Heat Kernel Embeddings, Differential Geometry and Graph Structure
Abstract
:1. Introduction
2. Heat Kernels on Graphs
2.1. Preliminaries
2.2. The Heat Equation
2.3. Geodesic Distance from the Heat Kernel
2.4. Heat Kernel Embedding
3. Geometric Graph Characterization
3.1. The Sectional Curvature
3.2. The Gaussian Curvature
4. Graph Similarity
4.1. Hausdorff Distance
- The classical Hausdorff distance is:
- The modified Hausdorff distance is:
4.2. Multidimensional Scaling
5. Experiments
5.1. Experimental Databases
5.1.1. The York Model House Dataset
5.1.2. The COIL Dataset

5.2. Experimenting with Real-World Data
- We compute the adjacency matrices of the Delaunay triangulations of the detected feature points in each image.
- From the adjacency matrices, we construct the normalised Laplacian matrix for each graph in the database.
- For each graph, we then use the heat kernel embedding defined in Section 2.2 to embed the nodes of each graph as points residing on a manifold in a Euclidean space.
- The Euclidean distance between pairs of points in the Euclidean space is obtained from the heat kernel embedding at the values of and using the formula deduced in Section 2.4.
- From the embeddings, we compute two curvature-based representations for the graphs. The first is the sectional curvature associated with the edges, outlined in Section 3.1. The second is the Gaussian curvature on the triangles of the Delaunay triangulations extracted from the graphs, as outlined in Section 3.2.
- Both the sectional and Gaussian curvatures are used as graph features for the purposes of gauging the similarity of graphs. The similarities are computed using both the classical Hausdorff distance and the robust modified variant of the Hausdorff distance.
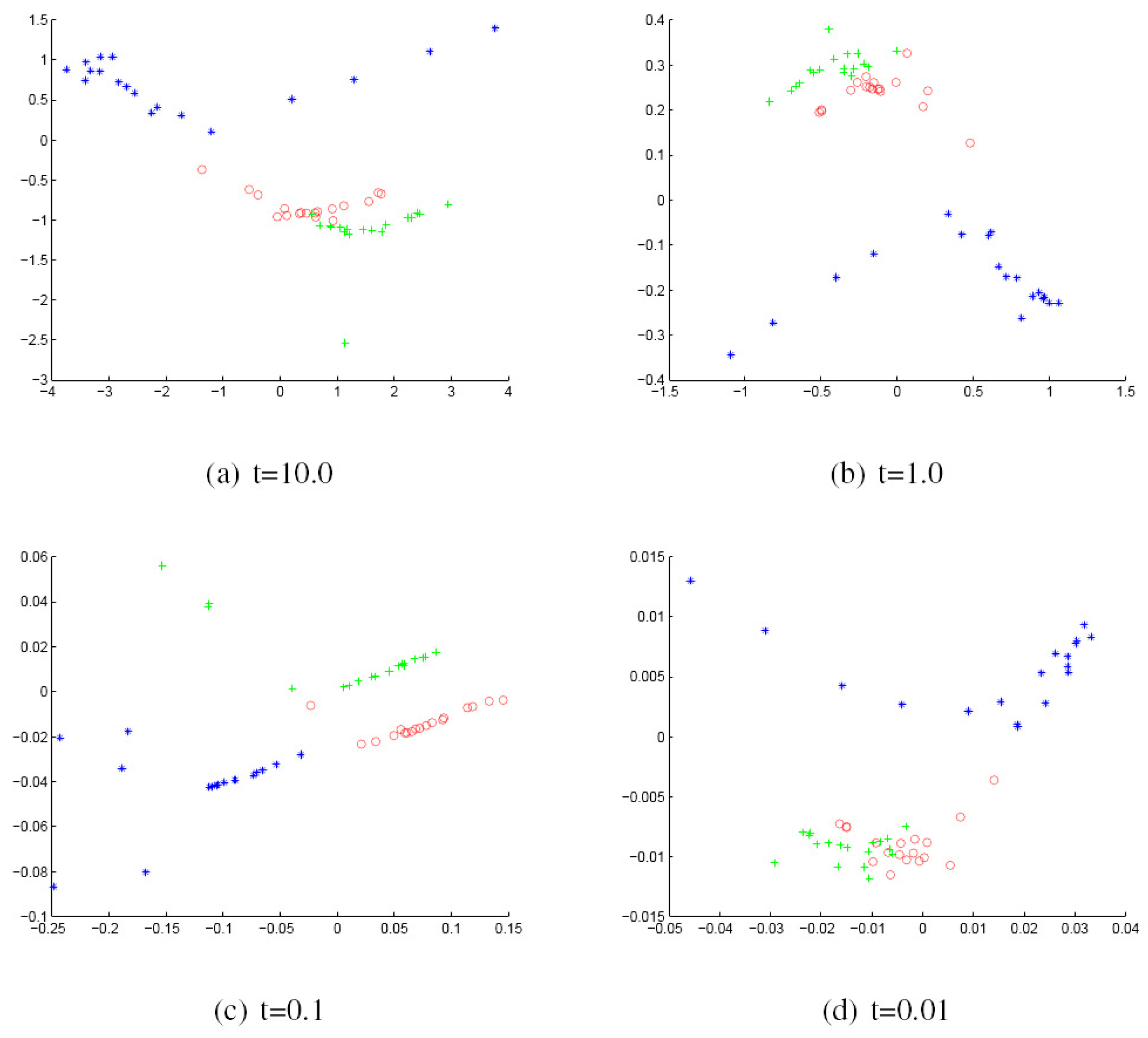
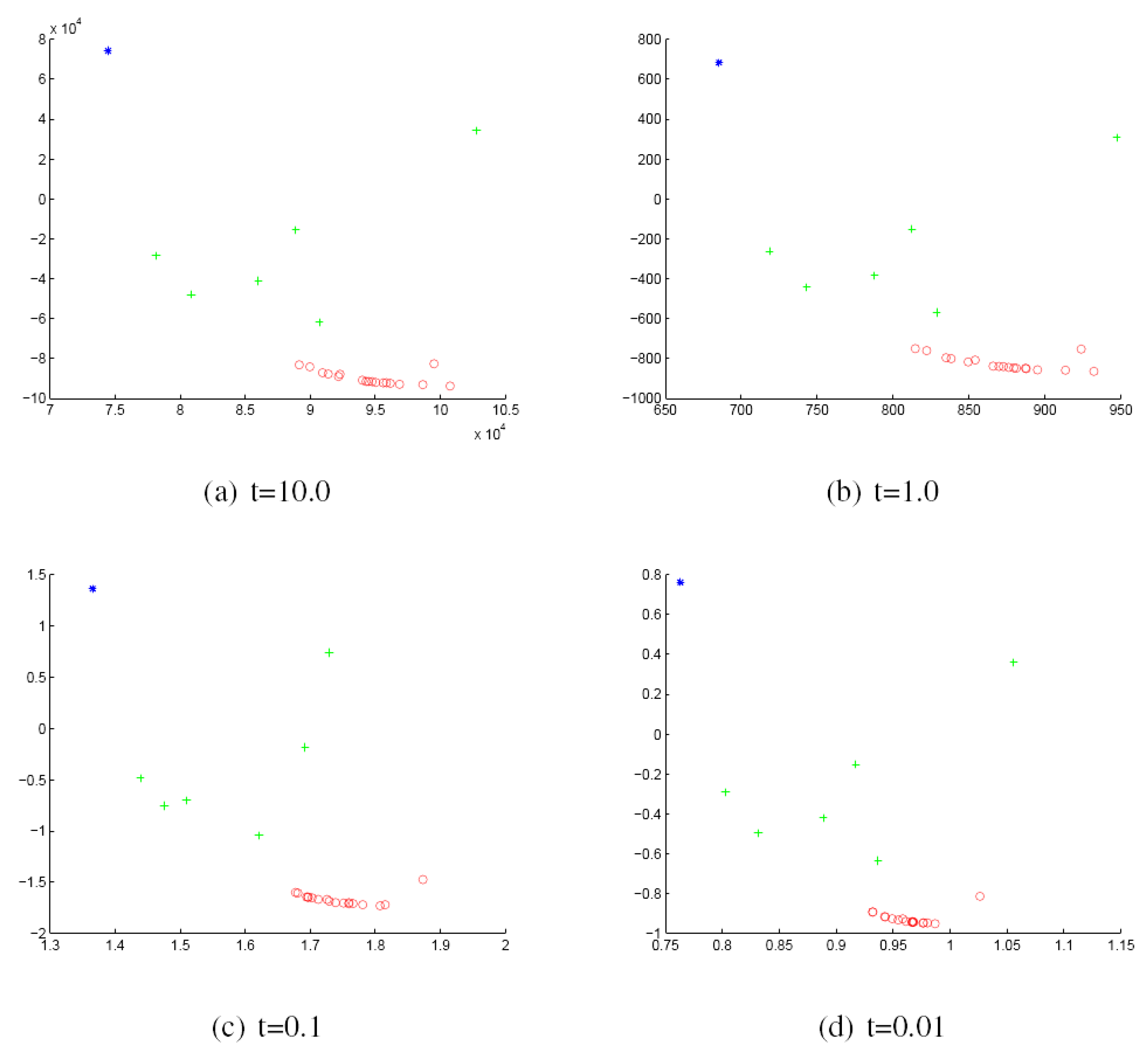
- Finally, we use the multidimensional scaling (MDS) procedure to embed the graphs into a low dimensional space where each graph is represented as a point in a 2D space.
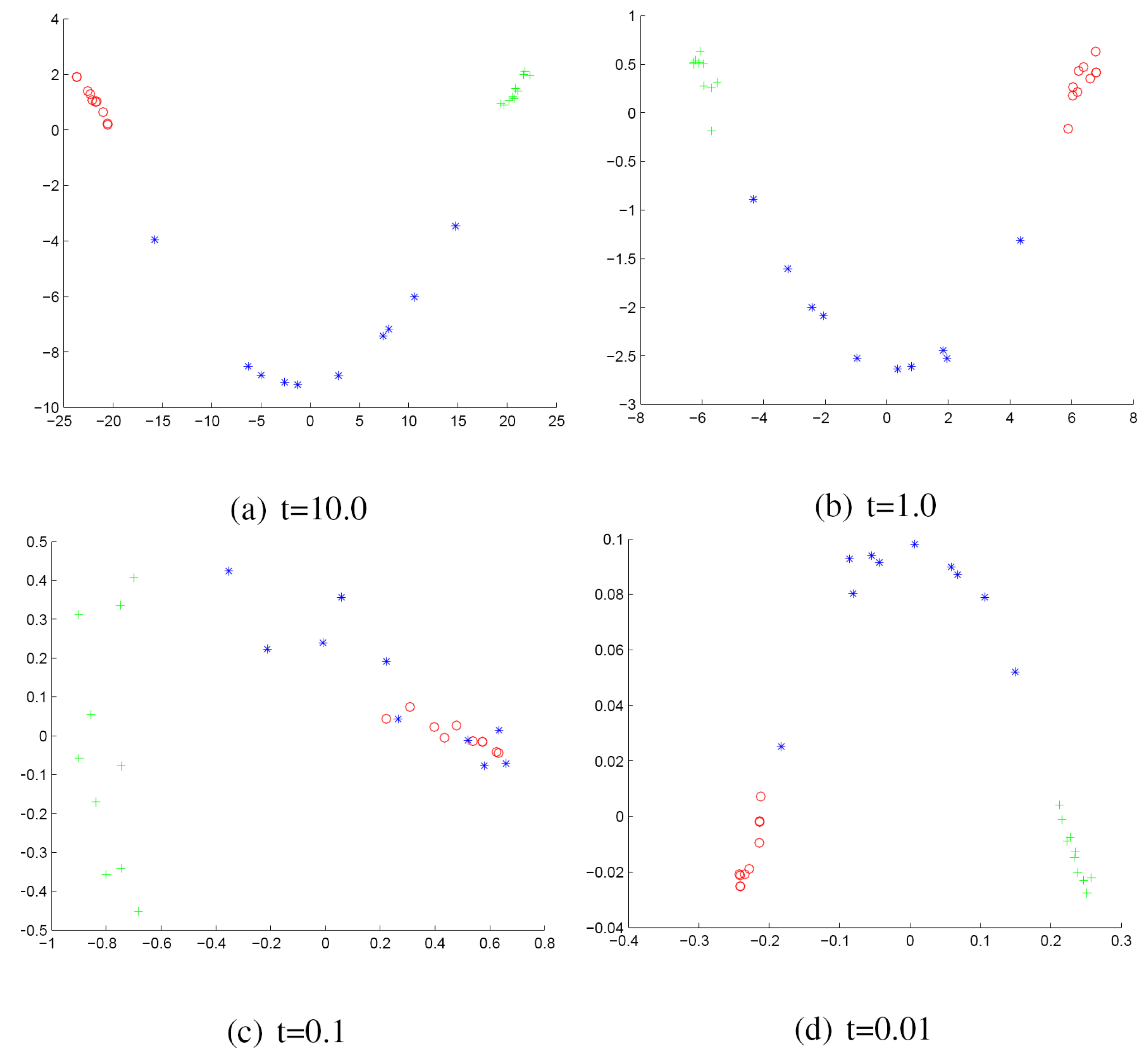

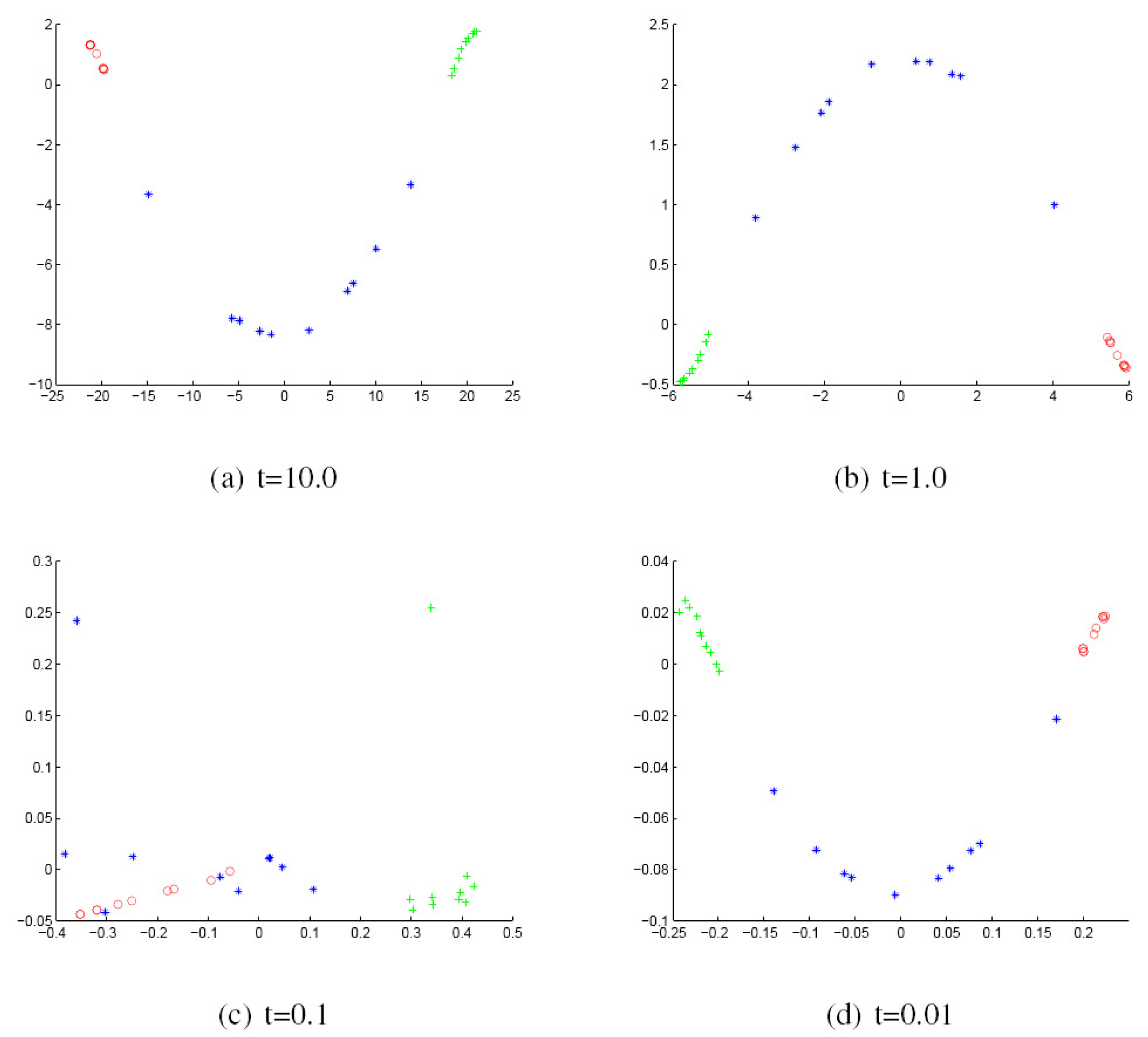

- We commence by computing the mean for each cluster.
- Then, we compute the distance from each point to each mean.
- If the distance from the correct mean is smaller than those to remaining means, then the classification is correct; if not, then the classification is incorrect.
- The rand index is:= (♯ incorrect ) / ( ♯ incorrect + ♯ correct ).
| t = 10 | t = 1.0 | t = 0.1 | t = 0.01 | ||
|---|---|---|---|---|---|
| HD | Sectional curvature | 0.1000 | 0.1667 | 0.4333 | 0.0333 |
| HD | Gaussian curvature | 0.5000 | 0.1333 | 0.1000 | 0.5000 |
| MHD | Sectional curvature | 0.1333 | 0.2333 | 0.1333 | 0.0333 |
| MHD | Gaussian curvature | 0.1667 | 0.0333 | 0.1333 | 0.4000 |
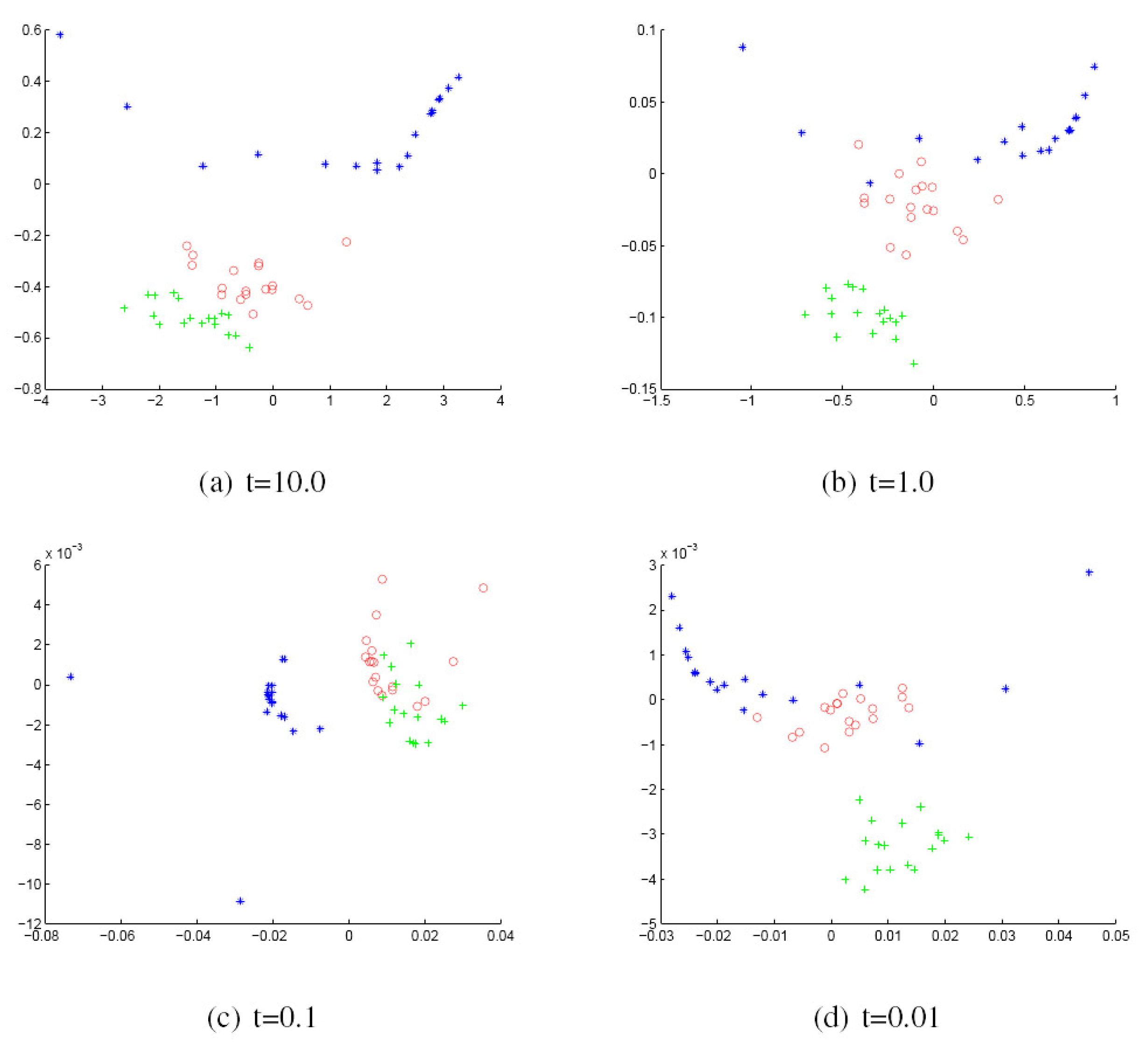
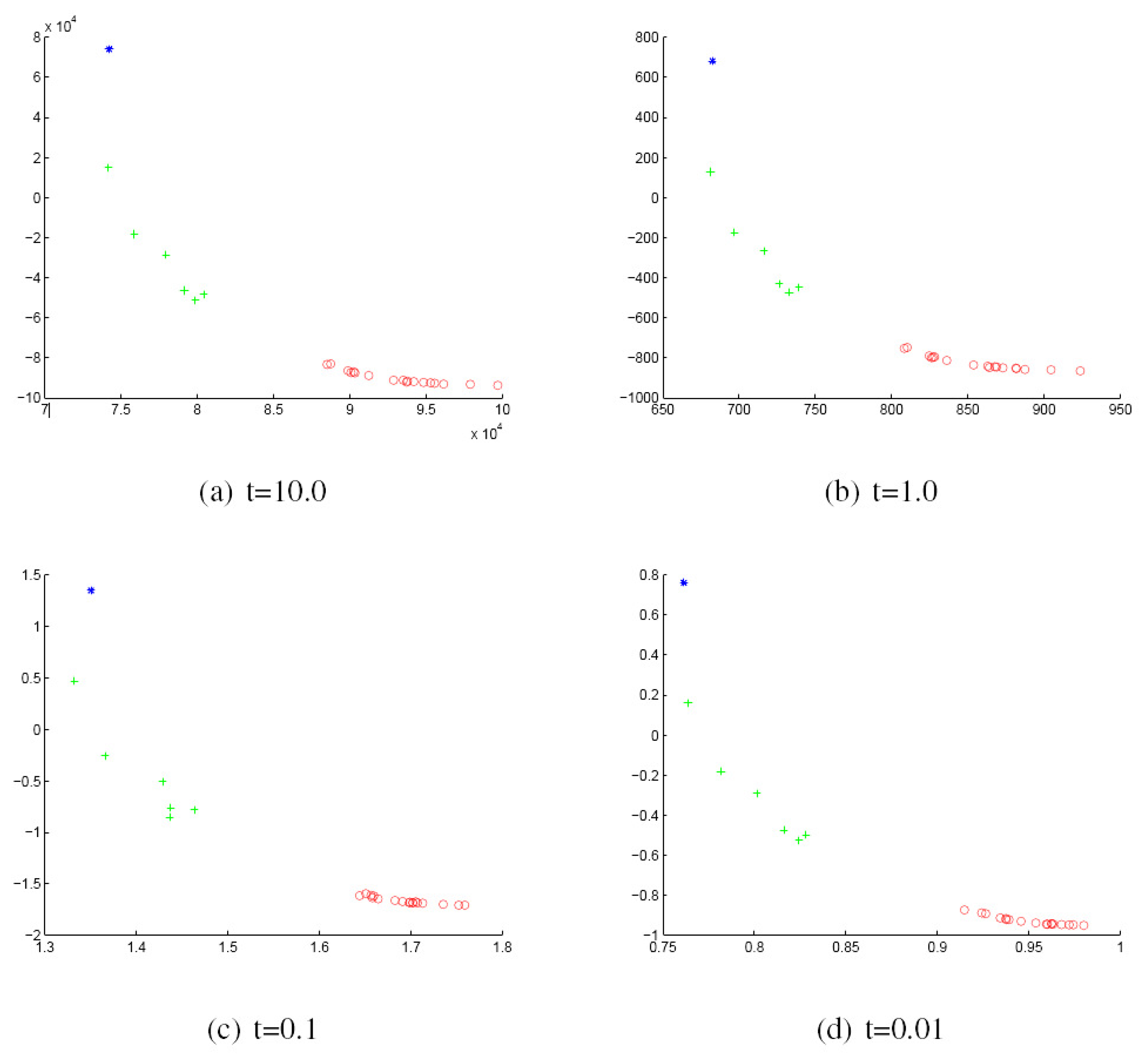
| t = 10 | t = 1.0 | t = 0.1 | t = 0.01 | ||
|---|---|---|---|---|---|
| HD | Sectional curvature | 0.1667 | 0.2037 | 0.2407 | 0.2037 |
| HD | Gaussian curvature | 0.2222 | 0.0000 | 0.0000 | 0.2222 |
| MHD | Sectional curvature | 0.1852 | 0.1852 | 0.1667 | 0.2222 |
| MHD | Gaussian curvature | 0.2222 | 0.0926 | 0.0000 | 0.2222 |
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Scholkopf, B.; Smola, A.; Muller, K.-R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Chung, F.R.K. Spectral Graph Theory; AMS: Ann Arbor, MI, USA, 1997; p. 92. [Google Scholar]
- De Verdi’ere, Y.C. Spectres De Graphes; Societe Mathematique de France: Paris, France, 1998. [Google Scholar]
- Linial, N.; London, E.; Rabinovich, Y. The geometry of graphs and some of its algorithmic applications. Combinatorica 1995, 15, 215–245. [Google Scholar] [CrossRef]
- Smola, A.; Kondor, R. Kernels and regularization on graphs. In Proceedings of the Conference on Learning Theory, Washington, DC, USA; 2003. [Google Scholar]
- Young, G.; Householder, A.S. Disscussion of a set of points in terms of their mutual distances. Psychometrika 1938, 3, 19–22. [Google Scholar] [CrossRef]
- Xiao, B.; Hancock, E.R. Heat kernel, Riemannian manifolds and Graph Embedding. LNCS 2004, 3138, 198–206. [Google Scholar]
- Atkins, J.E.; Boman, E.G.; Hendrickson, B. A Spectral Algorithm for Seriation and the Consecutive Ones Problem. SIAM J. Comput. 1998, 28, 297–310. [Google Scholar] [CrossRef]
- Shokoufandeh, A.; Dickinson, S.J.; Siddiqi, K.; Zucker, S.W. Indexing using a Spectral Encoding of Topological Structure. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; pp. 2491–2497.
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Umeyama, S. An eigendecomposition approach to weighted graph matching problems. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 695–703. [Google Scholar] [CrossRef]
- Luo, B.; Hancock, E.R. Structural Graph Matching Using the EM Algorithm and Singular Value Decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1120–1136. [Google Scholar]
- Yau, S.T.; Schoen, R.M. Lectures on Differential Geometry; Science Publication Co.: Somerville, MA, USA, 1988. [Google Scholar]
- Lebanon, G.; Lafferty, J.D. Hyperplane margin classifiers on the multinomial manifold. In Proceedings of the Twenty-First International Conference on Machine Learning, ICML’04, Banff, AB, Canada, 2004.
- Xiao, B.; Hancock, E.R. Trace Formula Analysis of Graphs. In Structural, Syntactic, and Statistical Pattern Recognition; Springer: Berlin, Germany, 2006; pp. 306–313. [Google Scholar]
- Spivak, M. A Comprehensive Introduction to Differential Geometry, 2nd ed.; Publish or Perish Inc.: Houston, TX, USA, 1979; Volume 1–5. [Google Scholar]
- Luxburg, U.V.; Belkin, M.; Bousquet, O. Consistency of Spectral Clustering; Technical Report 134; Max Planck Institute for Biological Cybernetics: Tubingen, Germany, 2004. [Google Scholar]
- Vaxman, A.; Ben-Chen, M.; Gotsman, C. A multi-resolution approach to heat kernels on discrete surfaces. ACM Trans. Graph. 2010, 29, 1–10. [Google Scholar] [CrossRef]
- Patane, G. wFEM heat kernel: Discretization and applications to shape analysis and retrieval. Comput. Aided Geom. Des. 2013, 30, 276–295. [Google Scholar] [CrossRef]
- Stillwell, J. Mathematics and Its History; Springer-Verlag: New York, NY, USA, 1974. [Google Scholar]
- Cox, T.; Cox, M. Multidimensional Scaling; Chapman-Hall: Boca Raton, FL, USA, 1994. [Google Scholar]
- Huttenlocher, D.; Klanderman, G.; Rucklidge, W. Comparing images using the Hausdorff distance. IEEE. Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Dubuisson, M.; Jain, A. A modified Hausdorff distance for object matching. In Proceedings of the International Conference on Pattern Recognition (ICPR), Jerusalem, Israel, 9–13 October 1994; pp. 566–568.
- Luo, B.; Wilson, R.C.; Hancock, E.R. Spectral embedding of graphs. Pattern Recogint. 2003, 36, 2213–2230. [Google Scholar] [CrossRef]
- Luo, B.; Cross, A.; Hancock, E.R. Corner detection via topographic analysis of vector potential. Pattern Recognit. Lett. 1999, 20, 635–650. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
ElGhawalby, H.; Hancock, E.R. Heat Kernel Embeddings, Differential Geometry and Graph Structure. Axioms 2015, 4, 275-293. https://doi.org/10.3390/axioms4030275
ElGhawalby H, Hancock ER. Heat Kernel Embeddings, Differential Geometry and Graph Structure. Axioms. 2015; 4(3):275-293. https://doi.org/10.3390/axioms4030275
Chicago/Turabian StyleElGhawalby, Hewayda, and Edwin R. Hancock. 2015. "Heat Kernel Embeddings, Differential Geometry and Graph Structure" Axioms 4, no. 3: 275-293. https://doi.org/10.3390/axioms4030275





