Study on SEAI Model of COVID-19 Based on Asymptomatic Infection
Abstract
:1. Introduction
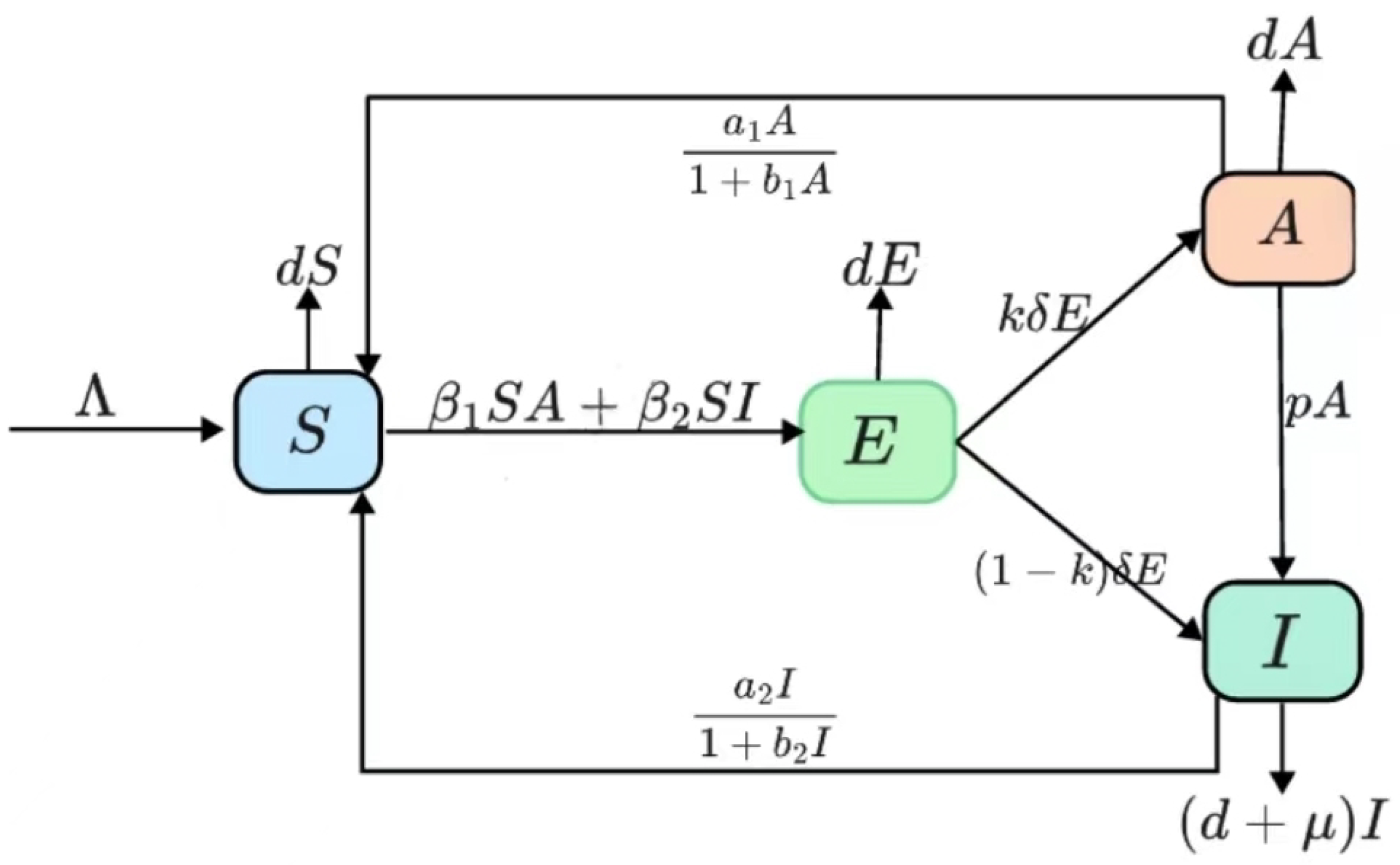
2. Model Formulation
3. Basic Regeneration Number and Equilibrium
3.1. Stability of Disease-Free Equilibrium
3.2. Stability of the Endemic Equilibrium
4. Persistence
5. Optimal Control Strategy
5.1. Existence of Optimal Control Solutions
- (1)
- For any control variable , the initial values of system (10) are all negative;
- (2)
- The control set is a closed and convex set;
- (3)
- The right-hand linear function of system (10) satisfies the initial conditions, ensuring boundedness on the control set U;
- (4)
- The integrand of the objective function (11) is convex on the control set U, and there exist constants and , such that
5.2. Optimal Control Solution
- : control system satisfaction
- : adjoint system satisfaction
- : minimum condition
6. Numerical Simulation
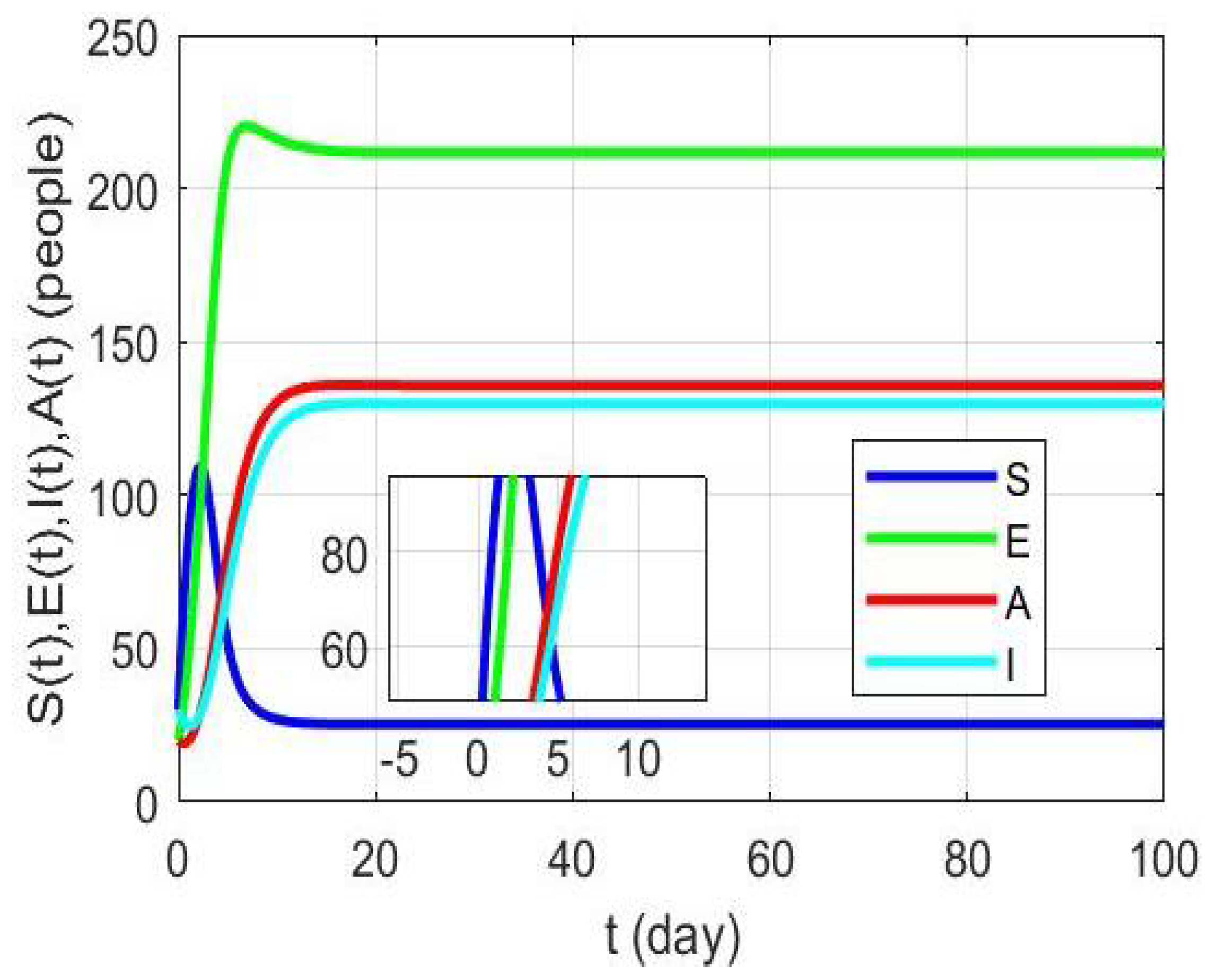
6.1. Stability of Balance Point
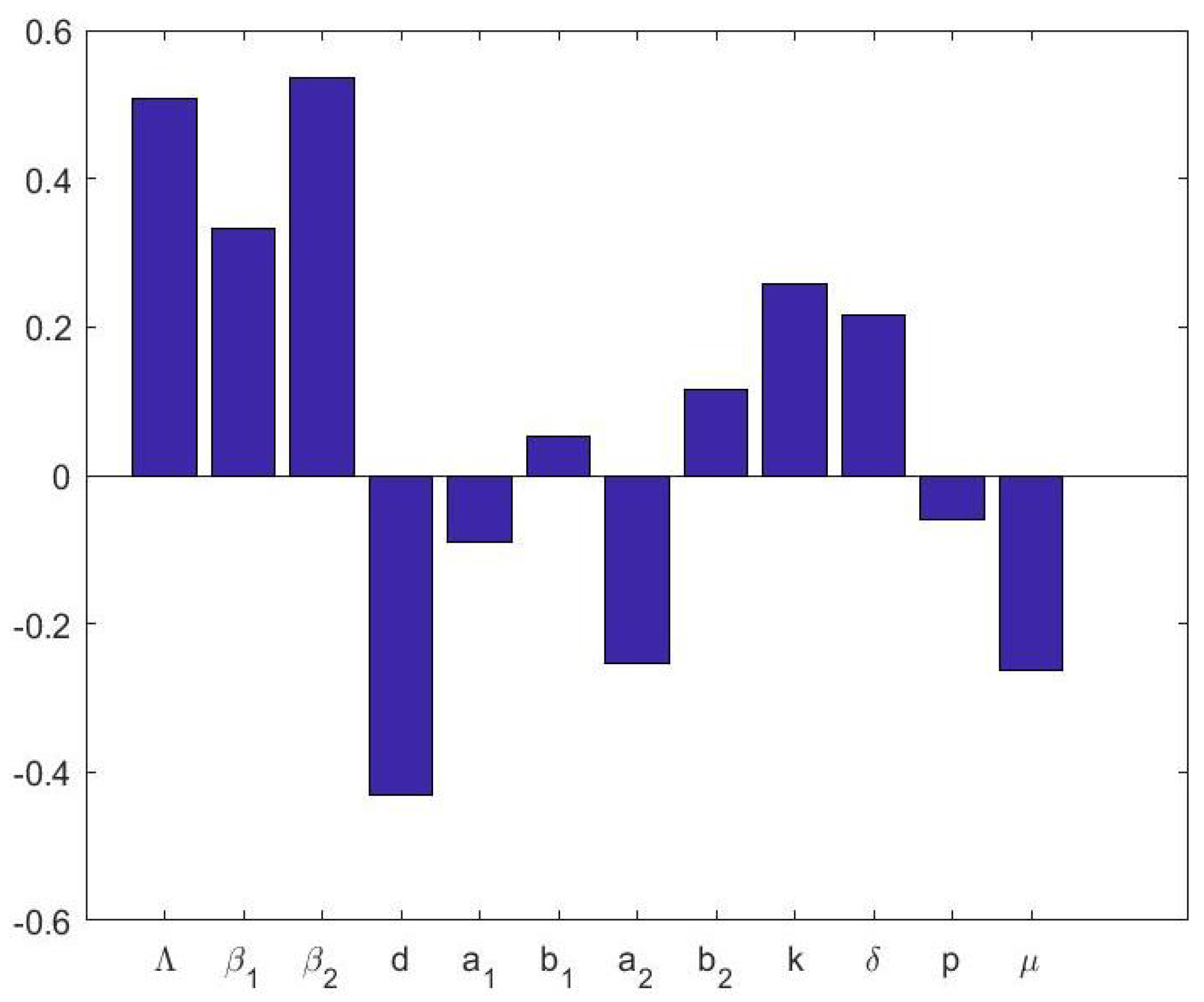
6.2. Sensitivity Analysis
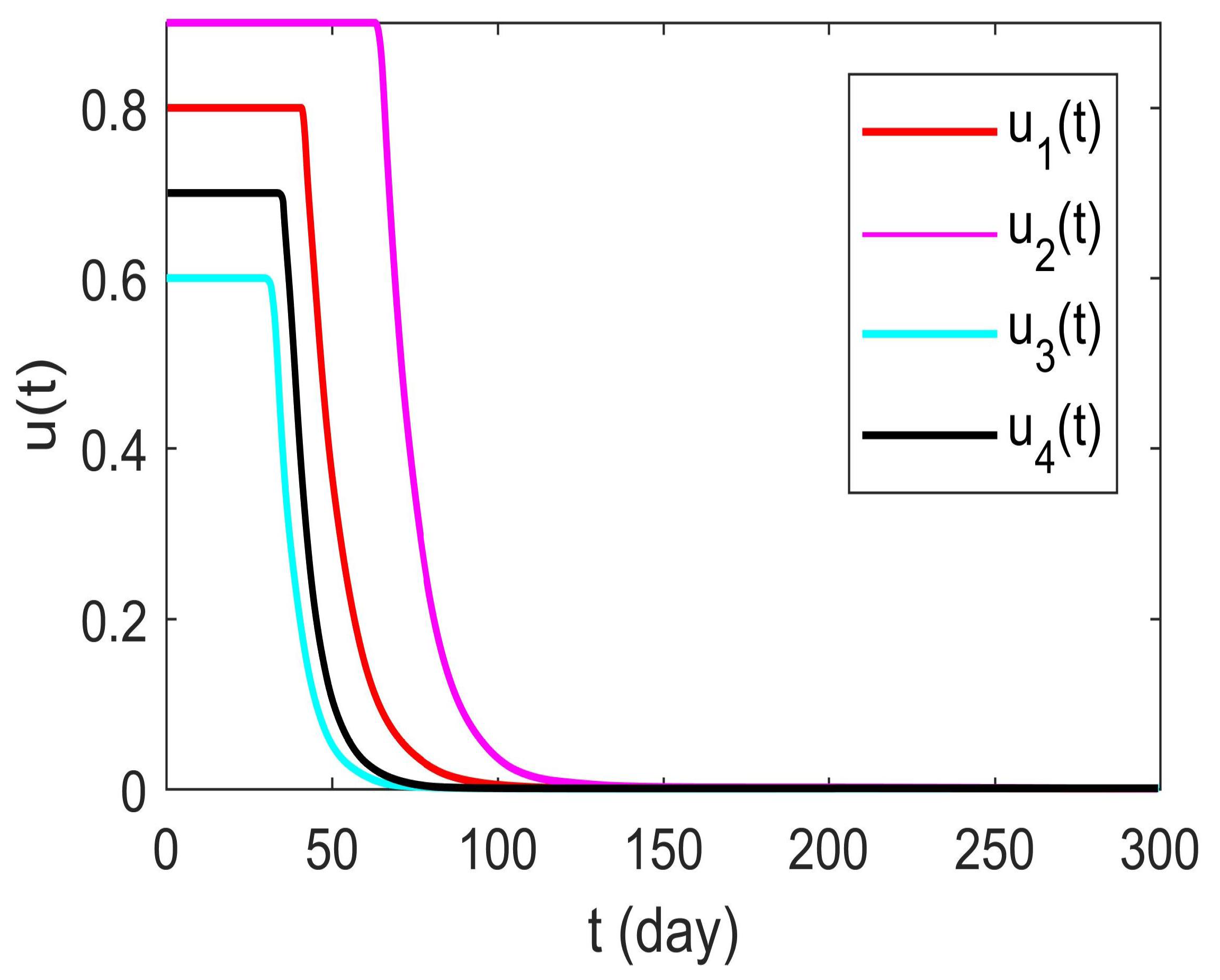
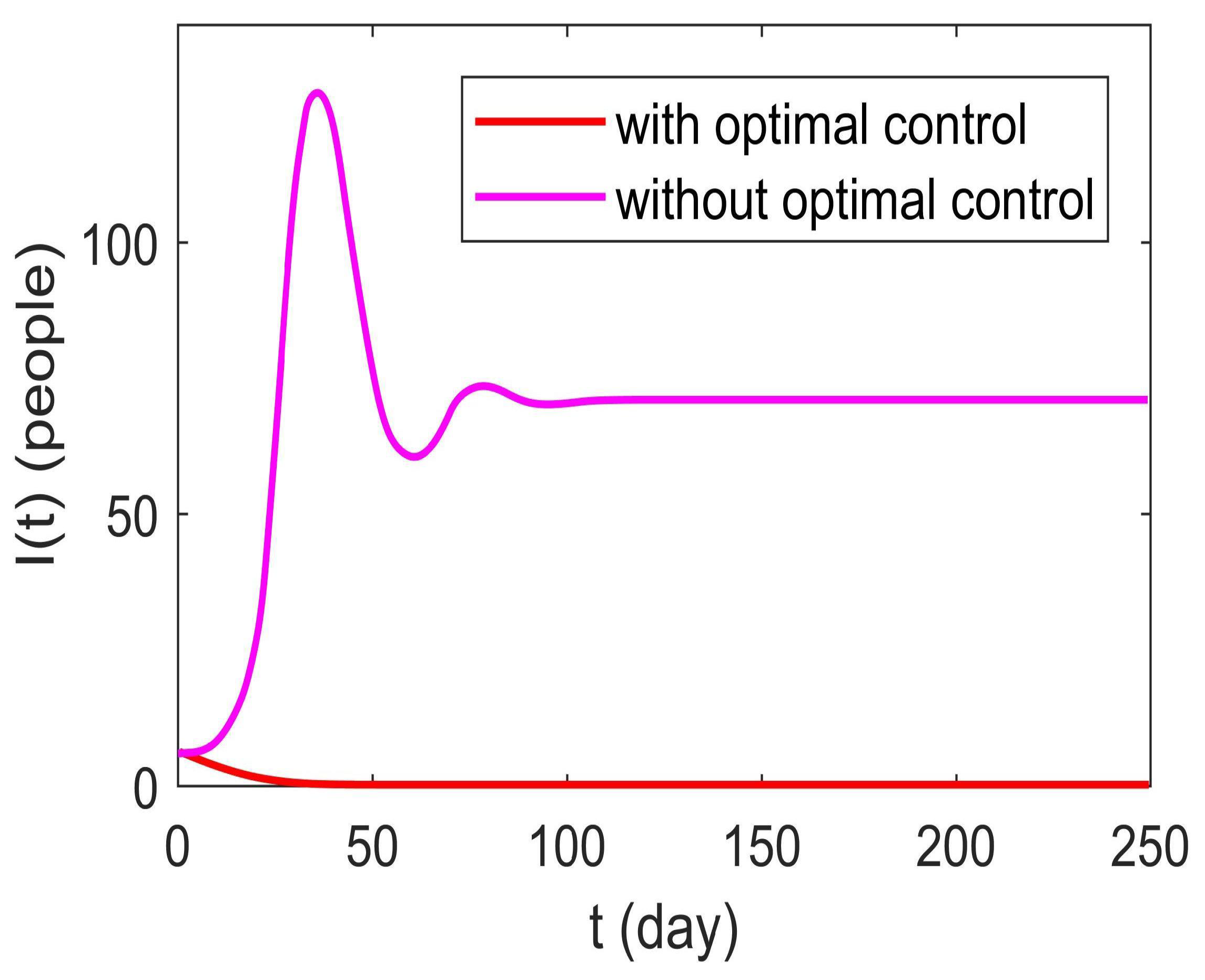
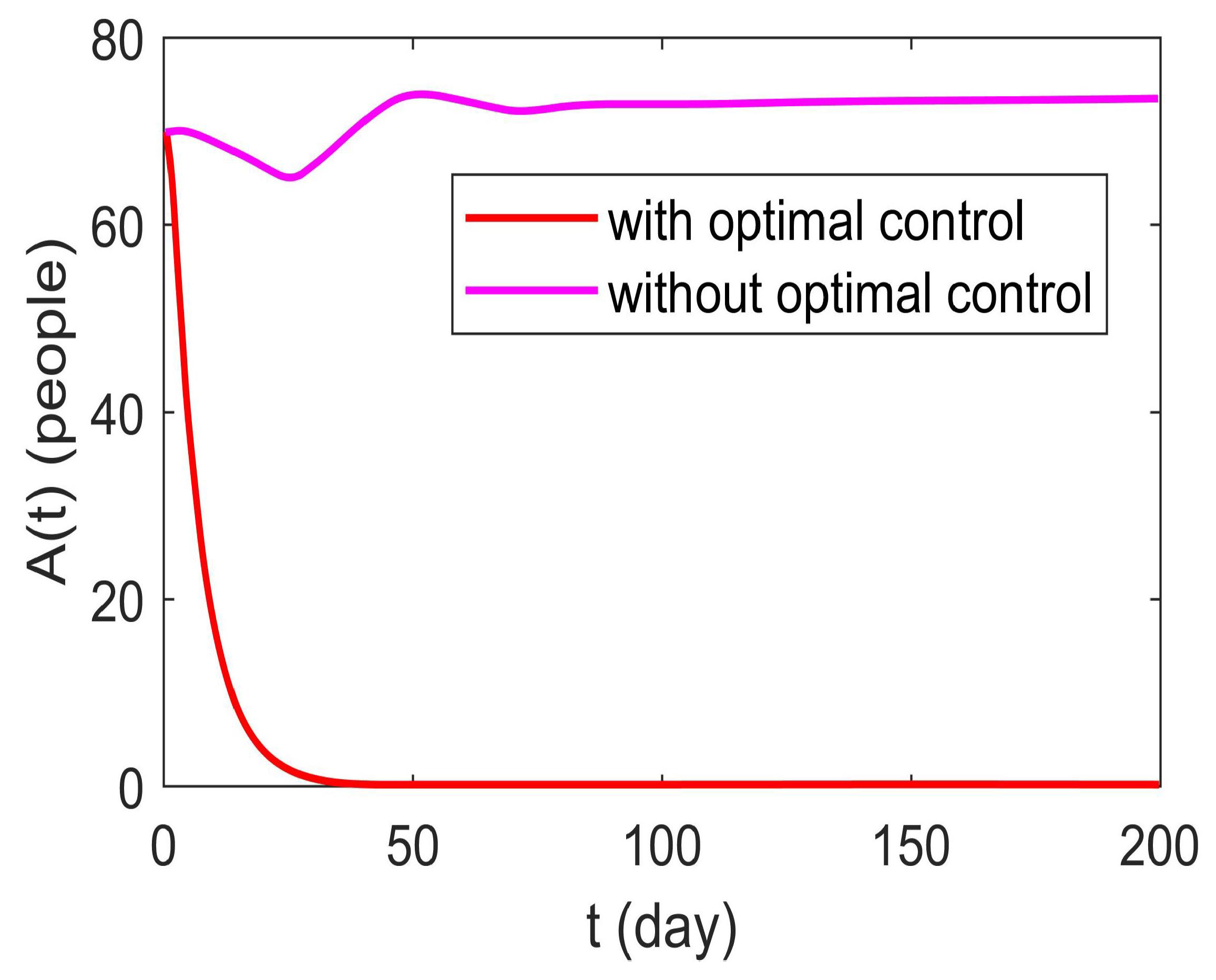
6.3. Optimal Control
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Kemp, M.; Nielsen, X.C.; Batels, M.D.; Hasman, H.; Nielsen, E.M. Whole genome sequencing for surveillance of bacterial infectious illnesses. Ugeskr. Laeger 2023, 185, V11220690. [Google Scholar] [PubMed]
- Muhitdinovna, D.M.; Usmanovna, R.R. Infectious diseases during Covid 19 and the issues of proper treatment. ACADEMICIA Int. Multidiscip. Res. J. 2020, 12, 195–197. [Google Scholar] [CrossRef]
- Das, M.; Samanta, G.; De la Sen, M. A fractional ordered covid-19 model incorporating comorbidity and vaccination. Mathematics 2021, 9, 2806. [Google Scholar] [CrossRef]
- Das, M.; Samanta, G. Stability analysis of a fractional ordered COVID-19 model. Comput. Math. Biophys. 2021, 9, 22–45. [Google Scholar] [CrossRef]
- Aakash, M.; Gunasundari, C.; Qasem, M. Mathematical modeling and simulation of SEIR model for COVID-19 outbreak: A case study of trivandrum. Front. Appl. Math. Stat. 2023, 9, 1124897. [Google Scholar]
- Hao, Z.; Liu, Y.; Guan, W.; Juan Pan Li, M.; Wu, J.; Liu, Y.; Kuang, H.; Yang, B. Syringa reticulata potently inhibits the activity of SARS-CoV-2 3CL protease. Biochem. Biophys. Rep. 2024, 37, 101626. [Google Scholar] [CrossRef]
- Yao, S.W.; Farman, M.; Amin, M.; Inc, M.; Akgul, A.; Ahmad, A. Fractional order COVID 19 model with transmission rout infected through environment. AIMS Math. 2022, 7, 5156–5174. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Khan, M.; Alshahrani, M.; Muhammad, T. A dynamical study of SARS-COV-2: A study of third wave. Results Phys. 2021, 29, 104705. [Google Scholar] [CrossRef]
- Kronbichler, A.; Kresse, D.; Yoon, S.; Yoon, S.; Lee, K.; Effenberger, M.; Shin, J. Asymptomatic patients as a source of COVID-19 infections: A systematic review and meta-analysis. Int. J. Infect. Dis. 2020, 98, 180–186. [Google Scholar] [CrossRef]
- Uzunova, G.; Pallanti, S.; Hollander, E. Presentation and management of anxiety in individuals with acute symptomatic or asymptomatic covid-19 infection, and in the post-covid-19 recovery phase. Int. J. Psychiatry Clin. Pract. 2021, 25, 115–131. [Google Scholar] [CrossRef]
- Stilianakis, N.; Drossinos, Y. Dynamics of infectious disease transmission by inhalable respiratory droplets. J. R. Soc. Interface 2010, 7, 1355–1366. [Google Scholar] [CrossRef]
- Zhai, Y.; Liu, Y.; Ding, N.; Fan, Z.; Fang, G. Improved SEIR model based on asymptomatic infection of COVID-19. In Proceedings of the 2021 4th International Conference on Advanced Electronic Materials. Computers and Software Engineering (AEMCSE), Changsha, China, 26–28 March 2021; pp. 652–655. [Google Scholar]
- Zhang, Y.; You, C.; Cai, Z.; Sun, J.; Zhou, X. Prediction of the COVID-19 outbreak based on a realistic stochastic model. MedRxiv 2020, 10, 21522. [Google Scholar]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the transmission risk of the 2019-ncov and its implication for public health interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Weng, D. Estimating the effects of asymptomatic and imported patients on covid-19 epidemic using mathematical modeling. J. Med. Virol. 2020, 92, 1995–2003. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Apio, C.; Park, T. Estimation of undetected asymptomatic covid-19 cases in south korea using a probabilistic model. Int. J. Environ. Res. Public Health 2021, 18, 4946. [Google Scholar] [CrossRef] [PubMed]
- Syangtan, G.; Bista, S.; Dawadi, P.; Rayamajhee, B.; Joshi, D. Asymptomatic SARS-CoV-2 carriers: A systematic review and meta-analysis. Front. Public Health 2021, 8, 587374. [Google Scholar] [CrossRef]
- Khan, T.; Ullah, R.; Zaman, G.; Khatib, Y. Modeling the dynamics of the SARS-CoV-2 virus in a population with asymptomatic and symptomatic infected individuals and vaccination. Phys. Scr. 2021, 96, 104009. [Google Scholar] [CrossRef]
- Tan, J.; Ge, Y.; Martinez, L.; Shen, Y. Transmission roles of symptomatic and asymptomatic COVID-19 cases: A modeling study. Epidemiol. Infect. 2022, 150, e171. [Google Scholar] [CrossRef] [PubMed]
- Dobrovolny, H.M. Modeling the role of asymptomatics in infection spread with application to SARS-CoV-2. PLoS ONE 2020, 15, e0236976. [Google Scholar] [CrossRef]
- Sun, T.; Wang, Y. Modeling COVID-19 epidemic in Heilongjiang province, China. Chaos Solitons Fractals 2020, 138, 109949. [Google Scholar] [CrossRef]
- Stehlé, J.; Voirin, N.; Barrat, A.; Cattuto, C.; Colizza, V.; Isella, L.; Régis, C.; Pinton, J.F.; Khanafer, N.; Van den Broeck, W.; et al. Simulation of an SEIR infectious disease model on the dynamic contact network of conference attendees. BMC Med. 2011, 9, 87. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Qin, K. Analysis of epidemic situation in novel coronavirus based on SEIR model. Comput. Appl. Softw. 2021, 38, 87–90. [Google Scholar]
- Zhou, L. Dynamic Model Analysis of Infectious Diseases with Limited Medical Resources. Ph.D. Thesis, Northeast Normal University, Changchun, China, 2012. [Google Scholar]
- Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Avram, F.; Adenane, R.; Basnarkov, L.; Johnston, M.D. Algorithmic approach for a unique definition of the next-generation matrix. Mathematics 2023, 12, 27. [Google Scholar] [CrossRef]
- Patil, A. Routh-hurwitz criterion for stability: An overview and its implementation on characteristic equation vectors using matlab. In Emerging Technologies in Data Mining and Information Security: Proceedings of IEMIS; Advances in Intelligent Systems and Computing; Springer: Singapore, 2020; Volume 1286, pp. 319–329. [Google Scholar]
- Bodson, M. Explaining the routh–hurwitz criterion. IEEE Control. Syst. Mag. 2020, 40, 45–51. [Google Scholar] [CrossRef]
- Gerbet, D.; Benack, K.R. Application of lasalle’s invariance principle on polynomial differential equations using quantifier elimination. IEEE Trans. Autom. Control 2021, 67, 3590–3597. [Google Scholar] [CrossRef]
- Anagnost, J.J.; Desoer, C.A. An elementary proof of the Routh-Hurwitz stability criterion. Circuits Syst. Signal Process. 1991, 10, 101–114. [Google Scholar] [CrossRef]
- Qin, W.; Xia, Y.; Yang, Y. An eco-epidemic model for assessing the application of integrated pest management strategies. Math. Biosci. Eng. 2023, 20, 16506–16527. [Google Scholar] [CrossRef]
- Ahmad, M.D.; Usman, M.; Khan, A.; Imran, M. Optimal control analysis of Ebola disease with control strategies of quarantine and vaccination. Infect. Dis. Poverty 2016, 5, 72. [Google Scholar] [CrossRef]
- Rogers, C. Deterministic Stochastic Optimal Control; Department of Statistics: Cambridge, UK, 2006; Volume 71, pp. 1–18. [Google Scholar]
- Li, K.; Zhu, G.; Ma, Z.; Chen, L. Dynamic stability of an siqs epidemic network and its optimal control. Commun. Nonlinear Sci. Numer. Simul. 2019, 66, 84–95. [Google Scholar] [CrossRef]
- Oshima, M.; Yamaguchi, Y.; Muramatsu, W.; Amano, H.; Bi, C.; Seto, H.; Bamba, S.; Morimoto, T. Study of charged particle activation analysis (I): Determination sensitivity for single element samples. J. Radioanal. Nucl. Chem. 2016, 308, 711–719. [Google Scholar] [CrossRef]
- Kuddus, M.; Rahman, A. Analysis of covid-19 using a modified slir model with nonlinear incidence. Results Phys. 2021, 27, 104478. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Wang, J.R. Fractional dynamic analysis and optimal control problem for an SEIQR model on complex networks. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 123123. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Definition | Unit |
|---|---|---|
| the constant input of population | ||
| d | the natural death rate of population | |
| the morbidity and mortality of symptomatic infected persons | ||
| p | the rate of transformation from asymptomatic infection to symptomatic infection | |
| the maximum cure rate for asymptomatic patients | ||
| the maximum cure rate for an infected person | ||
| resource constraints for treating asymptomatic patients | ||
| resource constraints for treating infected people | ||
| the infection rate of asymptomatic infected people to susceptible people | ||
| the infection rate of infected people with symptoms to susceptible people | ||
| the transfer rates of latent to infected persons | ||
| the rate at which latent persons develop asymptomatic infections | ||
| the rate at which latent persons become infected with symptoms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Xia, Y.; Qin, W. Study on SEAI Model of COVID-19 Based on Asymptomatic Infection. Axioms 2024, 13, 309. https://doi.org/10.3390/axioms13050309
Huang L, Xia Y, Qin W. Study on SEAI Model of COVID-19 Based on Asymptomatic Infection. Axioms. 2024; 13(5):309. https://doi.org/10.3390/axioms13050309
Chicago/Turabian StyleHuang, Lidong, Yue Xia, and Wenjie Qin. 2024. "Study on SEAI Model of COVID-19 Based on Asymptomatic Infection" Axioms 13, no. 5: 309. https://doi.org/10.3390/axioms13050309








