Asymptotical Stability Criteria for Exact Solutions and Numerical Solutions of Nonlinear Impulsive Neutral Delay Differential Equations

Abstract

In this paper, the idea of two transformations is first proposed and applied. Some new different sufficient conditions for the asymptotical stability of the exact solutions of nonlinear impulsive neutral delay differential equations (INDDEs) are obtained. A new numerical scheme for INDDEs is also constructed based on the idea. The numerical methods that can preserve the stability and asymptotical stability of the exact solutions are provided. Two numerical examples are provided to demonstrate the theoretical results.

1. Introduction

There is extensive use of impulsive differential equations in economics, engineering, biology, medicine, etc. In recent years, the theory of INDDEs has been the object of active research. Some scholars have investigated the existence, uniqueness, and continuous dependence of INDDEs (see [1,2]) and the oscillation of the first-order, second-order, and even-order of INDDEs (see [3,4,5]). In [6], the thermoelasticity of type III for Cosserat media has been studied. In [7], the asymptotic properties of the solutions of nonlinear, non-instantaneous impulsive differential equations has been studied. In [8], the Legendre spectral-collocation method is applied to delay the differential and stochastic delay differential equation. In [9], the convergence and superconvergence of collocation methods for one class of impulsive delay differential equations have been studied, respectively.

However, there are not many studies on the stability of INDDEs. In [10], the asymptotic behavior of some special nonlinear INDDEs were considered by establishing proper Lyapunov functions and certain analysis techniques. In [11], some results ensuring the global exponential stability of impulsive functional equations of neutral type were derived via impulsive delay inequality and certain analysis techniques that are very popular in the application of the dynamical analysis of neural networks. In [3], the authors developed the Razumikhin method for impulsive functional differential equations of neutral type and established some Razumikhin theorems. Recently, we found that there are errors in [12] (Stability of zero solution of linear INDDE with constant coefficients is studied, but zero is not the solution of the linear INDDE in [12]). All the above studies focus on the asymptotic stability of zero solutions, but in this paper we will study the stability of the exact solutions (not necessarily zero solutions) of INDDEs.

Usually, as is well known, it is difficult, sometime maybe impossible, to acquire the explicit solutions for INDDEs, so it is necessary to investigate the numerical methods for INDDEs. Numerical stability refers to the degree to which small perturbations of input data affect the output results of the algorithm when solving numerical problems using an algorithm. A numerically stable algorithm can produce accurate results that are not affected by input perturbations, while a numerically unstable algorithm may produce unpredictable results. Hence, it is necessary to investigate the asymptotical stability of numerical methods for INDDEs.

The stability of the exact solutions and the numerical solutions for NDDEs without impulsive perturbations has also been extensively studied (see [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]). There are many classic results found in the literature [14,21,22,28]. Recently, some new and important related developments have emerged. In papers [17,18,19,20], Guang-Da Hu and Taketomo Mitsui et al. studied the asymptotical stability of the exact solutions and the numerical solutions of linear NDDEs in real space and complex space, respectively. In [27], Wang and Li studied the stability and asymptotic stability of $\theta$-methods for nonlinear NDDEs with constant delay and with proportional delay. In [15], Enright and Hayashi established sufficient conditions for order of convergence results regarding continuous Runge–Kutta methods for NDDEs with state dependent delays. Zhang, Song, and Liu have studied the asymptotic stability of linear impulsive delay differential equations (IDDEs) (see [29]); the exponential stability of linear IDDEs (see [30]); and the stability and asymptotical stability of nonlinear IDDEs (see [31]. Based on their ideas, the problems of IDDEs are transformed into the problems of delay differential equations without impulsive perturbations. In this paper, this idea is applied to INDDEs for the first time, and to the best of our knowledge no article has previously been written regarding the stability of numerical methods for INDDEs.

The goal of this paper is to provide new different asymptotical stability criteria for exact solutions and numerical solutions of a class of nonlinear impulsive neutral differential equations (INDDEs). We will adopt the idea of two transformations to achieve our goal; the problems of the stability and asymptotical stability of INDDEs are first transformed into the problems of NDDEs without impulsive perturbations, and then transformed into the problems of ordinary differential equations with a forcing term. The organization of this paper is as follows. In Section 2, we first transform the problems of the stability and asymptotical stability of INDDEs into the problems of NDDEs without impulsive perturbations, and we then further transform them into the problems of ordinary different equations with a forcing term. On this basis, two general forms of criteria for the stability and asymptotical of INDDEs are established. Furthermore, when different transforms are chosen, different criterion for the stability and asymptotical stability can be obtained. For brevity, three different transforms are provided to achieve some specific different criteria for stability and asymptotical stability. In Section 3, based on the ideas in Section 2, we will derive the numerical methods of INDDEs, which can preserve the stability and asymptotical stability of the nonlinear INDDEs if corresponding continuous Runge–Kutta methods are $B{N}_f$-stable. 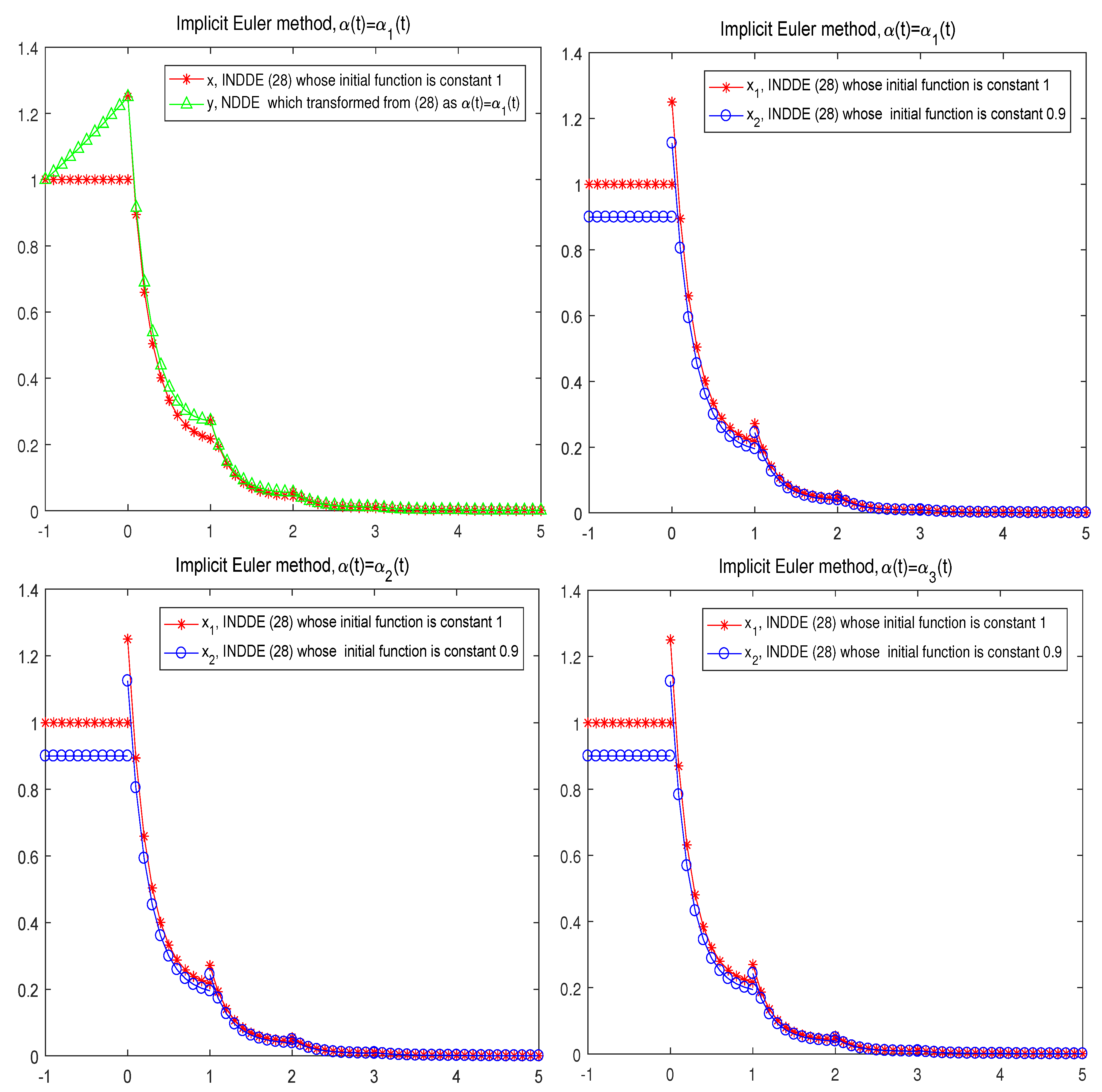In Section 4, one linear numerical example and one nonlinear numerical example are chosen to demonstrate the theoretical results.

2. Asymptotical Stability of the Exact Solutions

Firstly, the relationships between INDDEs and NDDEs are constructed in Section 2.1. Based on this idea, the general sufficient conditions for the asymptotical stability of the exact solutions of INDDEs are established in Section 2.2. Finally, the different special relationships between INDDEs and NDDEs are studied, and different sufficient conditions for the asymptotical stability of INDDEs are obtained in Section 2.3.

In this article, we will study the following nonlinear INDDEs:

$$\left\{\begin{array}{cc}\frac{d}{dt}\left(x(t)-G(t,x(t-\tau ))\right)=F(t,x(t),x(t-\tau )),\hfill & t\ge 0,t\ne k\tau ,\hfill \\ x(t)=\lambda x(t^{-}),\hfill & t=k\tau ,\hfill \\ x(t)=\psi (t),\hfill & t\in [-\tau ,0),\hfill \end{array}\right.$$

(1)

and the same equation with another initial function:

$$\left\{\begin{array}{cc}\frac{d}{dt}\left(\tilde{x}(t)-G(t,\tilde{x}(t-\tau ))\right)=F(t,\tilde{x}(t),\tilde{x}(t-\tau )),\hfill & t\ge 0,t\ne k\tau ,\hfill \\ \tilde{x}(t)=\lambda \tilde{x}(t^{-}),\hfill & t=k\tau ,\hfill \\ \tilde{x}(t)=\tilde{\psi }(t),\hfill & t\in [-\tau ,0),\hfill \end{array}\right.$$

(2)

where $\tau >0$, $\lambda \ne 0$, $\lambda \ne 1$, $k\in \mathbb{N}=\{0,1,2,\cdots \}$, $\psi$ and $\tilde{\psi }$ are continuous functions on $[-\tau ,0)$, and $\underset{t\to 0^{-}}{lim}\psi (t)$ and $\underset{t\to 0^{-}}{lim}\tilde{\psi }(t)$ exist. The right-hand derivative of $x(t)$ is written as $x^{\prime }(t)$. Assume that $\langle ·,·\rangle$ is a given inner product on ${\mathbb{C}}^d$ and $\parallel ·\parallel$ is the induced norm. Assume that the function $F:[0,\infty )\times {\mathbb{C}}^d\times {\mathbb{C}}^d\to {\mathbb{C}}^d$ is continuous in t and fulfills the following conditions: for arbitrary $x,x_1,x_2,y_1,y_2\in {\mathbb{C}}^d$ and arbitrary $t\in [0,+\infty )$, there are real value functions $X,Y$ from $[0,+\infty )$ to $\mathbb{R}$, such that

$$Y(t)\ge \underset{y_1\ne y_2,x}{sup}\frac{\Re (\langle H(t,y_1,x)-H(t,y_2,x),y_1-y_2\rangle )}{\parallel y_1-y_2{\parallel }^2}$$

(3)

$$X(t)\ge \underset{y,x_1\ne x_2}{sup}\frac{\parallel H(t,y,x_1)-H(t,y,x_2)\parallel }{\parallel x_1-x_2\parallel },$$

(4)

where $H(t,y,x)=F(t,y+G(t,x),x)$, which is the same as that in [14]. Assume that the function $G:[0,\infty )\times {\mathbb{C}}^d\to {\mathbb{C}}^d$ is continuous in t and fulfills the following conditions: for arbitrary $x,x_1,x_2,\in {\mathbb{C}}^d$ and arbitrary $t\in [0,+\infty )$, a real value function Z from $[0,+\infty )$ to $\mathbb{R}$ satisfies

$$Z(t)\ge \underset{x_1\ne x_2}{sup}\frac{\parallel G(t,x_1)-G(t,x_2)\parallel }{\parallel x_1-x_2\parallel }.$$

(5)

2.1. Relationships between INDDEs and NDDEs

In order to establish the relationships between INDDEs and NDDEs, setting the scalar function $\alpha :[-\tau ,\infty )\to \mathbb{C}$ satisfies the following:

(1)

for any $t\in [0,\infty )$, $\alpha (t)=\alpha (t-\tau )$;

(2)

$\alpha (t)$ is infinitely smooth on $[0,\tau )$;

(3)

$\alpha (0)=1$ and $\alpha (0^{-})=\lambda$;

(4)

$\underset{t\in [0,\tau )}{inf}|\alpha (t)|\ge m>0$.

Theorem 1. 

If $x(t)$ is the solution of INDDE (1), $y(t)=\alpha (t)x(t)$ for $t\in [-\tau ,+\infty )$, then $y(t)$ is the solution of the following NDDE:

$$\left\{\begin{array}{cc}\frac{d}{dt}\left(y(t)-I(t,y(t-\tau )\right)=J(t,y(t),y(t-\tau )),\hfill & t\ge 0,\hfill \\ y(t)=\mathsf{\Psi }(t),\hfill & t\in [-\tau ,0],\hfill \end{array}\right.$$

(6)

where

$$I(t,x)=\alpha (t)G(t,\frac{x}{\alpha (t)})$$

$$J(t,y,z)=\frac{{\alpha }^{\prime }(t)y}{\alpha (t)}-{\alpha }^{\prime }(t)G(t,\frac{z}{\alpha (t)})+\alpha (t)F(t,\frac{y}{\alpha (t)},\frac{z}{\alpha (t)})$$

and

$$\mathsf{\Psi }(t)=\left\{\begin{array}{c}\alpha (t)\psi (t),t\in [-\tau ,0),\hfill \\ \alpha (0^{-})\psi (0^{-}),t=0.\hfill \end{array}\right.$$

In reverse, assuming $y(t)$ is the solution of NDDE (6), $x(t)=\frac{y(t)}{\alpha (t)}$ for $t\in [-\tau ,+\infty )$, then $x(t)$ is the solution of INDDE (1).

Proof. 

(i) On $[k\tau ,(k+1)\tau )$, $k=-1,0,1,\cdots$, $\alpha (t)$ and $x(t)$ are continuous, which implies that $y(t)$ is continuous. We can obtain that

$$\begin{array}{ccc}\hfill y(k\tau )& =& y(k{\tau }^{+})=\alpha (k{\tau }^{+})x(k{\tau }^{+})\hfill \\ & =& \alpha (k\tau )\lambda x(k{\tau }^{-})=\alpha (0)\lambda x(k{\tau }^{-})\hfill \\ & =& \lambda x(k{\tau }^{-})\hfill \end{array}$$

and

$$\begin{array}{c}\hfill y(k{\tau }^{-})=\alpha (k{\tau }^{-})x(k{\tau }^{-})=\lambda x(k{\tau }^{-}),\end{array}$$

implying $y(k\tau )=y(k{\tau }^{+})=y(k{\tau }^{-}),k\in \mathbb{N}$. Consequently, $y(t)$ is continuous on $[-\tau ,\infty )$.

For $t\in [k\tau ,(k+1)\tau ),k\in \mathbb{N}$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \frac{d}{dt}[y(t)-I(t,y(t-\tau ))]=\frac{d}{dt}[y(t)-\alpha (t)G(t,\frac{y(t-\tau )}{\alpha (t)})]\hfill \\ \hfill & =\frac{d}{dt}[\alpha (t)x(t)-\alpha (t)G(t,x(t-\tau ))]\hfill \\ \hfill & ={\alpha }^{\prime }(t)x(t)-{\alpha }^{\prime }(t)G(t,x(t-\tau ))+\alpha (t)\frac{d}{dt}[x(t)-G(t,x(t-\tau ))]\hfill \\ \hfill & ={\alpha }^{\prime }(t)x(t)-{\alpha }^{\prime }(t)G(t,x(t-\tau ))+\alpha (t)F(t,x(t),x(t-\tau ))\hfill \\ \hfill & =\frac{{\alpha }^{\prime }(t)y(t)}{\alpha (t)}-{\alpha }^{\prime }(t)G(t,\frac{y(t-\tau )}{\alpha (t)})+\alpha (t)F(t,\frac{y(t)}{\alpha (t)},\frac{y(t-\tau )}{\alpha (t)})\hfill \\ \hfill & =J(t,y(t),y(t-\tau ))\hfill \end{array}\end{array}$$

(ii) Let $y(t)$ be the solution of (6). For $t\in [k\tau ,(k+1)\tau ),k\in \mathbb{N}$,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \frac{d}{dt}[x(t)-G(t,x(t-\tau ))]=\frac{d}{dt}[\frac{y(t)}{\alpha (t)}-G(t,\frac{y(t-\tau )}{\alpha (t)})]\hfill \\ \hfill & =\frac{y^{\prime }(t)}{\alpha (t)}-\frac{{\alpha }^{\prime }(t)y(t)}{{\alpha }^2(t)}-[\frac{1}{\alpha (t)}\frac{d}{dt}(\alpha (t)G(t,\frac{y(t-\tau )}{\alpha (t)}))-\frac{{\alpha }^{\prime }(t)}{\alpha (t)}G(t,\frac{y(t-\tau )}{\alpha (t)})]\hfill \\ \hfill & =\frac{1}{\alpha (t)}\frac{d}{dt}[y(t)-I(t,y(t-\tau ))]-\frac{{\alpha }^{\prime }(t)y(t)}{{\alpha }^2(t)}+\frac{{\alpha }^{\prime }(t)}{\alpha (t)}G(t,\frac{y(t-\tau )}{\alpha (t)})]\hfill \\ \hfill & =\frac{J(t,y(t),y(t-\tau ))}{\alpha (t)}-\frac{{\alpha }^{\prime }(t)y(t)}{{\alpha }^2(t)}+\frac{{\alpha }^{\prime }(t)}{\alpha (t)}G(t,\frac{y(t-\tau )}{\alpha (t)})]\hfill \\ \hfill & =F(t,\frac{y(t)}{\alpha (t)},\frac{y(t-\tau )}{\alpha (t)})=F(t,\frac{y(t)}{\alpha (t)},\frac{y(t-\tau )}{\alpha (t-\tau )})\hfill \\ \hfill & =F(t,x(t),x(t-\tau )).\hfill \end{array}\end{array}$$

We can easily see that

$$x(k\tau )=\frac{y(k\tau )}{\alpha (k\tau )}=\frac{y(k\tau )}{\alpha (0)}=y(k\tau )$$

and

$$x(k{\tau }^{-})=\underset{t\to k{\tau }^{-}}{lim}\frac{y(t)}{\alpha (t)}=\frac{y(k\tau )}{\alpha (k{\tau }^{-})}=\frac{y(k\tau )}{\alpha ({\tau }^{-})}=\frac{y(k\tau )}{\lambda },$$

implying that $x(k\tau )=\lambda x(k{\tau }^{-}),k\in \mathbb{N}$. Apparently, we obtain $x(t)=\frac{y(t)}{\alpha (t)}=\psi (t)$, $t\in [-\tau ,0)$. Therefore, $x(t)$ is the solution of INDDE (1). □

Since in Theorem 1, $\alpha (t)$ and $\frac{1}{\alpha (t)}$ are bounded for all $t\in \mathbb{R}$, we can obtain the following result.

Remark 1. 

The exact solution $x(t)$ of INDDE (1) is stable if and only if the exact solution $y(t)$ of NDDE (6) is stable when $y(t)=\alpha (t)x(t)$ for $t\in [-\tau ,+\infty )$. Moreover, the exact solution $x(t)$ of INDDE (1) is asymptotically stable if and only if the exact solution $y(t)$ of NDDE (6) is asymptotically stable when $y(t)=\alpha (t)x(t)$ for $t\in [-\tau ,+\infty )$.

2.2. Asymptotical Stability of INDDEs

According to Theorem 1, assuming $\tilde{y}(t)=\alpha (t)\tilde{x}(t)$, $t\ge -\tau$, then $\tilde{x}(t)$ is the solution of (2) if and only if $\tilde{y}(t)$ is the solution of the following equation:

$$\left\{\begin{array}{cc}\frac{d}{dt}\left(\tilde{y}(t)-I(t,\tilde{y}(t-\tau )\right)=J(t,\tilde{y}(t),\tilde{y}(t-\tau )),\hfill & t\ge 0,\hfill \\ \tilde{y}(t)=\tilde{\mathsf{\Psi }}(t),\hfill & t\in [-\tau ,0],\hfill \end{array}\right.$$

(7)

where

$$\tilde{\mathsf{\Psi }}(t)=\left\{\begin{array}{c}\alpha (t)\tilde{\psi }(t),t\in [-\tau ,0),\hfill \\ \alpha (0^{-})\tilde{\psi }(0^{-}),t=0.\hfill \end{array}\right.$$

Let

$$P(t)=y(t)-I(t,y(t-\tau )),\tilde{P}(t)=\tilde{y}(t)-I(t,\tilde{y}(t-\tau )),$$

$$Q(t,y,z)=J(t,y+I(t,z),z).$$

Then the NDDE (6) can be expressed as the following ordinary differential equations with forcing term:

$$\left\{\begin{array}{c}{P}^{\prime }(t)=Q(t,P(t),y(t-\tau )),t\ge 0,\hfill \\ P(0)=\mathsf{\Psi }(0)-I(0,\mathsf{\Psi }(-\tau )),\hfill \end{array}\right.$$

(8)

coupled with the algebraic recursion

$$y(t)=\left\{\begin{array}{c}\mathsf{\Psi }(t),t\in [-\tau ,0),\hfill \\ P(t)+I(t,y(t-\tau )),t\ge 0.\hfill \end{array}\right.$$

Analogously, the NDDE (7) can also be expressed in the following form:

$$\left\{\begin{array}{c}{\tilde{P}}^{\prime }(t)=Q(t,\tilde{P}(t),\tilde{y}(t-\tau )),t\ge 0,\hfill \\ \tilde{P}(0)=\tilde{\mathsf{\Psi }}(0)-I(0,\tilde{\mathsf{\Psi }}(-\tau )),\hfill \end{array}\right.$$

(9)

coupled with the algebraic recursion

$$\tilde{y}(t)=\left\{\begin{array}{c}\tilde{\mathsf{\Psi }}(t),t\in [-\tau ,0),\hfill \\ \tilde{P}(t)+I(t,\tilde{y}(t-\tau )),t\ge 0.\hfill \end{array}\right.$$

Theorem 2. 

Assume IDDEs (1) and (2) satisfy (3)–(5). If $Y(t)\le 0$, there exists a bounded function $r(t)$, integrable in any bounded interval, such that $r(t)\le 0$, $r(0)<0$,

$$\omega X(t)=r(t)\left(\Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})+\frac{Y(t)}{{\omega }^2}\right)$$

(10)

and a non-negative constant $\rho \le 1$, such that

$$\underset{0\le x\le t}{sup}|r(x)|+\omega Z(t)\le \rho ,t\ge 0,$$

(11)

then the solution of IDDEs (1) and (2) are bounded stable; that is

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{\omega \underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{|\lambda |\parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-mr(0)}\},t\ge 0.$$

Moreover, if $\rho <1$ and

$$\Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})+\frac{Y(t)}{{\omega }^2}\le Y_0<0,t\ge 0,$$

(12)

then IDDEs (1) and (2) are asymptotically stable; that is

$$\underset{t\to \infty }{lim}\parallel x(t)-\tilde{x}(t)\parallel =0.$$

Proof. 

We will apply inequalities (3)–(5) to prove that the function $Q:[0,\infty )\times {\mathbb{C}}^d\times {\mathbb{C}}^d\to {\mathbb{C}}^d$ is continuous in t and satisfies the following conditions: for arbitrary $y,y_1,y_2,x_1,x_2\in {\mathbb{C}}^d$, and $\forall t\in [0,+\infty )$,

$$\underset{y_1\ne y_2,x}{sup}\frac{\Re \left(\langle Q(t,y_1,x)-Q(t,y_2,x),y_1-y_2\rangle \right)}{\parallel y_1-y_2{\parallel }^2}\le \Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})+{\omega }^{2}Y(t),$$

(13)

$$\underset{y,x_1\ne x_2}{sup}\frac{\parallel Q(t,y,x_1)-Q(t,y,x_2)\parallel }{\parallel x_1-x_2\parallel }\le \omega X(t),$$

(14)

$$\underset{x_1\ne x_2}{sup}\frac{\parallel G(t,x_1)-G(t,x_2)\parallel }{\parallel x_1-x_2\parallel }\le \omega Z(t).$$

(15)

First, the inequality (13) can be proven as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \Re \langle Q(t,y_1,x)-Q(t,y_2,x),y_1-y_2,\rangle \hfill \\ \hfill & =\Re \langle J(t,y_1+I(t,x),x)-J(t,y_2+I(t,x),x),y_1-y_2,\rangle \hfill \\ \hfill & =\Re \langle \frac{{\alpha }^{\prime }(t)}{\alpha (t)}(y_1+I(t,x))-{\alpha }^{\prime }(t)G(t,\frac{x}{\alpha (t)})+\alpha (t)F(t,\frac{1}{\alpha (t)}(y_1+I(t,x)),\frac{x}{\alpha (t)})\hfill \\ \hfill & -[\frac{{\alpha }^{\prime }(t)}{\alpha (t)}(y_2+I(t,x))-{\alpha }^{\prime }(t)G(t,\frac{x}{\alpha (t)})+\alpha (t)F(t,\frac{1}{\alpha (t)}(y_2+I(t,x)),\frac{x}{\alpha (t)})],\hfill \\ \hfill & y_1-y_2\rangle \hfill \\ \hfill & =\Re \langle \frac{{\alpha }^{\prime }(t)}{\alpha (t)}(y_1-y_2)+\alpha (t)[F(t,\frac{1}{\alpha (t)}(y_1+I(t,x)),\frac{x}{\alpha (t)})\hfill \\ \hfill & -\alpha (t)F(t,\frac{1}{\alpha (t)}(y_2+I(t,x)),\frac{x}{\alpha (t)})],y_1-y_2\rangle \hfill \\ \hfill & =\Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})\parallel y_1-y_2{\parallel }^2+\Re (\alpha (t)\langle F(t,\frac{y_1}{\alpha (t)}+G(t,\frac{x}{\alpha (t)}),\frac{x}{\alpha (t)})\hfill \\ \hfill & -F(t,\frac{y_2}{\alpha (t)}+G(t,\frac{x}{\alpha (t)}),\frac{x}{\alpha (t)})),y_1-y_2\rangle )\hfill \\ \hfill & =\Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})\parallel y_1-y_2{\parallel }^2+{|\alpha (t)|}^2\Re (\langle H(t,\frac{y_1}{\alpha (t)},\frac{x}{\alpha (t)})-H(t,\frac{y_2}{\alpha (t)},\frac{x}{\alpha (t)}),\frac{y_1}{\alpha (t)}-\frac{y_2}{\alpha (t)}\rangle )\hfill \\ \hfill & \le \Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})\parallel y_1-y_2{\parallel }^2+|\alpha (t){|}^{2}Y(t){\parallel \frac{y_1}{\alpha (t)}-\frac{y_2}{\alpha (t)}\parallel }^2\hfill \end{array}\end{array}$$

which implies that, if $Y(t)\le 0$,

$$\Re \langle Q(t,y_1,x)-Q(t,y_2,x),y_1-y_2,\rangle \le [\Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})+\frac{Y(t)}{{\omega }^2}]{\parallel y_1-y_2\parallel }^2$$

(16)

and if $Y(t)\le \widehat{Y}$ and $\widehat{Y}>0$,

$$\Re \langle Q(t,y_1,x)-Q(t,y_2,x),y_1-y_2,\rangle \le [\Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})+{\omega }^2\widehat{Y}]{\parallel y_1-y_2\parallel }^2$$

(17)

Next, we will prove the inequality (14) as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \parallel Q(t,y,x_1)-Q(t,y,x_2)\parallel \hfill \\ \hfill & =\parallel J(t,y+I(t,x_1),x_1)-J(t,y+I(t,x_2),x_2)\parallel \hfill \\ \hfill & =\parallel \frac{{\alpha }^{\prime }(t)}{\alpha (t)}(y+I(t,x_1))-{\alpha }^{\prime }(t)G(t,\frac{x_1}{\alpha (t)})+\alpha (t)F(t,\frac{1}{\alpha (t)}(y+I(t,x_1)),\frac{x_1}{\alpha (t)})\hfill \\ \hfill & -[\frac{{\alpha }^{\prime }(t)}{\alpha (t)}(y+I(t,x_2))-{\alpha }^{\prime }(t)G(t,\frac{x_2}{\alpha (t)})+\alpha (t)F(t,\frac{1}{\alpha (t)}(y+I(t,x_2)),\frac{x_2}{\alpha (t)})]\parallel \hfill \\ \hfill & =\omega \parallel H(t,\frac{y}{\alpha (t)},\frac{x_1}{\alpha (t)})-H(t,\frac{y}{\alpha (t)},\frac{x_2}{\alpha (t)})\parallel \hfill \\ \hfill & \le \omega X(t)\parallel x_1-x_2\parallel \hfill \end{array}\end{array}$$

Finally, the inequality (15) can be proven as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \parallel I(t,x_1)-I(t,x_2)\parallel \hfill \\ \hfill & =\parallel \alpha (t)G(t,\frac{x_1}{\alpha (t)})-\alpha (t)G(t,\frac{x_2}{\alpha (t)})\parallel \hfill \\ \hfill & \le (\underset{t\ge 0}{sup}|\alpha (t)|)\parallel G(t,\frac{x_1}{\alpha (t)})-G(t,\frac{x_2}{\alpha (t)})\parallel \hfill \\ \hfill & \le Z(t)(\underset{t\ge 0}{sup}|\alpha (t)|)\parallel \frac{x_1}{\alpha (t)}-\frac{x_2}{\alpha (t)}\parallel \hfill \\ \hfill & \le \omega Z(t)\parallel x_1-x_2\parallel .\hfill \end{array}\end{array}$$

By [14] (Theorem 9.4.1) or [24] (Theorem 3.1, Theorem 4.2), we can obtain that

$$\parallel y(t)-\tilde{y}(t)\parallel \le max\{\underset{t\in [-\tau ,0)}{sup}\parallel \mathsf{\Psi }(t)-\tilde{\mathsf{\Psi }}(t)\parallel ,\frac{\parallel \mathsf{\Psi }(0)-\tilde{\mathsf{\Psi }}(0)\parallel }{-r(0)}\},t\ge 0$$

and

$$\underset{t\to \infty }{lim}\parallel y(t)-\tilde{y}(t)\parallel =0.$$

Because $x(t)=\frac{y(t)}{\alpha (t)}$, $t\ge -\tau$, we know the theorem holds. □

Theorem 3. 

Assume IDDEs (1) and (2) satisfy (3)–(5). If $Y(t)\le \widehat{Y}$, $\widehat{Y}>0$, there exists a bounded function $\overline{r}(t)$, integrable in any bounded interval, such that $\overline{r}(t)\le 0$, $\overline{r}(0)<0$,

$$\omega X(t)=\overline{r}(t)\left(\Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})+{\omega }^2\widehat{Y}\right)$$

(18)

and a non-negative constant $\overline{\rho }\le 1$, such that

$$\underset{0\le x\le t}{sup}|r(x)|+\omega Z(t)\le \overline{\rho },t\ge 0,$$

(19)

then the solution of IDDEs (1) and (2) are bounded stable; that is

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{\omega \underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{|\lambda |\parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m\overline{r}(0)}\},t\ge 0.$$

Moreover, if $\overline{\rho }<1$ and

$$\Re (\frac{{\alpha }^{\prime }(t)}{\alpha (t)})+{\omega }^2\widehat{Y}\le {\overline{Y}}_0<0,t\ge 0,$$

(20)

then IDDEs (1) and (2) are asymptotically stable; that is

$$\underset{t\to \infty }{lim}\parallel x(t)-\tilde{x}(t)\parallel =0.$$

2.3. Special Cases

When different functions of $\alpha (t)$ are chosen, different sufficient conditions for the bounded stability and asymptotical stability of the exact solutions of (1) and (2) can be obtained. For brevity, we only consider three of them.

Special Case I. Set ${\alpha }_1(t)={\lambda }^{\{\frac{t}{\tau }\}}$, $t\in [-\tau ,\infty )$, where $\{\frac{t}{\tau }\}=\frac{t}{\tau }-\lfloor \frac{t}{\tau }\rfloor$, $\lfloor \frac{t}{\tau }\rfloor$ denotes the floor function. The following theorem can be seen as a special case of Theorem 2 when $\alpha (t)={\alpha }_1(t)$.

Theorem 4. 

Let $x(t)$ be the solution of (1). If $z_1(t)={\lambda }^{\{\frac{t}{\tau }\}}x(t),t\in [-\tau ,\infty )$, then $z_1(t)$ is the solution of

$$\left\{\begin{array}{cc}\frac{d}{dt}[z_1(t)-I_1(t,z_1(t-\tau ))]=J_1(t,z_1(t),z_1(t-\tau )),\hfill & t\ge 0,\hfill \\ z_1(t)={\mathsf{\Psi }}_1(t),\hfill & t\in [-\tau ,0],\hfill \end{array}\right.$$

(21)

where

$$I_1(t,x))={\lambda }^{\{\frac{t}{\tau }\}}G(t,{\lambda }^{-\{\frac{t}{\tau }\}}x)$$

$$J_1(t,y,x)=(\frac{ln\lambda }{\tau })y-{\lambda }^{\{\frac{t}{\tau }\}}(\frac{ln\lambda }{\tau })G(t,{\lambda }^{-\{\frac{t}{\tau }\}}x)+{\lambda }^{\{\frac{t}{\tau }\}}F(t,{\lambda }^{-\{\frac{t}{\tau }\}}y,{\lambda }^{-\{\frac{t}{\tau }\}}x)$$

$${\mathsf{\Psi }}_1(t)=\left\{\begin{array}{c}{\lambda }^{\frac{t}{\tau }+1}\psi (t),t\in [-\tau ,0),\hfill \\ \lambda \psi (0^{-}),t=0.\hfill \end{array}\right.$$

Conversely, $x(t)$ is the solution of (1) if $z_1(t)$ is the solution of (21) and $x(t)={\lambda }^{-\{\frac{t}{\tau }\}}{z}_1(t),$$t\in [-\tau ,\infty )$.

Theorem 5. 

Assume IDDEs (1) and (2) satisfy inequalities (3)–(5). If $Y(t)\le 0$, there exists a bounded function $r_1(t)$, integrable in any bounded interval, such that $r_1(t)\le 0$ and $r_1(0)<0$,

$${\omega }_{1}X(t)=r_1(t)\left(\frac{ln|\lambda |}{\tau }+\frac{Y(t)}{{\omega }_1^2}\right)$$

and a non-negative constant ${\rho }_1\le 1$, such that

$$\underset{0\le x\le t}{sup}|r_1(x)|+{\omega }_{1}Z(t)\le {\rho }_1,t\ge 0,$$

then the solutions of IDDEs (1) and (2) are bounded stable,

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{{\omega }_1\underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{|\lambda |\parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m_1{r}_1(0)}\},t\ge 0.$$

where ${\omega }_1=max\{|\lambda |,\frac{1}{|\lambda |}\}$, $m_1=min\{1,|\lambda |\}$. Moreover, if ${\rho }_1<1$ and

$$\frac{ln|\lambda |}{\tau }+\frac{Y(t)}{{\omega }_1^2}\le Y_1<0,t\ge 0,$$

then IDDEs (1) and (2) are asymptotically stable.

Theorem 6. 

Assume IDDEs (1) and (2) satisfy inequalities (3)–(5). If $Y(t)\le \widehat{Y}$, $\widehat{Y}>0$, there exists a bounded function ${\overline{r}}_1(t)$, integrable in any bounded interval, such that ${\overline{r}}_1(t)\le 0$, ${\overline{r}}_1(0)<0$,

$${\omega }_{1}X(t)={\overline{r}}_1(t)\left(\frac{ln|\lambda |}{\tau }+{\omega }_1^2\widehat{Y}\right)$$

and a non-negative constant ${\overline{\rho }}_1\le 1$, such that

$$\underset{0\le x\le t}{sup}|r(x)|+{\omega }_{1}Z(t)\le {\overline{\rho }}_1,t\ge 0,$$

then the solutions of IDDEs (1) and (2) are bounded,

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{{\omega }_1\underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{|\lambda |\parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m_1{\overline{r}}_1(0)}\},t\ge 0.$$

Moreover, if ${\overline{\rho }}_1<1$ and

$$\frac{ln|\lambda |}{\tau }+{\omega }_1^2\widehat{Y}\le {\overline{Y}}_1<0,t\ge 0,$$

then IDDEs (1) and (2) are asymptotically stable.

Special Case II. Let ${\alpha }_2(t)=1+(\lambda -1)\{\frac{t}{\tau }\}$, $t\in [-\tau ,\infty )$, $\lambda >0$, $\lambda \ne 1$. The following theorem can be seen as a special case of Theorem 2 when $\alpha (t)={\alpha }_2(t)$.

Theorem 7. 

Assume that $x(t)$ is the solution of (1) and $z_2(t)=[1+(\lambda -1)\{\frac{t}{\tau }\}]x(t),$$t\in [-\tau ,\infty )$. Then $z_2(t)$ is the solution of

$$\left\{\begin{array}{cc}\frac{d}{dt}[z_2(t)-I_2(t,z_2(t-\tau ))]=J_2(t,z_2(t),z_2(t-\tau )),\hfill & t\ge 0,\hfill \\ z_2(t)={\mathsf{\Psi }}_2(t),\hfill & t\in [-\tau ,0],\hfill \end{array}\right.$$

(22)

where

$$I_2(t,x))={\alpha }_2(t)G(t,\frac{x}{{\alpha }_2(t)})=\left(1+(\lambda -1)\{\frac{t}{\tau }\}\right)G(t,\frac{x}{\left(1+(\lambda -1)\{\frac{t}{\tau }\}\right)})$$

$$J_2(t,y,x)=\frac{(\lambda -1)y}{\tau {\alpha }_2(t)}-\frac{\lambda -1}{\tau }G(t,\frac{x}{{\alpha }_2(t)})+{\alpha }_2(t)F(t,\frac{y}{{\alpha }_2(t)},\frac{x}{{\alpha }_2(t)})$$

$${\mathsf{\Psi }}_2(t)=\left\{\begin{array}{c}[1+(\lambda -1)(\frac{t}{\tau }+1)]\psi (t),t\in [-\tau ,0),\hfill \\ \lambda \psi (0^{-}),t=0.\hfill \end{array}\right.$$

Conversely, $x(t)$ is the solution of (1) if $z_2(t)$ is the solution of (22) and $x(t)=\frac{z_2(t)}{1+(\lambda -1)\{\frac{t}{\tau }\}},$$t\in [-\tau ,\infty )$.

Theorem 8. 

Assume that $\lambda \in \mathbb{R}$, $\lambda >0$, $\lambda \ne 1$, IDDEs (1) and (2) satisfy (3)–(5). If $Y(t)\le 0$, there exists a bounded function $r_2(t)$, integrable in any bounded interval, such that $r_2(t)\le 0$, $r_2(0)<0$,

$${\omega }_{2}X(t)=r(t)\left(\frac{\lambda -1}{\tau +(\lambda -1)\tau \{\frac{t}{\tau }\}}+\frac{Y(t)}{{\omega }_2^2}\right)$$

and a non-negative constant ${\rho }_2\le 1$, such that

$$\underset{0\le x\le t}{sup}|r_2(x)|+{\omega }_{2}Z(t)\le {\rho }_2,t\ge 0,$$

then the exact solutions of IDDEs (1) and (2) are bounded stable as follows:

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{{\omega }_2\underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{\lambda \parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m_2{r}_2(0)}\},t\ge 0,$$

where ${\omega }_2=max\{\lambda ,\frac{1}{\lambda }\}$, $m_2=min\{1,\lambda \}$. Moreover, if ${\rho }_2<1$ and there is a negative constant $Y_2$ such that

$$\frac{\lambda -1}{\tau +(\lambda -1)\tau \{\frac{t}{\tau }\}}+\frac{Y(t)}{{\omega }_2^2}\le Y_2<0,t\ge 0,$$

then IDDEs (1) and (2) are asymptotically stable.

Theorem 9. 

Assume that IDDEs (1) and (2) satisfy (3)–(5), $\lambda >0$ and $\lambda \ne 1$. If $Y(t)\le \widehat{Y}$, $\widehat{Y}>0$, there exists a bounded function ${\overline{r}}_2(t)$, integrable in any bounded interval, such that ${\overline{r}}_2(t)\le 0$, ${\overline{r}}_2(0)<0$,

$${\omega }_{2}X(t)=r(t)\left(\frac{\lambda -1}{\tau +(\lambda -1)\tau \{\frac{t}{\tau }\}}+{\omega }_2^2\widehat{Y}\right)$$

and a non-negative constant ${\overline{\rho }}_2\le 1$, such that

$$\underset{0\le x\le t}{sup}|r(x)|+{\omega }_{2}Z(t)\le {\overline{\rho }}_2,t\ge 0,$$

then the exact solutions of IDDEs (1) and (2) are bounded stable as follows:

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{{\omega }_2\underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{\lambda \parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m_2{\overline{r}}_2(0)}\},t\ge 0.$$

Moreover, if ${\overline{\rho }}_2<1$ and there is a negative constant ${\overline{Y}}_2$, such that

$$\frac{\lambda -1}{\tau +(\lambda -1)\tau \{\frac{t}{\tau }\}}+{\omega }_2^2\widehat{Y}\le {\overline{Y}}_2<0,t\ge 0,$$

then IDDEs (1) and (2) are asymptotically stable.

Because $\frac{\lambda -1}{\tau +(\lambda -1)\tau \{\frac{t}{\tau }\}}\le \frac{\lambda -1}{\tau }$ for all $\lambda >0$, $\forall t\in \mathbb{R}$, by Theorems 8 and 9, we can obtain the following two results.

Corollary 1. 

Assume that IDDEs (1) and (2) satisfy (3)–(5), $\lambda \ne 1$ and $\lambda >0$. If $Y(t)\le 0$, there exists a bounded function ${\tilde{r}}_2(t)$, integrable in any bounded interval, such that ${\tilde{r}}_2(t)\le 0$, ${\tilde{r}}_2(0)<0$,

$${\omega }_{2}X(t)={\tilde{r}}_2(t)\left(\frac{\lambda -1}{\tau }+\frac{Y(t)}{{\omega }_2^2}\right)$$

and a non-negative constant ${\tilde{\rho }}_2\le 1$, such that

$$\underset{0\le x\le t}{sup}|{\tilde{r}}_2(x)|+{\omega }_{2}Z(t)\le {\tilde{\rho }}_2,t\ge 0,$$

then the exact solutions of IDDEs (1) and (2) are bounded stable as follows:

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{{\omega }_2\underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{\lambda \parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m_2{\tilde{r}}_2(0)}\},t\ge 0.$$

Moreover, if ${\tilde{\rho }}_2<1$ and there is a positive constant $Y_2$, such that

$$\frac{\lambda -1}{\tau }+\frac{Y(t)}{{\omega }_2^2}\le Y_2<0,t\ge 0,$$

then IDDEs (1) and (2) are asymptotically stable.

Corollary 2. 

Assume that IDDEs (1) and (2) satisfy (3)–(5) and $\lambda >0$, $\lambda \ne 1$. If there exists a bounded function ${\check{r}}_2(t)$, integrable in any bounded interval, such that ${\check{r}}_2(t)\le 0$, ${\check{r}}_2(0)<0$,

$${\omega }_{2}X(t)={\check{r}}_2(t)\left(\frac{\lambda -1}{\tau }+{\omega }_2^2\widehat{Y}\right)$$

and a non-negative constant ${\check{\rho }}_2\le 1$, such that

$$\underset{0\le x\le t}{sup}|r(x)|+{\omega }_{2}Z(t)\le {\check{\rho }}_2,t\ge 0,$$

then the exact solutions of IDDEs (1) and (2) are bounded stable as follows:

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{{\omega }_2\underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{\lambda \parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m_2{\check{r}}_2(0)}\},t\ge 0.$$

Moreover, if ${\check{\rho }}_2<1$ and $\frac{\lambda -1}{\tau }+{\omega }_2^2\widehat{Y}<0,t\ge 0$, then IDDEs (1) and (2) are asymptotically stable.

Special Case III. Let ${\alpha }_3(t)=-{\{\frac{t}{\tau }\}}^2+\lambda \{\frac{t}{\tau }\}+1$, $t\in [-\tau ,\infty )$, $\lambda \in \mathbb{R}$, $\lambda >0$, $\lambda \ne 1$. The following theorem can be seen as a special case of Theorem 2 when $\alpha (t)={\alpha }_3(t)$.

Theorem 10. 

Let $x(t)$ be the solution of (1) and $z_3(t)=\left(-{\{\frac{t}{\tau }\}}^2+\lambda \{\frac{t}{\tau }\}+1\right)x(t),$$t\in [-\tau ,\infty )$. Then $z_3(t)$ is the solution of

$$\left\{\begin{array}{cc}\frac{d}{dt}[z_3(t)-I_3(t,z_3(t-\tau ))]=J_3(t,z_3(t),z_3(t-\tau )),\hfill & t\ge 0,\hfill \\ z_3(t)={\mathsf{\Psi }}_3(t),\hfill & t\in [-\tau ,0],\hfill \end{array}\right.$$

(23)

where

$$I_3(t,x))=(-{\{\frac{t}{\tau }\}}^2+\lambda \{\frac{t}{\tau }\}+1)G(t,\frac{x}{-{\{\frac{t}{\tau }\}}^2+\lambda \{\frac{t}{\tau }\}+1})$$

$$J_3(t,y,x)=\frac{(-2\{\frac{t}{\tau }\}+\lambda )y}{\tau {\alpha }_3(t)}-\frac{(-2\{\frac{t}{\tau }\}+\lambda )}{\tau }G(t,\frac{x}{{\alpha }_3(t)})+{\alpha }_3(t)F(t,\frac{y}{{\alpha }_3(t)},\frac{x}{{\alpha }_3(t)})$$

$${\mathsf{\Psi }}_3(t)=\left\{\begin{array}{c}[-{(\frac{t}{\tau }+1)}^2+\lambda (\frac{t}{\tau }+1)+1]\psi (t),t\in [-\tau ,0),\hfill \\ \lambda \psi (0^{-}),t=0.\hfill \end{array}\right.$$

Conversely, $x(t)$ is the solution of (1) if $z_3(t)$ is the solution of (23) and $x(t)=\frac{z_3(t)}{-{\{\frac{t}{\tau }\}}^2+\lambda \{\frac{t}{\tau }\}+1},$$t\in [-\tau ,\infty )$.

Theorem 11. 

Assume that $\lambda \in \mathbb{R}$ and $\lambda >0$, and IDDEs (1) and (2) satisfy inequalities (3)–(5). If $Y(t)\le 0$, there exists a bounded function $r_3(t)$, integrable in any bounded interval, such that $r_3(t)\le 0$, $r_3(0)<0$,

$${\omega }_{3}X(t)=r_3(t)\left(\Re (\frac{-2\{\frac{t}{\tau }\}+\lambda }{-{\{\frac{t}{\tau }\}}^2\tau +\lambda \tau \{\frac{t}{\tau }\}+\tau })+\frac{Y(t)}{{\omega }_3^2}\right)$$

and a non-negative constant ${\rho }_3\le 1$, such that

$$\underset{0\le x\le t}{sup}|r(x)|+{\omega }_{3}Z(t)\le {\rho }_3,t\ge 0,$$

then the exact solutions of IDDEs (1) and (2) are bounded stable as follows:

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{{\omega }_3\underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{\lambda \parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m_3{r}_3(0)}\},t\ge 0,$$

where $m_3=min\{1,\lambda \}$ and

$${\omega }_3=\left\{\begin{array}{c}\frac{\lambda }{4}+\frac{1}{\lambda },0<\lambda \le 1,\hfill \\ \frac{{\lambda }^2}{4}+1,1<\lambda \le 2,\hfill \\ \lambda ,\lambda >2.\hfill \end{array}\right.$$

Moreover, if ${\rho }_3<1$ and there is a positive constant $Y_3$, such that

$$\frac{-2\{\frac{t}{\tau }\}+\lambda }{-{\{\frac{t}{\tau }\}}^2\tau +\lambda \tau \{\frac{t}{\tau }\}+\tau }+\frac{Y(t)}{{\omega }_3^2}\le Y_3<0,t\ge 0,$$

then IDDEs (1) and (2) are asymptotically stable.

Because $\frac{-2\{\frac{t}{\tau }\}+\lambda }{-{\{\frac{t}{\tau }\}}^2\tau +\lambda \tau \{\frac{t}{\tau }\}+\tau }\le \frac{\lambda }{\tau }$ for all $\lambda >0$, $\forall t\in \mathbb{R}$, by Theorem 11, we can obtain the following corollary.

Corollary 3. 

Assume that $\lambda \in \mathbb{R}$ and $\lambda >0$, and the IDDEs (1) and (2) satisfy inequalities (3)–(5). If $Y(t)\le 0$, there exists a bounded integrable function ${\overline{r}}_3(t)$ in any bounded interval, such that ${\overline{r}}_3(t)\le 0$, ${\overline{r}}_3(0)<0$,

$${\omega }_{3}X(t)={\overline{r}}_3(t)(\frac{\lambda }{\tau }+\frac{Y(t)}{{\omega }_3^2})$$

and a non-negative constant ${\overline{\rho }}_3\le 1$, such that

$$\underset{0\le x\le t}{sup}|{\overline{r}}_3(x)|+{\omega }_{3}Z(t)\le {\overline{\rho }}_3,t\ge 0,$$

then the exact solutions of IDDEs (1) and (2) are bounded stable as follows:

$$\parallel x(t)-\tilde{x}(t)\parallel \le max\{{\omega }_3\underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{\lambda \parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-m_3{\overline{r}}_3(0)}\},t\ge 0.$$

Moreover, if ${\overline{\rho }}_3<1$ and there is a positive constant ${\overline{Y}}_3$, such that

$$\frac{\lambda }{\tau }+\frac{Y(t)}{{\omega }_3^2}\le {\overline{Y}}_3<0,t\ge 0,$$

then IDDEs (1) and (2) are asymptotically stable.

3. Numerical Methods for INDDEs

Firstly, based on the idea of transformations, the numerical methods for INDDEs are constructed. Furthermore, it is proven that the constructed numerical methods can preserve the boundary stability and asymptotical stability of the nonlinear INDDEs if corresponding continuous Runge–Kutta methods are $B{N}_f$-stable.

The numerical method for nonlinear INDDE (1) can be constructed as the following three steps.

Step 1. The numerical solution of (8) is computed by the following continuous Runge–Kutta method:

$$\left\{\begin{array}{c}{\mathsf{\Lambda }}_{n+1}^i=p_n+h{\displaystyle \sum _{j=1}^s}{a}_{ij}Q(t_{n+1}^j,{\mathsf{\Lambda }}_{n+1}^j,\eta (t_{n+1}^j-\tau )),i=1,2,\cdots ,s,\hfill \\ \lambda (t_n+\theta h)=p_n+h{\displaystyle \sum _{i=1}^s}{b}_i(\theta )Q(t_{n+1}^i,{\mathsf{\Lambda }}_{n+1}^i,\eta (t_{n+1}^i-\tau ))\hfill \\ p_{n+1}=\lambda (t_{n+1})=p_n+h{\displaystyle \sum _{i=1}^s}{b}_{i}Q(t_{n+1}^i,{\mathsf{\Lambda }}_{n+1}^i,\eta (t_{n+1}^i-\tau )),\hfill \end{array}\right.$$

(24)

where the stepsize $h=\frac{\tau }{m}$, m is a positive integer, $t_n=nh$, $t_{n+1}^i=t_n+c_{i}h$, and $c_i={\sum }_{j=1}^s{a}_{ij}$, $n\in \mathbb{N}$, $i=1,2,\cdots ,s$.

Step 2. The numerical solution of (6) can be computed by

$$\eta (t)=\lambda (t)+G(t,\eta (t-\tau )),t\ge 0,$$

(25)

where

$$\eta (t)=\mathsf{\Psi }(t),t\in [-\tau ,0].$$

Step 3. The numerical solution $\mu (t)$ of (1) can be computed by

$$\mu (t)=\frac{\eta (t)}{\alpha (t)},t\ge 0.$$

(26)

In the above process, the exact solution $P(t)$ of (8) is approximated by $\lambda (t)$ for all $t\ge 0$ and $P(t_n)$ is approximated by $p_n$, $n\in \mathbb{N}$; $y(t)$ of (6) is approximated by $\eta (t)$ and $x(t)$ of (1) is approximated by $\mu (t)$ for all $t\ge 0$.

Similarly, the numerical method for nonlinear INDDE (2) can be constructed as follows:

$$\left\{\begin{array}{c}{\tilde{\mathsf{\Lambda }}}_{n+1}^i=p_n+h{\displaystyle \sum _{j=1}^s}{a}_{ij}Q(t_{n+1}^j,{\tilde{\mathsf{\Lambda }}}_{n+1}^j,\tilde{\eta }(t_{n+1}^j-\tau )),i=1,2,\cdots ,s,\hfill \\ \tilde{\lambda }(t_n+\theta h)={\tilde{p}}_n+h{\displaystyle \sum _{i=1}^s}{b}_i(\theta )Q(t_{n+1}^i,{\tilde{\mathsf{\Lambda }}}_{n+1}^i,\tilde{\eta }(t_{n+1}^i-\tau )),\hfill \\ {\tilde{p}}_{n+1}=\tilde{\lambda }(t_{n+1})={\tilde{p}}_n+h{\displaystyle \sum _{i=1}^s}{b}_{i}Q(t_{n+1}^i,{\tilde{\mathsf{\Lambda }}}_{n+1}^i,\tilde{\eta }(t_{n+1}^i-\tau )),\hfill \\ \tilde{\eta }(t)=\tilde{\lambda }(t)+G(t,\tilde{\eta }(t-\tau )),t\ge 0,\hfill \\ \tilde{\mu }(t)=\frac{\tilde{\eta }(t)}{\alpha (t)},t\ge 0,\hfill \end{array}\right.$$

(27)

where

$$\tilde{\eta }(t)=\tilde{\mathsf{\Psi }}(t),t\in [-\tau ,0].$$

Theorem 12. 

Assume that IDDEs (1) and (2) satisfy inequalities (3)–(5), and assume the constructed numerical methods (24)–(27) are furnished by $B{N}_f$-stable continuous Runge–Kutta methods. If $Y(t)\le 0$, there exists a bounded function $r(t)$, integrable in any bounded interval, such that $r(t)\le 0$, $r(0)<0$, and (10) and (11) hold, then the numerical solution $\mu (t)$ obtained from (24)–(26) and $\tilde{\mu }(t)$ obtained from (27) are bounded, in the following sense:

$$\parallel \mu (t)-\tilde{\mu }(t)\parallel \le max\{\omega \underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{|\lambda |\parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-mr(0)}\},t\ge 0.$$

Moreover, if $\rho <1$ and (12) hold, then the numerical methods (24)–(27) for IDDEs (1) and (2), furnished by $B{N}_f$-stable continuous Runge–Kutta methods, are asymptotically stable; that is

$$\underset{t\to \infty }{lim}\parallel \mu (t)-\tilde{\mu }(t)\parallel =0.$$

Proof. 

By ref. [14] (Theorem 10.5.1)or ref. [24] (Theorem 6.1), the numerical methods (24) and (25), furnished by $B{N}_f$-stable continuous Runge–Kutta methods, are bounded; that is

$$\parallel \eta (t_n)-\tilde{\eta }(t_n)\parallel \le max\{\parallel \Phi (0)-\tilde{\Phi }(0)\parallel ,\kappa \}.$$

Moreover, ref. [14] (Theorem 10.5.1) or ref. [24] (Theorem 6.3), under the condition of Theorem 2, the numerical methods (24) and (25) furnished by $B{N}_f$-stable continuous Runge–Kutta methods, are also asymptotically stable; that is,

$$\underset{n\to +\infty }{lim}\parallel \eta (t_n)-\tilde{\eta }(t_n)\parallel =0.$$

Because of the relationship (26) between the numerical solutions INDDE and NDDE without impulsive perturbations, the theorem holds. □

Similar to Theorem 12, we can obtain that the constructed numerical methods (24)–(27), furnished by $B{N}_f$-stable continuous Runge–Kutta methods, preserve the boundary stability and asymptotical stability of the exact solutions, under the conditions of Theorem 3, as follows.

Theorem 13. 

Assume that IDDEs (1) and (2) satisfy inequalities (3)–(5), and assume the constructed numerical methods (24)–(27) are furnished by $B{N}_f$-stable continuous Runge–Kutta methods. If $Y(t)\le \widehat{Y}$, $\widehat{Y}>0$, there exists a bounded function $r(t)$ integrable in any bounded interval, such that $\overline{r}(t)\le 0$, $\overline{r}(0)<0$, (18) and (19) hold, then the numerical solution $\mu (t)$ obtained from (24)–(26) and $\tilde{\mu }(t)$ obtained from (27) are bounded stable, in the following sense:

$$\parallel \mu (t)-\tilde{\mu }(t)\parallel \le max\{\omega \underset{t\in [-\tau ,0)}{sup}\parallel \phi (t)-\tilde{\phi }(t)\parallel ,\frac{\lambda \parallel \phi (0^{-})-\tilde{\phi }(0^{-})\parallel }{-mr(0)}\},t\ge 0.$$

Moreover, if $\rho <1$ and (20) hold, then the numerical methods (24)–(27) for IDDEs (1) and (2), furnished by $B{N}_f$-stable continuous Runge–Kutta methods, are asymptotically stable.

4. Numerical Experiments

In this section, two numerical examples are chosen to confirm the theoretical results.

Example 1. 

Consider the following scalar linear INDDEs with different initial functions:

$$\left\{\begin{array}{cc}{x}^{\prime }(t)-c{x}^{\prime }(t-\tau )=ax(t)+bx(t-\tau ),\hfill & t\ge 0,t\ne k\tau ,k\in \mathbb{N},\hfill \\ x(k\tau )=\lambda x(k{\tau }^{-}),\hfill & \\ x(t)=\varphi (t),\hfill & t\in [-\tau ,0),\hfill \end{array}\right.$$

(28)

where a, b, c, and λ are real constants and $\varphi (t)$ is the continuous differential initial function on $[-\tau ,0)$. Obviously, the inequalities (3)–(5) are satisfied with $X(t)=|ac+b|$, $Y(t)=a$, $Z(t)=|c|$. There are many parameters that meet the conditions of the theorems. Obviously, when

$$a=-5,b=\frac{4}{5},c=\frac{1}{5},\lambda =\frac{5}{4},\tau =1,$$

we have

$$X(t)=|ac+b|=|-5\times \frac{1}{5}+\frac{4}{5}|=\frac{1}{5},Y(t)=a=-5,Z(t)=|c|=\frac{1}{5},$$

and

$${\omega }_1=max\{\frac{5}{4},\frac{4}{5}\}=\frac{5}{4}.$$

Obviously, there exists $r_1(t)$ as follows:

$$r_1(t)=\frac{\left(\frac{ln|\lambda |}{\tau }+\frac{Y(t)}{{\omega }_1^2}\right)}{{\omega }_{1}X(t)}=\frac{1}{4\left(-\frac{16}{5}+ln(\frac{5}{4})\right)}<0,$$

such that the first condition of Theorem 5 holds; that is

$${\omega }_{1}X(t)=r_1(t)\left(\frac{ln|\lambda |}{\tau }+\frac{Y(t)}{{\omega }_1^2}\right).$$

So we can obtain that

$$\underset{0\le x\le t}{sup}|r_1(x)|+{\omega }_{1}Z(t)={\rho }_1=|\frac{1}{4\left(-\frac{16}{5}+ln(\frac{5}{4})\right)}|+\frac{5}{4}\times \frac{1}{5}<1$$

and

$$\frac{ln|\lambda |}{\tau }+\frac{Y(t)}{{\omega }_1^2}=-\frac{5}{\frac{25}{16}}+ln(\frac{5}{4})=Y_1<0.$$

Hence, all the conditions of Theorem 5 hold. By Theorem 5, the exact solution of (28) is asymptotically stable.

Similarly, ${\omega }_2=max\{\frac{5}{4},\frac{4}{5}\}=\frac{5}{4}$ and there exists $r_2(t)$ as follows:

$$r_2(t)=\frac{\left(\frac{\lambda -1}{\tau }+\frac{Y(t)}{{\omega }_2^2}\right)}{{\omega }_{2}X(t)}=\frac{1}{4\left(\frac{1}{4}-\frac{16}{5}+\right)}<0,$$

such that the first condition of Corollary 1 holds; that is

$${\omega }_{2}X(t)=r_2(t)\left(\frac{\lambda -1}{\tau }+\frac{Y(t)}{{\omega }_2^2}\right).$$

Therefore, we can obtain that

$$\underset{0\le x\le t}{sup}|r_2(x)|+{\omega }_{2}Z(t)={\rho }_2=|\frac{1}{4\left(-\frac{16}{5}+\frac{1}{4}\right)}|+\frac{5}{4}\times \frac{1}{5}<1$$

and

$$\frac{\lambda -1}{\tau }+\frac{Y(t)}{{\omega }_2^2}=\frac{1}{4}-\frac{5}{\frac{25}{16}}=Y_2<0.$$

Hence, all the conditions of Corollary 1 hold. By Corollary 1, we also obtain that the exact solution of (28) is asymptotically stable.

Similarly, ${\omega }_3=\frac{{\lambda }^2}{4}+1=\frac{89}{64}$, and there exists $r_3(t)$ as follows:

$$r_3(t)=\frac{\left(\frac{\lambda }{\tau }+\frac{Y(t)}{{\omega }_3^2}\right)}{{\omega }_{3}X(t)}=\frac{89}{5\times 64\times \left(\frac{5}{4}-\frac{5\times {64}^2}{{89}^2}\right)}<0,$$

such that the first condition of Corollary 3 holds; that is

$${\omega }_{3}X(t)=r_3(t)\left(\frac{\lambda }{\tau }+\frac{Y(t)}{{\omega }_3^2}\right).$$

Therefore, we can obtain that

$$\underset{0\le x\le t}{sup}|r_3(x)|+{\omega }_{3}Z(t)={\rho }_3=|\frac{89}{5\times 64\times \left(\frac{5}{4}-\frac{5\times {64}^2}{{89}^2}\right)}|+\frac{89}{64}\times \frac{1}{5}<1$$

and

$$\frac{\lambda }{\tau }+\frac{Y(t)}{{\omega }_3^2}=\frac{5}{4}-5\times \frac{{64}^2}{{89}^2}=Y_3<0.$$

Hence, all the conditions of Corollary 3 hold. By Corollary 3, we also obtain that the exact solution of (28) is asymptotically stable.

By Theorem 12, we can obtain that the constructed numerical methods (24)–(27) for INDDE (28), furnished by $B{N}_f$-stable continuous Runge–Kutta methods, are asymptotically stable. From Figure 1 and Figure 2, we can roughly see the trend that the distances between the two numerical solutions (obtained from the constructed numerical methods (24)–(27) for linear INDDE (28), furnished by implicit Euler method or 2-stage Lobatto IIIC method with two different constant initial function 1 and 0.9) become smaller as the time increases.

Example 2. 

Consider the following scalar nonlinear INDDEs:

$$\left\{\begin{array}{cc}\frac{d}{dt}\left(x(t)-\nu cos(x(t-1))\right)=\beta x(t)+\gamma {\mathrm{e}}^{-t}sin(x(t-1)),\hfill & t\ge 0,t\ne k,k\in \mathbb{N},\hfill \\ x(k)=\lambda x(k^{-}),\hfill & \\ x(t)=\varphi (t),\hfill & t\in [-1,0),\hfill \end{array}\right.$$

(29)

where β, γ, ν, and λ are real constants and $\varphi (t)$ is the continuous differential initial functions on $[-1,0)$. It is easy to verify that the inequalities (3)–(5) are satisfied with $X(t)=|\beta \nu |+|\gamma |{\mathrm{e}}^{-t}$, $Y(t)=\beta$, $Z(t)=|\nu |$. We can see that the one-side Lipschitz coefficient $X(t)$ is non-negative, which is different from the general results of NDDEs without impulsive perturbations. The parameters β, γ, ν, and λ are chosen to satisfy the conditions of Theorem 6:

$$\beta =\frac{1}{10},\gamma =\frac{1}{50},\nu =\frac{1}{5},\lambda =\frac{1}{\mathrm{e}},$$

which implies that the exact solution of (29) is stable and asymptotically stable (See Figure 3 and Figure 4). We can see that the one-side Lipschitz coefficient $X(t)$ is non-negative, which is different from NDDEs’ (without impulsive perturbations) stability results of Bellen, Zennaro, et al. (See [14] (Theorem 9.4.1) or [24] (Theorem 3.1, Theorem 4.2)).

By Theorem 13, we can obtain that the constructed numerical methods (24)–(27) for nonlinear INDDE (29), furnished by $B{N}_f$-stable continuous Runge–Kutta methods, are asymptotically stable. From Figure 3 and Figure 4, we can roughly see the trend that the distances between the two numerical solutions (obtained from the constructed numerical methods (24)–(27) for INDDE (29), furnished by implicit Euler method or 2-stage Lobatto IIIC method with two different constant initial function 1 and 0.9) become smaller as the time increases.

In

Table 1. The errors between the numerical solutions obtained from (24)–(26) and the exact solution of (28) at $t=10$, when $\alpha (t)={\alpha }_1(t)={\lambda }^{\{t\}}$, $t\ge -1$.

	The Implicit Euler		2-Lobatto IIIC
m	AE	RE	AE	RE
10	3.6581941667 $\times {10}^{-8}$	0.0551236000	3.3993997914 $\times {10}^{-9}$	0.0051223952
20	1.6188740613 $\times {10}^{-8}$	0.0243940486	9.5844940891 $\times {10}^{-10}$	0.0014442422
40	7.5674842099 $\times {10}^{-9}$	0.0114030845	2.5770607279 $\times {10}^{-10}$	3.8832512532 $\times {10}^{-4}$
80	3.6514998468 $\times {10}^{-9}$	0.0055022726	6.7075180094 $\times {10}^{-11}$	1.0107242500 $\times {10}^{-4}$
Ratio	2.1571322845	2.1571322845	3.7026585356	3.7026585356

,

Table 2. The errors between the numerical solutions obtained from (24)–(26) and the exact solution of (28) at $t=10$, when $\alpha (t)={\alpha }_2(t)=1+(\lambda -1)\{t\}$, $t\ge -1$.

	The Implicit Euler		2-Lobatto IIIC
m	AE	RE	AE	RE
10	3.6469927694 $\times {10}^{-8}$	0.0549548115	3.3341478657 $\times {10}^{-9}$	0.0050240702
20	1.6145910077 $\times {10}^{-8}$	0.0243295093	9.2718600641 $\times {10}^{-10}$	0.0013971329
40	7.5491598720 $\times {10}^{-9}$	0.0113754724	2.4224957236 $\times {10}^{-10}$	$3.6503445423\times {10}^{-4}$
80	3.6430871304 $\times {10}^{-9}$	0.0054895959	6.7075212665 $\times {10}^{-11}$	$8.9455329107\times {10}^{-5}$
Ratio	2.1565761938	2.1565761938	3.8346733002	3.8346733002

,

Table 3. The errors between the numerical solutions obtained from (24)–(26) and the exact solution of (28) at $t=10$, when $\alpha (t)={\alpha }_3(t)=-{\{t\}}^2+\lambda \{t\}+1$, $t\ge -1$.

	The Implicit Euler		2-Lobatto IIIC
m	AE	RE	AE	RE
10	3.2928273582 $\times {10}^{-8}$	0.0496180603	3.5224011714 $\times {10}^{-9}$	0.0053077402
20	1.4792658001 $\times {10}^{-8}$	0.0222903577	9.9361388805 $\times {10}^{-10}$	0.0014972299
40	6.9719562429 $\times {10}^{-9}$	0.0105057116	2.6736493834 $\times {10}^{-10}$	4.0287961420 $\times {10}^{-4}$
80	3.3787413432 $\times {10}^{-9}$	0.0050912658	6.9626687974 $\times {10}^{-11}$	1.0491717188 $\times {10}^{-4}$
Ratio	2.1370673472	2.1370673472	3.7004462838	3.7004462838

,

Table 4. The errors between the numerical solutions obtained from (24)–(26) and the exact solution of (29) at $t=5$, when $\alpha (t)={\alpha }_1(t)$.

	The Implicit Euler		2-Lobatto IIIC
m	AE	RE	AE	RE
20	0.0022369766	0.2202504769	5.7299369527 $\times {10}^{-6}$	2.3107308782 $\times {10}^{-4}$
40	0.0011276564	0.1110279231	1.4405875293 $\times {10}^{-6}$	5.8095056092 $\times {10}^{-5}$
80	5.6614685412 $\times {10}^{-4}$	0.0557422526	3.6113985329 $\times {10}^{-7}$	1.4563807896 $\times {10}^{-5}$
160	2.8365495107 $\times {10}^{-4}$	0.0279283826	9.0363875351 $\times {10}^{-8}$	3.6441342859 $\times {10}^{-6}$
Ratio	1.9904827766	1.9904827766	3.9876695906	3.9876695906

,

Table 5. The errors between the numerical solutions obtained from (24)–(26) and the exact solution of (29) at $t=5$, when $\alpha (t)={\alpha }_2(t)$.

	The Implicit Euler		2-Lobatto IIIC
m	AE	RE	AE	RE
20	1.9815130517 $\times {10}^{-4}$	0.0195097711	2.3187856183 $\times {10}^{-5}$	9.4091835401 $\times {10}^{-4}$
40	1.0076686770 $\times {10}^{-4}$	0.0099214008	5.9673597828 $\times {10}^{-6}$	2.4210841877 $\times {10}^{-4}$
80	5.0814463184 $\times {10}^{-5}$	0.0050031391	1.5136126717 $\times {10}^{-6}$	6.1405921789 $\times {10}^{-5}$
160	2.5515894339 $\times {10}^{-5}$	0.0025122684	3.8502245644 $\times {10}^{-7}$	1.5462538456 $\times {10}^{-5}$
Ratio	1.9803170077	1.9803170077	3.9334584227	3.9334584227

and

Table 6. The errors between the numerical solutions obtained from (24)–(26) and the exact solution of (29) at $t=5$, when $\alpha (t)={\alpha }_3(t)$.

	The Implicit Euler		2-Lobatto IIIC
m	AE	RE	AE	RE
20	0.0046567801	0.4585012456	1.5888036813 $\times {10}^{-4}$	0.0064072219
40	0.0024075383	0.2370434701	4.2949208184 $\times {10}^{-5}$	0.0017320271
80	0.0012240906	0.1205225617	1.1161651179 $\times {10}^{-5}$	4.5011964909 $\times {10}^{-4}$
160	6.1718429346 $\times {10}^{-4}$	0.0607672605	2.8446726005 $\times {10}^{-6}$	1.1471806565 $\times {10}^{-4}$
Ratio	1.9614646923	1.9614646923	3.8236303912	3.8236303912

, AE denotes the absolute errors between the numerical solutions and the exact solution of INDDEs. Similarly, RE denotes the relative errors between the numerical solutions and the exact solution of INDDEs. As is well known, when the step size is halved, the global errors of the numerical methods of p-order convergence will become approximately the same as the original times. We can see from the tables that the average ratio of the absolute errors (or relative errors) between the numerical solutions obtained from (24)–(26), furnished by implicit Euler method and the exact solution of (28), is close to 2 (the reciprocal of $\frac{1}{2}$) and the average ratio of the absolute errors (or relative errors) between the numerical solutions obtained from (24)–(26), furnished by 2-stage Lobatto IIIC method and the exact solution of (29), is close to 4 (the reciprocal of $\frac{1}{2^2}$) when the step size doubles and three different kinds of the transformations are used. Hence, Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 roughly show that the constructed method, furnished by backward Euler method, is convergent of order 1 and by 2-stage Lobatto IIIC method is convergent of order 2 when the different transformations are chosen.

5. Conclusions and Future Works

In this paper, some new different asymptotical stability criteria are given for the exact solutions of a class of nonlinear INDDEs, based on the following idea: first the problems of the stability and asymptotical stability of INDDEs are transformed into the problems of NDDEs without impulsive perturbations, and then transformed into the problems of ordinary differential equations with a forcing term. Based on the above idea, some new sufficient conditions for the stability and asymptotical stability of the exact solutions of INDDEs are obtained and the numerical methods for INDDEs are constructed. Moreover, the numerical method is asymptotically stable if the corresponding continuous Runge–Kutta methods are $B{N}_f$-stable, under these different sufficient conditions.

In the future, we will study the asymptotical stability of more general INDDEs with the following characteristics: the size of the delay in continuous dynamics can be flexible, and there is no magnitude between the delay in continuous flow and impulsive delay. Finally, we propose the discontinuous Galerkin method (see [32]) as a stable and highly efficient alternative for solving INDDEs. Its application to these equations holds substantial potential and could produce promising outcomes.