Solutions of Time Fractional (1 + 3)-Dimensional Partial Differential Equations by the Natural Transform Decomposition Method (NTDM)
Abstract
:1. Introduction
2. Basic Definitions and Properties of the Natural Transform Method (NTM)
3. Natural Transform and Decomposition Method (NTDM)
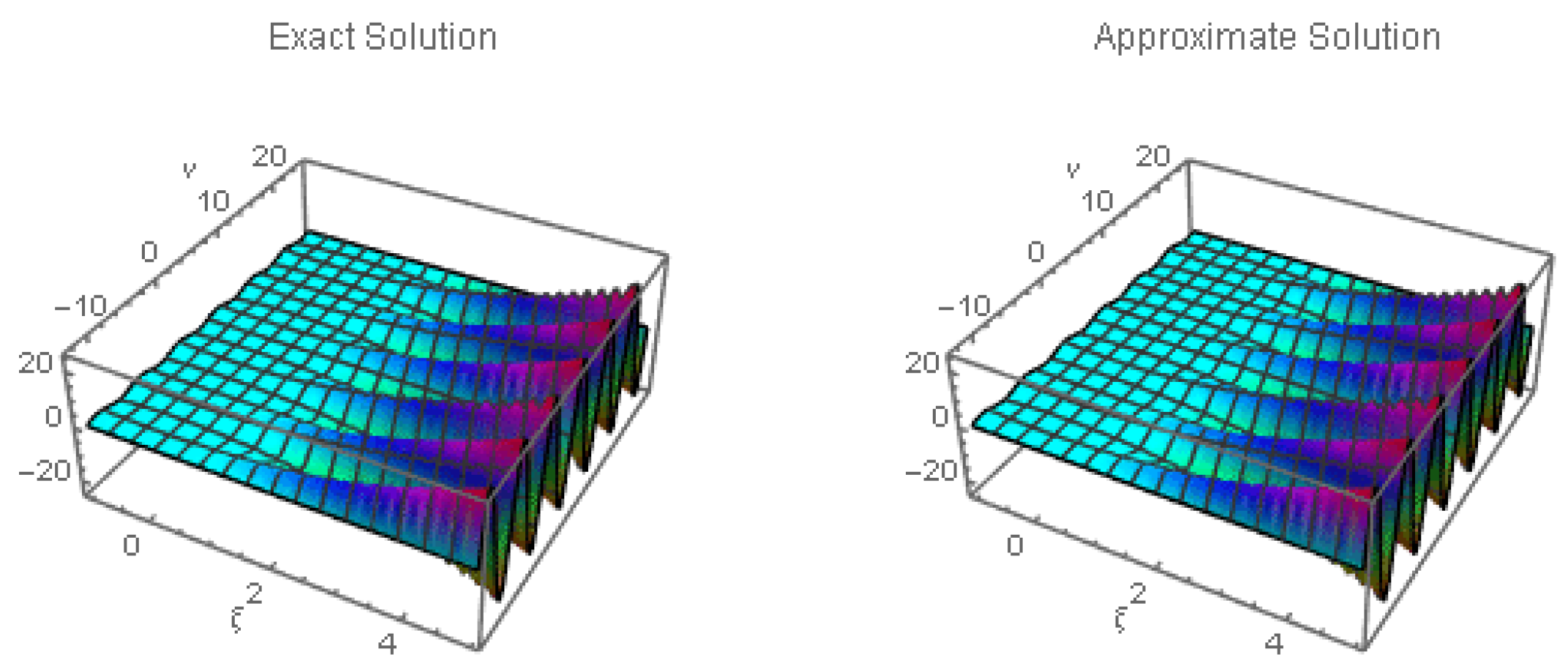
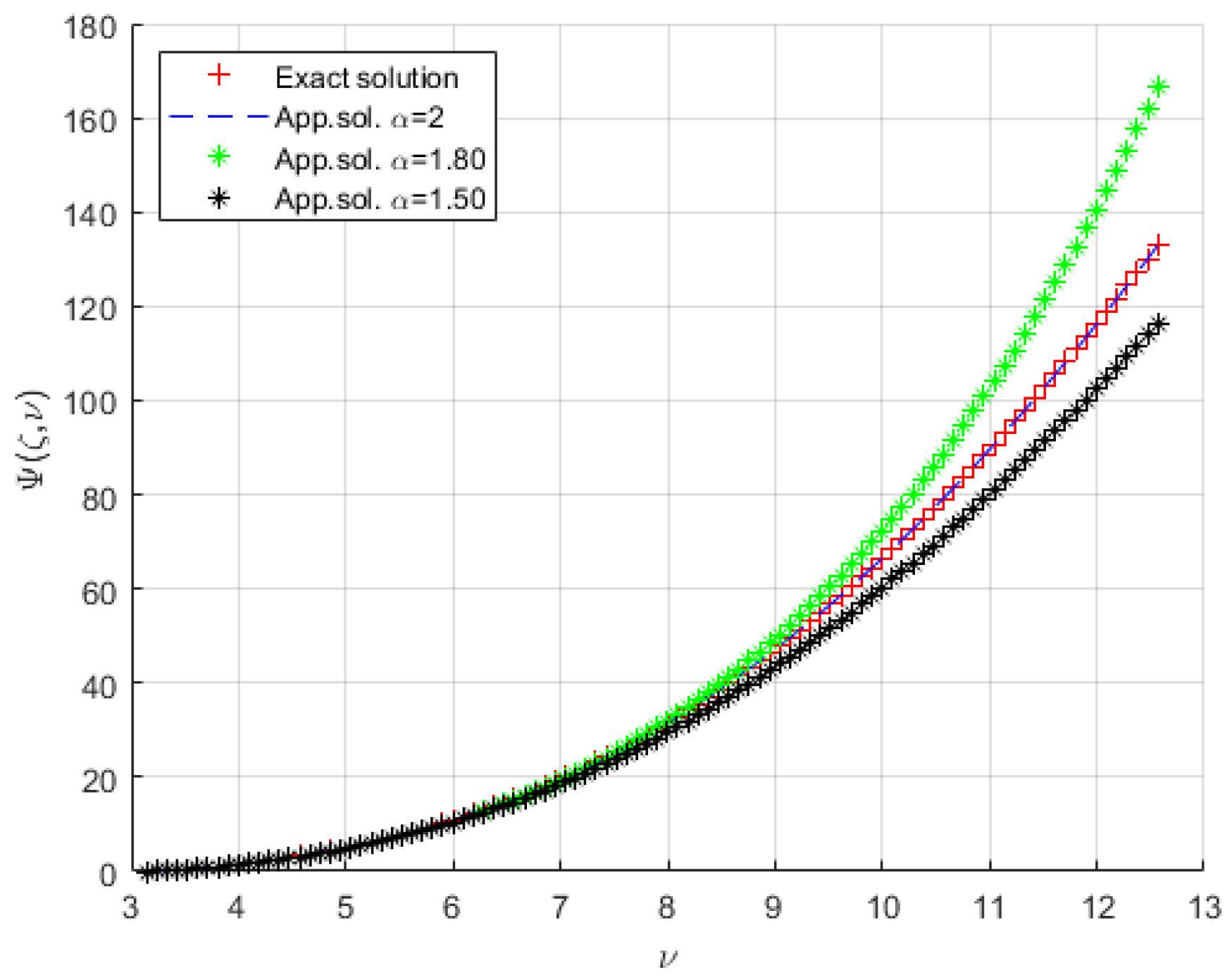
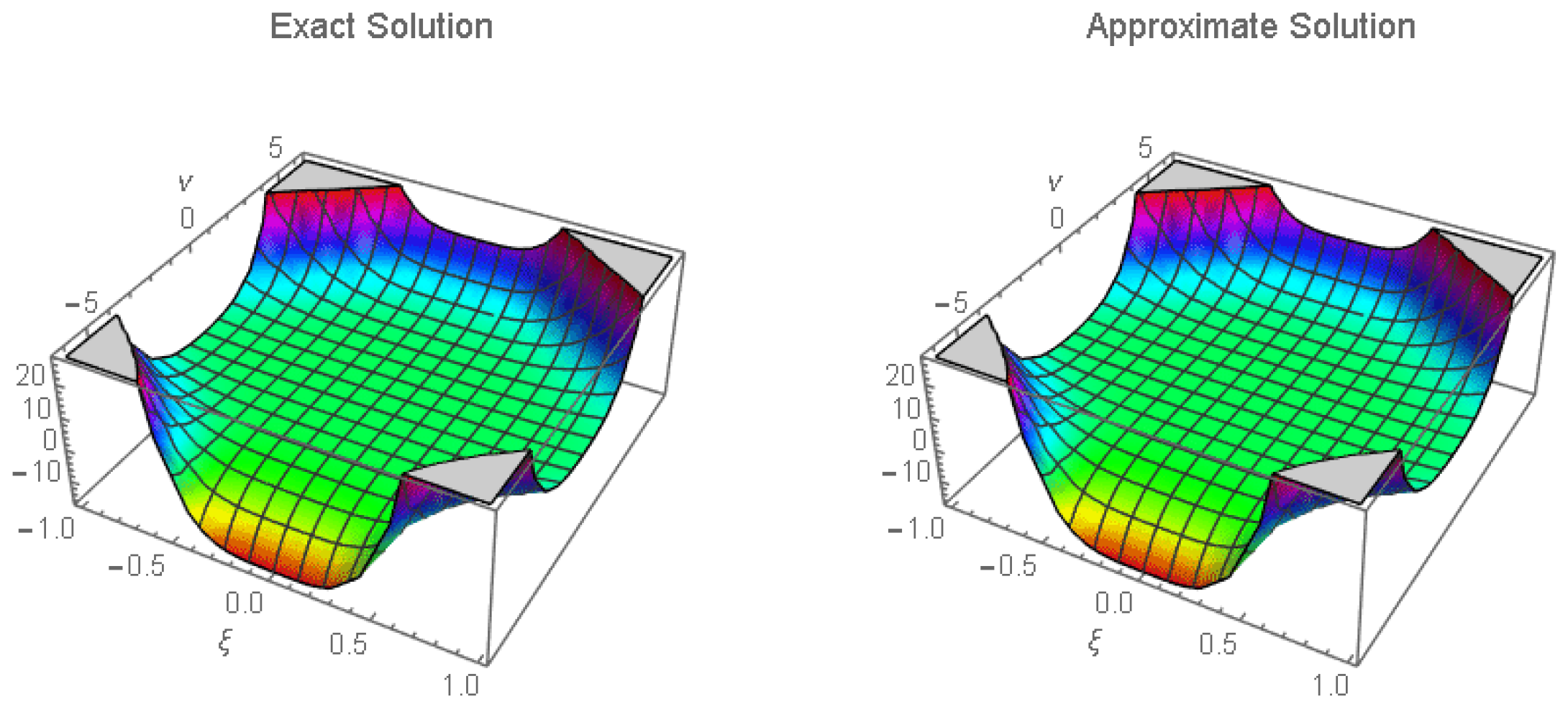
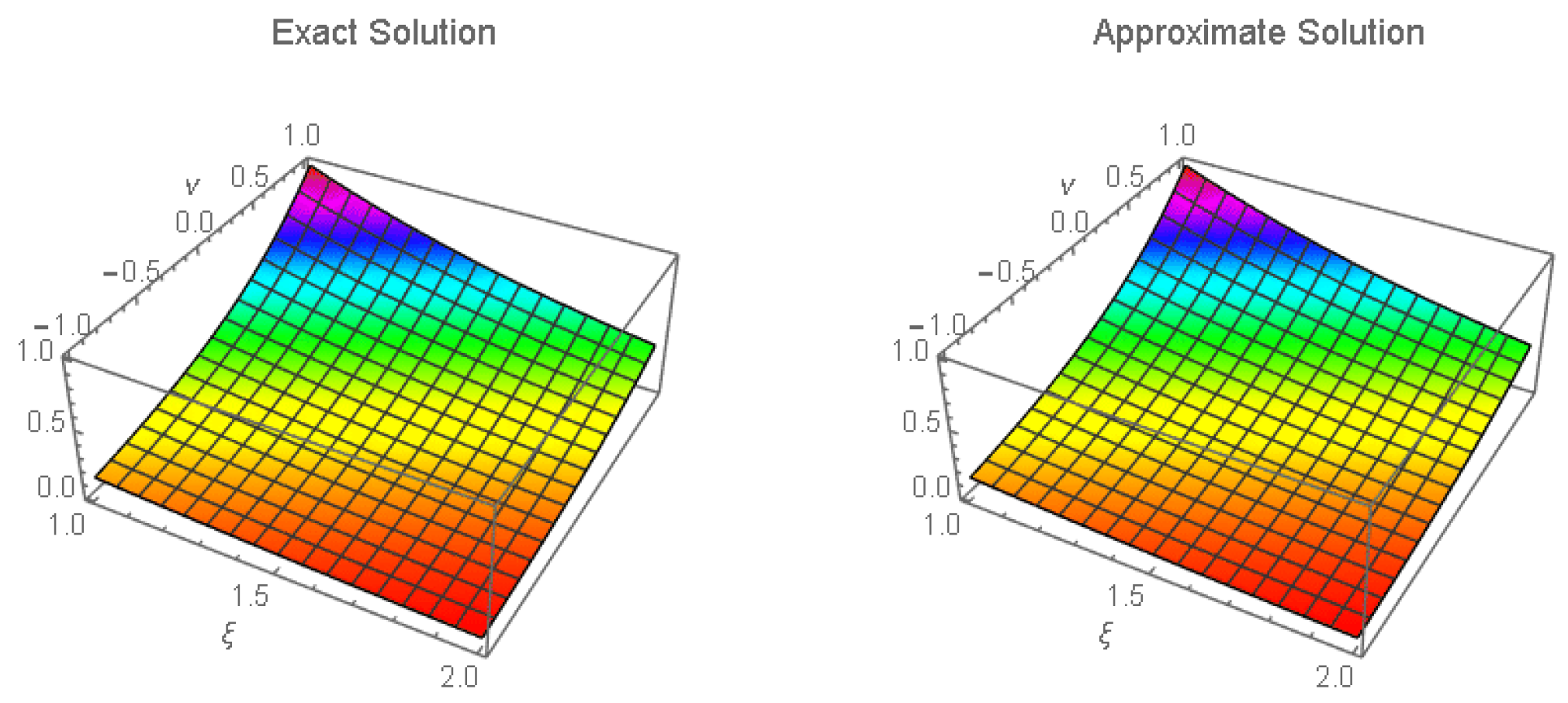
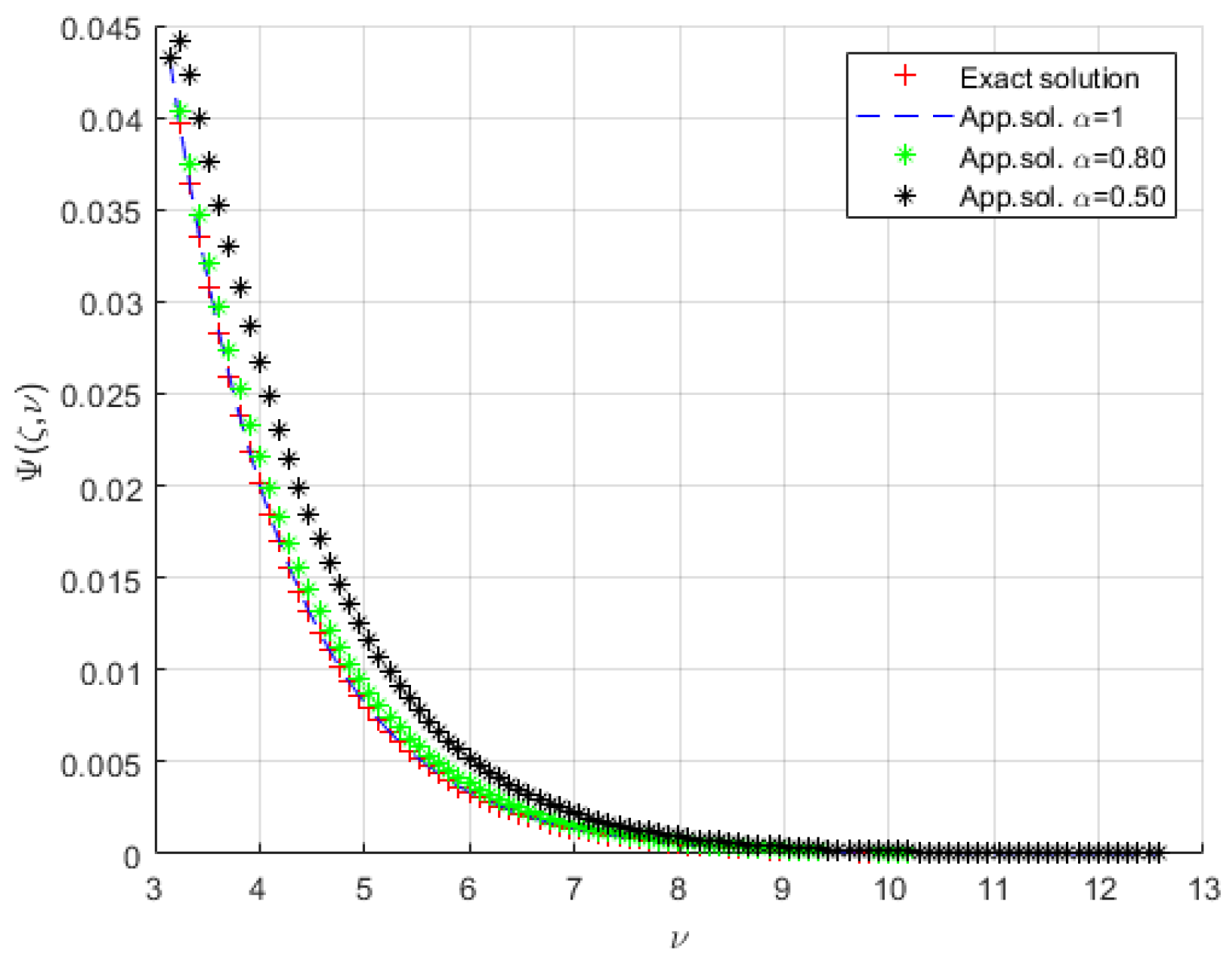
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Caputo, M. Elasticitae Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Caputo, M.; Mainardi, F. Linear models of dissipation in anelastic solids. Riv. del Nuovo Cimento. 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Garg, M.; Manohar, P. Numerical solution of fractional diffusion-wave equation with two space variables by matrix method. Fract. Calc. Appl. Anal. 2019, 13, 191–207. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Rawashdeh, M. An efficient approach for time-fractional damped Burger and time-sharma-tasso-Olver equations using the FRDTM. Appl. Math. Inf. Sci. 2015, 9, 1239–1246. [Google Scholar]
- Patel, T.; Meher, R. Thermal Analysis of porous fin with uniform magnetic field using Adomian decomposition Sumudu transform method. Nonlinear Eng. 2017, 6, 191–200. [Google Scholar] [CrossRef]
- Patel, T.; Patel, H.; Meher, R. Analytical study of atmospheric internal waves model with fractional approach. JOES 2022. [Google Scholar] [CrossRef]
- Omran, M.; Kiliçman, A. Natural transform of fractional order and some properties. Cogent Math. 2016, 3, 1251874. [Google Scholar] [CrossRef]
- Kazem, S. Exact solution of some linear fractional differential equations by Laplace transform. Int. J.Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Odibat, Z.; Momani, S.; Erturk, V.S. Generalized differential transform method: Application to differential equations of fractional order. Appl. Math. Comput. 2008, 197, 467–477. [Google Scholar] [CrossRef]
- Inc, M. The approximate and exact solutions of the space- and time-fractional Burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 2008, 345, 476–484. [Google Scholar] [CrossRef]
- Garg, M.; Sharma, A. Solution of space-time fractional telegraph equation by Adomian decomposition method. J. Inequal. Spec. Funct. 2011, 2, 1–7. [Google Scholar]
- Ray, S.S.; Bera, R.K. An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl. Math. Comput. 2005, 167, 561–571. [Google Scholar]
- Rawashdeh, M.; Solving, M.S. Nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
- Rawashdeh, M.S.; Al-Jammal, H. New approximate solutions to fractional nonlinear systems of partial differential equations using the FNDM. Adv. Differ. Equ. 2016, 2016, 235. [Google Scholar] [CrossRef]
- Rawashdeh, M.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Cherif, M.H.; Ziane, D.; Belghaba, K. Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Stud. 2018, 25, 753–764. [Google Scholar]
- Eltayeb, H.; Abdalla, Y.T.; Bachar, I.; Khabir, M.H. Fractional telegraph equation and its solution by natural transform decomposition method. Symmetry 2019, 11, 334. [Google Scholar] [CrossRef]
- Sarwar, S.; Alkhalaf, S.; Iqbal, S.; Zahid, M.A. A note on optimal homotopy asymptotic method for the solutions of fractional order heat- and wave-like partial differential equations. Comput. Math. Appl. 2015, 70, 942–953. [Google Scholar] [CrossRef]
- Katatbeh, Q.D.; Belgacem, F.B.M. Applications of the Sumudu transform to fractional differential equations. Nonlinear Stud. J. 2011, 18, 99–112. [Google Scholar]
- Kumar, D.; Singh, J.; An, K.A. Efficient approach for fractional Harry Dym equation by using Sumudu transform. Abstr. Appl. Anal. 2013, 2013, 608943. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Belgacem, F.B.M.; Silambarasan, R. Theory of natural transform. Math. Eng. Sci. Aerosp. (MESA) 2012, 3, 99–124. [Google Scholar]
- Marin, M.; Marinescu, C. Thermoelasticity of initially stressed bodies, asymptotic equipartition of energies. Int. J. Eng. Sci. 1998, 36, 73–86. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Al-Jammal, H. Theories and Applications of the Inverse Fractional Natural Transform Method. Adv. Differ. 2018, 2018, 222. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kumar, S.; Rashidi, M. New analytical method for gas dynamics equation arising in shock fronts. Comput. Phys. Commun. 2014, 185, 1947–1954. [Google Scholar] [CrossRef]
- Baccouch, M.; Temimi, H. A high-order space-time ultra-weak discontinuous Galerkin method for the second-order wave equation in one space dimension. J. Comput. Appl. Math. 2021, 389, 113331. [Google Scholar] [CrossRef]



| Exact | Absolute Error | |||||
|---|---|---|---|---|---|---|
| 0.5 | 0.0299640962 | 0.0293796164 | 0.0280835396 | 0.0299640962 | 0 | |
| 0.25 | 0.75 | 0.0513947958 | 0.0452272241 | 0.0384946707 | 0.0426024225 | 0.0087923732 |
| 1 | 0.0734500746 | 0.0501614436 | 0.0460926237 | 0.0010907754 | 0.0723592991 | |
| 0.5 | 0.1302738263 | 0.1175184656 | 0.1123341583 | 01198563846 | 0.0104174417 | |
| 0.50 | 0.75 | 0.2055791830 | 0.1809088961 | 0.153976827 | 0.1704096900 | 0.035169493 |
| 1 | 0.2938002984 | 0.2006457422 | 0.184370449 | 0.0043631016 | 0.2894371968 | |
| 0.5 | 0.5210953055 | 0.4700738629 | 0.4493366329 | 0.4794255386 | 0.0416697669 | |
| 1 | 0.75 | 0.8223167320 | 0.7236355851 | 0.6159147310 | 0.6816387600 | 0.140677972 |
| 1 | 1.175201193 | 0.8025829685 | 0.7374819794 | 0.0174524064 | 1.157748787 |
| Exact | Absolute Error | |||||
|---|---|---|---|---|---|---|
| 0.5 | 0.0064403174 | 0.0066750912 | 0.0072013111 | 0.0064403174 | 1 × 10 | |
| 0.25 | 0.75 | 0.0082695312 | 0.0084681072 | 00096675856 | 0.0082695313 | 6.7 × 10 |
| 1 | 0.0106182872 | 0.0074431273 | 0.0128345819 | 0.0106182883 | 1.19 × 10 | |
| 0.5 | 0.1030451762 | 0.1070299290 | 0.1152209783 | 0.0130450794 | 9.68 × 10 | |
| 0.50 | 0.75 | 0.1323130518 | 0.0885159904 | 0.1546813706 | 0.1323125010 | 5.508 × 10 |
| 1 | 0.1698925954 | 0.1190900375 | 0.2053533103 | 0.1698926143 | 1.89 × 10 | |
| 0.5 | 1.648721270 | 1.708823359 | 1.843435654 | 1.648721270 | 0 | |
| 1 | 0.75 | 2.117000000 | 2.232441653 | 2.474901931 | 2.117000017 | 1.7 × 10 |
| 1 | 2.718281526 | 1.905440600 | 3.285652963 | 2.718281828 | 3.02 × 10 |
| Exact | Absolute Error | |||||
|---|---|---|---|---|---|---|
| 0.5 | 0.386654 × 10 | 0.481388 × 10 | 0.103833 × 10 | 0.386668 × 10 | 1.39203 × 10 | |
| 0.25 | 0.75 | 0.665619 × 10 | 0.841673 × 10 | 0.157573 × 10 | 0.665783 × 10 | 1.647378 × 10 |
| 1 | 0.102321 × 10 | 0.129654 × 10 | 0.219436 × 10 | 1.024175 × 10 | 9.62711 × 10 | |
| 0.5 | 0.0001583735 | 0.0001971769 | 0.0004253023 | 1.583792 × 10 | 5.7017 × 10 | |
| 0.50 | 0.75 | 0.0002726376 | 0.0003447496 | 0.0006454195 | 2.727050 × 10 | 6.74765 × 10 |
| 1 | 0.0004191080 | 0.0005869575 | 0.0008988117 | 4.195023 × 10 | 3.9432705 × 10 | |
| 0.5 | 0.6486979167 | 0.8076367013 | 1.742038385 | 0.6487212707 | 2.3354 × 10 | |
| 1 | 0.75 | 1.116723633 | 1.412094400 | 2.643638290 | 1.117000017 | 2.76384 × 10 |
| 1 | 1.716666667 | 2.175242941 | 3.681533056 | 1.718281828 | 1.615161 × 10 |
| Exact | Absolute Error | |||||
|---|---|---|---|---|---|---|
| 0.5 | 1.284007229 | 1.501210297 | 2.135501642 | 1.284025417 | 1.8188 × 10 | |
| 0.25 | 0.75 | 1.648506023 | 1.968100996 | 2.837668354 | 1.648721271 | 2.15248 × 10 |
| 1 | 2.115742127 | 2.553826345 | 3.645981610 | 2.117000017 | 1.25789 × 10 | |
| 0.5 | 0.999985352 | 1.169143755 | 1.663130351 | 1 | 1.415448 × 10 | |
| 0.50 | 0.75 | 1.283857782 | 1.532758597 | 2.209978336 | 1.284025417 | 1.67635 × 10 |
| 1 | 1.647741626 | 1.988921957 | 2.839493333 | 1.648721271 | 9.79645 ×10 | |
| 0.5 | 0.6065220684 | 0.7091215329 | 1.008739549 | 0.6065306597 | 8.5913 ×10 | |
| 1 | 0.75 | 0.7786991072 | 0.9296650831 | 1.340419618 | 0.7788007831 | 1.01659 × 10 |
| 1 | 0.9994058152 | 1.206342147 | 1.722239764 | 1 | 5.941848 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gadallah, M.R.; Eltayeb, H. Solutions of Time Fractional (1 + 3)-Dimensional Partial Differential Equations by the Natural Transform Decomposition Method (NTDM). Axioms 2023, 12, 958. https://doi.org/10.3390/axioms12100958
Gadallah MR, Eltayeb H. Solutions of Time Fractional (1 + 3)-Dimensional Partial Differential Equations by the Natural Transform Decomposition Method (NTDM). Axioms. 2023; 12(10):958. https://doi.org/10.3390/axioms12100958
Chicago/Turabian StyleGadallah, Musa Rahamh, and Hassan Eltayeb. 2023. "Solutions of Time Fractional (1 + 3)-Dimensional Partial Differential Equations by the Natural Transform Decomposition Method (NTDM)" Axioms 12, no. 10: 958. https://doi.org/10.3390/axioms12100958






