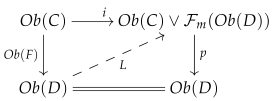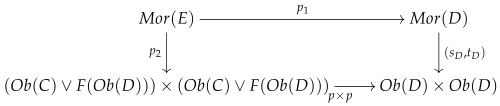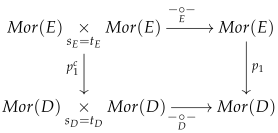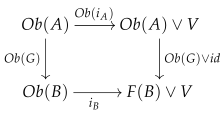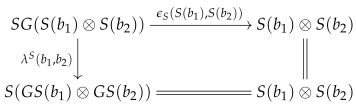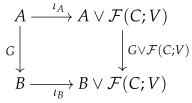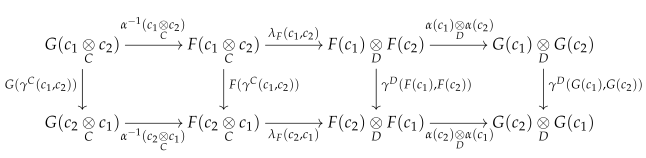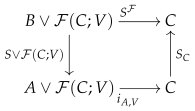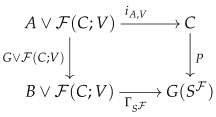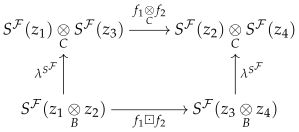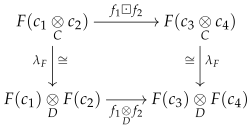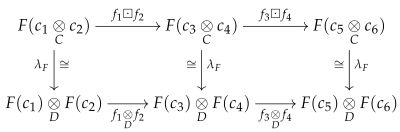1. Introduction
A
permutative category is a symmetric monoidal category whose associativity and unit natural isomorphisms are identities. Permutative categories have generated significant interest in topology. An infinite loop space machine was constructed on permutative categories in [
1]. A
K-theory (multi-)functor from a
multicategory of permutative categories into a symmetric monoidal category of symmetrical spectra, which preserves the multiplicative structure, was constructed in [
2]. In [
3], the
K-theory of [
2] was enhanced to a lax symmetric monoidal functor. It was shown in [
4] that permutative categories model connective spectra.
Every symmetric monoidal category is equivalent (by a symmetric monoidal functor) to a permutative category. The category of symmetric monoidal categories
does NOT have a model category structure; however, its subcategory of permutative categories and strict symmetric monoidal functors
carries a model category structure. The category
is isomorphic to the category of algebras over the (categorical) Barrat–Eccles operad. Using this fact, the model category structure follows from [
5] and ([
6], Thm. 4.5). This model category structure is called the
natural model category structure of permutative categories.
The main objective of this paper is to identify a class of cofibrations in the natural model category
called
free cofibrations such that every cofibration in
is a retract of a free cofibration. A desirable property of free cofibrations is that cobase changes along a free cofibration preserve acyclic fibrations in the natural model category
. This property allows us to prove our main result that the natural model category
is
left proper. Our primary motivation for proving the main result of this paper is the existence of left Bousfield localizations in combinatorial left-proper model categories ([
7], Thm. 4.7). The main result of this paper has allowed us to construct two left Bousfield localizations of the natural model category
which are the model category of (permutative) compact closed categories
[
8] and the model category of (permutative) Picard groupoids
[
9].
Finally in
Appendix A we present a construction of
Gabriel Factorization of a unital symmetric monoidal functor between permutative categories. Our construction factors a unital symmetric monoidal functor into an essentially surjective strict symmetric monoidal functor followed by a fully faithful unital symmetric monoidal functor.
Remark 1. Some proofs in this paper assume standard results in homotopical algebra. We would like to provide the uninformed reader a list of references to standard textbooks on the subject: [10,11,12]. 2. Free Cofibrations in
In this section, we define a class of maps called
free cofibrations in the natural model category of permutative categories
. We show that a strict symmetric monoidal functor is a cofibration in
if and only if it is a retract of a free cofibration. A characterization of cofibrations in
was formulated purely in terms of object functions (which are monoid homomorphisms) of the underlying strict symmetric monoidal functor in [
13]. In order to define free cofibrations, we will start by reviewing some basic notions of permutative categories:
Definition 1. A symmetric monoidal category is called a permutative category or a strict symmetric monoidal category if it is strictly associative and strictly unital.
Remark 2. A permutative category is an internal category in the category of monoids.
We recall that the forgetful functor has a left adjoint .
Definition 2. A monoid M is called a free monoid if there exists a (dotted) lifting monoid homomorphism whenever we have the following (outer) commutative diagram of monoid homomorphisms:where p is a surjective monoid homomorphism, and * is a zero object in the category of monoids. Definition 3. A free cofibration of permutative categories is a (strict symmetric monoidal) functor whose object function is the inclusion , where M is a free monoid and the coproduct is taken in the category of monoids.
The next proposition presents the desired characterization of cofibrations:
Proposition 1. A strict symmetric monoidal functor is a cofibration in if and only if it is a retract of a free cofibration by a map that fixes C.
Proof. Let us first assume that F is a retract of a free cofibration . We observe that the object function of a free cofibration has the left lifting property with respect to all surjective monoid homomorphisms; therefore, each free cofibration is a cofibration in . A retract of a cofibration is again a cofibration. Thus, F is a cofibration in .
Conversely, let us assume that
F is a cofibration in
. We have the following (outer) commutative diagram in the category of monoids
where
is the free monoid generated by the set
,
i is the inclusion into the coproduct, and
. The summand
is the counit of the reflection:
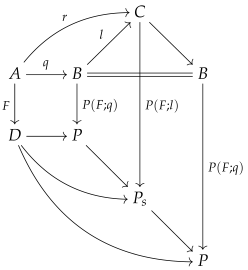
Since the right vertical homomorphism of monoids is surjective and F is a cofibration by assumption, there therefore exists a (dotted) lifting homomorphism L which makes the whole diagram commutative. Thus, is a retract of the inclusion i in the category of monoids. We will construct a strict symmetric monoidal functor whose object function is the inclusion i and show that F is a retract of I. We begin by constructing the category E:
The object set of E is . The morphism monoid of E is defined by the following pullback square in the category of monoids:
We will denote the projection map
in the above Cartesian square by
. This pair will be source and target maps for the proposed category
E. The projection map
in the above Cartesian diagram restricts to a map between the set of composable arrows in
E and
D:
Now, we observe the composite factors through as follows:
The map
in the above commutative diagram provides the composition of category
E. Finally, we define the symmetry natural transformation of
E as follows:
for each pair of objects
. This defines a permutative category
, where the tensor product is uniquely determined by the monoid structures on
and
.
The commutative diagrams (
1) and (
2) and the definition of the symmetry natural transformation (
3) together imply that there is a strict symmetric monoidal functor
whose object homomorphism is
p and morphism homomorphism is
. Further,
P is surjective on objects and also fully faithful. This implies that
P is an acyclic fibration in the natural model category
.
Now, we construct the free cofibration
mentioned above. The object homomorphism of
I is the inclusion
. The morphism homomorphism of
I is defined as follows:
In other words, for each morphism . Now, we have the following (outer) commutative diagram in :
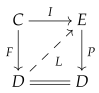
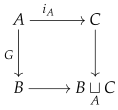
Since F is a cofibration and P is an acyclic fibration in the natural model category , there exists a (dotted) lifting arrow L which makes the entire diagram commutative. This implies that F is a retract of the free cofibration I in the natural model category . □
3. Left Properness of the Natural Model Category
In this section we show that the natural model category of permutative categories is left proper. We recall that a model category is left proper if the cobase change of a weak-equivalence along a cofibration is again a weak-equivalence. We will first show that the cobase change of a weak-equivalence along a free cofibration is a weak-equivalence. Using this intermediate result, we will prove the left properness of .
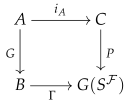
Let
be an acyclic fibration in
and
be a free cofibration. Therefore, the object monoid of
C can be written as a coproduct
, where
V is a free monoid. We observe that the following commutative square is co-Cartesian:
We will construct the following pushout square in :
A strict symmetric monoidal functor
is an acyclic fibration in
if and only if there exists a unital symmetric monoidal section ([
13], Cor. 3.5(3))
such that
and a monoidal natural isomorphism
. Let us fix such a section
and natural isomorphism
.
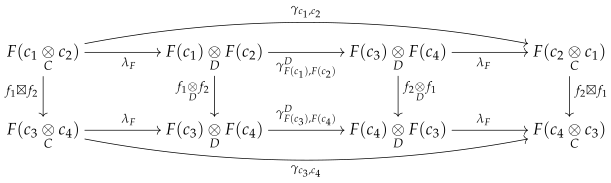
Remark 3. The above characterization of acyclic fibrations implies that is a left-adjoint-right-inverse of . This means that is a counit of an adjoint equivalence whose unit is the identity natural transformation. This further implies that . In other words, for each , we have the following equality: Since it follows from ([13], Cor. 3.5(3)) that the unit natural transformation η is the identity, . Remark 4. Let be a pair of objects in B. Since is a monoidal natural transformation, we have the following commutative diagram:
This further implies that The unital symmetric monoidal functor
S gives us the following unital symmetric monoidal functor:
where
is the full permutative subcategory of
C whose object set is the (free) monoid
V, and the notation
is an abbreviation for the coproduct of functors
. We observe that
is a section of the strict symmetric monoidal functor
i.e.,
. Moreover, we obtain a monoidal natural isomorphism
Hence, the functor
is an acyclic fibration in the natural model category
by ([
13], Cor. 3.5(3)).
We observe the free cofibration
factors as follows:
where
is the inclusion into the coproduct, and
is the unique map induced by the inclusions
and
Remark 5. The following commutative square is a co-Cartesian:
We observe that the object monoid of
C is the same as the object monoid of
, namely the coproduct
. This implies that for each
there is the following isomorphism in
C:
Now, it follows from ([
13], Prop. 2.7) that there exists a (uniquely defined) functor
and a natural isomorphism
. The functor
is defined on objects as follows:
The following lemma now tells us that is a unital symmetric monoidal functor, and is a monoidal natural isomorphism:
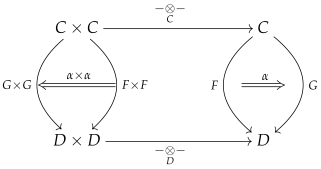
Lemma 1. Given a unital oplax symmetric monoidal functor between two symmetric monoidal categories C and D, a functor and a unital natural isomorphism , there is a unique natural isomorphism which enhances G to a unital oplax symmetric monoidal functor such that α is a monoidal natural isomorphism. If is unital symmetric monoidal, then so is .
Proof. We consider the following diagram:
This diagram helps us define a composite natural isomorphism
as follows:
This composite natural isomorphism is the unique natural isomorphism which makes
a unital monoidal natural isomorphism. Now, we have to check that
is a unital monoidal natural isomorphism with respect to the above definition. Clearly,
is unital because both
and
are unital natural isomorphisms. We first check the symmetry condition ([
13], Defn. 2.4 OL. 2). This condition is satisfied because the following composite diagram commutes
The condition ([
13], Defn. 2.4 OL. 3) follows from the following equalities
If
is a symmetric monoidal functor, then so is
because (
6) is a natural isomorphism. □
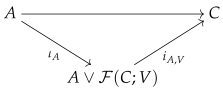
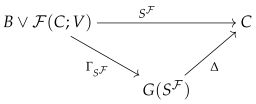
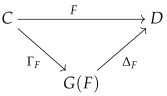
The section provides us with a unital symmetric monoidal functor which we denote by . The unital symmetric monoidal functor has the following Gabriel factorization:
By Lemma A1, is a permutative category structure. In addition, by the same lemma, is a strict symmetric monoidal functor.
Remark 6. The following diagram of unital symmetric monoidal functors is commutative:
The above commutative diagram implies that for each object , .
We claim that there exists a strict symmetric monoidal functor
such that the following diagram, in
, is co-Cartesian:
where
. The object function of the functor
P is the monoid homomorphism
For any pair of objects
, we observe the following equality:
Now, we define the morphism function of
P as follows:
where
f is a morphism in
C. The functoriality of
P follows from that of
.
The object function of
P is a monoid homomorphism; therefore,
for each pair of objects
. The following commutative diagram shows that
for each pair of maps
:
Thus, we have defined a strict symmetric monoidal functor P which is fully faithful. Further, each object of is isomorphic to one in the image of P. Thus, P is an equivalence of categories.
Proposition 2. The commutative square (7) is co-Cartesian. Proof. In order to show that (
7) is co-Cartesian, it is sufficient to show that the following commutative square is co-Cartesian in light of factorization (
4) and Remark 5:
We will show that whenever we have the following (outer) commutative diagram, there exists a unique dotted arrow
L which makes the whole diagram commutative in
:
Since
is the identity, the object homomorphism
has to be the same as
. In order to make the diagram commutative, we define
. The morphism function of
L is defined as follows:
for each pair of objects
. This defines a functor
L which makes the diagram above commutative (in
). In order to verify that
L is a strict symmetric monoidal functor, it is sufficient to show that for each pair of maps
,
in
,
We recall that the map
is defined by the following commutative diagram:
Since
R is a strict symmetric monoidal functor,
. Now, it sufficient to show that
in order to establish the equalities in (
8). We observe that
. Since
is an acyclic fibration, it follows from Remark 4 that
. Since
, it follows that
. The uniqueness of the object functor of
L is obvious. The uniqueness of the morphism homomorphism of
L can be easily checked. □
The main objective of this section is to show that the natural model category is left proper. The next lemma serves as a first step in proving the main result. The lemma follows from the above discussion:
Lemma 2. In the natural model category , a pushout of a weak-equivalence along a free cofibration is a weak-equivalence.
Proof. In light of the facts that each weak equivalence in a model category can be factored as an acyclic cofibration followed by an acyclic fibration and acyclic cofibrations are closed under cobase change, it is sufficient to see that the cobase change of an acyclic fibration is a weak-equivalence. This follows from the discussion above. □
Now, we state and prove the main result of this paper:
Theorem 1. The natural model category of permutative categories is a left proper model category.
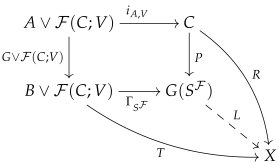
Proof. We will show that a pushout
of a weak equivalence
in
along a cofibration
in
is a weak-equivalence. We consider the following commutative diagram:
Since F is a cofibration, by Proposition 1 there exists a free cofibration such that F is a retract of r by a map that fixes A. The top left commutative square in the above diagram is co-Cartesian. The map is a pushout of F along the free cofibration r and therefore a weak-equivalence by Lemma 2. Now, the result follows from the observation that the diagonal composite in the above diagram is the identity map and the commutativity of the above diagram. □