Automatic Sleep Staging Based on Single-Channel EEG Signal Using Null Space Pursuit Decomposition Algorithm
Abstract
1. Introduction
- (1)
- An automatic sleep scoring method based on single-channel EEG is proposed.
- (2)
- A new signal processing technique, NSP decomposition, is used for sleep staging.
- (3)
- The effectiveness of this method is verified by statistical analysis and graphical analysis.
- (4)
- Compared with the existing schemes, the performance of this scheme is promising.
- (5)
- The automation of the classification method avoids the manual time-consuming nature and subjectivity of scoring.
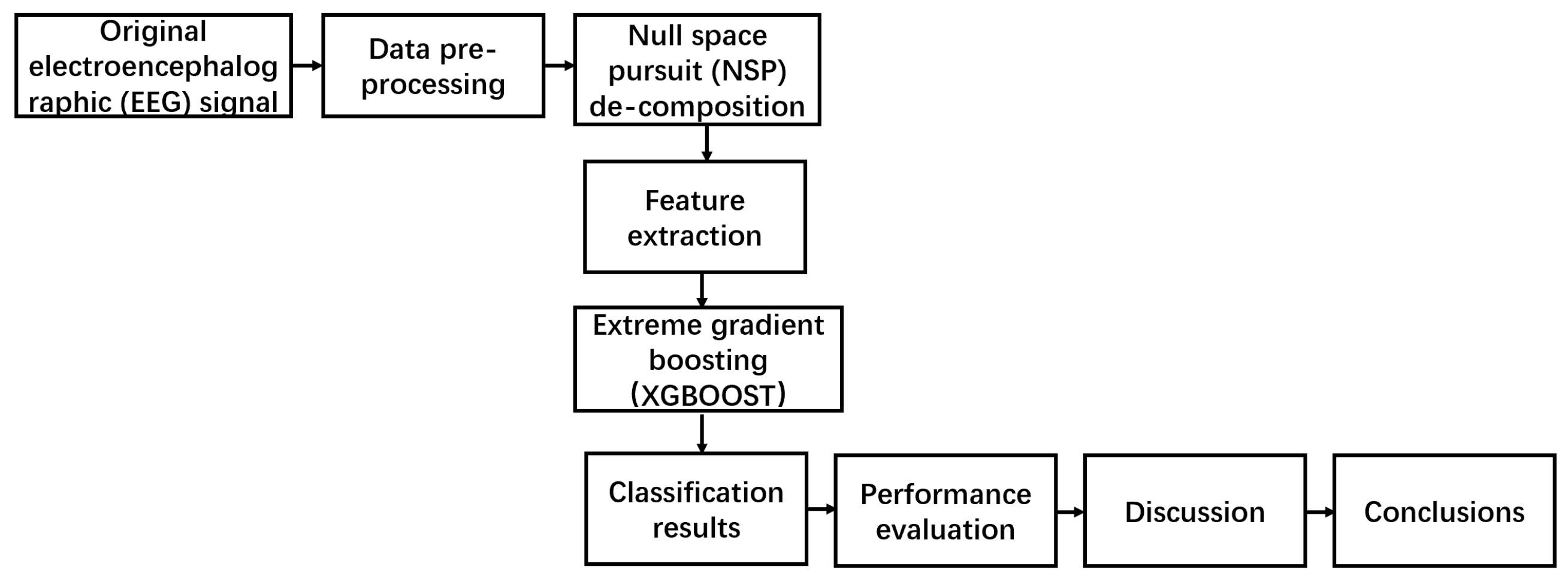
2. Materials and Methods
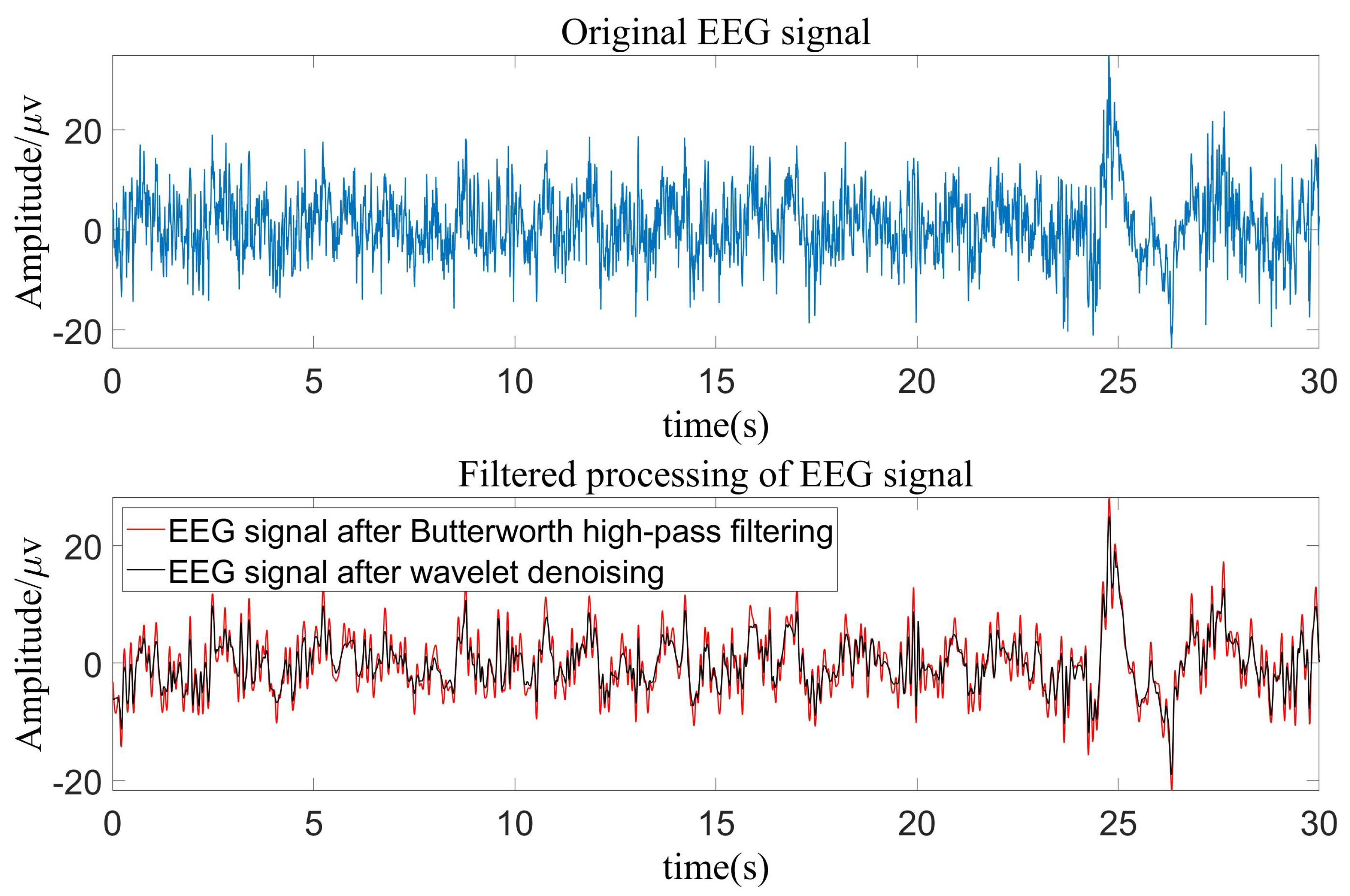
2.1. Datasets and Data Preprocessing
2.2. Methods
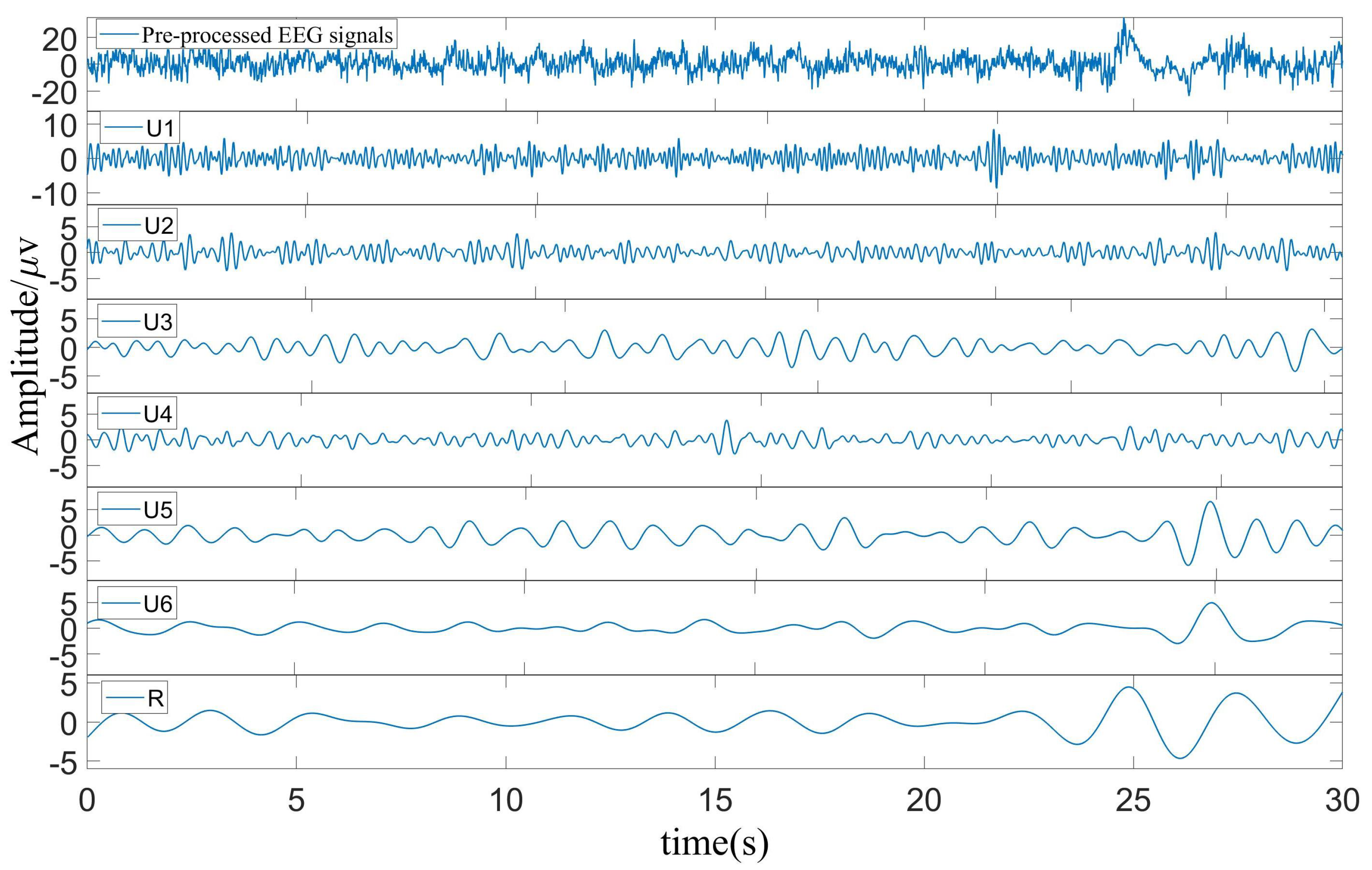
2.2.1. NSP Algorithms
2.2.2. Feature Extraction
2.2.3. Classification Algorithms
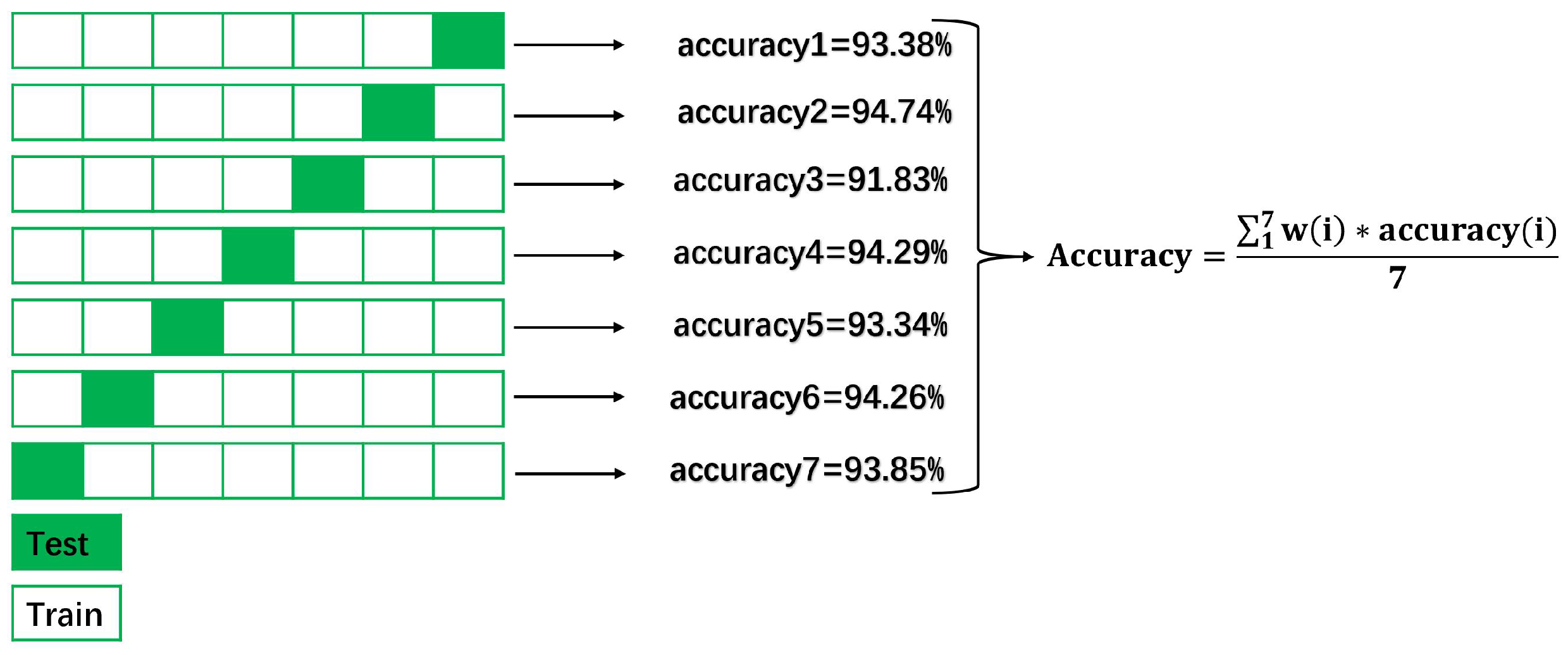
2.2.4. Model Evaluation
3. Results
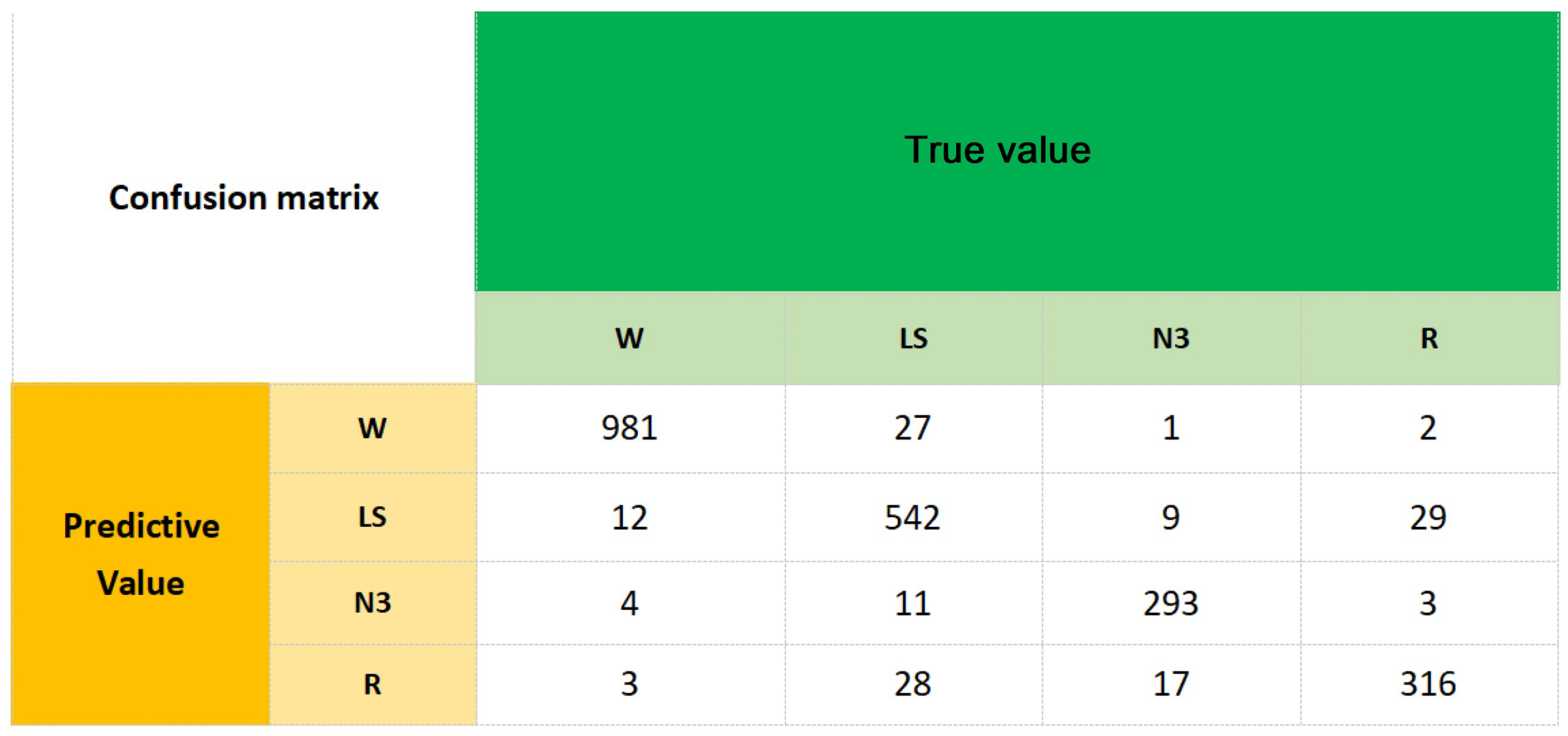
3.1. Analysis of Classification Results
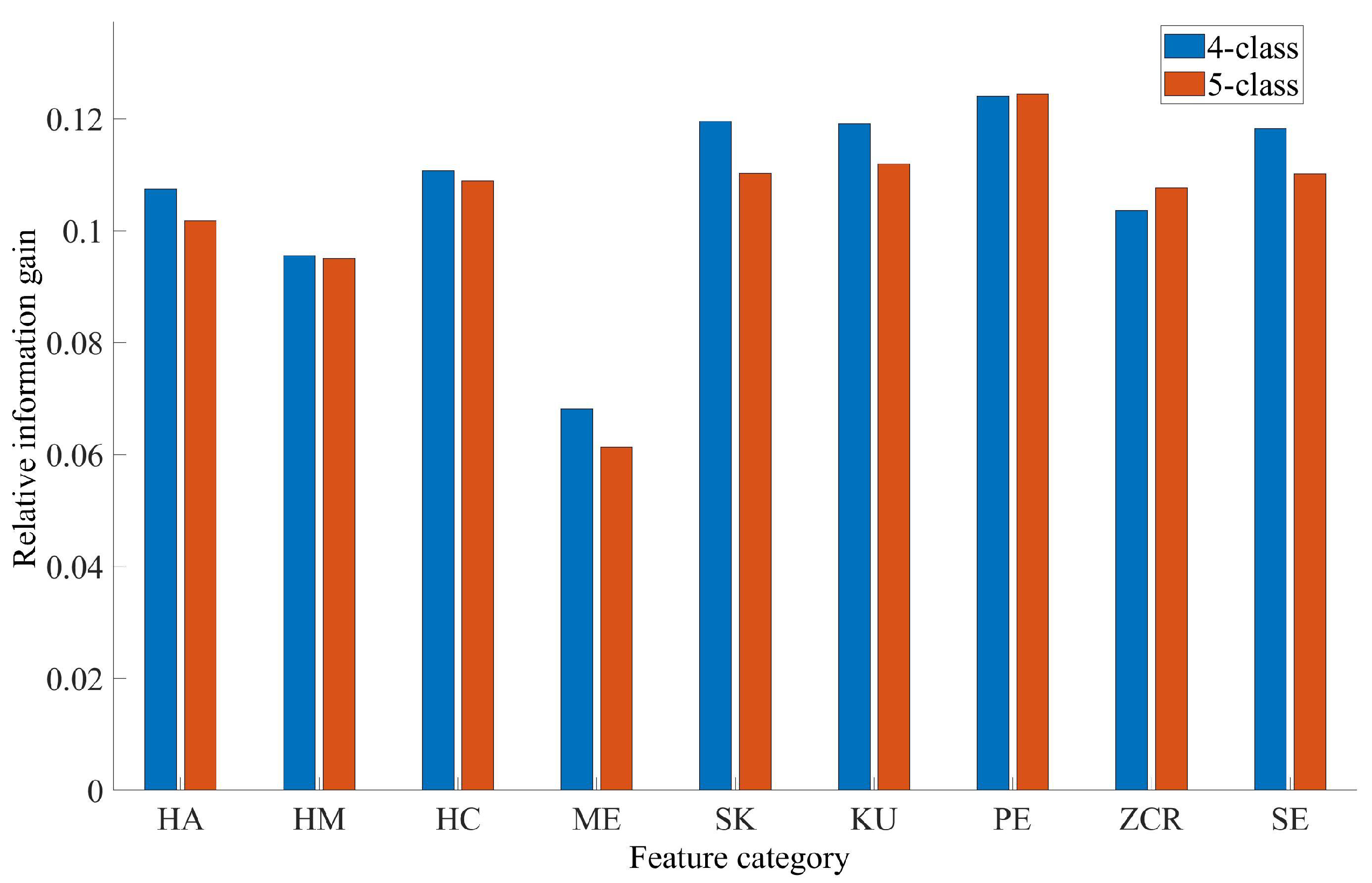
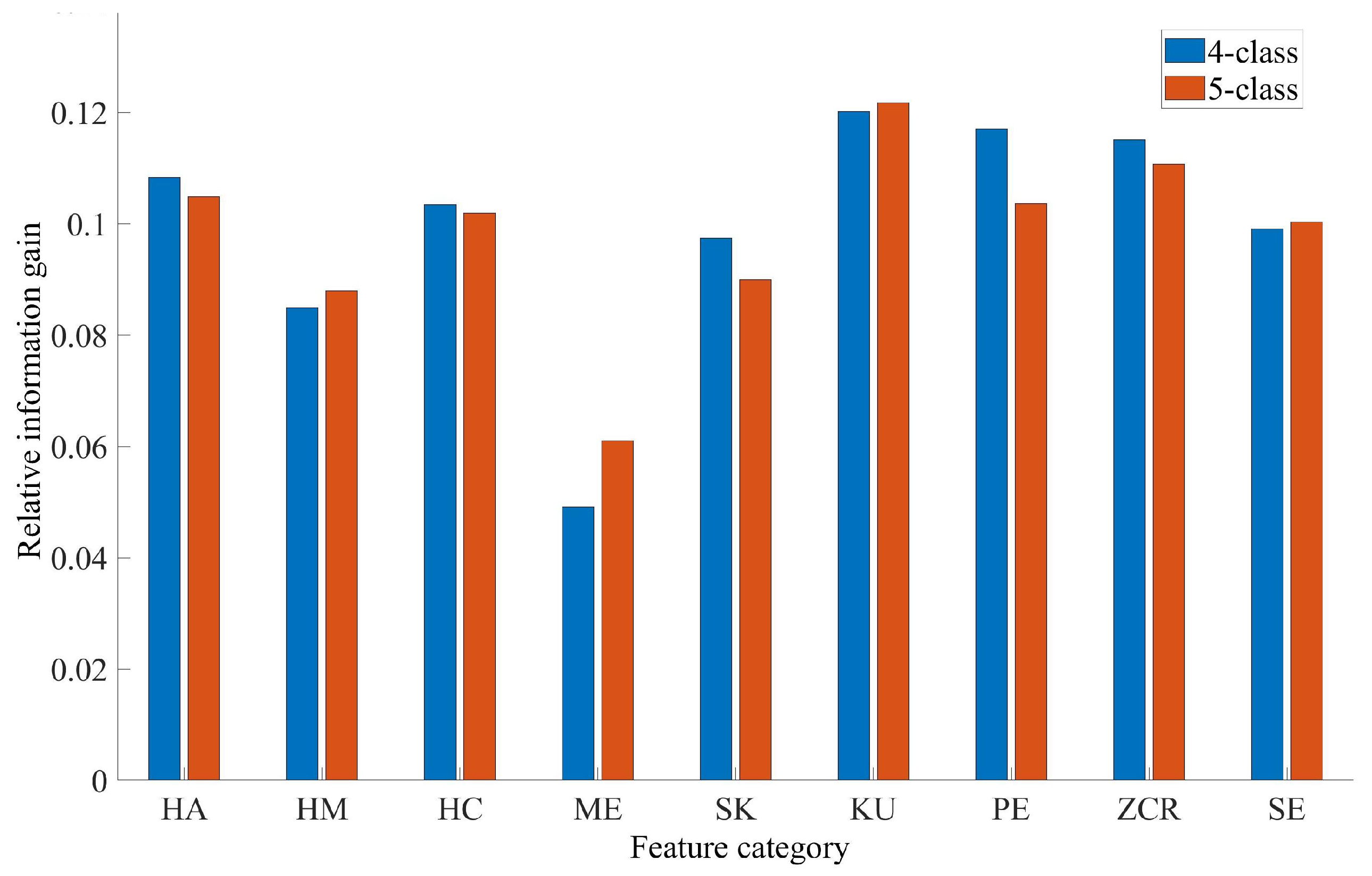
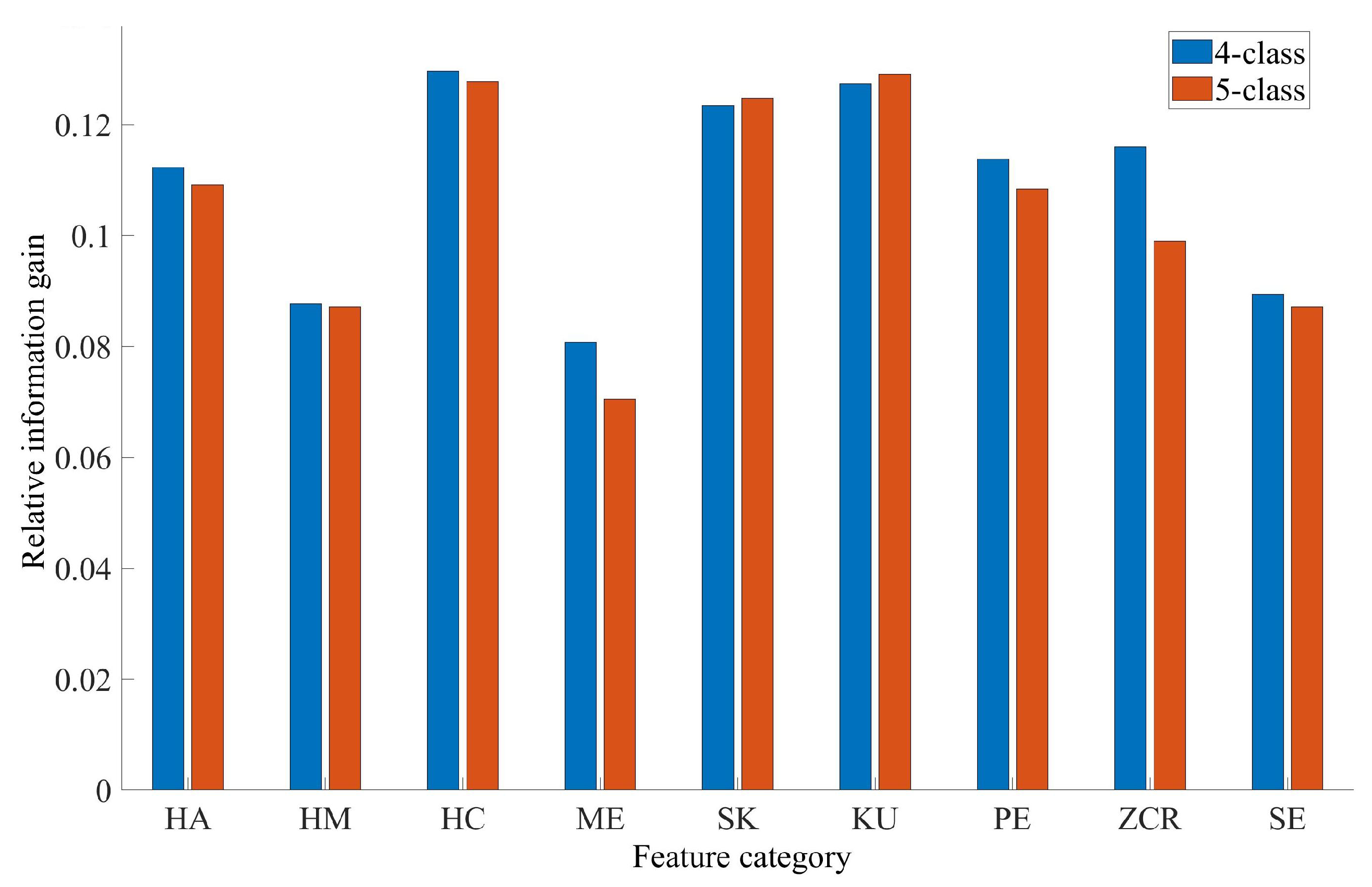
3.2. Feature Importance Analysis Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Younes, M. The case for using digital EEG analysis in clinical sleep medicine. Sleep Sci. Pract. 2017, 1. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Y.; Wang, Q.; Wang, X. Comparative analysis of different characteristics of automatic sleep stages. Comput. Methods Programs Biomed. 2019, 175, 53–72. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Loparo, K.A.; Kelly, M.R.; Kaplan, R.F. Evaluation of an automated single-channel sleep staging algorithm. Nat. Sci. Sleep 2015, 7, 101–111. [Google Scholar] [PubMed]
- Wolpert, E.A. A manual of standardized terminology, Techniques and scoring system for sleep stages of human subjects. Arch. Gen. Psychiatry. 1969, 20, 246–247. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Ashkenazy, Y.; Ivanov, P.C.; Bunde, A.; Havlin, S.; Penzel, T.; Peter, J.H.; Stanley, H.E. Characterization of sleep stages by correlations in the magnitude and sign of heartbeat increments. Phys. Rev. E 2002, 65, 051908. [Google Scholar] [CrossRef]
- Ferri, R.; Rundo, F.; Novelli, L.; Terzano, M.G.; Parrino, L.; Bruni, O. A new quantitative automatic method for the measurement of non-rapid eye movement sleep electroencephalographic amplitude variability. J. Sleep Res. 2012, 21, 212–220. [Google Scholar] [CrossRef] [PubMed]
- Singh, J.; Keer, N. Overview of Telemedicine and Sleep Disorders. Sleep Med. Clin. 2020, 15, 341–346. [Google Scholar] [CrossRef]
- Alickovic, E.; Subasi, A. Ensemble SVM Method for Automatic Sleep Stage Classification. IEEE Trans. Instrum. Meas. 2018, 67, 1258–1265. [Google Scholar] [CrossRef]
- Punjabi, N.M.; Shifa, N.; Dorffner, G.; Patil, S.; Pien, G.; Aurora, R.N. Computer-assisted automated scoring of polysomnograms using the somnolyzer system. Sleep 2015, 38, 1555–1566. [Google Scholar] [CrossRef]
- Koley, B.; Dey, D. An ensemble system for automatic sleep stage classification using single channel EEG signal. Comput. Biol. Med. 2012, 42, 1186–1195. [Google Scholar] [CrossRef]
- Zhu, G.; Li, Y.; Wen, P. Analysis and Classification of Sleep Stages Based on Difference Visibility Graphs From a Single-Channel EEG Signal. IEEE J. Biomed. Health Inform. 2014, 18, 1813–1821. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.R.; Subasi, A. A decision support system for automated identification of sleep stages from single-channel EEG signals. Knowl.-Based Syst. 2017, 128, 115–124. [Google Scholar] [CrossRef]
- Liu, C.; Tan, B.; Fu, M.; Li, J.; Wang, J.; Hou, F.; Yang, A. Automatic sleep staging with a single-channel EEG based on ensemble empirical mode decomposition. Phys. A Stat. Mech. Its Appl. 2021, 567, 125685. [Google Scholar] [CrossRef]
- Peng, S.L.; Hwang, W.L. Null Space Pursuit: An Operator-based Approach to Adaptive Signal Separation. IEEE Trans. Signal Process. 2010, 58, 2475–2483. [Google Scholar] [CrossRef]
- The Sleep-EDF Database. Available online: https://physionet.org/content/sleep-edfx/1.0.0/ (accessed on 15 October 2021).
- The SHHS Database. Available online: https://physionet.org/content/shhpsgdb/1.0.0/ (accessed on 13 November 2021).
- The DREAMS Subjects Database. Available online: https://rdrr.io/github/boupetch/rmdf/man/download_dreams_subjects.html (accessed on 11 November 2021).
- Hassan, A.R.; Bhuiyan, M.I.H. Automated identification of sleep states from EEG signals by means of ensemble empirical mode decomposition and random under sampling boosting. Comput. Methods Programs Biomed. 2017, 140, 201–210. [Google Scholar] [CrossRef] [PubMed]
- Seifpour, S.; Niknazar, H.; Mikaeili, M.; Nasrabadi, A.M. A new automatic sleep staging system based on statistical behavior of local extrema using single channel EEG signal. Expert Syst. Appl. 2018, 104, 277–293. [Google Scholar] [CrossRef]
- Quan, S.F.; Howard, B.V.; Iber, C.; Kiley, J.p.; Nieto, F.j.; O’Connor, G.T.; Rapoport, D.M.; Redline, S.; Robbins, J.; Samet, J.M.; et al. The sleep heart health study: Design, rationale and methods. Sleep 1997, 20, 1077–1085. [Google Scholar] [PubMed]
- Redline, S.; Sanders, M.H.; Lind, B.K.; Quan, S.F.; Iber, C.; Gottlieb, D.J.; Bonekat, W.H.; Rapoport, D.M.; Smith, P.L.; Kiley, J.P. Methods for obtaining and analyzing unattended polysomnography data for a multicenter study. Sleep 1998, 21, 759–767. [Google Scholar]
- Pan, Q.; Zhang, L.; Dai, G.; Zhang, H. Two denoising methods by wavelet transform. IEEE Trans. Signal Process. 1999, 47, 3401–3406. [Google Scholar] [CrossRef]
- Grobbelaar, M.; Phadikar, S.; Ghaderpour, E.; Struck, A.F.; Sinha, N.; Ghosh, R.; Ahmed, M.Z.I. A Survey on Denoising Techniques of Electroencephalogram Signals Using Wavelet Transform. Signals 2022, 3, 577–586. [Google Scholar] [CrossRef]
- Fu, K.; Qu, J.; Chai, Y.; Dong, Y. Classification of seizure based on the time frequency image of EEG signals using HHT and SVM. Biomed. Signal Process. Control 2014, 13, 15–22. [Google Scholar] [CrossRef]
- Skowronek, J.; Mckinney, M. Features for audio classification: Percussiveness of sounds. Intell. Algorithms Ambient. Biomed. Comput. 2006, 7, 103–118. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.J.; Bolbecker, A.R.; Howell, J.; Rass, O.; Sporns, O.; Hetrick, W.P.; Breier, A.; O’Donnell, B.F. Disturbed resting state EEG synchronization in bipolar disorder: A graph-theoretic analysis. Neuroimage Clin. 2013, 2, 414–423. [Google Scholar] [CrossRef]
- Cecchin, T.; Ranta, R.; Koessler, L.; Caspary, O.; Vespignani, H.; Maillard, L. Seizure lateralization in scalp EEG using Hjorth parameters. Clin. Neurophysiol. 2010, 121, 290–300. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. International Biometric Society. 1977, 33, 159–174. [Google Scholar] [CrossRef]
- Koprinska, I. Feature Selection for Brain-Computer Interfaces. In Proceedings of the Pacific-Asia conference on Knowledge of Discovery and Data Mining, New Frontiers in Applied Data Mining, Bangkok, Thailand, 27–30 April 2010; Volume 5669, pp. 106–117. [Google Scholar]
- Mamun, M.; Al-Kadi, M.; Marufuzzaman, M. Effectiveness of Wavelet Denoising on Electroencephalogram Signals. J. Appl. Res. Technol. 2013, 11, 156–160. [Google Scholar] [CrossRef]
- Phadikar, S.; Sinha, N.; Ghosh, R.; Ghaderpour, E. Automatic Muscle Artifacts Identification and Removal from Single-Channel EEG Using Wavelet Transform with Meta-Heuristically Optimized Non-Local Means Filter. Sensors 2022, 22, 2948. [Google Scholar] [CrossRef]
| Database | Demographics | Electroencephalographic(EEG) | ||||
|---|---|---|---|---|---|---|
| Subjects | Age | Gender | Lead | Frequency | Epochs | |
| Sleep-EDF | 8 | 4M/4F | Pz-Oz | 100 | 15188 | |
| DREAMS | 20 | 4M/16F | Cz-A1 | 200 | 20242 | |
| SHHS | 111 | 20M/91F | C4-A1 | 125 | 113347 | |
| Feature | Computing Formula | Feature Description |
|---|---|---|
| Mean | ME describes the middle point of the sample set. | |
| Skewness | SK is a measure of the asymmetry of the probability distribution of real variables [24]. | |
| Kurtosis | KU is a measure of the kurtosis of the probability distribution of real-valued variables [24]. | |
| Zero crossing rate | ZCR is the change rate of the signal sampling point symbol [25]. | |
| Sample entropy | SE is often used to measure the complexity of time series [26]. | |
| Permutation entropy | PE can quickly and accurately respond to the sudden change of the signal, which is a standard to measure the complexity of the signal [27]. | |
| Flexibility | HA represents the fluctuation degree of the EEG signal [28]. | |
| Complexity | HM represents the slope of the EEG signal [28]. | |
| Mobility | HC represents the change rate of the slope of the EEG signal [28,29]. |
| Model Evaluation | Computing Formula |
|---|---|
| Accuracy | |
| Specificity | |
| Sensitivity |
| Database | 4-Class Classifier | ||||
|---|---|---|---|---|---|
| W | LS | N3 | R | ||
| Sleep-EDF | specificity | 97.65% | 97.00% | 96.08% | 91.51% |
| sensitivity | 98.1% | 89.14% | 91.56% | 95.75% | |
| DREAMS | specificity | 95.23% | 93.87% | 92.15% | 83.24% |
| sensitivity | 96.11% | 92.87% | 90.06% | 80.42% | |
| SHHS | specificity | 94.06% | 90.53% | 88.32% | 95.84% |
| sensitivity | 90.08% | 93.74% | 92.51% | 94.73% | |
| Database | 5-Class Classifier | |||||
|---|---|---|---|---|---|---|
| W | N1 | N2 | N3 | R | ||
| Sleep-EDF | specificity | 96.41% | 94.46% | 93.63% | 93.11% | 85.38% |
| sensitivity | 98.67% | 47.36% | 90.57% | 90.68% | 85.60% | |
| proportion | 53.03% | 3.1% | 23.9% | 8.8% | 11.17% | |
| DREAMS | specificity | 93.96% | 91.47% | 89.81% | 87.39% | 81.53% |
| sensitivity | 95.18% | 59.32% | 89.85% | 92.12% | 83.10% | |
| proportion | 35% | 3.4% | 28.6% | 13% | 20% | |
| SHHS | specificity | 95.84% | 92.03% | 91.00% | 89.69% | 84.33% |
| sensitivity | 94.73% | 9.21% | 92.00% | 89.09% | 81.90% | |
| proportion | 27.65% | 2.6% | 39.4% | 14.8% | 15.55% | |
| Database | 4-Class Classifier | 5-Class Classifier | |
|---|---|---|---|
| Sleep-EDF | Accuracy | 93.59% | 92.89% |
| Kappa | 0.8924 | 0.8837 | |
| DREAMS | Accuracy | 91.32% | 90.01% |
| Kappa | 0.8619 | 0.8392 | |
| SHHS | Accuracy | 90.25% | 88.37% |
| Kappa | 0.8412 | 0.8238 |
| Database | Year | Name | Decomposition Algorithm | Features ang Signal Channel | Classifiers | 4-Class | 5-Class |
|---|---|---|---|---|---|---|---|
| Sleep-EDF | 2014 | Zhu | Degree distribution based on difference visibility (Pz-Oz) | Support vector machine | 89.3% | 88.9% | |
| 2017 | Hassan | Tunable-Q factor wavelet transform | Four statistical moments (Pz-Oz) | Bagging | 94.36% | 93.69% | |
| 2018 | Seifpour | Statistical behavior of local extrema (Fpz-Cz) | Support vector machine | 92.8% | 91.8% | ||
| 2021 | Cong Liu | Ensemble empiricar model algorithm (EEMD) | Mean, skewness, kurtosis, time domain, and nonlinear dynamics features (Pz-Oz) | XGBOOST | 93.1% | 91.9% | |
| In this work | NSP | Mean, skewness, kurtosis, time domain, and nonlinear dynamics features (Pz-Oz) | XGBOOST | 93.59% | 92.89% | ||
| DREAMS Subjects | 2017 | Hassan | EEMD | Statistical features (Cz-A1) | Random under sampling boosting | 80.0% | 74.6% |
| 2017 | Hassan | Tunable-Q factor wavelet transform | Four statistical moments (Cz-A1) | Bagging | 83.78% | 78.95% | |
| 2018 | Seifpour | Statistical behavior of local extrema (Cz-A1) | Support vector machine | 83.3% | |||
| 2021 | Cong Liu | EEMD | Mean, skewness, kurtosis, time domain, and nonlinear dynamics features (Cz-A1) | XGBOOST | 86.4% | 83.4% | |
| In this work | NSP | Mean, skewness, kurtosis, time domain, and nonlinear dynamics features (Cz-A1) | XGBOOST | 91.32% | 90.01% | ||
| SHHS | 2021 | Cong Liu | EEMD | Mean, skewness, kurtosis, time domain, and nonlinear dynamics features (C4-A1) | XGBOOST | 87.5% | 85.8% |
| In this work | NSP | Mean, skewness, kurtosis, time domain, and nonlinear dynamics features (C4-A1) | XGBOOST | 90.25% | 88.37% | ||
| Database | 4-Class Classifier | 5-Class Classifier | |
|---|---|---|---|
| Sleep-EDF | Accuracy of using NSP | 93.59% | 92.89% |
| Accuracy without NSP | 89.56% | 88.20% | |
| DREAMS | Accuracy of using NSP | 91.32% | 90.01% |
| Accuracy without NSP | 84.34% | 82.63% | |
| SHHS | Accuracy of using NSP | 90.25% | 88.37% |
| Accuracy without NSP | 85.73% | 81.58% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, W.; Linghu, R.; Li, H.; Hou, F. Automatic Sleep Staging Based on Single-Channel EEG Signal Using Null Space Pursuit Decomposition Algorithm. Axioms 2023, 12, 30. https://doi.org/10.3390/axioms12010030
Xiao W, Linghu R, Li H, Hou F. Automatic Sleep Staging Based on Single-Channel EEG Signal Using Null Space Pursuit Decomposition Algorithm. Axioms. 2023; 12(1):30. https://doi.org/10.3390/axioms12010030
Chicago/Turabian StyleXiao, Weiwei, Rongqian Linghu, Huan Li, and Fengzhen Hou. 2023. "Automatic Sleep Staging Based on Single-Channel EEG Signal Using Null Space Pursuit Decomposition Algorithm" Axioms 12, no. 1: 30. https://doi.org/10.3390/axioms12010030
APA StyleXiao, W., Linghu, R., Li, H., & Hou, F. (2023). Automatic Sleep Staging Based on Single-Channel EEG Signal Using Null Space Pursuit Decomposition Algorithm. Axioms, 12(1), 30. https://doi.org/10.3390/axioms12010030





