The Hecke Bicategory
Abstract
:1. Introduction
1.1. Matrices and Spans
1.2. Groupoidification and Enriched Bicategories
1.3. The Hecke Bicategory
1.4. Spans of Groupoids and Cocontinuous Functors
1.5. The Categorified Hecke Algebra and Zamolodchikov Equation
2. Matrices, Spans and G-Sets
2.1. Spans as Matrices




2.2. Permutation Representations
- G-sets (with finitely many orbits) as objects,
- G-equivariant functions as morphisms,
- permutation representations of G as objects,
- intertwining operators as morphisms.
2.3. Spans of G-Sets

- a set of objects x, y, z …,
- for each pair of objects, a set of morphisms,
- for each pair of morphisms, a set of 2-morphisms,
- 1-morphisms x → y of as objects,
- 2-morphisms:of as morphisms, and a vertical compositionof 2-morphisms of .
- for each triple of objects , a horizontal composition functoron 1-morphisms and 2-morphisms,
- for each object x, an identity-assigning functor ,
- for objects , an associator natural isomorphism
- for pairs of objects , left and right unitor natural isomorphismsall of which is required to satisfy associativity and unit axioms:
- sets as objects,
- spans of sets as morphisms,
- maps of spans of sets as 2-morphisms.

- G-sets as objects,
- spans of G-sets as morphisms,
- maps of spans of G-sets as 2-morphisms.
3. Groupoidification and Enriched Bicategories
3.1. Action Groupoids and Groupoid Cardinality
- elements of X as objects,
- pairs as morphisms , where .
3.2. Degroupoidification
- (tame) groupoids as objects,
- spans of groupoids as 1-morphisms,
- isomorphism classes of maps of spans of groupoids as 2-morphisms.



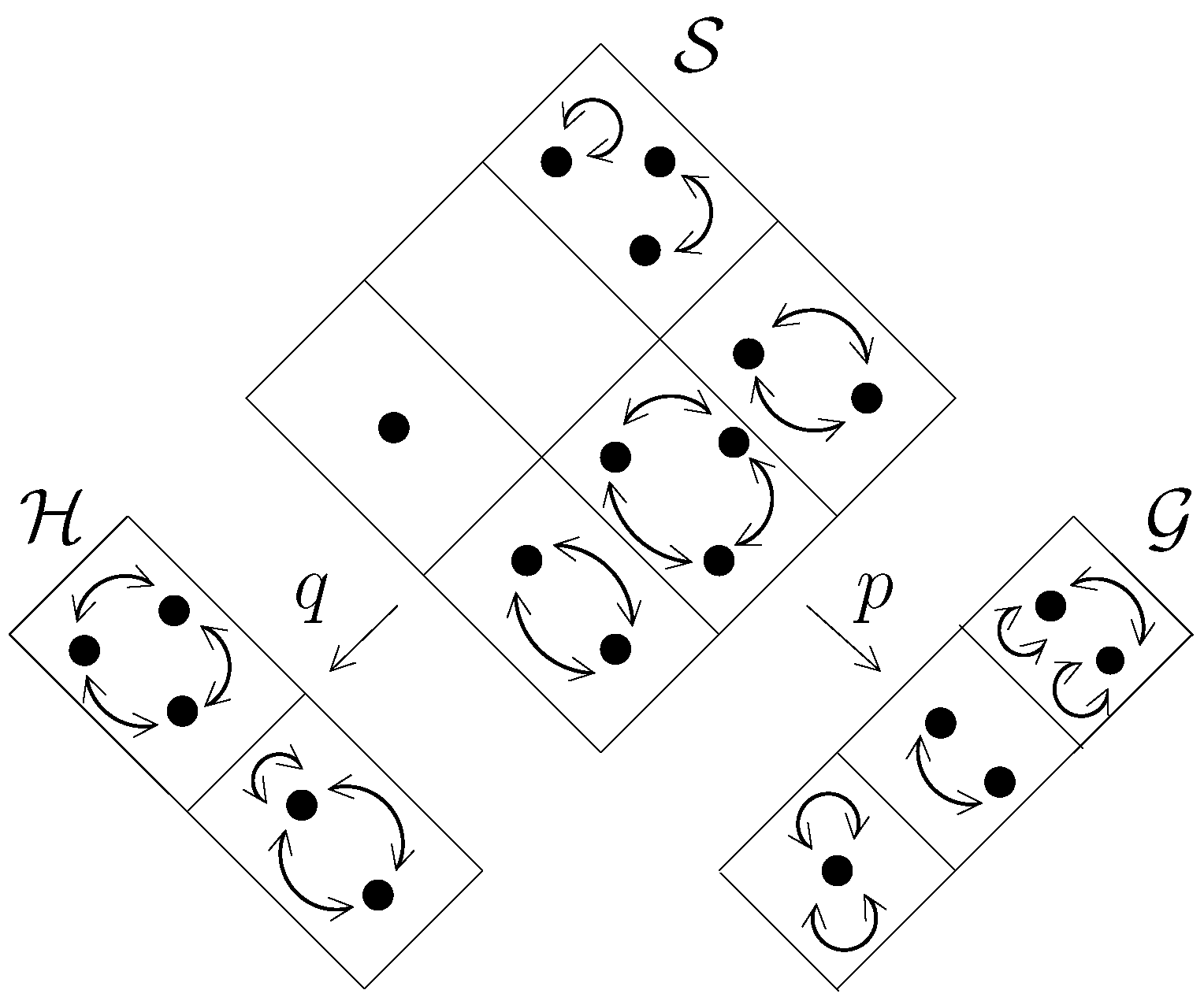

- objects v of , such that , as objects,
- morphisms in as morphisms.







3.3. Enriched Bicategories
- a set of objects ,
- for each pair of objects , an object ,
- composition and identity-assigning maps that are morphisms in .
- a collection of objects ,
- for every pair of objects , a hom-object , which we will often denote ,
- a morphism called compositionfor each triple of objects ,
- an identity-assigning morphismfor each object ,
- an invertible 2-morphism called the associatorfor each quadruple of objects ;
- and invertible 2-morphisms called the right unitor and left unitorfor every pair of objects ;
- and axioms given by closed surface diagrams, the more interesting of the two being the permutahedron [4].
4. A Categorification Theorem
4.1. The Hecke Bicategory
- G-sets as objects,
- for each pair of G-sets , an object of , the action groupoid:
- compositionis the span of groupoids,
- for each G-set X, an identity assigning span from the terminal groupoid 1 to ,
- invertible 2-morphisms in assuming the role of the associator and left and right unitors.
4.2. A Categorification of the Hecke Algebroid
- permutation representations of G as objects,
- for each pair of permutation representations , the vector space
5. Spans of Groupoids and Cocontinuous Functors
5.1. The Monoidal 2-Category Cocont
- presheaves on as objects,
- natural transformations as morphisms.
- nice toposes as objects,
- cocontinuous functors as 1-morphisms,
- natural transformations as 2-morphisms.
5.2. From Spans of Groupoids to Cocontinuous Functors



5.3. Spans of G-Sets as Nice toposes
- G-sets as objects,
- for each pair of G-sets , an object of Cocont:
- compositionis the cocontinuous functor ,
- for each G-set X, an identity assigning cocontinuous functor from the topos to ,
- invertible 2-morphisms in Cocont assuming the role of the associator and left and right unitors.



6. The Categorified Hecke Algebra and Zamolodchikov Equation
6.1. The Hecke Algebra
6.2. Categorified Generators and the Zamolodchikov Equation
- is drawn as no edge at all,
- is drawn as a single edge,
- is drawn as a double edge,
- is drawn as a triple edge.







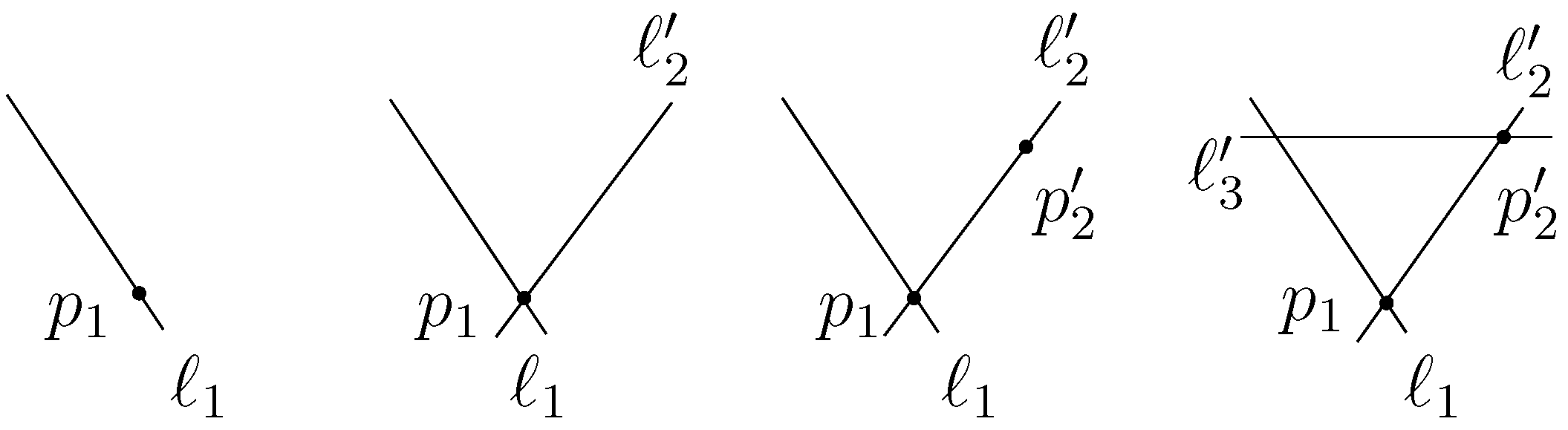
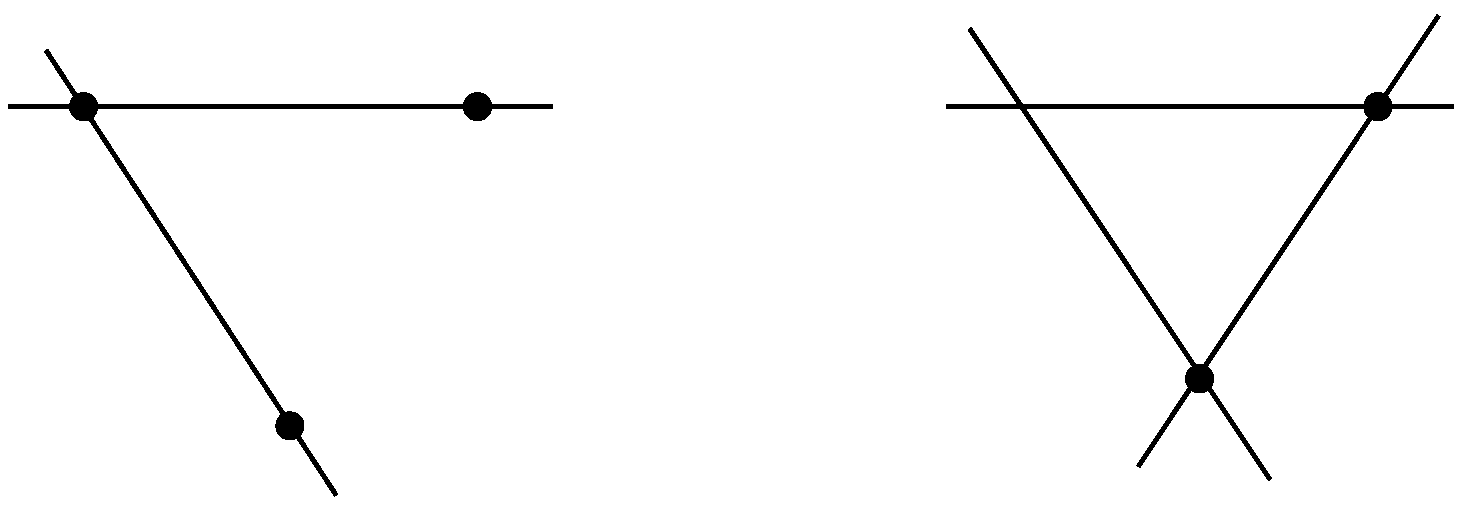


Acknowledgments
References
- Baez, J.; Hoffnung, A.E.; Walker, C. Higher Dimensional Algebra VII: Groupoidification. In Theory and Applications of Categories; 2010; Volume 24, pp. 489–553. Available online: http://arxiv.org/abs/0908.4305.
- Hoffnung, A.E. Spans in 2-categories: A monoidal tricategory. Available online: http://arxiv.org/abs/1112.0560 (accessed on 22 September 2012).
- Baez, J.; Hoffnung, A.E. Higher dimensional Algebra VIII: The Hecke bicategory. Available online: http://math.ucr.edu/home/baez/hecke.pdf (accessed on 19 September 2012).
- Carmody, S.M. Cobordism Categories. Ph.D. Thesis, University of Cambridge, Cambridge, MA, USA, 1995. [Google Scholar]
- Forcey, S. Quotients of the multiplihedron as categorified associahedra. Available online: http://arxiv.org/PS_cache/arxiv/pdf/0803/0803.2694v4.pdf (accessed on 19 September 2012).
- Baez, J.; Dolan, J. From Finite Sets to Feynman Diagrams. In Mathematics Unlimited—2001 and Beyond; Engquist, B., Schmid, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 29–50. [Google Scholar]
- Kelly, G.M. Basic Concepts of Enriched Category Theory; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Kapranov, M.; Voevodsky, V. 2-Categories and Zamolodchikov Tetrahedra Equations. In Proceedings of Symposia in Pure Mathematics, Providence, RI, USA, 1994; Volume 56, Part 2. pp. 177–260.
- Baez, J.; Langford, L. Higher-Dimensional Algebra IV: 2-tangles. Adv. Math. 2003, 180, 705–764. [Google Scholar] [CrossRef]
- Kazhdan, D.; Lusztig, G. Representations of Coxeter groups and Hecke algebras, Invent. Math. 1979, 53, 165–184. [Google Scholar]
- Rouquier, R. Categorification of the braid groups. Available online: http://arxiv.org/abs/math/0409593 (accessed on 19 September 2012).
- Soergel, W. The combinatorics of Harish-Chandra bimodules, J. Reine Angew. Math. 1992, 429, 49–74. [Google Scholar]
- Khovanov, M. A categorification of the Jones polynomial. Duke Math. J. 2000, 101, 359–426. [Google Scholar] [CrossRef]
- Bernstein, J.; Frenkel, I.; Khovanov, M. A categorification of the Temperley-Lieb algebra and Schur quotients of U(sl2) via projective and Zuckerman functors. Selecta Math. 1999, 5, 199–241. [Google Scholar] [CrossRef]
- Stroppel, C. Categorification of the Temperley-Lieb category, tangles, and cobordisms via projective functors. Duke Math. J. 2005, 126, 547–596. [Google Scholar] [CrossRef]
- Elias, B.; Khovanov, M. Diagrammatics for Soergel Categories, 2009. Available online: http://arxiv.org/abs/0902.4700 (accessed on 19 September 2012).
- Webster, B.; Williamson, G. A geometric model for Hochschild homology of Soergel bimodules. Geom. Topol. 2008, 12, 1243–1263. [Google Scholar] [CrossRef]
- Bénabou, J. Introduction to Bicategories. In Reports of the Midwest Category Seminar; Springer-Verlag: Berlin/Heidelberg, Germany, 1967; pp. 1–77. [Google Scholar]
- Leinster, T. Basic bicategories. Available online: http://arxiv.org/abs/math/9810017 (accessed on 19 September 2012).
- Fiore, M.; Leinster, T. Objects of categories as complex numbers. Adv. Math. 2005, 190, 264–277. [Google Scholar] [CrossRef]
- Kim, M.A. Lefschetz trace formula for equivariant cohomology. Ann. Sci. École Norm. Sup. 1995, 28, 669–688. [Google Scholar]
- Leinster, T. The Euler characteristic of a category. Doc. Math. 2008, 13, 21–49. [Google Scholar]
- Weinstein, A. The Volume of a Differentiable Stack. In Proceedings of the Poisson, Lausanne, Switzerland, July 2008; Available online: http://arxiv.org/abs/0809.2130 (accessed on 19 September 2012).
- Street, R. Fibrations and Yoneda’s lemma in a 2-category. In Category Seminar; Springer: Berlin/Heidelberg, Germany, 1974; Volume 420, pp. 104–133. [Google Scholar]
- Weber, M. Strict 2-toposes. Available online: http://arxiv.org/abs/math/0606393 (accessed on 19 September 2012).
- Gordon, R.; Power, A.J.; Street, R. Coherence for tricategories. Mem. Am. Math. Soc. 1995, 117, 1–81. [Google Scholar] [CrossRef]
- Gurski, N. An algebraic theory of tricategories. Ph.D. Thesis, University of Chicago, Chicago, IL, USA, June 2006. [Google Scholar]
- Moerdijk, I. Toposes and Groupoids. In Categorical Algebra and Its Applications; Springer: Berlin/Heidelberg, Germany, 1988; Volume 1348, pp. 280–298. [Google Scholar]
- Johnstone, P.T. Sketches of an Elephant: A Topos Theory Compendium; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Mac Lane, S.; Moerdijk, I. Sheaves in Geometry and Logic: A First Introduction to Topos Theory; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Brown, K. Buildings; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Bump, D. Lie Groups; Springer: New York, NY, USA, 2004. [Google Scholar]
- Humphreys, J. Reflection Groups and Coxeter Groups; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Jones, V. Hecke algebra representations of braid groups and link polynomials. Ann. Math. 1987, 126, 335–388. [Google Scholar] [CrossRef]
- Carter, J.S.; Saito, M. Knotted Surfaces and Their Diagrams; American Mathematical Society: Providence, RI, USA, 1998. [Google Scholar]
- Baez, J.; Crans, A. Higher-dimensional algebra VI: Lie 2-algebras. Theory Appl. Categ. 2004, 12, 492–528. [Google Scholar]
- Baez, J.; Neuchl, M. Higher-dimensional algebra I: Braided monoidal categories. Adv. Math. 1996, 121, 196–244. [Google Scholar] [CrossRef]
- McCrudden, P. Balanced coalgebroids. Theory Appl. Categ. 2000, 7, 71–147. [Google Scholar]
© 2012 by the author licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hoffnung, A.E. The Hecke Bicategory. Axioms 2012, 1, 291-323. https://doi.org/10.3390/axioms1030291
Hoffnung AE. The Hecke Bicategory. Axioms. 2012; 1(3):291-323. https://doi.org/10.3390/axioms1030291
Chicago/Turabian StyleHoffnung, Alexander E. 2012. "The Hecke Bicategory" Axioms 1, no. 3: 291-323. https://doi.org/10.3390/axioms1030291
APA StyleHoffnung, A. E. (2012). The Hecke Bicategory. Axioms, 1(3), 291-323. https://doi.org/10.3390/axioms1030291









