A Hybrid Approach for Joint Simulation of Geometallurgical Variables with Inequality Constraint
Abstract
:1. Introduction
2. Materials and Methods
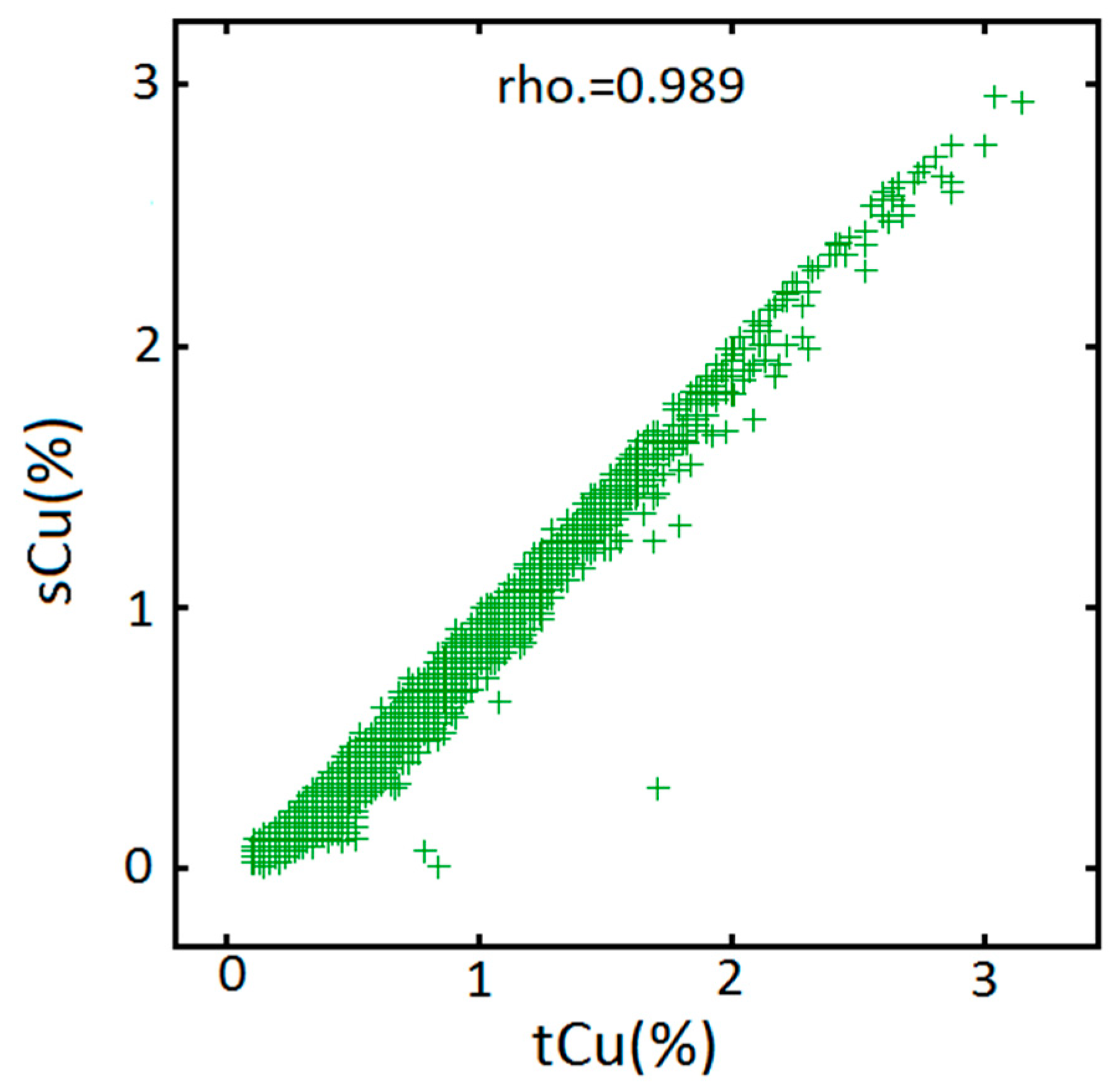
2.1. Inequality Constraint
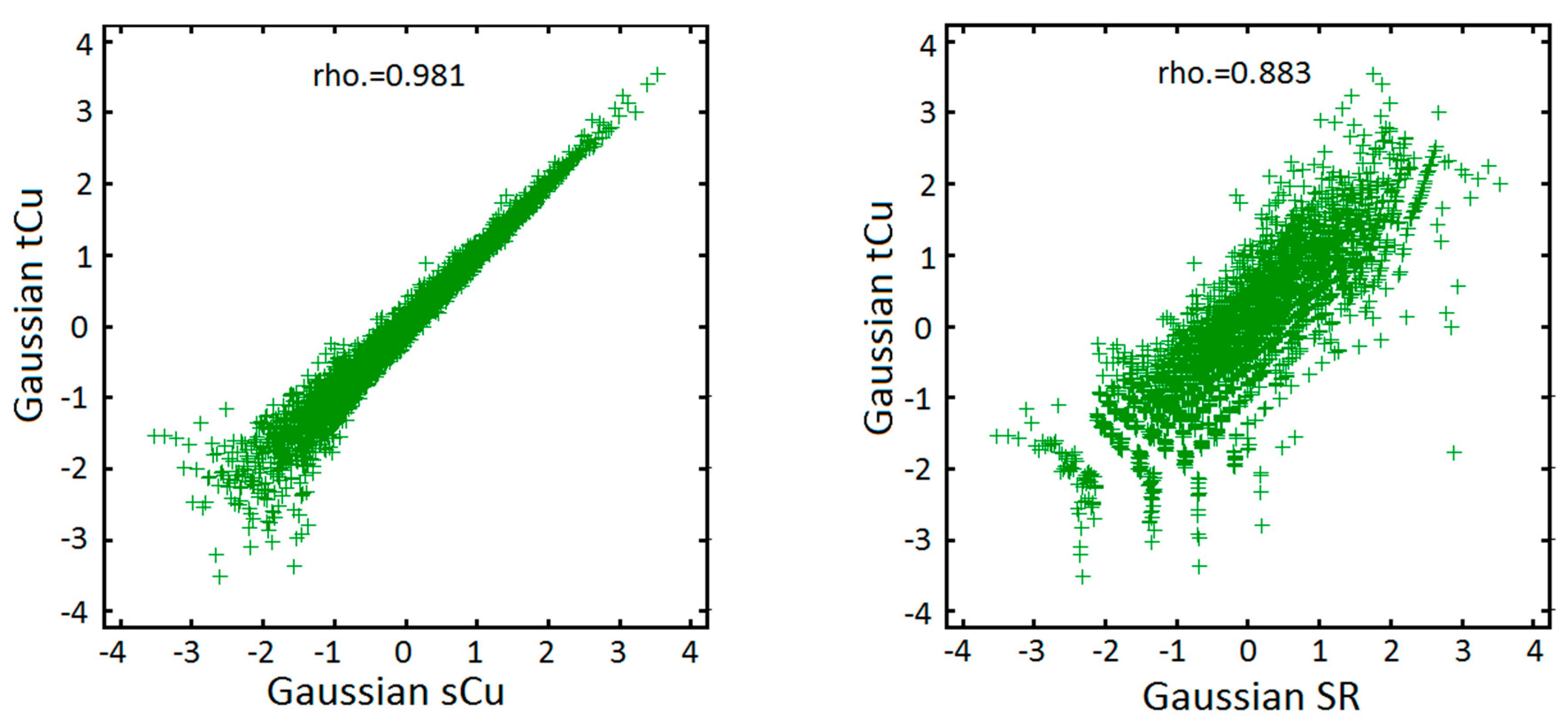
2.2. Minimum/Maximum Autocorrelation Factor (MAF)
- Transform the original variables to normal score values with a mean of zero and variance one this can be implemented by normal score transformation methodologies such as Gaussian anamorphosis [32] or quantile-based approach [33].where is the standard normal cumulative distribution function, is the cumulative distribution function of the original variable and, is the normal score value.
- Compute the experimental variance-covariance matrix : since we are dealing with normal score values, this matrix is identical to the sample correlation matrix. In the case of two variables, this matrix is given by:where the principal diagonal element equals one which is identical to the total variance. The upper and lower diagonal elements and equal the linear correlation coefficient between two normal score variables and , respectively.
- Perform the spectral decomposition of above matrix to derive the orthonormal eigenvectors matrix , associated with the underlying diagonal eigenvalues matrix , such that:It is necessary to check that the entries of are in decreasing order.
- Calculate the PCA transformations at locations by:where PCA(u) are the scores with normal standard distribution due to the priori multivariate Gaussian assumption.
- Choose a proper nonzero lag distance and calculate the sample covariance and cross-covariance matrices over the scores, so its related spectral decomposition with diagonal eigenvalues matrix and orthonormal eigenvectors matrix is:It is worth mentioning that since the scores are standard values, the variance-covariance matrix is identical to correlogram matrix.
- Finally, the MAF factors at location can be derived:The back transformation is performed through the inverse of matrix :
- Convert the original cross-correlated variables to the new variables free of inequality constraint
- Transform the declustered converted variables into normal score data (Gaussian random field with mean 0 and variance 1) (Equation (1))
- Transform the normal score data into orthogonal MAF factors (Equation (6)).
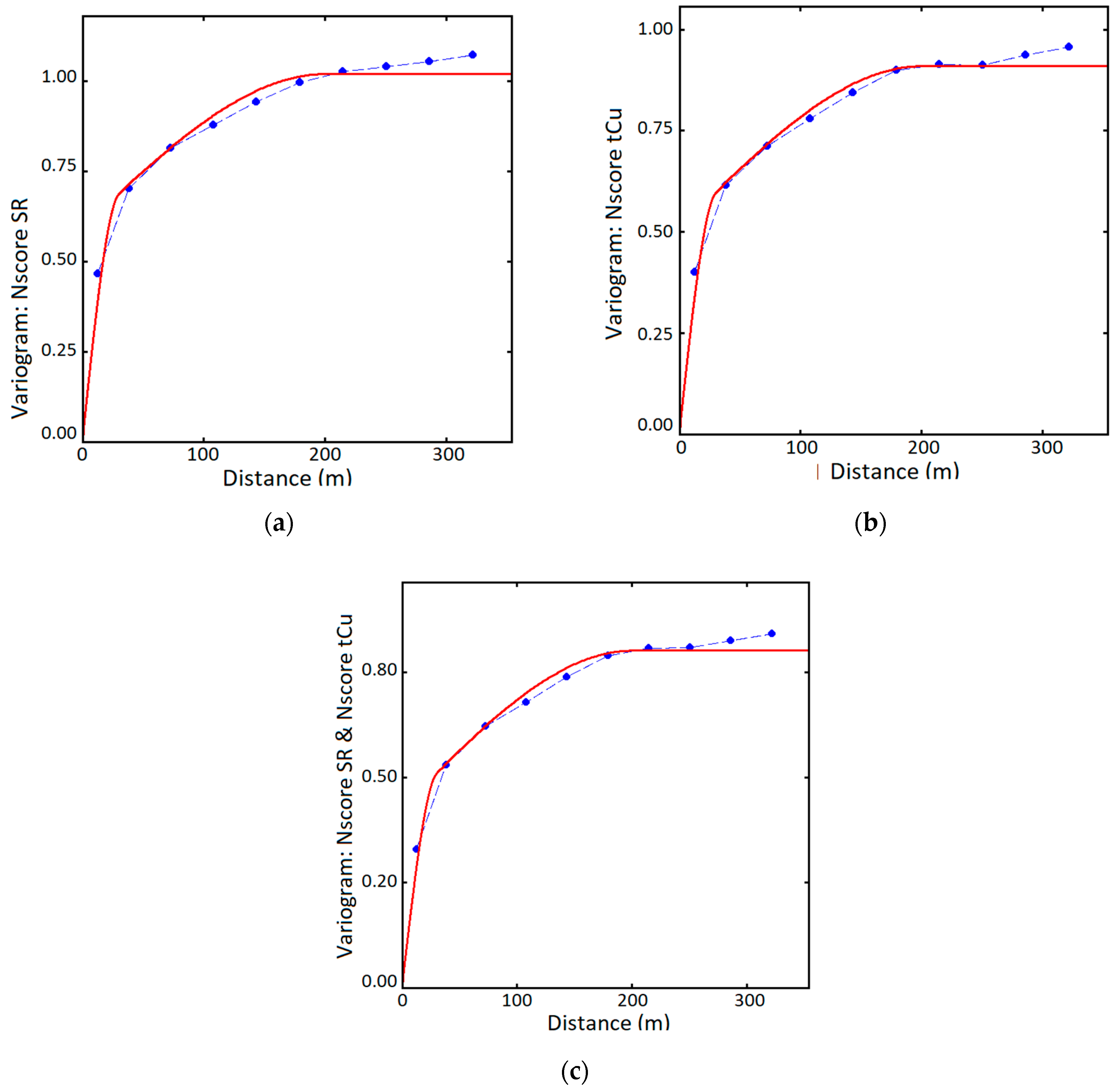
- Calculate the experimental variograms for each MAF factor
- Independent Gaussian simulation of MAF factors
- Back-transformation of the simulation results (realizations) into normal score space (Equation (7))
- Back-transformation of the normal score realizations into the original space in order to restitute the intrinsic cross-correlation
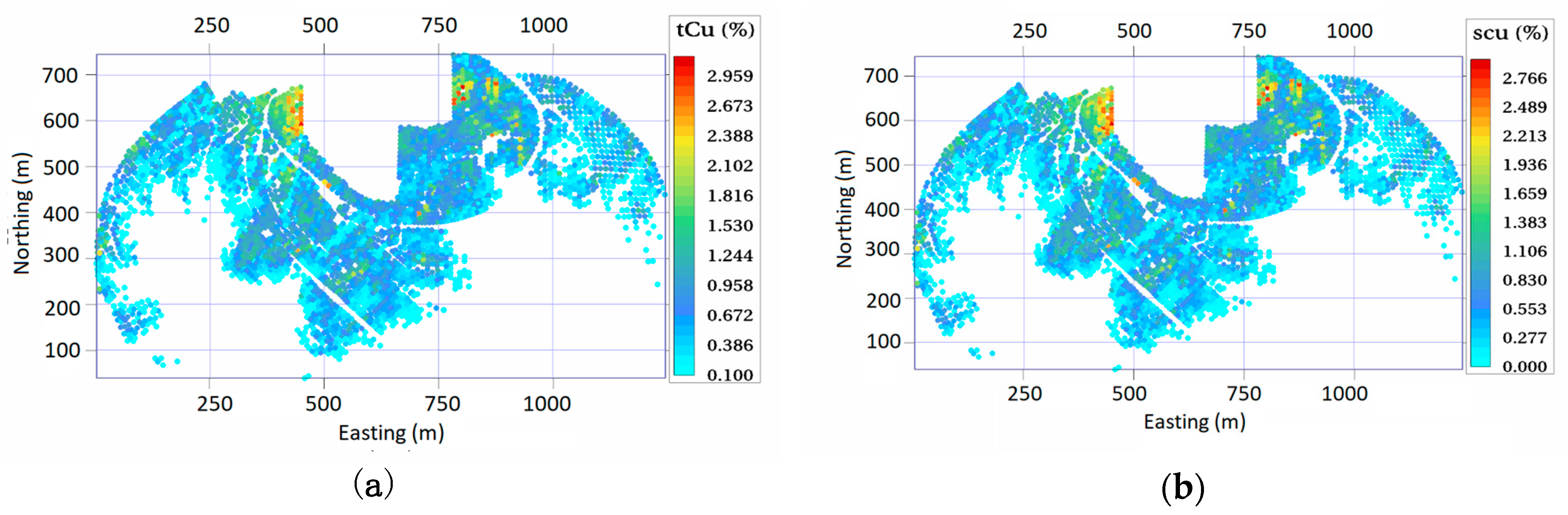
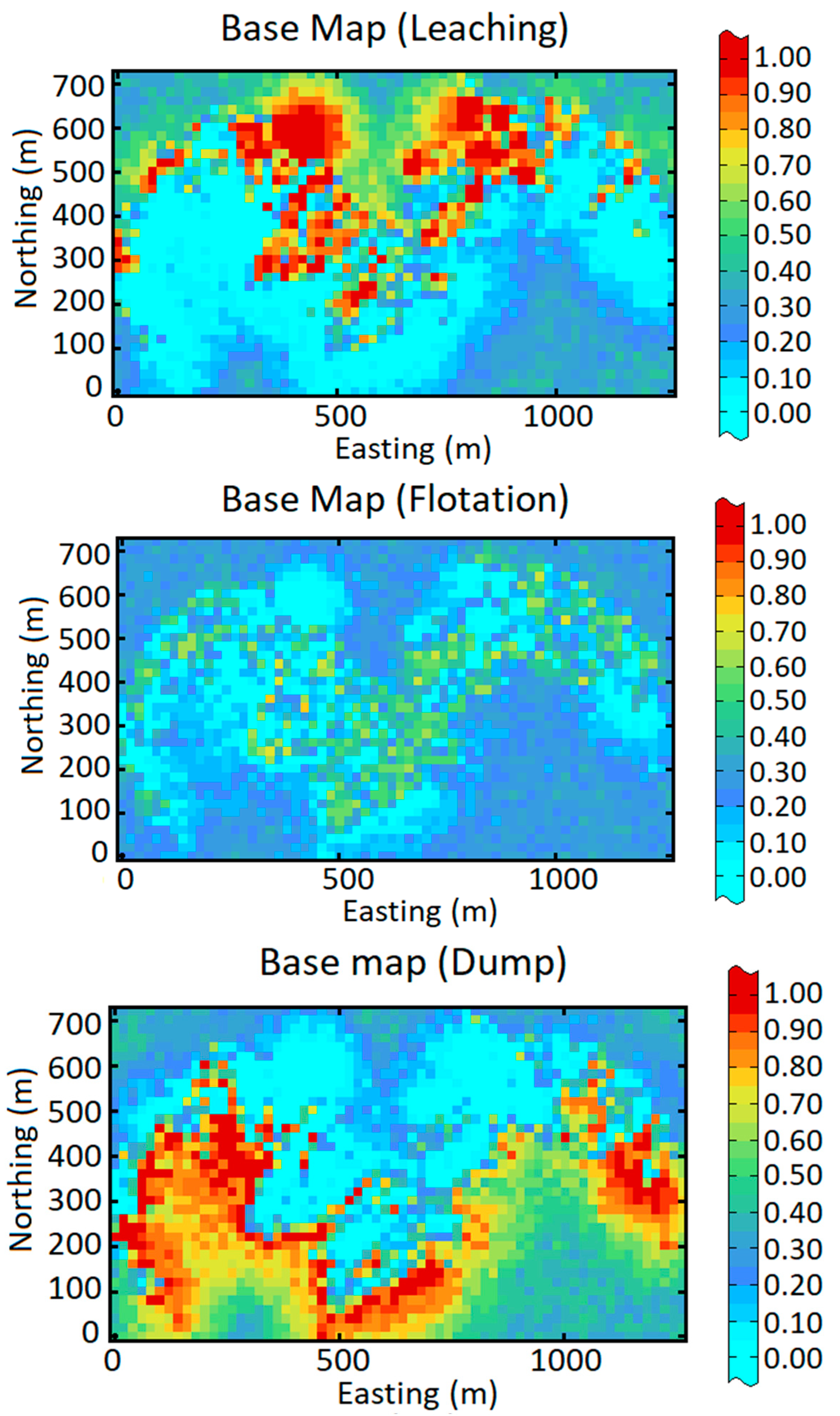
3. Application to an Actual Case study
3.1. Conventional Co-Simulation
3.2. Joint Simulation with MAF Transformation
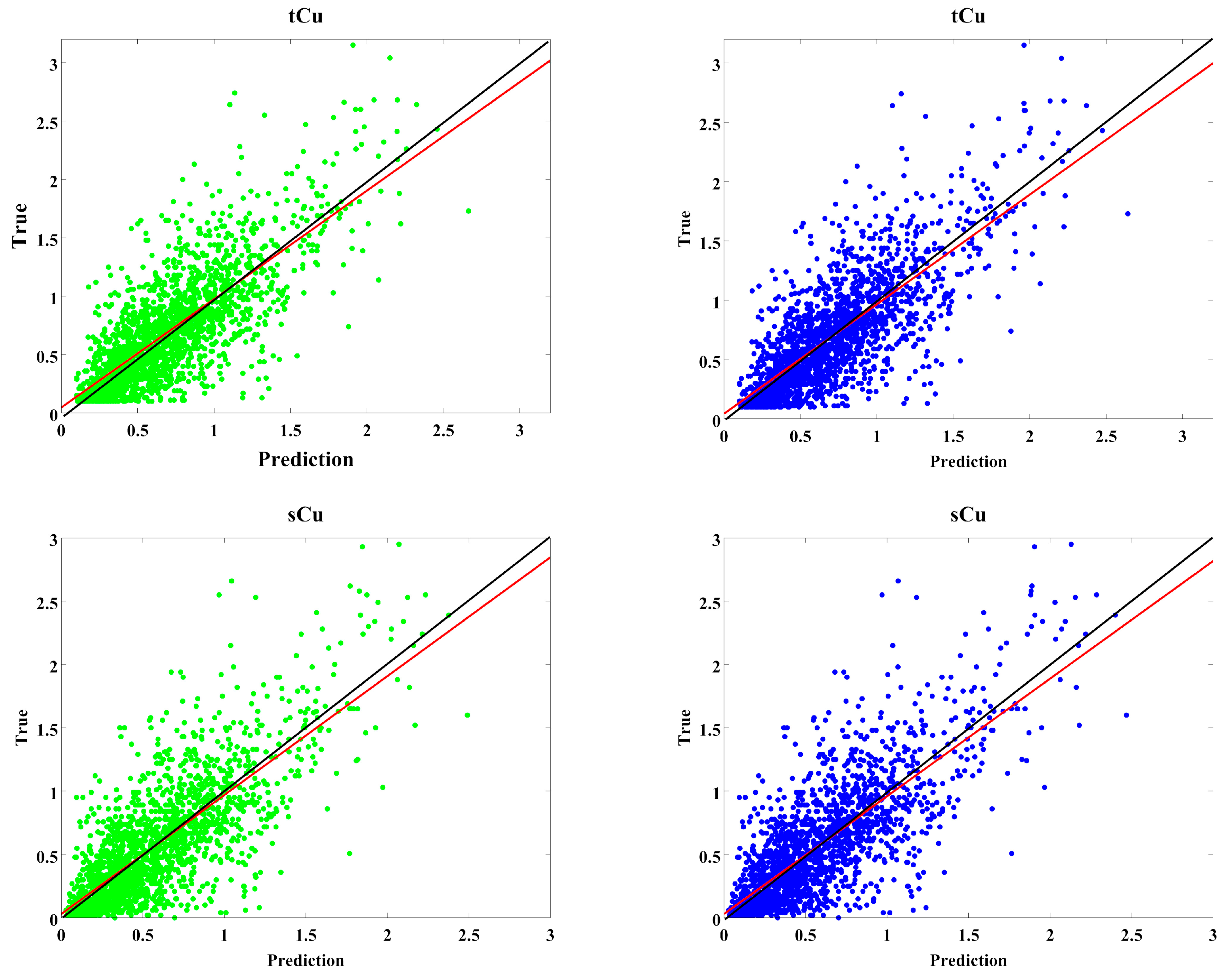
3.3. Validation of Results
3.3.1. Validation of Global Statistical Parameter
3.3.2. Validation of Local Statistical Parameter
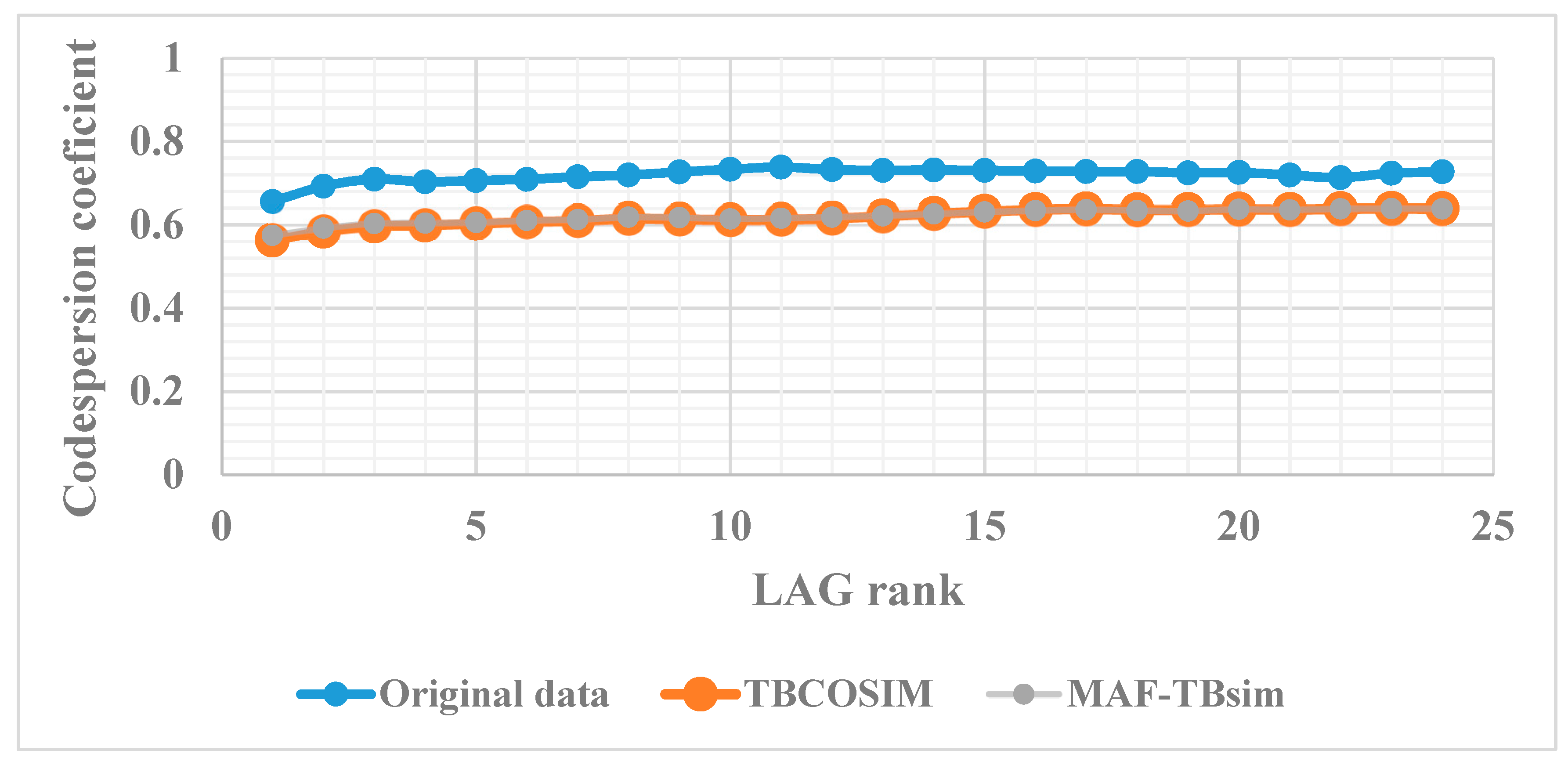
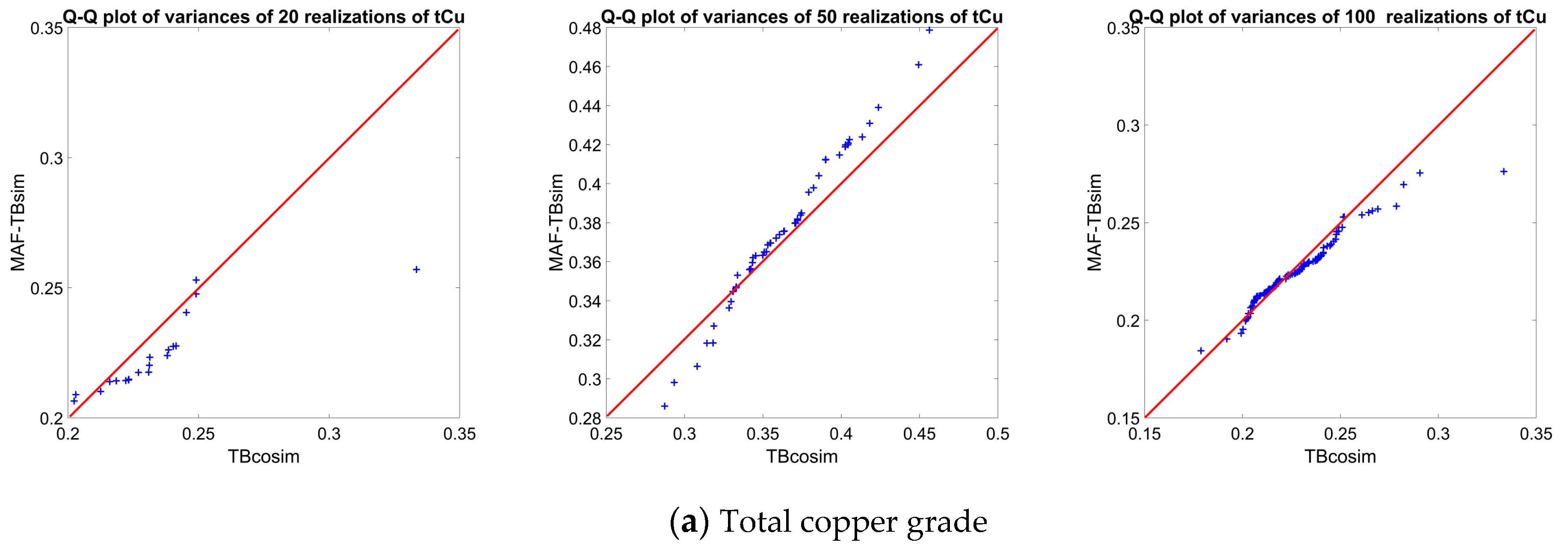
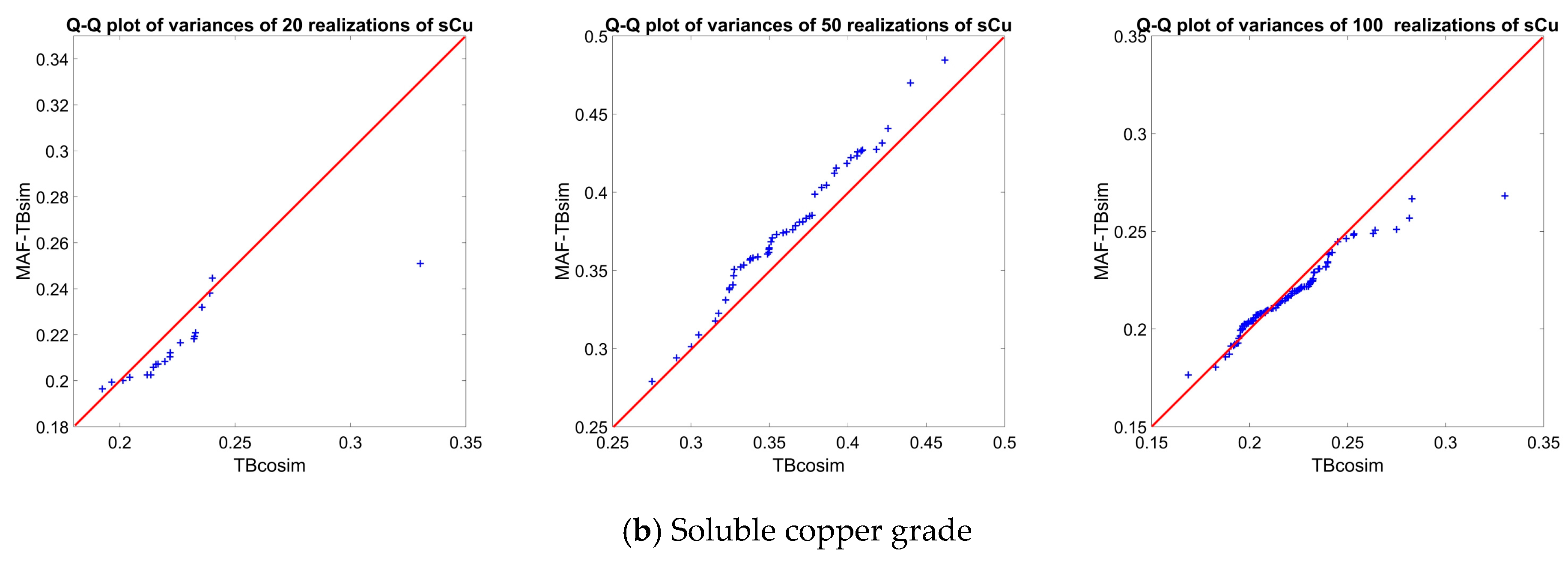
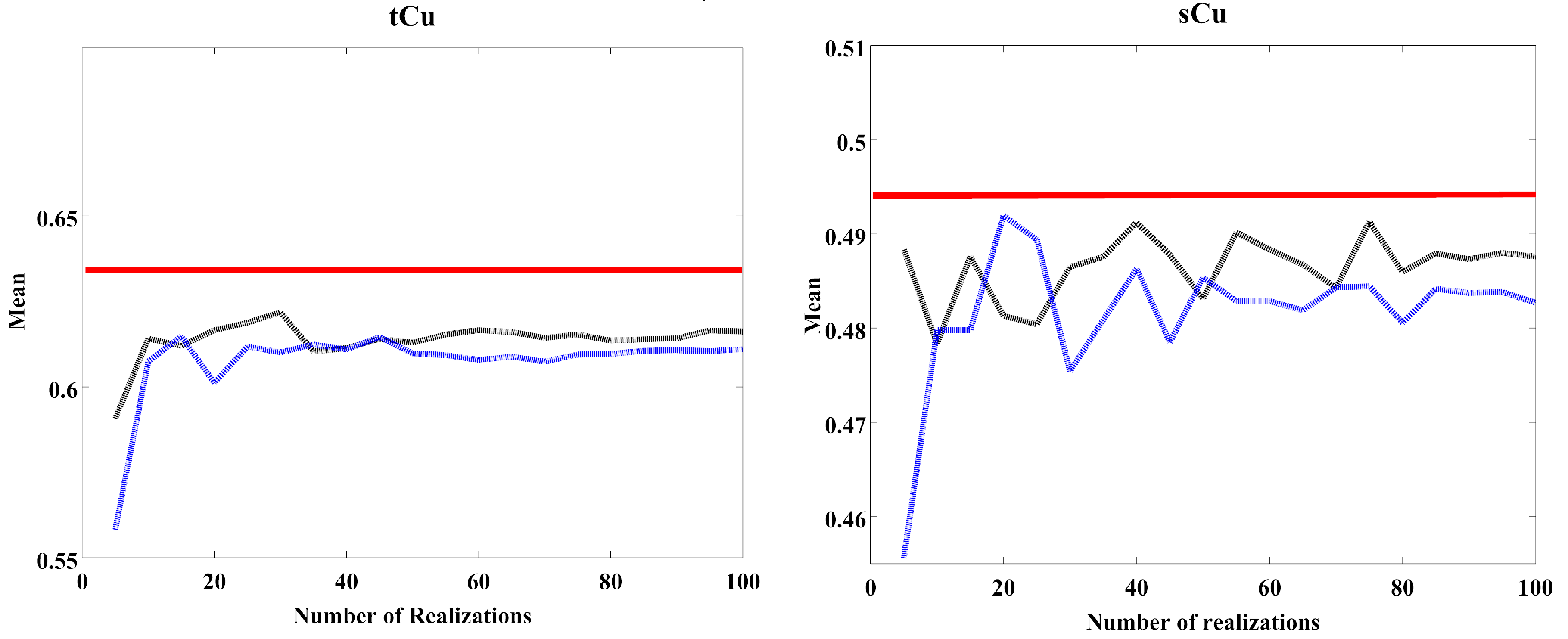
3.3.3. Sensitivity Analysis of the Number of Simulations
3.3.4. Post Processing the Realizations: Probabilistic Domaining of Geometallurgical Domains
3.3.5. Validation against Actual Data
4. Discussion on Application and Limitations of the Proposed Approach
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Macfarlane, A.S.; Williams, T.P. Optimizing value on a copper mine by adopting a geometallurgical solution. J. South. Afr. Inst. Min. Metall. 2014, 114, 929–935. [Google Scholar]
- Almeida, J.A. Modelling of cement raw material compositional indices with direct sequential cosimulation. Eng. Geol. 2010, 114, 26–33. [Google Scholar] [CrossRef]
- Tercan, A.E.; Sohrabian, B. Multivariate geostatistical simulation of coal quality by independent components. Int. J. Coal Geol. 2013, 112, 53–66. [Google Scholar] [CrossRef]
- Brissette, M.; Mihajlovic, V.; Sanuri, S. Geometallurgy: New accurate test work to meet required accuracies of mining project development. In Proceedings of the XXVII International Mineral Processing Congress, Santiago, Chile, 20–24 October 2014. [Google Scholar]
- Deutsch, J.L.; Szymanski, J.; Etsell, T.H. Metallurgical Variable Re-expression for Geostatistics. In Geostatistical and Geospatial Approaches for the Characterization of Natural Resources in the Environment; Springer: Cham, Switzerland, 2016; pp. 83–88. [Google Scholar]
- Tolosana-Delgado, R.; Mueller, U.; van den Boogaart, K.G.; Ward, C.; Gutzmer, J. Improving processing by adaption to conditional geostatistical simulation of block compositions. J. South. Afr. Inst. Min. Metall. 2015, 115, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Emery, X. Co-simulating total and soluble copper grades in an oxide ore deposit. Math. Geosci. 2012, 44, 27–46. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Asghari, O. Simulation of geometallurgical variables through stepwise conditional transformation in Sungun copper deposit, Iran. Arab. J. Geosci. 2015, 8, 3821–3831. [Google Scholar] [CrossRef]
- Bai, S.; Fu, X.; Li, C.; Wen, S. Process improvement and kinetic study on copper leaching from low-grade cuprite ores. Physicochem. Probl. Miner. Process 2018, 54, 300–310. [Google Scholar]
- Pizarro, S.; Emery, X. Geostatistical joint modelling of total and soluble copper grades. In Proceedings of the 2nd International Seminar on Geology for the Mining Industry GEOMIN 2011, Antofagasta, Chile, 8–10 June 2011; Beniscelli, J., Kuyvenhoven, R., Hoal, K.O., Eds.; Gecamin Ltda: Santiago, Chile, 2011. [Google Scholar]
- Cáceres, A.; Riquelme, R.; Emery, X.; Díaz, J.; Fuster, G. Total and soluble copper grade estimation using minimum/maximum autocorrelation factors and multigaussian kriging. In Proceedings of the 2nd International Seminar on Geology for the Mining Industry GEOMIN 2011, Antofagasta, Chile, 8–10 June 2011; Beniscelli, J., Kuyvenhoven, R., Hoal, K.O., Eds.; Gecamin Ltda: Santiago, Chile, 2011. [Google Scholar]
- Lange, W.; Emery, X. Joint simulation of total and soluble copper grades in an oxide copper deposit. In Proceedings of the 5th International Conference on Innovation in Mine Operations, Santiago, Chile, 20–22 June 2012; Kuyvenhoven, R., Morales, J.E., Vega, C., Eds.; Gecamin Ltda: Santiago, Chile, 2012; pp. 62–63. [Google Scholar]
- Dubrule, O.; Kostov, C. An interpolation method taking into account inequality constraints: I. Methodology. Math. Geol. 1986, 18, 33–51. [Google Scholar] [CrossRef]
- Leuangthong, O.; Deutsch, C.V. Stepwise conditional transformation for simulation of multiple variables. Math. Geol. 2003, 35, 155–173. [Google Scholar] [CrossRef]
- Abildin, Y.; Madani, N.; Topal, E. Geostatistical Modelling of Geometallurgical Variables through Turning Bands Approach. In Proceedings of the 25th World Mining Congress, Astana, Kazakhstan (WMC 2018), Astana, Kazakhstan, 19–22 June 2018. [Google Scholar]
- Emery, X. Testing the correctness of the sequential algorithm for simulating Gaussian random fields. Stoch. Environ. Res. Risk Assess. 2004, 18, 401–413. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Goovaerts, P. Spatial orthogonality of the principal components computed from coregionalized variables. Math. Geol. 1993, 25, 281–302. [Google Scholar] [CrossRef]
- Bandarian, E.M.; Bloom, L.M.; Mueller, U.A. Direct minimum/maximum autocorrelation factors within the framework of a two structure linear model of coregionalisation. Comput. Geosci. 2008, 34, 190–200. [Google Scholar] [CrossRef]
- Switzer, P.; Green, A.A. Min/max autocorrelation factors for multivariate spatial imagery. Comput. Sci. Stat. 1985, 16, 13–16. [Google Scholar]
- Maleki, M.; Madani, N. Multivariate Geostatistical Analysis: An application to ore body evaluation. Iran. J. Earth Sci. 2017, 8, 173–184. [Google Scholar]
- Kim, H.J.; Song, Y.; Lee, K.H. Inequality constraint in least-squares inversion of geophysical data. Earth Planets Space 1999, 51, 255–259. [Google Scholar] [CrossRef] [Green Version]
- Abrahamsen, P.; Benth, F.E. Kriging with Inequality Constraints. Math. Geol. 2001, 33, 719–744. [Google Scholar] [CrossRef]
- Journel, A.G. Constrained interpolation and qualitative information—The soft kriging approach. Math. Geol. 1986, 18, 269–286. [Google Scholar] [CrossRef]
- Vargas-Guzmán, J.A.; Dimitrakopoulos, R. Successive nonparametric estimation of conditional distributions. Math. Geol. 2003, 35, 39–52. [Google Scholar] [CrossRef]
- Tran, T.T.; Murphy, M.; Glacken, I. Semivariogram structures used in multivariate conditional simulation via minimum/maximum autocorrelation factors. In Proceedings of the XI International Congress, IAMG, Liège, Belgium, 3–8 September 2006. [Google Scholar]
- Davis, B.M.; Greenes, K.A. Estimation using spatially distributed multivariate data: An example with coal quality. J. Int. Assoc. Math. Geol. 1983, 15, 287–300. [Google Scholar] [CrossRef]
- Suro-Perez, V.; Journel, A.G. Indicator principal component kriging. Math. Geol. 1991, 23, 759–788. [Google Scholar] [CrossRef]
- Rondon, O. Teaching aid: Minimum/maximum autocorrelation factors for joint simulation of attributes. Math. Geosci. 2012, 44, 469–504. [Google Scholar] [CrossRef]
- Desbarats, A.J. Geostatistical modeling of regionalized grain-size distributions using min/max autocorrelation factors. In geoENV III—Geostatistics for Environmental Applications; Springer: Dordrecht, The Netherlands, 2001; pp. 441–452. [Google Scholar]
- Desbarats, A.J.; Dimitrakopoulos, R. Geostatistical simulation of regionalized pore-size distributions using min/max autocorrelation factors. Math. Geol. 2000, 32, 919–942. [Google Scholar] [CrossRef]
- Rivoirard, J. Introduction to Disjunctive Kriging and Non-Linear Geostatistics; No. 551.021 R626i; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide, 2nd ed.; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Emery, X.; Lantuéjoul, C. Tbsim: A computer program for conditional simulation of three-dimensional gaussian random fields via the turning bands method. Comput. Geosci. 2006, 32, 1615–1628. [Google Scholar] [CrossRef]
- Paravarzar, S.; Emery, X.; Madani, N. Comparing sequential Gaussian and turning bands algorithms for cosimulating grades in multi-element deposits. Comptes Rendus Geosci. 2015, 347, 84–93. [Google Scholar] [CrossRef]
- Madani, N.; Ortiz, J. Geostatistical Simulation of Cross-Correlated Variables: A Case Study through Cerro Matoso Nickel-Laterite Deposit. In Proceedings of the 26th International Symposium on Mine Planning and Equipment Selection, Luleå, Sweden, 29–31 August 2017. [Google Scholar]
- Eze, P.N.; Madani, N.; Adoko, A.C. Multivariate Mapping of Heavy Metals Spatial Contamination in a Cu–Ni Exploration Field (Botswana) Using Turning Bands Co-simulation Algorithm. Nat. Resour. Res. 2018, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Rossi, M.; Deutsch, C.V. Mineral Resource Estimation; Springer: New York, NY, USA, 2014. [Google Scholar]
- Emery, X. A turning bands program for conditional co-simulation of cross-correlated Gaussian random fields. Comput. Geosci. 2008, 34, 1850–1862. [Google Scholar] [CrossRef]
- Chilès, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Goulard, M.; Voltz, M. Linear corregionalization model: Tools for estimation and choice of cross variogram matrix. Math. Geol. 1992, 30, 589–615. [Google Scholar]
- Emery, X. Iterative algorithms for fitting a linear model of coregionalization. Comput. Geosci. 2010, 36, 1150–1160. [Google Scholar] [CrossRef]
- Madani, N.; Emery, X. A comparison of search strategies to design the cokriging neighborhood for predicting coregionalized variables. Stoch. Environ. Res. Risk Assess. 2018, 1–17. [Google Scholar] [CrossRef]
- Lantuejoul, C. Geostatistical Simulation, Models and Algorithms; Springer: Berlin/Heidelberg, Germany, 2002; p. 256. [Google Scholar]
- Emery, X. Conditioning simulations of Gaussian random fields by ordinary kriging. Math. Geol. 2007, 39, 607–623. [Google Scholar] [CrossRef]
- Deutsch, C.V. All Realizations All the Time. In Handbook of Mathematical Geosciences; Daya Sagar, B., Cheng, Q., Agterberg, F., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Jakab, N. Stochastic modeling in geology: Determining the sufficient number of models. Central Eur. Geol. 2017, 60, 135–151. [Google Scholar] [CrossRef] [Green Version]
- Pyrcz, M.; Deutsch, C.V. Geostatistical Reservoir Modeling; Oxford University Press: New York, NY, USA, 2014. [Google Scholar]
- Emery, X.; Ortiz, J.M. Enhanced coregionalization analysis for simulating vector Gaussian random fields. Comput. Geosci. 2012, 42, 126–135. [Google Scholar] [CrossRef]



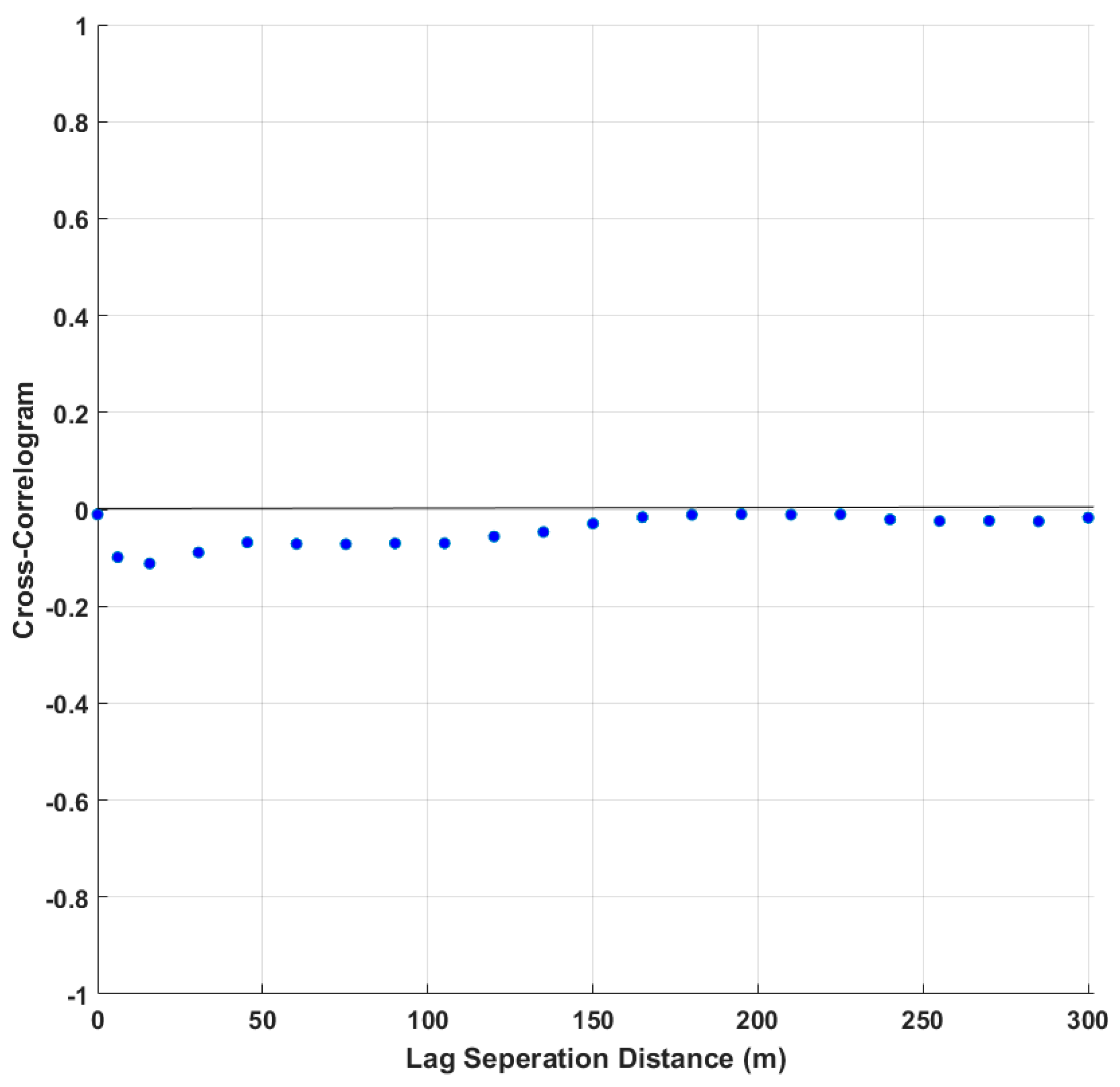
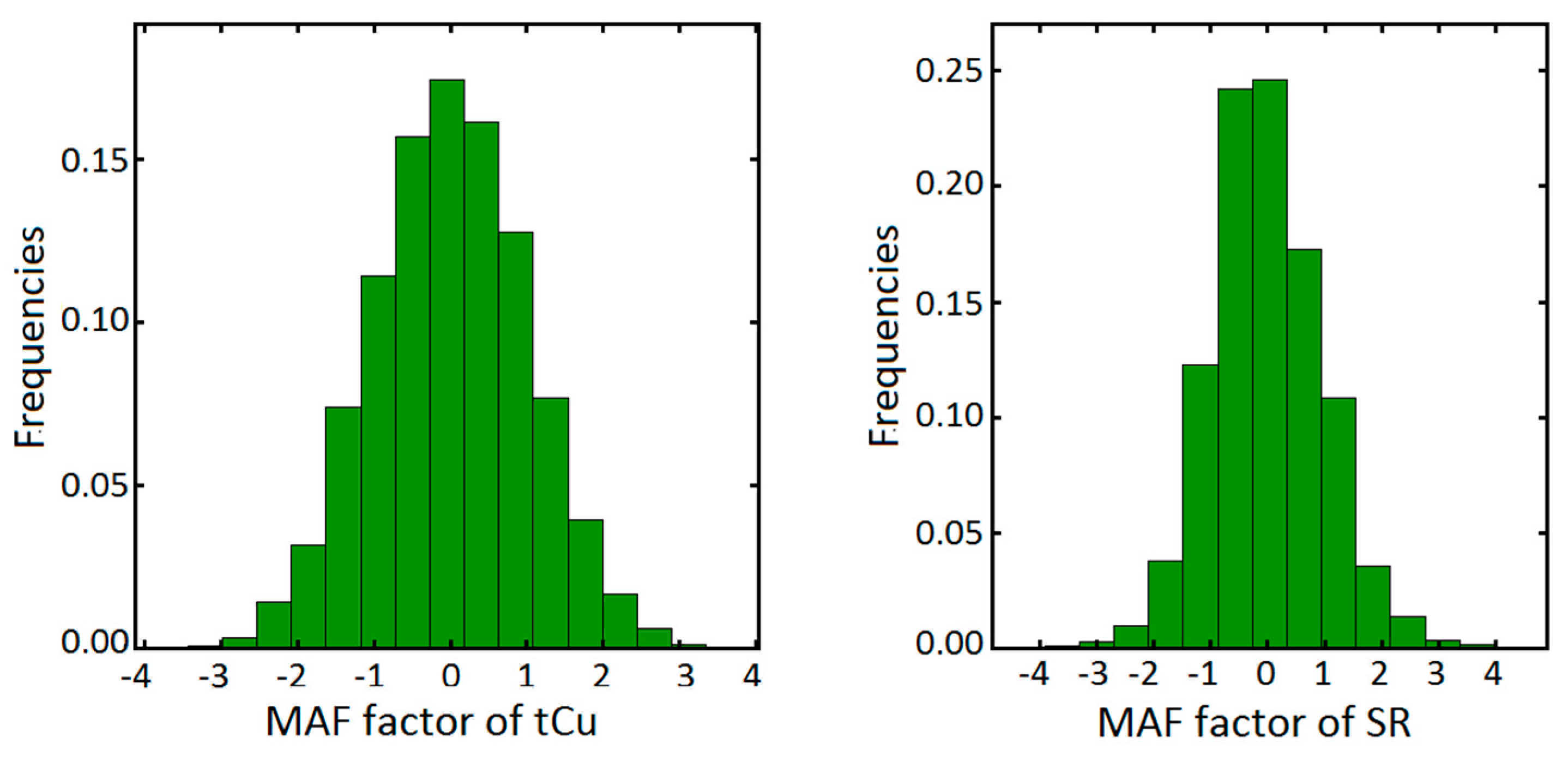
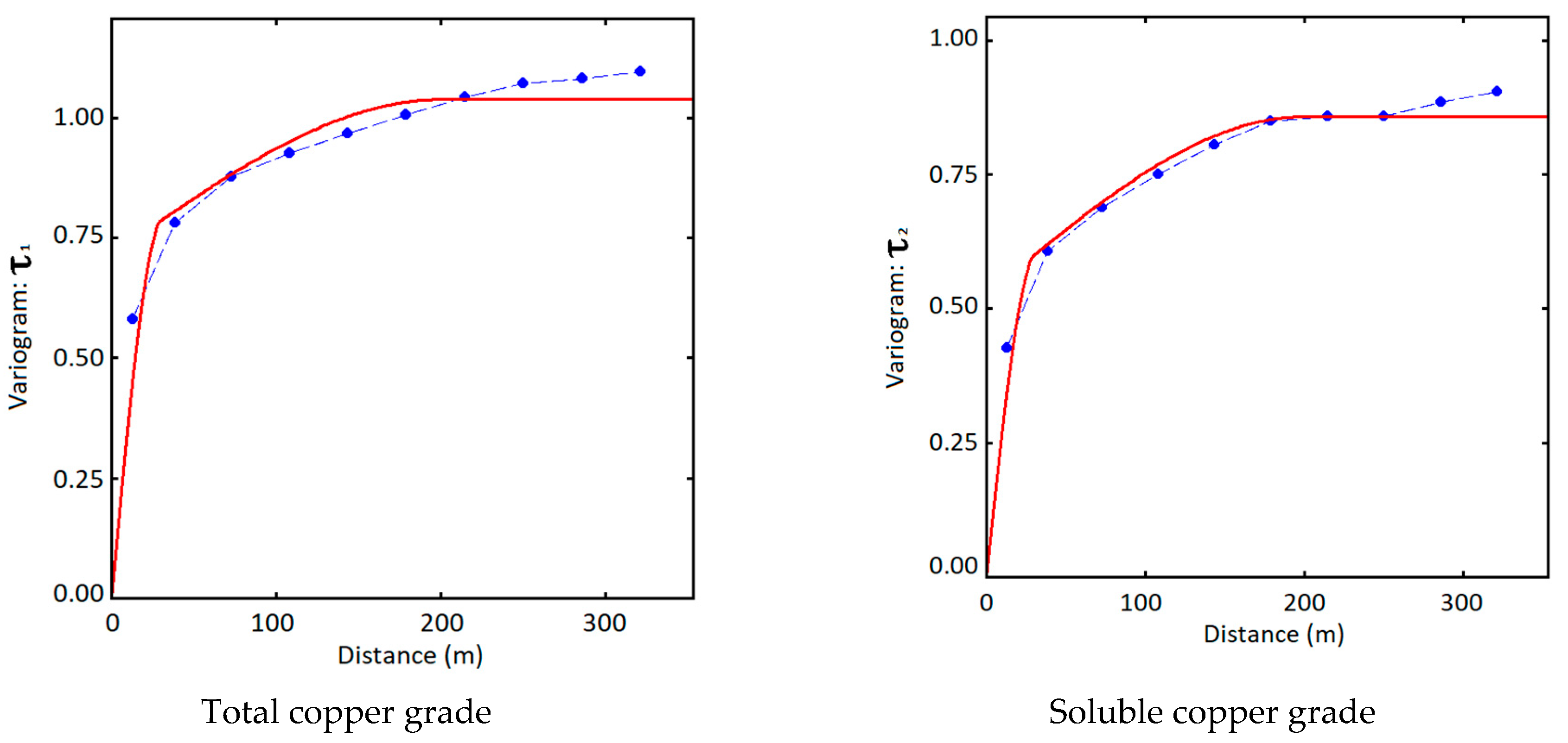

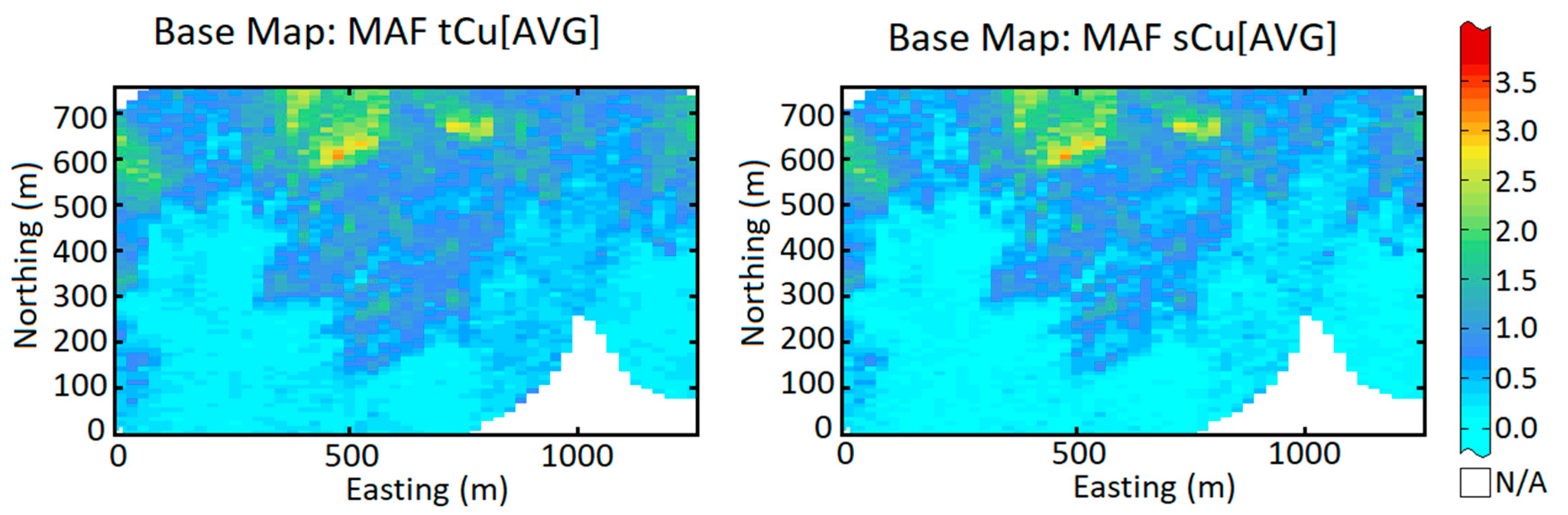



| Variable | Mean | Variance | Maximum | Minimum | COV | |
|---|---|---|---|---|---|---|
| Original | tCu(%) | 0.723 | 0.233 | 3.150 | 0.100 | 0.667 |
| sCu(%) | 0.587 | 0.232 | 2.950 | 0.000 | 0.820 | |
| Declustered | tCu(%) | 0.632 | 0.209 | 3.150 | 0.100 | 0.723 |
| sCu(%) | 0.493 | 0.203 | 2.950 | 0.000 | 0.913 |
| Mean | Variance | Correlation | |||
|---|---|---|---|---|---|
| Parameters | tCu(%) | sCu(%) | tCu(%) | sCu(%) | tCu(%) vs sCu(%) |
| Original | 0.723 | 0.587 | 0.233 | 0.232 | 0.991 |
| Declustred | 0.632 | 0.493 | 0.209 | 0.203 | 0.989 |
| Average TBcosim | 0.616 | 0.487 | 0.228 | 0.219 | 0.990 |
| Average MAF | 0.611 | 0.483 | 0.225 | 0.216 | 0.990 |
| tCu | sCu | |
|---|---|---|
| TBCOSIM | 0.284 | 0.678 |
| MAF | 0.268 | 0.667 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abildin, Y.; Madani, N.; Topal, E. A Hybrid Approach for Joint Simulation of Geometallurgical Variables with Inequality Constraint. Minerals 2019, 9, 24. https://doi.org/10.3390/min9010024
Abildin Y, Madani N, Topal E. A Hybrid Approach for Joint Simulation of Geometallurgical Variables with Inequality Constraint. Minerals. 2019; 9(1):24. https://doi.org/10.3390/min9010024
Chicago/Turabian StyleAbildin, Yerniyaz, Nasser Madani, and Erkan Topal. 2019. "A Hybrid Approach for Joint Simulation of Geometallurgical Variables with Inequality Constraint" Minerals 9, no. 1: 24. https://doi.org/10.3390/min9010024




