Computational Redox Potential Predictions: Applications to Inorganic and Organic Aqueous Complexes, and Complexes Adsorbed to Mineral Surfaces
Abstract
:1. Introduction
2. Theory of Redox Potential Predictions
2.1. Aqueous Solutions
2.2. Non-Aqueous Solutions
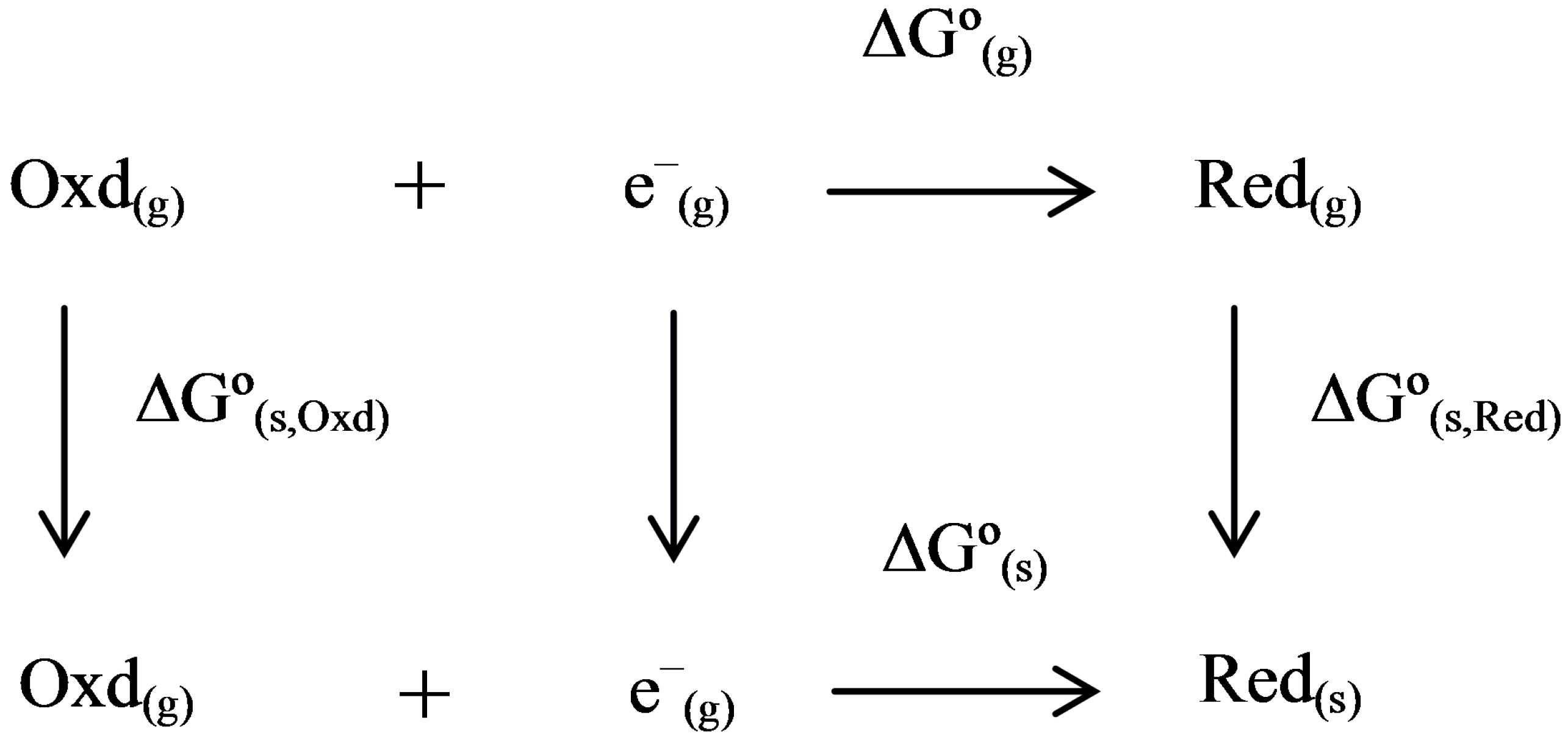
2.3. Thermodynamic Cycle
2.4. Methods Used to Calculate the Gibbs Free Energy and Redox Potential of a Redox Reaction
2.4.1. Direct Method
| Solvents | Trassatti | Fawcett | Kelly a | Kelly b |
|---|---|---|---|---|
| Water | 4.44 | 4.42 | 4.24 | 4.28 |
| Methanol | 4.19 | 4.17 | 4.34 | 4.38 |
| Ethanol | 4.21 | 4.24 | - | - |
| Acetonitrile | 4.60 | 4.59 | 4.48 | 4.52 |
| Dimethylsulfoxide | - | 3.83 | 3.92 | 3.96 |
2.4.2. Isodesmic Method
3. Computational Methods
3.1. DFT or Wave Function Based Methods
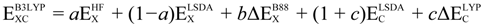
 is the Hartree-Fock exchange energy,
is the Hartree-Fock exchange energy,  the local spin density approximation, B88 the Becke’s exchange functional, a, b, and c are semi-empirical parameters and the corresponding values are 0.20, 0.72, and 0.81, respectively. The LYP term corresponds to the Lee Yang Parr correlational functional [53]. The subscript C refers to correlation whereas the X refers to exchange.
the local spin density approximation, B88 the Becke’s exchange functional, a, b, and c are semi-empirical parameters and the corresponding values are 0.20, 0.72, and 0.81, respectively. The LYP term corresponds to the Lee Yang Parr correlational functional [53]. The subscript C refers to correlation whereas the X refers to exchange.3.1.1. Choice of DFT Functional
3.1.2. Basis Set Choice
3.2. Solvation
3.3. Spin-Orbit Coupling
3.4. Molecular Dynamics Simulations
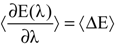
 with respect to the integration parameter, η taking values from 0 to 1 produces the free energy difference between the reactant and the product, here this free energy difference corresponds to the reduction free energy of the redox reaction.
with respect to the integration parameter, η taking values from 0 to 1 produces the free energy difference between the reactant and the product, here this free energy difference corresponds to the reduction free energy of the redox reaction.
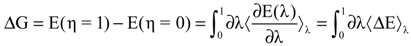
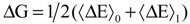
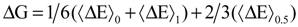
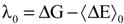
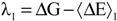
4. Applications
4.1. Organics
4.2. Inorganic Compounds
4.3. Metal Complexes
4.3.1. Transition Metal Complexes
4.3.2. Actinides
4.4. Actinyl(VI/V), Pyrite-Actinyl(VI/V), and Mackinawite-Actinyl(VI/V) Redox Potential Calculations
4.4.1. Computational Details
4.4.2. Hydration of [AnO2(H2O)5]2+/+ Complexes (An = U, Np, and Pu)
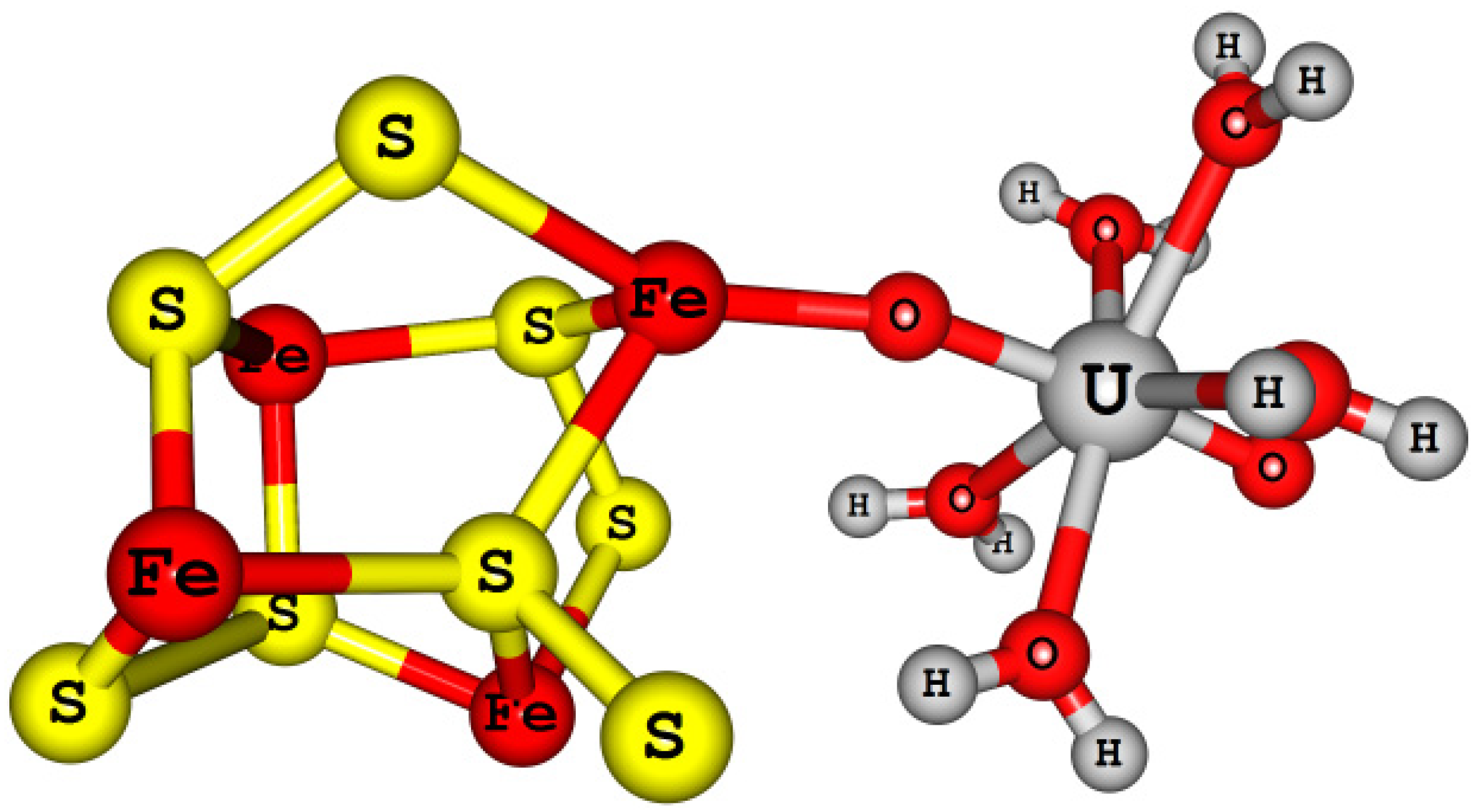
4.4.3. Actinyl (An = U, Np, and Pu) Adsorption/Reduction to Small Pyrite Clusters [Fe4S8-AnO2(H2O)5]2+/+
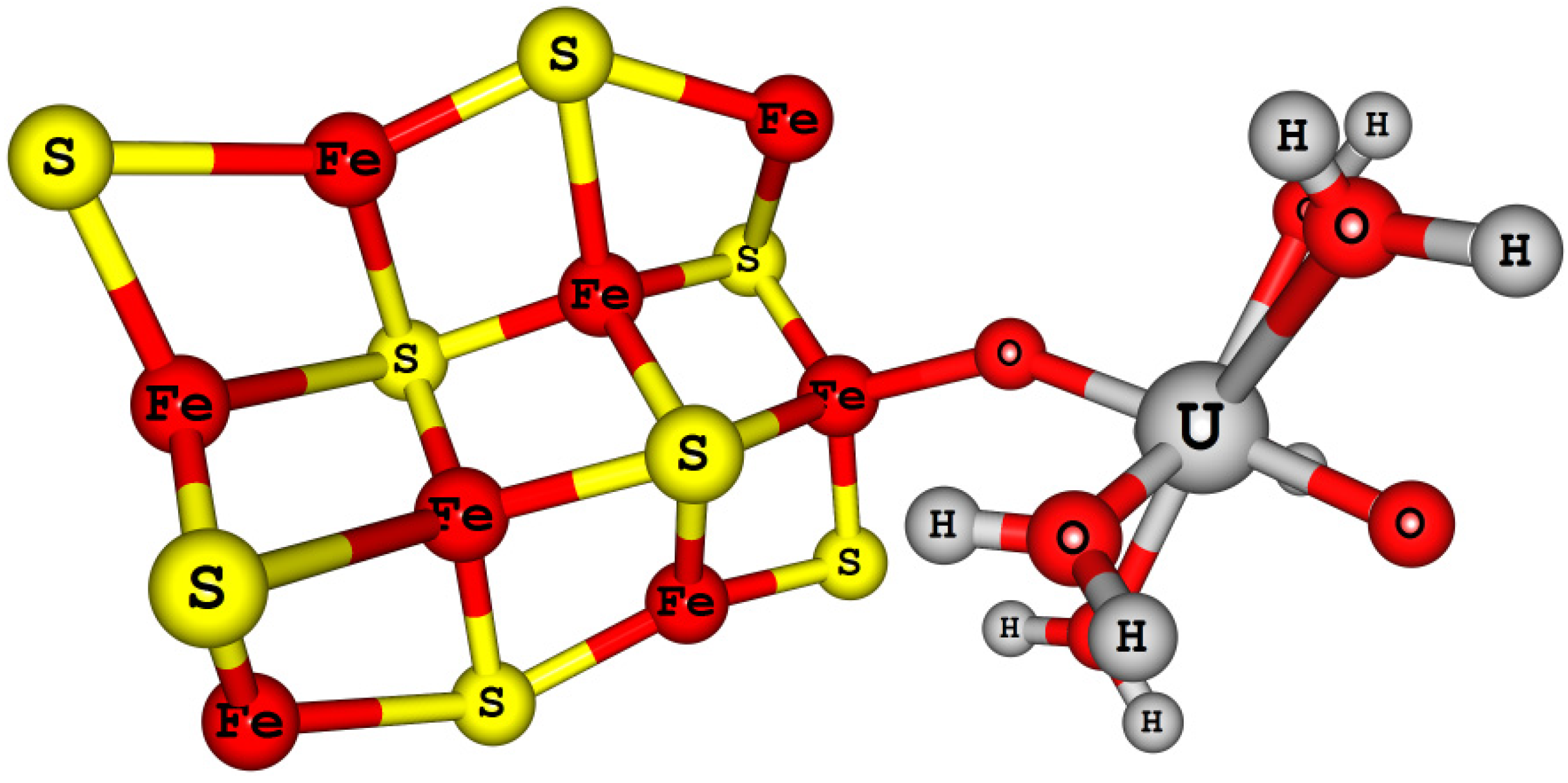
4.4.4. Actinyl (An = U, Np, and Pu) Adsorption/Reduction on Small Mackinawite Clusters [Fe8S8-AnO2(H2O)5]2+/+
| Models | Experimental | [AnO2(H2O)5]2+/+ | [Fe4S8-AnO2(H2O)5]2+/+ | [Fe8S8-AnO2(H2O)5]2+/+ | |||||
|---|---|---|---|---|---|---|---|---|---|
| Opt. a | Adiabatic b | Opt. | Adiabatic b | Opt. | Adiabatic b | ||||
| E0 | E0+SOc | E0 | E0+SOc | E0 | E0 | E0 | E0 | ||
| U | 0.088 | −0.173 | 0.137 | −0.504 | −0.194 | 0.017 | 0.145 | −0.256 | 0.234 |
| Np | 1.159 | 0.820 | 1.210 | 0.471 | 0.861 | 0.036 | 0.154 | −0.267 | −0.699 |
| Pu | 0.936 | 1.332 | 1.422 | 0.975 | 1.065 | 0.036 | 0.163 | 3.174 | −0.658 |
| MUE | - | 0.33 | 0.20 | 0.44 | 0.24 | ||||
4.5. Redox Potentials of Li Ion Battery Materials, Semiconductors, and Surfaces
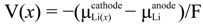
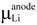 is the chemical potential of Li. Integrating the above equation (x1 = 0 and x2 = 1) gives the average voltage
is the chemical potential of Li. Integrating the above equation (x1 = 0 and x2 = 1) gives the average voltage 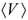 for the Li insertion between Lix1MOy and Lix2MOy compositions. From the total energies of the Lix1MOy and Lix2MOy and Li species, the average voltage
for the Li insertion between Lix1MOy and Lix2MOy compositions. From the total energies of the Lix1MOy and Lix2MOy and Li species, the average voltage 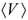 can be determined using the expression shown below:
can be determined using the expression shown below: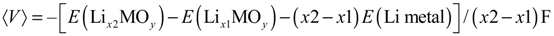
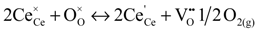
 is the Ce4+ ion in its lattice position and
is the Ce4+ ion in its lattice position and  is the oxygen atom in its lattice position. On the right hand side of the equation, the first term designates Ce3+ and the next term designates an oxygen vacancy. Moreover, the Ce(4+/3+) reduction free energies in mixed oxides such as CeO2–MO (M = Zr, Ca, Mn, Ni, and Zn) and CeO2–M2O3 (M = Sc, Mn, Y, Gd, and La) [157,160] were modeled using this approach. The Ce (4+/3+) reduction free energies were found to decrease when the content of divalent metal increased in CeO2–MO mixed oxides. Similarly, in CeO2–M2O3 mixed oxides, an increase in trivalent metal was found to predict a decrease in the Ce(4+/3+) reduction free energies. Although reduction free energies for the Ce (4+/3+) reduction process in cerium oxide materials were modeled using classical molecular dynamics approaches, these studies did not include reference electrode systems.
is the oxygen atom in its lattice position. On the right hand side of the equation, the first term designates Ce3+ and the next term designates an oxygen vacancy. Moreover, the Ce(4+/3+) reduction free energies in mixed oxides such as CeO2–MO (M = Zr, Ca, Mn, Ni, and Zn) and CeO2–M2O3 (M = Sc, Mn, Y, Gd, and La) [157,160] were modeled using this approach. The Ce (4+/3+) reduction free energies were found to decrease when the content of divalent metal increased in CeO2–MO mixed oxides. Similarly, in CeO2–M2O3 mixed oxides, an increase in trivalent metal was found to predict a decrease in the Ce(4+/3+) reduction free energies. Although reduction free energies for the Ce (4+/3+) reduction process in cerium oxide materials were modeled using classical molecular dynamics approaches, these studies did not include reference electrode systems.5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Levina, A.; Lay, P.A. Mechanistic studies of relevance to the biological activities of chromium. Coord. Chem. Rev. 2005, 249, 281–298. [Google Scholar] [CrossRef]
- Sundararajan, M.; Campbell, A.J.; Hillier, I.H. How do enzymes reduce metals? The mechanism of the reduction of Cr(VI) in chromate by cytochrome c7 proteins proposed from DFT calculations. Faraday Discuss. 2011, 148, 195–205. [Google Scholar] [CrossRef]
- Mullet, M.; Demoisson, F.; Humbert, B.; Michot, L.J.; Vantelon, D. Aqueous Cr(VI) reduction by pyrite: Speciation and characterisation of the solid phases by X-ray photoelectron, Raman and X-ray absorption spectroscopies. Geochim. Cosmochim. Acta 2007, 71, 3257–3271. [Google Scholar] [CrossRef]
- Fendorf, S.; Berkeley, L. Reduction of hexavalent chromium by amorphous iron sulfide. Environ. Sci. Technol. 1997, 31, 2039–2044. [Google Scholar] [CrossRef]
- Mullet, M.; Boursiquot, S.; Ehrhardt, J.-J. Removal of hexavalent chromium from solutions by mackinawite, tetragonal FeS. Colloids Surf. A Physicochem. Eng. Asp. 2004, 244, 77–85. [Google Scholar] [CrossRef]
- Hughes, M.F. Arsenic toxicity and potential mechanisms of action. Toxicol. Lett. 2002, 133, 1–16. [Google Scholar] [CrossRef]
- Sun, F.; Dempsey, B.A.; Osseo-Asare, K.A. As(V) and As(III) reactions on pristine pyrite and on surface-oxidized pyrite. J. Colloid Interface Sci. 2012, 388, 170–175. [Google Scholar] [CrossRef]
- Wolthers, M.; Charlet, L.; van Der Weijden, C.H.; van der Linde, P.R.; Rickard, D. Arsenic mobility in the ambient sulfidic environment: Sorption of arsenic(V) and arsenic(III) onto disordered mackinawite. Geochim. Cosmochim. Acta 2005, 69, 3483–3492. [Google Scholar] [CrossRef]
- Renock, D.; Mueller, M.; Yuan, K.; Ewing, R.C.; Becker, U. The energetics and kinetics of uranyl reduction on pyrite, hematite, and magnetite surfaces: A powder microelectrode study. Geochim. Cosmochim. Acta 2013, 118, 56–71. [Google Scholar] [CrossRef]
- Scott, T.B.; Riba Tort, O.; Allen, G.C. Aqueous uptake of uranium onto pyrite surfaces; Reactivity of fresh versus weathered material. Geochim. Cosmochim. Acta 2007, 71, 5044–5053. [Google Scholar] [CrossRef]
- Moyes, L.N.; Jones, M.J.; Pattrick, R.A.D. An X-ray absorption spectroscopy study of neptunium ( V ) reactions with mackinawite (FeS). Environ. Sci. Technol. 2002, 36, 179–183. [Google Scholar] [CrossRef]
- Kirsch, R.; Fellhauer, D.; Altmaier, M.; Neck, V.; Rossberg, A.; Fangh, T.; Charlet, L.; Scheinost, A.C. Oxidation state and local structure of plutonium reacted with magnetite, mackinawite, and chukanovite. Environ. Sci. Technol. 2011, 45, 7267–7274. [Google Scholar] [CrossRef]
- Bruggeman, C.; Maes, N. Uptake of uranium(VI) by pyrite under boom clay conditions: Influence of dissolved organic carbon. Environ. Sci. Technol. 2010, 44, 4210–4216. [Google Scholar] [CrossRef]
- Latta, D.E.; Pearce, C.I.; Rosso, K.M.; Kemner, K.M.; Boyanov, M.I. Reaction of UVI with titanium-substituted magnetite: Influence of Ti on UIV speciation. Environ. Sci. Technol. 2013, 47, 4121–4130. [Google Scholar] [CrossRef]
- Morris, D.E. Redox energetics and kinetics of uranyl coordination complexes in aqueous solution. Inorg. Chem. 2002, 41, 3542–3547. [Google Scholar] [CrossRef]
- Austin, J.P.; Sundararajan, M.; Vincent, M.A.; Hillier, I.H. The geometric structures, vibrational frequencies and redox properties of the actinyl coordination complexes ([AnO2(L)n]m; An = U, Pu, Np; L = H2O, Cl−, CO32−, CH3CO2−, OH−) in aqueous solution, studied by density functional theory methods. Dalt. Trans. 2009, 5902–5909. [Google Scholar]
- Steele, H.; Taylor, R.J. A theoretical study of the inner-sphere disproportionation reaction mechanism of the pentavalent actinyl ions. Inorg. Chem. 2007, 46, 6311–6318. [Google Scholar] [CrossRef]
- Alessi, D.S.; Uster, B.; Veeramani, H.; Suvorova, E.I.; Lezama-Pacheco, J.S.; Stubbs, J.E.; Bargar, J.R.; Bernier-Latmani, R. Quantitative separation of monomeric U(IV) from UO2 in products of U(VI) reduction. Environ. Sci. Technol. 2012, 46, 6150–6157. [Google Scholar] [CrossRef]
- Wall, J.D.; Krumholz, L.R. Uranium reduction. Annu. Rev. Microbiol. 2006, 60, 149–166. [Google Scholar] [CrossRef]
- Renshaw, J.C.; Butchins, L.J.C.; Livens, F.R.; May, I.; Charnock, J.M.; Lloyd, J.R. Bioreduction of uranium: Environmental implications of a pentavalent intermediate. Environ. Sci. Technol. 2005, 39, 5657–5660. [Google Scholar] [CrossRef]
- Lovley, D.R.; Phillips, E.J.P.; Survey, U.S.G. Bioremediation of uranium contamination with enzymatic uranium reduction. Envirn. Sci. Technol. 1992, 26, 2228–2234. [Google Scholar] [CrossRef]
- Luo, W.; Wu, W.-M.; Yan, T.; Criddle, C.S.; Jardine, P.M.; Zhou, J.; Gu, B. Influence of bicarbonate, sulfate, and electron donors on biological reduction of uranium and microbial community composition. Appl. Microbiol. Biotechnol. 2007, 77, 713–721. [Google Scholar] [CrossRef]
- Sundararajan, M.; Campbell, A.J.; Hillier, I.H. Catalytic cycles for the reduction of [UO2]2+ by cytochrome c7 proteins proposed from DFT calculations. J. Phys. Chem. A 2008, 112, 4451–4457. [Google Scholar] [CrossRef]
- Sundararajan, M.; Assary, R.S.; Hillier, I.H.; Vaughan, D.J. The mechanism of the reduction of [AnO2]2+ (An = U, Np, Pu) in aqueous solution, and by Fe(II) containing proteins and mineral surfaces, probed by DFT calculations. Dalt. Trans. 2011, 40, 11156–11163. [Google Scholar] [CrossRef]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Single-ion solvation free energies and the normal hydrogen electrode potential in methanol , acetonitrile , and dimethyl sulfoxide. J. Phys. Chem. B 2007, 111, 408–422. [Google Scholar] [CrossRef]
- Trasatti, S. The absolute electrode potential: An explanatory note. Pure Appl. Chem. 1986, 58, 955–966. [Google Scholar]
- Fawcett, W.R.; Acta, S.E. The ionic work function and its role in estimating absolute electrode potentials. Langmuir 2008, 24, 9868–9875. [Google Scholar] [CrossRef]
- Reiss, H. The absolute potential of the standard hydrogen electrode: A new estimate. J. Phys. Chem. 1985, 89, 4207–4213. [Google Scholar] [CrossRef]
- Hansen, W.N.; Kolb, D.M. The work function of emersed electrodes. J. Electroanal. Chem. Interfacial Electrochem. 1979, 100, 493–500. [Google Scholar] [CrossRef]
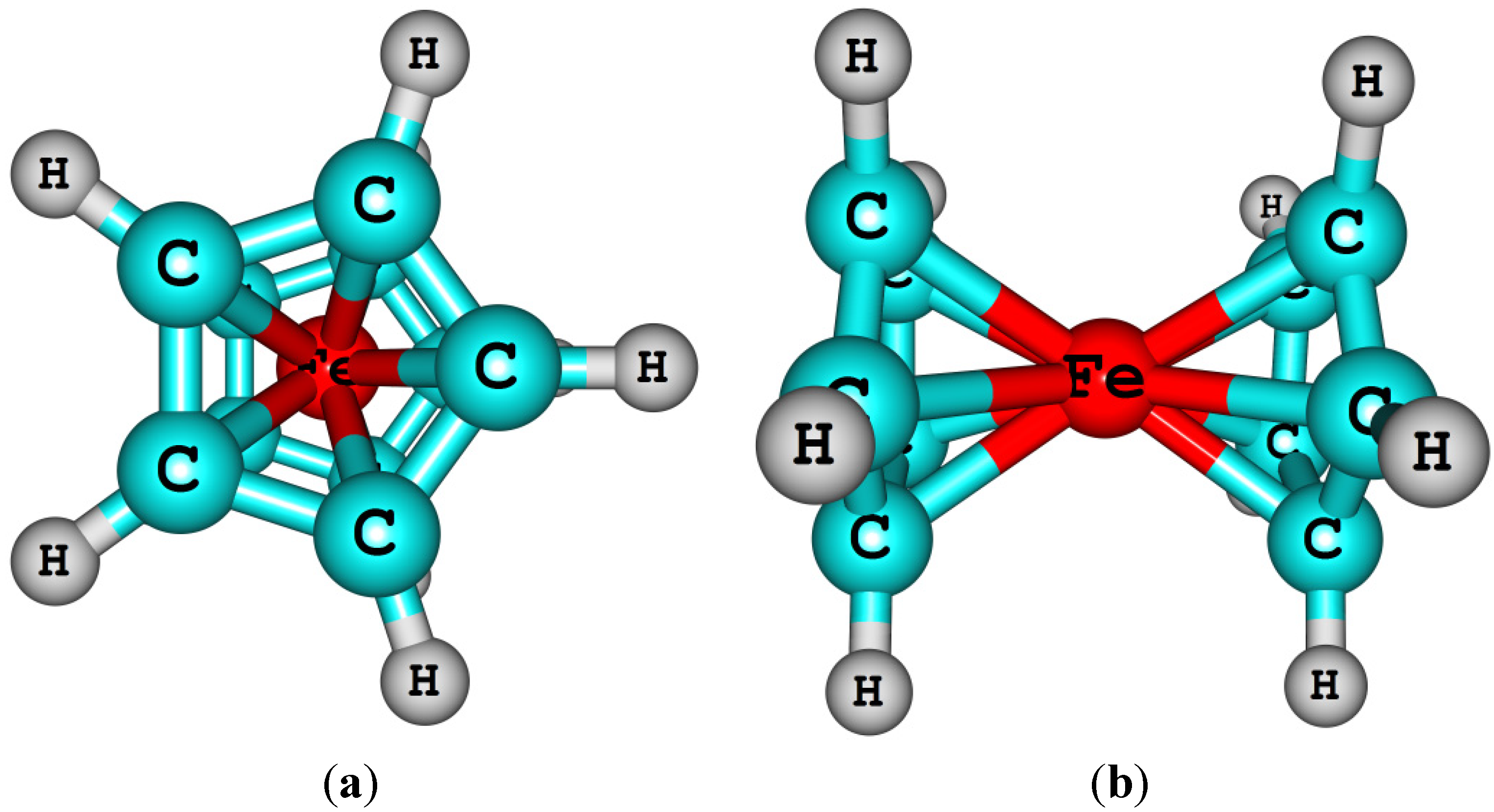
- Coriani, S.; Haaland, A.; Helgaker, T.; Jørgensen, P. The equilibrium structure of ferrocene. Chemphyschem 2006, 7, 245–249. [Google Scholar] [CrossRef]
- Gritzner, G.; Kuta, J. Recommendations on reporting electrode potenitals in nonaqueous solvents. Pure Appl. Chem. 1982, 54, 1527–1532. [Google Scholar]
- Pavlishchuk, V.V.; Addison, A.W. Conversion constants for redox potentials measured versus different reference electrodes in acetonitrile solutions at 25 °C. Inorganica Chim. Acta 2000, 298, 97–102. [Google Scholar] [CrossRef]
- Isse, A.A.; Gennaro, A. Absolute potential of the standard hydrogen electrode and the problem of interconversion of potentials in different solvents. J. Phys. Chem. B 2010, 114, 7894–7899. [Google Scholar] [CrossRef]
- Konezny, S.J.; Doherty, M.D.; Luca, O.R.; Crabtree, R.H.; Soloveichik, G.L.; Batista, V.S. Reduction of systematic uncertainty in DFT redox potentials of transition-metal complexes. J. Phys. Chem. C 2012, 116, 6349–6356. [Google Scholar]
- Bartmess, J.E. Thermodynamics of the electron and the proton. J. Phys. Chem. 1994, 98, 6420–6424. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry Theories and Models, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2004; pp. 378–379. [Google Scholar]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Aqueous solvation free energies of ions and ion—Water clusters based on an accurate value for the absolute aqueous solvation free energy of the proton. J. Phys. Chem. B 2006, 110, 16066–16081. [Google Scholar] [CrossRef]
- Namazian, M.; Almodarresieh, H.A.; Noorbala, M.R.; Zare, H.R. DFT calculation of electrode potentials for substituted quinones in aqueous solution. Chem. Phys. Lett. 2004, 396, 424–428. [Google Scholar] [CrossRef]
- Zhu, X.-Q.; Wang, C.-H.; Liang, H. Scales of oxidation potentials, pK(a), and BDE of various hydroquinones and catechols in DMSO. J. Org. Chem. 2010, 75, 7240–7257. [Google Scholar] [CrossRef]
- Alizadeh, K.; Shamsipur, M. Calculation of the two-step reduction potentials of some quinones in acetonitrile. J. Mol. Struct. Theochem. 2008, 862, 39–43. [Google Scholar] [CrossRef]
- Zhu, X.-Q.; Wang, C.-H. Accurate estimation of the one-electron reduction potentials of various substituted quinones in DMSO and CH3CN. J. Org. Chem. 2010, 75, 5037–5047. [Google Scholar] [CrossRef]
- Fernandez, L.E.; Horvath, S.; Hammes-Schi, S. Theoretical analysis of the sequential proton-coupled electron transfer mechanisms for H2 oxidation and production pathways catalyzed by nickel molecular electrocatalysts. J. Phys. Chem. C 2012, 3171–3180. [Google Scholar] [CrossRef]
- Solis, B.H.; Hammes-Schiffer, S. Computational study of anomalous reduction potentials for hydrogen evolution catalyzed by cobalt dithiolene complexes. J. Am. Chem. Soc. 2012, 134, 15253–15256. [Google Scholar] [CrossRef]
- Solis, B.H.; Hammes-Schiffer, S. Substituent effects on cobalt diglyoxime catalysts for hydrogen evolution. J. Am. Chem. Soc. 2011, 133, 19036–19039. [Google Scholar] [CrossRef]
- Arumugam, K. Redox Chemistry of Actinyl Complexes in Solution: A DFT Study. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2012. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for density functional theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2007, 120, 215–241. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. [Google Scholar] [CrossRef]
- Becke, A.D. Density-fnnctional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Castro, L. Calculations of one-electron redox potentials of oxoiron(IV) porphyrin complexes. J. Chem. Theory Comput. 2013, 10, 243–251. [Google Scholar] [CrossRef]
- Roy, L.E.; Jakubikova, E.; Guthrie, M.G.; Batista, E.R. Calculation of one-electron redox potentials revisited. Is it possible to calculate accurate potentials with density functional methods? J. Phys. Chem. A 2009, 113, 6745–6750. [Google Scholar]
- Roy, L.E.; Batista, E.R.; Hay, P.J. Theoretical studies on the redox potentials of Fe dinuclear complexes as models for hydrogenase. Inorg. Chem. 2008, 47, 9228–9237. [Google Scholar] [CrossRef]
- Austin, J.P.; Burton, N.A.; Hillier, I.H.; Sundararajan, M.; Vincent, M.A. Which density functional should be used to study actinyl complexes? Phys. Chem. Chem. Phys. 2009, 11, 1143–1145. [Google Scholar] [CrossRef]
- Steele, H.M.; Guillaumont, D.; Moisy, P. Density functional theory calculations of the redox potentials of actinide(VI)/actinide(V) couple in water. J. Phys. Chem. A 2013, 117, 4500–4505. [Google Scholar] [CrossRef]
- Jaque, P.; Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Computational electrochemistry: The aqueous Ru3+|Ru2+ reduction potential. J. Phys. Chem. C 2007, 111, 5783–5799. [Google Scholar] [CrossRef]
- Baik, M.-H.; Friesner, R.A. Computing redox potentials in solution: Density functional theory as a tool for rational design of redox agents. J. Phys. Chem. A 2002, 106, 7407–7412. [Google Scholar] [CrossRef]
- Mennucci, B.; Tomasi, J.; Cammi, R.; Cheeseman, J.R.; Frisch, M.J.; Devlin, F.J.; Gabriel, S.; Stephens, P.J. Polarizable continuum model (PCM) Calculations of solvent effects on optical rotations of chiral molecules. J. Phys. Chem. A 2002, 106, 6102–6113. [Google Scholar] [CrossRef]
- Klamt, A.; Schuurmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2 1993, 1993, 799–805. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in soluion by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic propoerties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Mennucci, B.; Cancès, E.; Tomasi, J. Evaluation of solvent effects in isotropic and anisotropic dielectrics and in ionic solutions with a unified integral equation method: theoretical bases, computational implementation, and numerical applications. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Burger, T.; Lohrenz, J.C.W. Refinement and parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Edinger, S.R.; Cortis, C.; Shenkin, P.S.; Friesner, R.A. Solvation free energies of peptides: Comparison of approximate continuum solvation models with accurate solution of the Poisson–Boltzmann equation. J. Phys. Chem. B 1997, 101, 1190–1197. [Google Scholar] [CrossRef]
- Friedrichs, M.; Zhou, R.; Edinger, S.R.; Friesner, R.A. Poisson–Boltzmann analytical gradients for molecular modeling calculations. J. Phys. Chem. B 1999, 103, 3057–3061. [Google Scholar] [CrossRef]
- Marten, B.; Kim, K.; Cortis, C.; Friesner, R.A.; Murphy, R.B.; Ringnalda, M.N.; Sitkoff, D.; Honig, B. New model for calculation of solvation free energies: Correction of self-consistent reaction field continuum dielectric theory for short-range hydrogen-bonding effects. J. Phys. Chem. 1996, 100, 11775–11788. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H.P.; Izmaylov, A.F.; Bloino, J.; Zheng, G.; Sonnenberg, J.L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J.A., Jr.; Peralta, J.E.; Ogliaro, F.; Bearpark, M.; Heyd, J.J.; Brothers, E.; Kudin, K.N.; Staroverov, V.N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J.C.; Iyengar, S.S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, J.M.; Klene, M.; Knox, J.E.; Cross, J.B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R.E.; Yazyev, O.; Austin, A.J.; Cammi, R.; Pomelli, C.; Ochterski, J.W.; Martin, R.L.; Morokuma, K.; Zakrzewski, V.G.; Voth, G.A.; Salvador, P.; Dannenberg, J.J.; Dapprich, S.; Daniels, A.D.; Farkas, Ö.; Foresman, J.B.; Ortiz, J.V.; Cioslowski, J.; Fox, D.J. Gaussian 09, Revision A.02, Gaussian, Inc.: Wallingford, CT, USA, 2009.
- Takano, Y.; Houk, K.N.; Angeles, L. Benchmarking the conductor-like polarizable continuum model (CPCM) for aqueous solvation free energies of neutral and ionic organic molecules. J. Chem. Theory Comput. 2005, 1, 70–77. [Google Scholar] [CrossRef]
- Methods, I.S.; Chiorescu, I.; Deubel, D.V.; Arion, V.B.; Keppler, B.K. Computational electrochemistry of ruthenium anticancer agents. Unprecedented benchmarking of implicit solvation methods. J. Chem. Theory Comput. 2008, 4, 499–506. [Google Scholar] [CrossRef]
- Bondi, A. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Uudsemaa, M.; Tamm, T. Density-functional theory calculations of aqueous redox potentials of fourth-period transition metals. J. Phys. Chem. A 2003, 107, 9997–10003. [Google Scholar] [CrossRef]
- Keith, T.A.; Frisch, M.J. Inclusion of explicit solvent molecules in a self-consistent-reaction field model of solvation. ACS Symp. Ser. 1994, 569, 22–35. [Google Scholar] [CrossRef]
- Hughes, T.F.; Friesner, R.A. Development of accurate DFT methods for computing redox potentials of transition metal complexes: Results for model complexes and application to cytochrome P450. J. Chem. Theory Comput. 2012, 8, 442–459. [Google Scholar] [CrossRef]
- Srnec, M.; Chalupský, J.; Fojta, M.; Zendlová, L.; Havran, L.; Hocek, M.; Kývala, M.; Rulísek, L. Effect of spin-orbit coupling on reduction potentials of octahedral ruthenium(II/III) and osmium(II/III) complexes. J. Am. Chem. Soc. 2008, 130, 10947–10954. [Google Scholar] [CrossRef]
- Hay, P.J.; Martin, R.L.; Schreckenbach, G. Theoretical studies of the properties and solution chemistry of AnO22+ and AnO2+ aquo complexes for An = U , Np , and Pu. J. Phys. Chem. A 2000, 104, 6259–6270. [Google Scholar] [CrossRef]
- Wang, L.-P.; Van Voorhis, T. A polarizable QM/MM explicit solvent model for computational electrochemistry in water. J. Chem. Theory Comput. 2012, 8, 610–617. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.; Cui, Q. Free energy perturbation calculations with combined QM/MM potentials complications, simplifications, and applications to redox potential calculations. J. Phys. Chem. B 2003, 107, 8643–8653. [Google Scholar] [CrossRef]
- Formaneck, M.S.; Li, G.; Zhang, X.; Cui, Q. Calculating accurate redox potentials in enzymes with a combined QM/MM free energy perturbation approach. J. Theor. Comput. Chem. 2002, 1, 53–67. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, H.; Hu, X.; Yang, W. Calculating solution redox free energies with ab initio quantum mechanical/molecular mechanical minimum free energy path method. J. Chem. Phys. 2009, 130, 164111. [Google Scholar] [CrossRef]
- Costanzo, F.; Sulpizi, M.; Della Valle, R.G.; Sprik, M. The oxidation of tyrosine and tryptophan studied by a molecular dynamics normal hydrogen electrode. J. Chem. Phys. 2011, 134, 244508. [Google Scholar] [CrossRef]
- Rauschnot, J.C.; Yang, C.; Yang, V.; Bhattacharyya, S. Theoretical determination of the redox potentials of NRH:Quinone oxidoreductase 2 using quantum mechanical/molecular mechanical simulations. J. Phys. Chem. B 2009, 113, 8149–8157. [Google Scholar] [CrossRef]
- Oxidase, C.; Bhattacharyya, S.; Stankovich, M.T.; Truhlar, D.G.; Gao, J. Combined quantum mechanical and molecular mechanical simulations of one- and two-electron reduction potentials of flavin cofactor in water, medium-chain acyl-CoA dehydrogenase, and cholesterol oxidase. J. Phys. Chem. A 2007, 111, 5729–5742. [Google Scholar] [CrossRef]
- Van den Bosch, M.; Swart, M.; Snijders, J.G.; Berendsen, H.J.C.; Mark, A.E.; Oostenbrink, C.; van Gunsteren, W.F.; Canters, G.W. Calculation of the redox potential of the protein azurin and some mutants. Chembiochem 2005, 6, 738–746. [Google Scholar] [CrossRef]
- Blumberger, J.; Tateyama, Y.; Sprik, M. Ab initio molecular dynamics simulation of redox reactions in solution. Comput. Phys. Commun. 2005, 169, 256–261. [Google Scholar] [CrossRef]
- VandeVondele, J.; Ayala, R.; Sulpizi, M.; Sprik, M. Redox free energies and one-electron energy levels in density functional theory based ab initio molecular dynamics. J. Electroanal. Chem. 2007, 607, 113–120. [Google Scholar]
- Adriaanse, C.; Cheng, J.; Chau, V.; Sulpizi, M.; VandeVondele, J.; Sprik, M. Aqueous redox chemistry and the electronic band structure of liquid water. J. Phys. Chem. Lett. 2012, 3, 3411–3415. [Google Scholar] [CrossRef]
- Blumberger, J.; Sprik, M. Ab initio molecular dynamics simulation of the aqueous Ru2+/Ru3+ redox reaction: The Marcus perspective. J. Phys. Chem. B 2005, 109, 6793–6804. [Google Scholar] [CrossRef]
- Kamerlin, S.C.L.; Haranczyk, M.; Warshel, A. Progress in ab initio QM/MM free-energy simulations of electrostatic energies in proteins: accelerated QM/MM studies of pKa, redox reactions and solvation free energies. J. Phys. Chem. B 2009, 113, 1253–1272. [Google Scholar] [CrossRef]
- Cheng, J.; Sulpizi, M.; Sprik, M. Redox potentials and pKa for benzoquinone from density functional theory based molecular dynamics. J. Chem. Phys. 2009, 131, 154504. [Google Scholar] [CrossRef]
- Evans, D.H. One-electron and two-electron transfers in electrochemistry and homogeneous solution reactions. Chem. Rev. 2008, 108, 2113–2144. [Google Scholar] [CrossRef]
- Costentin, C. Electrochemical approach to the mechanistic study of proton-coupled electron transfer. Chem. Rev. 2008, 108, 2145–2179. [Google Scholar] [CrossRef]
- Savéant, J.-M. Molecular catalysis of electrochemical reactions. Mechanistic aspects. Chem. Rev. 2008, 108, 2348–2378. [Google Scholar] [CrossRef]
- Yoshida, J.; Kataoka, K.; Horcajada, R.; Nagaki, A. Modern strategies in electroorganic synthesis. Chem. Rev. 2008, 108, 2265–2299. [Google Scholar] [CrossRef]
- Keith, J.A.; Carter, E.A. Theoretical insights into pyridinium-based photoelectrocatalytic reduction of CO2. J. Am. Chem. Soc. 2012, 134, 7580–7583. [Google Scholar] [CrossRef]
- Namazian, M.; Coote, M.L. Accurate calculation of absolute one-electron redox potentials of some para-quinone derivatives in acetonitrile. J. Phys. Chem. A 2007, 3, 7227–7232. [Google Scholar] [CrossRef]
- Gogoll, A.; Strømme, M.; Sjo, M. Investigation of the redox chemistry of isoindole-4,7-diones. J. Phys. Chem. C 2013, 117, 894–901. [Google Scholar] [CrossRef]
- Karlsson, C.; Ja, E.; Strømme, M.; Sjo, M. Computational electrochemistry study of 16 isoindole-4,7-diones as candidates for organic cathode materials. J. Phys. Chem. C 2012, 116, 3793–2801. [Google Scholar] [CrossRef]
- Francke, R.; Little, R.D. Optimizing Electron transfer mediators based on arylimidazoles by ring fusion: Synthesis, electrochemistry and computational analysis of 2-aryl-1-methylphenanthro[9,10-d]imidazoles. J. Am. Chem. Soc. 2013, 136, 427–435. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, L.; Yu, H.-Z.; Wang, Y.-M.; Guo, Q.-X. Quantum-chemical predictions of absolute standard redox potentials of diverse organic molecules and free radicals in acetonitrile. J. Am. Chem. Soc. 2005, 127, 7227–7234. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, L.; Wang, Y.-M.; Li, J.-N.; Yu, T.-Q.; Guo, Q.-X. Quantum-chemical predictions of redox potentials of organic anions in dimethyl sulfoxide and reevaluation of bond dissociation enthalpies measured by the electrochemical methods. J. Phys. Chem. A 2006, 110, 5874–5886. [Google Scholar] [CrossRef]
- Lynch, E.J.; Speelman, A.L.; Curry, B.A.; Murillo, C.S.; Gillmore, J.G. Expanding and testing a computational method for predicting the ground state reduction potentials of organic molecules on the basis of empirical correlation to experiment. J. Org. Chem. 2012, 77, 6423–6430. [Google Scholar] [CrossRef]
- Bogart, J.A.; Lee, H.B.; Boreen, M.A.; Jun, M.; Schelter, E.J. Fine-tuning the oxidative ability of persistent radicals: Electrochemical and computational studies of substituted 2-pyridylhydroxylamines. J. Org. Chem. 2013, 78, 6344–6349. [Google Scholar] [CrossRef]
- Davis, A.P.; Fry, A.J. Experimental and computed absolute redox potentials of polycyclic aromatic hydrocarbons are highly linearly correlated over a wide range of structures and potentials. J. Phys. Chem. A 2010, 114, 12299–12304. [Google Scholar] [CrossRef]
- Blinco, J.P.; Hodgson, J.L.; Morrow, B.J.; Walker, J.R.; Will, G.D.; Coote, M.L.; Bottle, S.E. Experimental and theoretical studies of the redox potentials of cyclic nitroxides. J. Org. Chem. 2008, 73, 6763–6771. [Google Scholar] [CrossRef]
- Hodgson, J.L.; Namazian, M.; Bottle, S.E.; Coote, M.L. One-electron oxidation and reduction potentials of nitroxide antioxidants: A theoretical study. J. Phys. Chem. A 2007, 111, 13595–13605. [Google Scholar] [CrossRef]
- Guerard, J.J.; Arey, J.S. Critical evaluation of implicit solvent models for predicting aqueous oxidation potentials of neutral organic compounds. J. Chem. Theory Comput. 2013, 9, 5046–5058. [Google Scholar] [CrossRef]
- Psciuk, B.T.; Lord, R.L.; Munk, B.H.; Schlegel, H.B. Theoretical determination of one-electron oxidation potentials for nucleic acid bases. J. Chem. Theory Comput. 2012, 8, 5107–5123. [Google Scholar] [CrossRef]
- Psciuk, B.T.; Schlegel, H.B. Computational prediction of one-electron reduction potentials and acid dissociation constants for guanine oxidation intermediates and products. J. Phys. Chem. B 2013, 117, 9518–9531. [Google Scholar] [CrossRef]
- Baik, M.-H.; Silverman, J.S.; Yang, I.V.; Ropp, P.A.; Szalai, V.A.; Yang, W.; Thorp, H.H. Using density functional theory to design DNA base analogues with low oxidation potentials. J. Phys. Chem. B 2001, 105, 6437–6444. [Google Scholar] [CrossRef]
- Crespo-Hernandez, C.E.; Arce, R.; Ishikawa, Y.; Gorb, L.; Leszczynski, J.; Close, D.M. Ab initio ionization energy thresholds of DNA and RNA bases in gas phase and in aqueous solution. J. Phys. Chem. A 2004, 108, 6373–6377. [Google Scholar] [CrossRef]
- Paukku, Y.; Hill, G. Theoretical determination of one-electron redox potentials for DNA bases, base pairs, and stacks. J. Phys. Chem. A 2011, 115, 4804–4810. [Google Scholar] [CrossRef]
- Lin, M.-J.; Liu, W.-X.; Peng, C.R.; Lu, W.-C. A First-principles method for predicting redox potentials of nucleobases and the metabolites in aqueous solution. Acta Phys. Chim. Sin. 2011, 27, 595–603. [Google Scholar]
- Li, X.-L.; Fu, Y. Theoretical study of reduction potentials of substituted flavins. J. Mol. Struct. Theochem 2008, 856, 112–118. [Google Scholar] [CrossRef]
- North, M.A.; Bhattacharyya, S.; Truhlar, D.G. Improved density functional description of the electrochemistry and structure-property descriptors of substituted flavins. J. Phys. Chem. B 2010, 114, 14907–14915. [Google Scholar] [CrossRef]
- Walsh, J.D.; Miller, A. Flavin reduction potential tuning by substitution and bending. J. Mol. Struct. Theochem 2003, 623, 185–195. [Google Scholar] [CrossRef]
- Wade, K. The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds. J. Chem. Soc. D Chem. Commun. 1971, 1971, 792–793. [Google Scholar] [CrossRef]
- Welch, A.J. The significance and impact of Wade’s rules. Chem. Commun. 2013, 49, 3615–3616. [Google Scholar] [CrossRef]
- Wahab, A.; Stepp, B.; Douvris, C.; Valášek, M.; Štursa, J.; Klíma, J.; Piqueras, M.-C.; Crespo, R.; Ludvík, J.; Michl, J. Measured and calculated oxidation potentials of 1-X-12-Y-CB11Me10− anions. Inorg. Chem. 2012, 51, 5128–5137. [Google Scholar] [CrossRef]
- Boeré, R.T.; Bolli, C.; Finze, M.; Himmelspach, A.; Knapp, C.; Roemmele, T.L. Quantum-chemical and electrochemical investigation of the electrochemical windows of halogenated carborate anions. Chemistry 2013, 19, 1784–1795. [Google Scholar]
- Lee, T.B.; Mckee, M.L. Redox energetics of Hypercloso boron hydrides BnHn (n = 6–13) and B12X12 (X = F, Cl, OH, and CH3). Inorg. Chem. 2012, 51, 4205–4214. [Google Scholar] [CrossRef]
- Moens, J.; Geerlings, P.; Roos, G. A conceptual DFT approach for the evaluation and interpretation of redox potentials. Chem. Eur. J. 2007, 13, 8174–8184. [Google Scholar] [CrossRef]
- Li, J.; Fisher, C.L.; Chen, J.L.; Bashford, D.; Noodleman, L. Calculation of redox potentials and pka values of hydrated transition metal cations by a combined density functional and continuum dielectric theory. Inorg. Chem. 1996, 35, 4694–4702. [Google Scholar] [CrossRef]
- Chen, S.; Wang, L.-W. Thermodynamic oxidation and reduction potentials of photocatalytic semiconductors in aqueous solution. Chem. Mater. 2012, 24, 3659–3666. [Google Scholar] [CrossRef]
- Matsui, T.; Kitagawa, Y.; Shigeta, Y.; Okumura, M. A density functional theory based protocol to compute the redox potential of transition metal complex with the correction of pseudo-counterion: General theory and applications. J. Chem. Theory Comput. 2013, 9, 2974–2980. [Google Scholar] [CrossRef]
- Moens, J.; De Proft, F.; Geerlings, P. A density functional theory study on ligand additive effects on redox potentials. Phys. Chem. Chem. Phys. 2010, 12, 13174–13181. [Google Scholar] [CrossRef]
- Haines, D.E.; O’Hanlon, D.C.; Manna, J.; Jones, M.K.; Shaner, S.E.; Sun, J.; Hopkins, M.D. Oxidation-potential tuning of tungsten-alkylidyne complexes over a 2 V range. Inorg. Chem. 2013, 52, 9650–9658. [Google Scholar] [CrossRef]
- Holland, J.P.; Green, J.C.; Dilworth, J.R. Probing the mechanism of hypoxia selectivity of copper bis(thiosemicarbazonato) complexes: DFT calculation of redox potentials and absolute acidities in solution. Dalt. Trans. 2006, 783–794. [Google Scholar] [CrossRef]
- Berard, J.J.; Schreckenbach, G.; Arnold, P.L.; Patel, D.; Love, J.B. Computational density functional study of polypyrrolic macrocycles: analysis of actinyl-oxo to 3d transition metal bonding. Inorg. Chem. 2008, 47, 11583–11592. [Google Scholar] [CrossRef]
- Shamov, G.A.; Schreckenbach, G. Density functional studies of actinyl aquo complexes studied using small-core effective core potentials and a scalar four-component relativistic method. J. Phys. Chem. A 2005, 109, 10961–10974. [Google Scholar] [CrossRef]
- Shamov, G.A.; Schreckenbach, G. Relativistic density functional theory study of dioxoactinide(VI) and -(V) complexation with alaskaphyrin and related Schiff-base macrocyclic ligands. J. Phys. Chem. A 2006, 110, 9486–9499. [Google Scholar] [CrossRef]
- Horowitz, S.E.; Marston, J.B. Strong correlations in actinide redox reactions. J. Chem. Phys. 2011, 134, 064510. [Google Scholar] [CrossRef]
- Tsushima, S.; Wahlgren, U.; Grenthe, I. Quantum chemical calculations of reduction potentials of AnO22+/AnO2+ (An = U, Np, Pu, Am) and Fe3+/Fe2+ couples. J. Phys. Chem. A 2006, 9175–9182. [Google Scholar] [CrossRef]
- Schreckenbach, G.; Shamov, G.A. Theoretical actinide molecular science. Acc. Chem. Res. 2010, 43, 19–29. [Google Scholar] [CrossRef]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A., III; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Rappe, A.K.; Colwell, K.S.; Casewit, C.J. Application of a universal force field to metal complexes. Inorg. Chem. 1993, 3438–3450. [Google Scholar]
- Elkechai, A.; Boucekkine, A.; Belkhiri, L.; Amarouche, M.; Clappe, C.; Hauchard, D.; Ephritikhine, M. A DFT and experimental investigation of the electron affinity of the triscyclopentadienyl uranium complexes Cp3UX. Dalt. Trans. 2009, 2009, 2843–2849. [Google Scholar]
- Elkechai, A.; Meskaldji, S.; Boucekkine, A.; Belkhiri, L.; Bouchet, D.; Amarouche, M.; Clappe, C.; Hauchard, D.; Ephritikhine, M. A relativistic DFT study of the electron affinity of the biscyclopentadienyl uranium complexes Cp*2UX2. J. Mol. Struct. Theochem 2010, 954, 115–123. [Google Scholar] [CrossRef]
- Elkechai, A.; Boucekkine, A.; Belkhiri, L.; Hauchard, D.; Clappe, C.; Ephritikhine, M. Electron affinities of biscyclopentadienyl and phospholyl uranium(IV) borohydride complexes: Experimental and DFT studies. Comptes Rendus Chim. 2010, 13, 860–869. [Google Scholar] [CrossRef]
- Elkechai, A.; Mani, Y.; Boucekkine, A.; Ephritikhine, M. Density functional theory investigation of the redox properties of tricyclopentadienyl- and phospholyluranium(IV) chloride complexes. Inorg. Chem. 2012, 51, 6943–6952. [Google Scholar] [CrossRef]
- Küchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted pseudopotentials for the actinides. Parameter sets and test calculations for thorium and thorium monoxide. J. Chem. Phys. 1994, 100, 7535–7542. [Google Scholar]
- Cao, Z.; Balasubramanian, K. Theoretical studies of UO2(H2O)n2+, NpO2(H2O)n+, and PuO2(H22O)n2+ complexes (n = 4–6) in aqueous solution and gas phase. J. Chem. Phys. 2005, 123, 114309. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
- Meng, Y.S.; Arroyo-de Dompablo, M.E. First principles computational materials design for energy storage materials in lithium ion batteries. Energy Environ. Sci. 2009, 2, 589–609. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, F.; Meng, Y.; Ceder, G. First-principles study of surface properties of LiFePO4: Surface energy, structure, Wulff shape, and surface redox potential. Phys. Rev. B 2007, 76, 165435. [Google Scholar] [CrossRef]
- Zhou, F.; Cococcioni, M.; Marianetti, C.; Morgan, D.; Ceder, G. First-principles prediction of redox potentials in transition-metal compounds with LDA+U. Phys. Rev. B 2004, 70, 235121. [Google Scholar] [CrossRef]
- Chevrier, V.L.; Ong, S.P.; Armiento, R.; Chan, M.K.Y.; Ceder, G. Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds. Phys. Rev. B 2010, 82, 075122. [Google Scholar] [CrossRef]
- Hautier, G.; Jain, A.; Ong, S.P.; Kang, B.; Moore, C.; Doe, R.; Ceder, G. Phosphates as lithium-ion battery cathodes: An evaluation based on high-throughput ab initio calculations. Chem. Mater. 2011, 23, 3495–3508. [Google Scholar] [CrossRef]
- Mueller, T.; Hautier, G.; Jain, A.; Ceder, G. Evaluation of tavorite-structured cathode materials for lithium-ion batteries using high-throughput computing. Chem. Mater. 2011, 23, 3854–3862. [Google Scholar] [CrossRef]
- Balducci, G.; Kas, J.; Fornasiero, P.; Graziani, M.; Islam, M.S. Surface and reduction energetics of the CeO2–ZrOO2 catalysts. J. Phys. Chem. B 1998, 102, 557–561. [Google Scholar] [CrossRef]
- Balducci, G.; Kas, J.; Fornasiero, P.; Graziani, M.; Islam, M.S.; Gale, J.D. Computer simulation studies of bulk reduction and oxygen migration in CeO2–ZrOO2 solid solutions. J. Phys. Chem. B 1997, 101, 1750–1753. [Google Scholar] [CrossRef]
- Balducci, G.; Islam, M.S.; Kašpar, J.; Fornasiero, P.; Graziani, M. Bulk reduction and oxygen migration in the ceria-based oxides. Chem. Mater. 2000, 12, 677–681. [Google Scholar] [CrossRef]
- Balducci, G.; Islam, M.S.; Kas, J.; Fornasiero, P. Reduction process in CeO2–MO and CeO2–M2O2 mixed oxides: A computer simulation study. Chem. Mater. 2003, 15, 3781–3785. [Google Scholar] [CrossRef]
- Speight, J.G. Lange’s Handbook of Chemistry, 16th ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Zanoni, R.; Cossi, M.; Iozzi, M.F.; Cattaruzza, F.; Dalchiele, E.A.; Decker, F.; Marrani, A.G.; Valori, M. Tuning the redox potential in molecular monolayers covalently bound to H–Si(100) electrodes via distinct C–C tethering arms. Superlattices Microstruct. 2008, 44, 542–549. [Google Scholar] [CrossRef]
- Boccia, A.; Decker, F.; Marrani, A.G.; Stranges, S.; Zanoni, R.; Cossi, M.; Iozzi, M.F. Role of the extent of -electron conjugation in visible-light assisted molecular anchoring on Si(111) surfaces. Superlattices Microstruct. 2009, 46, 30–33. [Google Scholar] [CrossRef]
- Pro, T.; Buckley, J.; Huang, K.; Calborean, A.; Marc, G.; Delapierre, G.; Member, S.; Duclairoir, F.; Marchon, J.; Jalaguier, E.; Maldivi, P.; De Salvo, B.; Deleonibus, S. Investigation of hybrid molecular/silicon memories with redox-active molecules acting as storage media. IEEE Trans. Nanotechnol. 2009, 8, 204–213. [Google Scholar] [CrossRef]
- Pro, T.; Buckley, J.; Barattin, R.; Calborean, A.; Aiello, V.; Nicotra, G.; Gély, M.; Delapierre, G.; Jalaguier, E.; Duclairoir, F.; Chevalier, N.; Lombardo, S.; Maldivi, P.; Ghibaudo, G.; De Salvo, B.; Deleonibus, S. From atomistic to device level investigation of hybrid redox molecular/silicon field-effect memory devices. IEEE Trans. Nanotechnol. 2011, 10, 275–283. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Arumugam, K.; Becker, U. Computational Redox Potential Predictions: Applications to Inorganic and Organic Aqueous Complexes, and Complexes Adsorbed to Mineral Surfaces. Minerals 2014, 4, 345-387. https://doi.org/10.3390/min4020345
Arumugam K, Becker U. Computational Redox Potential Predictions: Applications to Inorganic and Organic Aqueous Complexes, and Complexes Adsorbed to Mineral Surfaces. Minerals. 2014; 4(2):345-387. https://doi.org/10.3390/min4020345
Chicago/Turabian StyleArumugam, Krishnamoorthy, and Udo Becker. 2014. "Computational Redox Potential Predictions: Applications to Inorganic and Organic Aqueous Complexes, and Complexes Adsorbed to Mineral Surfaces" Minerals 4, no. 2: 345-387. https://doi.org/10.3390/min4020345




