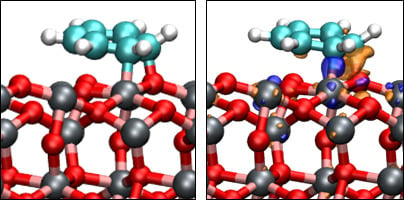
A Density Functional Theory Study of the Adsorption of Benzene on Hematite (α-Fe2O3) Surfaces
Abstract
:1. Introduction
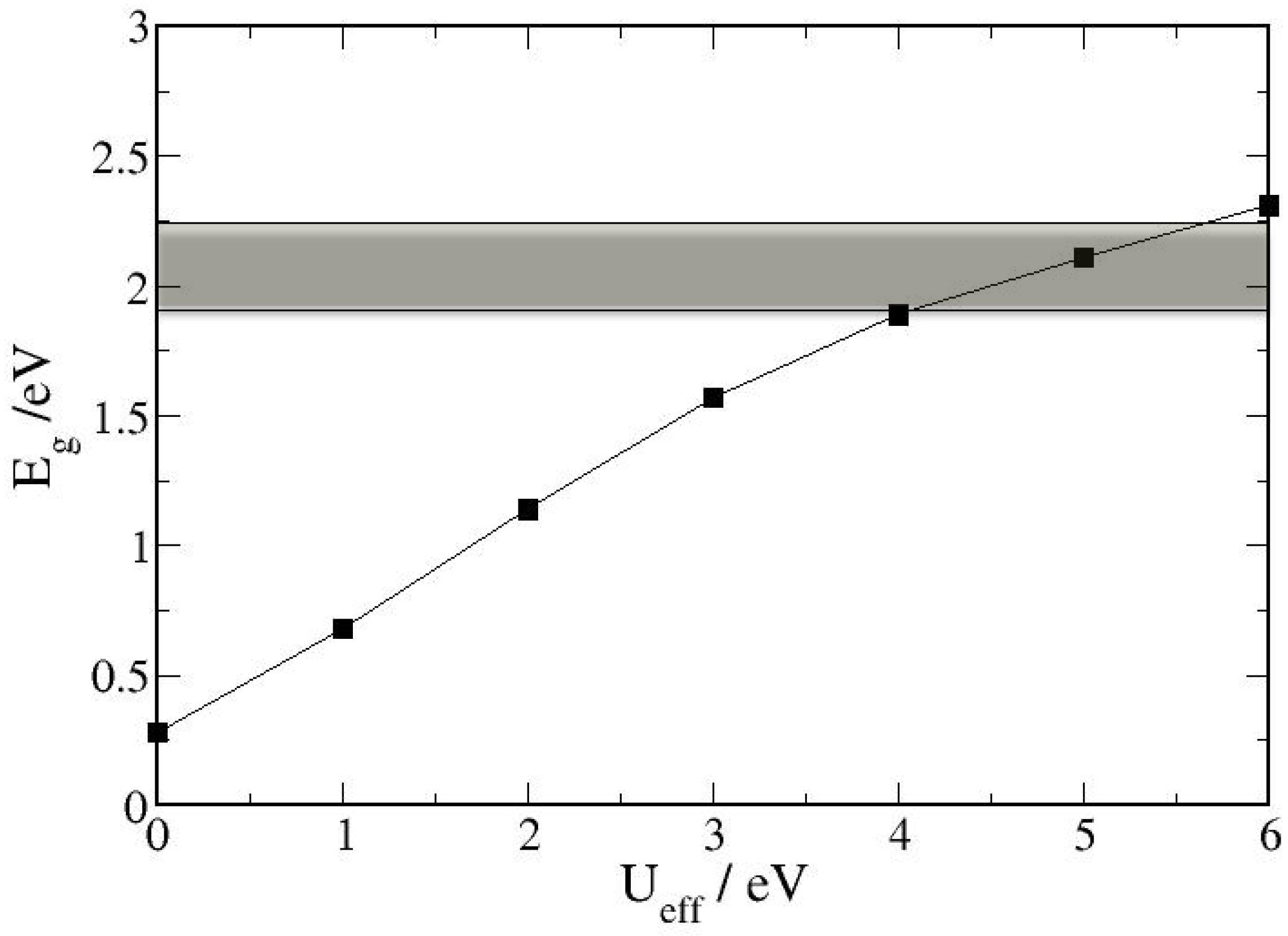
2. Computational Methods
3. Results and Discussion
3.1. Bulk α-Fe2O3 Structure

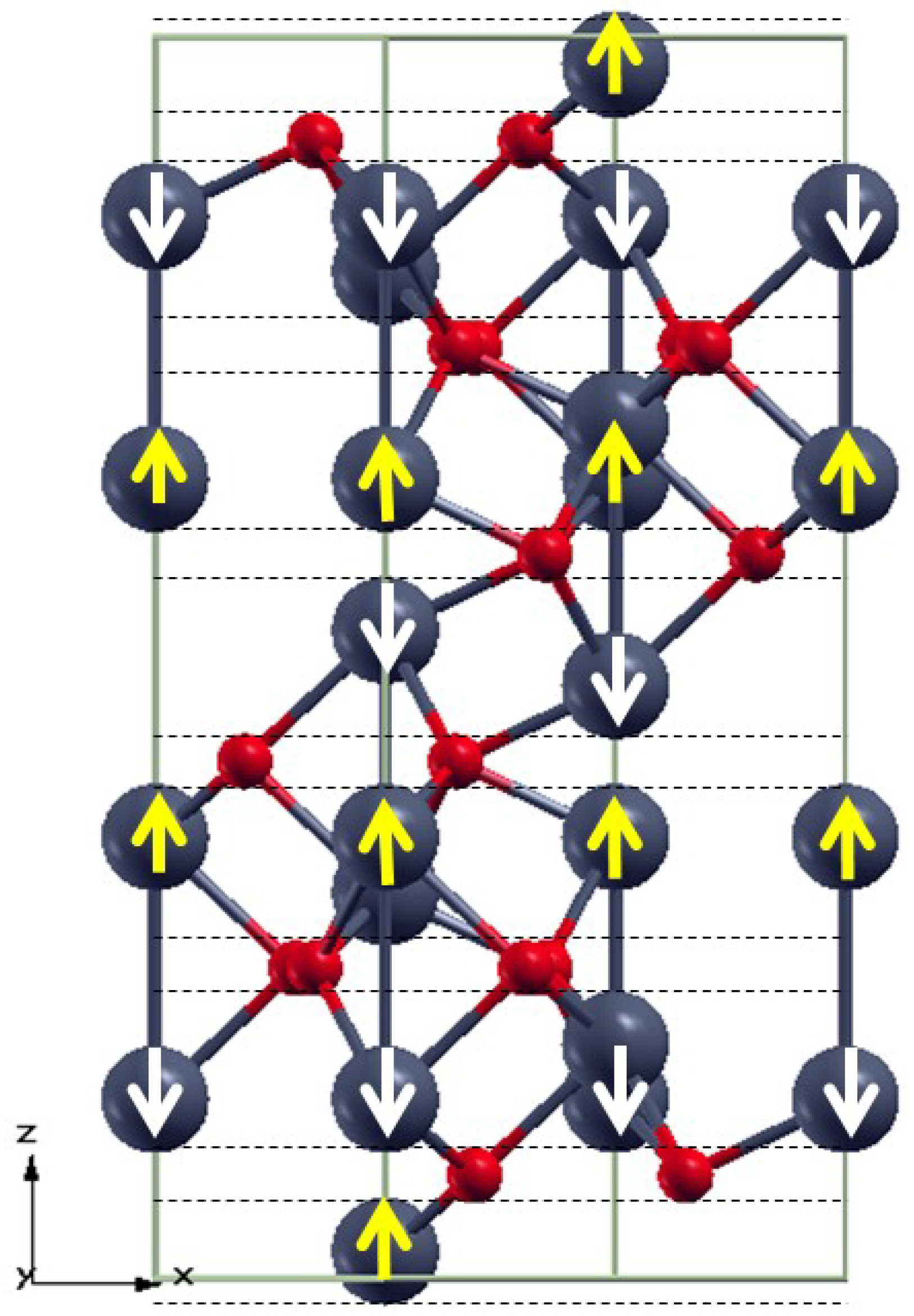
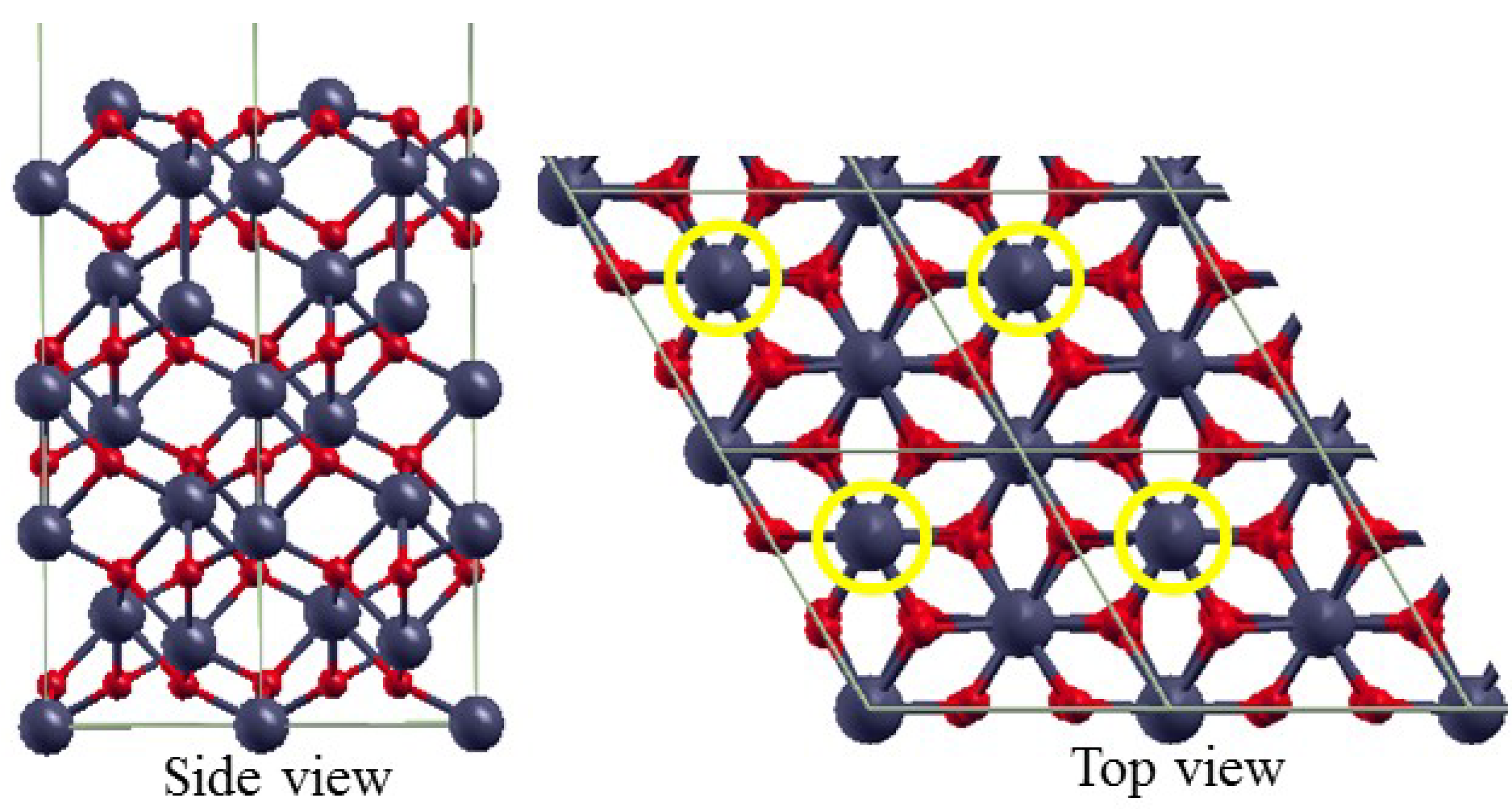
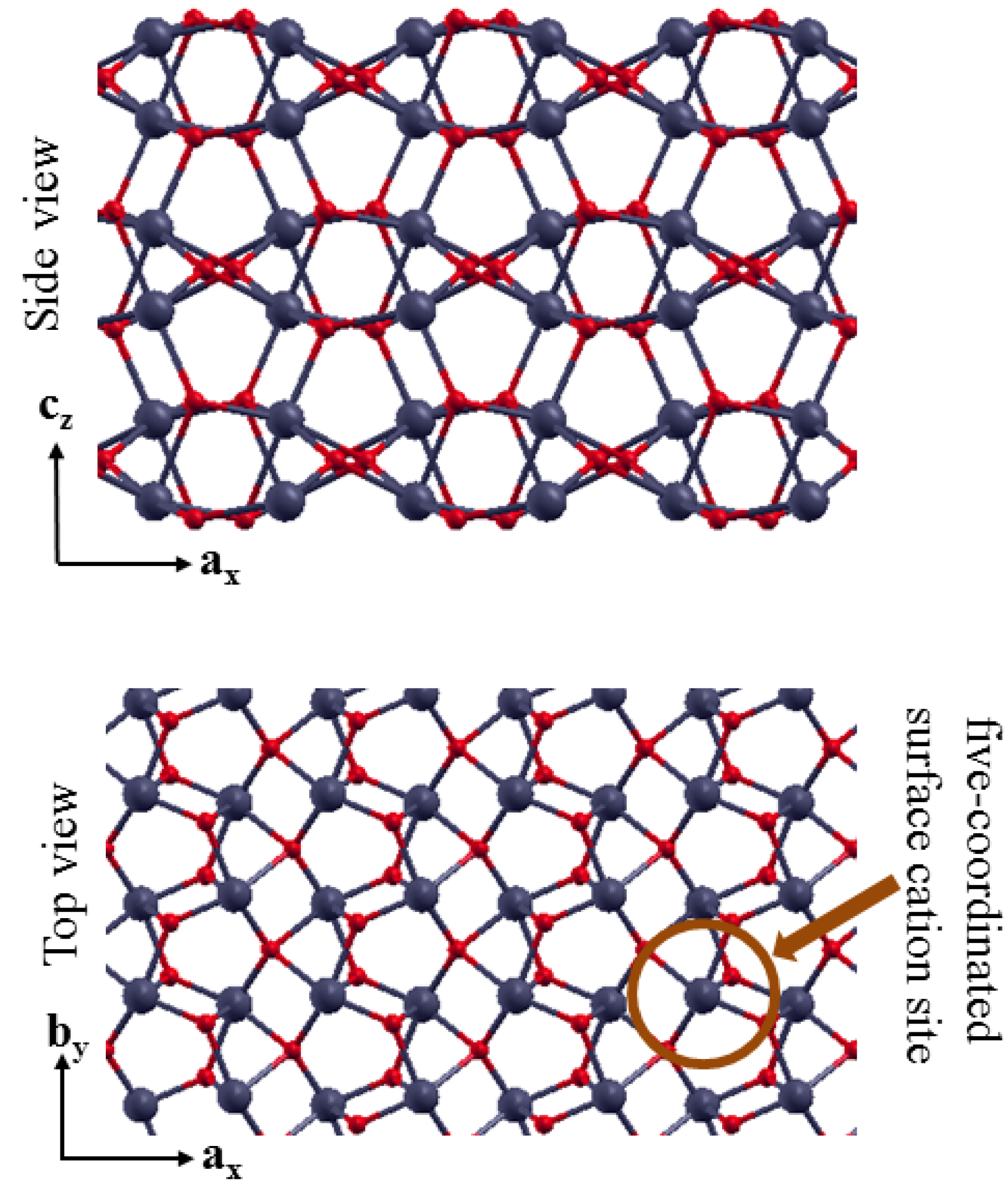
3.2. The Structure of α-Fe2O3 Surfaces
| Investigations | L1-L2 (bulk = 0.85) | L2-L3 (bulk = 0.85) | L3-L4 (bulk = 0.61) | L4-L5 (bulk = 0.85) |
|---|---|---|---|---|
| Theory (This work) | 0.40 (−52%) | 0.91 (+8%) | 0.45 (−26%) | 1.05 (+23%) |
| Theory (Wang et al. [62]) | 0.36 (−57%) | 0.90 (+7%) | 0.46 (−23%) | 0.97 (+15%) |
| Theory (Wasserman et al. [65]) | 0.43 (−49%) | 0.82 (−3%) | 0.36 (−40%) | 1.02 (+21%) |
| Theory (de Leeuw et al. [63]) | 0.21 (−76%) | 0.90 (+7%) | 0.42 (−31%) | 0.97 (+15%) |
| XPD (X-ray photoelectron diffraction) (Thevuthasan et al. [151]) | 0.50 (−41%) | 1.0 (+18%) | 0.55 (−9%) | 1.24 (+47%) |
| Plane (hkil) | Mackrodt [153] | Reeves and Mann [154] | de Leeuw [63] | This work |
|---|---|---|---|---|
| {0001}-Fe | 1.53 | 2.31 | 1.78 | 1.66 |
| {0001}-O | – | – | 2.63 | 2.59 |
| {1010} | 2.36 | 2.35 | 1.99 | 2.19 |
| {0112} | 1.47 | – | 1.88 | 1.92 |
| {1110} | 2.03 | – | 2.03 | 1.97 |
| {1011} | 2.41 | 2.84 | 2.34 | 2.29 |
| {1111} | – | – | 1.93 | 2.33 |

3.3. Benzene Adsorption
| Parameters | Experiment [159] | This work |
|---|---|---|
| d(C‒H)/Å | 1.101 | 1.091 |
| d(C‒C)/Å | 1.399 | 1.400 |
| <C‒C‒C/° | 120.0 | 119.9 |
| <C‒C‒H/° | 120.0 | 120.0 |
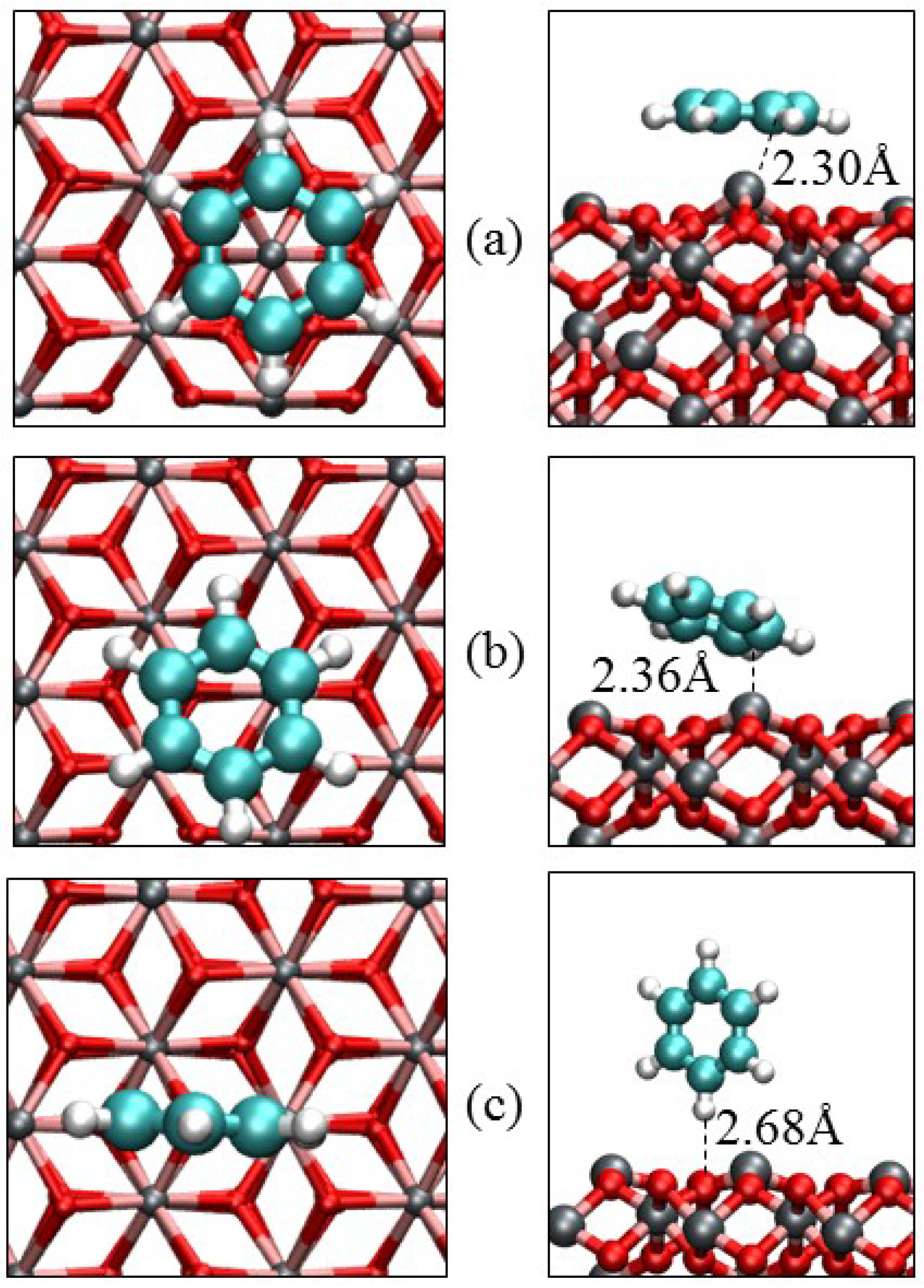
| Parameters | α-Fe2O3(0001) | α-Fe2O3(0112) | |||
|---|---|---|---|---|---|
| Parallel | Slant | Vertical | Parallel | Vertical | |
| Eads/eV | −1.17 | −0.79 | −0.28 | −1.52 | −0.41 |
| Qmol/e‒ | −0.07 | −0.05 | 0.00 | −0.23 | −0.00 |
| Fe‒C/Å | 2.301 | 2.363 | – | 1.952 | – |
| O‒C/Å | 3.001 | 3.065 | – | 1.631 | – |
| O‒H/Å | 3.106 | 2.701 | 2.682 | 3.001 | 2.300 |
| d(C‒H)/Å | 1.093 | 1.091 | 1.090 | 1.104 | 1.091 |
| d(C‒C)/Å | 1.421 | 1.411 | 1.401 | 1.503 | 1.401 |
| <C‒C‒C/° | 119.9 | 119.8 | 120.0 | 116.9 | 120.0 |
| <C‒C‒H/° | 120.3 | 120.2 | 120.0 | 117.4 | 119.9 |

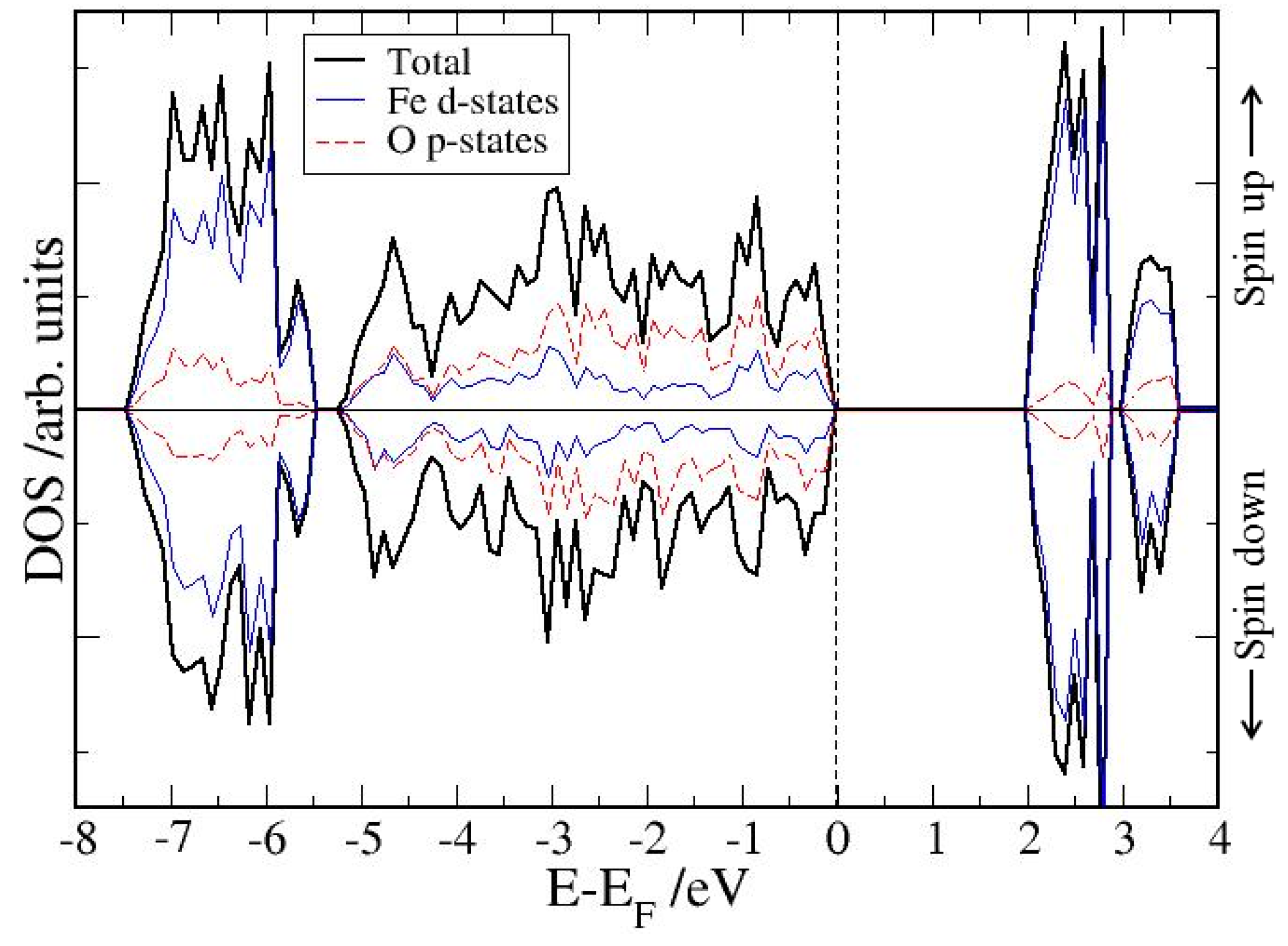
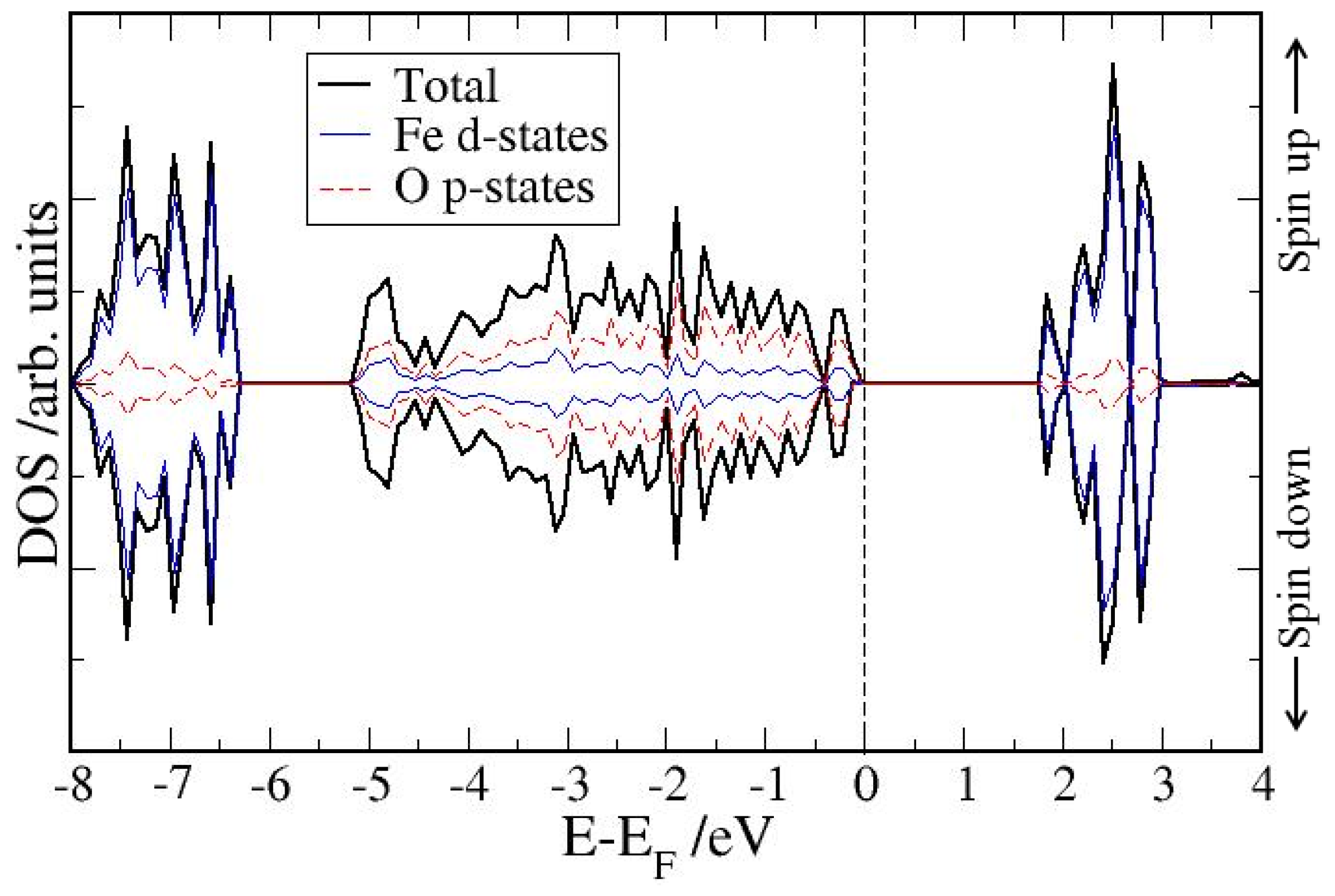
4. Electronic Structures

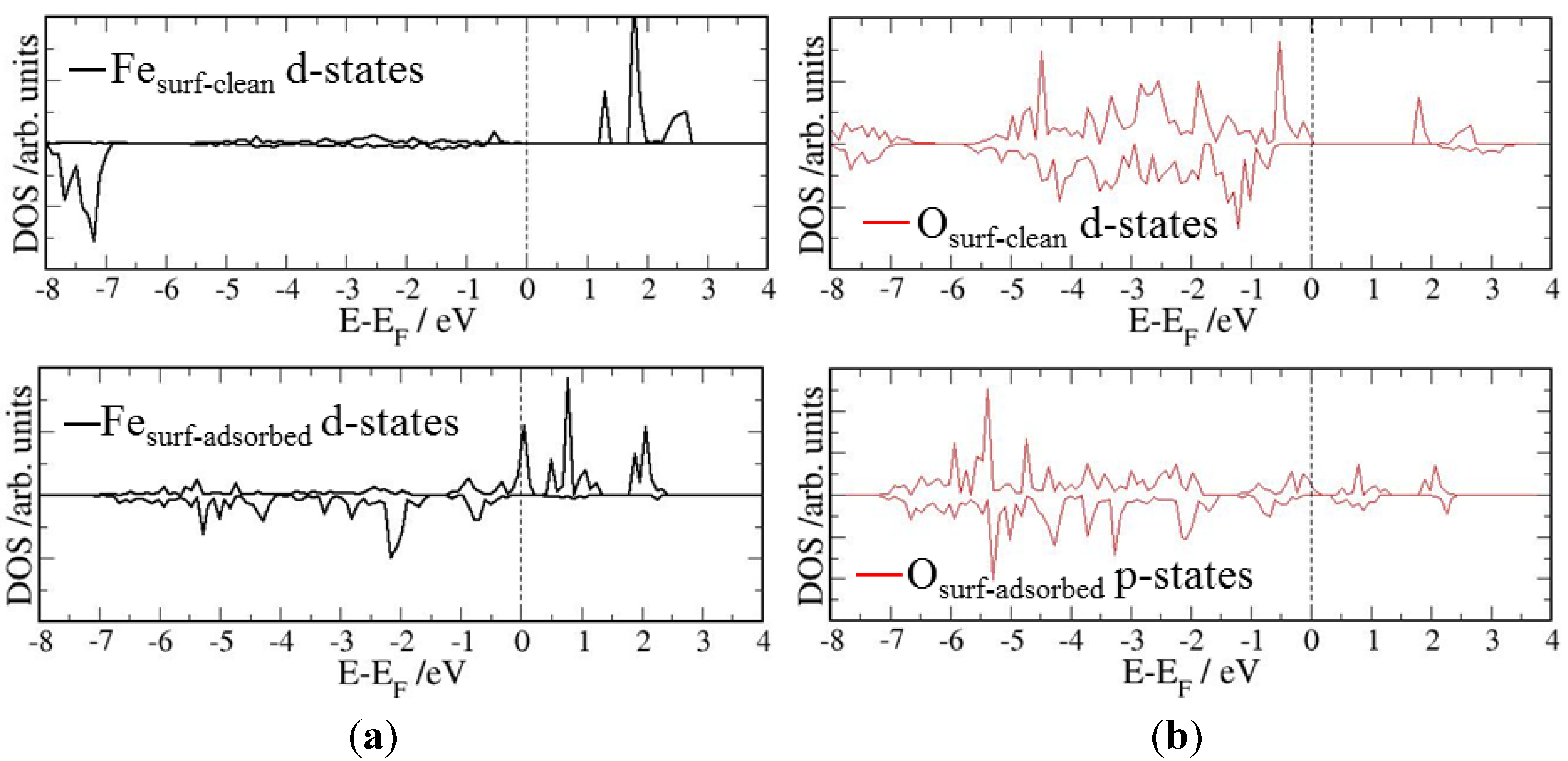
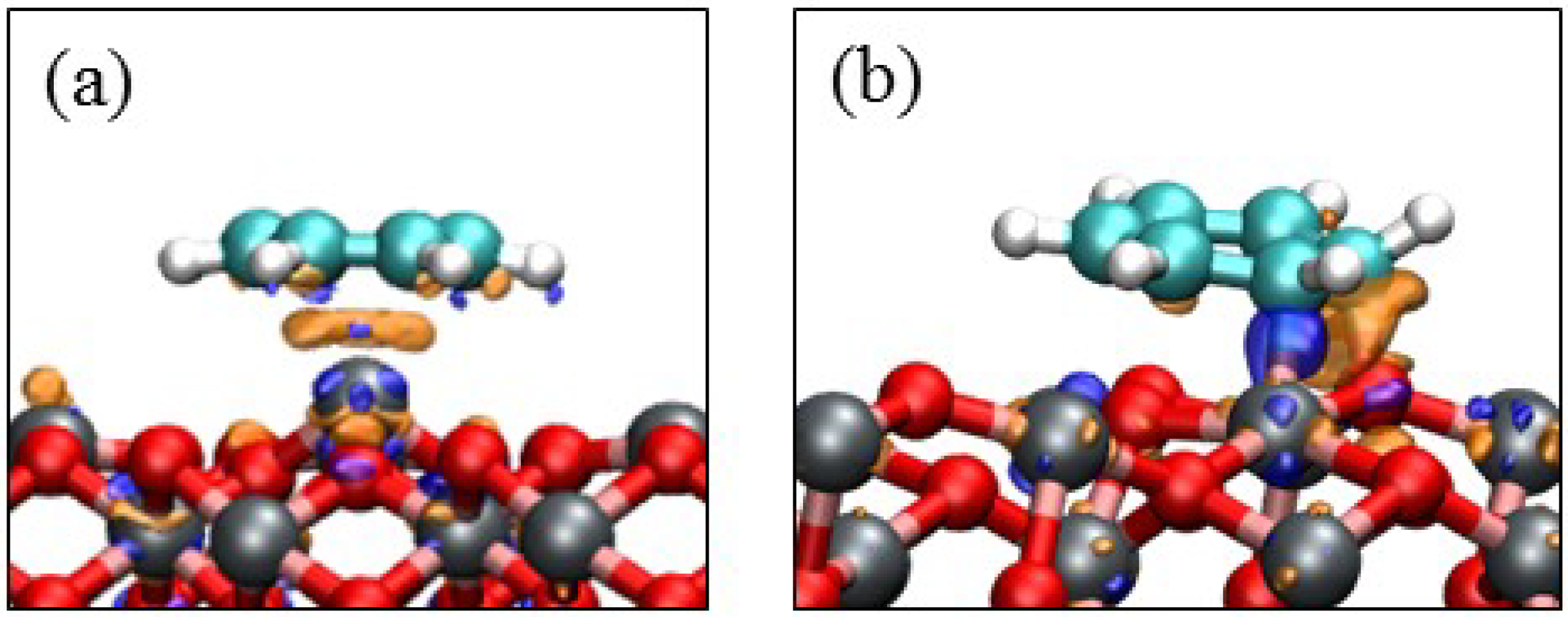
| Surface | Adsorption mode | Interacting Fe magnetic moment (μβ) | |
|---|---|---|---|
| Clean surface | Adsorbed surface | ||
| (0001) | Parallel | 3.97 | 3.65 |
| Slant | 3.97 | 3.78 | |
| Vertical | 3.97 | 3.91 | |
| (0112) | Parallel | 4.01 | 3.49 |
| Vertical | 4.01 | 3.98 | |
5. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Cornell, R.M.; Schwertmann, U. Iron Oxides in the Laboratory: Preparation and Characterization, 2nd ed.; Wiley-VCH: New York, NY, USA, 2000. [Google Scholar]
- Cornell, R.M.; Schwertmann, U. The Iron Oxides: Structure, Properties, Reactions, Occurrences, and Uses, 2nd ed.; Wiley-VCH: New York, NY, USA, 2003. [Google Scholar]
- Teja, A.S.; Koh, P.Y. Synthesis, properties, and applications of magnetic iron oxide nanoparticles. Prog. Cryst. Growth Charact. Mater. 2009, 55, 22–45. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Simchi, I.; Imani, M. Recent advances in surface engineering of superparamagnetic iron oxide nanoparticles for biomedical applications. J. Iran. Chem. Soc. 2010, 7, S1–S27. [Google Scholar] [CrossRef]
- Wang, G.; Liu, T.; Luo, Y.; Zhao, Y.; Ren, Z.; Bai, J.; Wang, H. Preparation of Fe2O3/graphene composite and its electrochemical performance as an anode material for lithium ion batteries. J. Alloys Compd. 2011, 509, L216–L220. [Google Scholar] [CrossRef]
- Singh, J.; Srivastava, M.; Dutta, J.; Dutta, P.K. Preparation and properties of hybrid monodispersed magnetic α-Fe2O3 based chitosan nanocomposite film for industrial and biomedical applications. Int. J. Biol. Macromol. 2011, 48, 170–176. [Google Scholar] [CrossRef]
- Hassan, M.F.; Guo, Z.; Chen, Z.; Liu, H. α-Fe2O3 as an anode material with capacity rise and high rate capability for lithium-ion batteries. Mater. Res. Bull. 2011, 46, 858–864. [Google Scholar] [CrossRef]
- Gupta, A.K.; Gupta, M. Synthesis and surface engineering of iron oxide nanoparticles for biomedical applications. Biomaterials 2005, 26, 3995–4021. [Google Scholar] [CrossRef]
- Twigg, M.V. Catalyst Handbook; Wolfe Publishing: London, UK, 1989. [Google Scholar]
- Xu, L.; Bao, S.; O’Brien, R.J.; Houpt, D.J.; Davis, B.H. Iron fischer-tropsch catalysis-properties of an ultrafine iron oxide catalyst. Fuel Sci. Technol. Int. 1994, 12, 1323–1353. [Google Scholar] [CrossRef]
- Jung, H.; Thomson, W.J. Dynamic X-ray diffraction study of an unsupported iron catalyst in Fischer-Tropsch synthesis. J. Catal. 1993, 139, 375–382. [Google Scholar] [CrossRef]
- Appl, M. Ammonia, 2. Production Processes. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH: Hoboken, NJ, USA, 2011; Volume 3, pp. 227–261. [Google Scholar]
- Lei, Y.; Cant, N.W.; Trimm, D.L. Activity patterns for the water gas shift reaction over supported precious metal catalysts. Catal. Lett. 2005, 103, 133–136. [Google Scholar] [CrossRef]
- Huang, C.S.; Xu, L.; Davis, B.H. Fischer-Tropsch synthesis: Impact of pretreatment of ultrafine iron oxide upon catalyst structure and selectivity. Fuel Sci. Technol. Int. 1993, 11, 639–664. [Google Scholar] [CrossRef]
- Mimura, N.; Takahara, I.; Ando, M. Dehydrogenation of ethylbenzene over iron oxide-based catalyst in the presence of carbon dioxide. Catal. Today 1998, 45, 61–64. [Google Scholar] [CrossRef]
- Zscherpel, D.; Weiss, W.; Schlogl, R. Adsorption and dehydrogenation of ethylbenzene on ultrathin iron oxide model catalyst films. Surf. Sci. 1997, 382, 326–335. [Google Scholar] [CrossRef]
- Chang, J.S.; Park, S.E.; Park, M.S. Beneficial effect of carbon dioxide in dehydrogenation of ethylbenzene to styrene over zeolite-supported iron oxide catalyst. Chem. Lett. 1997, 26, 1123–1124. [Google Scholar] [CrossRef]
- Mendoza, E.A.; Sunil, D.; Wolkow, E.; Gafney, H.D.; Rafailovich, M.H.; Sokolov, J.; Long, G.G.; Jemian, P.R.; Schwartz, S.A.; Wilkens, B.J. Effect of photodeposited iron oxide and tin oxide on the consolidation of porous Vycor glass. Appl. Phys. Lett. 1990, 57, 209–211. [Google Scholar] [CrossRef]
- Morsi, M.M.; El-Shennawi, A.W.A. Joint effect of gamma irradiation and TiO2 nucleation on the crystallization of (Li2, R)O aluminosilicate glass with and without iron oxide addition. Ceram. Int. 1993, 19, 333–338. [Google Scholar] [CrossRef]
- Burkhard, D.J.M. Elastic properties of alkali silicate glasses with iron oxide: Relation to glass structure. Solid State Commun. 1997, 101, 903–907. [Google Scholar] [CrossRef]
- Suber, L.; Imperatori, P.; Ausanio, G.; Fabbri, F.; Hofmeister, H. Synthesis, morphology, and magnetic characterization of iron oxide nanowires and nanotubes. J. Phys. Chem. B 2005, 109, 7103–7109. [Google Scholar] [CrossRef]
- Xiong, Y.; Ye, J.; Gu, X.; Chen, Q. Synthesis and magnetic properties of iron oxide nanoparticles/C and α-Fe/iron oxide nanoparticles/C composites. J. Magn. Magn. Mater. 2008, 320, 107–112. [Google Scholar] [CrossRef]
- Fujishiro, Y.; Uchida, S.; Sato, T. Synthesis and photochemical properties of semiconductor pillared layered compounds. Int. J. Inorg. Mater. 1999, 1, 67–72. [Google Scholar] [CrossRef]
- Peng, X.; Qian, X.; Mao, H.; Wang, A.Y.; Chen, Z.; Nie, S.; Shin, D.M. Targeted magnetic iron oxide nanoparticles for tumor imaging and therapy. Int. J. Nanomed. 2008, 3, 311–321. [Google Scholar]
- Yu, M.; Park, J.; Jeong, Y.Y.; Moon, W.K.; Jon, S. Integrin-targeting thermally cross-linked superparamagnetic iron oxide nanoparticles for combined cancer imaging and drug delivery. Nanotechnology 2010, 21. [Google Scholar] [CrossRef]
- Waychunas, G.A.; Kim, C.S.; Banfield, J.F. Nanoparticulate iron oxide minerals in soils and sediments: Unique properties and contaminant scavenging mechanisms. J. Nanopart. Res. 2005, 7, 409–433. [Google Scholar] [CrossRef]
- Nassar, N.N. Iron Oxide Nanoadsorbents for Removal of Various Pollutants from Wastewater: An Overview. In Application of Adsorbents for Water Pollution Control; Bentham Science Publishers: Sharjah, United Arab Emirates, 2012; pp. 81–118. [Google Scholar]
- Xu, P.; Zeng, G.M.; Huang, D.L.; Feng, C.L.; Hu, S.; Zhao, M.H.; Lai, C.; Wei, Z.; Huang, C.; Xie, G.X.; et al. Use of iron oxide nanomaterials in wastewater treatment: A review. Sci. Total Environ. 2012, 424, 1–10. [Google Scholar] [CrossRef]
- Tunega, D.; Gerzabek, M.H.; Haberhauer, G.; Totsched, K.U.; Lischka, H. Model study on sorption of polycyclic aromatic hydrocarbons to goethite. J. Colloid Interface Sci. 2009, 330, 244–249. [Google Scholar] [CrossRef]
- Rebhun, M.; Kalabo, R.; Grossman, L.; Manka, J.; Rav-Acha, C. Sorption of organics on clay and synthetic humic-clay complexes simulating aquifer processes. Water Res. 1992, 26, 79–84. [Google Scholar] [CrossRef]
- Lijestrand, M.H.; Lo, I.M.-C.; Shimizu, Y. Sorption of humic materials onto inorganic surfaces for the mitigation of facilitated pollutant transport processes. Water Sci. Technol. 1992, 26, 1221–1228. [Google Scholar]
- Knezovich, J.P.; Harrison, F.L.; Wilhelm, R.G. The bioavailability of sediment-sorbed organic chemicals. Water Air Soil Pollut. 1987, 32, 233–245. [Google Scholar]
- Fendorf, S.; Eick, M.J.; Grossl, P.; Sparks, D.L. Arsenate and chromate retention mechanisms on goethite. 1. Surf. Struct. Environ. Sci. Technol. 1997, 31, 315–320. [Google Scholar] [CrossRef]
- Waychunas, G.A.; Rea, B.A.; Fuller, C.C.; Davis, J.A. Surface chemistry of ferrihydrite: Part 1. EXAFS studies of the geometry of coprecipitated and adsorbed arsenate. Geochim. Cosmochim. Acta 1993, 57, 2251–2269. [Google Scholar] [CrossRef]
- Waychunas, G.A.; Davis, J.A.; Fuller, C.C. Geometry of sorbed arsenate on ferrihydrite and crystalline FeOOH: Re-evaluation of EXAFS results and topological factors in predicting sorbate geometry, and evidence for monodentate complexes. Geochim. Cosmochim. Acta 1995, 59, 3655–3661. [Google Scholar] [CrossRef]
- Hsia, T.H.; Lo, S.L.; Lin, C.F.; Lee, D.Y. Characterization of arsenate adsorption on hydrous iron oxide using chemical and physical methods. Colloids Surf. A Physicochem. Eng. Asp. 1994, 85, 1–7. [Google Scholar] [CrossRef]
- Sun, X.H.; Doner, H.E. An investigation of arsenate and arsenite bonding structures on goethite by FTIR. Soil Sci. 1996, 161, 865–872. [Google Scholar] [CrossRef]
- Manning, B.A.; Fendorf, S.E.; Goldberg, S. Surface structures and stability of arsenic(III) on goethite: Spectroscopic evidence for inner-sphere complexes. Environ. Sci. Technol. 1998, 32, 2383–2388. [Google Scholar] [CrossRef]
- Manning, B.A.; Hunt, M.L.; Amrhein, C.; Yarmoff, J.A. Arsenic(III) and Arsenic(V) reactions with zerovalent iron corrosion products. Environ. Sci. Technol. 2002, 36, 5455–5546. [Google Scholar] [CrossRef]
- Foster, A.L.; Brown, G.E., Jr.; Tingle, T.N.; Parks, G.A. Quantitative arsenic speciation in mine tailings using X-ray absorption spectroscopy. Am. Mineral. 1998, 83, 553–568. [Google Scholar]
- Farquhar, M.L.; Charnock, J.M.; Livens, F.R.; Vaughan, D.J. Mechanisms of arsenic uptake from aqueous solution by interaction with goethite, lepidocrocite, mackinawite, and pyrite: An X-ray absorption spectroscopy study. Environ. Sci. Technol. 2002, 36, 1757–1762. [Google Scholar] [CrossRef]
- Ona-Nguema, G.; Morin, G.; Juillot, F.; Brown, G.E., Jr.; Calas, G. EXAFS analysis of arsenite adsorption onto two-line ferrihydrite, hematite, goethite, and lepidocrocite. Environ. Sci. Technol. 2005, 39, 9147–9155. [Google Scholar] [CrossRef]
- Wang, Y.; Morin, G.; Ona-Nguema, G.; Juillot, J.; Guyot, F.; Calas, G.; Brown, G.E., Jr. Evidence for different surface speciation of arsenite and arsenate on green rust: An EXAFS and XANES study. Environ. Sci. Technol. 2010, 44, 109–115. [Google Scholar] [CrossRef]
- Goldberg, S.; Johnston, C.T. Mechanisms of arsenic adsorption on amorphous oxides evaluated using macroscopic measurements, vibrational spectroscopy, and surface complexation modelling. J. Colloid Interface Sci. 2001, 234, 204–216. [Google Scholar] [CrossRef]
- Wu, H.; Lin, Y.; Wu, J.; Zeng, L.; Zeng, D.; Du, J. Surface adsorption of iron oxide minerals for phenol and dissolved organic matter. Earth Sci. Front. 2008, 15, 133–141. [Google Scholar] [CrossRef]
- McBride, M.B.; Kung, K.H. Adsorption of phenol substituted phenols by iron-oxides. Environ. Toxicol. Chem. 1991, 10, 441–448. [Google Scholar] [CrossRef]
- Beentjes, P.C.J.; Brand, J.D.; Dewit, J.H.W. Interaction of ester and acid groups containing organic compounds with iron oxide surfaces. J. Adhes. Sci. Technol. 2006, 20, 1–18. [Google Scholar] [CrossRef]
- Parfitt, R.L.; Farmer, V.C.; Russell, J.D. Adsorption on hydrous oxides. 1. Oxalate and benzoate on goethite. J. Soil Sci. 1977, 28, 29–39. [Google Scholar] [CrossRef]
- Hwang, Y.K.; Lenhart, J.J. Surface complexation modeling of dual-mode adsorption of organic acids: Phthalic acid adsorption onto hematite. J. Colloid Interface Sci. 2009, 336, 200–207. [Google Scholar] [CrossRef]
- Angove, M.J.; Fernandes, M.B.; Ikhsan, J. The sorption of anthracene onto goethite and kaolinite in the presence of some benzene carboxylic acids. J. Colloid Interface Sci. 2002, 247, 282–289. [Google Scholar] [CrossRef]
- Boily, J.-F.; Fein, J.B. Adsorption of Pb(II) and benzenecarboxylates onto corundum. Chem. Geol. 1998, 148, 157–175. [Google Scholar] [CrossRef]
- Das, M.R.; Bordoloi, D.; Borthakur, P.C.; Mahiuddin, S. Kinetics and adsorption of benzoate and salicylate at the natural hematite-water interface. Colloids Surf. A Physicochem. Eng. Asp. 2005, 254, 49–55. [Google Scholar] [CrossRef]
- Huda, M.N.; Walsh, Y.; Yan, Y.; Wei, S.-H.; Al-Jassim, M.N. Electronic, structural, and magnetic effects of 3d transition metals in hematite. J. Appl. Phys. 2010, 107. [Google Scholar] [CrossRef]
- Rohrbach, A.; Hafner, J.; Kresse, G. Ab initio study of the (0001) surfaces of hematite and chromia: Influence of strong electronic correlations. Phys. Rev. B. 2004, 70. [Google Scholar] [CrossRef]
- Rollmann, G.; Rohrbach, A.; Entel, P.; Hafner, J. First-principles calculation of the structure and magnetic phases of hematite. Phys. Rev. B 2004, 69. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Velev, J.; Butler, W.H.; Sarker, S.K.; Bengone, O. Effect of electron correlations on the electronic and magnetic structure of Ti-doped α-hematite. Phys. Rev. B. 2004, 69, 174429:1–174429:8. [Google Scholar]
- Lee, J.; Han, S. Thermodynamics of native point defects in α-Fe2O3: An ab initio study. Phys. Chem. Chem. Phys. 2013, 15, 18906–18914. [Google Scholar] [CrossRef]
- Rivera, R.; Pinto, H.P.; Stashans, A.; Piedra, L. Density functional theory study of Al-doped hematite. Phys. Scr. 2012, 85. [Google Scholar] [CrossRef]
- Meng, X.Y.; Qin, G.W.; Li, S.; Wen, X.H.; Ren, Y.P.; Pei, W.L.; Zuo, L. Enhanced photoelectrochemical activity for Cu and Ti doped hematite: The first principles calculations. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
- Liao, P.; Toroker, M.C.; Carter, E.A. Electron transport in pure and doped hematite. Nano Lett. 2011, 11, 1775–1781. [Google Scholar] [CrossRef]
- Trainor, T.P.; Chaka, A.M.; Eng, P.J.; Newville, M.; Waychunas, C.A.; Catalano, J.C.; Brown, G.E., Jr. Structure and reactivity of the hydrated hematite (0001) surface. Surf. Sci. 2004, 573, 204–224. [Google Scholar] [CrossRef]
- Wang, X.G.; Weiss, W.; Shaikhutdinov, S.K.; Ritter, M.; Petersen, M.; Wagner, F.; Schlögl, R.; Scheffler, M. The hematite (α-Fe2O3) (0001) surface: Evidence for domains of distinct chemistry. Phys. Rev. Lett. 1998, 81, 1038–1041. [Google Scholar] [CrossRef]
- De Leeuw, N.H.; Cooper, T.G. Surface simulation studies of the hydration of white rust Fe(OH)2, goethite α-FeO(OH) and hematite α-Fe2O3. Geochim. Cosmochim. Acta 2007, 71, 1655–1673. [Google Scholar] [CrossRef]
- Rustad, J.R.; Wasserman, E.; Felmy, A.R. Molecular modeling of the surface charging of hematite—II. Optimal proton distribution and simulation of surface charge versus pH relationships. Surf. Sci. 1999, 424, 28–35. [Google Scholar] [CrossRef]
- Wasserman, E.; Rustad, J.R.; Felmy, A.R.; Hay, B.P.; Halley, J.W. Ewald methods for polarizable surfaces with application to hydroxylation and hydrogen bonding on the (012) and (001)surfaces of alpha-Fe2O3. Surf. Sci. 1997, 385, 217–239. [Google Scholar] [CrossRef]
- Jones, F.; Rohl, A.L.; Farrow, J.B.; Bronswijk, W.V. Molecular modeling of water adsorption on hematite. Phys. Chem. Chem. Phys. 2000, 2, 3209–3216. [Google Scholar] [CrossRef]
- Nguyen, M.-T.; Seriani, N.; Gebauer, R. Water adsorption and dissociation on α-Fe2O3(0001): PBE+U calculations. J. Chem. Phys. 2013, 138. [Google Scholar] [CrossRef]
- Yin, S.; Ma, X.; Ellis, D.E. Initial stages of H2O adsorption and hydroxylation of Fe-terminated alpha-Fe2O3(0001) surface. Surf. Sci. 2007, 601, 2426–2437. [Google Scholar] [CrossRef]
- Lo, C.S.; Tanwar, K.S.; Chaka, A.M.; Trainor, T.P. Density functional theory study of the clean and hydrated hematite (1102) surfaces. Phys. Rev. B 2007, 75, 075425:1–075425:15. [Google Scholar]
- Tanwar, K.S.; Lo, C.S.; Eng, P.J.; Catalano, J.G.; Walko, D.A.; Brown, G.E., Jr.; Waychunas, G.A.; Chaka, A.M.; Trainor, T.P. Surface diffraction study of the hydrated hematite (1102) surface. Surf. Sci. 2007, 601, 460–474. [Google Scholar] [CrossRef]
- Parker, S.C.; de Leeuw, N.H.; Redfern, S.E. Atomistic simulation of oxide surfaces and their reactivity with water. Faraday Discuss. 1999, 114, 381–393. [Google Scholar] [CrossRef]
- Lado-Touriňo, I.; Tsobnang, F. Using computational approaches to model hematite surfaces. Comput. Mater. Sci. 2000, 17, 243–248. [Google Scholar] [CrossRef]
- Rustad, J.R.; Felmy, A.R.; Hay, B.P. Molecular statics calculations for iron oxide and oxyhydroxide minerals: Toward a flexible model of the reactive mineral-water interface. Geochim. Cosmochim. Acta 1996, 60, 1553–1562. [Google Scholar] [CrossRef]
- Shroll, R.M.; Straatsma, T.P. Molecular dynamics simulations of the goethite-water interface. Mol. Simul. 2003, 29, 1–11. [Google Scholar] [CrossRef]
- Rakovan, J.; Becker, U.; Hochella, M.F. Aspects of goethite surface microtopography, structure, chemistry, and reactivity. Am. Mineral. 1999, 84, 884–894. [Google Scholar]
- Sherman, D.M.; Randall, S.R. Surface complexation of arsenie(V) to iron(III) (hydr)oxides: Structural mechanism from ab initio molecular geometries and EXAFS spectroscopy. Geochim. Cosmochim. Acta 2003, 67, 4223–4230. [Google Scholar] [CrossRef]
- Blanchard, M.; Morin, G.; Lazzeri, M.; Balan, E.; Dabo, I. First-principles simulation of arsenate adsorption on the (112) surface of hematite. Geochim. Cosmochim. Acta 2012, 86, 182–195. [Google Scholar] [CrossRef]
- Yin, S.; Ellis, D.E. DFF studies of Cr(VI) complex adsorption on hydroxylated hematite (1102) surfaces. Surf. Sci. 2009, 603, 736–746. [Google Scholar] [CrossRef]
- Kwon, K.D.; Kubicki, J.D. Molecular orbital theory study on surface complex structures of phosphates to iron hydroxides: Calculation of vibrational frequencies and adsorption energies. Langmuir 2004, 20, 9249–9254. [Google Scholar] [CrossRef]
- Persson, P.; Nilsson, N.; Sjöberg, S. Structure and bonding of orthophosphate ions at the iron oxide aqueous interface. J. Colloid Interface Sci. 1996, 177, 263–275. [Google Scholar] [CrossRef]
- Arai, Y.; Sparks, D.L. ATR-FTIR spectroscopic investigation on phosphate adsorption mechanisms at the ferrihydrite-water interface. J. Colloid Interface Sci. 2001, 241, 317–326. [Google Scholar] [CrossRef]
- Kubicki, J.D.; Kwon, K.D.; Paul, K.W.; Sparks, D.L. Surface complex structures modelled with quantum chemical calculations: Carbonate, phosphate, sulphate, arsenate and arsenite. Eur. J. Soil Sci. 2007, 58, 932–944. [Google Scholar] [CrossRef]
- Acelas, N.Y.; Mejia, S.M.; Mondragón, F.; Flórez, E. Density functional theory characterization of phosphate and sulfate adsorption on Fe-(hydr)oxide: Reactivity, pH effect, estimation of Gibbs free energies, and topological analysis of hydrogen bonds. Comput. Theor. Chem. 2013, 1005, 16–24. [Google Scholar]
- Grossl, P.R.; Sparks, D.L. Evaluation of contaminant ion adsorption/desorption on goethite using pressure jump relaxation kinetics. Geoderma 1995, 67, 87–101. [Google Scholar] [CrossRef]
- Grossl, P.R.; Eick, M.; Sparks, D.L.; Goldberg, S.; Ainsworth, C.C. Arsenate and chromate retention mechanisms on goethite. 2. Kinetic evaluation using a pressure-jump relaxation technique. Environ. Sci. Technol. 1997, 31, 321–326. [Google Scholar] [CrossRef]
- Catalano, J.G.; Zhang, Z.; Fenter, P.; Bedzyk, M.J. Inner-sphere adsorption geometry of Se(IV) at the hematite (100)-water interface. J. Colloid Interface Sci. 2006, 297, 665–671. [Google Scholar] [CrossRef]
- Mason, S.E.; Trainor, T.P.; Goffinet, C.J. DFT study of Sb(III) and Sb(V) adsorption and heterogeneous oxidation on hydrated oxide surfaces. Comput. Theor. Chem. 2012, 987, 103–114. [Google Scholar] [CrossRef]
- Aquino, A.J.A.; Tunega, D.; Haberhauer, G.; Gerzabek, M.H.; Lischka, H. Quantum chemical adsorption studies on the (110) surface of the mineral goethite. Phys. Chem. C 2007, 111, 877–885. [Google Scholar]
- Han, K.N.; Healy, T.W.; Fuerstenau, D.W. The mechanism of adsorption of fatty acids and other surfactants at the oxide-water interface. J. Colloid Interface Sci. 1973, 44, 407–414. [Google Scholar] [CrossRef]
- Aquino, A.J.A.; Tunega, D.; Haberhauer, G.; Gerzabek, M.H.; Lischka, H. Interaction of the 2.4-dichlorophenoxyacetic acid herbicide with soil organic matter moieties: A theoretical study. Eur. J. Soil Sci. 2007, 58, 889–899. [Google Scholar] [CrossRef]
- San-Miguel, M.A.; Rodger, P.A. Simulation of deposition of wax to iron oxide surfaces. Mol. Simul. 2001, 26, 193–216. [Google Scholar] [CrossRef]
- San-Miguel, M.A.; Rodger, P.M. Wax deposition onto Fe2O3 surfaces. Phys. Chem. Chem. Phys. 2003, 5, 575–581. [Google Scholar] [CrossRef]
- San-Miguel, M.A.; Rodger, P.M. Templates of wax deposition? Phys. Chem. Chem. Phys. 2010, 12, 3887–3894. [Google Scholar] [CrossRef]
- Amellal, S.; Boivin, A.; Ganier, C.P.; Schiavon, M. High sorption of phenanthrene in agricultural soils. Agron. Sustain. Dev. 2006, 26, 99–106. [Google Scholar] [CrossRef]
- Weigand, H.; Totsche, K.U.; Kögel-Knaber, I.; Annwiler, E.; Richnow, H.H.; Michaelis, W. Fate of anthracene in contaminated soil: Transport and biochemical transformation under unsaturated flow conditions. Eur. J. Soil Sci. 2002, 53, 71–81. [Google Scholar] [CrossRef]
- Weigand, H.; Totsche, K.U.; Mansfeldt, T.; Kögel-Knaber, I. Release and mobility of polycyclic aromatic hydrocarbons and iron-cyanide complexes in contaminated soil. J. Plant Nutr. Soil Sci. 2001, 164, 643–649. [Google Scholar] [CrossRef]
- Weigand, H.; Totche, K.U.; Huwe, B.; Kögel-Knaber, I. PAH mobility in contaminated industrial soils: A Markov chain approach to the spatial variability of soil properties and PAH levels. Geoderma 2001, 102, 371–389. [Google Scholar] [CrossRef]
- Laor, Y.; Farmer, W.J.; Aochi, Y.; Strom, P.F. Phenanthrene binding and sorption to dissolved and to mineral-associated humic acid. Water Res. 1998, 32, 1923–1931. [Google Scholar] [CrossRef]
- Ping, L.F.; Luo, Y.M.; Wu, L.H.; Qian, W.; Song, J.; Christie, P. Phenanthrene adsorption by soils treated with humic substances under different pH and temperature conditions. Environ. Geochem. Health 2006, 28, 189–195. [Google Scholar] [CrossRef] [Green Version]
- Rügner, H.; Kleneidam, S.; Grathwohl, P. Long term sorption kinetics of phenanthrene in aquifer materials. Environ. Sci. Technol. 1999, 33, 1645–1651. [Google Scholar] [CrossRef]
- Chiou, C.T.; McGroddy, S.E.; Kile, D.E. Partition characteristics of polycyclic aromatic hydrocarbons on soils and sediments. Environ. Sci. Technol. 1998, 32, 264–269. [Google Scholar] [CrossRef]
- Means, J.C.; Wood, S.G.; Hassett, J.J.; Banwart, W.L. Sorption of polynuclear aromatic hydrocarbons by sediments and soils. Environ. Sci. Technol. 1980, 14, 1524–1528. [Google Scholar] [CrossRef]
- Stauffer, T.B.; MacIntyre, W.G. Sorption of low-polarity organic compounds on oxide minerals and aquifer material. Environ. Toxicol. Chem. 1986, 5, 949–955. [Google Scholar]
- Piatt, J.J.; Backhus, D.A.; Capel, P.D.; Eisenreich, S.J. Temperature-dependent sorption of naphthalene, phenanthrene, and pyrene to low organic carbon aquifer sediments. Environ. Sci. Technol. 1996, 30, 751–760. [Google Scholar] [CrossRef]
- Xia, G.; Ball, W.P. Adsorption-partitioning uptake of nine low-polarity organic chemicals on a natural sorbent. Environ. Sci. Technol. 1999, 33, 262–269. [Google Scholar] [CrossRef]
- Allen-King, R.M.; Grathwohl, P.; Ball, W.P. New modeling paradigms for the sorption of hydrophobic organic chemicals to heterogeneous carbonaceous matter in soils, sediments, and rocks. Adv. Water Res. 2002, 25, 985–1016. [Google Scholar] [CrossRef]
- Mader, B.T.; Goss, K.U.; Eisenreich, S.J. Sorption of nonionic, hydrophobic organic chemicals to mineral surfaces. Environ. Sci. Technol. 1997, 31, 1079–1086. [Google Scholar] [CrossRef]
- Ma, J.C.; Dougherty, D.A. The cation-π interaction. Chem. Rev. 1997, 97, 1303–1324. [Google Scholar] [CrossRef]
- Zaric, S.D. Metal ligand aromatic cation-π interactions. Eur. J. Inorg. Chem. 2003, 12, 2197–2209. [Google Scholar] [CrossRef]
- Zhu, D.; Herbert, B.E.; Schlautman, M.A.; Carraway, E.R.; Hur, J. Cation-π bonding: A new perspective on the sorption of polycyclic aromatic hydrocarbons to mineral surfaces. J. Environ. Qual. 2004, 33, 1322–1330. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter 1994, 6, 8245–8257. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Liechtenstein, A.I.; Castell, M.R.; Briggs, G.A.D.; Sutton, A.P. Surface states on NiO (100) and the origin of the contrast reversal in atomically resolved scanning tunneling microscope images. Phys. Rev. B 1997, 56, 4900–4908. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Rohrbach, A.; Hafner, J.; Kresse, G. Electronic correlation effects in transition-metal sulfides. J. Phys. Condens. Matter 2003, 15, 979–996. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Dzade, N.Y.; Roldan, A.; de Leeuw, N.H. Adsorption of methylamine on mackinawite (FeS) surfaces: A density functional theory study. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef]
- Irrera, S.; Roldan, A.; Portalone, G.; de Leeuw, N.H. The role of hydrogen bonding and proton transfer in the formation of uracil networks on the gold (100) surface: A density functional theory approach. J. Phys. Chem. C 2013, 117, 3949–3957. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Rohr, F.; Baumer, M.; Freund, H.J.; Mejias, J.A.; Staemmler, V.; Muller, S.; Hammer, L.; Heinz, K. Strong relaxations at the Cr2O3(0001) surface as determined via low-energy electron diffraction and molecular dynamics simulations. Surf. Sci. 1997, 372, L291–L297. [Google Scholar] [CrossRef]
- Mackrodt, W.C.; Davey, R.J.; Black, S.N.; Docherty, R. The morphology of α-Al2O3 and α-Fe2O3: The importance of surface relaxation. J. Cryst. Growth 1987, 80, 441–446. [Google Scholar] [CrossRef]
- Ching, W.Y.; Xu, Y.-N. First-principles calculation of electronic, optical, and structural properties of α-Al2O3. J. Am. Ceram. Soc. 1994, 77, 404–411. [Google Scholar] [CrossRef]
- Freier, S.; Greenshpan, P.; Hillman, P.; Shechter, H. The antiferromagnetic curie point in α-Fe2O3. Phys. Lett. 1962, 2, 191–192. [Google Scholar] [CrossRef]
- Lielmezs, J.; Chaklader, A.C.D. Reversible thermal effect in α-Fe2O3 at 690 ± 5 °C. J. Appl. Phys. 1965, 36, 866–867. [Google Scholar] [CrossRef]
- Punkkinen, M.P.J.; Kokko, K.; Hergert, W.; Väyrynen, I.J. Fe2O3 within the LSDA+U approach. J. Phys. Condens. Matter 1999, 11, 2341–2349. [Google Scholar] [CrossRef]
- Sandratskii, L.M.; Uhl, M.; Kübler, J. Band theory for electronic and magnetic properties of α-Fe2O3. J. Phys. Condens. Matter 1996, 8, 983–989. [Google Scholar] [CrossRef]
- Uozumi, T.; Okada, K.; Kotani, A. Theory of photoemission spectra for M2O3 (M = Ti, V, Cr, Mn, Fe) compounds. J. Electron. Spectrosc. Relat. Phenom. 1996, 78, 103–106. [Google Scholar] [CrossRef]
- Fujimori, A.; Saeki, M.; Kimizuka, N.; Taniguchi, M.; Suga, M. Photoemission satellites and electronic structure of Fe2O3. Phys. Rev. B 1989, 34, 7318–7333. [Google Scholar]
- Ciccacci, F.; Braicovich, L.; Puppin, E.; Vescovo, E. Empty electron states in Fe2O3 by ultraviolet inverse-photoemission spectroscopy. Phys. Rev. B 1991, 44, 10444–10448. [Google Scholar] [CrossRef]
- Sivula, K.; Le Formal, F.; Grätzel, M. Solar water splitting: Progress using hematite (α-Fe2O3) photoelectrodes. ChemSusChem 2011, 4, 432–439. [Google Scholar] [CrossRef]
- Coey, J.; Sawatzky, G. A study of hyperfine interactions in the system (Fe1−xRhx)2O3 using the Mossbauer effect (Bonding parameters). J. Phys. C 1971, 4, 2386–2407. [Google Scholar] [CrossRef]
- Kren, E.; Szabo, P.; Konczos, G. Neutron diffraction studies on the (1−x)Fe2O3-xRh2O3 system. Phys. Lett. 1965, 19, 103–104. [Google Scholar] [CrossRef]
- Kiejna, A.; Pabisiak, T. Surface properties of clean and Au or Pd covered hematite (α-Fe2O3) (0001). J. Phys. Condens. Matter 24, 095003:1–095003:16.
- Liao, P.; Carter, E.A. Testing variations of the GW approximation on strongly correlated transition metal oxides: Hematite (α-Fe2O3) as a benchmark. Phys. Chem. Chem. Phys. 2011, 13, 15189–15199. [Google Scholar] [CrossRef]
- Barteau, M.A. Site requirements of reactions on oxide surfaces. J. Vac. Technol. A 1993, 11, 2162–2168. [Google Scholar] [CrossRef]
- Kurtz, R.; Henrich, V.E. Geometric structure of the α-Fe2O3(001) surface: A LEED and XPS study. Surf. Sci. 1983, 129, 345–354. [Google Scholar] [CrossRef]
- Lad, R.J.; Henrich, V.E. Structure of α-Fe2O3 single crystal surfaces following Ar+ ion bombardment and annealing in O2. Surf. Sci. 1988, 193, 81–93. [Google Scholar] [CrossRef]
- Ritter, M.; Weiss, W. Fe3O4(111) surface structure determined by LEED crystallography. Surf. Sci. 1999, 432, 81–94. [Google Scholar] [CrossRef]
- Ketteler, G.; Weiss, W.; Ranke, W. Surface structures of α-Fe2O3(0001) phases determined by LEED crystallography. Surf. Rev. Lett. 2001, 8, 661–683. [Google Scholar] [CrossRef]
- Lübbe, M.; Moritz, W. A LEED analysis of the clean surfaces of α-Fe2O3(0001) and α-Cr2O3(0001) bulk single crystals. J. Phys. Condens. Matter 2009, 21, 134010:1–134010:9. [Google Scholar]
- Eggleston, C.M.; Hochella, M.F. The structure of hematite {001} surfaces by scanning tunneling microscopy: Image interpretation, surface relaxation, and step structure. Am. Mineral. 1992, 77, 911–922. [Google Scholar]
- Condon, N.G.; Murray, P.W.; Leibsle, F.M.; Thornton, G.; Lennie, A.R.; Vaughan, D.J. Fe3O4(111) termination of α-Fe2O3(0001). Surf. Sci. 1994, 310, L609–L613. [Google Scholar] [CrossRef]
- Condon, N.G.; Leibsle, F.M.; Lennie, A.R.; Murray, P.W.; Vaughan, D.J.; Thornton, G. Biphase ordering of iron oxide surfaces. Phys. Rev. Lett. 1995, 75, 1961–1964. [Google Scholar] [CrossRef]
- Condon, N.G.; Leibsle, F.M.; Lennie, A.R.; Murray, P.W.; Parker, T.M.; Vaughan, D.J.; Thornton, G. Scanning tunnelling microscopy studies of α-Fe2O3(0001). Surf. Sci. 1998, 397, 278–287. [Google Scholar] [CrossRef]
- Shaikhutdinov, S.K.; Weiss, W. Oxygen pressure dependence of the α-Fe2O3(0001) surface structure. Surf. Sci. 1999, 432, L627–L634. [Google Scholar] [CrossRef]
- Chambers, S.A.; Yi, S.I. Fe termination for α-Fe2O3(0001) as grown by oxygen-plasma-assisted molecular beam epitaxy. Surf. Sci. 1999, 439, L785–L791. [Google Scholar] [CrossRef]
- Thevuthasan, S.; Kim, Y.J.; Yi, S.I.; Chambers, S.A.; Morais, J.; Denecke, R.; Fadley, C.S.; Liu, P.; Kendelewica, T.; Brown, G.E., Jr. Surface structure of MBE-grown α-Fe2O3(0001) by intermediate-energy X-ray photoelectron diffraction. Surf. Sci. 1999, 425, 276–286. [Google Scholar] [CrossRef]
- Greene, M.E.; Chiaramonti, A.N.; Christensen, S.T.; Cao, L.; Bedzyk, M.J.; Hersam, M.C. Controlled nanoscale morphology of hematite (0001) surfaces grown by chemical vapor transport. Adv. Mater. 2005, 17, 1765–1768. [Google Scholar] [CrossRef]
- Mackrodt, W.C. Atomistic simulation of oxide surfaces. Phys. Chem. Miner. 1988, 15, 228–237. [Google Scholar] [CrossRef]
- Reeves, N.J.; Mann, S. Influence of inorganic and organic additives on the tailored synthesis of iron oxides. J. Chem. Soc. Faraday Trans. 1991, 87, 3875–3880. [Google Scholar] [CrossRef]
- Jin, J.; Ma, X.; Kim, C.-Y.; Ellis, D.E.; Bedzyk, M.J. Adsorption of V on a hematite (0001) surface and its oxidation: Submonolayer coverage. Surf. Sci. 2007, 601, 3082–3098. [Google Scholar] [CrossRef]
- Henderson, M.A. Insights into the (1 × 1)-to-(2 × 1) phase transition of the α-Fe2O3 (012) surface using EELS, LEED and water TPD. Surf. Sci. 2002, 515, 253–262. [Google Scholar] [CrossRef]
- Henderson, M.A.; Joyce, S.A.; Rustad, J.R. Interaction of water with the (1 × 1) and (2 × 1) surfaces of α-Fe2O3 (012). Surf. Sci. 1998, 417, 66–81. [Google Scholar] [CrossRef]
- Chatman, S.; Zarzyckib, P.; Rosso, K.M. Surface potentials of (001), (012), (113) hematite (α-Fe2O3) crystal faces in aqueous solution. Phys. Chem. Chem. Phys. 2013, 15, 13911–13921. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 91st ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Bader, R.F.W. Atoms in Molecules—A Quantum Theory; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Knickelbein, M.B. Nickel clusters: The influence of adsorbates on magnetic moments. J. Chem. Phys. 2002, 116, 9703–9711. [Google Scholar] [CrossRef]
- Błoński, P.; Kiejna, A.; Hafner, J. Theoretical study of oxygen adsorption at the Fe(110) and (100) surfaces. Surf. Sci. 2005, 590, 88–100. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dzade, N.Y.; Roldan, A.; De Leeuw, N.H. A Density Functional Theory Study of the Adsorption of Benzene on Hematite (α-Fe2O3) Surfaces. Minerals 2014, 4, 89-115. https://doi.org/10.3390/min4010089
Dzade NY, Roldan A, De Leeuw NH. A Density Functional Theory Study of the Adsorption of Benzene on Hematite (α-Fe2O3) Surfaces. Minerals. 2014; 4(1):89-115. https://doi.org/10.3390/min4010089
Chicago/Turabian StyleDzade, Nelson Y., Alberto Roldan, and Nora H. De Leeuw. 2014. "A Density Functional Theory Study of the Adsorption of Benzene on Hematite (α-Fe2O3) Surfaces" Minerals 4, no. 1: 89-115. https://doi.org/10.3390/min4010089