Some Remarks on the Electrical Conductivity of Hydrous Silicate Minerals in the Earth Crust, Upper Mantle and Subduction Zone at High Temperatures and High Pressures
Abstract
:1. Introduction
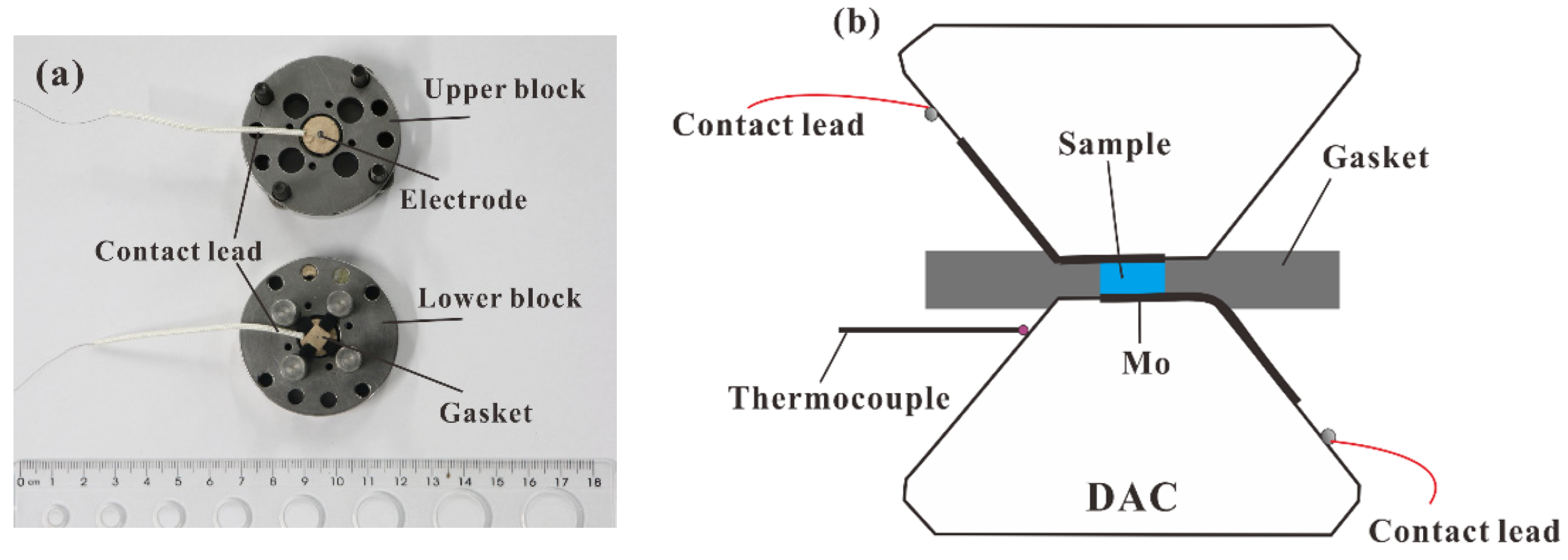
2. High-Pressure Apparatus for the EC Measurements and FT-IR Observation
3. Experimental Theory and Measurement Methods
4. Electrical Conductivity of Hydrous Minerals
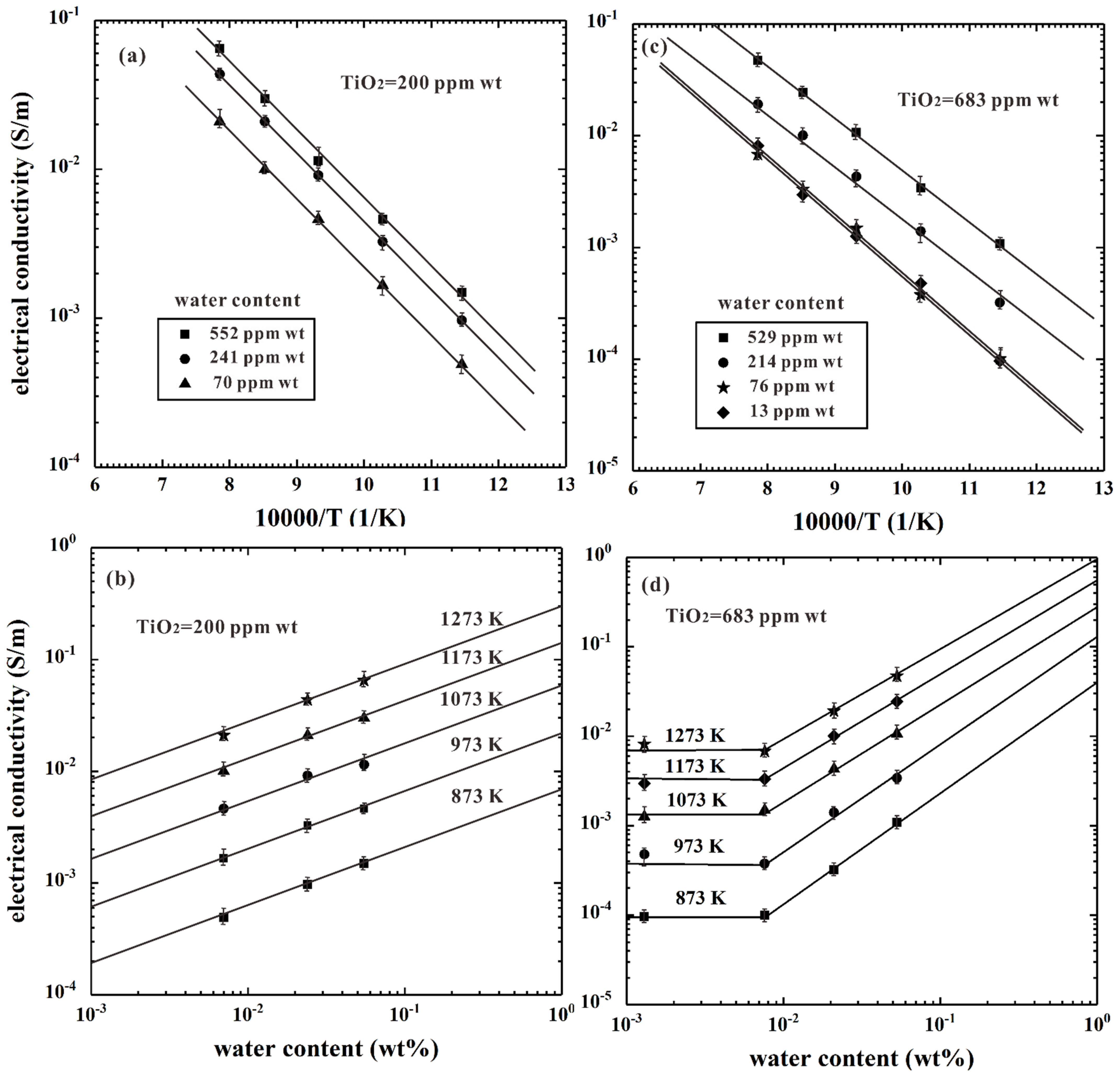
4.1. Electrical Conductivity of Ti-Bearing Hydrous Olivine
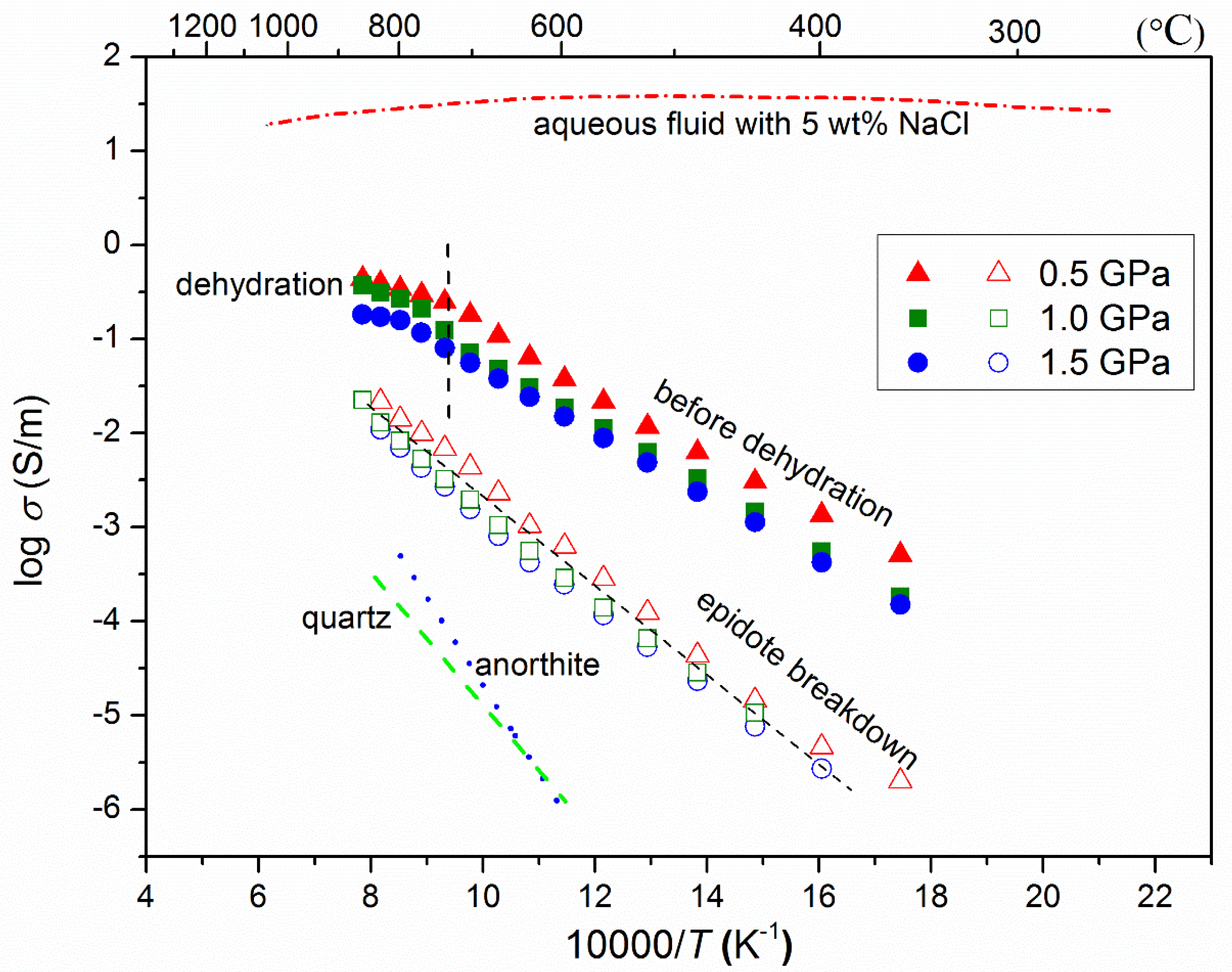
4.2. Electrical Conductivity of Hydrous Epidote
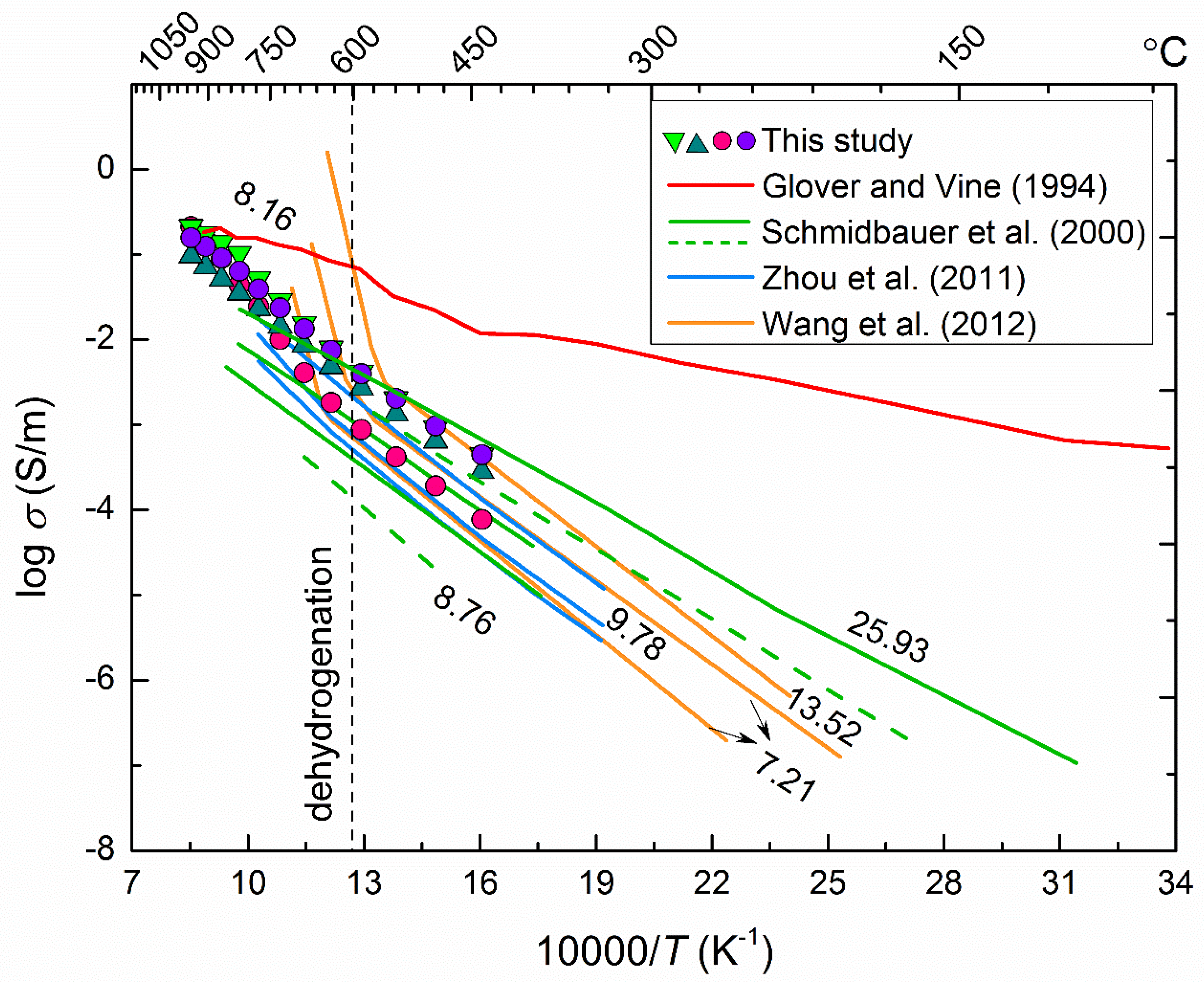
4.3. Electrical Conductivity of Hydrous Amphibole
4.4. Electrical Conductivity of Hydrous Kaolinite
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zheng, Y.; Hermann, J. Geochemistry of continental subduction-zone fluids. Earth Planets Space 2014, 66, 93. [Google Scholar] [CrossRef] [Green Version]
- Karato, S. The role of hydrogen in the electrical conductivity of the upper mantle. Nature 1990, 347, 272–273. [Google Scholar] [CrossRef]
- Selway, K.; O’Donnell, J.; Özaydin, S. Upper mantle melt distribution from petrologically constrained magnetotellurics. Geochem. Geophys. Geosyst. 2019, 20, 3328–3346. [Google Scholar] [CrossRef]
- Selway, K. Negligible effect of hydrogen content on plate strength in East Africa. Nat. Geosci. 2015, 8, 543–546. [Google Scholar] [CrossRef]
- Selway, K. On the causes of electrical conductivity anomalies in tectonically stable lithosphere. Sur. Geophys. 2014, 35, 219–257. [Google Scholar] [CrossRef]
- Selway, K.; Hand, M.; Heinson, G.; Payne, J. Magnetotelluric constraints on subduction polarity: Reversing reconstruction models for Proterozoic Australia. Geology 2009, 37, 799–802. [Google Scholar] [CrossRef]
- Förster, M.; Selway, K. Melting of subducted sediments reconciles geophysical images of subduction zones. Nat. Commun. 2021, 12, 1320. [Google Scholar] [CrossRef]
- Yang, B.; Egbert, G.; Zhang, H.; Meqbel, N.; Hu, X. Electrical resistivity imaging of continental United States from three-dimensional inversion of EarthScope USArray magnetotelluric data. Earth Planet. Sci. Lett. 2021, 576, 117244. [Google Scholar] [CrossRef]
- Dai, L.; Karato, S. Electrical conductivity of Ti-bearing hydrous olivine aggregates at high temperature and high pressure. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020309. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, Q.; Xu, X.; Fei, H.; Yang, X. High electrical conductivity of olivine at oxidizing conditions of the shallow mantle and geophysical implications. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022739. [Google Scholar] [CrossRef]
- Sun, C.; Tang, G.; Fortin, J.; Borgomano, J.V.; Wang, S. Dispersion and attenuation of elastic wave velocities: Impact of microstructure heterogeneity and local measurements. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020132. [Google Scholar] [CrossRef]
- Horikawa, T.; Katsura, M.; Yokota, T.; Nakashima, S. Effects of pore water distributions on P-wave velocity–water saturation relations in partially saturated sandstones. Geophys. J. Int. 2021, 226, 1558–1573. [Google Scholar] [CrossRef]
- Mohiuddin, A.; Karato, S.; Girard, J. Slab weakening during the olivine to ringwoodite transition in the mantle. Nat. Geosci. 2020, 13, 170–174. [Google Scholar] [CrossRef]
- Zhang, Z.; Karato, S. The effect of pressure on grain-growth kinetics in olivine aggregates with some geophysical applications. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020886. [Google Scholar] [CrossRef]
- Sun, W.; Yoshino, T.; Sakamoto, N.; Yurimoto, H. Supercritical fluid in the mantle transition zone deduced from H–D interdiffusion of wadsleyite. Earth Planet. Sci. Lett. 2018, 484, 309–317. [Google Scholar] [CrossRef]
- Fei, H.; Koizumi, S.; Sakamoto, N.; Hashiguchi, M.; Yurimoto, H.; Marquardt, K.; Miyajima, N.; Katsura, T. Pressure, temperature, water content, and oxygen fugacity dependence of the Mg grain-boundary diffusion coefficient in forsterite. Am. Mineral. 2018, 103, 1354–1361. [Google Scholar] [CrossRef]
- Tielke, J.; Mecklenburgh, J.; Mariani, E.; Wheeler, J. The influence of water on the strength of olivine dislocation slip systems. J. Geophys. Res. Solid Earth 2019, 124, 6542–6559. [Google Scholar] [CrossRef]
- Zhang, G.; Mei, S.; Song, M. Effect of water on the dislocation creep of enstatite aggregates at 300 MPa. Geophys. Res. Lett. 2020, 47, e2019GL085895. [Google Scholar] [CrossRef]
- Précigout, J.; Prigent, C.; Palasse, L.; Pochon, A. Water pumping in mantle shear zones. Nat. Commun. 2017, 8, 15736. [Google Scholar] [CrossRef]
- Speciale, P.; Behr, W.; Hirth, G.; Tokle, L. Rates of olivine grain growth during dynamic recrystallization and postdeformation annealing. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020415. [Google Scholar] [CrossRef]
- Huang, X.; Xu, Y.; Karato, S. Water content in the transition zone from electrical conductivity of wadsleyite and ringwoodite. Nature 2005, 434, 746–749. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Bai, W.; Xu, Y.; Karato, S. Influence of hydrogen on electrical conductivity of wadsleyite and ringwoodite with its geodynamics implications. Acta Petrol. Sin. 2005, 21, 1743–1748. [Google Scholar]
- Huang, X.; Wang, X.; Chen, Z.; Bai, W. The experimental research on electrical conductivity for minerals and rocks under condition of upper mantle. Sci. Sin. Terrae 2017, 47, 518–529. [Google Scholar]
- Wang, D.; Mookherjee, M.; Xu, Y.; Karato, S. The effect of water on the electrical conductivity of olivine. Nature 2006, 443, 977–980. [Google Scholar] [CrossRef]
- Dai, L.; Karato, S. Electrical conductivity of wadsleyite at high temperatures and high pressures. Earth Planet. Sci. Lett. 2009, 287, 277–283. [Google Scholar] [CrossRef]
- Dai, L.; Karato, S. Electrical conductivity of pyrope-rich garnet at high temperature and high pressure. Phys. Earth Planet. Inter. 2009, 176, 83–88. [Google Scholar] [CrossRef]
- Dai, L.; Karato, S. Electrical conductivity of orthopyroxene: Implications for the water content of the asthenosphere. Proc. Jpn. Acad. 2009, 85, 466–475. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Karato, S. High and highly anisotropic electrical conductivity of the asthenosphere due to hydrogen diffusion in olivine. Earth Planet. Sci Lett. 2014, 408, 79–86. [Google Scholar] [CrossRef]
- Dai, L.; Karato, S. The effect of pressure on the electrical conductivity of olivine under the hydrogen-rich conditions. Phys. Earth Planet. Inter. 2014, 232, 51–56. [Google Scholar] [CrossRef]
- Dai, L.; Karato, S. Influence of oxygen fugacity on the electrical conductivity of hydrous olivine: Implications for the mechanism of conduction. Phys. Earth Planet. Inter. 2014, 232, 57–60. [Google Scholar] [CrossRef]
- Dai, L.; Karato, S. Influence of FeO and H on the electrical conductivity of olivine. Phys. Earth Planet. Inter. 2014, 237, 73–79. [Google Scholar] [CrossRef]
- Karato, S.; Dai, L. Comments on “Electrical conductivity of wadsleyite as a function of temperature and water content” by Manthilake et al. Phys. Earth Planet. Inter. 2009, 174, 19–21. [Google Scholar] [CrossRef]
- Hu, H.; Dai, L.; Li, H.; Hui, K.; Sun, W. Influence of dehydration on the electrical conductivity of epidote and implications for high-conductivity anomalies in subduction zones. J. Geophys. Res. Solid Earth 2017, 122, 2751–2762. [Google Scholar] [CrossRef]
- Hu, H.; Dai, L.; Li, H.; Sun, W.; Li, B. Effect of dehydrogenation on the electrical conductivity of Fe-bearing amphibole: Implications for high conductivity anomalies in subduction zones and continental crust. Earth Planet. Sci Lett. 2018, 498, 27–37. [Google Scholar] [CrossRef]
- Dai, L.; Hu, H.; Jiang, J.; Sun, W.; Li, H.; Wang, M.; Vallianatos, F.; Saltas, V. An overview of the experimental studies on the electrical conductivity of major minerals in the upper mantle and transition zone. Materials 2020, 13, 408. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Dai, L.; Kim, D.Y.; Li, H.; Karato, S. Thermal ionization of hydrogen in hydrous olivine with enhanced and anisotropic conductivity. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022939. [Google Scholar] [CrossRef]
- Shan, S.; Xiao, C.; Li, H.; Xu, L.; Lin, S.; Li, S. In Situ electrical conductivity measurements of porous water-containing rock materials under high temperature and high pressure conditions in an autoclave. Rev. Sci. Instrum. 2021, 92, 095104. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Hu, H.; Shan, S. Novel technique to control oxygen fugacity during high-pressure measurements of grain boundary conductivities of rocks. Rev. Sci. Instrum. 2009, 80, 033903. [Google Scholar] [CrossRef]
- Gwanmesia, G.; Whitaker, M.; Dai, L.; James, A.; Chen, H.; Triplett, R.; Cai, N. The elastic properties of β-Mg2SiO4 containing 0.73 wt.% of H2O to 10 GPa and 600 K by ultrasonic interferometry with synchrotron x-radiation. Minerals 2020, 10, 209. [Google Scholar] [CrossRef] [Green Version]
- Paterson, M. The determination of hydroxyl by infrared absorption in quartz, silicate glass and similar materials. Bull. De Minéralogie 1982, 105, 20–29. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Hu, H.; Shan, S.; Jiang, J.; Hui, K. The effect of chemical composition and oxygen fugacity on the electrical conductivity of dry and hydrous garnet at high temperatures and pressures. Contrib. Mineral. Petrol. 2012, 163, 689–700. [Google Scholar] [CrossRef]
- Dai, L.; Hu, H.; Li, H.; Hui, K.; Jiang, J.; Li, J.; Sun, W. Electrical conductivity of gabbro: The effects of temperature, pressure and oxygen fugacity. Eur. J. Mineral. 2015, 27, 215–224. [Google Scholar] [CrossRef]
- Dai, L.; Jiang, J.; Li, H.; Hu, H.; Hui, K. Electrical conductivity of hydrous natural basalt at high temperatures and high pressures. J. Appl. Geophys. 2015, 112, 290–297. [Google Scholar] [CrossRef]
- Sun, W.; Dai, L.; Li, H.; Hu, H.; Wu, L.; Jiang, J. Electrical conductivity of mudstone (before and after dehydration at high PT) and a test of high conductivity layers in the crust. Am. Mineral. 2017, 102, 2450–2456. [Google Scholar] [CrossRef]
- Sun, W.; Dai, L.; Li, H.; Hu, H.; Jiang, J.; Hui, K. Effect of dehydration on the electrical conductivity of phyllite at high temperatures and pressures. Mineral. Petrol. 2017, 111, 853–863. [Google Scholar] [CrossRef]
- Dai, L.; Hu, H.; Sun, W.; Li, H.; Liu, C.; Wang, M. Influence of high conductive magnetite impurity on the electrical conductivity of dry olivine aggregates at high temperature and high pressure. Minerals 2019, 9, 44. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Sun, W.; Li, H.; Hu, H.; Wu, L.; Jiang, J. Effect of chemical composition on the electrical conductivity of gneiss at high temperatures and pressures. Solid Earth 2018, 9, 233–245. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Hu, H.; Li, H.; Sun, W.; Jiang, J. Influence of anisotropy on the electrical conductivity and diffusion coefficient of dry K-feldspar: Implications for the mechanism of conduction. Chin. Phys. B 2018, 27, 028703. [Google Scholar] [CrossRef]
- Dai, L.; Hu, H.; Li, H.; Wu, L.; Hui, K.; Jiang, J.; Sun, W. Influence of temperature, pressure, and oxygen fugacity on the electrical conductivity of dry eclogite, and geophysical implications. Geochem. Geophys. Geosyst. 2016, 17, 2394–2407. [Google Scholar] [CrossRef]
- Dai, L.; Hu, H.; Li, H.; Jiang, J.; Hui, K. Influence of temperature, pressure, and chemical composition on the electrical conductivity of granite. Am. Mineral. 2014, 99, 1420–1428. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Hu, H.; Jiang, J.; Hui, K.; Shan, S. Electrical conductivity of Alm82Py15Grs3 almandine-rich garnet determined by impedance spectroscopy at high temperatures and high pressures. Tectonophysics 2013, 608, 1086–1093. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Hu, H.; Shan, S. In-Situ control of oxygen fugacity for laboratory measurements of electrical conductivity of minerals and rocks in multi-anvil press. Chin. Phys. B 2011, 20, 049101. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Li, C.; Hu, H.; Shan, S. The electrical conductivity of dry polycrystalline olivine compacts at high temperatures and pressures. Mineral. Mag. 2010, 74, 849–857. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Hu, H.; Shan, S. Experimental study of grain boundary electrical conductivities of dry synthetic peridotite under high-temperature, high-pressure, and different oxygen fugacity conditions. J. Geophys. Res. Solid Earth 2008, 113, B12211. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Li, H.; Deng, H.; Liu, C.; Su, G.; Shan, S.; Zhang, L.; Wang, R. In-Situ control of different oxygen fugacity experimental study on the electrical conductivity of lherzolite at high temperature and high pressure. J. Phys. Chem. Solids 2008, 69, 101–110. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Liu, C.; Su, G.; Shan, S. Experimental measurement on the electrical conductivity of pyroxenite at high temperature and high pressure under different oxygen fugacities. High Press. Res. 2006, 26, 193–202. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Liu, C.; Cui, T.; Shan, S.; Yang, C.; Liu, Q.; Deng, H. Experimental measurement on the electrical conductivity of single crystal olivine at high temperature and high pressure under different oxygen fugacities. Prog. Nat. Sci. 2006, 16, 387–393. [Google Scholar] [CrossRef]
- Dai, L.; Li, H.; Liu, C.; Shan, S.; Cui, T.; Su, G. Experimental study on the electrical conductivity of orthopyroxene at high temperature and high pressure under different oxygen fugacities. Acta Geol. Sin. Engl. 2005, 79, 803–809. [Google Scholar]
- Dai, L.; Li, H.; Liu, C.; Su, G.; Cui, T. In Situ control of oxygen fugacity experimental study on the crystallographic anisotropy of the electrical conductivities of diopside at high temperature and high pressure. Acta Petrol. Sin. 2005, 21, 1737–1742. [Google Scholar]
- Hu, H.; Dai, L.; Li, H.; Hui, K.; Li, J. Temperature and pressure dependence of electrical conductivity in synthetic anorthite. Solid State Ion. 2015, 276, 136–141. [Google Scholar] [CrossRef]
- Hu, H.; Dai, L.; Li, H.; Jiang, J.; Hui, K. Electrical conductivity of K-feldspar at high temperature and high pressure. Mineral. Petrol. 2014, 108, 609–618. [Google Scholar] [CrossRef]
- Hu, H.; Li, H.; Dai, L.; Shan, S.; Zhu, C. Electrical conductivity of alkali feldspar solid solutions at high temperatures and high pressures. Phys. Chem. Mineral. 2013, 40, 51–62. [Google Scholar] [CrossRef]
- Hu, H.; Li, H.; Dai, L.; Shan, S.; Zhu, C. Electrical conductivity of albite at high temperatures and high pressures. Am. Miner. 2011, 96, 1821–1827. [Google Scholar] [CrossRef]
- Hui, K.; Dai, L.; Li, H.; Hu, H.; Jiang, J.; Sun, W.; Zhang, H. Experimental study on the electrical conductivity of pyroxene andesite at high temperature and high pressure. Pure Appl. Geophys. 2017, 174, 1033–1041. [Google Scholar] [CrossRef]
- Hui, K.; Zhang, H.; Li, H.; Dai, L.; Hu, H.; Jiang, J.; Sun, W. Experimental study on the electrical conductivity of quartz andesite at high temperature and high pressure: Evidence of grain boundary transport. Solid Earth 2015, 6, 1037–1043. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Dai, L.; Hu, H.; Jiang, J.; Wang, M.; Hu, Z.; Jing, C. Influence of saline fluids on the electrical conductivity of olivine aggregates at high temperature and high pressure and its geological implications. Front. Earth Sci. 2021, 9, 749896. [Google Scholar] [CrossRef]
- Sun, W.; Jiang, J.; Dai, L.; Hu, H.; Wang, M.; Qi, Y.; Li, H. Electrical properties of dry polycrystalline olivine mixed with various chromite contents: Implications for the high-conductivity anomalies in subduction zones. Geosci. Front. 2021, 12, 101178. [Google Scholar] [CrossRef]
- Sun, W.; Dai, L.; Li, H.; Hu, H.; Jiang, J.; Wang, M. Electrical conductivity of clinopyroxene-NaCl-H2O system at high temperatures and pressures: Implications for high-conductivity anomalies in the deep crust and subduction zone. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019093. [Google Scholar] [CrossRef]
- Sun, W.; Dai, L.; Li, H.; Hu, H.; Jiang, J.; Liu, C. Experimental study on the electrical properties of carbonaceous slate: A special natural rock with unusually high conductivity at high temperatures and pressures. High Temp. High Press. 2019, 48, 455–467. [Google Scholar] [CrossRef]
- Sun, W.; Dai, L.; Li, H.; Hu, H.; Liu, C. Effect of temperature, pressure and chemical composition on the electrical conductivity of granulite and geophysical implications. J. Mineral. Petrol. Sci. 2019, 114, 87–98. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Dai, L.; Li, H.; Hu, H.; Liu, C.; Wang, M. Effect of temperature, pressure and chemical compositions on the electrical conductivity of schist: Implications for electrical structures under the Tibetan plateau. Materials 2019, 12, 961. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, L.; Pu, C.; Li, H.; Hu, H.; Liu, K.; Yang, L.; Hong, M. Characterization of metallization and amorphization for GaP under different hydrostatic environments in diamond anvil cell up to 40.0 GPa. Rev. Sci. Instrum. 2019, 90, 066103. [Google Scholar] [CrossRef] [PubMed]
- Hong, M.; Dai, L.; Hu, H.; Yang, L.; Zhang, X. Pressure-induced structural phase transitions in natural kaolinite investigated by Raman spectroscopy and electrical conductivity. Am. Mineral. 2022, in press. [Google Scholar] [CrossRef]
- Liu, K.; Dai, L.; Li, H.; Hu, H.; Zhuang, Y.; Yang, L.; Pu, C.; Hong, M. Pressure-induced phase transitions for goethite investigated by Raman spectroscopy and electrical conductivity. High Press. Res. 2019, 39, 106–116. [Google Scholar] [CrossRef]
- Pu, C.; Dai, L.; Li, H.; Hu, H.; Zhuang, Y.; Liu, K.; Yang, L.; Hong, M. High–pressure electrical conductivity and Raman spectroscopic study of chalcanthite. Spectrosc. Lett. 2018, 51, 531–539. [Google Scholar] [CrossRef]
- Yang, L.; Dai, L.; Li, H.; Hu, H.; Hong, M.; Zhang, X. The phase transition and dehydration in epsomite under high temperature and high pressure. Crystals 2020, 10, 75. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Dai, L.; Li, H.; Hu, H.; Zhuang, Y.; Liu, K.; Pu, C.; Hong, M. Pressure-induced structural phase transition and dehydration for gypsum investigated by Raman spectroscopy and electrical conductivity. Chem. Phys. Lett. 2018, 706, 151–157. [Google Scholar] [CrossRef]
- Dai, L.; Liu, K.; Li, H.; Wu, L.; Hu, H.; Zhuang, Y.; Yang, L.; Pu, C.; Liu, P. Pressure-induced irreversible metallization accompanying the phase transitions in Sb2S3. Phys. Rev. B 2018, 97, 024103. [Google Scholar] [CrossRef]
- Dai, L.; Zhuang, Y.; Li, H.; Wu, L.; Hu, H.; Liu, K.; Yang, L.; Pu, C. Pressure-induced irreversible amorphization and metallization with a structural phase transition in arsenic telluride. J. Mater. Chem. C 2017, 5, 12157–12162. [Google Scholar] [CrossRef]
- Dai, L.; Wu, L.; Li, H.; Hu, H.; Zhuang, Y.; Liu, K. Evidence of the pressure-induced conductivity switching of yttrium-doped SrTiO3. J. Phys Condens. Matt. 2016, 28, 475501. [Google Scholar] [CrossRef]
- Dai, L.; Wu, L.; Li, H.; Hu, H.; Zhuang, Y.; Liu, K. Pressure-induced phase-transition and improvement of the micro dielectric properties in yttrium-doped SrZrO3. Europhys. Lett. 2016, 114, 56003. [Google Scholar] [CrossRef]
- Hong, M.; Dai, L.; Hu, H.; Zhang, X. Pressure-induced structural phase transition and metallization in Ga2Se3 up to 40.2 GPa under non-hydrostatic and hydrostatic environments. Crystals 2021, 11, 746. [Google Scholar] [CrossRef]
- Hong, M.; Dai, L.; Li, H.; Hu, H.; Liu, K.; Yang, L.; Pu, C. Structural phase transition and metallization of nanocrystalline rutile investigated by high-pressure Raman spectroscopy and electrical conductivity. Minerals 2019, 9, 441. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Dai, L.; Li, H.; Hu, H.; Yang, L.; Pu, C.; Hong, M. Evidences for phase transition and metallization in β-In2S3 at high pressure. Chem. Phys. 2019, 524, 63–69. [Google Scholar] [CrossRef]
- Liu, K.; Dai, L.; Li, H.; Hu, H.; Yang, L.; Pu, C.; Hong, M. Phase transition and metallization of orpiment by Raman spectroscopy, electrical conductivity and theoretical calculation under high pressure. Materials 2019, 12, 784. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Dai, L.; Li, H.; Hu, H.; Wu, L.; Zhuang, Y.; Pu, C.; Yang, L. Migration of impurity level reflected in the electrical conductivity variation for natural pyrite at high temperature and high pressure. Phys. Chem. Miner. 2018, 45, 85–92. [Google Scholar] [CrossRef]
- Pu, C.; Dai, L.; Li, H.; Hu, H.; Liu, K.; Yang, L.; Hong, M. Pressure-induced phase transitions of ZnSe under different pressure environments. AIP Adv. 2019, 9, 025004. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Dai, L.; Li, H.; Hu, H.; Zhuang, Y.; Liu, K. Anomalous phase transition of Bi-doped Zn2GeO4 investigated by electrical conductivity and Raman spectroscopy under high pressure. J. Appl. Phys. 2017, 121, 125901. [Google Scholar] [CrossRef]
- Wu, L.; Dai, L.; Li, H.; Zhuang, Y.; Liu, K. Pressure-induced improvement of grain boundary properties in Y-doped BaZrO3. J. Phys. D Appl. Phys. 2016, 49, 345102. [Google Scholar] [CrossRef]
- Yang, L.; Jiang, J.; Dai, L.; Hu, H.; Hong, M.; Zhang, X.; Li, H.; Liu, P. High-pressure structural phase transition and metallization in Ga2S3 under non-hydrostatic and hydrostatic conditions up to 36.4 GPa. J. Mater. Chem. C 2021, 9, 2912–2918. [Google Scholar] [CrossRef]
- Yang, L.; Dai, L.; Li, H.; Hu, H.; Hong, M.; Zhang, X.; Liu, P. High-pressure investigations on the isostructural phase transition and metallization in realgar with diamond anvil cells. Geosci. Front. 2021, 12, 1031–1037. [Google Scholar] [CrossRef]
- Yang, L.; Dai, L.; Li, H.; Hu, H.; Liu, K.; Pu, C.; Hong, M.; Liu, P. Characterization of the pressure-induced phase transition of metallization for MoTe2 under different hydrostatic environments. AIP Adv. 2019, 9, 065104. [Google Scholar] [CrossRef]
- Yang, L.; Dai, L.; Li, H.; Hu, H.; Liu, K.; Pu, C.; Hong, M.; Liu, P. Pressure-induced metallization in MoSe2 under different pressure conditions. RSC Adv. 2019, 9, 5794–5803. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Dai, L.; Hu, H.; Hong, M. Pressure-induced metallic phase transition in gallium arsenide up to 24.3 GPa under hydrostatic conditions. Mod. Phys. Lett. B 2021, 35, 2150460. [Google Scholar] [CrossRef]
- Zhuang, Y.; Dai, L.; Li, H.; Hu, H.; Liu, K.; Yang, L.; Pu, C.; Hong, M. Pressure induced reversible metallization and phase transition in Zinc Telluride. Mod. Phys. Lett. B 2018, 34, 1850342. [Google Scholar] [CrossRef]
- Zhuang, Y.; Dai, L.; Li, H.; Hu, H.; Liu, K.; Yang, L.; Pu, C.; Hong, M.; Liu, P. Deviatoric stresses promoted metallization in rhenium disulfide. J. Phys. D Appl. Phys. 2018, 51, 165101. [Google Scholar] [CrossRef]
- Zhuang, Y.; Dai, L.; Wu, L.; Li, H.; Hu, H.; Liu, K.; Yang, L.; Pu, C. Pressure-induced permanent metallization with reversible structural transition in molybdenum disulfide. Appl. Phys. Lett. 2017, 110, 122103. [Google Scholar] [CrossRef]
- Manthilake, G.; Koga, K.; Peng, Y.; Mookherjee, M. Halogen bearing amphiboles, aqueous fluids, and melts in subduction zones: Insights on halogen cycle from electrical conductivity. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021339. [Google Scholar] [CrossRef]
- Manthilake, G.; Peng, Y.; Koga, K.; Mookherjee, M. Tracking slab surface temperatures with electrical conductivity of glaucophane. Sci. Rep. 2021, 11, 18014. [Google Scholar] [CrossRef]
- Manthilake, G.; Schiavi, F.; Zhao, C.; Mookherjee, M.; Bouhifd, M.; Jouffret, L. The electrical conductivity of Liebermannite: Implications for water transport into the Earth’s lower mantle. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020094. [Google Scholar] [CrossRef]
- Manthilake, G.; Bolfan-Casanova, N.; Novella, D.; Mookherjee, M.; Andrault, D. Dehydration of chlorite explains anomalously high electrical conductivity in the mantle wedges. Sci. Adv. 2016, 2, e1501631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manthilake, G.; Mookherjee, M.; Bolfan-Casanova, N.; Andrault, D. Electrical conductivity of lawsonite and dehydrating fluids at high pressures and temperatures. Geophys. Res. Lett. 2015, 42, 7398–7405. [Google Scholar] [CrossRef] [Green Version]
- Saltas, V.; Pentari, D.; Vallianatos, F. Complex electrical conductivity of biotite and muscovite micas at elevated temperatures: A comparative study. Materials 2020, 13, 3513. [Google Scholar] [CrossRef]
- Saltas, V.; Fitilis, I.; Vallianatos, F. A combined complex electrical impedance and acoustic emission study in limestone samples under uniaxial loading. Tectonophysics 2014, 637, 198–206. [Google Scholar] [CrossRef]
- Saltas, V.; Chatzistamou, V.; Pentari, D.; Paris, E.; Triantis, D.; Fitilis, I.; Vallianatos, F. Complex electrical conductivity measurements of a KTB amphibolite sample at elevated temperatures. Mater. Chem. Phys. 2013, 139, 169–175. [Google Scholar] [CrossRef]
- Saltas, V.; Vallianatos, F.; Gidarakos, E. Charge transport in diatomaceous earth studied by broadband dielectric spectroscopy. Appl. Clay Sci. 2013, 80–81, 226–235. [Google Scholar] [CrossRef]
- Huebner, J.; Dillenburg, R. Impedance spectra of hot, dry silicate minerals and rock: Qualitative interpretation of spectra. Am. Mineral. 1995, 80, 46–64. [Google Scholar] [CrossRef]
- Macdonald, J.; Barsoukov, E. Impedance Spectroscopy: Theory, Experiment, and Applications, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2005; pp. 1–595. [Google Scholar]
- Ter Heege, J.; Renner, J. In situ impedance spectroscopy on pyrophyllite and CaCO3 at high pressure and temperature: Phase transformations and kinetics of atomistic transport. Phys. Chem. Miner. 2007, 34, 445–465. [Google Scholar] [CrossRef]
- Cline, C., II; Faul, U.; David, E.; Berry, A.; Jackson, I. Redox-influenced seismic properties of upper-mantle olivine. Nature 2018, 555, 355–358. [Google Scholar] [CrossRef]
- Tollan, P.; Smith, R.; O’Neill, H.; Hermann, J. The responses of four main substitution mechanisms of H in olivine to H2O activity at 1050 °C and 3 GPa. Prog. Earth Planet. Sci. 2017, 4, 14. [Google Scholar] [CrossRef]
- Poli, S.; Schmidt, M. Experimental subsolidus studies on epidote minerals. Rev. Mineral. Geochem. 2004, 56, 171–195. [Google Scholar] [CrossRef]
- Bagdassarov, N.; Delépine, N. α–β inversion in quartz from low frequency electrical impedance spectroscopy. J. Phys. Chem. Solids 2004, 65, 1517–1526. [Google Scholar] [CrossRef]
- Sinmyo, R.; Keppler, H. Electrical conductivity of NaCl-bearing aqueous fluids to 600 °C and 1 GPa. Contrib. Mineral. Petrol. 2017, 172, 4. [Google Scholar] [CrossRef]
- Christensen, N.; Mooney, W. Seismic velocity structure and composition of the continental crust: A global view. J. Geophys. Res. Solid Earth 1995, 100, 9761–9788. [Google Scholar] [CrossRef]
- Schmidbauer, E.; Kunzmann, T.; Fehr, T.; Hochleitner, R. Electrical resistivity and 57Fe Mossbauer spectra of Fe-bearing calcic amphiboles. Phys. Chem. Miner. 2000, 27, 347–356. [Google Scholar] [CrossRef]
- Phillips, M.; Popp, R.; Clowe, C. Structural adjustments accompanying oxidation-dehydrogenation in amphiboles. Am. Mineral. 1988, 73, 500–506. [Google Scholar]
- Glover, P.; Vine, F. Electrical conductivity of the continental crust. Geophys. Res. Lett. 1994, 21, 2357–2360. [Google Scholar] [CrossRef]
- Zhou, W.; Fan, D.; Liu, Y.; Xie, H. Measurements of wave velocity and electrical conductivity of an amphibolite from southwestern margin of the Tarim Basin at pressures to 1.0 GPa and temperatures to 700 °C: Comparison with field observations. Geophys. J. Int. 2011, 187, 1393–1404. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Guo, Y.; Yu, Y.; Karato, S. Electrical conductivity of amphibole-bearing rocks: Influence of dehydration. Contrib. Mineral. Petrol. 2012, 164, 17–25. [Google Scholar] [CrossRef]
- Reynard, B.; Mibe, K.; de Moortèle, B.V. Electrical conductivity of the serpentinised mantle and fluid flow in subduction zones. Earth Planet. Sci. Lett. 2011, 307, 387–394. [Google Scholar] [CrossRef]
- Wang, D.; Karato, S. Electrical conductivity of talc aggregates at 0.5 GPa: Influence of dehydration. Phys. Chem. Miner. 2013, 40, 11–17. [Google Scholar] [CrossRef]
- Guo, X.; Yoshino, T. Pressure-induced enhancement of proton conduction in brucite. Geophys. Res. Lett. 2014, 41, 813–819. [Google Scholar] [CrossRef]
- Balan, E.; Calas, G.; Bish, D. Kaolin-group minerals: From hydrogen-bonded layers to environmental recorders. Elements 2014, 10, 183–188. [Google Scholar] [CrossRef]
- Schroeder, P.; Erickson, G. Kaolin: From ancient porcelains to nanocomposites. Elements 2014, 10, 177–182. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Dai, L.; Sun, W.; Zhuang, Y.; Liu, K.; Yang, L.; Pu, C.; Hong, M.; Wang, M.; Hu, Z.; et al. Some Remarks on the Electrical Conductivity of Hydrous Silicate Minerals in the Earth Crust, Upper Mantle and Subduction Zone at High Temperatures and High Pressures. Minerals 2022, 12, 161. https://doi.org/10.3390/min12020161
Hu H, Dai L, Sun W, Zhuang Y, Liu K, Yang L, Pu C, Hong M, Wang M, Hu Z, et al. Some Remarks on the Electrical Conductivity of Hydrous Silicate Minerals in the Earth Crust, Upper Mantle and Subduction Zone at High Temperatures and High Pressures. Minerals. 2022; 12(2):161. https://doi.org/10.3390/min12020161
Chicago/Turabian StyleHu, Haiying, Lidong Dai, Wenqing Sun, Yukai Zhuang, Kaixiang Liu, Linfei Yang, Chang Pu, Meiling Hong, Mengqi Wang, Ziming Hu, and et al. 2022. "Some Remarks on the Electrical Conductivity of Hydrous Silicate Minerals in the Earth Crust, Upper Mantle and Subduction Zone at High Temperatures and High Pressures" Minerals 12, no. 2: 161. https://doi.org/10.3390/min12020161






