Measurement of 3D-Shape Preferred Orientation (SPO) Using Synchrotron μ-CT: Applications for Estimation of Fault Motion Sense in a Fault Gouge
Abstract
:1. Introduction
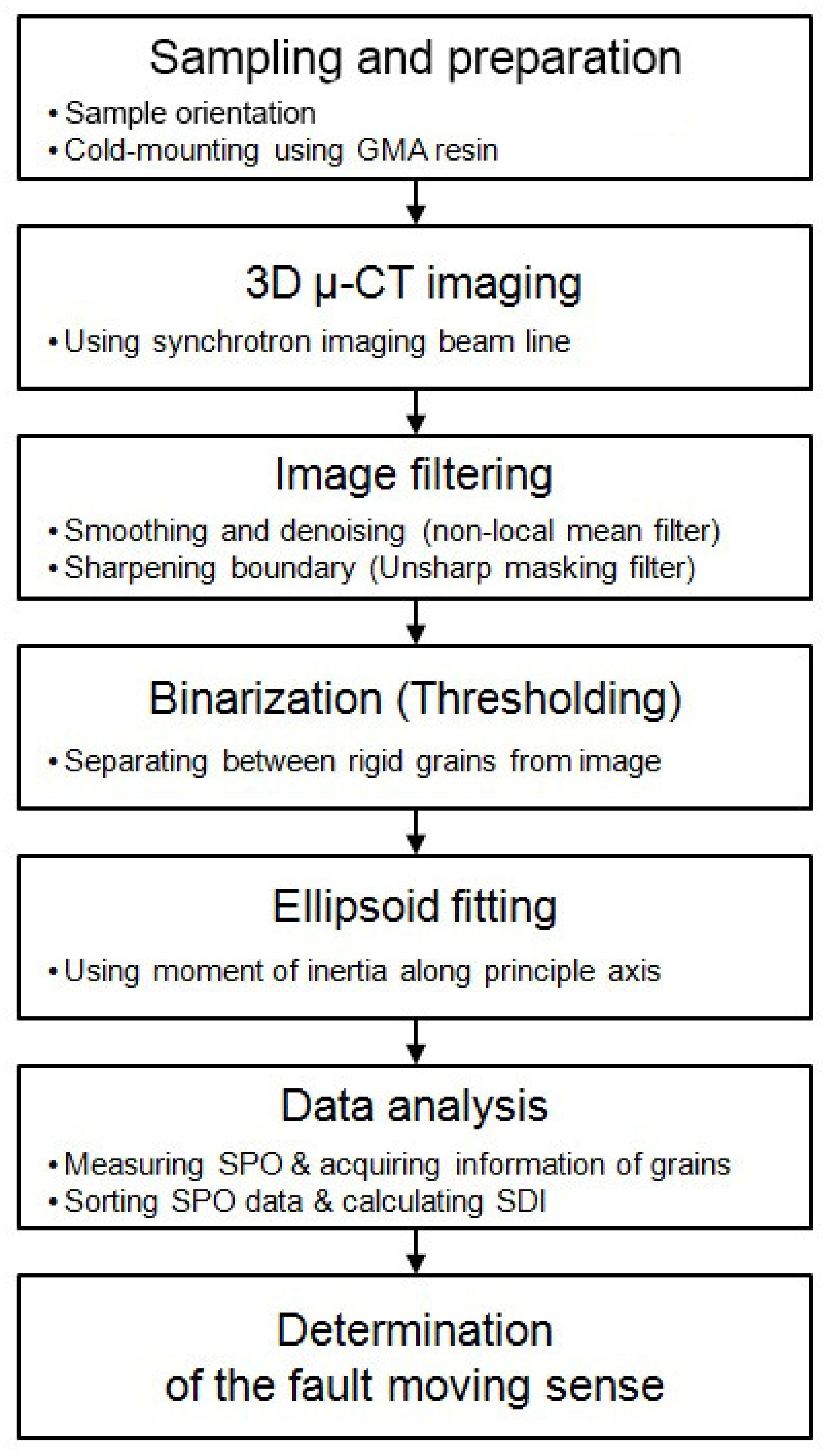
2. SPO Method Development
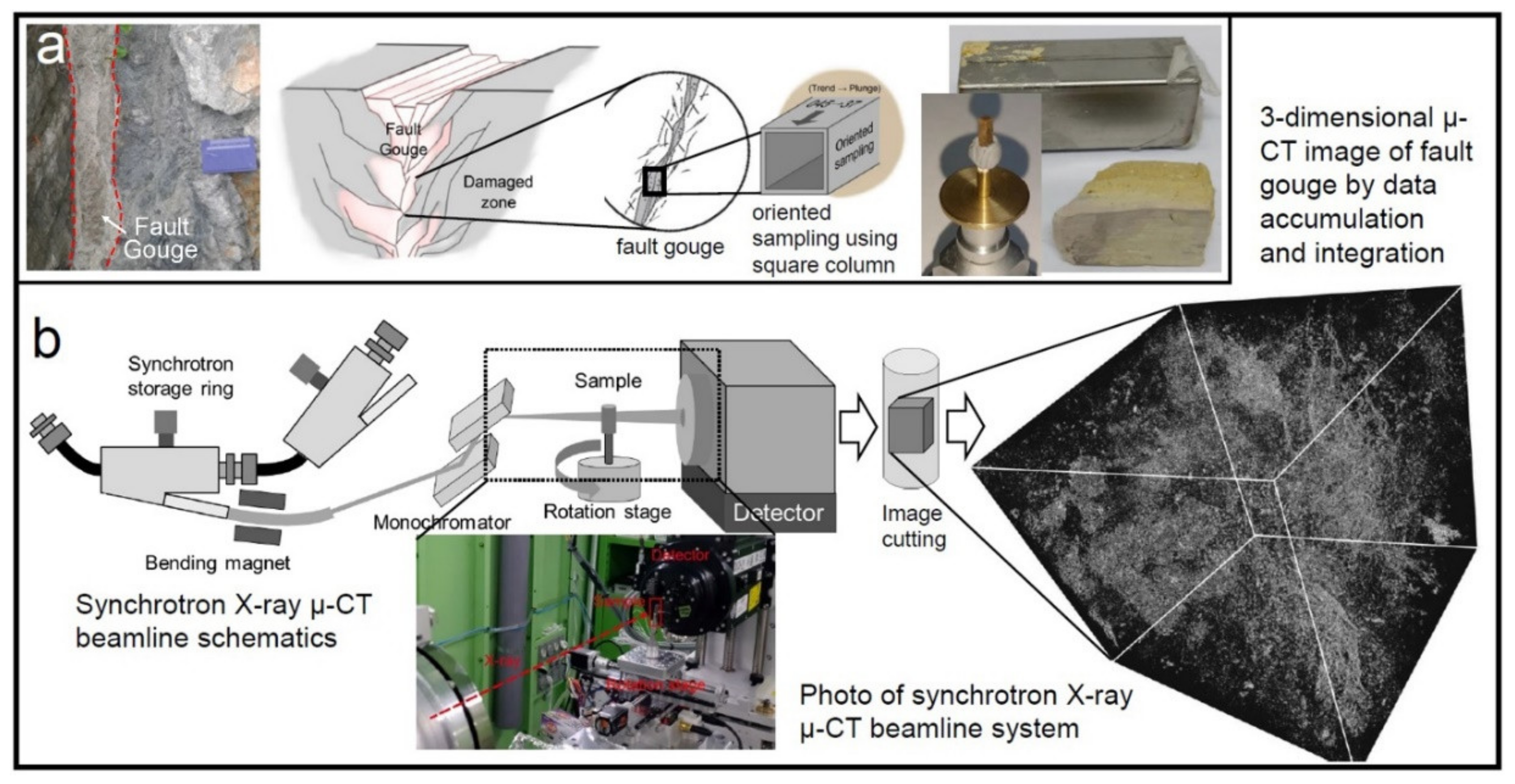
2.1. μ-CT Imaging
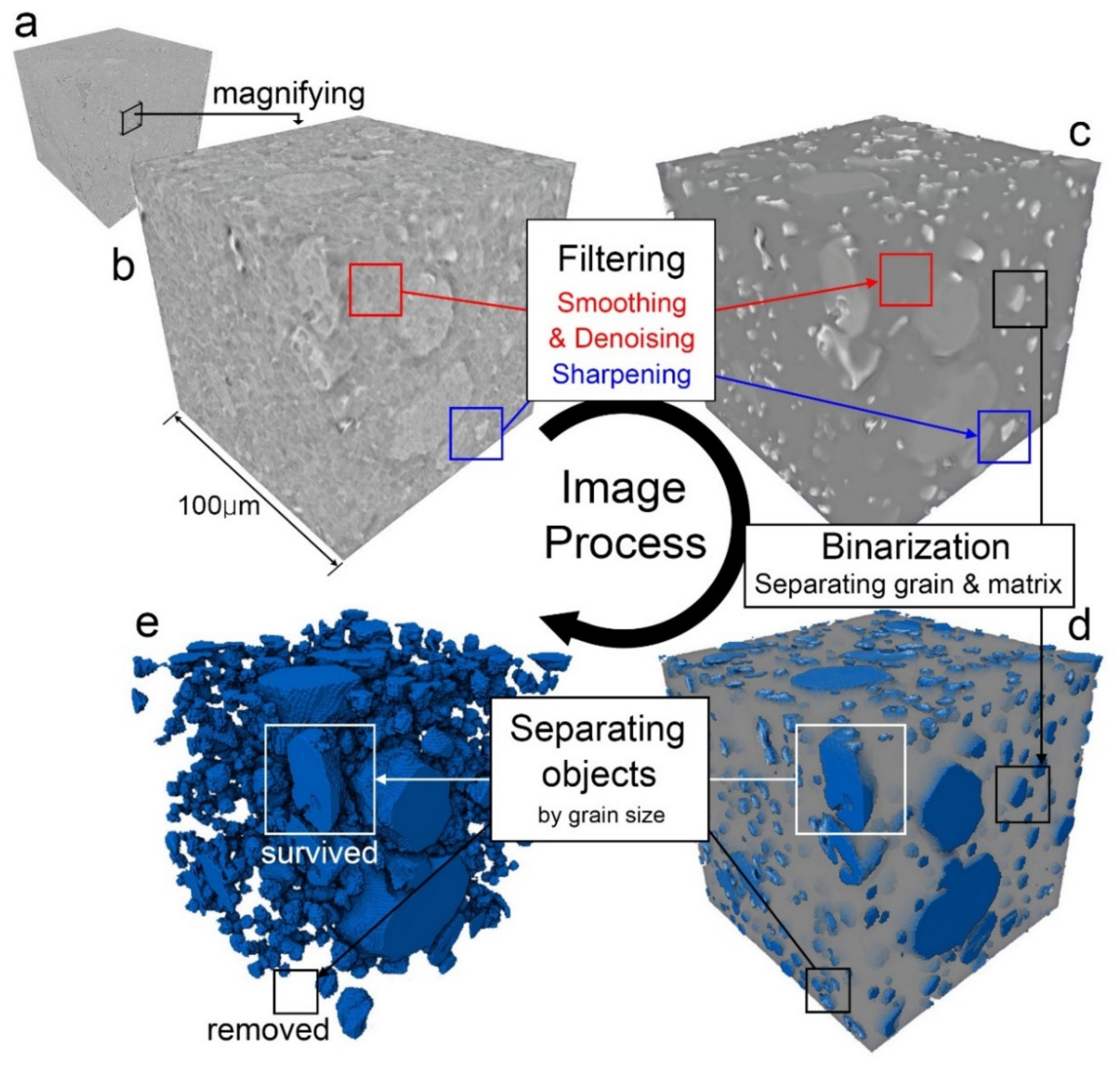
2.2. Image Processing and Ellipsoid Fitting
2.3. Data Analysis
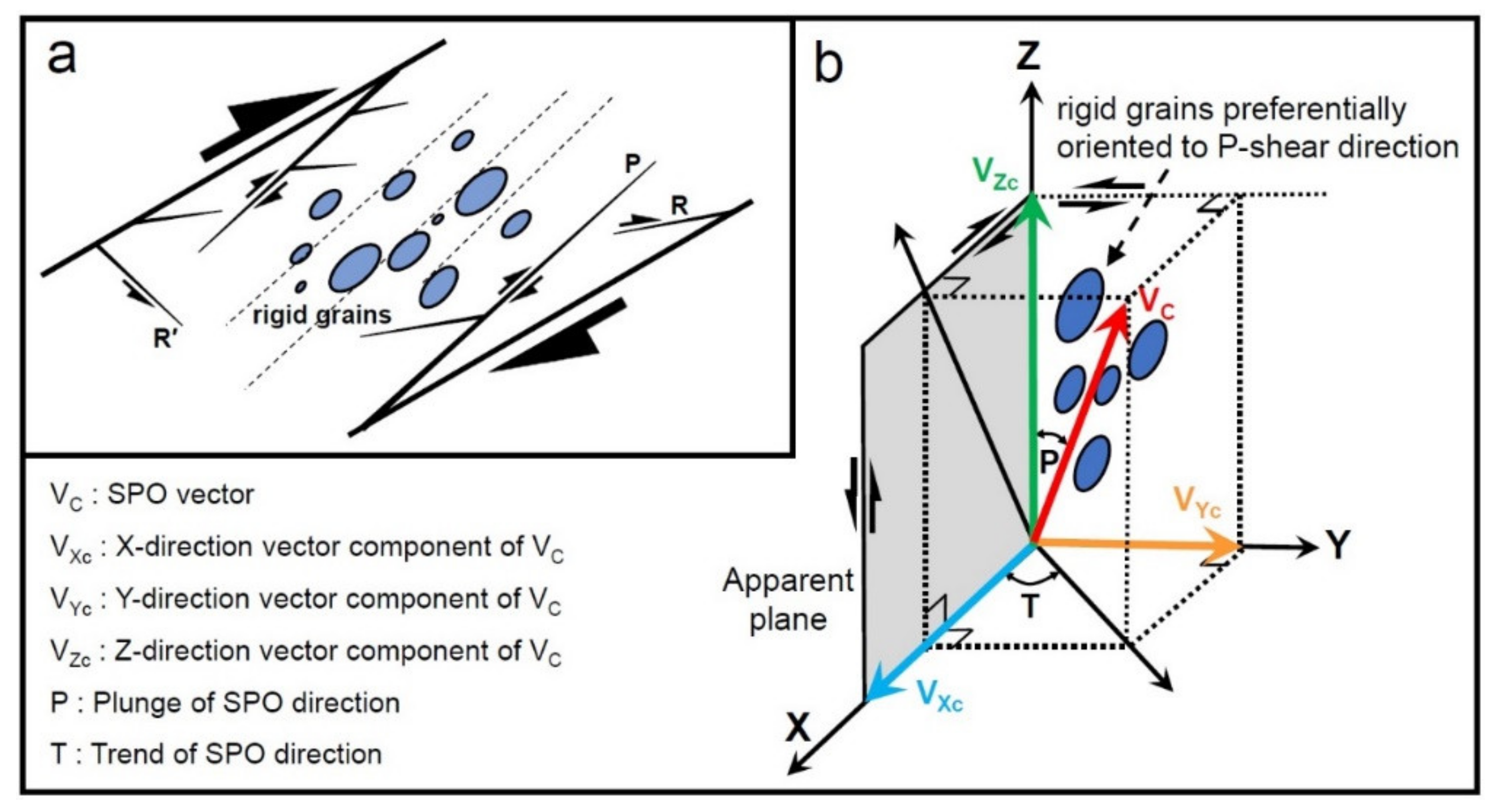
2.3.1. SPO Measurement
2.3.2. SPO Distribution Index
3. Application of the 3D- SPO Method for a Fault Gouge Sample
3.1. Sample Preparation
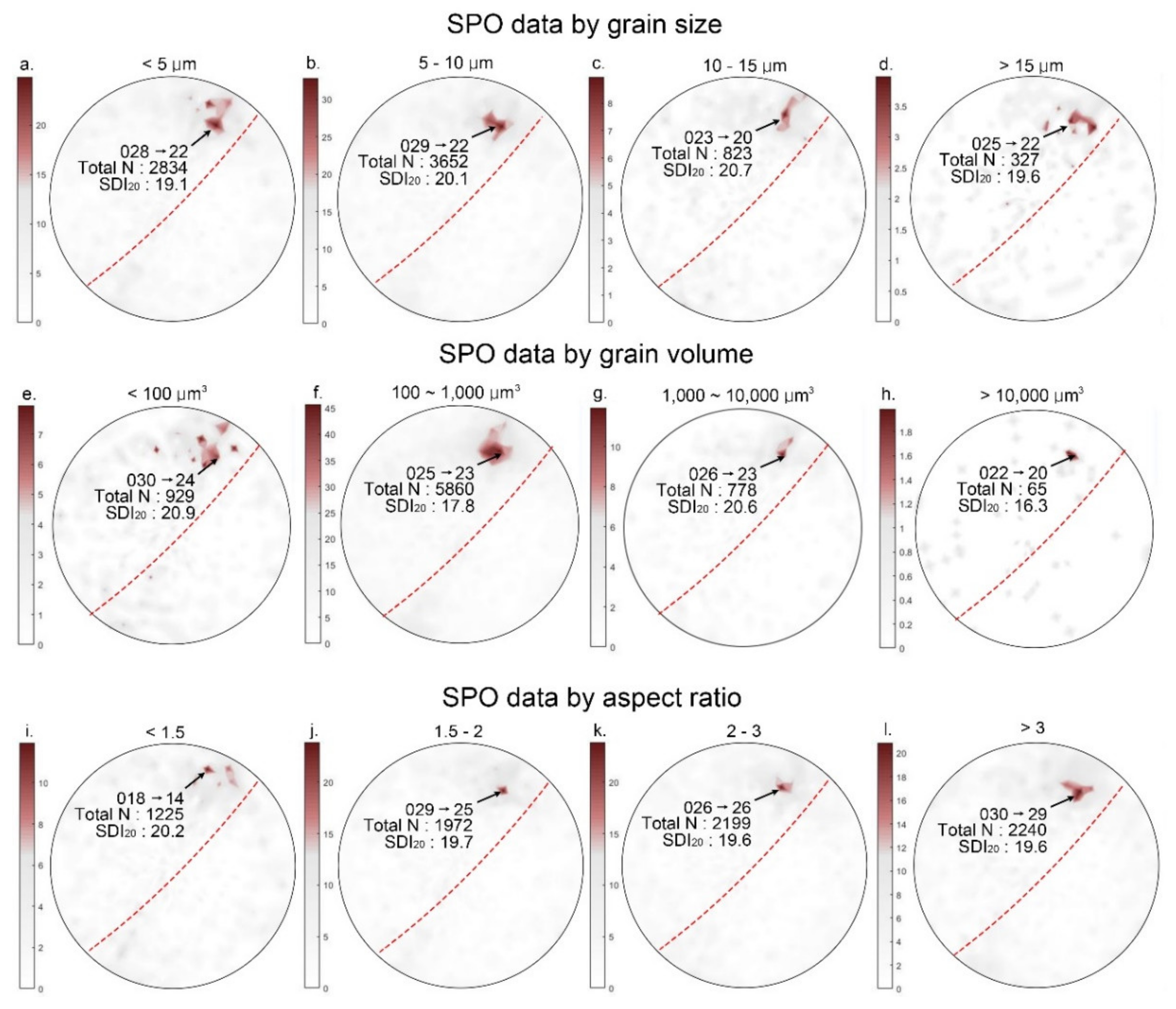
3.2. SPO Data of Fault Gouge Sample
4. Discussions
4.1. SPO Data Interpretation and Implication
4.2. Estimation of Fault Motion Direction
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, W.H.; Chen, C.H. Static stress transferred by the 1999 Chi-Chi, Taiwan, earthquake: Effects on the stability of the surrounding fault systems and aftershock triggering with a 3D fault-slip model. Bull. Seismol. Soc. Am. 2001, 91, 1041–1052. [Google Scholar] [CrossRef]
- Rochette, P.; Jackson, M.; Aubourg, C. Rock magnetism and the interpretation of anisotropy of magnetic susceptibility. Rev. Geophys. 1992, 30, 209–226. [Google Scholar] [CrossRef]
- Van der Pluijm, B.A.; Ho, N.-C.; Peacor, D.R. High-resolution X-ray texture goniometry. J. Struct. Geol. 1994, 16, 1029–1032. [Google Scholar] [CrossRef] [Green Version]
- Wenk, H.-R.; Kanitpanyacharoen, W.; Voltolini, M. Preferred orientation of phyllosilicates: Comparison of fault gouge, shale and schist. J. Struct. Geol. 2010, 32, 478–489. [Google Scholar] [CrossRef]
- Vernet, E.; Casas-Sainz, A.M.; Roman-Berdiel, T.; Marcen, M.; Osacar, M.C. Variable magnetic fabrics under heterogeneous deformation across a shallow fault zone in the Iberian Chain (Monroyo thrust, N Spain). J. Iber. Geol. 2019, 45, 111–127. [Google Scholar] [CrossRef]
- Roman-Berdiel, T.; Casas-Sainz, A.M.; Oliva-Urcia, B.; Calvin, P.; Villalain, J.J. On the influence of magnetic mineralogy in the tectonic interpretation of anisotropy of magnetic susceptibility in cataclastic fault zones. Geophys. J. Int. 2019, 216, 1043–1061. [Google Scholar] [CrossRef]
- Woodcock, N.H.; Mort, K. Classification of fault breccias and related fault rocks. Geol. Mag. 2008, 145, 435–440. [Google Scholar] [CrossRef] [Green Version]
- Freeman, B. The motion of rigid ellipsoidal particles in slow flows. Tectonophysics 1985, 113, 163–183. [Google Scholar] [CrossRef]
- Passchier, C.W.; Simpson, C. Porphyroclast systems as kinematic indicators. J. Struct. Geol. 1986, 8, 831–843. [Google Scholar] [CrossRef]
- Ildefonse, B.; Mancktelow, N.S. Deformation around rigid particles: The influence of slip at the particle/matrix interface. Tectonophysics 1993, 221, 345–359. [Google Scholar] [CrossRef]
- Arbaret, L.; Mancktelow, N.S.; Burg, J.-P. Effect of shape and orientation on rigid particle rotation and matrix deformation in simple shear flow. J. Struct. Geol. 2001, 23, 113–125. [Google Scholar] [CrossRef] [Green Version]
- Masuda, T.; Michibayashi, K.; Ohta, H. Shape preferred orientation of rigid particles in a viscous matrix: Re-evaluation to determine kinematic parameters of ductile deformation. J. Struct. Geol. 1995, 17, 115–129. [Google Scholar] [CrossRef]
- Shelley, D. Asymmetric shape preferred orientations as shear-sense indicators. J. Struct. Geol. 1995, 17, 509–517. [Google Scholar] [CrossRef]
- Cladouhos, T.T. Shape preferred orientation of survivor grains in fault gouge. J. Struct. Geol. 1999, 21, 419–436. [Google Scholar] [CrossRef]
- Agbogun, H.M.D.; Al Tom, A.; Hussein Esam, M.A. Three dimestional imaging of porosity and tracer concentration distributions in a dolostone sample during diffusion experiments using X-ray micro-CT. J. Contam. Hydrol. 2013, 145, 44–53. [Google Scholar] [CrossRef] [PubMed]
- Boone, M.A.; De Kock, T.; Bultreys, T.; De Schutter, G.; Vontobel, P.; Van Hoorebeke, L.; Cnudde, V. 3D mapping of water in oolithic limestone at atmospheric and vacuum saturation using X-ray micro-CT differential imaging. Mater. Charact. 2014, 97, 150–160. [Google Scholar] [CrossRef]
- Sayab, M.; Miettinen, A.; Aerden, D.; Karell, F. Orthogonal switching of AMS axes during type-2 fold interference: Insights from integrated X-ray computed tomography, AMS and 3D petrography. J. Struct. Geol. 2017, 103, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Prichard, H.M.; Barnes, S.J.; Godel, B. A mechanism for chromite growth in ophiolite complexes: Evidence from 3D high-resolution X-ray computed tomography images of chromite grains in Harold’s Grave chromitite in the Shetland ophiolite. Mineral. Mag. 2018, 82, 457–470. [Google Scholar] [CrossRef]
- Saur, H.; Senechal, P.; Boiron, T.; Aubourg, C.; Derluyn, H.; Moonen, P. First investigation of quartz and calcite shape fabrics in strained shales by means of X-ray tomography. J. Struct. Geol. 2020, 130, 103905. [Google Scholar] [CrossRef]
- Lim, J.H.; Seo, S.J.; Kim, H.Y.; Ryu, S.; Huang, J.Y.; Lee, C.S.; Seo, I.D.; Kim, S.G.; Lee, D.; Cho, M.H. Station for structural studies on macro objects: Beamline 6C Bio Medical Imaging at the Pohang Light Source-II. Biodesign 2017, 5, 53–61. [Google Scholar]
- Li, Z.; Yu, L.; Trzasko, J.D.; Lake, D.S.; Blezek, D.J.; Gletcher, J.G.; McCollough, C.H.; Manduca, A. Adaptive nonlocal means filtering based on local noise level for CT denoising. Med. Phys. 2014, 41, 011908. [Google Scholar] [CrossRef] [PubMed]
- Deng, G. A generalized unsharp masking algoritm. IEEE Trans. Image Process. 2011, 20, 1249–1261. [Google Scholar] [CrossRef] [PubMed]
- Kang, D.H.; Lee, J.H.; Choo, J.; Yun, T.S. Pore directivity of soils subjected to shearing: Numerical simulation and image processing. In Proceedings of the GeoCongress 2012: State of the Art in Practice and Geotechnical Engineering, Oakland, CA, USA, 25–29 March 2012; Hryciw, R.D., Athanasopoulos-Zekkos, A., Yesiller, N., Eds.; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2012; pp. 2342–2351. [Google Scholar]
- Workman, H.J.; Hollingsworth, C.A. Concerning the orientation distribution function of rigid particles in a suspension which is undergoing simple shear flow. J. Colloid Interface Sci. 1969, 29, 664–669. [Google Scholar] [CrossRef]
- Jelinek, V.; Kropacek, V. Statistical processing of anisotropy of magnetic susceptibility measured on groups of specimens. Studia Geophys. Geod. 1978, 22, 50–62. [Google Scholar] [CrossRef]
- Wenk, H.R.; Voltolini, M.; Kern, H.; Popp, T.; Mazurek, M. Anisotropy in shale from Mont Terri. Lead. Edge 2008, 27, 742–748. [Google Scholar] [CrossRef]
- Ree, J.H.; Lee, Y.J.; Rhodes, E.J.; Park, Y.; Kwon, S.T.; Chwae, U.; Jeon, J.S.; Lee, B. Quarternary reactivation of Tertiary faults in the southeastern Korean Peninsula: Age constraint by optically stimulated luminescence dating. Isl. Arc 2003, 12, 1–12. [Google Scholar] [CrossRef]
- Jeong, G.Y.; Cheong, C.S. Recurrent events on a Quarternary fault recorded in the mineralogy and micromorphology of a weathering profile, Yangsan Fault System, Korea. Quart. Res. 2005, 64, 221–233. [Google Scholar] [CrossRef]
- Chough, S.K.; Sohn, Y.K. Tectonic and sedimentary evolution of a Cretaceous continental arc-backarc system in the Korean peninsula: New view. Earth Sci. Rev. 2010, 101, 225–249. [Google Scholar] [CrossRef]
- Kim, C.M.; Han, R.; Jeong, G.Y.; Jeong, J.O.; Son, M. Internal structure and materials of the Yangsan fault, Bogyeongsa area, Pohang, South Korea. Geosci. J. 2016, 20, 759–773. [Google Scholar] [CrossRef]
- Sim, H.; Song, Y.; Son, M.; Park, C.; Choi, W.; Khulganakhuu, C. Reactivated timings of Yangsan Fault in the northern Pohang area, Korea. Econ. Environ. Geol. 2017, 50, 97–104. [Google Scholar] [CrossRef]
- Passchier, C.W.; Trouw, R.A. Microtectonics, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005; pp. 136–141. [Google Scholar]
- Sills, D.W. The Fabric of Clasts, Veins and Foliations within the Actively Creeping Zones of the San Andreas Fault at SAFOD: Implications for Deformation Processes. Master’s Thesis, University of Texas A&M, College Station, TX, USA, 2010. [Google Scholar]


| N | Length of Axis | Direction Vector of z-Axis (Vc) | Trend and Plunge of Direction of z-Axis (Vc) | Angle | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | Vxc | Vyc | Vzc | Ta | Pa | To | Po | θ | |
| 1 | 3.28 | 4.18 | 6.18 | 0.686 | 0.147 | 0.713 | 258 | 45.5 | 21.2 | 26.0 | 23.7 |
| 2 | 2.11 | 2.94 | 3.28 | 0.603 | −0.796 | 0.052 | 323 | 57.6 | 250 | 45.6 | 20.8 |
| 3 | 3.41 | 4.57 | 5.68 | −0.406 | −0.906 | 0.122 | 24.1 | 7.03 | 213 | 12.3 | 10.6 |
| 4 | 3.57 | 4.09 | 9.05 | 0.229 | 0.961 | 0.157 | 193 | 9.06 | 50.9 | 6.80 | 5.3 |
| 5 | 1.87 | 5.29 | 9.79 | 0.415 | 0.742 | 0.527 | 209 | 31.8 | 60.2 | 21.6 | 11.9 |
| … | |||||||||||
| 7632 | 2.00 | 3.56 | 10.7 | −0.075 | −0.890 | 0.449 | 4.80 | 26.7 | 99.9 | 61.7 | 17.8 |
| 7633 | 3.72 | 9.49 | 12.7 | 0.237 | 0.601 | 0.763 | 202 | 49.8 | 12.6 | 20.7 | 31.6 |
| 7634 | 3.16 | 3.97 | 6.33 | −0.246 | −0.951 | 0.190 | 14.5 | 10.9 | 30.6 | 14.6 | 14.8 |
| 7635 | 2.30 | 2.95 | 8.45 | −0.526 | −0.245 | 0.814 | 66.0 | 54.5 | 99.3 | 23.6 | 44.5 |
| 7636 | 3.08 | 4.81 | 6.03 | 0.967 | −0.142 | 0.213 | 278 | 12.3 | 248 | 67.0 | 13.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sim, H.; Song, Y.; Kim, J.; Yang, E.; Yun, T.S.; Lim, J.-H. Measurement of 3D-Shape Preferred Orientation (SPO) Using Synchrotron μ-CT: Applications for Estimation of Fault Motion Sense in a Fault Gouge. Minerals 2020, 10, 528. https://doi.org/10.3390/min10060528
Sim H, Song Y, Kim J, Yang E, Yun TS, Lim J-H. Measurement of 3D-Shape Preferred Orientation (SPO) Using Synchrotron μ-CT: Applications for Estimation of Fault Motion Sense in a Fault Gouge. Minerals. 2020; 10(6):528. https://doi.org/10.3390/min10060528
Chicago/Turabian StyleSim, Ho, Yungoo Song, Jaehun Kim, Eomzi Yang, Tae Sup Yun, and Jae-Hong Lim. 2020. "Measurement of 3D-Shape Preferred Orientation (SPO) Using Synchrotron μ-CT: Applications for Estimation of Fault Motion Sense in a Fault Gouge" Minerals 10, no. 6: 528. https://doi.org/10.3390/min10060528





