Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation
Abstract
1. Introduction
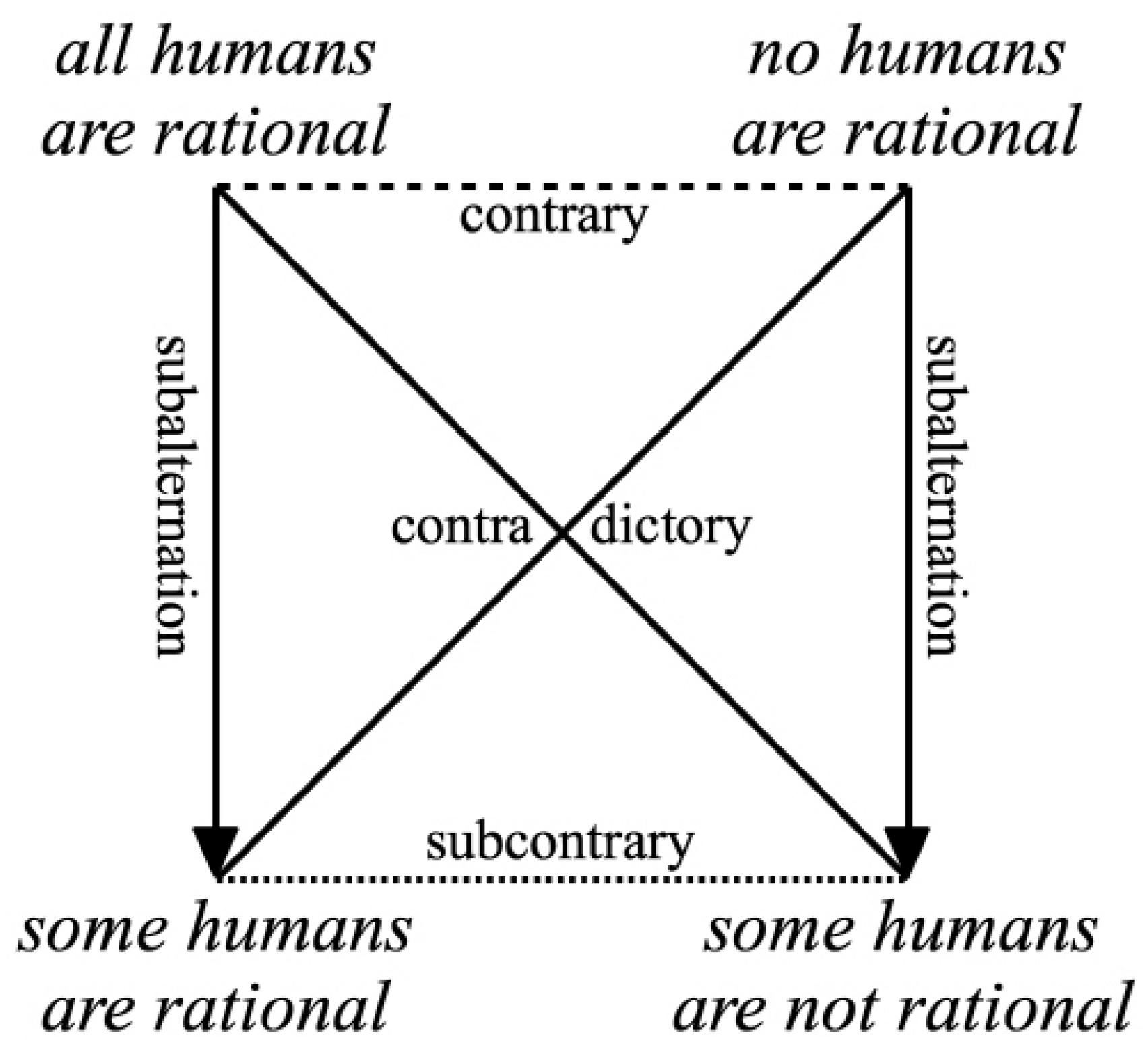
2. The Boolean Algebra and Its Polyhedral Hasse Diagram
| contradictory () | iff | and | , | |
| contrary (C) | iff | and | , | |
| subcontrary () | iff | and | , | |
| in subalternation () | iff | and | . |
3. Polyhedral Aristotelian Diagrams for
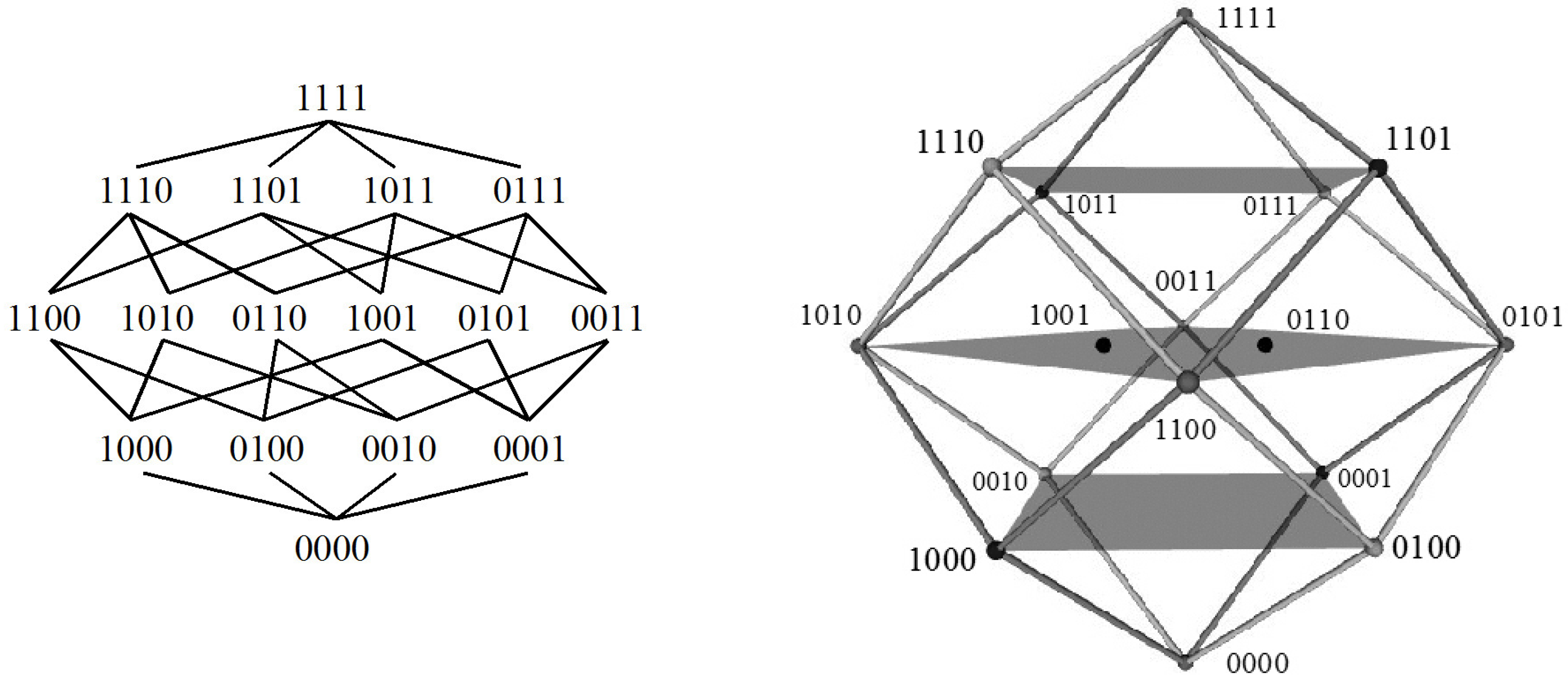
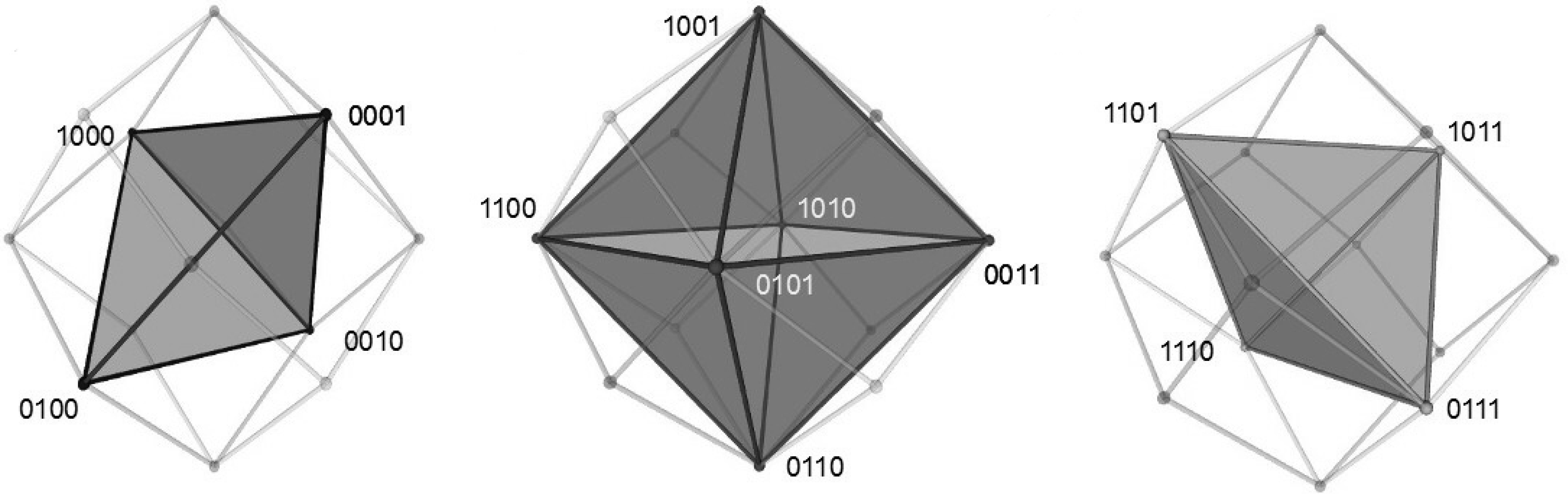
3.1. The Aristotelian Rhombic Dodecahedron for
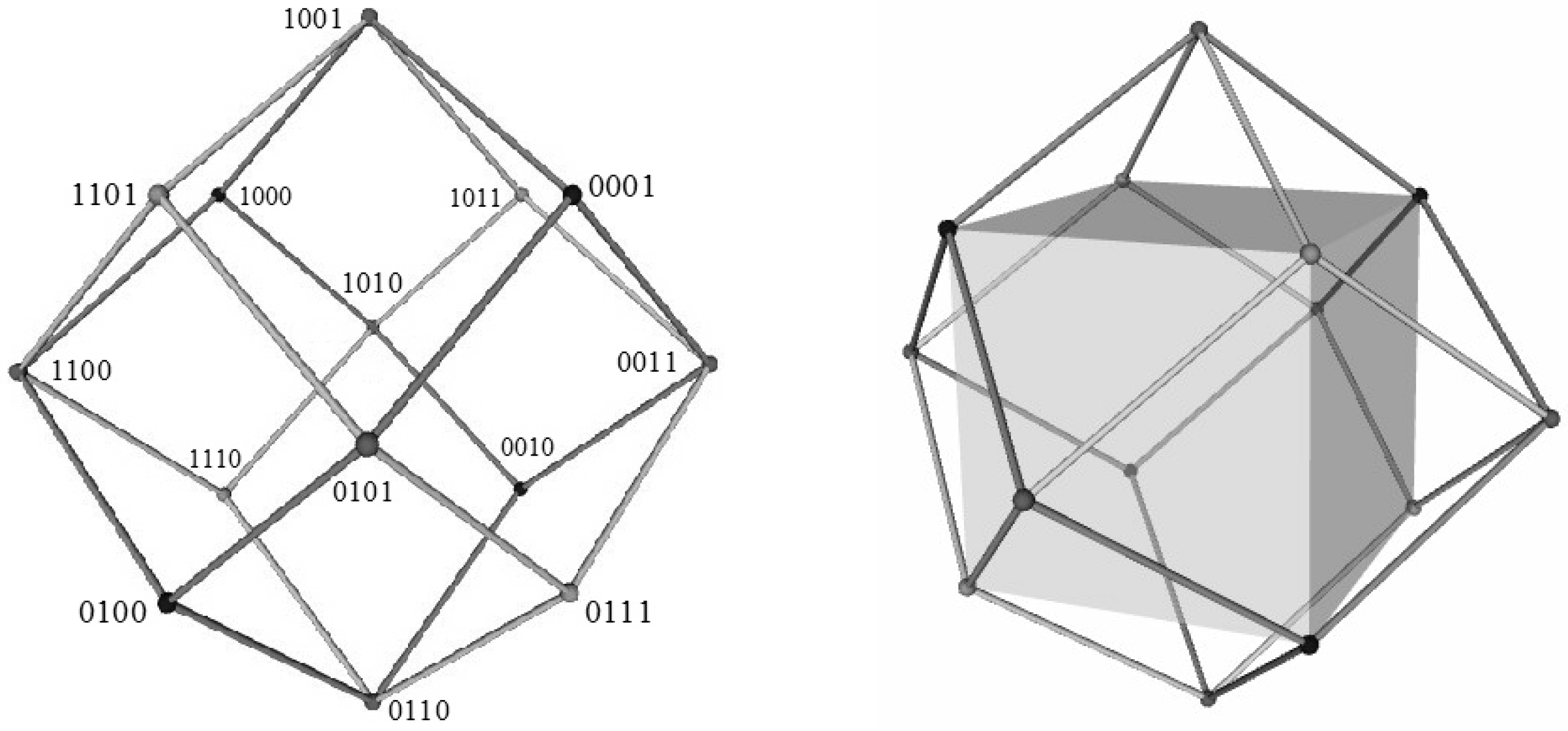
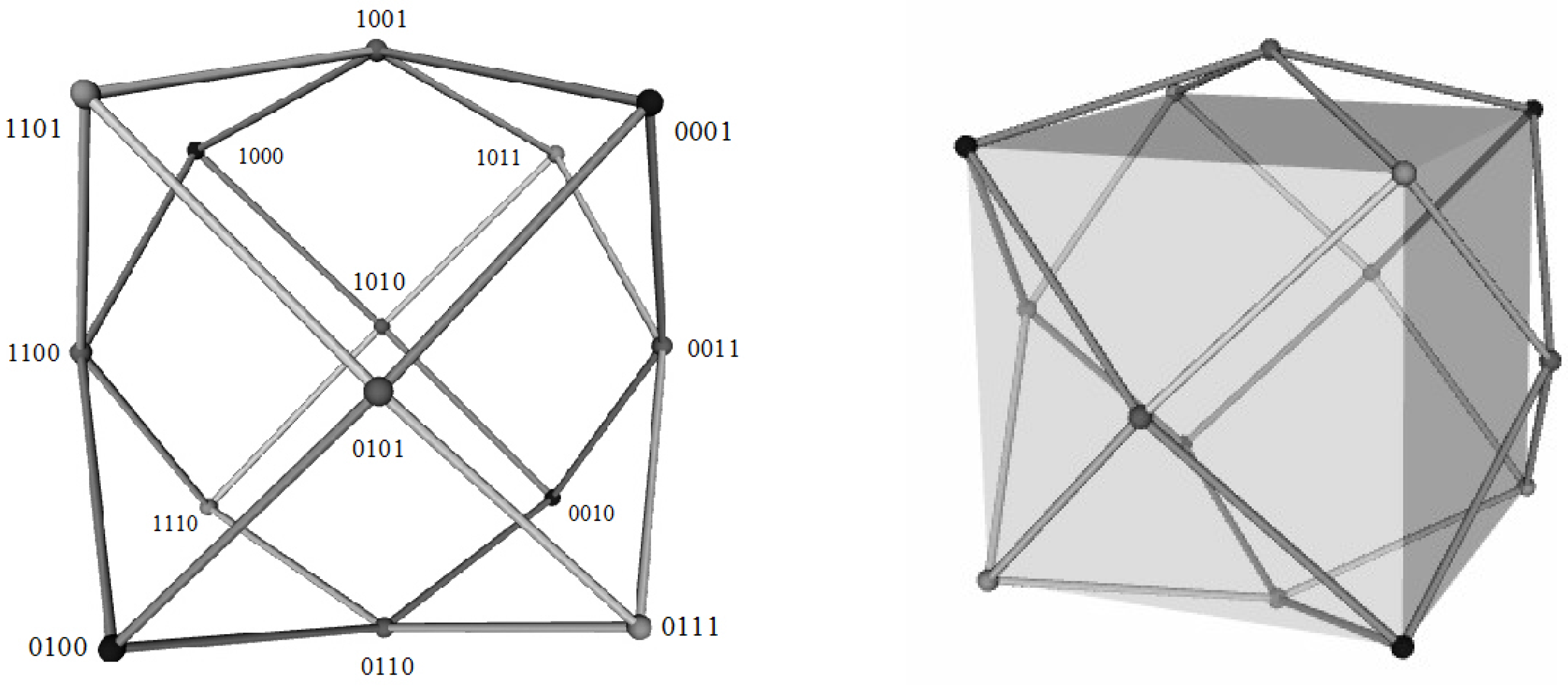
3.2. The Aristotelian Tetrakis Hexahedron for
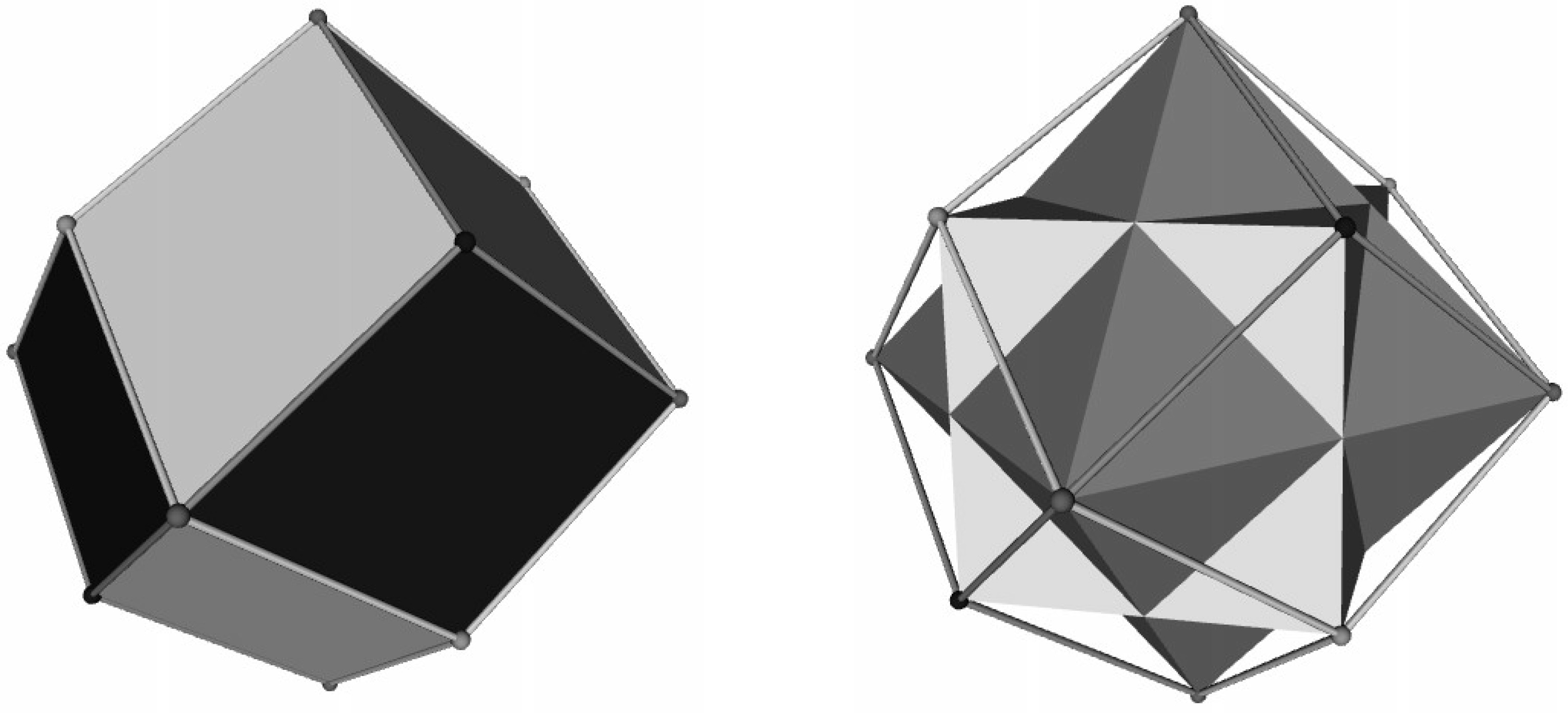
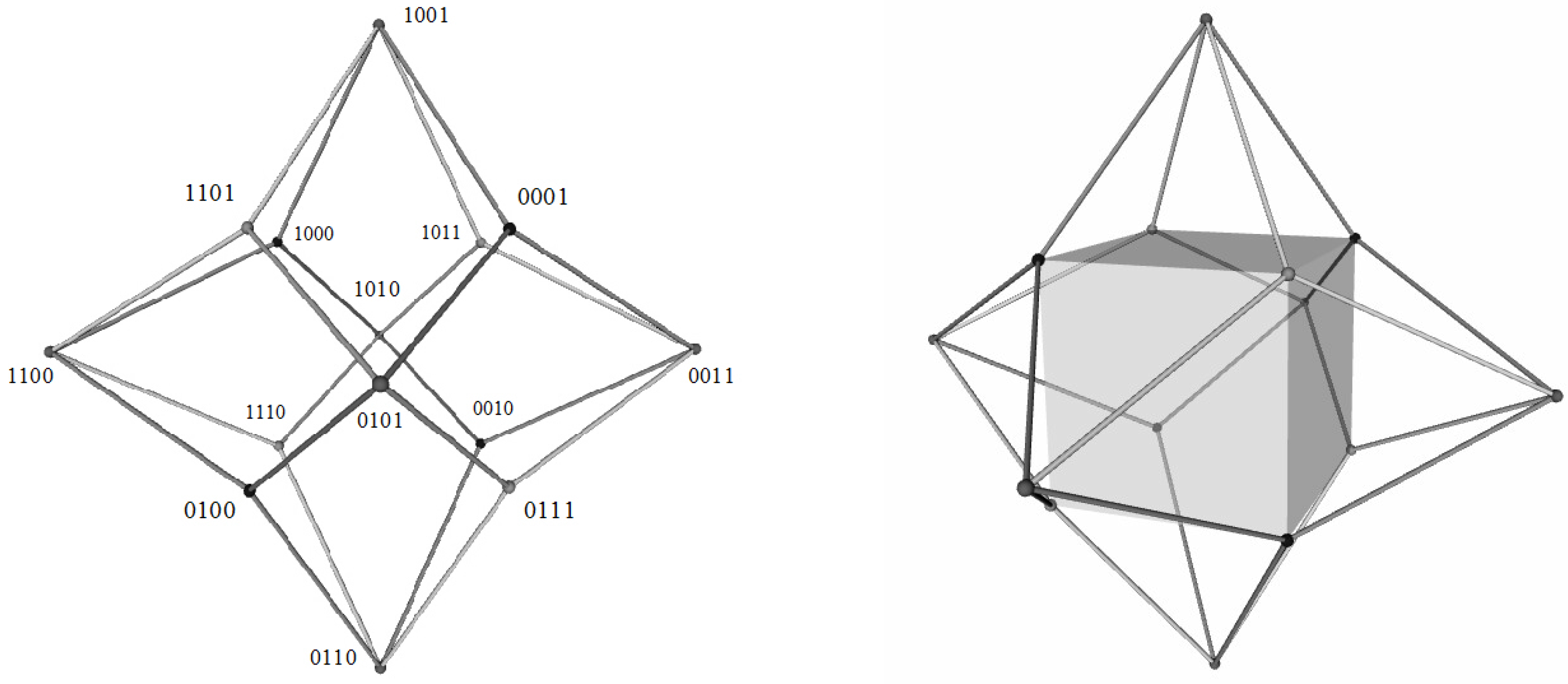
3.3. The Aristotelian Tetraicosahedron for
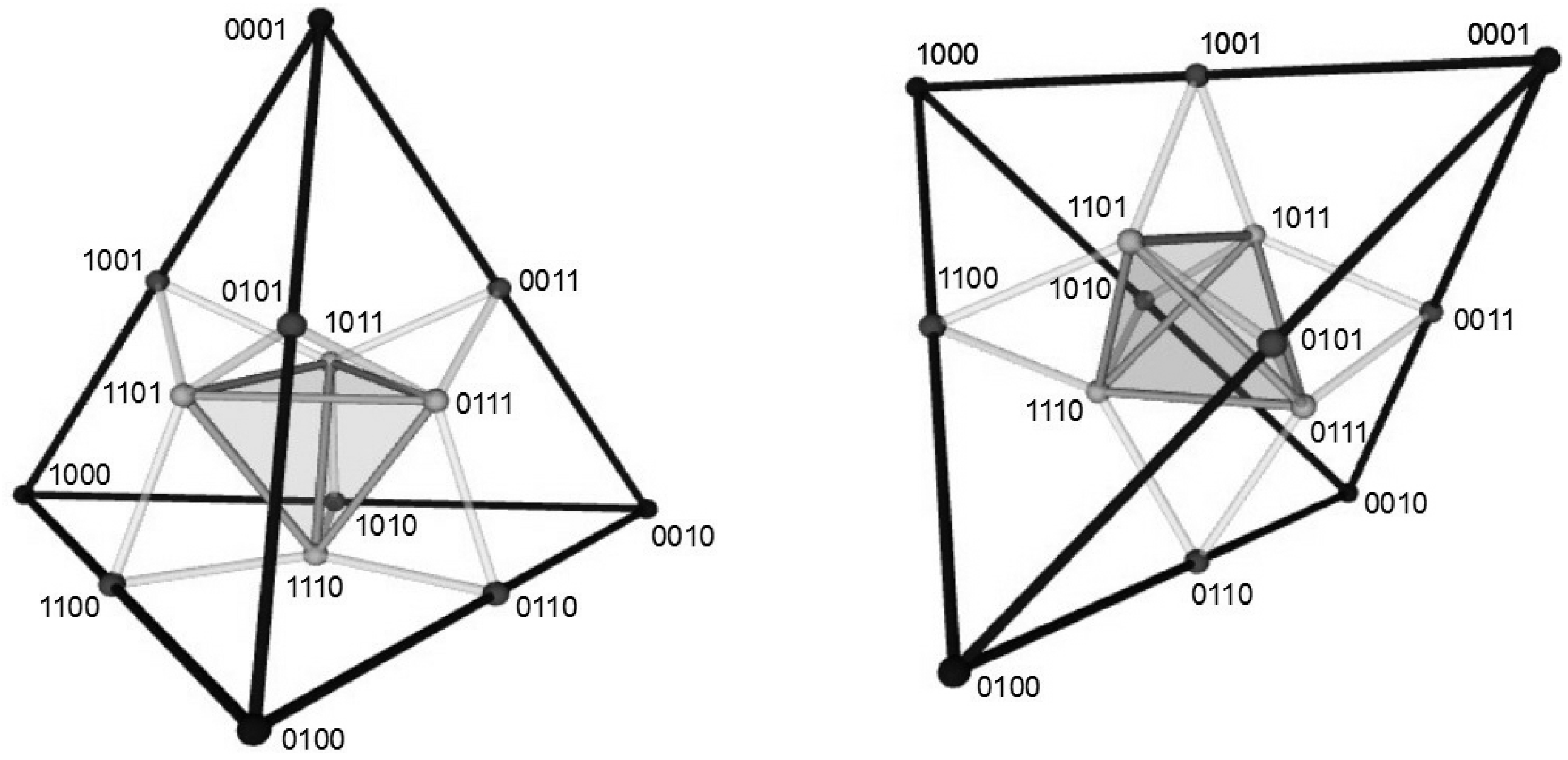
3.4. The Aristotelian Nested Tetrahedron for
3.5. Summary
4. A Comparative Analysis of Logical and Geometrical Distance
4.1. Logical and Geometrical Distance in the Aristotelian Rhombic Dodecahedron for
4.2. Logical and Geometrical Distance in the Aristotelian Tetrakis Hexahedron for
4.3. Logical and Geometrical Distance in the Aristotelian Tetraicosahedron for
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet .
- , so ,
- , so .
4.4. Logical and Geometrical Distance in the Aristotelian Nested Tetrahedron for
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet ,
- if and , then and yet .
- , so ,
- , so .
4.5. Summary
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Parsons, T. The Traditional Square of Opposition. In Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; CSLI: Stanford, CA, USA, 2012. [Google Scholar]
- Read, S. John Buridan’s Theory of Consequence and His Octagons of Opposition. In Around and Beyond the Square of Opposition; Béziau, J.Y., Jacquette, D., Eds.; Springer: Basel, Switzerland, 2012; pp. 93–110. [Google Scholar]
- Lenzen, W. Leibniz’s Logic and the “Cube of Opposition”. Log. Univ. 2016, 10, 171–189. [Google Scholar] [CrossRef]
- Kienzler, W. The Logical Square and the Table of Oppositions. Five Puzzles about the Traditional Square of Opposition Solved by Taking up a Hint from Frege. Log. Anal. Hist. Philos. 2013, 15, 398–413. [Google Scholar]
- Beller, S. Deontic reasoning reviewed: Psychological questions, empirical findings, and current theories. Cognit. Process. 2010, 11, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Mikhail, J. Universal moral grammar: Theory, evidence and the future. Trends Cognit. Sci. 2007, 11, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Abrusci, V.M.; Casadio, C.; Medaglia, M.T.; Porcaro, C. Universal vs. Particular Reasoning: A Study with Neuroimaging Techniques. Log. J. IGPL 2013, 21, 1017–1027. [Google Scholar] [CrossRef]
- Saurí, R.; Pustejovsky, J. FactBank: A Corpus Annotated with Event Factuality. Lang. Resour. Eval. 2009, 43, 227–268. [Google Scholar] [CrossRef]
- Joerden, J. Logik im Recht; Springer: Berlin, Germany, 2010. [Google Scholar]
- O’Reilly, D. Using the Square of Opposition to Illustrate the Deontic and Alethic Relations Constituting Rights. Univ. Tor. Law J. 1995, 45, 279–310. [Google Scholar] [CrossRef]
- Vranes, E. The Definition of ‘Norm Conflict’ in International Law and Legal Theory. Eur. J. Int. Law 2006, 17, 395–418. [Google Scholar] [CrossRef]
- Dekker, P. Not Only Barbara. J. Log. Lang. Inf. 2015, 24, 95–129. [Google Scholar] [CrossRef]
- Horn, L.R. A Natural History of Negation; University of Chicago Press: Chicago, IL, USA, 1989. [Google Scholar]
- Seuren, P.; Jaspers, D. Logico-Cognitive Structure in the Lexicon. Language 2014, 90, 607–643. [Google Scholar] [CrossRef]
- Van der Auwera, J. Modality: The Three-layered Scalar Square. J. Semant. 1996, 13, 181–195. [Google Scholar] [CrossRef]
- Glöckner, I. Fuzzy Quantifiers; Springer: Berlin, Germany, 2006. [Google Scholar]
- Murinová, P.; Novák, V. Analysis of Generalized Square of Opposition with Intermediate Quantifiers. Fuzzy Sets Syst. 2014, 242, 89–113. [Google Scholar] [CrossRef]
- Murinová, P.; Novák, V. Graded Generalized Hexagon in Fuzzy Natural Logic. In Information Processing and Management of Uncertainty in Knowledge-Based Systems 2016, Part II; Carvalho, J.P., Lesot, M.J., Kaymak, U., Vieiram, S., Bouchon-Meunier, B., Yager, R.R., Eds.; CCIS 611; Springer: Berlin, Germany, 2016; pp. 36–47. [Google Scholar]
- Murinová, P.; Novák, V. Syllogisms and 5-Square of Opposition with Intermediate Quantifiers in Fuzzy Natural Logic. Log. Univ. 2016, 10, 339–357. [Google Scholar] [CrossRef]
- Trillas, E.; Seising, R. Turning Around the Ideas of ‘Meaning’ and ‘Complement’. In Fuzzy Technology; Collan, M., Fedrizzi, M., Kacprzyk, J., Eds.; SFSC 335; Springer: Berlin, Germany, 2016; pp. 3–31. [Google Scholar]
- Carnielli, W.; Pizzi, C. Modalities and Multimodalities; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Demey, L. Structures of Oppositions for Public Announcement Logic. In Around and Beyond the Square of Opposition; Béziau, J.Y., Jacquette, D., Eds.; Springer: Basel, Switzerland, 2012; pp. 313–339. [Google Scholar]
- Fitting, M.; Mendelsohn, R.L. First-Order Modal Logic; Kluwer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Lenzen, W. How to Square Knowledge and Belief. In Around and Beyond the Square of Opposition; Béziau, J.Y., Jacquette, D., Eds.; Springer: Basel, Switzerland, 2012; pp. 305–311. [Google Scholar]
- Luzeaux, D.; Sallantin, J.; Dartnell, C. Logical Extensions of Aristotle’s Square. Log. Univ. 2008, 2, 167–187. [Google Scholar] [CrossRef]
- Gilio, A.; Pfeifer, N.; Sanfilippo, G. Transitivity in Coherence-Based Probability Logic. J. Appl. Log. 2016, 14, 46–64. [Google Scholar] [CrossRef]
- Pfeifer, N.; Sanfilippo, G. Square of Opposition under Coherence. In Soft Methods for Data Science; AISC 456; Springer: Berlin, Germany, 2017; pp. 407–414. [Google Scholar]
- Pfeifer, N.; Sanfilippo, G. Probabilistic Squares and Hexagons of Opposition under Coherence. Int. J. Approx. Reason. 2017, 88, 282–294. [Google Scholar] [CrossRef]
- Amgoud, L.; Besnard, P.; Hunter, A. Foundations for a Logic of Arguments. In Logical Reasoning and Computation: Essays Dedicated to Luis Fariñas del Cerro; Cabalar, P., Herzig, M.D.A., Pearce, D., Eds.; IRIT: Toulouse, France, 2016; pp. 95–107. [Google Scholar]
- Amgoud, L.; Prade, H. Can AI Models Capture Natural Language Argumentation? Int. J. Cognit. Inf. Nat. Intell. 2012, 6, 19–32. [Google Scholar] [CrossRef]
- Amgoud, L.; Prade, H. Towards a Logic of Argumentation. In Scalable Uncertainty Management 2012; LNCS 7520; Springer: Berlin, Germany, 2012; pp. 558–565. [Google Scholar]
- Amgoud, L.; Prade, H. A Formal Concept View of Formal Argumentation. In Symbolic and Quantiative Approaches to Resoning with Uncertainty (ECSQARU 2013); van der Gaag, L.C., Ed.; LNCS 7958; Springer: Berlin, Germany, 2013; pp. 1–12. [Google Scholar]
- Ciucci, D.; Dubois, D.; Prade, H. Structures of Opposition in Fuzzy Rough Sets. Fundam. Inform. 2015, 142, 1–19. [Google Scholar] [CrossRef]
- Ciucci, D.; Dubois, D.; Prade, H. Structures of opposition induced by relations. The Boolean and the gradual cases. Ann. Math. Artif. Intell. 2016, 76, 351–373. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Gradual Structures of Oppositions. In Enric Trillas: A Passion for Fuzzy Sets; Magdalena, L., Verdegay, J.L., Esteva, F., Eds.; SFSC 322; Springer: Berlin, Germany, 2015; pp. 79–91. [Google Scholar]
- Dubois, D.; Prade, H.; Rico, A. Graded Cubes of Opposition and Possibility Theory with Fuzzy Events. Int. J. Approx. Reason. 2017, in press. [Google Scholar] [CrossRef]
- Ciucci, D.; Dubois, D.; Prade, H. The Structure of Oppositions in Rough Set Theory and Formal Concept Analysis—Toward a New Bridge between the Two Settings. In Foundations of Information and Knowledge Systems (FoIKS 2014); Beierle, C., Meghini, C., Eds.; LNCS 8367; Springer: Berlin, Germany, 2014; pp. 154–173. [Google Scholar]
- Dubois, D.; Prade, H. From Blanché’s Hexagonal Organization of Concepts to Formal Concept Analysis and Possibility Theory. Log. Univ. 2012, 6, 149–169. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Formal Concept Analysis from the Standpoint of Possibility Theory. In Formal Concept Analysis (ICFCA 2015); Baixeries, J., Sacarea, C., Ojeda-Aciego, M., Eds.; LNCS 9113; Springer: Berlin, Germany, 2015; pp. 21–38. [Google Scholar]
- Ciucci, D.; Dubois, D.; Prade, H. Oppositions in Rough Set Theory. In Rough Sets and Knowledge Technology; Li, T., Nguyen, H.S., Wang, G., Grzymala-Busse, J., Janicki, R., Hassanien, A.E., Yu, H., Eds.; LNCS 7414; Springer: Berlin, Germany, 2012; pp. 504–513. [Google Scholar]
- Yao, Y. Duality in Rough Set Theory Based on the Square of Opposition. Fundam. Inform. 2013, 127, 49–64. [Google Scholar]
- Dubois, D.; Prade, H.; Rico, A. The Cube of Opposition—A Structure underlying many Knowledge Representation Formalisms. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence (IJCAI 2015); Yang, Q., Wooldridge, M., Eds.; AAAI Press: Palo Alto, CA, USA, 2015; pp. 2933–2939. [Google Scholar]
- Dubois, D.; Prade, H.; Rico, A. The Cube of Opposition and the Complete Appraisal of Situations by Means of Sugeno Integrals. In Foundations of Intelligent Systems (ISMIS 2015); LNCS 9384; Springer: Berlin, Germany, 2015; pp. 197–207. [Google Scholar]
- Dubois, D.; Prade, H.; Rico, A. Organizing Families of Aggregation Operators into a Cube of Opposition. In Granular, Soft and Fuzzy Approaches for Intelligent Systems; Kacprzyk, J., Filev, D., Beliakov, G., Eds.; Springer: Berlin, Germany, 2017; pp. 27–45. [Google Scholar]
- Miclet, L.; Prade, H. Analogical Proportions and Square of Oppositions. In Information Processing and Management of Uncertainty in Knowledge-Based Systems 2014, Part II; CCIS 442; Springer: Berlin, Germany, 2014; pp. 324–334. [Google Scholar]
- Prade, H.; Richard, G. From Analogical Proportion to Logical Proportions. Log. Univ. 2013, 7, 441–505. [Google Scholar] [CrossRef]
- Prade, H.; Richard, G. Picking the one that does not fit—A matter of logical proportions. In Proceedings of the 8th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT-13); Pasi, G., Montero, J., Ciucci, D., Eds.; Atlantis Press: Amsterdam, The Netherlands, 2013; pp. 392–399. [Google Scholar]
- Prade, H.; Richard, G. On Different Ways to be (dis)similar to Elements in a Set. Boolean Analysis and Graded Extension. In Information Processing and Management of Uncertainty in Knowledge-Based Systems 2016, Part II; CCIS 611; Springer: Berlin, Germany, 2016; pp. 605–618. [Google Scholar]
- Prade, H.; Richard, G. From the Structures of Opposition Between Similarity and Dissimilarity Indicators to Logical Proportions. In Representation and Reality in Humans, Other Living Organisms and Intelligent Machines; Dodig-Crnkovic, G., Giovagnoli, R., Eds.; Springer: Berlin, Germany, 2017; pp. 279–299. [Google Scholar]
- Smessaert, H.; Demey, L. Logical Geometries and Information in the Square of Opposition. J. Log. Lang. Inf. 2014, 23, 527–565. [Google Scholar] [CrossRef]
- Demey, L.; Smessaert, H. Combinatorial Bitstring Semantics for Arbitrary Logical Fragments. J. Philos. Log. 2017. [Google Scholar] [CrossRef]
- Demey, L. Interactively Illustrating the Context-Sensitivity of Aristotelian Diagrams. In Modeling and Using Context; Christiansen, H., Stojanovic, I., Papadopoulos, G., Eds.; LNCS 9405; Springer: Berlin, Germany, 2015; pp. 331–345. [Google Scholar]
- Demey, L.; Smessaert, H. Shape Heuristics in Aristotelian Diagrams. In Shapes 3.0 Proceedings; Kutz, O., Borgo, S., Bhatt, M., Eds.; Workshop Proceedings 1616; CEUR: Aachen, Germany, 2016; pp. 35–45. [Google Scholar]
- Demey, L.; Smessaert, H. The Interaction between Logic and Geometry in Aristotelian Diagrams. In Diagrammatic Representation and Inference; Jamnik, M., Uesaka, Y., Elzer Schwartz, S., Eds.; LNCS 9781; Springer: Berlin, Germany, 2016; pp. 67–82. [Google Scholar]
- Smessaert, H.; Demey, L. Visualising the Boolean Algebra in 3D. In Diagrammatic Representation and Inference; Jamnik, M., Uesaka, Y., Elzer Schwartz, S., Eds.; LNCS 9781; Springer: Berlin, Germany, 2016; pp. 289–292. [Google Scholar]
- Demey, L.; Smessaert, H. The Relationship between Aristotelian and Hasse Diagrams. In Diagrammatic Representation and Inference; Dwyer, T., Purchase, H., Delaney, A., Eds.; LNCS 8578; Springer: Berlin, Germany, 2014; pp. 213–227. [Google Scholar]
- Demey, L.; Smessaert, H. Geometric and Cognitive Differences between Aristotelian Diagrams for the Boolean Algebra . 2017. submitted. [Google Scholar]
- Kruja, E.; Marks, J.; Blair, A.; Waters, R. A Short Note on the History of Graph Drawing. In Graph Drawing (GD 2001); Mutzel, P., Jünger, M., Leipert, S., Eds.; LNCS 2265; Springer: Berlin, Germany, 2002; pp. 272–286. [Google Scholar]
- Ford, B.J. Images of Science: A History of Scientific Illustration; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Moretti, A. The Geometry of Logical Opposition. Ph.D. Thesis, University of Neuchâtel, Neuenburg, Switzerland, 2009. [Google Scholar]
- Smessaert, H. On the 3D Visualisation of Logical Relations. Log. Univ. 2009, 3, 303–332. [Google Scholar] [CrossRef]
- Béziau, J.Y. New light on the square of oppositions and its nameless corner. Log. Investig. 2003, 10, 218–232. [Google Scholar]
- Smessaert, H.; Demey, L. Béziau’s Contributions to the Logical Geometry of Modalities and Quantifiers. In The Road to Universal Logic; Koslow, A., Buchsbaum, A., Eds.; Springer: Basel, Switzerland, 2015; pp. 475–493. [Google Scholar]
- Pellissier, R. Setting n-Opposition. Log. Univ. 2008, 2, 235–263. [Google Scholar] [CrossRef]
- Moretti, A. The Geometry of Standard Deontic Logic. Log. Univ. 2009, 3, 19–57. [Google Scholar] [CrossRef]
- Tversky, B. Prolegomenon to Scientific Visualizations. In Visualization in Science Education; Gilbert, J.K., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 29–42. [Google Scholar]
- Tversky, B. Visualizing Thought. Top. Cognit. Sci. 2011, 3, 499–535. [Google Scholar] [CrossRef] [PubMed]
- Moretti, A. Was Lewis Carroll an Amazing Oppositional Geometer? Hist. Philos. Log. 2014, 35, 383–409. [Google Scholar] [CrossRef]
- Smessaert, H.; Demey, L. Logical and Geometrical Complementarities between Aristotelian Diagrams. In Diagrammatic Representation and Inference; Dwyer, T., Purchase, H., Delaney, A., Eds.; LNCS 8578; Springer: Berlin, Germany, 2014; pp. 246–260. [Google Scholar]
- Givant, S.; Halmos, P. Introduction to Boolean Algebras; Springer: New York, NY, USA, 2009. [Google Scholar]
- Smessaert, H.; Demey, L. The Unreasonable Effectiveness of Bitstrings in Logical Geometry. In The Square of Opposition: A Cornerstone of Thought; Béziau, J.Y., Basti, G., Eds.; Springer: Basel, Switzerland, 2017; pp. 197–214. [Google Scholar]
- Demey, L.; Smessaert, H. Metalogical Decorations of Logical Diagrams. Log. Univ. 2016, 10, 233–292. [Google Scholar] [CrossRef]
- Demey, L. Metalogic, Metalanguage and Logical Geometry. 2017. submitted. [Google Scholar]
- Davey, B.; Priestley, H. Introduction to Lattices and Order; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Kauffman, L.H. The Mathematics of Charles Sanders Peirce. Cybern. Hum. Knowing 2001, 8, 79–110. [Google Scholar]
- Zellweger, S. Untapped potential in Peirce’s iconic notation for the sixteen binary connectives. In Studies in the Logic of Charles Peirce; Houser, N., Roberts, D.D., Van Evra, J., Eds.; Indiana University Press: Bloomington, IN, USA, 1997; pp. 334–386. [Google Scholar]
- Harary, F.; Hayes, J.P.; Wu, H.J. A Survey of the Theory of Hypercube Graphs. Comput. Math. Appl. 1988, 15, 277–289. [Google Scholar] [CrossRef]
- Coxeter, H.S.M. Regular Polytopes; Dover Publications: New York, NY, USA, 1973. [Google Scholar]
- Larkin, J.; Simon, H. Why a Diagram is (Sometimes) Worth Ten Thousand Words. Cognit. Sci. 1987, 11, 65–99. [Google Scholar] [CrossRef]
- Conway, J.H.; Burgiel, H.; Goodman-Strauss, C. The Symmetries of Things; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Wenninger, M. Polyhedron Models; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Wenninger, M. Dual Models; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Coxeter, H.S.M. Regular and Semiregular Polyhedra. In Shaping Space. Exploring Polyhedra in Nature, Art, and the Geometrical Imagination; Senechal, M., Ed.; Springer: New York, NY, USA, 2013; pp. 41–52. [Google Scholar]
- Walter, M.; Pedersen, J.; Wenninger, M.; Schattschneider, D.; Loeb, A.L.; Demaine, E.; Demaine, M.; Hart, V. Six Recipes for Making Polyhedra. In Shaping Space. Exploring Polyhedra in Nature, Art, and the Geometrical Imagination; Senechal, M., Ed.; Springer: New York, NY, USA, 2013; pp. 13–40. [Google Scholar]
- Sauriol, P. Remarques sur la Théorie de l’hexagone logique de Blanché. Dialogue 1968, 7, 374–390. [Google Scholar] [CrossRef]
- Johnson, N.W. Convex Polyhedra with Regular Faces. Can. J. Math. 1966, 18, 169–200. [Google Scholar] [CrossRef]
- Carroll, L. Symbolic Logic. Edited, with Annotations and an Introduction by William Warren Bartley III; Clarkson N. Potter: New York, NY, USA, 1977. [Google Scholar]
- Roth, R.M. Introduction to Coding Theory; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Deza, M.M.; Deza, E. Encyclopedia of Distances; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Demey, L.; Smessaert, H. Logische geometrie en pragmatiek. In Patroon en Argument; Van De Velde, F., Smessaert, H., Van Eynde, F., Verbrugge, S., Eds.; Leuven University Press: Leuven, Belgium, 2014; pp. 553–564. [Google Scholar]
- Peterson, P. On the Logic of “Few”, “Many”, and “Most”. Notre Dame J. Form. Log. 1979, 20, 155–179. [Google Scholar] [CrossRef]
- Demey, L.; Smessaert, H. The Logical Geometry of the Boolean Algebra . 2017. Unpublished work. [Google Scholar]
| 0000 | ||||
| 1000 | ||||
| 0100 | ||||
| 0010 | ||||
| 0001 | ||||
| 1100 | ||||
| 1010 | ||||
| 1001 | ||||
| 0110 | ||||
| 0101 | ||||
| 0011 | ||||
| 1110 | ||||
| 1101 | ||||
| 1011 | ||||
| 0111 | ||||
| 1111 |
| Elements | Rhombic Dodecahedron | Tetrakis Hexahedron | Tetraicosahedron | Nested Tetrahedron |
|---|---|---|---|---|
| (RDH) | (THH) | (TIH) | (NTH) | |
| vertices | 14 | 14 | 14 | 4 |
| edges | 24 | 36 | 36 | 6 |
| faces | 12 | 24 | 24 | 4 |
| Example | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1000-1100 | 1.73 | 1.5 | 2 | 1.41 | |
| 1 | 2 | 3 | 1100-1110 | 1.73 | 1.5 | 2 | 0.82 | |
| 2 | 1 | 3 | 1000-1110 | 2 | 2 | 2 | 1.63 | |
| 2 | 1 | 1 | 1000-0001 | 2.83 | 2.83 | 2.83 | 2.83 | |
| 2 | 3 | 3 | 1110-0111 | 2.83 | 2.83 | 2.83 | 0.94 | |
| 2 | 2 | 2 | 1100-0110 | 2.83 | 2.12 | 3.41 | 1.41 | |
| 3 | 1 | 2 | 1000-0110 | 3.32 | 2.87 | 3.70 | 2.45 | |
| 3 | 2 | 3 | 1100-0111 | 3.32 | 2.87 | 3.70 | 1.41 | |
| 4 | 1 | 3 | 1000-0111 | 3.46 | 3.46 | 3.46 | 2.31 | |
| 4 | 2 | 2 | 1100-0011 | 4 | 3 | 4.83 | 2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demey, L.; Smessaert, H. Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation. Symmetry 2017, 9, 204. https://doi.org/10.3390/sym9100204
Demey L, Smessaert H. Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation. Symmetry. 2017; 9(10):204. https://doi.org/10.3390/sym9100204
Chicago/Turabian StyleDemey, Lorenz, and Hans Smessaert. 2017. "Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation" Symmetry 9, no. 10: 204. https://doi.org/10.3390/sym9100204
APA StyleDemey, L., & Smessaert, H. (2017). Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation. Symmetry, 9(10), 204. https://doi.org/10.3390/sym9100204





