1. Introduction
In a historical perspective, the recent enormous growth of interest in the experimental as well as theoretical aspects of optical systems exhibiting various anomalous (typically, complex and space-dependent) forms of refraction index
(mostly in two dimensions, with
) may be traced back to the influential theoretical letter [
1] in which Carl Bender with his student Stefan Boettcher recalled the traditional parity-time symmetry
alias symmetry and transferred its use from relativistic quantum field physics (e.g., [
2]) to the Krein-space-related spectral-theory mathematics [
3,
4]. In this manner Bender with Boettcher opened the Pandora’s box of possible applications of the concept of
symmetry
of Hamiltonians
H in non-relativistic quantum mechanics [
5]. In parallel, their study inspired also generalizations of mathematically similar theories in several other branches of physics including even the classical mechanics and, first of all, classical optics (also [
6]; updated historical and contextual remarks and also many related fresh as well as older references may be found, e.g., in the physics-reviewing chapter [
7] and/or in the more mathematics-oriented rest of monograph [
8]).
The combination of the
symmetric quantum theory with the predominantly experimental nature of the study of gain-loss systems in classical optics proved unexpectedly fortunate and productive. In the past, the collaboration between the two communities of researchers materialized, i.a., during the series of dedicated international conferences [
9]. There also seem to be no reasons for a decrease of intensity of this mutual inspiration in the future. In what follows, the latter optimistic expectation is to be supported constructively, via a toy-model study of the systems and instants at which, in the language of quantum physicists, the
symmetry becomes spontaneously broken.
We intend to present here several new ideas in the field, with emphasis upon their possible experimental testability in classical optics as well as upon their potentially deep impact during the future development of quantum theory and of its various less standard phenomenological applications.
2. The Context of Quantum Mechanics
Our basic methodical idea is that it makes sense to develop further the recently revealed intimate formal relationship between the theoretically appealing quantum theories exhibiting symmetry (typically, in the Schrödinger equation) and the experimentally realizable classical optical systems built, basically, on the solutions of the formally similar Maxwell equations in paraxial approximation. Briefly, all of these systems may be characterized by the various specific forms of the balance between the sinks and sources, causing the gain and loss in the electromagnetic radiation in general and in the intensity of the light in optical settings in particular.
On the less pragmatic level of theoretical speculations we would like to point out here that in both the classical and quantum contexts of propagation dynamics the most interesting phenomena may be expected to occur, in the language of optics, in the domains of a “deeply complex” refraction. In the parallel language of abstract quantum theory, one should speak about the anomalously-looking dynamical regime of an apparently “deeply non-unitary” evolution,
i.e., with reference to the famous Stone’s theorem [
10], about the regime in which the quantum Hamiltonian appears “deeply non-self-adjoint”.
Once we recall the unifying terminology of mathematics we reveal that a common background of study may be found in the classical Kato’s book on linear operators [
11]. The author explained there the necessary mathematical concepts via a methodically extremely efficient replacement of complicated differential generators of evolution by the mere
dimensional matrices
, mostly of the first nontrivial dimension
. In this manner, Kato was able to circumvent virtually all of the inessential technical complications which mar, typically, the wider acceptance of the mathematically very complicated differential-operator quantum Hamiltonians of Bender and Boettcher [
12]. At the same time, the use of the matrix models with
may be also expected to facilitate the building of bridges between the simplified matrix forms of toy-model
symmetric quantum Hamiltonians
and their optical analogs which would be much more accessible to the experimental testing.
The above-mentioned ambiguous concepts of the “deeply complex” refraction and/or of the “deeply non-self-adjoint” operators of observables lose immediately their misleading flavor after one recalls the Kato’s terminology. Indeed, one immediately imagines that the
qualitative features of the generic evolution law
(
i.e., of quantum Schrödinger equation or of its formally equivalent paraxial-approximation analogue in classical optics) are really best understood when the complicated differential operators
H (
i.e., typically, the Bender’s and Boettcher’s
symmetric Hamiltonians
with complex potentials
such that
[
1]) are approximated or entirely replaced by the suitable toy-model matrices
for which
performs Hermitian conjugation while the parity-simulating
may be virtually arbitrary invertible matrix, exhibiting usually just the involution-representation property
.
A particularly friendly class of time-dependent (and, incidentally, real)
N by
N matrices
representing a quantum observable (
i.e., admissibly but not necessarily just the evolution operators
H entering Equation (
2)) was constructed and studied in [
13]. Speaking, for the sake of brevity, just the language of quantum theory from now on, the concept of the “deeply non-self-adjoint” dynamical regime was given there an entirely rigorous mathematical meaning. Moreover, the very first element of the family
(where
t may denote either time or another variable parameter) was chosen equivalent to one of the Kato’s illustrative examples.
Due to the latter incidental coincidence of toy models we imagined, later, that the physics-inspired “deeply non-self-adjoint” operators are strictly those in which the parameter (
i.e., in our model (
3), time
t) lies sufficiently close to its so called “exceptional point” value
at which, by definition [
11], the matrix in question acquires a non-diagonalizable, Jordan-block-equivalent form. For our most elementary toy model (
3) there exists strictly one EP value which is real,
[
14].
After the toy-model specification of
, the “physical” solutions of Schrödinger Equation (
2) would cease to be acceptable at the EP value of time. This immediately leads to the interesting questions of what can happen and what happens under which circumstances (
i.e., what is the physical meaning and dynamics of the system) in the EP vicinity, at the small and positive differences
. The latter problem will be addressed in what follows.
5. The Context of Quantum Cosmology
We have to admit that the most extreme contrast between the expected feasibility of an experimental optical simulation and an absolute inaccessibility of any experimental study in an analogous quantum setting may and should be sought in the framework of quantum cosmology. The existence of such a challenge has already been noticed in a conference contribution [
34]. Its mathematically highly challenging nature was emphasized there, together with its deep relevance for several characteristic quantum cosmology scenarios. At the same time we were only able to work there, non-numerically, with the two by two matrix observables. Still we believe that before a transfer of the quantum-evolution problems from the speculative cosmology to the experimental domain of classical optics one should succeed in moving from the two by two toy-model matrices to the higher matrix dimensions
.
5.1. Problems with Quantization
In the recent literature devoted to cosmology the singularities predicted by classical theory are widely believed to be smeared out after quantization. In particular, the spatial degeneracy at Big Bang is often replaced by its Big-Bounce alternative [
35,
36]. We propose that such a strong belief should be weakened. Constructively, we intend to show that the survival of the singularities sampled by Big Bang could find one of its possible explanations in the exceptional-point (EP, [
11]) interpretation of the Big-Bang time
.
We shall describe an elementary, very schematic family of non-covariant toy-model realization of such a possibility. We will work with a schematic, empty Universe which is quantized in a non-covariant version of Heisenberg picture [
37]. In such a setting the classical Big Bang singularity may survive the quantization.
In the model the mechanism of the unfolding of the singularity after Big Bang will be shown to carry certain, not fully clarified features including, e.g., a strong initial anisotropy of Hilbert space which weakens and isotropizes in finite time. We believe that such a result could offer also a hint or nonstandard key to the existence and/or quantum-theoretical origin of the Inflation period in the evolution of the Universe.
5.2. The Consistent Quantum Singularity at Big Bang
Let us now return to the question of the most interesting physical interpretations of operator
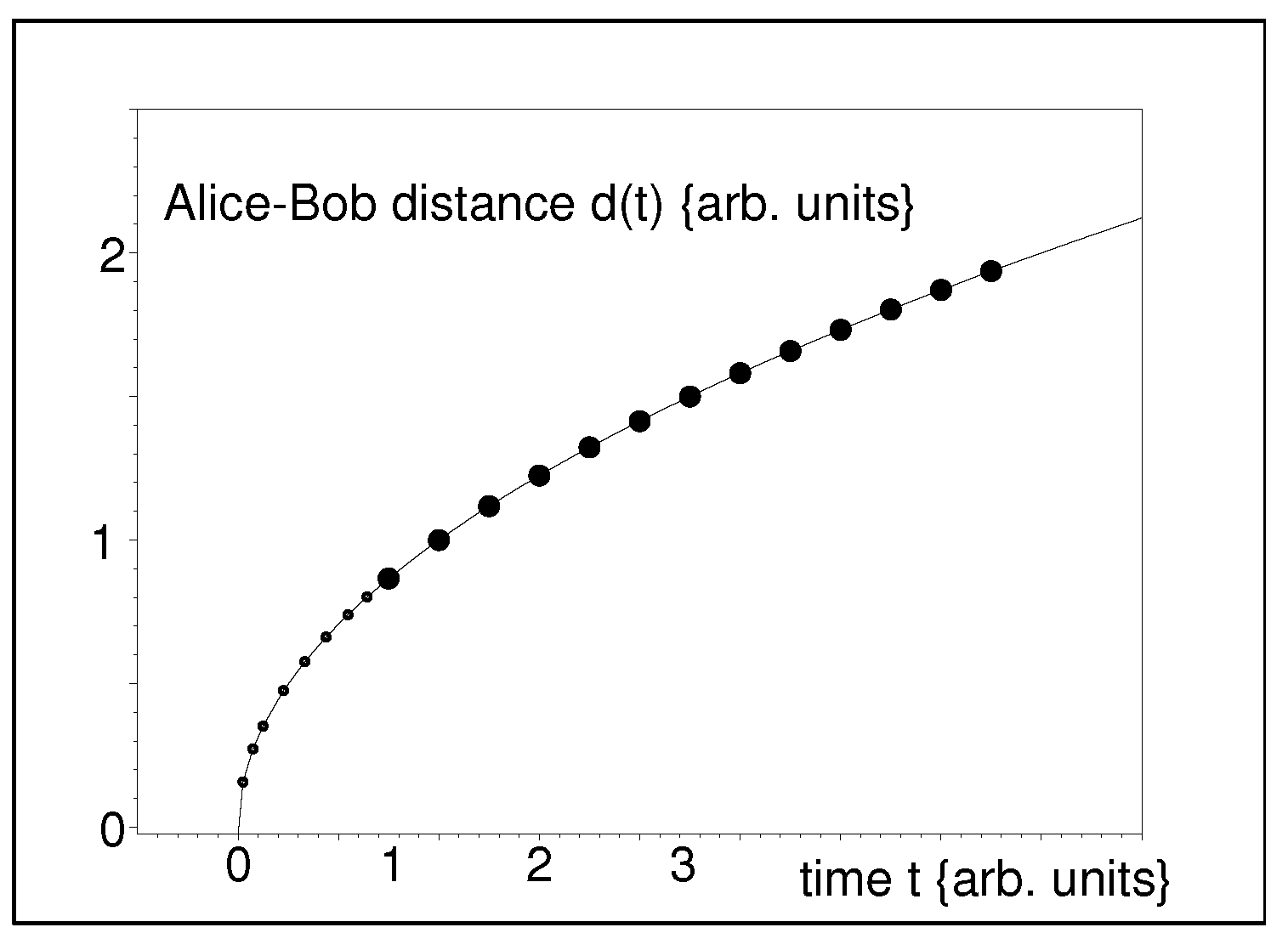
. Basically, the answer lies in the possibility of treating this operator as the distance between two observers in an empty space (Universe). In a cosmology-oriented
Gedankenexperiment, such a pair of observers (let us call them, say, Alice and Bob—they may be perceived as attached, say, to different Galaxies) are assumed to measure their (classical) distance
(cf.
Figure 1). Once they extrapolate their data to remote past, they may reveal the existence of the Big Bang singularity,
Hypothetically, Alice and Bob may have started their experiment very early after the Big Bang. In such a case one should recall the principle of classical-quantum correspondence and replace the real curve by the pencil of self-adjoint operators defined in the above-mentioned alternative physical Hilbert space . In Heisenberg picture (and, say, in pure state), the wave function of the Alice’s and Bob’s Universe will be time-independent while, under adiabatic hypothesis, their measured distance will smoothly continue the classical curve and, moreover, it will coincide, in the case of a luckily chosen quantum theory, with one of the eigenvalues of the toy-model operator .
A decisive weakness of the whole argument has already been noticed by Ashtekar
et al. [
35,
38,
39]. The essence of the problem may be seen in the incompatibility of the quantized version of the degeneracy of eigenvalues (
6) with the self-adjoint nature of the underlying operator. Indeed, from the purely mathematical point of view the eigenvalues of
may degenerate
either at a complex value of the EP Big Bang time
or after an emergence of some mysterious
ad hoc symmetry at some real value of
. Both of these possibilities look, clearly, unacceptable.
In the manner which was already proposed in the not too successful illustrative construction [
34], the escape out of such an apparent no-go theorem may be provided by the time-dependent generalization (cf. [
24,
40]) of the Dyson’s [
15]
non-unitary isospectral change of representation. As long as we realize all of our constructions solely in the auxiliary Hilbert space
, the mapping (
4) leads to the manifestly non-Hermitian operator representation
of the observable Alice-Bob distance. Hence, there are no formal objections against the critical EP time of the Big Bang being real (and, for simplicity, shifted to the origin,
).
6. Toy Models
In the language of mathematics, the problem we intend to discuss here is the problem of the behavior of a quantum/classical system near its
multiple, degenerate exceptional-point singularity. We believe that a particularly suitable class of models suitable for such a study are the discrete,
N by
N matrix models. Their purely formally motivated but remarkably transparent class was proposed in Refs. [
13,
18,
19]. In what follows, the low-dimensional toy models of this class will be explored as most suitable candidates for bridging the existing gaps between the formulation of certain quantum-cosmological hypotheses and some future experimental optical simulations and tests of structures and stability of their descriptive properties.
6.1. Toy Model Matrices with
For times
(
i.e., long after the passage of the system through its exceptional point—in a way inspired by cosmology [
41,
42] let us call this passage, briefly, “Big Bang”) our
toy-model operator (
3) (representing any generic observable quantity—in the light of our forthcoming, phenomenology-oriented applications of the formalism let us call this observable, for the sake of brevity, “distance”) is self-adjoint even in the friendly Hilbert space
. Due to the extreme simplicity of such an illustrative model we may recall constraint
(in
)
alias (in
) and construct all of the Hermitizing inner-product metrics
,
i.e., all of the eligible, manifestly time-dependent physical Hilbert spaces
[
43,
44]. The exhaustive, complete menu of our Hilbert space metrics (HSMs) at
,
is defined in terms of a single [
25] free real parameter
α such that
. Both of the eigenvalues of the metric are positive,
At any time
each choice of
α specifies a different inner product,
i.e., a different, potentially physical Hilbert space
. This means that the physical contents of the model described by operator (
3) and by the related HSM
will vary with
α.
One of the most successful strategies of removal of such an unpleasant ambiguity was proposed by Bender
et al. [
45]. They recommended the use of ansatz
where
(in the diagonal matrix form where
) mimics parity and where
(such that
) mimics charge. In our case this conjecture leads to formula
and to constraint
, with several remarkable consequences. Firstly, the choice of
minimizes the anisotropy
of the Hilbert-space geometry at all
. Secondly, as long as we have
, the anisotropy will vanish yielding the trivial, isotropic-metric limit
at
.
As long as the smooth continuation of Equation (
3) to the larger times
would make our only observable
manifestly Hermitian, the related physical HSM matrix could be kept trivial as well,
at
. In this case the interval of times in which the HSM matrix
is anomalous will be finite, yielding
at all
.
Obviously, our
model with “Big Bang” at
reminds us of the elementary cosmological model of [
23]. Once we accept such a cosmological interpretation of our present quantum evolution model, the finite interval of times
could be, in the same spirit, tentatively identified with the Inflation period, or with its initial quantized-evolution phase at least. The same terminological convention will be accepted to hold for the whole
family of hiddenly Hermitian
N by
N matrices of [
13,
18] involving Equation (
3) as its most elementary special case.
6.2. Toy-Model Matrices with
The first nontrivial, three-by-three candidate for the crypto-Hermitian distance operator has the non-Hermitian real matrix form
with
, with the real spectrum
and with the triple EP value
.
The construction of the corresponding general two-parametric Hermitizing metrics (we skip its presentation) as well as of its specific and unique product form remains routine. In terms of antidigonal unit matrix J with Kronecker-delta elements , we get the following result.
Lemma 1. For the crypto-Hermitian distance operator of the form (11) at times the requirement makes the Hermitizing HSM unique, Although one of the eigenvalues loses its positivity beyond the Big Bang boundary, i.e., at , the effect is spurious because it occurs at unphysical, purely imaginary times t. The behavior of the eigenvalues near alias is more important because it shows that the end-of-Inflation limit of the conventional Dirac’s metric is reached in a finite time after the Big Bang.
What remains to be proved or disproved is the minimal-anisotropy property of the physical and unique Hilbert space
with metric (
12). In order to shorten the analysis let us skip the detailed description of the fully general case and let us merely consider the following one-parametric subset of all of the solutions of Equation (
7),
For all of these HSM candidates guaranteeing the Hermiticity of operator
in
we may evaluate the eigenvalues,
and demonstrate that the choice of the free parameter
g which would guarantee the minimal anisotropy of the geometry of Hilbert space
is unique and equal to
. Such a result may be given the form of the following two lemmas.
Lemma 2. Whenever there exists a real such that the HSM candidate (13) is positive definite if and only if . Proof. The use of ansatz
in Equation (
14) (with, say,
) converts the inequality
into relation
i.e.,
Thus, at each choice of the inequality will hold in a non-empty interval of small t. ☐
Lemma 3. Whenever , metric (13) is not isotropic at the “end-of-Inflation” time . Proof. follows from an immediate inspection of formula (
13). ☐
The
single requirement of minimal anisotropy makes the metric optimal at
and
,
i.e., at
both of the ends of the Inflation-resembling interval. The deviations of the roots (
14) from their minimal-anisotropy extreme at
are easily described. The middle root (forming an inverted parabola in
τ) remains positive for
. The change of the sign of the smaller
(which is positive for all
at
) may take place at the curves
(= the shared upper boundary of the domain of positivity for
) and
(= the lower boundary) in the
plane. Whenever
, the Inflation-resembling evolution has no natural end because the time-dependent Hilbert-space geometry remains anisotropic at
alias .
6.3. Toy-Model Matrices with
The latter two Lemmas offer a hint for an extrapolation of the pattern to the larger Hilbert-space dimensions
. With the next operator
(with the real spectrum
and with the quadruple EP value
), we get beyond the scope of the general analytic metric-operator results of [
19]. Fortunately, even our
example still admits a non-numerical treatment.
Lemma 4. Manifestly time-dependent matrix (15) is Hermitian with respect to the manifestly time-dependent HSM matrix The eigenvalues of the latter matrix form the ordered set and satisfy the positivity requirements during all Inflation, i.e.
, at all times . Proof. The verification of the hidden Hermiticity (
7) of operator (
15) was performed using the routine, computer-assisted linear algebra. At
these manipulations are still feasible and provide, as a byproduct, the closed-form eigenvalues of the physical Hilbert-space metric. ☐
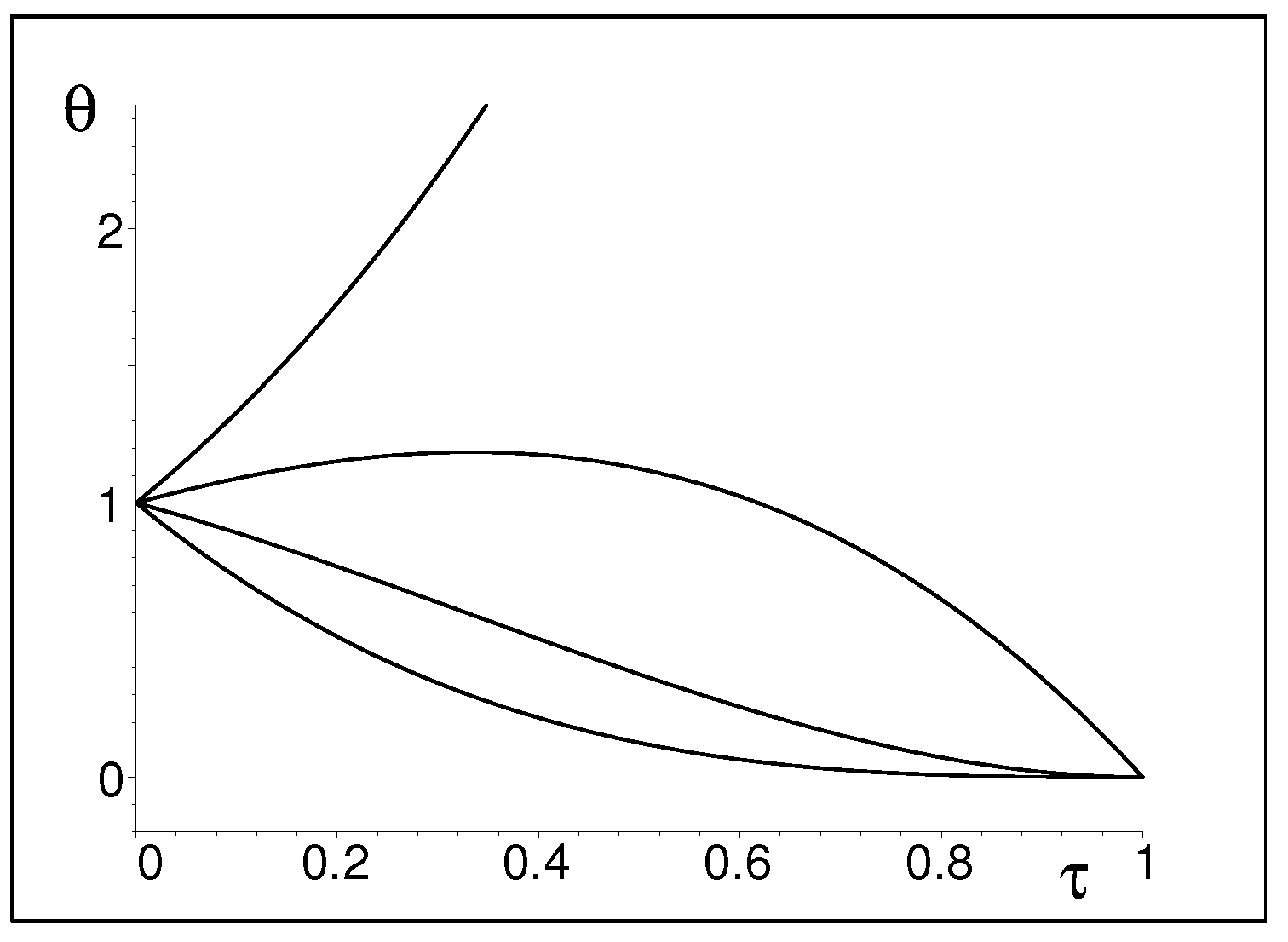
Figure 2 offers the graphical illustration of the latter observation. The time-variation of the eigenvalues is shown to start from the absence of any isotropy of Hilbert space
at Big Bang instant
. Immediately after the Big Bang the degenerate
plet of the vanishing eigenvalues of the metric is seen to unfold in a hierarchical, ordered manner. The smooth increase of the isotropy during Inflation ends, at
, by the ultimate disappearance of the anisotropy. This marks the end of the Inflation at finite time.
7. Discussion
It is important to keep in mind that our present matrix models still represent just a very schematic realization of the underlying idea of the quantization of the measurable distance between Alice and Bob. Naturally, in the context of a not yet existing full fledged quantum cosmology we are still far from any truly realistic picture. At the same time it is quite plausible that that the basic features our elementary toy models may be rather realistic even under our drastic simplifications.
First of all we believe that our present purely pedagogical restriction of attention to the smallest dimensions N of the spatial grid is not too relevant and that the underlying background-independent quantum dynamics of the expanding Universe at short times will remain qualitatively unchanged at all of the finite matrix dimensions N.
It is possible to claim that on the purely mathematical side our present results clearly support the idea of the feasibility of quantization in which several traditional “no-go” expectations are circumvented via the identification of the spatiotemporal coordinates of quantum catastrophes like Big Bang with the Kato’s exceptional-point parameters of the theory.
On the purely formal level we connected here the implementation of this idea with an active use of the manifestly time-dependent forms of quantum theory in which the observables exhibit a hidden Hermiticity,
i.e., in which the (perhaps, necessarily needed) new physical degrees of freedom emerge as rrepresented by the Hilbert-space inner-product metric Θ. Then, in a way paralleling the phenomenological quantum-catastrophe perspective of [
20] the initial choice of the cryptohermitian operators of observables (
i.e., in our simplified models, of the “quantized distance” matrices
) represents one of the most efficient strategies in model-building.
Via a detailed analysis of our models we showed that even when any form of the dynamical input information is allowed to be manifestly time-dependent, the technical manipulations (and, first of all, the constructions of physical metric) remain—at least conceptually - feasible. Thus, in methodical sense we may be quite assertive, opposing, e.g., the scepticism [
6,
46,
47,
48], and joining opinions [
49,
50], the authors of which managed to clarify several comparatively widespread though just more or less purely terminological misunderstandings.
Naturally, also our present constructions combine the clarification of the innovative methodology with a concrete sample of its possible immediate impact upon the predictions to be made by any realistic theory in quantum cosmology. In such an applied-theory context we are persuaded that especially the present, virtually serendipitous discovery of possible connection between the process of quantization and the emergence of the Inflation-resembling short time-period after the Big Bang sounds quite inspiring.
The generalization of the formalism in which the coupling
λ in Hamiltonians
would vary with time appeared to require a thorough change of the formalism [
24,
40]. Moreover, it also proved accompanied by a perceivable loss of its simplicity [
34,
51,
52,
53,
54,
55]. Fortunately, the major part of these discouraging shortcomings disappears after one disconnects the toy-model matrices from their early role of Hamiltonians (
i.e., roughly speaking, of the energy operators). Such a change of interpretation formed in fact the core of our present message. Marginally, let us add that the methodical relevance of the time-dependent observables (sampled by (
3), (
11) and (
15),
etc.) in quantum cosmology was preliminarily communicated also in a recent conference [
56]. The videorecorded form [
57] of the talk on the webpage of the conference might be also recalled as a predecessor and/or complement of the present text.
8. Summary
Via toy-model examples we managed here to demonstrate that the spatial Big Bang singularity of classical cosmology need not necessarily be replaced by a regularized Big Bounce after quantization. Our demonstration proceeded, constructively, via a non-covariant, highly schematic model of an empty one-dimensional Universe in which a pair of experimentalists (Alice and Bob) measure their distance.
As an unpredicted byproduct of the study of toy models we revealed that in their cosmological phenomenological implementations the Big Bang appears followed by a finite anomalous evolution period carrying multiple features of a hypothetical “Inflation”. Thus, the period of Inflation appears naturally identified with the period of an anisotropy of the “physical” Hilbert space of the hypothetical (i.e., “multiverse”) quantum states of the non-stationary, evolving Universe. In other words, during the evolutionary stage which mimics (explains?) Inflation one encounters a step-by-step weakening of the anisotropy of the Hilbert space of states of the Universe.
Thus, with the Big Bang singularity identified with the Kato’s exceptional point, the Inflation period is explained as a purely quantum phenomenon. In this sense our present results may be directly related to our older quantum-cosmology-related conjecture [
34] where we already tried to work, constructively, with a doublet of the non-Hermitian operators of observables. Unfortunately, the latter conjecture was based on an inefficient strategy as long as we kept the Hamiltonian
maximally elementary (
i.e., constant and parameter-independent) while having started our constructions from the time-dependent set of eligible Hermitizing metrics
. This made the older construction of the present spatial-geometry observable
(which would characterize the Big Bang or Big Crunch in the respective limits
) prohibitively complicated. Due to the emergent technical complications we only managed to construct the relevant resulting
at
.
In the present paper we made use of a much more efficient strategy. It was based, in essence, just on a reversal of the flow of the construction. Thus, we started now directly from a suitable initial choice of the time-dependent candidates
) for the “geometry” observable (viz., the Alice-Bob distance). Having made use of the discretization philosophy as advocated and tested in [
58], manifestly non-Hermitian matrices
were chosen also here, playing the role of the operators of an observable distance. Thus, the time-dependent eigenvalues of
were assumed to be measured and given the cosmological toy-model geometrical meaning.