Nutritional Stress Causes Heterogeneous Relationships with Multi-Trait FA in Lesser Black-Backed Gull Chicks: An Aviary Experiment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Manipulations
2.1.1. General Procedure
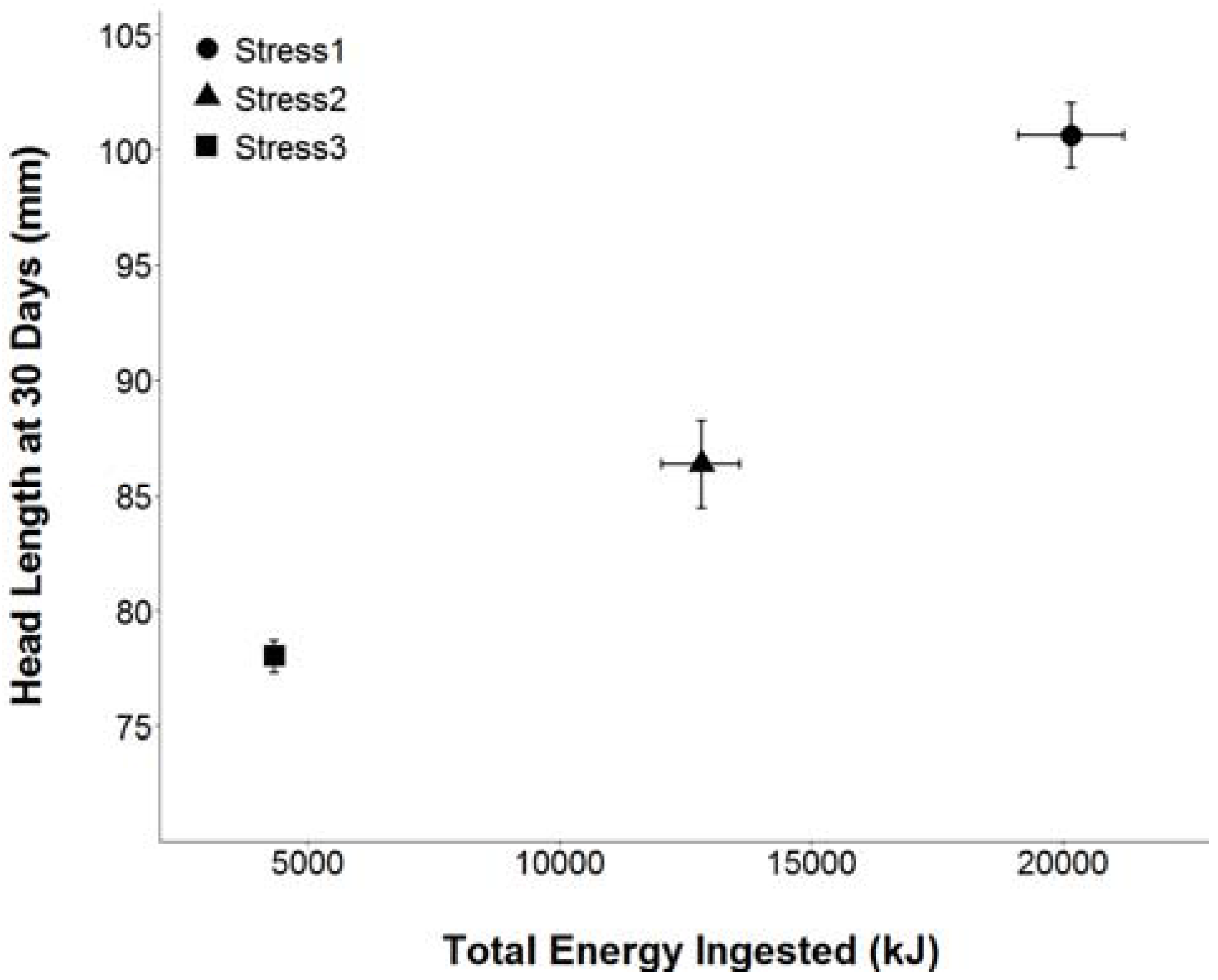
2.1.2. Diet Treatments
2.1.3. Measurements
2.1.4. Animal Welfare
2.2. Data Analyses
2.2.1. Fluctuating Asymmetry Estimation
2.2.2. Hypothesis Testing
3. Results
3.1. FA Estimation
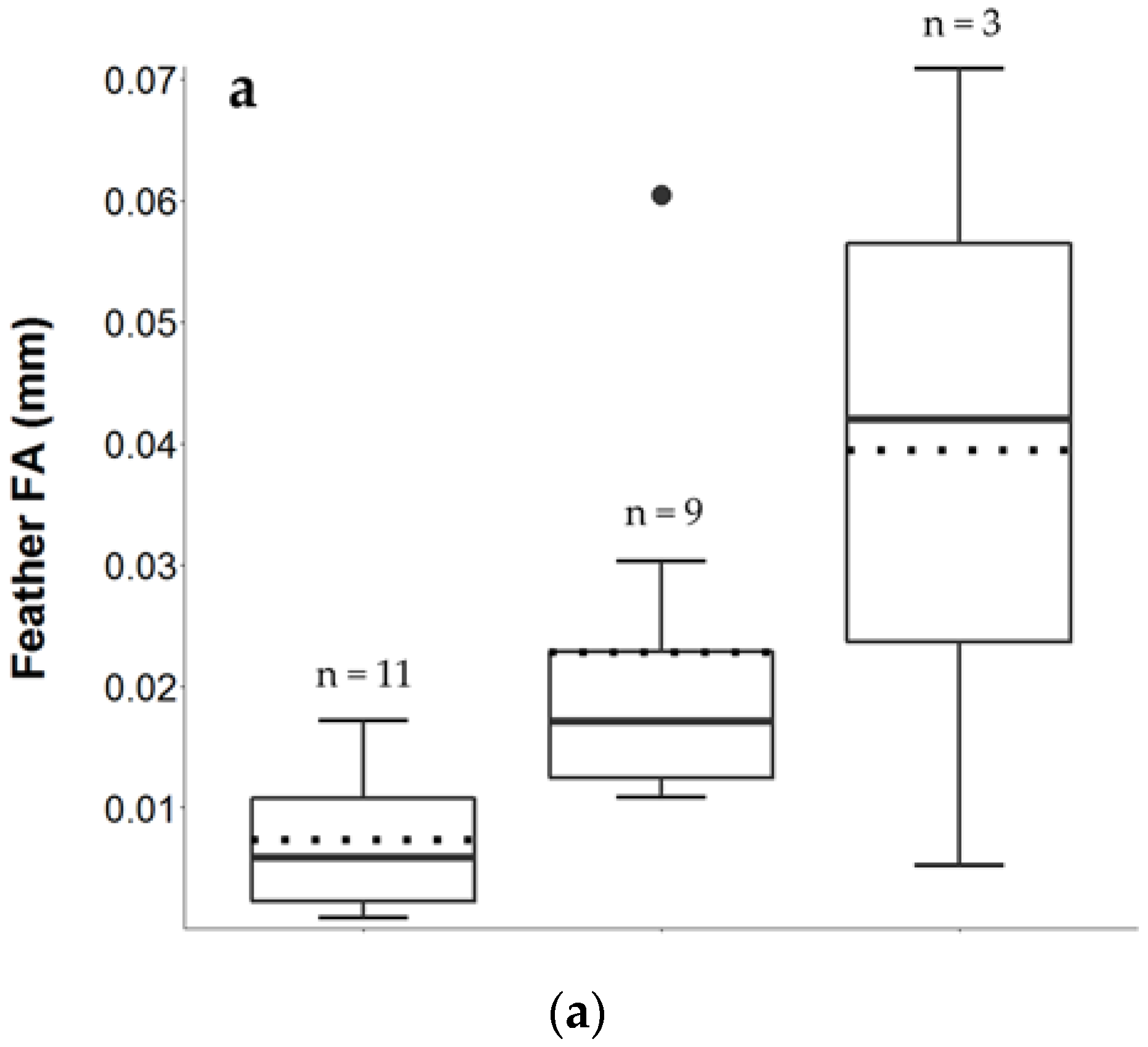
3.2. Feather FA
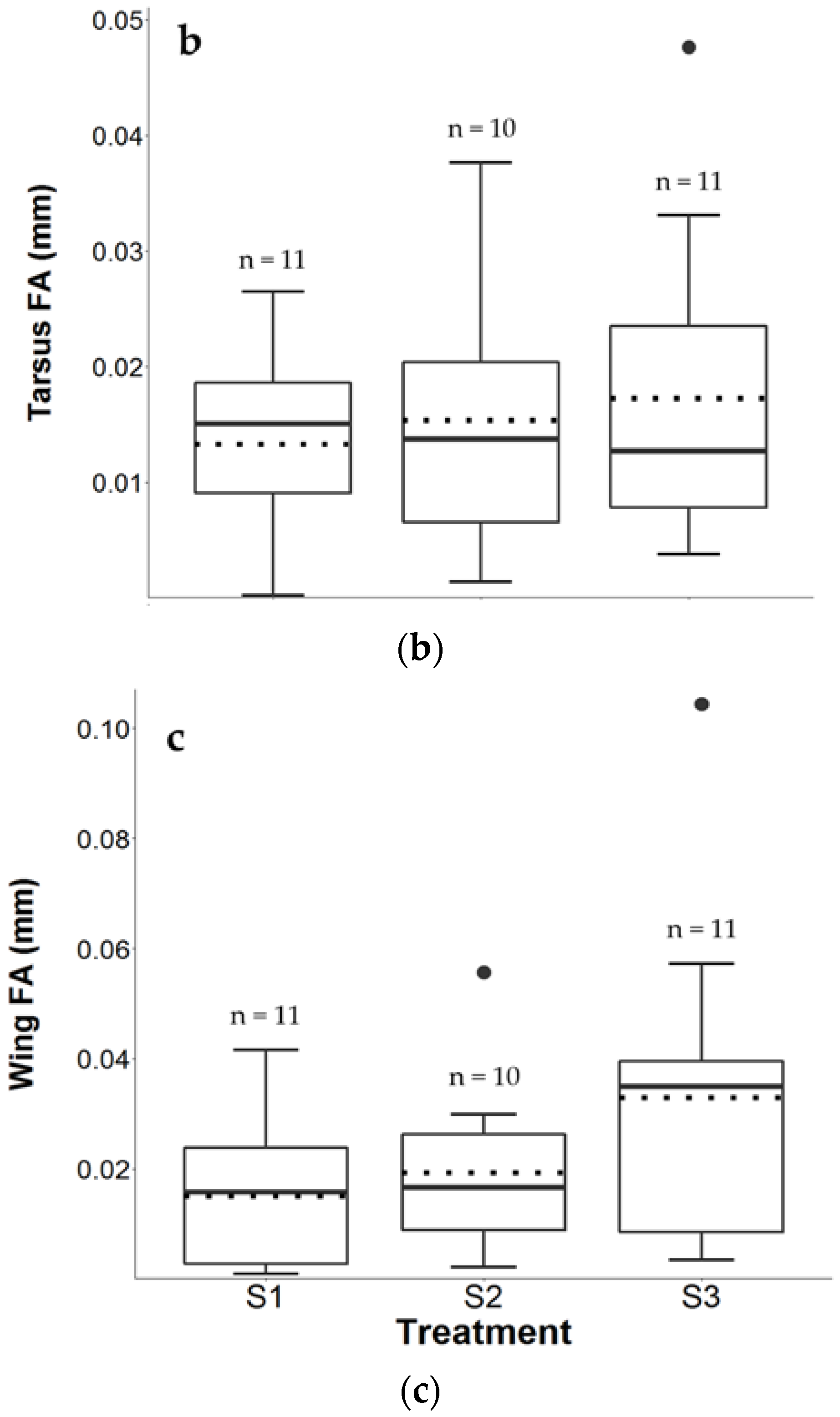
3.3. Tarsus FA
3.4. Wing FA
3.5. Multi-Trait FA
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Adams, S.M.; Giesy, J.P.; Tremblay, L.A.; Eason, C.T. The use of biomarkers in ecological risk assessment: Recommendations from the Christchurch conference on Biomarkers in Ecotoxicology. Biomarkers 2001, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Tomkins, J.L.; Andrews, S. Fluctuating Asymmetry. Encycl. Life Sci. 2001. [Google Scholar] [CrossRef]
- Palmer, A.R. Fluctuating asymmetry analyses: A primer. In Developmental Instability: Its Origins and Evolutionary Implications; Springer: Dordrecht, The Netherlands, 1994; Volume 93, pp. 335–364. [Google Scholar]
- Lens, L.; Dongen, S.; Kark, S.; Matthysen, E. Fluctuating asymmetry as an indicator of fitness: Can we bridge the gap between studies? Biol. Rev. 2002, 77, 27–38. [Google Scholar] [CrossRef] [PubMed]
- Leary, R.F.; Allendorf, F.W. Fluctuating asymmetry as an indicator of stress: Implications for conservation biology. Trends Ecol. Evol. 1989, 4, 214–217. [Google Scholar] [CrossRef]
- Moller, A.P. Developmental stability and fitness: A review. Am. Nat. 1997, 149, 916–932. [Google Scholar] [CrossRef] [PubMed]
- Clarke, G.M. Fluctuating asymmetry of invertebrate populations as a biological indicator of environmental quality. Environ. Pollut. 1993, 82, 207–211. [Google Scholar] [CrossRef]
- Palmer, A.R. Waltzing with asymmetry: Is fluctuating asymmetry a powerful new tool for biologists or just an alluring new dance step? Bioscience 1996, 46, 518–532. [Google Scholar] [CrossRef]
- Clarke, G.M.; McKenzie, L.J. Fluctuating asymmetry as a quality control indicator for insect mass rearing processes. J. Econ. Entomol. 1992, 85, 2045–2050. [Google Scholar] [CrossRef]
- Clarke, G.M. Relationships Between Developmental Stability and Fitness: Application for Conservation Biology. Conserv. Biol. 1995, 9, 18–24. [Google Scholar] [CrossRef]
- Lens, L.; Eggermont, H. Fluctuating asymmetry as a putative marker of human-induced stress in avian conservation. Bird Conserv. Int. 2008, 18, S125–S143. [Google Scholar] [CrossRef]
- Bjorksten, T.A.; Fowler, K.; Pomiankowski, A. What does sexual trait FA tell us about stress? Trends Ecol. Evol. 2000, 15, 163–166. [Google Scholar] [CrossRef]
- Leung, B.; Forbes, M.R. Fluctuating asymmetry in relation to stress and fitness Effects of trait type as revealed by meta-analysis. Ecoscience 1996, 3, 400–413. [Google Scholar] [CrossRef]
- Swaddle, J.P.; Witter, M.S. Food, Feathers and Fluctuating Asymmetries. R. Soc. 1994, 255, 147–152. [Google Scholar] [CrossRef]
- Nilsson, J. Energetic stress and the degree of fluctuating asymmetry: Implications for a long-lasting, honest signal. Evol. Ecol. 1994, 8, 248–255. [Google Scholar] [CrossRef]
- Grieco, F. Greater food availability reduces tarsus asymmetry in nestling blue tits. Condor 2003, 105, 599–603. [Google Scholar] [CrossRef]
- Sillanpää, S.; Salminen, J.-P.; Eeva, T. Fluctuating asymmetry in great tit nestlings in relation to diet quality, calcium availability and pollution exposure. Sci. Total Environ. 2010, 408, 3303–3309. [Google Scholar] [CrossRef] [PubMed]
- Vangestel, C.; Lens, L. Does fluctuating asymmetry constitute a sensitive biomarker of nutritional stress in house sparrows (Passer domesticus)? Ecol. Indic. 2011, 11, 389–394. [Google Scholar] [CrossRef]
- Regulation, E.C. No. 1380/2013 of the European Parliament and of the Council of 11 December 2013 on the Common Fisheries Policy, Amending Council Regulations (EC) No. 1954/2003 and (EC) No. 1224/2009 and repealing Council Regulations (EC) No. 2371/2002 and (EC). Off. J. Eur. Union 2013, 354, 22–61. [Google Scholar]
- Bicknell, A.W.J.; Oro, D.; Camphuysen, K.C.J.; Votier, S.C. Potential consequences of discard reform for seabird communities. J. Appl. Ecol. 2013, 50, 649–658. [Google Scholar] [CrossRef]
- Sommerfeld, J.; Mendel, B.; Fock, H.O.; Garthe, S. Combining bird-borne tracking and vessel monitoring system data to assess discard use by a scavenging marine predator, the lesser black-backed gull Larus fuscus. Mar. Biol. 2016, 163, 1–11. [Google Scholar] [CrossRef]
- Hume, R. Complete Birds of Britain and Europe, 1st ed.; Dorling Kindersley: London, UK, 2002. [Google Scholar]
- Isaksson, N.; Evans, T.J.; Shamoun-Baranes, J.; Åkesson, S. Land or sea? Foraging area choice during breeding by an omnivorous gull. Mov. Ecol. 2016, 4, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Harris, M.P. Aspectes of the breeding biology of the gulls Larus argentatus, L. fuscus and L. marinus. Ibis 1964, 106, 432–456. [Google Scholar] [CrossRef]
- Del Hoyo, J.; Elliott, A.; Sargatal, J. Handbook of the Birds of the World, Vol. 3: Hoatzin to Auks; Lynx Edicions: Barcelona, Spain, 1996. [Google Scholar]
- Research Institute for Nature and Forest (INBO), Brussels, Belgium. Unpublished work. 2012.
- Sotillo, A.; Ghent University, Ghent, Belgium. Unpublished work. 2014.
- Smith, J.A.; van den Broek, F.A.R.; Martorell, J.C.; Hackbarth, H.; Ruksenas, O.; Zeller, W. Principles and practice in ethical review of animal experiments across Europe: Summary of the report of a FELASA working group on ethical evaluation of animal experiments. Lab. Anim. 2007, 41, 143–160. [Google Scholar] [CrossRef] [PubMed]
- Van Dongen, S.; Molenberghs, G.; Matthysen, E. The statistical analysis of fluctuating asymmetry: REML estimation of a mixed regression model. J. Evol. Biol. 1999, 12, 94–102. [Google Scholar] [CrossRef]
- Tests in Linear Mixed Effects Models, version 2.0-32; lmerTest; Danmarks Tekniske Universitet: Copenhagen, Denmark, 2016.
- Leung, B.; Forbes, M.; Houle, D. Fluctuating Asymmetry as a Bioindicator of Stress: Comparing Efficacy of Analyses Involving Multiple Traits. Am. Nat. 2000, 155, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Palestis, B.G. Fluctuating Asymmetry in Common Tern (Sterna Hirundo) Chicks Varies with Hatching Order and Clutch Size. Auk 2009, 126, 815–822. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Multi-Model Inference (MuMIn), version 1.15.6; R Foundation for Statistical Computing: Vienna, Austria, 2015.
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using Ime4. Statistics, 2015; arXiv:1406.5823. [Google Scholar]
- R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Copenhagen, Denmark, 2015.
- RStudio Team. RStudio: Integrated Development for R; RStudio: Boston, MA, USA, 2015. [Google Scholar]
- Lens, L.; Van Dongen, S.; Matthysen, E. Fluctuating asymmetry as an early warning system in the critically endangered Taita Thrush. Conserv. Biol. 2002, 16, 479–487. [Google Scholar] [CrossRef]
- Maul, J.D.; Farris, J.L. Monitoring Exposure of Northern Cardinals, Cardinalis Cardinalis, to Cholinesterase—Inhibiting Pesticides: Enzyme Activity, Reactivations, and Indicators of Environmental Stress. Environ. Toxicol. 2005, 24, 1721–1730. [Google Scholar] [CrossRef]
- Swaddle, J.P.; Witter, M.S. On the ontogeny of developmental stability in a stabilized trait. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1997, 264, 329–334. [Google Scholar] [CrossRef]
- Chippindale, A.K.; Palmer, A.R. Persistence of subtle departures from symmetry over multiple molts in individual brachyuran crabs: Relevance to developmental stability. Genetica 1993, 89, 185–199. [Google Scholar] [CrossRef]
- Aparicio, J.M. Patterns of fluctuating asymmetry in developing primary feathers: A test of the compensational growth hypothesis. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1998, 265, 2353–2357. [Google Scholar] [CrossRef]
- Clarke, G.M. The genetic basis of developmental stability. IV. Individual and population asymmetry parameters. Heredity 1998, 80, 553–561. [Google Scholar] [CrossRef]
- Rasmuson, M. Fluctuating asymmetry—Indicator of what? Hereditas 2002, 136, 177–183. [Google Scholar] [CrossRef] [PubMed]
- Aparicio, J.M.; Bonal, R. Why do some traits show higher fluctuating asymmetry than others? A test of hypotheses with tail feathers of birds. Heredity 2002, 89, 139–144. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.R.; Strobeck, C. Fluctuating Asymmetry: Measurement, Analysis, Patterns. Annu. Rev. Ecol. Syst. 1986, 17, 391–421. [Google Scholar] [CrossRef]
- Gummer, D.L.; Brigham, R.M. Does fluctuating asymmetry reflect the importance of traits in little brown bats (Myotis lucifugus)? Can. J. Zool. 1995, 73, 990–992. [Google Scholar] [CrossRef]
- Boonekamp, J.J.; Dijkstra, R.; Dijkstra, C.; Verhulst, S. Canalization of development reduces the utility of traits as fitness biomarkers: Feather fault bars in nestling birds. Funct. Ecol. 2016. [Google Scholar] [CrossRef]
- Thomas, A.L. The aerodynamic costs of asymmetry in the wings and tail of birds: Asymmetric birds can’t fly round tight corners. Proc. R. Soc. Lond. B Biol. Sci. 1993, 1341, 181–189. [Google Scholar] [CrossRef]
| Trait | n | Directional Asymmetry (DA) | Variance Components | Likelihood Ratio Test | ||||
|---|---|---|---|---|---|---|---|---|
| Mean ± SE | t-Statistic (df) | p | VFA | VME | χ2 | p | ||
| Feather | 23 | 0.1594 ± 0.3942 | 0.404 (22.57) | 0.690 | 3.48 | 0.14 | 166.90 | <0.001 |
| Tarsus | 32 | 0.3702 ± 0.1780 | 2.080 (31.26) | 0.046 | 1.01 | 0.01 | 222.46 | <0.001 |
| Wing | 32 | 0.2500 ± 0.7354 | 0.340 (30.99) | 0.736 | 16.74 | 0.56 | 118.47 | <0.001 |
| Treatment Contrast | Hatching Period | Estimate (SE) | Lower CI | Upper CI |
|---|---|---|---|---|
| S1–S2 | Early | −0.0121 (0.0067) | −0.0296 | 0.0055 |
| S1–S3 | Early | −0.0635 (0.0101) | −0.0898 | −0.0373 |
| S2–S3 | Early | −0.0515 (0.0107) | −0.0792 | −0.0238 |
| S1–S2 | Intermediate | −0.0069 (0.0067) | −0.0244 | 0.0106 |
| S1–S3 | Intermediate | −0.0133 (0.0084) | −0.0351 | 0.0086 |
| S2–S3 | Intermediate | −0.0063 (0.0077) | −0.0264 | 0.0137 |
| S1–S2 | Late | −0.0563 (0.0107) | −0.0840 | −0.0286 |
| S1–S3 | Late | |||
| S2–S3 | Late |
| Treatment Contrast | Hatching Period | Estimate (SE) | Lower CI | Upper CI |
|---|---|---|---|---|
| S1–S2 | Early | 0.0072 (0.0133) | −0.0262 | 0.0406 |
| S1–S3 | Early | −0.0325 (0.0193) | −0.0809 | 0.0160 |
| S2–S3 | Early | −0.0397 (0.0140) | −0.0749 | −0.0044 |
| S1–S2 | Intermediate | −0.0002 (0.0127) | −0.0320 | 0.0316 |
| S1–S3 | Intermediate | −0.0034 (0.0199) | −0.0533 | 0.0465 |
| S2–S3 | Intermediate | −0.0032 (0.0111) | −0.0311 | 0.0246 |
| S1–S2 | Late | −0.0229 (0.0229) | −0.0805 | 0.0347 |
| S1–S3 | Late | 0.00001 (0.0227) | −0.0571 | 0.0571 |
| S2–S3 | Late | 0.0229 (0.0106) | −0.0037 | 0.0494 |
| Treatment Contrast | Estimate (SE) | Lower CI | Upper CI |
|---|---|---|---|
| S1–S2 | −0.0238 (0.0567) | −0.1648 | 0.1172 |
| S1–S3 | −0.0693 (0.0803) | −0.2689 | 0.1303 |
| S2–S3 | −0.0456 (0.0385) | −0.1414 | 0.0502 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, T.; Santos, C.S.A.; Sotillo, A.; De Neve, L.; Stienen, E.W.M.; Müller, W.; Lens, L. Nutritional Stress Causes Heterogeneous Relationships with Multi-Trait FA in Lesser Black-Backed Gull Chicks: An Aviary Experiment. Symmetry 2016, 8, 133. https://doi.org/10.3390/sym8110133
Gupta T, Santos CSA, Sotillo A, De Neve L, Stienen EWM, Müller W, Lens L. Nutritional Stress Causes Heterogeneous Relationships with Multi-Trait FA in Lesser Black-Backed Gull Chicks: An Aviary Experiment. Symmetry. 2016; 8(11):133. https://doi.org/10.3390/sym8110133
Chicago/Turabian StyleGupta, Trisha, Cátia S. A. Santos, Alejandro Sotillo, Liesbeth De Neve, Eric W. M. Stienen, Wendt Müller, and Luc Lens. 2016. "Nutritional Stress Causes Heterogeneous Relationships with Multi-Trait FA in Lesser Black-Backed Gull Chicks: An Aviary Experiment" Symmetry 8, no. 11: 133. https://doi.org/10.3390/sym8110133
APA StyleGupta, T., Santos, C. S. A., Sotillo, A., De Neve, L., Stienen, E. W. M., Müller, W., & Lens, L. (2016). Nutritional Stress Causes Heterogeneous Relationships with Multi-Trait FA in Lesser Black-Backed Gull Chicks: An Aviary Experiment. Symmetry, 8(11), 133. https://doi.org/10.3390/sym8110133






