Symmetry Perspectives on Some Auxetic Body-Bar Frameworks
Abstract
: Scalar mobility counting rules and their symmetry extensions are reviewed for finite frameworks and also for infinite periodic frameworks of the bar-and-joint, body-joint and body-bar types. A recently published symmetry criterion for the existence of equiauxetic character of an infinite framework is applied to two long known but apparently little studied hinged-hexagon frameworks, and is shown to detect auxetic behaviour in both. In contrast, for double-link frameworks based on triangular and square tessellations, other affine deformations can mix with the isotropic expansion mode.1. Introduction
Use of counting rules in the study of rigidity and mobility of frameworks has a venerable history, going back to Maxwell's 1864 rule for bar-and-joint frameworks [1], and its extension (due to Calladine [2]) to account for the balance between the numbers of mechanisms (m) and states of self-stress (s). Mobility criteria for body-and-joint assemblies involving counting of degrees of freedom and constraints also appeared early on the scene [3, 4]. In recent years, extensions of these classic counting rules have been made, employing arguments based on point-group symmetry. It turns out that “counting with symmetry” can often detect mechanisms and/or states of self-stress that cancel out in purely numerical terms in the balance m − s, but have different characteristic symmetries and do not cancel in the reducible representation Γ(m) − Γ(s) [5]. Examples of this symmetry-based approach include symmetry-adapted versions of the Maxwell Rule [5], the mobility criterion for body and joint assemblies [6], and for bar-body systems [7]. Symmetry analyses have dealt with classes of system such as rotating rings of tetrahedra [8], [N]-loops [9] toroidal deltahedra [10] and various mechanical toys and models [11–13]. Symmetry arguments have been used to derive conditions for the existence of isostatic frameworks [14] and to discuss the flexibility of protein molecules [15]. Attention from the mathematical, engineering and materials-science communities has now started to shift to periodic systems. Several different mathematical approaches towards the treatment of periodic systems are described in the proceedings of the 2012 conference on Rigidity of Periodic and Symmetric Structures in Nature and Engineering [15–18].
Direct extension of symmetric Maxwell and mobility rules from point groups and finite objects to unit-cell symmetry in infinite repetitive systems [18] gives criteria for detection of repetitive (zero-wavevector) mechanisms and states of self-stress. In turn, analysis of these periodic mobility rules leads to a symmetry-based criterion for “equiauxetic” behaviour [19]. Auxetic materials have the property that they respond to stretching along one direction by expansion along the transverse direction(s). Equiauxetic materials manage this in such a way that they have Poisson's ratio −1.
The new symmetry theorem for equiauxetics gives an opportunity to look back at some frameworks that were first discussed [20–23] before the term “auxetic” came into use [24] and to see how the symmetry viewpoint enhances understanding. The particular frameworks that we have in mind are hinged versions of hexagonal tessellations where rigid hexagons are linked by either one or two pin-jointed bars per edge. (See Figure 1, the movement of which was described in a near-forty-year old sketch by one of the present authors (T.T.).) The mechanism of the single-link version appeared in Figure 6 of [20] and later in Figure 4.2.17 of [21] and in the appendix to [22]. A model of the double-link version was published in [22] and [23]. In the double-link framework, pairing enforces parallel geometry for the two hexagon edges that are coincident in the fully closed position.
As the analysis with a periodic symmetry extension of the mobility criterion for body-bar frameworks will show, both frameworks have an auxetic expansion mode. Connection patterns with one and two bars were later used as the inspiration for the construction of families of expanding polyhedra [12,13], which in turn were intended to serve as mechanical models for aspects of pH-induced swelling of virus particles [25]. Again, symmetry analysis proved especially helpful in understanding the mechanisms in such “expandohedra” [12].
In view of the interdisciplinary nature of the material in this paper, it seems useful to give a short lexicon of equivalences between mathematical and engineering/materials science terminology used here. “Mechanisms” and “states of self-stress” are vectors in the left-nullspace and nullspace, respectively, of the equilibrium matrix, a matrix which describes the relationship between internal and external forces in a structure [26]. The “numbers” of mechanisms and states-of-self-stress are the dimensions of these spaces. Any mechanism must also be a vector in the nullspace of the square symmetric “stiffness” matrix for an unstressed structure [27], and hence is an eigenvector, or mode, with a corresponding zero eigenvalue (stiffness). For the remaining definitions, we take a repetitive structure considered as a meta-material that is loaded in a longitudinal direction. The “Poisson's ratio” is the negative of the ratio of the strain (change in length/original length) in the perpendicular direction to that in the longitudinal direction. For traditional materials, which get thinner when stretched, Poisson's ratio is positive, but for auxetic materials, Poisson's ratio is negative. In the thermodynamic limit, Poisson's ratio reaches − 1. An “equiauxetic mode” is thus a zero stiffness eigenvector that corresponds to equal expansion/contraction in perpendicular directions.
2. Counting and Symmetry Versions of Periodic Mobility Rules
2.1. Pin-Jointed Frameworks
Maxwell's 1864 rule for pin-jointed frameworks [1], in the extension due to Calladine [2] is
The scalar counting rule (1) is simply the character of the full symmetry equation under the identity operation. Each additional class of symmetry operations has the possibility of generating an extra counting relation, and extra information for the analysis. It has been said with some justification that each conventional counting rule is just the tip of a symmetry-counting iceberg.
For periodic pin-jointed frameworks, the behaviour of a representative unit cell is considered, and we look for mechanisms and states of self-stress that are propagated by translation of the unit cell, i.e., that correspond to zero wavevector [30]. Furthermore, as discussed in [18], in the periodic case the admissible deformations of the unit cell (excluding rigid-body motions) are: (in 2D) stretches in two orthogonal directions and a single shear; (in 3D) stretches in three orthogonal directions and three independent shears. The periodic equivalent of Equation (1) is therefore
The symmetry equivalent of Equation (4) in both 2D and 3D (with the appropriate definitions of ΓT and ΓR) is
2.2. Body-and-Joint Frameworks
Equation (5) is effectively the symmetry-adapted mobility criterion for a periodic bar-and-joint framework. It is also useful to develop the equivalent criteria for body-and-joint and body-bar models.
For a finite system consisting of n bodies connected by g joints, where joint i permits fi relative freedoms, the mobility (number of relative degrees of freedom) for this composite system can be found by imagining first gluing all the joints rigidly and then restoring the appropriate freedoms at each joint [3,4]. The result is
The symmetry extensions of Equations (6) and (7) are couched in terms of the so-called contact polyhedronC, which has vertices defined by the rigid elements of the structure, and edges defined by the joints connecting them. The result for a finite body-and-joint system in both 2D and 3D is [6]
Contributions to Γfreedoms are calculated according to the type of the joint, and its placement with respect to symmetry elements [6,12,13]. Conversion of Equation (8) to deal with periodic systems follows the reasoning used for bar-and-joint frameworks, and yields
2.3. Body-Bar Frameworks
Finally, we deal briefly with body-bar frameworks. If n bodies are connected by b bars, the Tay counting rule [33] gives
We can derive this counting rule directly from the body-joint Equation (6), if we consider a bar to be a joint that removes five degrees of freedom. For body-bar frameworks, however, it is simpler to begin with body freedoms and impose the bar constraints, rather than working through the gluing and freeing-up procedure used for the various types of hinge in body-hinge arrangements. The symmetry extension of Equation (10) is found by noting the scalar nature of the constraints imposed by bars. The set of bar constraints that act to reduce the freedom of the bodies span Γ(b) which is equal to Γ(e, C), the permutation representation of the edges of the contact polyhedron. The result for a finite body-bar framework is [7]
The adaptation of this formula to periodic symmetry does not appear to have been stated explicitly elsewhere, but it is easily seen to be
3. Symmetry and Equiauxetic Frameworks
The type of auxetic behaviour that can be detected by symmetry is, as mentioned earlier, equiauxetic, implying equal expansion/contraction in all directions and a Poisson's ratio of −1. We note that a Poisson's ratio of −1 is a limiting property for an isotropic material treated as a continuum, as in classical elasticity theory it implies that the ratio of the bulk modulus to shear modulus must be zero, and that the Young's Modulus must also vanish. Symmetry-adapted mobility criteria such as Equations (5), (9) and (12) can be used to provide a sufficient condition for the existence of equiauxetic behaviour in any periodic framework for which we can calculate Γ(m) − Γ(s). The essential idea is that an equiauxetic mode must be one that does not distinguish between orthogonal directions, i.e., it must preserve rotational equivalence of x and y directions in 2D, or x, y and z in 3D. In 2D, the group must contain a rotational axis of order at least 3, and in 3D the group must be cubic. In both cases, the mode must belong to a non-degenerate representation.
For an equiauxetic mode to exist in 2D or 3D, it is therefore sufficient that Γ(m) − Γ(s) should contain a positive weight of some non-degenerate mode of the correct type. What is the “correct” type? The possible representations of auxetic modes in 2D have been listed [19]: they are those of A type in groups with six-fold, four-fold or three-fold rotational axes, or of B type in groups with a six-fold axis. (Representations of type A and B have character +1 and −1, respectively, under the generator rotation for the principal axis.) In 3D they are those of A type in the cubic groups.
The hinged-hexagon frameworks that are the subject of the present paper belong to plane group p6, which has a factor group isomorphic to
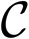
4. Two-Dimensional Hinged-Hexagon Frameworks
The single-link version of the hinged-hexagon framework is shown in Figure 1a, and the contact polyhedron C1 for this framework is given in Figure 1b. The bodies associated with the vertices of C1 are rigid hexagons. The pin-jointed bars, are associated with the edges of C1 and connect adjacent hexagons to give a locally chiral 6-fold symmetry. The plane group of this 2D structure is therefore p6, and the relevant point group is
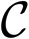
A suitable unit cell is the rhombus shown in Figure 1d with 6-fold rotational axes at the corners, additional 3-fold axes inside the cell, and 2-fold rotational axes at the cell centre and the centres of the sides. We explore periodic behaviour of the infinite framework by varying k, the number of copies of the smallest unit cell along each side of a larger unit cell that retains the rhomboidal shape. In the present case, n is also equal to the number of hexagons per side of the enlarged cell. The dashed lines in Figure 1c illustrate the choices k × k = 1 × 1, 2 × 2, 3 × 3 and 4 × 4. For all k, there is one hexagon on the unique 6-fold rotational axis. For odd k one bar lies on each of the three distinct 2-fold axis within the unit cell, whereas for even k no bar lies on any 2-fold axis.
A word about the method of calculation of the characters χ(S) for periodic systems may be in order. In finite frameworks, as noted earlier, the character χobject(S) for a set of scalars or objects without directional behaviour is simply found by counting the number of objects in the set that are unshifted by operation S. In the case of a periodic framework, the procedure for calculating the character in the factor group is essentially the same, except that objects are counted either if unshifted within the unit cell, or if moved outside the unit cell but to a position where they can be shifted back to the original position by a lattice translation. Boundary conditions are taken into account by attributing fractional weights to objects on the edges and corners of the unit cell, or by considering distinct set members only. Where necessary, resolution of the transformed object is taken into account. Translations and rotations may be taken as centred in the unit cell and their character can be taken from the standard tables [29].
4.1. Single-Link Framework
The calculation of the net mobility Γ(m) − Γ(s) for the single-link hexagonal framework (shown in Figure 1a) is set out below in the usual tabular form [5]:
Group
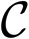 6 6 | E | C6 | C3 | ||||
| Γ(υ, C) × (ΓT + ΓR) | k2 | 1 | 1 | 1 | 4 | 1 | 1 |
| 3 | 2 | 0 | −1 | −1 | 0 | 2 | |
| −Γ(e, C) + (ΓT × ΓT) − ΓT − ΓR | 3k2 | 2 | 0 | −1 | −4 | 0 | 2 |
| −3k2 | 0 | 0 | −3 | 0 | 0 | 0 | |
| 1 | −1 | 1 | 5 | 5 | 1 | −1 | |
| = Γ(m) − Γ(s) | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Experimentation with physical models of finite portions of the single-link hexagon framework give an impression of floppiness, suggesting that there may be extra flexibility to be identified, but the periodic analysis indicates that these are likely to be boundary effects not present in the infinite framework.
4.2. Double-Link Framework
For the double-link hexagonal framework (shown in Figure 1c), the corresponding calculation is:
Group
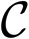 6 6 | E | C6 | C3 | ||||
| Γ(υ, C) × (ΓT + ΓR) | k2 | 1 | 1 | 1 | 4 | 1 | 1 |
| 3 | 2 | 0 | −1 | −1 | 0 | 2 | |
| −Γ(e, C) + (ΓT × ΓT) − ΓT − ΓR | 3k2 | 2 | 0 | −1 | −4 | 0 | 2 |
| −6k2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | −1 | 1 | 5 | 5 | 1 | −1 | |
| = Γ(m) − Γ(s) | 1 − 3k2 | 1 | 1 | 4 | 1 | 1 | 1 |
With k = 1, these equations give Γ(m) − Γ(s) = 2A + E2 − (A + B + E1 + E2) = A − B − E1, as before. The case k = 1 is a special one, as Equation (13) predicts a totally symmetric equiauxetic mechanism, and the argument used for the single-link framework again applies: equivalence of all bars implies that the mechanism is not blocked and hence finite for general displacements of the framework along the path. However, reasoning based on symmetry alone is not helpful for k > 1, since, from Equation (13) all irreducible representations of
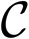
5. Frameworks based on Other Regular Tessellations
For completeness, we briefly consider the linked frameworks that can be based on the other regular tessellations of the plane, by equilateral triangles and by squares. Simple counting shows that a single-link framework based on either of these tessellations will be highly under-constrained. However, the double-link cases are potentially more interesting. In the case of the double-link triangular framework, each body has six constraining bars, with each bar joined to one neighbour, and hence this framework will be locally isostatic [35]. The double-link square framework, with eight shared bars per body, is clearly over-constrained.
5.1. Double-Link Framework based on the Triangular Tessellation
The arrangement of bodies and bars in this framework and the corresponding contact polyhedron and unit cell are shown in Figure 2. The plane group is p6 and the point group is
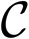
Group
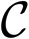 6 6 | E | C6 | C3 | C2 | |||
| Γ(υ, C) × (ΓT + ΓR) | 2k2 | 0 | 2 | 0 | 2 | 0 | |
| 3 | 2 | 0 | −1 | 0 | 2 | ||
| −Γ(e, C) + (ΓT × ΓT) − ΓT − ΓR | 6k2 | 0 | 0 | 0 | 0 | 0 | |
| −6k2 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | −1 | 1 | 5 | 1 | −1 | ||
| = Γ(m) − Γ(s) | 1 | −1 | 1 | 5 | 1 | −1 | |
An interesting feature of the calculation for this framework is that Γ(m) − Γ(s) evaluates to exactly (ΓT × ΓT) − Γt − Γr, the representation of the affine deformations of the unit cell denoted by Γa in previous work [19]. This results from the exact cancellation of body freedoms and bar constraints, which is an instance of the symmetry extension of the notion of local isostaticity introduced in [18]. We note that the present body-bar example is locally symmetry-isostatic for all k, as is the bar-and-joint distorted kagome lattice of space group p31m [18].
Specifically, the calculation shows here that, for all k, Γ(m) − Γ(s) = A + E2 − E1, indicating a constant set of three mechanisms consisting of an isotropic expansion mode and a pair of shear deformations, which is perhaps best understood as a set of independent dilations across three lines at 120° to each other, and a pair of states of self-stress. It is straightforward to find the forms of the E1 pair of states of self-stress from the fact that they transform under the operations of the group in the same way as the pair of translations {Tx, Ty} in the plane. For each state of self-stress in this {x, y}-like pair, the bars in each double-link pair are under equal and opposite tension and compression.
For this framework, isotropic expansion is possible, but is not the only allowed affine deformation, and therefore a general motion of the framework will mix isotropic expansion and shear deformation.
5.2. Double-Link Framework based on the Square Tessellation
The arrangement of bodies and bars in this framework and the corresponding contact polyhedron and unit cell are shown in Figure 3. The plane group is p4 and the point group is
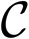
Group
 4 4 | E | ||||||
| Γ(υ, C) × (ΓT + ΓR) | k2 | 1 | 2 | 1 | 4 | 1 | 2 |
| 3 | 1 | 1 | −1 | −1 | 1 | 1 | |
| −Γ(e, C) + (ΓT × ΓT) − ΓT − ΓR | 3k2 | 1 | 2 | −1 | −4 | 1 | 2 |
| −4k2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | −1 | −1 | 5 | 5 | −1 | −1 | |
| = Γ (m) − Γ(s) | 1 − k2 | 0 | 1 | 4 | 1 | 0 | 1 |
The mobility for general k is therefore:
As with the triangular framework, isotropic expansion here is not the only allowed affine deformation of the double-link square tessellation.
6. Conclusions
Auxetic materials and substances have a huge variety of actual and proposed applications, from shock absorbers and self-cleaning filters to tunable photonics and strain amplifiers on the molecular scale (to take just the selection of proposals cited in the introduction of one recent paper [36]).
Analysis of some examples of hinged frameworks using periodic symmetry reveal the essential equiauxetic mechanism shared by these systems. We note that a comprehensive catalogue of 2D periodic frameworks considered as candidates for auxetic behaviour has been compiled [37]. (See also [36].) Some of these can be considered as periodic arrays of rigid plates, variously hinged: Star Tilings A, B and C in the catalogue correspond to single-hinge versions of the triangular, square and hexagonal tessellations of the plane, respectively.
In periodic structures found in Nature, the system can often be considered to be free from boundary effects, in that the number of unit cells is of the order of Avogadro's Number which for practical purposes is effectively infinite, and the system is considered to obey strict 2D or 3D toroidal boundary conditions. Engineered structures consist of much numbers of units that are smaller by many orders of magnitude, and edge/perimeter/boundary effects may be significant, especially in small physical models as we noted above for single-link hexagon frameworks. Analysis using ideal periodic symmetry gives a criterion for identifying what is a bulk property and what a boundary effect in these cases.
Finally, we note that, although we have taken an “analytical” approach here, using essentially only pencil-and-paper calculations and human reasoning about the interplay in the counting between stresses and mechanisms, it is clear that there is scope for building automated algorithms that incorporate finite and periodic point-group symmetry to reach these conclusions.
Acknowledgments
P.W. Fowler acknowledges support from the Royal Society/Leverhulme Trust in the form of a Senior Research Fellowship for 2013. T. Tarnai is grateful for financial support under OKTA grant K81146.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maxwell, J.C. On the calculation of the equilibrium and stiffness of frames. Philos. Mag. 1864, 27, 294–299. [Google Scholar]
- Calladine, C.R. Buckminster Fuller's “Tensegrity” structures and Clerk Maxwell's rules for the construction of stiff frames. Int. J. Solids Struct. 1978, 14, 161–172. [Google Scholar]
- Grübler, M. Getriebelehre; Springer: Berlin, Germany, 1917. [Google Scholar]
- Kutzbach, K. Mechanische Leitungsverzweigung, ihre Gesetze und Anwendungen. Maschinenbau Betr. 1929, 8, 710–716, in German. [Google Scholar]
- Fowler, P.W.; Guest, S.D. A symmetry extension of Maxwell's rule for rigidity of frames. Int. J. Solids Struct. 2000, 37, 1793–1804. [Google Scholar]
- Guest, S.D.; Fowler, P.W. A symmetry-extended mobility rule. Mech. Mach. Theory 2005, 40, 1002–1014. [Google Scholar]
- Guest, S.D.; Schulze, B.; Whiteley, W.J. When is a body-bar structure isostatic? Int. J. Solids Struct. 2010, 47, 2745–2754. [Google Scholar]
- Fowler, P.W.; Guest, S.D. A symmetry analysis of mechanisms in rotating rings of tetrahedra. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 1829–1846. [Google Scholar]
- Guest, S.D.; Fowler, P.W. Mobility of ‘N-loops’: Bodies cyclically connected by intersecting revolute hinges. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 63–77. [Google Scholar]
- Fowler, P.W.; Guest, S.D. Symmetry and states of self-stress in triangulated toroidal frames. Int. J. Solids Struct. 2002, 39, 4385–4393. [Google Scholar]
- Chen, Y.; Guest, S.D.; Fowler, P.W. Two-Orbit Switch-Pitch Structures. J. IASS 2012, 53, 157–162. [Google Scholar]
- Kovács, F.; Tarnai, T.; Fowler, P.W.; Guest, S.D. A class of expandable polyhedral structures. Int. J. Solids Struct. 2004, 41, 1119–1137. [Google Scholar]
- Kovács, F.; Tarnai, T.; Guest, S.D.; Fowler, P.W. Double-link expandohedra: A mechanical model for expansion of a virus. Proc. R. Soc. A Math. Phys. Eng. Sci. 2004, 460, 3191–3202. [Google Scholar]
- Connelly, R.; Fowler, P.W.; Guest, S.D.; Schulze, B.; Whiteley, W.J. When is a symmetric pin-jointed framework isostatic? Int. J. Solids Struct. 2009, 46, 762–773. [Google Scholar]
- Schulze, B.; Sljoka, A.; Whiteley, W. How does symmetry impact the flexibility of proteins? Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef]
- Power, S.C. Polynomials for crystal frameworks and the rigid unit mode spectrum. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef]
- Borcea, C.S.; Streinu, I. Frameworks with crystallographic symmetry. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef]
- Guest, S.D.; Fowler, P.W. Symmetry-extended counting rules for periodic frameworks. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef]
- Mitschke, H.; Schröder-Turk, G.E.; Mecke, K.; Fowler, P.W.; Guest, S.D. Symmetry detection of auxetic behaviour in 2D frameworks. Europhys. Lett. 2013, 102. [Google Scholar] [CrossRef]
- Kollár, L. Continuum method of analysis for double layer space trusses of “hexagonal over triangular mesh”. Acta Tech. Acad. Sci. Hung. 1978, 86, 55–77. [Google Scholar]
- Kollár, L.; Hegedűs, I. Analysis and Design of Space Frames by the Continuum Method; Akadémiai Kiadó: Budapest, Hungary, 1985. [Google Scholar]
- Tarnai, T. Folded Structures; Hungarian Academy of Sciences: Budapest, Hungary, 1999; in Hungarian. [Google Scholar]
- Tarnai, T. Folded Structures. Symmetry Art Sci. 2002, 2, 147–159. [Google Scholar]
- Caddock, B.D.; Evans, K.E. Microporous materials with negative Poisson's ratio. I. Microstructure and mechanical properties. J. Phys. D Appl. Phys. 1989, 22, 1877–1887. [Google Scholar]
- Speir, J.A.; Munshi, S.; Wang, G.; Baker, T.S.; Johnson, J.E. Structures of the native and swollen forms of cowpea chlorotic mottle virus determined by X-ray crystallography and cryo-electron microscopy. Structure 1995, 3, 63–78. [Google Scholar]
- Pellegrino, S.; Calladine, C.R. Matrix analysis of statically and kinematically indeterminate frameworks. Int. J. Solids Struct. 1986, 22, 409–428. [Google Scholar]
- Guest, S.D. The stiffness of prestressed frameworks: A unifying approach. Int. J. Solids Struct. 2006, 43, 842–854. [Google Scholar]
- Bishop, D.M. Group Theory and Chemistry; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Atkins, P.W.; Child, M.S.; Phillips, C.S.G. Tables for Group Theory; Oxford University Press: Oxford, UK, 1970. [Google Scholar]
- Dove, M.T. Introduction to Lattice Dynamics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Guest, S.D.; Hutchinson, J.W. On the determinacy of repetitive structures. J. Mech. Phys. Solids 2003, 51, 383–391. [Google Scholar]
- Burns, G.; Glazer, A.M. Space Groups for Solid State Scientists; Academic Press: New York, NY, USA, 1990. [Google Scholar]
- Tay, T.-S. Rigidity of multi-graphs. I. Linking rigid bodies in n-space. J. Comb. Theory Ser. B 1984, 36, 95–112. [Google Scholar]
- Guest, S.D.; Fowler, P.W. Symmetry conditions and finite mechanisms. J. Mech. Mater. Struct. 2007, 2, 293–301. [Google Scholar]
- Kapko, V.; Treacy, M.M.J.; Thorpe, M.F.; Guest, S.D. On the collapse of locally isostatic networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 3517–3530. [Google Scholar]
- Mitschke, H.; Robins, V.; Mecke, K.; Schröder-Turk, G.E. Finite auxetic deformations of plane tessellations. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469. [Google Scholar] [CrossRef]
- Mitschke, H. Deformations of Skeletal Structures. Master's Thesis; Universität Erlangen-Nürnberg: Erlangen, Germany, 17 August 2009. Available online: http://theorie1.physik.fau.de/research/theses/2009-dipl-hmitschke.html accessed on 13 May 2014). [Google Scholar]
 6, with one 6-fold axis, two additional 3-fold axes and three additional 2-fold axes (at cell centre and centres of left/right and top/bottom edges).
6, with one 6-fold axis, two additional 3-fold axes and three additional 2-fold axes (at cell centre and centres of left/right and top/bottom edges).
 6, with one 6-fold axis, two additional 3-fold axes and three additional 2-fold axes (at cell centre and centres of left/right and top/bottom edges).
6, with one 6-fold axis, two additional 3-fold axes and three additional 2-fold axes (at cell centre and centres of left/right and top/bottom edges).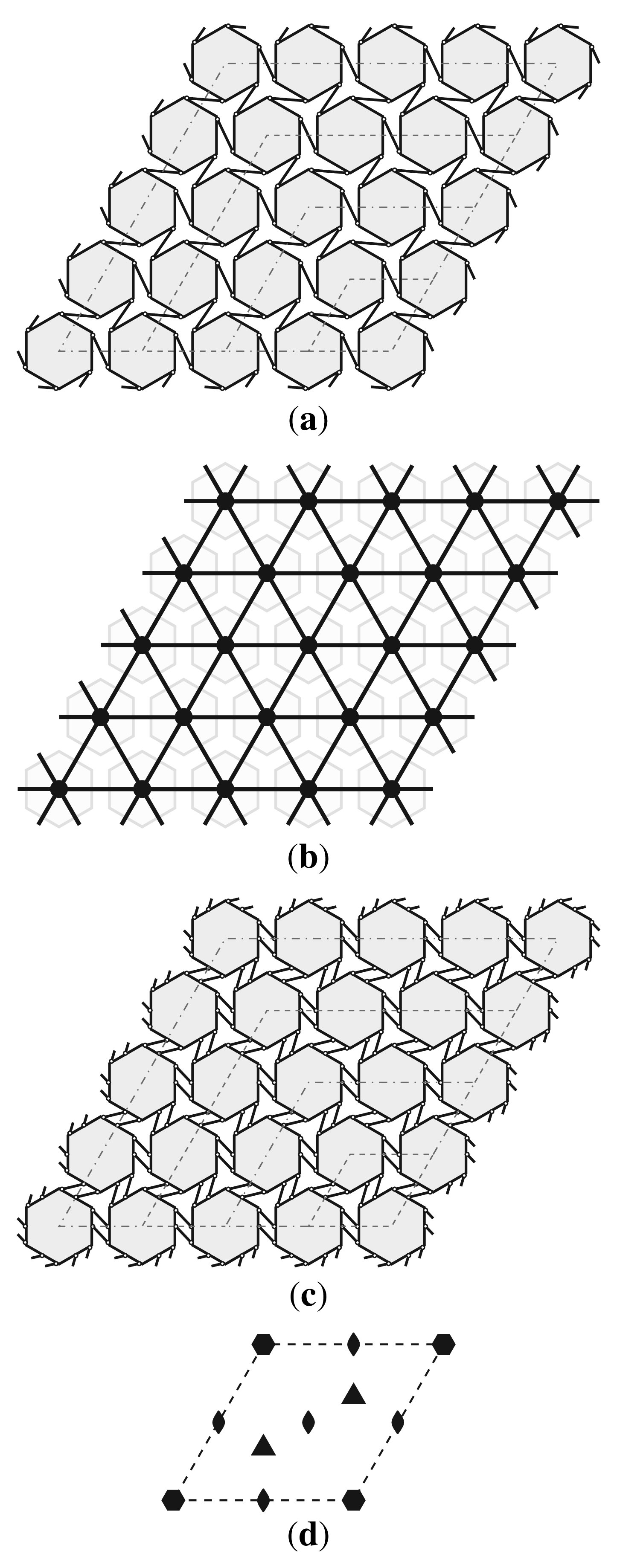
 6, with one 6-fold axis, two additional 3-fold axes and three additional 2-fold axes (at cell centre and centres of left/right and top/bottom edges).
6, with one 6-fold axis, two additional 3-fold axes and three additional 2-fold axes (at cell centre and centres of left/right and top/bottom edges).
 6, with one 6-fold axis, two additional 3-fold axes and three additional 2-fold axes (at cell centre and centres of left/right and top/bottom edges).
6, with one 6-fold axis, two additional 3-fold axes and three additional 2-fold axes (at cell centre and centres of left/right and top/bottom edges).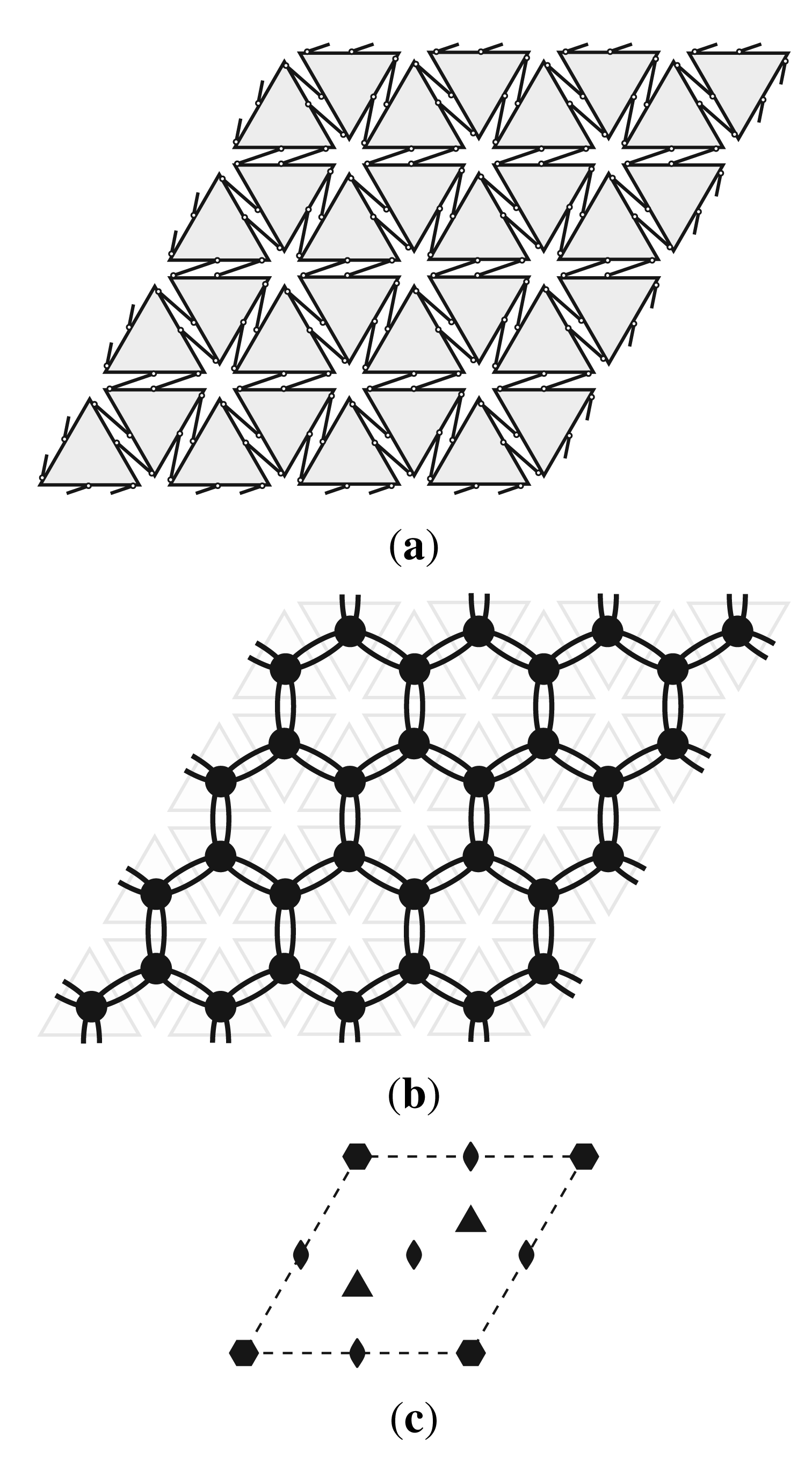
 4, with two 4-fold axes (at cell centre and corners) and two additional 2-fold axes (at centres of left/right and top/bottom edges).
4, with two 4-fold axes (at cell centre and corners) and two additional 2-fold axes (at centres of left/right and top/bottom edges).
 4, with two 4-fold axes (at cell centre and corners) and two additional 2-fold axes (at centres of left/right and top/bottom edges).
4, with two 4-fold axes (at cell centre and corners) and two additional 2-fold axes (at centres of left/right and top/bottom edges).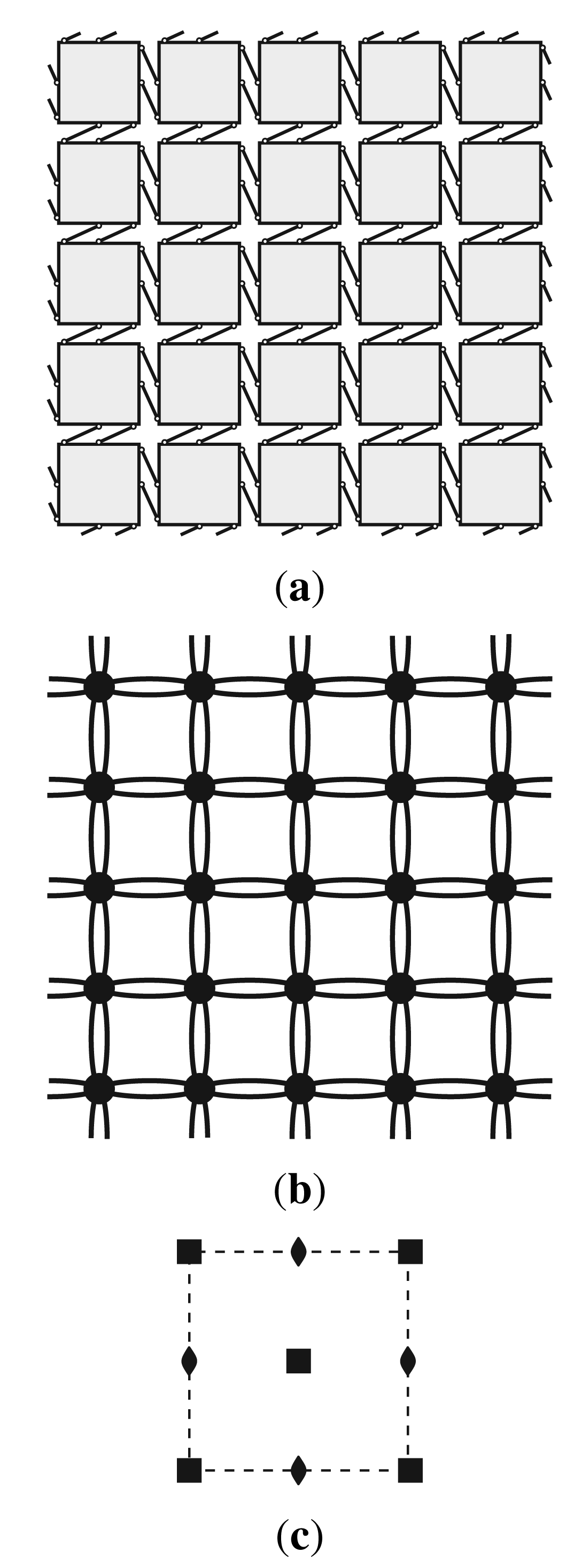
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fowler, P.W.; Guest, S.D.; Tarnai, T. Symmetry Perspectives on Some Auxetic Body-Bar Frameworks. Symmetry 2014, 6, 368-382. https://doi.org/10.3390/sym6020368
Fowler PW, Guest SD, Tarnai T. Symmetry Perspectives on Some Auxetic Body-Bar Frameworks. Symmetry. 2014; 6(2):368-382. https://doi.org/10.3390/sym6020368
Chicago/Turabian StyleFowler, Patrick W., Simon D. Guest, and Tibor Tarnai. 2014. "Symmetry Perspectives on Some Auxetic Body-Bar Frameworks" Symmetry 6, no. 2: 368-382. https://doi.org/10.3390/sym6020368



