Quantum Local Symmetry of the D-Dimensional Non-Linear Sigma Model: A Functional Approach
Abstract
: We summarize recent progress on the symmetric subtraction of the Non-Linear Sigma Model in D dimensions, based on the validity of a certain Local Functional Equation (LFE) encoding the invariance of the SU(2) Haar measure under local left transformations. The deformation of the classical non-linearly realized symmetry at the quantum level is analyzed by cohomological tools. It is shown that all the divergences of the one-particle irreducible (1-PI) amplitudes (both on-shell and off-shell) can be classified according to the solutions of the LFE. Applications to the non-linearly realized Yang-Mills theory and to the electroweak theory, which is directly relevant to the model-independent analysis of LHC data, are briefly addressed.1. Introduction
The purpose of this paper is to provide an introduction to the recent advances in the study of the renormalization properties of the SU(2) Non-Linear Sigma Model (NLSM) and of the quantum deformation of the underlying non-linearly realized classical SU(2) local symmetry. The results reviewed here are based mainly on References [1–19].
The linear sigma model was originally proposed a long time ago in [20] in the context of elementary particle physics. In this model the pseudoscalar pion fields φ⃗ form a chiral multiplet together with a scalar field σ, with (σ, φ⃗) transforming linearly as a vector under O(4) ∼ SU(2) × SU(2)/Z2. If one considers instead the model on the manifold defined by
The first step in this direction was to obtain a phenomenological lagrangian directly, by making use of a pion field with non-linear transformation properties dictated by chiral symmetry from the beginning. After the seminal work of Reference [21] for the chiral SU(2) × SU(2) group, non-linearly realized symmetries were soon generalized to arbitrary groups in [22,23] and have since then become a very popular tool [24].
Modern applications involve, e.g., Chiral Perturbation Theory [25–28], low energy electroweak theories [29] as well as gravity [30].
Effective field theories usually exhibit an infinite number of interaction terms, that can be organized according to the increasing number of derivatives. By dimensional arguments, the interaction terms must then be suppressed by some large mass scale M (so that one expects that the theory is reliable at energies well below M) (For a modern introduction to the problem, see e.g., [31]). In the spirit of the phenomenological lagrangians, the tree-level effective action is used to compute physical quantities up to a given order in the momentum expansion. Only a finite number of derivative interaction vertices contribute to that order, thus allowing to express the physical observables one is interested in through a finite number of parameters (to be eventually fixed by comparison with experimental data). Then the theory can be used to make predictions at the given order of accuracy in the low-energy expansion.
The problem of the mathematically consistent evaluation of quantum corrections in this class of models has a very long history. On general grounds, the derivative couplings tend to worsen the ultraviolet (UV) behavior of the theory, since UV divergent contributions arise in the Feynman amplitudes that cannot be compensated by a multiplicative renormalization of the fields and a redefinition of the mass parameters and the coupling constants in the classical action (truncated at some given order in the momentum expansion). Under these circumstances, one says that the theory is non-renormalizable (A compact introduction to renormalization theory is given in [32]).
It should be stressed that the key point here is the instability of the classical action: no matter how many terms are kept in the derivative expansion of the tree-level action, there exists a sufficiently high loop order where UV divergences appear that cannot be reabsorbed into the classical action. On the other hand, if in a non-anomalous and non-renormalizable gauge theory one allows for infinitely many terms in the classical action (all those compatible with the symmetries of the theory), then UV divergences can indeed be reabsorbed by preserving the Batalin-Vilkovisky master equation [33] and the model is said to be renormalizable in the modern sense [34].
Sometimes symmetries are so powerful in constraining the UV divergences that the non-linear theory proves to be indeed renormalizable (although not by power-counting), like for instance the NLSM in two dimensions [35,36] (For a more recent introduction to the subject, see e.g., [37]).
In four dimensions the situation is much less favorable. It has been found many years ago that already at one loop level in the four-dimensional NLSM there exists an infinite number of one-particle irreducible (1-PI) divergent pion amplitudes. Many attempts were then made in the literature in order to classify such divergent terms. Global SU(2) chiral symmetry is not preserved already at one loop level [38–40]. Moreover it turns out that some of the non-symmetric terms can be reabsorbed by a redefinition of the fields [40–43], however in the off-shell four-point ϕa amplitudes some divergent parts arise that cannot be reabsorbed by field redefinitions unless derivatives are allowed [40]. These technical difficulties prevented such attempts to evolve into a mathematically consistent subtraction procedure.
More recently it has been pointed out [1] that one can get the full control on the ultraviolet divergences of the ϕ′s-amplitudes by exploiting the constraints stemming from the presence of a certain local symmetry, associated with the introduction of a SU(2) background field connection into the theory. This symmetry in encoded in functional form in the so-called Local Functional Equation (LFE) [1]. It turns out that the fundamental divergent amplitudes are not those associated with the quantum fields of the theory, namely the pions, but those corresponding to the background connection and to the composite operator implementing the non-linear constraint [1,2]. These amplitudes are named ancestor amplitudes.
At every order in the loop expansion there is only a finite number of divergent ancestor amplitudes. They uniquely fix the divergent amplitudes involving the pions. Moreover, non-renormalizability of this theory in four dimensions can be traced back to the instability of the classical non-linear local symmetry, that gets deformed by quantum corrections. These results hold for the full off-shell amplitudes [3].
A comment is in order here. In Reference [4] it has been argued that Minimal Subtraction is a symmetric scheme, fulfilling all the symmetries of the NLSM in the LFE approach. This in particular entails that all finite parts of the needed higher order counterterms are consistently set to zero. It should be stressed that this is not the most general solution compatible with the symmetries and the WPC, that is commonly used in the spirit of the most popular effective field theory point of view. Indeed, these finite parts are constrained neither by the LFE nor by the WPC and thus, mathematically, they can be freely chosen, as far as they are introduced at the order prescribed by the WPC and without violating the LFE.
The four dimensional SU(2) NLSM provides a relatively simple playground where to test the approach based on the LFE, that can be further generalized to the SU(N) case (and possibly even to a more general Lie group).
Moreover, when the background vector field becomes dynamical, the SU(2) NLSM action allows one to generate a mass term for the gauge field à la Stückelberg [44,45]. The resulting non-linear implementation of the spontaneous symmetry breaking mechanism (as opposed to the linear Higgs mechanism) is widely used in the context of electroweak low energy effective field theories, that are a very important tool in the model-independent analysis of LHC data [46–49].
2. The Classical Non-Linear Sigma Model
The classical SU(2) NLSM in D dimensions is defined by the action
Equation (2) is invariant under a global SU(2)L × SU(2)R chiral transformation
We notice that such a global transformation is non-linearly realized, as can be easily seen by looking at its infinitesimal version. E.g., for the left transformation one finds:
Perturbative quantization of the NLSM requires to carry out the path-integral
The presence of two derivatives in the interaction term is the cause (in dimensions greater than 2) of severe UV divergences, leading to the non-renormalizability of the theory.
3. The Approach based on the Local Functional Equation
Some years ago it was recognized that the most effective classification of the UV divergences (both for on-shell and off-shell amplitudes) of the NLSM cannot be achieved in terms of the quantized fields ϕa, as it usually happens in power-counting renormalizable theories, but rather through the so-called ancestor amplitudes, i.e., the Green's functions of certain composite operators, whose knowledge completely determines the amplitudes involving at least one ϕa-leg. This property follows as a consequence of the existence of an additional local functional identity, the so-called Local Functional Equation (LFE) [1].
The LFE stems from the local SU(2)L-symmetry that can be established from the gauge transformation of the flat connection Fμ associated with the matrix Ω:
In order to implement the classical local SU(2)L invariance at the quantum level, one needs to define the composite operator ϕ0 in Equation (4) by coupling it in the classical action to an external source k0 through the term
The important observation now is that the variation of full one-particle irreducible (1-PI) vertex functional Γ(0) = S + Sext is linear in the quantized fields ϕa, i.e.,
In the following Section we are going to give a compact and self-contained presentation of the algebraic techniques used to deal with bilinear functional equations like the LFE in Equation (18).
4. Ancestor Amplitudes and the Weak Power-Counting
We are going to discuss in this Section the consequences of the LFE for the full vertex functional. The imposition of a quantum symmetry in a non-power-counting renormalizable theory is a subtle problem, since in general there is no control on the dimensions of the possible breaking terms as strong as the one guaranteed by the Quantum Action Principle (QAP) in the renormalizable case. Let us discuss the latter case first.
4.1. Renormalizable Theories and the Quantum Action Principle
If the tree-level functional Γ(0) is power-counting renormalizable, the renormalization procedure [51] provides a way to compute all higher-order terms in the loop expansion of the full vertex functional , depending on the set of quantized fields Φ and external sources collectively denoted by χ, by fixing order by order only a finite set of action-like normalization conditions. One says that the classical action is therefore stable under radiative corrections, namely the number of free parameters does not increase with the loop order.
This procedure is a recursive one, since it allows to construct Γ(n) once Γ(j), j < n are known. From a combinatorial point of view, it turns out that Γ is the generating functional of the 1-PI renormalized Feynman amplitudes.
A desirable feature of power-counting renormalizable theories is that the dependence of 1-PI Green's functions under an infinitesimal variations of the quantized fields and of the parameters of the model is controlled by the so-called Quantum Action Principle (QAP) [52-55] and can be expressed as the insertion of certain local operators with UV dimensions determined by their tree-level approximation (i.e., a polynomial in the fields, the external sources and derivatives thereof).
Let us now consider a certain symmetry δ of the tree-level Γ(0) classical action. Under the condition that the symmetry δ is non-anomalous [56], it can be extended to the full vertex functional Γ . In many cases of physical interest the proof that the symmetry is non-anomalous can be performed by making use of cohomological tools. Namely one writes the functional equation associated with the δ-invariance of the tree-level vertex functional as follows:
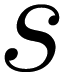 0 according to
0 according to
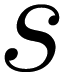 0 is also nilpotent, as a consequence of the nilpotency of δ and of the tree-level invariance in Equation (19). By exploiting this fact and by applying
0 is also nilpotent, as a consequence of the nilpotency of δ and of the tree-level invariance in Equation (19). By exploiting this fact and by applying
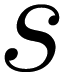 0 on both sides of Equation (20) one finds
0 on both sides of Equation (20) one finds
The problem of establishing whether the functional identity
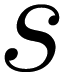 0) of the operator
0) of the operator
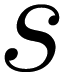 0 in the space of integrated local polynomials in the fields, the external sources and their derivatives. Two
0 in the space of integrated local polynomials in the fields, the external sources and their derivatives. Two
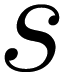 0-invariant integrated local polynomials
0-invariant integrated local polynomials
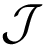 1 and
1 and
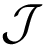 2 belong to the same cohomology class in H(
2 belong to the same cohomology class in H(
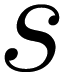 0) if and only if
0) if and only if
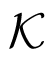 . In particular, H(
. In particular, H(
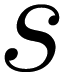 0) is empty if the only cohomology class is the one of the zero element, so that the condition that
0) is empty if the only cohomology class is the one of the zero element, so that the condition that
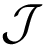 1 is
1 is
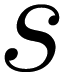 0-invariant implies that
0-invariant implies that
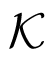 . Hence if one can prove that the cohomology of the operator
. Hence if one can prove that the cohomology of the operator
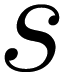 0 is empty in the space of breaking terms, then Equation (25) must be fulfilled by some choice of the functional Ξ(n). Moreover it must be checked that the UV dimensions of the possible counterterms Ξ(n) are compatible with the action-like condition, so that renormalizability of the theory is not violated. An extensive review of BRST cohomologies for gauge theories is given in [61].
0 is empty in the space of breaking terms, then Equation (25) must be fulfilled by some choice of the functional Ξ(n). Moreover it must be checked that the UV dimensions of the possible counterterms Ξ(n) are compatible with the action-like condition, so that renormalizability of the theory is not violated. An extensive review of BRST cohomologies for gauge theories is given in [61].4.2. Non-Renormalizable Theories
The QAP does not in general hold for non-renormalizable theories. This does not come as a surprise, since the appearance of UV divergences with higher and higher degree, as one goes up with the loop order, prevents to characterize the induced breaking of a functional identity in terms of a polynomial of a given finite degree (independent of the loop order).
Moreover for the NLSM another important difference must be stressed: the basic Green's functions of the theory are not those of the quantized fields ϕa, but those of the flat connection coupled to the external vector source J̃aμ and of the non-linear constraint ϕ0 (coupled to K0). This result follows from the invertibility of
Γ[J̃, K0] is the generating functional of the so called ancestor amplitudes, i.e., the 1-PI amplitudes involving only external J̃ and K0 legs.
It is therefore reasonable to assume the LFE in Equation (28) as the starting point for the quantization of the theory.
From a path-integral point of view, Equation (28) implies that one is performing an integration over the SU(2)-invariant Haar measure of the group, namely one is computing
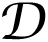 Ω(ϕ) the SU(2) Haar measure (in the coordinate representation spanned by the fields ϕa). This clarifies the geometrical meaning of the LFE.
Ω(ϕ) the SU(2) Haar measure (in the coordinate representation spanned by the fields ϕa). This clarifies the geometrical meaning of the LFE.4.3. Weak Power-Counting
As we have already noticed, in four dimensions the NLSM is non power-counting renormalizable, since already at one loop level an infinite number of divergent ϕ-amplitudes exists. One may wonder whether the UV behavior of the ancestor amplitudes (the boundary conditions to the LFE) is better. It turns out that this is indeed the case and one finds that in D dimensions a n-th loop Feynman amplitude
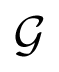
For instance, in D = 4 and at one loop order, Equation (30) reduces to
By taking into account Lorentz-invariance and global su(2)r symmetry, the list of UV divergent amplitudes reduces to
It should be emphasized that the model is not power-counting renormalizable, even when ancestor amplitudes are considered, since according to Equation (30) the number of UV divergent amplitudes increases as the loop order n grows.
A special case is the 2-dimensional NLSM. For D = 2 Equation (30) yields
A comment is in order here. In References [24,25] the external fields are the sources of connected Green's functions of certain quark-antiquark currents. The ancestor amplitudes in the NLSM, in the approach based on the LFE, do not have a direct physical interpretation of this type, however they have a very clear geometrical meaning. First of all, J̃μ is the source coupled to the flat connection naturally associated with the group element Ω. On the other hand, K0 is the unique scalar source required, in the special case of the SU(2) group, in order to control the renormalization of the non-linear classical SU(2) transformation of the ϕa's and thus plays the role of the so-called antifields [33,50]. The extension to a general Lie group G is addressed at the end of Section 5.
5. Cohomological Analysis of the LFE
In order to study the properties of the LFE, it is very convenient to introduce a fictious BRST operator s by promoting the gauge parameters αa(x) to classical anticommuting ghosts ωa(x). I.e., one sets
The introduction of the ghosts allows to define a grading w.r.t. the conserved ghost number. ω has ghost number +1, while all the other fields and sources have ghost number zero. (The ghost number was called the Faddeev-Popov (ΦΠ) charge in [2].)
In terms of the operator s we can write the n-th order projection (n ≥ 1) of the LFE in Equation (28) as follows:
Suppose now that all divergences have been recursively subtracted up to order n−1. At the n-th order the UV divergent part can only come from the term involving Γ(n) in Equation (35) and therefore, if the LFE holds, one gets a condition on the UV divergent part of Γ(n):
By the nilpotency of s, solving Equation (36) is equivalent to computing the cohomology of the BRST operator s in the space of local functionals in J̃, φ, K0 and their derivatives with ghost number zero. This can be achieved by using the techniques developed in [62].
One first builds invariant combinations in one-to-one correspondence with the ancestor variables J̃aμ and K0. For that purpose it is more convenient to switch back to matrix notation. The difference Iμ = Fμ − J̃μ transforms in the adjoint representation of SU(2), being the difference of two gauge connections. Thus the conjugate of such a difference w.r.t. Ω
One can also prove that the following combination
In terms of the new variables K̅0 and jμ and by differentiating Equation (36) w.r.t. ωa one gets
The subtraction strategy is thus the following. One computes the divergent part of the properly normalized ancestor amplitudes that are superficially divergent at a given loop order according to the WPC formula in Equation (30). Then the replacement J̃aμ→ jaμ and K0 → K̅0 is carried out. This gives the full set of counterterms required to make the theory finite at order n in the loop expansion.
As an example, we give here the explicit form of the one-loop divergent counterterms for the NLSM in D = 4 [2] (notice that we have set g = 1 according to our conventions in this paper):
The invariants in the combination 6 + 27 generate the counterterms in the first line between square brackets; these counterterms are globally SU(2) invariant. The other terms are generated by invariants involving the source K0. In [39,40] they were constructed by means of a (non-locally invertible) field redefinition of ϕa. The full set of mixed four point amplitudes involving at least one ϕa legs and the external sources J̃μ and K0 can be found in [2].
The correspondence with the linear sigma model in the large coupling limit has been studied in [5].
The massive NLSM in the LFE formulation has been studied in [15], while the symmetric subtraction procedure for the LFE associated with polar coordinates in the simplest case of the free complex scalar field has been given in [16].
In the SU(2) NLSM just one scalar source K0 is sufficient in order to formulate the LFE. For an arbitrary Lie group G the LFE can always be written if one introduces a full set of antifields , as follows. Let us denote by Ω(ϕI) the group element belonging to G, parameterized by local coordinates ϕI. Then under an infinitesimal left G-transformation of parameters αJ
6. Higher Loops
At orders n > 1 the LFE for Γ(n) is an inhomogeneous equation
For that purpose it is convenient to redefine the ghost according to
By the nilpotency of s the following consistency condition must hold for Δ(n):
The explicit dependence on ϕa only appears through lower order terms. Hence it does not influence the n-th order ancestor amplitudes.
The solution of Equation (49) can be written in compact form by using a homotopy operator. Indeed Γ(n) will be the sum of a n-th order contribution s(n), depending only on jaμ and K̅0, plus a lower order term:
An important remark is in order here. The theory remains finite and respects the LFE if one adds to Γ(n) some integrated local monomials in jaμ and k̅0 and ordinary derivatives thereof (with finite coefficients), compatible with Lorentz symmetry and global SU(2) invariance, while respecting the WPC condition in Equation (30):
This observation suggests that these finite parameters cannot be easily understood as physical free parameters of the theory, since they cannot appear in the tree-level action. It was then proposed to define the model by choosing the symmetric subtraction scheme discussed in Section 5 and by considering as physical parameters only those present in the classical action plus the scale of the radiative corrections Λ [4]. While acceptable on physical grounds, from the mathematical point of view one may wonder whether there is some deeper reason justifying such a strategy. We will comment briefly on this point in the Conclusions.
7. Applications to Yang-Mills and the Electroweak Theory
When the vector source J̃aμ becomes a dynamical gauge field, the NLSM action gives rise to the Stuckelberg mass term [67].
The subtraction procedure based on the LFE has been used to implement a mathematically consistent formulation of non-linearly realized massive Yang-Mills theory. SU(2) Yang-Mills in the LFE formalism has been formulated in [6]. The pseudo-Goldstone fields take over the role of the ϕa fields of the NLSM. Their Green's functions are fixed by the LFE. The WPC proves to be very restrictive, since by imposing the WPC condition it turns out that the only allowed classical solution is the usual Yang-Mills theory plus the Stuckelberg mass term.
This is a very powerful (and somehow surprising) result. Indeed all possible monomials constructed out of jaμ and ordinary derivatives thereof are gauge-invariant and therefore they could be used as interaction vertices in the classical action.
Otherwise said, the peculiar structure of the Yang-Mills action
The approach based on the LFE can also be used for non-perturbative studies of Yang-Mills theory on the lattice. The phase diagram of SU(2) Yang-Mills has been considered in [17]. Emerging evidence is being accumulated about the formation of isospin scalar bound states [18] in the supposedly confined phase of the theory [19].
An analytic approach based on the massless bound-state formalism for the implementation of the Schwinger mechanism in non-Abelian gauge theories has been presented in [75–77].
A very important physical application of non-linearly realized gauge theories is the formulation of a non-linearly realized electroweak theory, based on the group SU(2) × U(1). The set of gauge fields comprises the SU(2) fields Aaμ and the hypercharge U(1) gauge connection Bμ. By using the technique of bleached variables one can first construct SU(2) invariant variables in one-to-one correspondence with [8]:
The inclusion of physical scalar resonances in the non-linearly realized electroweak model, while respecting the WPC, yields some definite prediction for the Beyond the Standard Model (BSM) sector. Indeed it turns out that it is impossible to add a scalar singlet without breaking the WPC condition. The minimal solution requires a SU(2) doublet of scalars, leading to a CP-even physical field (to be identified with the recently discovered scalar resonance at 125.6 GeV) and to three additional heavier physical states, one CP-odd and neutral and two charged ones [13]. The proof of the WPC in this model and the BRST identification of physical states has been given in [14].
The WPC and the symmetries of the theory select uniquely the tree-level action of the non-linearly realized electroweak model. As in the NLSM case, mathematically additional finite counterterms are allowed at higher orders in the loop expansion. In [4] it has been argued that they cannot be interpreted as additional physical parameters (unlike in the effective field theory approach), on the basis of the observation that they are forbidden at tree-level by the WPC, and this strategy has been consistently applied in [7,11].
The question remains open of whether a Renormalization Group equation exists, involving a finite change in the higher order subtractions, in such a way to compensate the change in the sliding scale Λ of the radiative corrections. We notice that in this case the finite higher order counterterms would be a function of the tree-level parameters only (unlike in the conventional effective field theory approach, where they are treated as independent extra free parameters). This issue deserves further investigation, since obviously the possibility of running the scale Λ in a mathematically consistent way would allow to obtain physical predictions of the same observables applicable in different energy regimes.
8. Conclusions
The LFE makes it apparent that the independent amplitudes of the NLSM are not those of the quantum fields, over which the path-integral is carried out, but rather those of the background connection J̃μ and of the source k0, coupled to the solution of the non-linear constraint ϕ0. The WPC can be formulated only for these ancestor amplitudes; the LFE in turn fixes the descendant amplitudes, involving at least one pion external leg. Within this formulation, the minimal symmetric subtraction discussed in Section 5 is natural, since it provides a way to implement the idea that the number of ancestor interaction vertices, appearing in the classical action and compatible with the WPC, must be finite.
However, it should be stressed that the most general solution to the LFE, compatible with the WPC, does not forbid to choose different finite parts of the higher order symmetric counterterms (as in the most standard view of effective field theories, where such arbitrariness is associated with extra free parameters of the non-renormalizable theory), as far as they are introduced at the order prescribed by the WPC condition and without violating the LFE.
In this connection it should be noticed that the addition of the symmetric finite renormalizations in Equation (59), that are allowed by the symmetries of the theory, is equivalent to a change in the Hopf algebra [81,82] of the model. This is because the finite counterterms in Equation (59) modify the set of 1-PI Feynman diagrams on which the Hopf algebra is constructed, as a dual of the enveloping algebra of the Lie algebra of Feynman graphs. The approach to renormalization based on Hopf algebras is known to be equivalent [83] to the traditional approach based on the Bogoliubov recursive formula and its explicit solution through the Zimmermann's forest formula [84]. For models endowed with a WPC it might provide new insights into the structure of the UV divergences of the theory. This connection seems to deserve further investigations.
Acknowledgments
It is a pleasure to acknowledge many enlightening discussions with R. Ferrari. Useful comments and a careful reading of the manuscript by D. Bettinelli are also gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
Appendix
One-Loop Invariants
We report here the invariants controlling the one-loop divergences of the NLSM in D = 4 [2].
References
- Ferrari, R. Endowing the nonlinear sigma model with a flat connection structure: A way to renormalization. JHEP 2005. [Google Scholar] [CrossRef]
- Ferrari, R.; Quadri, A. A Weak power-counting theorem for the renormalization of the non-linear sigma model in four dimensions. Int. J. Theor. Phys. 2006, 45, 2497–2515. [Google Scholar]
- Bettinelli, D.; Ferrari, R.; Quadri, A. Path-integral over non-linearly realized groups and Hierarchy solutions. JHEP 2007. [Google Scholar] [CrossRef]
- Bettinelli, D.; Ferrari, R.; Quadri, A. Further Comments on the Symmetric Subtraction of the Nonlinear Sigma Model. Int. J. Mod. Phys. 2008, A23, 211–232. [Google Scholar]
- Bettinelli, D.; Ferrari, R.; Quadri, A. The Hierarchy principle and the large mass limit of the linear sigma model. Int. J. Theor. Phys. 2007, 46, 2560–2590. [Google Scholar]
- Bettinelli, D.; Ferrari, R.; Quadri, A. A Massive Yang-Mills Theory based on the Nonlinearly Realized Gauge Group. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Bettinelli, D.; Ferrari, R.; Quadri, A. One-loop self-energy and counterterms in a massive Yang-Mills theory based on the nonlinearly realized gauge group. Phys. Rev. D 2008, 7. [Google Scholar] [CrossRef]
- Bettinelli, D.; Ferrari, R.; Quadri, A. Gauge Dependence in the Nonlinearly Realized Massive SU(2) Gauge Theory. J. General. Lie Theor. Appl. 2008, 2, 122–126. [Google Scholar]
- Bettinelli, D.; Ferrari, R.; Quadri, A. The SU(2) × U(1) Electroweak Model based on the Nonlinearly Realized Gauge Group. Int. J. Mod. Phys. 2009, A24, 2639–2654. [Google Scholar]
- Bettinelli, D.; Ferrari, R.; Quadri, A. The SU(2) × U(1) Electroweak Model based on the Nonlinearly Realized Gauge Group. II. Functional Equations and the Weak Power-Counting. Acta Phys. Polon. 2010, B41, 597–628. [Google Scholar]
- Bettinelli, D.; Ferrari, R.; Quadri, A. One-loop Self-energies in the Electroweak Model with Nonlinearly Realized Gauge Group. Phys. Rev. D 2009, 79. [Google Scholar] [CrossRef]
- Quadri, A. The Algebra of Physical Observables in Nonlinearly Realized Gauge Theories. Eur. Phys. J. 2010, C70, 479–489. [Google Scholar]
- Binosi, D.; Quadri, A. Scalar Resonances in the Non-linearly Realized Electroweak Theory. JHEP 2013, 1302. [Google Scholar] [CrossRef]
- Bettinelli, D.; Quadri, A. The Stueckelberg Mechanism in the presence of Physical Scalar Resonances. Phys. Rev. D 2013, 88. [Google Scholar] [CrossRef]
- Ferrari, R. A Symmetric Approach to the Massive Nonlinear Sigma Model. J. Math. Phys. 2011, 52, 092303:1–092303:16. [Google Scholar]
- Ferrari, R. On the Renormalization of the Complex Scalar Free Field Theory. J. Math. Phys. 2010, 51, 032305:1–032305:20. [Google Scholar]
- Ferrari, R. On the Phase Diagram of Massive Yang-Mills. Acta Phys. Polon. 2012, B43, 1965–1980. [Google Scholar]
- Ferrari, R. On the Spectrum of Lattice Massive SU(2) YangMills. Acta Phys. Polon. 2013, B44, 1871–1885. [Google Scholar]
- Ferrari, R. Metamorphosis versus Decoupling in Nonabelian Gauge Theories at Very High Energies. Acta Phys. Polon. 2012, B43, 1735–1767. [Google Scholar]
- Gell-Mann, M.; Levy, M. The axial vector current in beta decay. Nuovo Cim. 1960, 16, 705–726. [Google Scholar]
- Weinberg, S. Nonlinear realizations of chiral symmetry. Phys. Rev. 1968, 166, 1568–1577. [Google Scholar]
- Coleman, S.R.; Wess, J.; Zumino, B. Structure of phenomenological Lagrangians. 1. Phys. Rev. 1969, 177, 2239–2247. [Google Scholar]
- Callan, C.G., Jr.; Coleman, S.R.; Wess, J.; Zumino, B. Structure of phenomenological Lagrangians. 2. Phys. Rev. 1969, 177, 2247–2250. [Google Scholar]
- Weinberg, S. Phenomenological Lagrangians. Physica 1979, A96, 327–340. [Google Scholar]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory to One Loop. Ann. Phys. 1984, 158, 142–210. [Google Scholar]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory: Expansions in the Mass of the Strange Quark. Nucl. Phys. B 1985, 250, 465–516. [Google Scholar]
- Bijnens, J.; Colangelo, G.; Ecker, G. Renormalization of chiral perturbation theory to order p**6. Ann. Phys. 2000, 280, 100–139. [Google Scholar]
- Ecker, G.; Gasser, J.; Leutwyler, H.; Pich, A.; de Rafael, E. Chiral Lagrangians for Massive Spin 1 Fields. Phys. Lett. B 1989, 223, 425–432. [Google Scholar]
- Buchmuller, W.; Wyler, D. Effective Lagrangian Analysis of New Interactions and Flavor Conservation. Nucl. Phys. B 1986, 268, 621–653. [Google Scholar]
- Donoghue, J.F. Introduction to the effective field theory description of gravity. Available online: http://arxiv.org/abs/grqc/9512024 (accessed on 15 April 2014).
- Weinberg, S. The Quantum Theory of Fields. Vol. 2: Modern Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Itzykson, C.; Zuber, J. Quantum Field Theory; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Gomis, J.; Paris, J.; Samuel, S. Antibracket, antifields and gauge theory quantization. Phys. Rep. 1995, 259, 1–145. [Google Scholar]
- Gomis, J.; Weinberg, S. Are nonrenormalizable gauge theories renormalizable? Nucl. Phys. B 1996, 469, 473–487. [Google Scholar]
- Brezin, E.; Zinn-Justin, J.; Le Guillou, J. Renormalization of the Nonlinear Sigma Model in (Two + Epsilon) Dimension. Phys. Rev. D 1976, 14, 2615–2621. [Google Scholar]
- Becchi, C.; Piguet, O. On the Renormalization of Two-dimensional Chiral Models. Nucl. Phys. B 1989, 315, 153–165. [Google Scholar]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Ecker, G.; Honerkamp, J. Application of invariant renormalization to the nonlinear chiral invariant pion lagrangian in the one-loop approximation. Nucl. Phys. B 1971, 35, 481–492. [Google Scholar]
- Appelquist, T.; Bernard, C.W. The Nonlinear σ Model in the Loop Expansion. Phys. Rev. D 1981, 23. [Google Scholar] [CrossRef]
- Tataru, L. One Loop Divergences of the Nonlinear Chiral Theory. Phys. Rev. D 1975, 12, 3351–3352. [Google Scholar]
- Gerstein, I.; Jackiw, R.; Weinberg, S.; Lee, B. Chiral loops. Phys. Rev. D 1971, 3, 2486–2492. [Google Scholar]
- Charap, J. Closed-loop calculations using a chiral-invariant lagrangian. Phys. Rev. D 1970, 2, 1554–1561. [Google Scholar]
- Honerkamp, J.; Meetz, K. Chiral-invariant perturbation theory. Phys. Rev. D 1971, 3, 1996–1998. [Google Scholar]
- Stueckelberg, E. Interaction forces in electrodynamics and in the field theory of nuclear forces. Helv. Phys. Acta 1938, 11, 299–328. [Google Scholar]
- Ruegg, H.; Ruiz-Altaba, M. The Stueckelberg field. Int. J. Mod. Phys. 2004, A19, 3265–3348. [Google Scholar]
- Altarelli, G.; Mangano, M.L. Electroweak Physics. Proceedings of CERN Workshop on Standard Model Physics (and More) at the LHC, CERN, Geneva, Switzerland, 25–26 May 1999.
- Azatov, A.; Contino, R.; Galloway, J. Model-Independent Bounds on a Light Higgs. JHEP 2012, 1204. [Google Scholar] [CrossRef]
- Contino, R. The Higgs as a Composite Nambu-Goldstone Boson. Available online: http://arxiv.org/abs/1005.4269 (accessed on 15 April 2014).
- Espinosa, J.; Grojean, C.; Muhlleitner, M.; Trott, M. First Glimpses at Higgs' face. JHEP 2012, 1212. [Google Scholar] [CrossRef]
- Zinn-Justin, J. Renormalization of Gauge Theories—Unbroken and broken. Phys. Rev. D 1974, 9, 933–946. [Google Scholar]
- Velo, G.; Wightman, A. Renormalization Theory. Proceedings of the NATO Advanced Study Institute, Erice, Sicily, Italy, 17–31 August 1975.
- Breitenlohner, P.; Maison, D. Dimensional Renormalization and the Action Principle. Commun. Math. Phys. 1977, 52, 11–38. [Google Scholar]
- Lam, Y.M.P. Perturbation Lagrangian theory for scalar fields: Ward-Takahasi identity and current algebra. Phys. Rev. D 1972, 6, 2145–2161. [Google Scholar]
- Lam, Y.M.P. Perturbation lagrangian theory for Dirac fields—Ward-Takahashi identity and current algebra. Phys. Rev. D 1972, 6, 2161–2167. [Google Scholar]
- Lowenstein, J. Normal product quantization of currents in Lagrangian field theory. Phys. Rev. D 1971, 4, 2281–2290. [Google Scholar]
- Piguet, O.; Sorella, S. Algebraic renormalization: Perturbative renormalization, symmetries and anomalies. Lect. Notes Phys. 1995, M28, 1–134. [Google Scholar]
- Becchi, C.; Rouet, A.; Stora, R. Renormalization of Gauge Theories. Ann. Phys. 1976, 98, 287–321. [Google Scholar]
- Becchi, C.; Rouet, A.; Stora, R. Renormalization of the Abelian Higgs-Kibble Model. Commun. Math. Phys. 1975, 42, 127–162. [Google Scholar]
- Becchi, C.; Rouet, A.; Stora, R. The Abelian Higgs-Kibble Model. Unitarity of the S Operator. Phys. Lett. B 1974, 52, 344–346. [Google Scholar]
- Wess, J.; Zumino, B. Consequences of anomalous Ward identities. Phys. Lett. B 1971, 37, 95–97. [Google Scholar]
- Barnich, G.; Brandt, F.; Henneaux, M. Local BRST cohomology in gauge theories. Phys. Rep. 2000, 338, 439–569. [Google Scholar]
- Henneaux, M.; Wilch, A. Local BRST cohomology of the gauged principal nonlinear sigma model. Phys. Rev. D 1998, 58, 025017:1–025017:14. [Google Scholar]
- Quadri, A. Slavnov-Taylor parameterization of Yang-Mills theory with massive fermions in the presence of singlet axial-vector currents. JHEP 2005, 0506. [Google Scholar] [CrossRef]
- Quadri, A. Higher order nonsymmetric counterterms in pure Yang-Mills theory. J. Phys. G 2004, 30, 677–689. [Google Scholar]
- Quadri, A. Slavnov-Taylor parameterization for the quantum restoration of BRST symmetries in anomaly free gauge theories. JHEP 2003, 0304. [Google Scholar] [CrossRef]
- Quadri, A. Algebraic properties of BRST coupled doublets. JHEP 2002, 0205. [Google Scholar] [CrossRef]
- Ferrari, R.; Quadri, A. Physical unitarity for massive non-Abelian gauge theories in the Landau gauge: Stueckelberg and Higgs. JHEP 2004, 0411. [Google Scholar] [CrossRef]
- Froissart, M. Asymptotic behavior and subtractions in the Mandelstam representation. Phys. Rev. 1961, 123, 1053–1057. [Google Scholar]
- Cornwall, J.M.; Levin, D.N.; Tiktopoulos, G. Derivation of Gauge Invariance from High-Energy Unitarity Bounds on the s Matrix. Phys. Rev. D 1974, 10, 1145–1167. [Google Scholar]
- Lee, B.W.; Quigg, C.; Thacker, H. Weak Interactions at Very High-Energies: The Role of the Higgs Boson Mass. Phys. Rev. D 1977, 16, 1519–1531. [Google Scholar]
- Weldon, H.A. The Effects of Multiple Higgs Bosons on Tree Unitarity. Phys. Rev. D 1984, 30, 1547–1558. [Google Scholar]
- Chanowitz, M.S.; Gaillard, M.K. The TeV Physics of Strongly Interacting W's and Z's. Nucl. Phys. B 1985, 261, 379–431. [Google Scholar]
- Gounaris, G.; Kogerler, R.; Neufeld, H. Relationship Between Longitudinally Polarized Vector Bosons and their Unphysical Scalar Partners. Phys. Rev. D 1986, 34, 3257–3259. [Google Scholar]
- Bettinelli, D.; Ferrari, R.; Quadri, A. Of Higgs, Unitarity and other Questions. Proc. Steklov Inst. Math. 2011, 272, 22–38. [Google Scholar]
- Aguilar, A.; Ibanez, D.; Mathieu, V.; Papavassiliou, J. Massless bound-state excitations and the Schwinger mechanism in QCD. Phys. Rev. D 2012, 85. [Google Scholar] [CrossRef]
- Aguilar, A.; Binosi, D.; Papavassiliou, J. The dynamical equation of the effective gluon mass. Phys. Rev. D 2011, 84. [Google Scholar] [CrossRef]
- Ibaez, D.; Papavassiliou, J. Gluon mass generation in the massless bound-state formalism. Phys. Rev. D 2013, 87. [Google Scholar] [CrossRef]
- Broken symmetries, massless particles and gauge fields. Phys. Lett. 1964, 12, 132–133.
- Broken Symmetries and the Masses of Gauge Bosons. Phys. Rev. Lett. 1964, 13, 508–509.
- Englert, F.; Brout, R. Broken Symmetry and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 1964, 13, 321–323. [Google Scholar]
- Connes, A.; Kreimer, D. Renormalization in quantum field theory and the Riemann-Hilbert problem. 1. The Hopf algebra structure of graphs and the main theorem. Commun. Math. Phys. 2000, 210, 249–273. [Google Scholar]
- Connes, A.; Kreimer, D. Renormalization in quantum field theory and the Riemann-Hilbert problem. 2. The beta function, diffeomorphisms and the renormalization group. Commun. Math. Phys. 2001, 216, 215–241. [Google Scholar]
- Ebrahimi-Fard, K.; Patras, F. Exponential renormalization. Ann. Henri Poincare 2010, 11, 943–971. [Google Scholar]
- Zimmermann, W. Convergence of Bogolyubov's method of renormalization in momentum space. Commun. Math. Phys. 1969, 15, 208–234. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Quadri, A. Quantum Local Symmetry of the D-Dimensional Non-Linear Sigma Model: A Functional Approach. Symmetry 2014, 6, 234-255. https://doi.org/10.3390/sym6020234
Quadri A. Quantum Local Symmetry of the D-Dimensional Non-Linear Sigma Model: A Functional Approach. Symmetry. 2014; 6(2):234-255. https://doi.org/10.3390/sym6020234
Chicago/Turabian StyleQuadri, Andrea. 2014. "Quantum Local Symmetry of the D-Dimensional Non-Linear Sigma Model: A Functional Approach" Symmetry 6, no. 2: 234-255. https://doi.org/10.3390/sym6020234
APA StyleQuadri, A. (2014). Quantum Local Symmetry of the D-Dimensional Non-Linear Sigma Model: A Functional Approach. Symmetry, 6(2), 234-255. https://doi.org/10.3390/sym6020234



