Topological Symmetry Groups of Small Complete Graphs
Abstract
: Topological symmetry groups were originally introduced to study the symmetries of non-rigid molecules, but have since been used to study the symmetries of any graph embedded in ℝ3. In this paper, we determine for each complete graph Kn with n ≤ 6, what groups can occur as topological symmetry groups or orientation preserving topological symmetry groups of some embedding of the graph in ℝ3.1. Introduction
Molecular symmetries are important in many areas of chemistry. Symmetry is used in interpreting results in crystallography, spectroscopy, and quantum chemistry, as well as in analyzing the electron structure of a molecule. Symmetry is also used in designing new pharmaceutical products. But what is meant by a “symmetry” depends on the rigidity of the molecule in question.
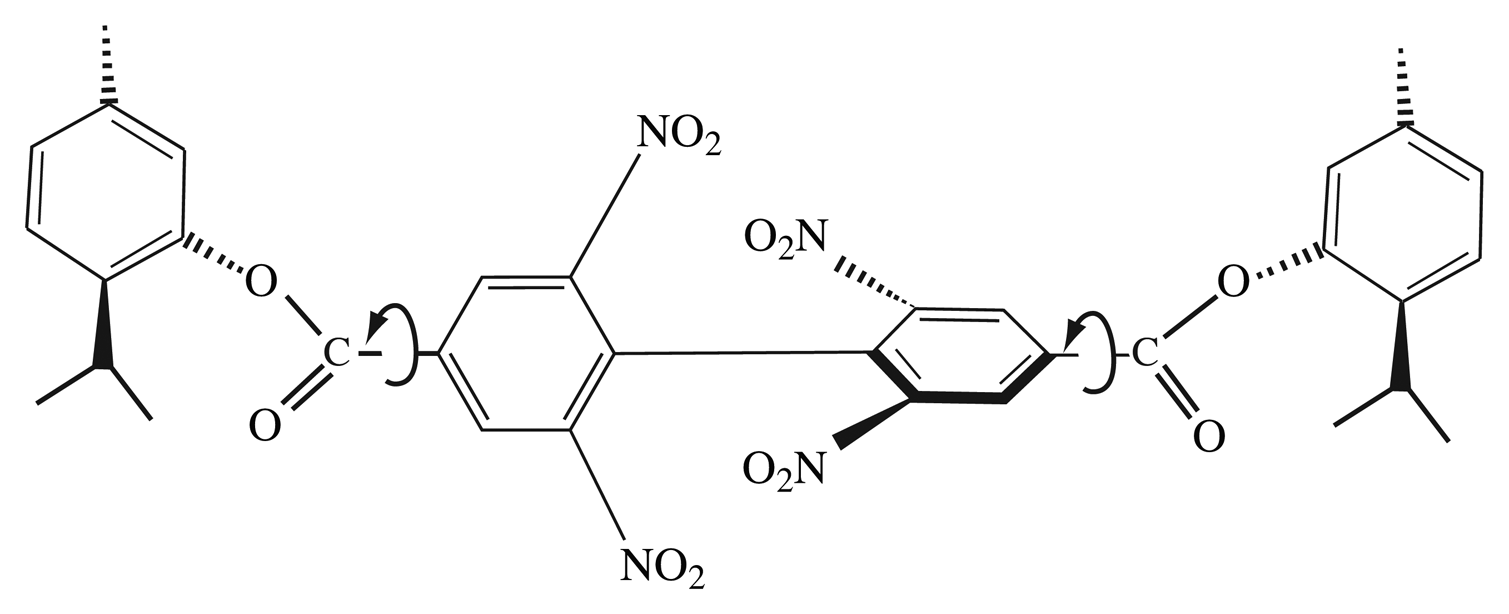
For rigid molecules, the group of rotations, reflections, and combinations of rotations and reflections, is an effective way of representing molecular symmetries. This group is known as the point group, of the molecule because it fixes a point of ℝ3. However, some molecules can rotate around particular bonds, and large molecules can even be somewhat flexible. For example, supramolecular structures constructed through self-assembly may be somewhat conformationally flexible. Even relatively small molecules may contain rigid molecular subparts that rotate on hinges around particular bonds. For example, the left and right sides of the biphenyl derivative illustrated in Figure 1 rotate simultaneously, independent of the central part of the molecule. Because of these rotating pieces, this molecule is achiral though it cannot be rigidly superimposed on its mirror form. A detailed discussion of the achirality of this molecule can be found in [1].
In general, the amount of rigidity of a given molecule depends on its chemistry not just its geometry. Thus a purely mathematical definition of molecular symmetries that accurately reflects the behavior of all molecules is impossible. However, for non-rigid molecules, a topological approach to classifying symmetries including achirality can add important information beyond what is obtained from the point group. Such an approach could be useful to the study of supramolecular chirality, since structures constructed through self-assembly may be large and somewhat flexible or contain subparts that can rotate around covalent or non-convalent bonds.
The topological symmetry group was first introduced by Jon Simon in 1987 in order to classify the symmetries of non-rigid molecules [2]. By comparing the topological symmetry group and the orientation preserving topological symmetry group of a particular structure, one can see whether the structure is achiral and if so, understand how its achirality fits together with its other topological symmetries.
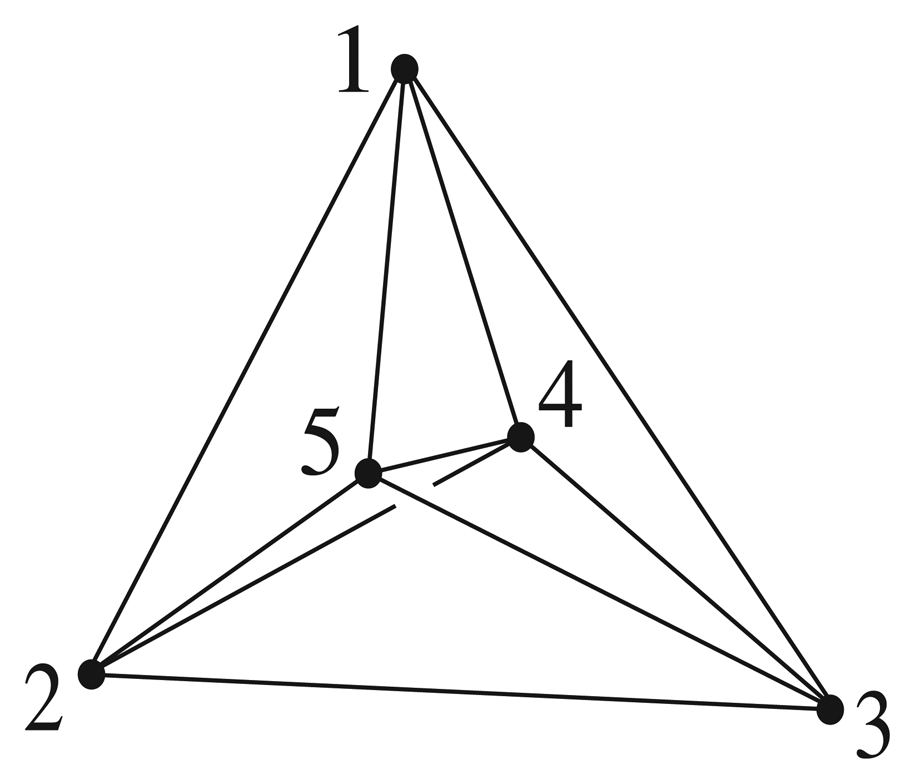
In this paper, we determine both the topological symmetry groups and the orientation preserving topological symmetry groups of structures whose underlying form is that of a complete graph with no more than six vertices. A complete graph, Kn, is defined to be a graph with n vertices which has an edge between every pair of vertices. In Figure 2 we illustrate embeddings of the complete graphs K3, K4, and K5. The class of complete graphs is an interesting class to consider because the automorphism group of Kn is the symmetric group Sn, which is the largest automorphism group of any graph with n vertices. For small values of n, there exist molecules whose underlying topological structure has the form of Kn. For example, a tetrahedral supramolecular cluster has the underlying structure of the complete graph K4. If such a cluster contains a central atom which is bonded to the four corners of the tetrahedron, then the structure has the form of the complete graph K5 (as illustrated on the right in Figure 2).
2. Background and Terminology
Though it may seem strange from the point of view of a chemist, the study of symmetries of embedded graphs is more convenient to carry out in the 3-dimensional sphere S3 = ℝ3 ∪ {∞} rather than in Euclidean 3-space, ℝ3. In particular, in ℝ3 every rigid motion is a rotation, reflection, translation, or a combination of these operations. Whereas, in S3 glide rotations provide an additional type of rigid motion. While a topological approach to the study of symmetries does not require us to focus on rigid motions, for the purpose of illustration it is preferable to display rigid motions rather than isotopies whenever possible. Thus throughout the paper we work in S3 rather than in ℝ3.
Definition 1
The topological symmetry group of a graph Γ embedded in S3 is the subgroup of the automorphism group of the graph, Aut(Γ), induced by homeomorphisms of the pair (S3, Γ). The orientation preserving topological symmetry group, TSG+(Γ), is the subgroup of Aut(Γ) induced by orientation preserving homeomorphisms of (S3, Γ).
It should be noted that for any homeomorphism h of (S3, Γ), there is a homeomorphism g of (S3, Γ) which fixes a point p not on Γ such that g and h induce the same automorphism on Γ. By choosing p to be the point at ∞, we can restrict g to a homeomorphism of (ℝ3, Γ). On the other hand if we start with an embedded graph Γ in ℝ3 and a homeomorphism g of (ℝ3, Γ), we can consider Γ to be embedded in S3 = ℝ3 ∪ {∞} and extend g to a homeomorphism of S3 simply by fixing the point at ∞. It follows that the topological symmetry group of Γ in S3 is the same as the topological symmetry group of Γ in ℝ3. Thus we lose no information by working with graphs in S3 rather than graphs in ℝ3.
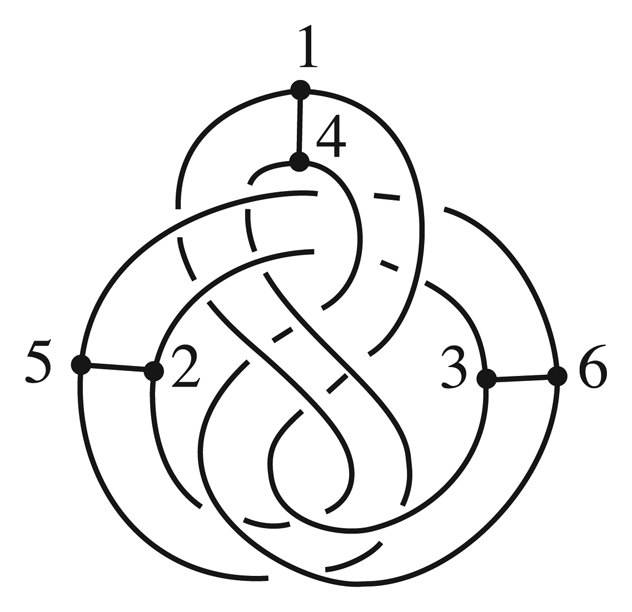
It was shown in [3] that the set of orientation preserving topological symmetry groups of 3-connected graphs embedded in S3 is the same up to isomorphism as the set of finite subgroups of the group of orientation preserving diffeomorphisms of S3, Diff+(S3). However, even for a 3-connected embedded graph Γ, the automorphisms in TSG(Γ) are not necessarily induced by finite order homeomorphisms of (S3, Γ).
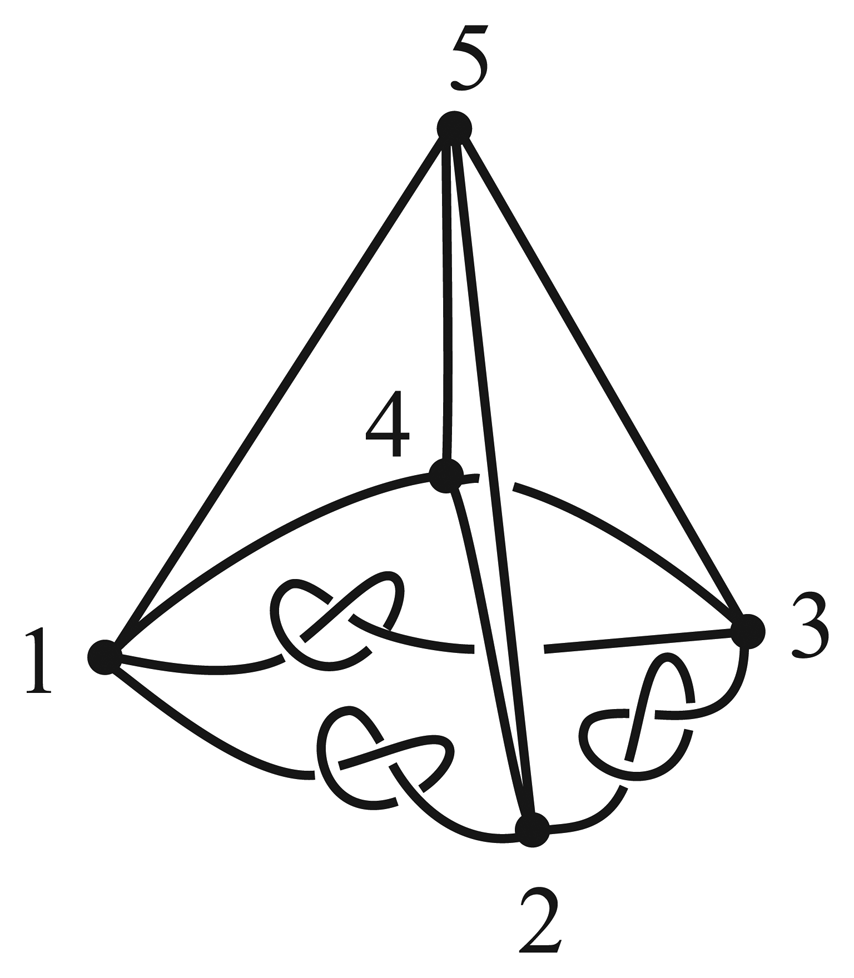
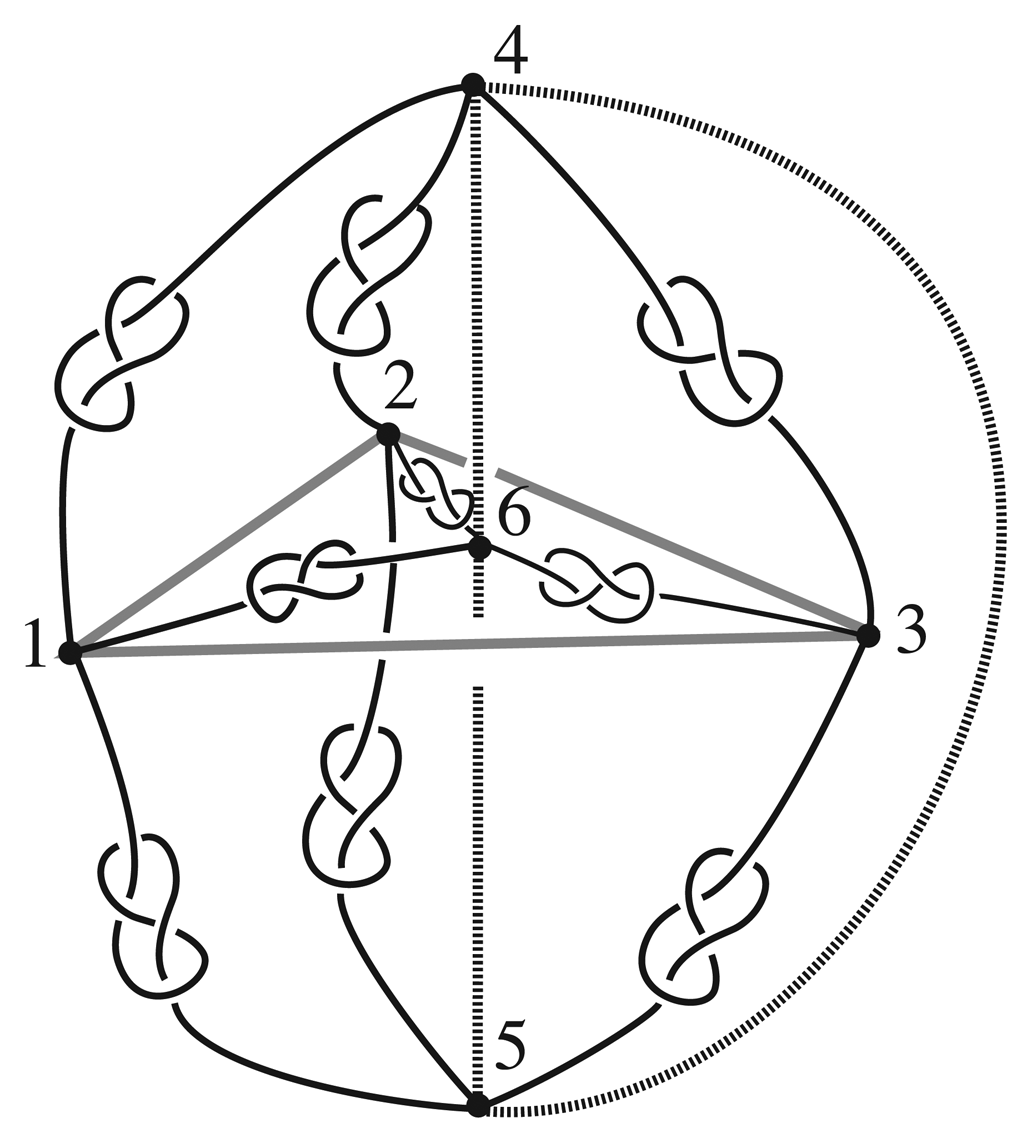
For example, consider the embedded 3-connected graph Γ illustrated in Figure 3. The automorphism (153426) is induced by a homeomorphism that slithers the graph along itself while interchanging the inner and outer knots in the graph. On the other hand, the automorphism (153426) cannot be induced by a finite order homeomorphism of S3 because there is no order three homeomorphism of S3 taking a figure eight knot to itself [4,5] and the embedded graph in Figure 3 cannot be pointwise fixed by a finite order homeomorphism of S3 [6].
On the other hand, Flapan proved the following theorem which we will make use of later in the paper.
Finite Order Theorem
[7] Let φ be a non-trivial automorphism of a 3-connected graph γ which is induced by a homeomorphism h of (S3, Γ) for some embedding Γ ofγ in S3. Then for some embedding Γ of γ in S3, the automorphism φ is induced by a finite order homeomorphism, f of (S3, Γ), and f is orientation reversing if and only ifh is orientation reversing.
In the definition of the topological symmetry group, we start with a particular embedding Γ of a graph γ in S3 and then determine the subgroup of the automorphism group of γ which is induced by homeomorphisms of (S3,Γ). However, sometimes it is more convenient to consider all possible subgroups of the automorphism group of an abstract graph, and ask which of these subgroups can be the topological symmetry group or orientation preserving topological symmetry group of some embedding of the graph in S3. The following definition gives us the terminology to talk about topological symmetry groups from this point of view.
Definition 2
An automorphism f of an abstract graph, γ, is said to be realizable if there exists an embedding Γ of γ in S3 such that f is induced by a homeomorphism of (S3, Γ). A group G is said to be realizable for γ if there exists an embedding Γ of γ in S3 such that TSG(Γ) = G. If there exists an embedding Γ such that TSG+(Γ) = G, then we say G is positively realizable for γ.
It is natural to ask whether every finite group is realizable. In fact, it was shown in [3] that the alternating group Am is realizable for some graph if and only if m < 5. Furthermore, in [8] it was shown that for every closed, connected, orientable, irreducible 3-manifold M, there exists an alternating group Am which is not isomorphic to the topological symmetry group of any graph embedded in M.
3. Topological Symmetry Groups of Compete Graphs
For the special class of complete graphs Kn embedded in S3, Flapan, Naimi, and Tamvakis obtained the following result.
Complete Graph Theorem
[9] A finite group H is isomorphic to TSG+(Γ) for some embedding Γ of a complete graph in S3 if and only if H is a finite subgroup of SO(3) or a subgroup of Dm × Dmfor some odd m.
This left open the question of what topological symmetry groups and orientation preserving topological symmetry groups are possible for embeddings of a particular complete graph Kn in S3. For each n > 6, this question was answered for orientation preserving topological symmetry groups in the series of papers [10-13]. These papers make use of a result that for n > 6, only a few types of automorphisms of Kn are realizable [7]. There are no comparable results available for automorphisms of Kn when n ≤ 6.
In the current paper, we determine which groups are realizable and which groups are positively realizable for each Kn with n < 6. This is the first family of graphs for which both the realizable and the positively realizable groups have been determined.
For n ≤ 3, this question is easy to answer. In particular, since K1 is a single vertex, the only realizable or positively realizable group is the trivial group. Since K2 is a single edge, the only realizable or positively realizable group is ℤ2.
For n = 3, we know that Aut(K3) ≅ S3 ≅ D3, and hence every realizable or positively realizable group for K3 must be a subgroup of D3. Note that for any embedding of K3 in S3, the graph can be “slithered” along itself to obtain an automorphism of order 3 which is induced by an orientation preserving homeomorphism. Thus the topological symmetry group and orientation preserving topological symmetry group of any embedding of K3 will contain an element of order 3. Thus neither the trivial group nor Z2 is realizable or positively realizable for K3. If Γ is a planar embedding of K3 in S3, then TSG(Γ) = TSG+(Γ) ≅ D3. Recall that the trefoil knot 31 is chiral while the knot 817 is negative achiral and non-invertible. Thus if Γ is the knot 817, then no orientation preserving homeomorphism of (S3, Γ) inverts Γ, but there is an orientation reversing homeomorphism of (S3, Γ) which inverts Γ. Whereas, if Γ is the knot 817#31, then there is no homeomorphism of (S3, Γ) which inverts Γ. Table 1 summarizes our results for K3.
Determining which groups are realizable and positively realizable for K4, K5, and K6 is the main point of this paper. In each case, we will first determine the positively realizable groups and then use the fact that either TSG+(Γ) = TSG(Γ) or TSG+(Γ) is a normal subgroup of TSG(Γ) of index 2 to help us determine the realizable groups.
4. Topological Symmetry Groups of K4
In addition to the Complete Graph Theorem given above, we will make use of the following results in our analysis of positively realizable groups for Kn with n ≥ 4.
A4 Theorem
[11] A complete graph Km with m ≥ 4 has an embedding Γ in S3 such that TSG+(Γ) ≅ A4 if and only ifm ≡ 0, 1, 4, 5, 8 (mod 12).
A5 Theorem
[11] A complete graph Km with m ≥ 4 has an embedding Γ in S3 such that TSG+(Γ) ≅ A5 if and only ifm ≡ 0, 1, 5, 20 (mod 60).
S4 Theorem
[11] A complete graph Km with m ≥ 4 has an embedding Γ in S3 such that TSG+(Γ) ≅ S4 if and only if m ≡ 0, 4, 8, 12, 20 (mod 24).
Subgroup Theorem
[12] Let Γ be an embedding of a 3-connected graph γ in S3 with an edge that is not poinwise fixed by any non-trivial element of TSG+(Γ). Then every subgroup of TSG+(Γ) is positively realizable for γ.
It was shown in [12] that adding a local knot to an edge of a 3-connected graph is well-defined and that any homeomorphism of S3 taking the graph to itself must take an edge with a given knot to an edge with the same knot. Furthermore, any orientation preserving homeomorphism of S3 taking the graph to itself must take an edge with a given non-invertible knot to an edge with the same knot oriented in the same way Thus for n > 3, adding a distinct knot to each edge of an embedding of Kn in S3 will create an embedding Δ where TSG(Δ) and TSG+(Δ) are both trivial. Hence we do not include the trivial group in our list of realizable and positively realizable groups for Kn when n > 3.
Finally, observe that for n > 3, for a given embedding Γ of Kn we can add identical chiral knots (whose mirror image do not occur in Γ) to every edge of Γ to get an embedding Γ such that TSG(Γ′) = TSG+(Γ). Thus every group which is positively realizable for Kn is also realizable for Kn. We will use this observation in the rest of our analysis.
The following is a complete list of all the non-trivial subgroups of Aut(K4) ≅ S4 up to isomorphism: S4, A4, D4, D3, D2, ℤ4, ℤ3, ℤ2.
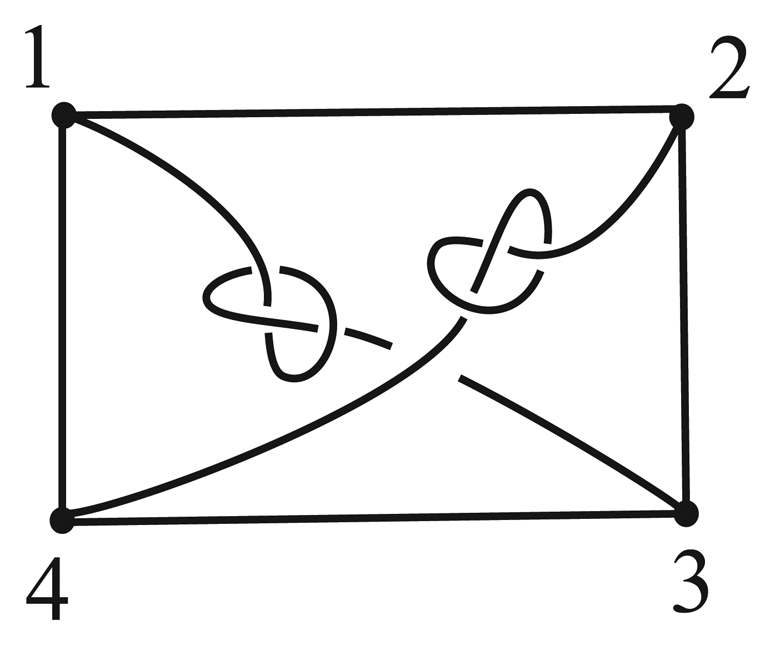
We will show that all of these groups are positively realizable, and hence all of the groups will also be realizable. First consider the embedding Γ of K4 illustrated in Figure 4. The square must go to itself under any homeomorphism of (S3, Γ). Hence TSG+(Γ) is a subgroup of D4. In order to obtain the automorphism (1234), we rotate the square clockwise by 90° and pull under . We can obtain the transposition (13) by first rotating the figure by 180° about the axis which contains vertices 2 and 4 and then pulling under . Thus TSG+(Γ) ≅ D4. Furthermore, since the edge is not pointwise fixed by any non-trivial element of TSG+(Γ), by the Subgroup Theorem the groups ℤ4, D2 and ℤ2 are each positively realizable for K4.
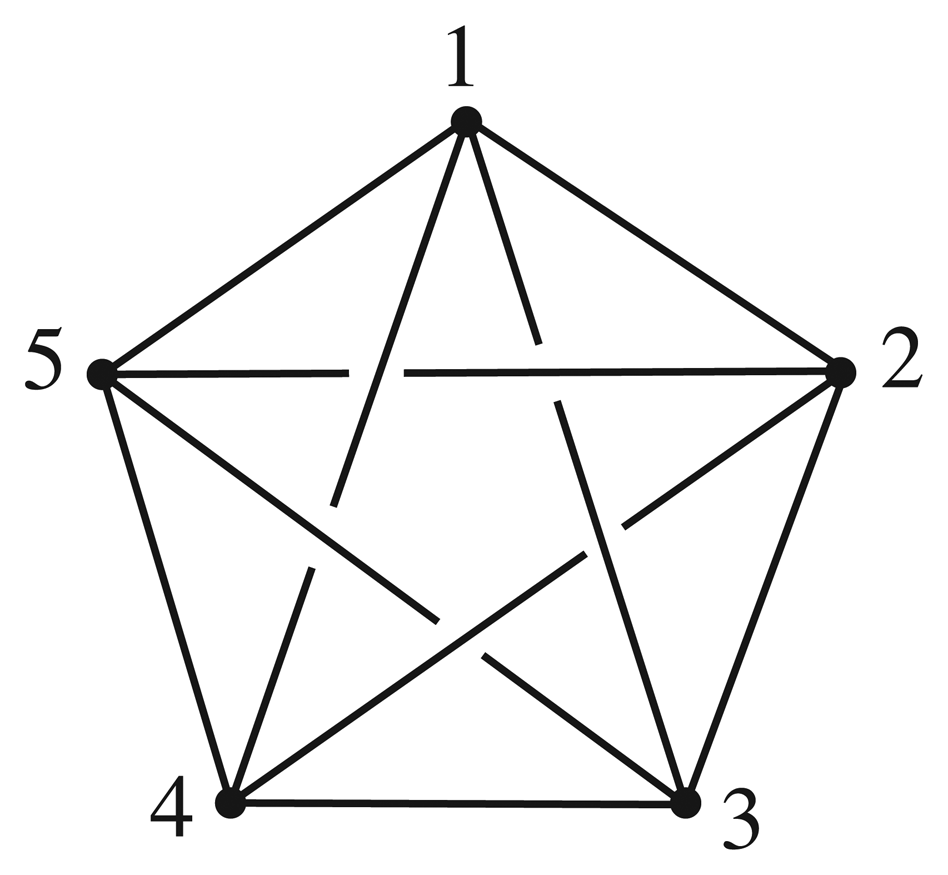
Next, consider the embedding, Γ of K4 illustrated in Figure 5. All homeomorphisms of (S3, Γ) fix vertex 4. Hence TSG+(Γ) is a subgroup of D3. The automorphism (123) is induced by a rotation, and the automorphism (12) is induced by turning the figure upside down and then pushing vertex 4 back up through the centre of 123. Thus TSG+(Γ) = D3. Since the edge 12 is not pointwise fixed by any non-trivial element of TSG+(Γ), by the Subgroup Theorem, the group Z3 is also positively realizable for K4.
Thus every subgroup of Aut(K4) is positively realizable. Now by adding appropriate equivalent chiral knots to each edge, all subgroups of Aut(K4) are also realizable. We summarize our results for K4 in Table 2.
5. Topological Symmetry Groups of K5
The following is a complete list of all the non-trivial subgroups of Aut(K5) ≅ S5:
The lemma below follows immediately from the Finite Order Theorem [7] (stated in the introduction) together with Smith Theory [6].
Lemma 1
Let n > 3 and let φ be a non-trivial automorphism of Kn which is induced by a homeomorphism h of (S3, Γ) for some embedding Γ of Kn in S3. If h is orientation reversing, then φ fixes at most 4 vertices. Ifh is orientation preserving, then φ fixes at most 3 vertices, and if φ has even order, then φ fixes at most 2 vertices.
We now prove the following lemma.
Lemma 2
Let n > 3 and let Γ be an embedding of Kn in S3 such that TSG+(Γ) contains an element φ of even order m > 2. Then φ does not fix any vertex or interchange any pair of vertices.
Proof
By the Finite Order Theorem, Kn can be re-embedded as Γ so that φ is induced on Γ by a finite order orientation preserving homeomorphism h of (S3, Γ′). Suppose that φ fixes a vertex or interchanges a pair of vertices of Γ. Then fix(h) is non-empty, and hence by Smith Theory, fix(h) ≅ S1. Let r = m/2. Then hr induces an involution on the vertices of Γ, and this involution can be written as a product (a1b1) … (aqbq) of disjoint transpositions of vertices. Now for each i, hr fixes a point on the edge aib. But fix(hr) contains fix(h) and thus by Smith Theory fix(hr) = fix(h). Hence h fixes a point on each edge aibi. Thus h induces also (a1 b1) … (aqbq) on the vertices of Γ′. But this contradicts the hypothesis that the order of φ is m > 2.
By Lemma 2, there is no embedding of K5 in S3 such that TSG+(Γ) contains an element of order 4 or of order 6. It follows that TSG+(Γ) cannot be D6, ℤ6, D4 or ℤ4.
Consider the embedding Γ of K5 illustrated in Figure 6. The knotted cycle 13524 must be setwise invariant under every homeomorphism of Γ. Thus TSG+(Γ) ≤ D5. The automorphism (12345) is induced by rotating Γ, and (25)(34) is induced by turning the graph over. Hence TSG+(Γ) = 〈(12345;, (25)(34)〉 ≅ D5. Since the edge is not pointwise fixed by any non-trivial element of TSG+(Γ), by the Subgroup Theorem the groups ℤ5 and ℤ2 are also positively realizable for K5.
Next consider the embedding Γ of K5 illustrated in Figure 7. The triangle must go to itself under any homeomorphism. Also by Lemma 1, any orientation preserving homeomorphism which fixes vertices 1, 2, and 3 induces a trivial automorphism on K5. Thus TSG+(Γ) ≤ D3. The automorphism (123) is induced by a rotation. Also the automorphism (45)(12) is induced by pulling vertex 4 down through the centre of triangle while pulling vertex 5 into the centre of the figure then rotating by 180° about the line through vertex 3 and the midpoint of the edge . Thus TSG+(Γ) = 〈(123;, (45)(12)〉 ≅ D3. Since the edge is not pointwise fixed by any non-trivial element of TSG+(Γ), by the Subgroup Theorem, the group ℤ3 is positively realizable for K5.
Lastly, consider the embedding Γ of K5 illustrated in Figure 8 with vertex 5 at infinity. The square must go to itself under any homeomorphism. Hence TSG+(Γ) ≤ D4. The automorphism (13)(24) is induced by rotating the square by 180°. By turning over the figure we obtain (12)(34). By Lemma 2, TSG+(Γ) cannot contain an element of order 4. Thus TSG+(Γ) = 〈(13)(24;, (12)(34)〉 ≅ D2.
We summarize our results on positive realizability for K5 in Table 3.
Again by adding appropriate equivalent chiral knots to each edge, all of the positively realizable groups for K5 are also realizable. Thus we only need to determine realizability for the groups S5, S4, ℤ5 ⋊ ℤ4, D6, D4, ℤ6,andℤ4.
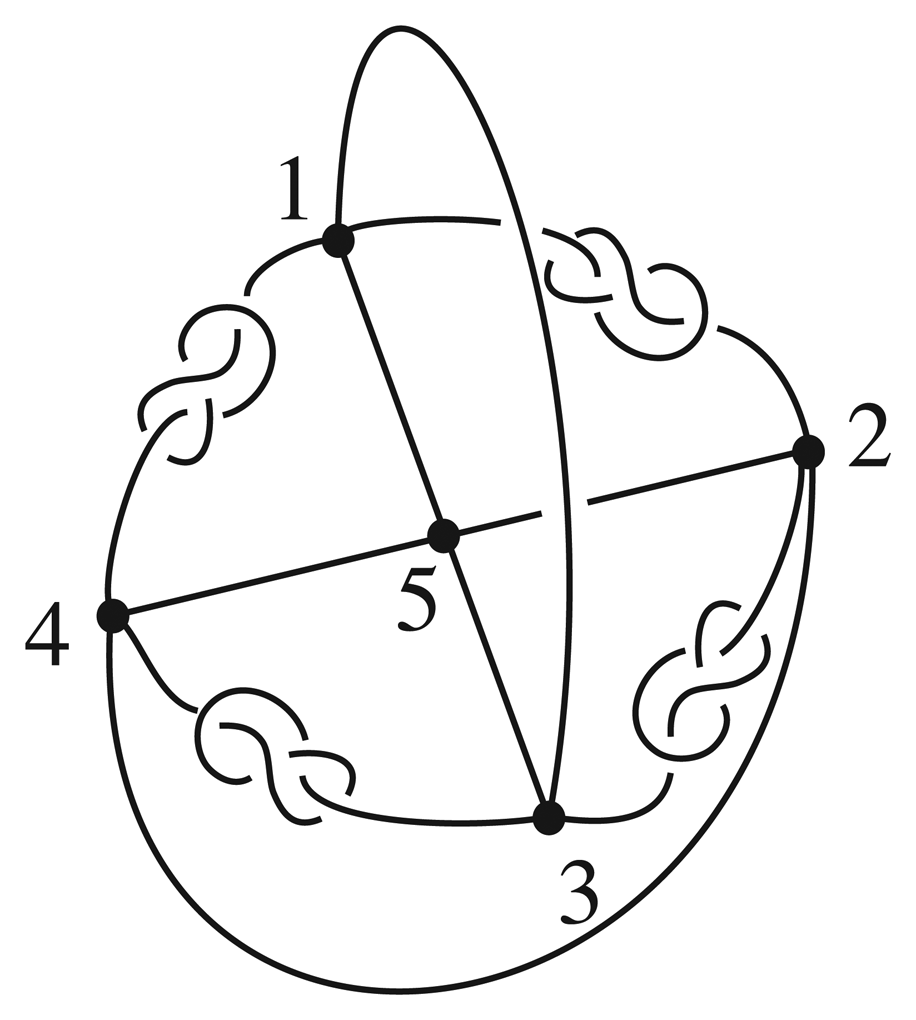
Let Γ be the embedding of K5 illustrated in Figure 9. Any transposition which fixes vertex 5 is induced by a reflection through the plane containing the three vertices fixed by the transposition. To see that any transposition involving vertex 5 can be achieved, consider the automorphism (15). Pull through the triangle and then turn over the embedding so that vertex 5 is at the top, vertex 1 is in the centre and vertices 3 and 4 are switched. Now reflect in the plane containing vertices 1, 5, and 2 in order to switch vertices 3 and 4 back. All other transpositions involving vertex 5 can be induced by a similar sequence of moves. Hence TSG(Γ) ≅ S5.
We create a new embedding Γ from Figure 9 by adding the achiral figure eight knot, 41, to all edges containing vertex 5. Now every homeomorphism of (S3, Γ) fixes vertex 5, yet all transpositions fixing vertex 5 are still possible. Thus TSG(Γ′) ≅ S4.
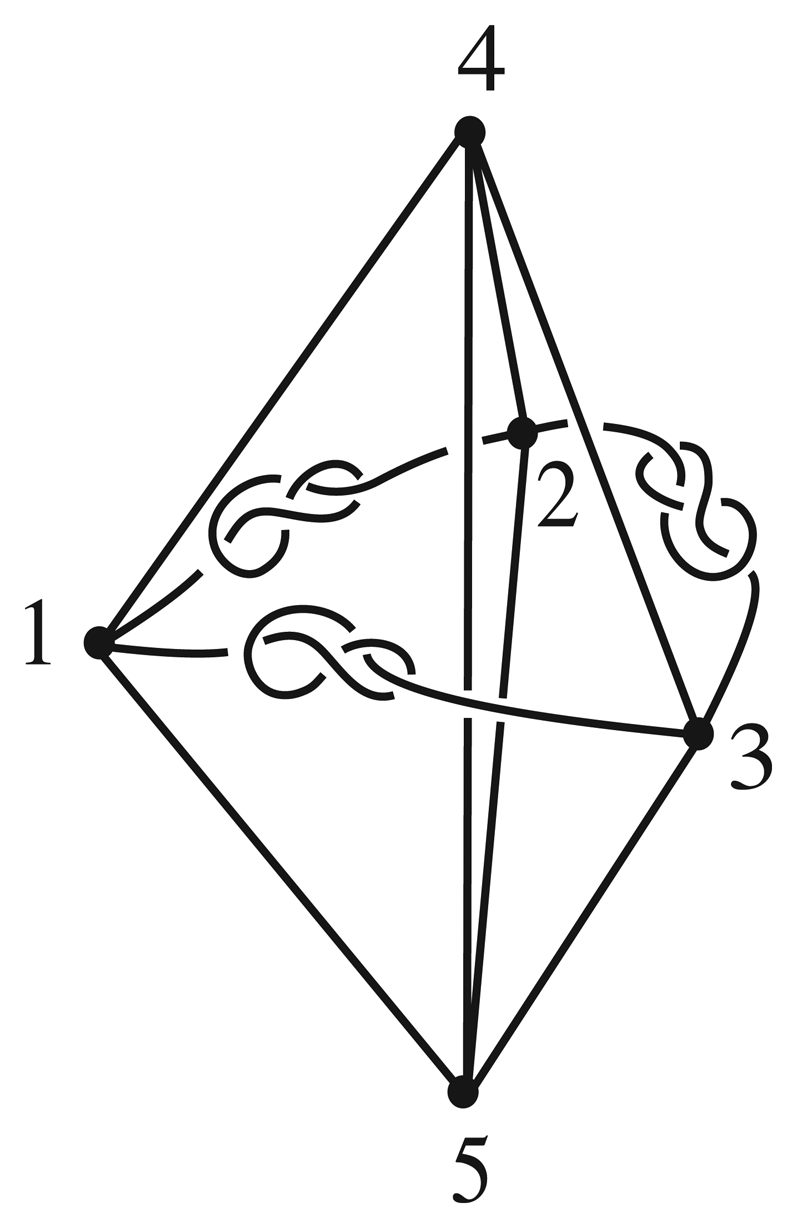
In order to prove D4 is realizable for K5 consider the embedding Γ illustrated in Figure 10. Every homeomorphism of (S3, Γ) takes to itself, so TSG(Γ) ≤ D4. The automorphism (1234) is induced by rotating the graph by 90° about a vertical line through vertex 5, then reflecting in the plane containing the vertices 1, 2, 3, 4, and finally isotoping the knots into position. Furthermore, reflecting in the plane containing or and then isotoping the knots into position yields the transposition (24) or (13) respectively. Hence TSG(Γ) ≅ D4.
We obtain a new embedding Γ by replacing the invertible 41 knots in Figure 10 with the knot 12427, which is positive achiral but non-invertible [16]. Since 12427 is neither negative achiral nor invertible, no homeomorphism of (S3, Γ) can invert . Thus TSG(Γ′) ≅ ℤ4.
Next let Γ denote the embedding of K5 illustrated in Figure 11. Every homeomorphism of (S3, Γ) takes to itself, so TSG(Γ) ≤ D6. The 3-cycle (123) is induced by a rotation. Each transposition involving only vertices 1, 2, and 3 is induced by a reflection in the plane containing and the remaining fixed vertex followed by an isotopy. The transposition (45) is induced by a reflection in the plane containing vertices 1, 2 and 3 followed by an isotopy. Thus TSG(Γ) ≅ D6, generated by (123), (23), and (45).
We obtain a new embedding Γ′ by replacing the 41 knots in Figure 11 by 12427 knots. Then the triangle cannot be inverted. Thus TSG(Γ′) ≅ ℤ6, generated by (123) and (45).
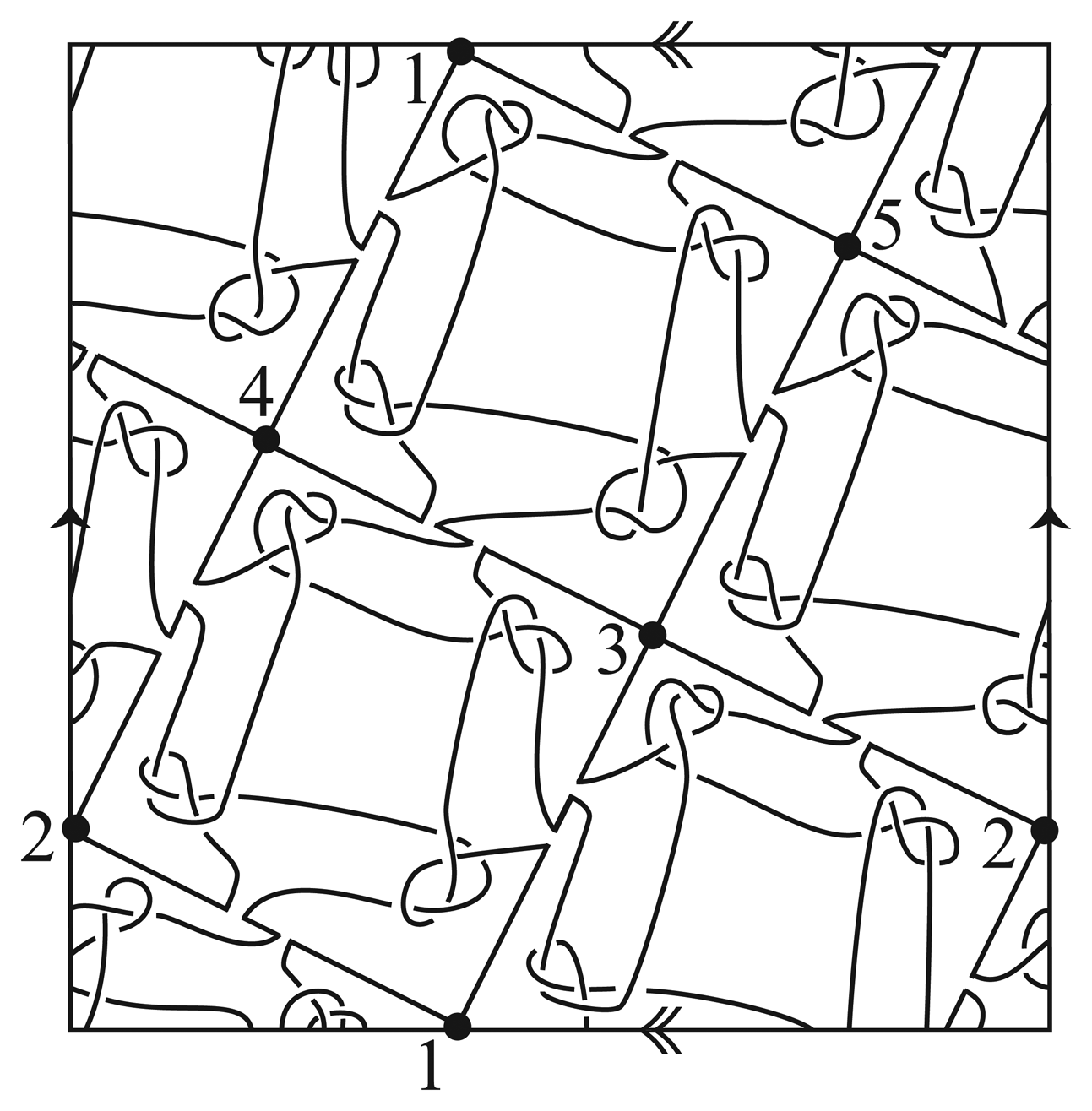
It is more difficult to show that ℤ5 × ℤ4 is realizable for K5, so we define our embedding in two steps. First we create an embedding Γ of K5 on a torus T that is standardly embedded in S3. In Figure 12, we illustrate Γ on a flat torus. Let f denote a glide rotation of S3 which rotates the torus longitudinally by 4π/5 while rotating it meridinally by 8π/5. Thus f takes Γ to itself inducing the automorphism (12345).
Let g denote the homeomorphism obtained by rotating S3 about a (1, 1) curve on the torus T, followed by a reflection through a sphere meeting T in two longitudes, and then a meridional rotation of T by 6π/5. In Figure 13, we illustrate the step-by-step action of g on T, showing that g takes Γ to itself inducing (2431).
The homeomorphisms f and g induce the automorphisms φ = (12345) and ψ = (2431) respectively. Observe that φ5 = ψ4 = 1 and ψφ = φψ2. Thus 〈φ, ψ〉 ≅ ℤ5 ⋊ ℤ4 ≤ TSG(Γ) ≤ S5. Note however that the embedding in Figure 12 is isotopic to the embedding of K5 in Figure 9. Thus TSG(Γ) ≅ S5.
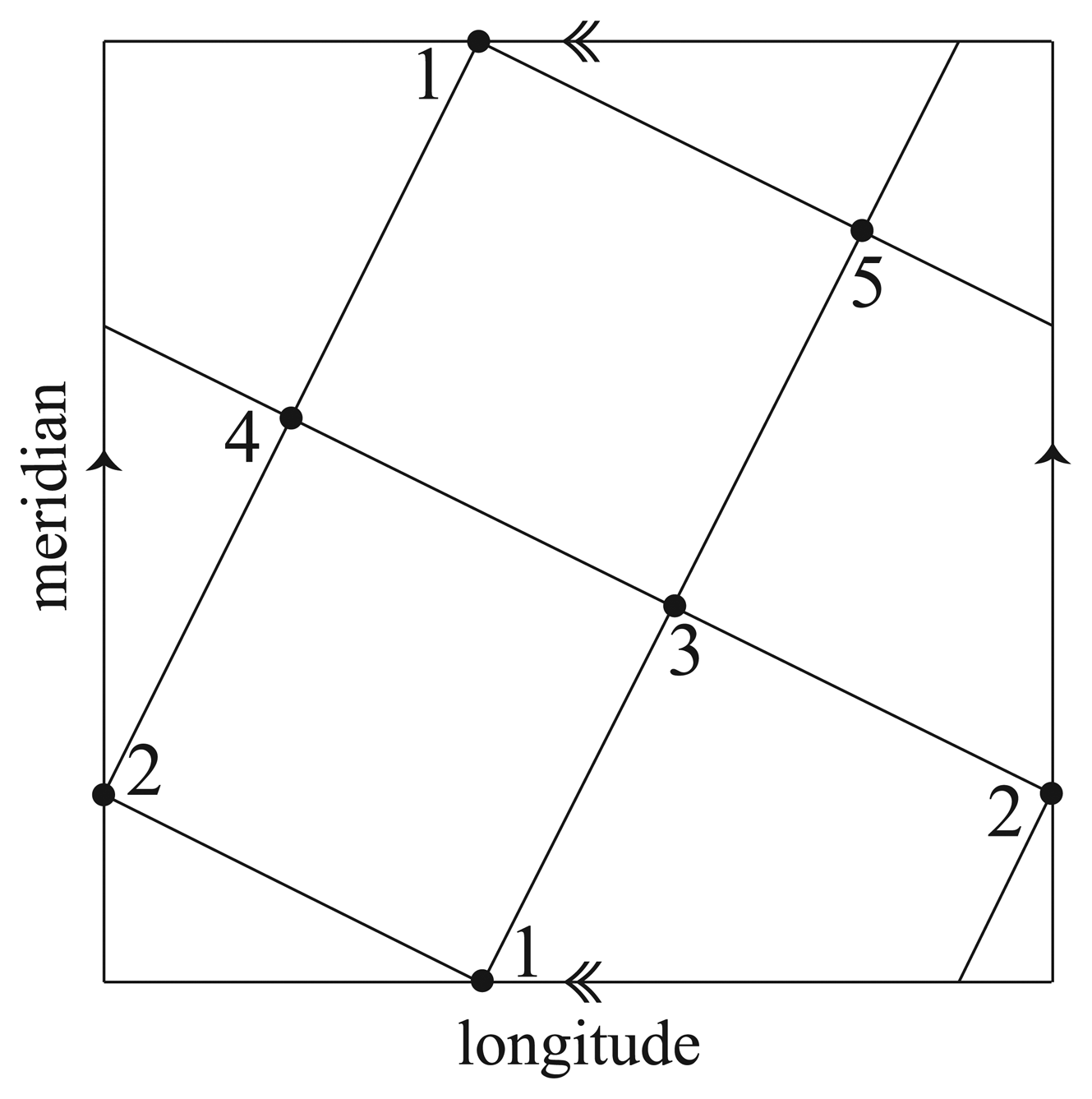
In order to obtain the group ℤ5 ⋊ ℤ4, we now consider the embedding Γ of K5 whose projection on a torus is illustrated in Figure 14. Observe that the projection of Γ′ in every square of the grid given by Γ on the torus is identical. Thus the homeomorphism f which took Γ to itself inducing the automorphism φ = (12345) on Γ also takes Γ′ to itself inducing φ on Γ′.
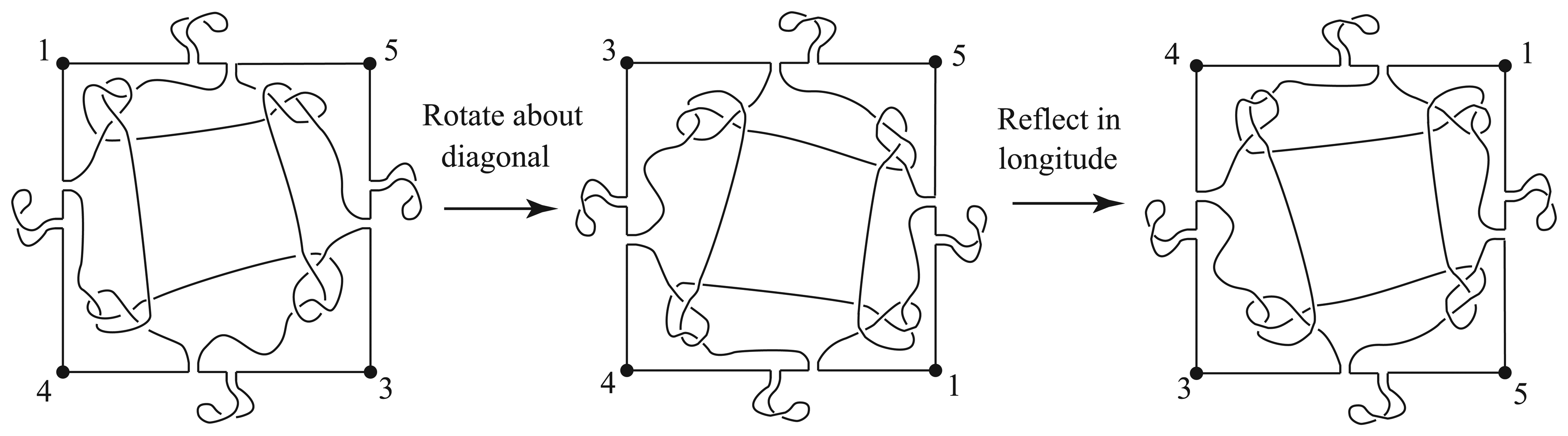
Recall that g was the homeomorphism of (S3, Γ) obtained by rotating S3 about a (1, 1) curve on the torus T, followed by a reflection through a sphere meeting T in two longitudes, and then a meridional rotation of T by 6π/5. In order to see what g does to Γ′, we focus on the square of Γ′. Figure 15 illustrates a rotation of the square about a diagonal, then a reflection of the square across a longitude. The result of these two actions takes the projection of the knot to an identical projection. Thus after rotating the torus meridionally by 6π/5, we see that g takes Γ′ to itself inducing the automorphism ψ = (2431). It now follows that ℤ5 ⋊ ℤ4 ≤ TSG(Γ′) < S5.
In order to prove that TSG(Γ′) ≅ ℤ5 ⋊ ℤ4, we need to show TSG(Γ′) ≇ S5. We prove this by showing that the automorphism (15) cannot be induced by a homeomorphism of (S3, Γ′).
From Figure 15 we see that the square is the knot 41#41#41#41. In order to see what would happen to this knot if the transposition (15) were induced by a homeomorphism of (S3, Γ), we consider the square . In Figures 16 and 17 we isotop to a projection with only 10 crossings. This means that cannot be the knot 41#41#41#41. It follows that the automorphism (15) cannot be induced by a homeomorphism of (S3, Γ). Hence TSG(Γ′) ≇ S5. However, the only subgroup of S5 that contains ℤ5 ⋊ ℤ4 and is not S5 is the group ℤ5 ⋊ ℤ4. Thus in fact TSG(Γ′) ≅ ℤ5 ⋊ ℤ4.
Thus every subgroup of Aut(K5) is realizable for K5. Table 4 summarizes our results for TSG(K5).
6. Topological Symmetry Groups of K6
The following is a complete list of all the subgroups of Aut(K6) ≅ S6: S6, A6, s5, A5, S2[S3] (B[A] represents a wreath product of A by B.), S4 × ℤ2, A4 × ℤ2, S4, A4, ℤ5 ⋊ ℤ4, D3 × D3, (ℤ3 × ℤ3) ⋊ ℤ4, (ℤ3 × ℤ3) ⋊ ℤ2, D3 × ℤ3, ℤ3 × ℤ3, D6, D5, D4, D4 × ℤ2, D3, D2, ℤ6, ℤ5, ℤ4, ℤ4 × ℤ2, ℤ3, ℤ2, ℤ2 × ℤ2 × ℤ2 (see [17] and independently verified using the program GAP).
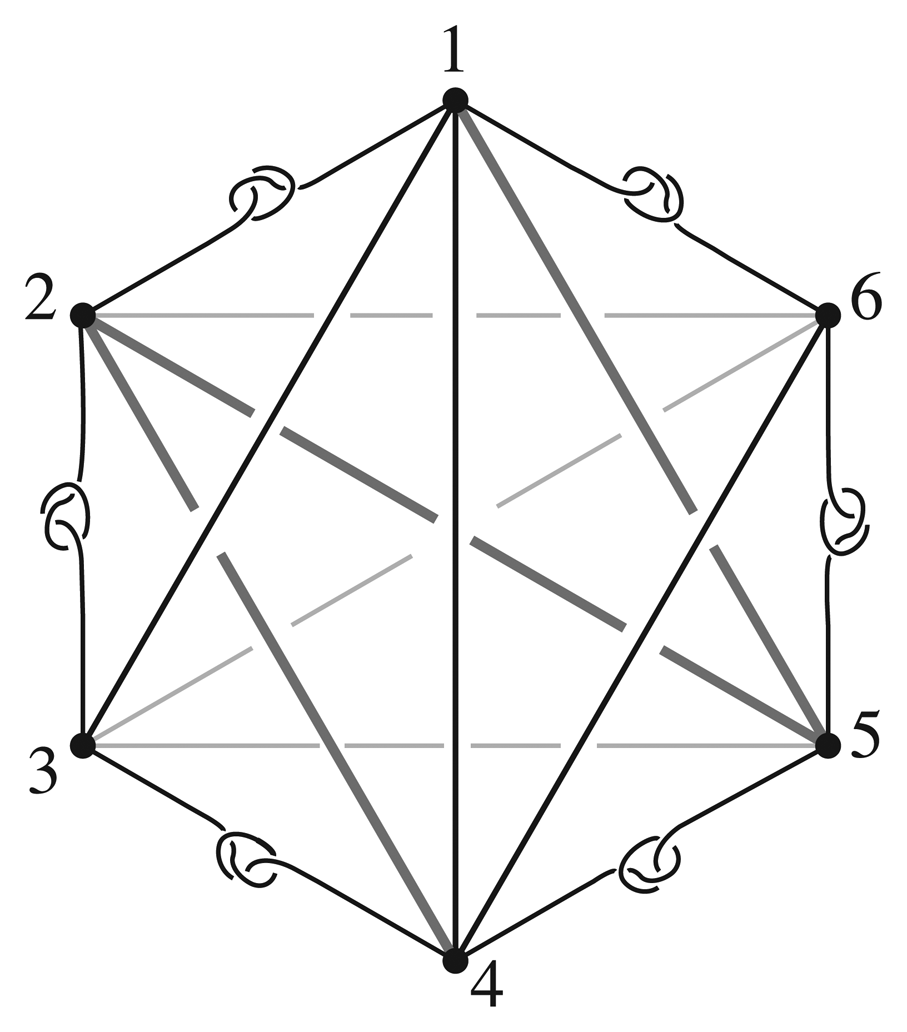
Consider the embedding Γ of K6 illustrated in Figure 18. There are three paths in Γ on different levels that look like the letter “Z” which are highlighted in Figure 18. The top Z-path is , the middle Z-path is , and the bottom Z-path is . The knotted cycle must be setwise invariant under every homeomorphism of Γ, and hence TSG+(Γ) < D6. The automorphism (123456) is induced by a glide rotation that cyclically permutes the Z-paths. Consider the homeomorphism obtained by rotating Γ by 180° about the line through vertices 2 and 5 and then pulling the edges and to the top level while pushing the lower edges down. The result of this homeomorphism is that the top Z-path goes to the top Z-path , the middle Z-path goes to to middle Z-path , and the bottom Z-path goes to the bottom Z-path . Thus the homeomorphism leaves Γ setwise invariant inducing the automorphism (13)(46). It follows that TSG+(Γ) = 〈(123456;, (13)(46)〉 ≅ D6. Finally, since the edge is not pointwise fixed by any non-trivial element of TSG+(Γ), by the Subgroup Theorem the groups ℤ6, D3, ℤ3, D2 and ℤ2 are positively realizable for K6.
Consider the embedding, Γ of K6 illustrated in Figure 19 with vertex 6 at infinity. The automorphisms (13524) and (25)(34) are induced by rotations. Also since 13524 is the only 5-cycle which is knotted, is setwise invariant under every homeomorphism of (S3, Γ). Hence TSG+(Γ) ≅ D5. Also since 15 is not pointwise fixed under any homeomorphism, by the Subgroup Theorem, ℤ5 is positively realizable for K6.
Next consider the embedding, Γ of K6 illustrated in Figure 20. The automorphisms (123)(456) and (123)(465) are induced by glide rotations and (45)(12) is induced by turning the figure upside down. Also if we consider the circles and as cores of complementary solid tori, then (14)(25)(36) is induced by an orientation preserving homeomorphism that switches the two solid tori.
Observe that every homeomorphism of (S3, Γ) takes the pair of triangles to itself, since this is the only pair of complementary triangles not containing knots. The automorphism group of the union of two triangles is S2[S3] [18]. Thus TSG+(Γ) ≤ S2[S3]. Note that the transpositions (12) and (45) are each induced by a reflection followed by an isotopy. Thus TSG(Γ) ≅ S2[S3], since (123)(456), (123)(465), (12) and (14)(25)(36) generate S2[S3]. However, by the Complete Graph Theorem, TSG+(Γ) ≇ S2[S3]. Thus TSG+(Γ) must be an index 2 subgroup of S2[S3] containing f = (123)(456), g = (123)(465), φ = (45)(12) and ψ = (14)(25)(36). Observe that φψ is the involution (42)(51)(36), and f commutes with ψ and also fφψ = φψf-1, while g commutes with φψ and gψ = ψg-1. Thus S2[S3] ≥ TSG+(Γ) ≥ 〈f,φψ〉 × (g,ψ) ≅ D3 × D3. It follows that TSG+(Γ) ≅ D3 × D3.
The subgroup 〈f, g, ψ〉 is isomorphic to D3 × ℤ3 because ψ commutes with f and gψ = ψg-1. We add the non-invertible knot 817 to every edge of the triangles and to obtain an embedding Γ1. Now the automorphism φ = (45)(12) cannot be induced by an orientation preserving homeomorphism of (S3, Γ1). However, f, g, and ψ are still induced by orientation preserving homeomorphisms. Thus TSG+(Γ1) ≅ D3 × ℤ3 since D3 × ℤ3 is a maximal subgroup of D3 x D3.
Also 〈f, g, φ〉 is isomorphic to (ℤ3 × ℤ3) ⋊ ℤ2 because fφ = φf-1 and gφ = φg-1. Again starting with Γ in Figure 20, we place 52 knots on the edges of the triangle 123 so that ψ is no longer induced. Thus creating and embedding Γ2 with TSG+(Γ2) ≅ (ℤ3 × ℤ3) ⋊ ℤ2 since (ℤ3 × ℤ3) ⋊ ℤ2 is a maximal subgroup of D3 × D3.
Finally 〈f, g〉 is isomorphic to ℤ3 × ℤ3. If we place equivalent non-invertible knots on each edge of the triangle and a another set (distinct from the first set) of equivalent non-invertible knots on each edge of we obtain an embedding Γ3 with TSG+(Γ3) ≅ ℤ3 × ℤ3 since ℤ3 × ℤ3 is a maximal subgroup of (ℤ3 × ℤ3) ⋊ ℤ2.
We summarize our results on positively realizability for K6 in Table 5. Note in the last few lines of the table we list multiple groups per line, since all of these groups are not positively realizable for the same reason.
By adding appropriate equivalent chiral knots to each edge, every group which is positively realizable for K6 is also realizable for K6. Thus we only need to determine realizability for the groups S6, A6, S5, A5, S4 × ℤ2, A4 × ℤ2, S4, A4, ℤ5 ⋊ ℤ4, (ℤ3 × ℤ3) ⋊ ℤ4, D4, D4 × ℤ2, ℤ4, ℤ4 × ℤ2, and ℤ2 × ℤ2 × ℤ2. Note that in Figure 20 we already determined that S2[S3] is realizable for K6.
Let Γ4 be the embedding of K6 illustrated in Figure 20 with a left handed trefoil added to each edge of and a right handed trefoil added to each edge of . The pair of triangles are setwise invariant since no other edges contain trefoils. Both (123)(456) and (123)(465) are induced by homeomorphisms of (Γ4,S3). Also if we reflect in the plane containing vertices 4, 5, 6, and 1 then all the trefoils switch from left-handed to right-handed and vice versa. If we then interchange the complementary solid tori which have the triangles as cores followed by an isotopy, we obtain an orientation reversing homeomorphism that induces the order 4 automorphism (14)(25)(36)(23) = (14)(2536). Now 〈(14)(2536;, (123)(456), (123)(465)〉 ≅ (ℤ3 × ℤ3) ⋊ ℤ4.
We see as follows that TSG(Γ4) cannot be larger than (ℤ3 × ℤ3) ⋊ ℤ4. Suppose that the automorphism (12) is induced by a homeomorphism f. By Lemma 1, f must be orientation reversing. But , which is impossible because 456 contains only right handed trefoils. Thus TSG(Γ4) ≇ S2[S3]. Note that the only proper subgroup of S2[S3] containing (ℤ3 × ℤ3) ⋊ ℤ4 is (ℤ3 × ℤ3) ⋊ ℤ4. Thus TSG(Γ4) ≅ (ℤ3 × ℤ3) ⋊ ℤ4.
Now let Γ be the embedding of K6 illustrated in Figure 21. Observe that the linking number , but . Thus the automorphism (56) cannot be induced by a homeomorphism of (S3,Γ). Since every homeomorphism of (S3,Γ) takes to itself, it follows that TSG(Γ) ≤ D4. The automorphism (1234)(56) is induced by a rotation followed by a reflection and an isotopy. In addition the automorphism (14)(23)(56) is induced by turning the figure upside down. Thus TSG(Γ) ≅ D4 generated by the automorphisms (1234)(56) and (14)(23)(56).
Now let Γ be obtained from Figure 21 by replacing the knot 41 with the non-invertible and positively achiral knot 12427. Then the square can no longer be inverted. In this case (1234)(56) generates TSG(Γ′) and thus TSG(Γ′) ≅ ℤ 4.
For the next few groups we will use the following lemma.
4-Cycle Theorem
[19] For any embedding Γ of K6 in S3, and any labelling of the vertices of K6 by the numbers 1 through 6, there is no homeomorphism of (S3,Γ) which induces the automorphism (1234).
Consider the subgroup ℤ5 ⋊ ℤ4 ≤ Aut(K6). The presentation of ℤ5 ⋊ ℤ4 as a subgroup of S6 gives the relation x-1yx = y2 for some elements x, y ∈ ℤ5 ⋊ ℤ4 of orders 4 and 5 respectively. Suppose that for some embedding Γ of K6, we have TSG(Γ) ≅ ℤ5 ⋊ ℤ4. Without loss of generality, we can assume that y = (12345) satisfies the relation x-1yx = y2. By the 4-Cycle Theorem, any order 4 element of TSG(Γ) must be of the form x = (abcd)(ef). However, there is no element in Aut(K6) of the form x = (abcd)(ef) that together with y = (12345) satisfies this relation. Thus there can be no embedding Γ of K6 in S3 such that TSG(Γ) ≅ ℤ5 ⋊ ℤ4.
Now consider the subgroup ℤ4 × ℤ2 ≤ Aut(K6). By the 4-Cycle Theorem, without loss of generality we may assume that if TSG(Γ) contains an element of order 4 for some embedding Γ of K6, then TSG(Γ) contains the element (1234)(56). Computation shows that the only transposition in Aut(K6) that commutes with (1234)(56) is (56), which cannot be an element of TSG(Γ) since this would imply that (1234) is an element of TSG(Γ). Furthermore the only order 2 element of Aut(K6) that commutes with (1234)(56) and is not a transposition is (13)(24), which is already in the group generated by (1234)(56). Thus there is no embedding Γ of K6 in S3 such that TSG(Γ) contains the group ℤ4 × ℤ2. This rules out all of the groups S4 × ℤ2, D4 × ℤ2 and ℤ4 × ℤ2 as possible topological symmetry groups for embeddings of K6 in S3.
For the group ℤ2 × ℤ2 × ℤ2 we will use the following result.
Conway Gordon
[20] For any embedding Γ of K6 in S3, the mod 2 sum of the linking numbers of all pairs of complementary triangles in Γ is 1.
Now suppose that for some embedding Γ of K6 in S3 we have TSG(Γ) ≅ ℤ2 × ℤ2 × ℤ2. It can be shown that the subgroup ℤ2 × ℤ2 × ℤ2 ≤ Aut(K6) contains three disjoint transpositions. Without loss of generality we can assume that TSG(Γ) contains (13), (24), and (56), which are induced by homeomorphisms h, f, and g of (S3, Γ) respectively. Since any three vertices of Γ determine a pair of disjoint triangles, we can use a triple of vertices to represent a pair of disjoint triangles. For example, we use the triple 123 to denote the pair of triangles and . With this notation, the orbits of the ten pairs of disjoint triangles in K6 under the group 〈(13;, (24), (56)〉 are:
Table 6 summarizes our realizability results for K6. Recall that for n = 4 and n = 5 every subgroup of Sn is realizable for Kn. However, as we see from Table 6, this is not true for n = 6.
7. Conclusions
We have classified all groups which can occur as the topological symmetry group or orientation preserving topological symmetry group of an embedded complete graph with no more than six vertices. Our results show that a number of groups can occur as a topological symmetry group but not as an orientation preserving topological symmetry group for a particular Kn. This gives us a collection of groups which can only occur for achiral embeddings of the graph in question.
The topological symmetry group includes all of the symmetries induced by the point group together with any symmetries that occur as the result of any flexibility or rotation of subparts of a structure around specific bonds. Thus the topological symmetry group gives us more information about the symmetries and possible achirality of supramolecular structures than could be obtained from the point group. Since complete graphs with no more than six vertices may occur as supramolecular clusters, these results could be of interest in the future study of supramolecular chirality.
Acknowledgments
The first author would like to thank Claremont Graduate University for its support while he pursued the study of Topological Symmetry Groups for his Ph.D Thesis. The second author would like to thank the Institute for Mathematics and its Applications at the University of Minnesota for its hospitality while she was a long term visitor in the fall of 2013.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Flapan, E. When Topology Meets Chemistry; Cambridge University Press: Cambridge, UK, the Mathematical Association of America: Washington, DC, USA; 2000. [Google Scholar]
- Simon, J. A Topological Approach to the Stereochemistry of Nonrigid Molecules. Stud. Phys. Theor. Chem. 1987, 51, 43–75. [Google Scholar]
- Flapan, E.; Naimi, R.; Pommersheim, J.; Tamvakis, H. Topological symmetry groups of graphs embedded in the 3-sphere. Comment. Math. Helv. 2005, 80, 317–354. [Google Scholar]
- Hartley, R. On knots with free period. Canad. J. Math. 1981, 33, 91–102. [Google Scholar]
- Trotter, H.F. Periodic automorphisms of groups and knots. Duke J. Math. 1961, 28, 553–557. [Google Scholar]
- Smith, P.A. Transformations of Finite Period II. Ann. Math. 1939, 40, 690–711. [Google Scholar]
- Flapan, E. Rigidity of Graph Symmetries in the 3-Sphere. J. Knot Theory Ramif. 1995, 4, 373–388. [Google Scholar]
- Flapan, E.; Tamvakis, H. Topological symmetry groups of graphs in 3-manifolds. Proc. Am. Math. Soc. 2013, 141, 1423–1436. [Google Scholar]
- Flapan, E.; Naimi, R.; Tamvakis, H. Topological symmetry groups of complete graphs in the 3-sphere. J. Lond. Math. Soc. 2006, 73, 237–251. [Google Scholar]
- Chambers, D.; Flapan, E.; O'Brien, J. Topological symmetry groups of K4r+3. Discret. Contin. Dyn. Syst. 2011, 4, 1401–1411. [Google Scholar]
- Flapan, E.; Mellor, B.; Naimi, R. Complete graphs whose topological symmetry groups are polyhedral. Algebr. Geom. Topol. 2011, 11, 1405–1433. [Google Scholar]
- Flapan, E.; Mellor, B.; Naimi, R. Spatial graphs with local knots. Rev. Matemática Complut. 2012, 25, 493–510. [Google Scholar]
- Flapan, E.; Mellor, B.; Naimi, R.; Yoshizawa, M. Classificaton of topological symmetry groups of Kn. Topol. Proc. 2014, 43, 209–233. [Google Scholar]
- Götz, P. The Subgroup of S5. Available online: http://schmidt.nuigalway.ie/subgroups/s5.pdf (accessed on 4 April 2014).
- Wikipedia. Subgroup structure of symmetric group:S5. Available online: http://groupprops.subwiki.org/wiki/Subgroup_structure_of_symmetric_group:S5 (accessed on 4 April 2014).
- Hoste, J.; Thistlethwaite, M. Knotscape software application. Available online: http://www.math.utk.edu/∼morwen/knotscape.html (accessed March 2013).
- Götz, P. The Subgroup of S6. Available online: http://schmidt.nuigalway.ie/subgroups/s6.pdf (accessed April 2013).
- Frucht, R. On the groups of repeated graphs. Bull. Am. Math. Soc. 1949, 55, 418–420. [Google Scholar]
- Flapan, E. Symmetries of Möbius Ladders. Math. Ann. 1989, 283, 271–283. [Google Scholar]
- Conway, J.; Gordon, C. Knots and links in spatial graphs. J. Graph Theory 1983, 7, 445–453. [Google Scholar]








| Embedding | TSG(Γ) | TSG+(Γ) |
|---|---|---|
| Planar | D3 | D3 |
| 817 | D3 | ℤ3 |
| 817 #31 | ℤ3 | ℤ3 |
| Subgroup | Realizable/Positively Realizable | Reason |
|---|---|---|
| S4 | Yes | By S4 Theorem |
| A4 | Yes | By A4 Theorem |
| D4 | Yes | By Figure 4 |
| D3 | Yes | By Figure 5 |
| D2 | Yes | By Subgroup Theorem |
| ℤ4 | Yes | By Subgroup Theorem |
| ℤ3 | Yes | By Subgroup Theorem |
| ℤ2 | Yes | By Subgroup Theorem |
| Subgroup | Positively Realizable | Reason |
|---|---|---|
| S5 | No | By Complete Graph Theorem |
| A5 | Yes | By A5 Theorem |
| ℤ5 ⋊ ℤ4 | No | By Complete Graph Theorem |
| S4 | No | By S4 Theorem |
| A4 | Yes | By A4 Theorem |
| D6 | No | By Lemma 2 |
| D5 | Yes | By Figure 6 |
| D4 | No | By Lemma 2 |
| D3 | Yes | By Figure 7 |
| D2 | Yes | By Figure 8 |
| ℤ6 | No | By Lemma 2 |
| ℤ5 | Yes | By Subgroup Theorem |
| ℤ4 | No | By Lemma 2 |
| ℤ3 | Yes | By Subgroup Theorem |
| ℤ2 | Yes | By Subgroup Theorem |
| Subgroup | Realizable | Reason |
|---|---|---|
| S5 | Yes | By Figure 9 |
| A5 | Yes | Positively realizable |
| S4 | Yes | By modifying Figure 9 |
| A4 | Yes | Positively realizable |
| D6 | Yes | By Figure 11 |
| D5 | Yes | Positively realizable |
| D4 | Yes | By Figure 10 |
| D3 | Yes | Positively realizable |
| D2 | Yes | Positively realizable |
| ℤ6 | Yes | By modifying Figure 11 |
| ℤ5⋊ℤ4 | Yes | By Figure 14 |
| ℤ5 | Yes | Positively realizable |
| ℤ4 | Yes | By modifying Figure 10 |
| ℤ3 | Yes | Positively realizable |
| ℤ2 | Yes | Positively realizable |
| Subgroup | Positively Realizable | Reason |
|---|---|---|
| A5 | No | By A5 Theorem |
| S4 | No | By S4 Theorem |
| A4 | No | By A4 Theorem |
| D6 | Yes | By Figure 18 |
| D5 | Yes | By Figure 19 |
| D4 | No | By Lemma 2 |
| D3×D3 | Yes | By Figure 20 |
| D3×ℤ3 | Yes | By modifying Figure 20 |
| D3 | Yes | By Subgroup Theorem |
| D2 | Yes | By Subgroup Theorem |
| ℤ6 | Yes | By Subgroup Theorem |
| ℤ5 | Yes | By Subgroup Theorem |
| ℤ4 | No | By Lemma 2 |
| (ℤ3 × ℤ3) x ℤ2 | Yes | By modifying Figure 20 |
| ℤ3 ×ℤ3 | Yes | By modifying Figure 20 |
| ℤ3 | Yes | By Subgroup Theorem |
| ℤ2 | Yes | By Subgroup Theorem |
| S6,A 6,S5,S 2[S 3],S4×ℤ2,A4×ℤ2 | No | By Complete Graph Theorem |
| ℤ5 ⋊ ℤ4, (ℤ3 × ℤ3) ⋊ ℤ4, D4 × ℤ2 | No | By Complete Graph Theorem |
| ℤ4 ×ℤ2, ℤ2 ×ℤ2 ×ℤ2 | No | By Complete Graph Theorem |
| Subgroup | Realizable | Reason |
|---|---|---|
| S6 | No | TSG+(K6) cannot be S6 or A6 |
| A6 | No | TSG+(K6) cannot be A6 |
| S5 | No | TSG+(K6) cannot be S5 or A5 |
| A5 | No | TSG+(K6) cannot be A5 |
| S4 × ℤ2 | No | TSG+(K6) cannot be S4 × ℤ2 or S4 |
| S4 | No | TSG+(K6) cannot be S4 or A4 |
| A4 × ℤ2 | No | TSG+(K6)cannotbeA4 × ℤ2orA4 |
| A4 | No | TSG+(K6) cannot be A4 |
| D6 | Yes | Positively realizable |
| D5 | Yes | Positively realizable |
| D4×ℤ2 | No | TSG+(K6) cannot be D4 × ℤ2, D4, ℤ4 × ℤ2, ℤ2 × ℤ2 × ℤ2 |
| D4 | Yes | By Figure 21 |
| S2[S3] | Yes | By Figure 20 |
| D3 × D3 | Yes | Positively realizable |
| D3 × ℤ3 | Yes | Positively realizable |
| D3 | Yes | Positively realizable |
| D2 | Yes | Positively realizable |
| ℤ6 | Yes | Positively realizable |
| ℤ5×ℤ4 | No | By 4-Cycle Theorem |
| ℤ5 | Yes | Positively realizable |
| ℤ4×ℤ2 | No | By 4-Cycle Theorem |
| ℤ4 | Yes | By modifying Figure 21 |
| (ℤ3 × ℤ3) ⋊ ℤ4 | Yes | By modifying Figure 20 |
| (ℤ3 × ℤ3) ⋊ ℤ2 | Yes | Positively realizable |
| ℤ3×ℤ3 | Yes | Positively realizable |
| ℤ3 | Yes | Positively realizable |
| ℤ2 x ℤ2 × ℤ2 | No | By Conway Gordon Theorem |
| ℤ2 | Yes | Positively realizable |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chambers, D.; Flapan, E. Topological Symmetry Groups of Small Complete Graphs. Symmetry 2014, 6, 189-209. https://doi.org/10.3390/sym6020189
Chambers D, Flapan E. Topological Symmetry Groups of Small Complete Graphs. Symmetry. 2014; 6(2):189-209. https://doi.org/10.3390/sym6020189
Chicago/Turabian StyleChambers, Dwayne, and Erica Flapan. 2014. "Topological Symmetry Groups of Small Complete Graphs" Symmetry 6, no. 2: 189-209. https://doi.org/10.3390/sym6020189




