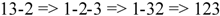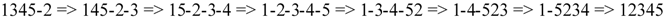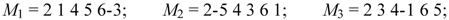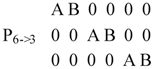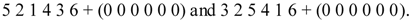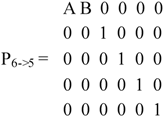A Higher Dimensional Description of the Structure of β-Mn

Abstract

The structure of β-Mn crystallizes in space group P4₁32. The pseudo 8-fold nature of the 4₁ axes makes it constitute an approximant to the octagonal quasicrystals. In this paper we analyze why a five-dimensional super space group containing mutually perpendicular 8-fold axes cannot generate P4₁32 on projection to 3-d space and how this may instead be accomplished from a six-dimensional model. A procedure for generating the actual structure of β-Mn lifted to six-dimensional space is given.

1. Introduction

The octagonal quasi crystals (oQC) discovered by Kuo and his co-workers [1,2], in the late 1980s are elusive for many reasons. They are difficult to make as attested to by the small number of oQCs found so far, and they are all, so far, produced by rapid quenching. Sample quality is therefore limited. The structural models suggested have been produced either by manually fitting distorted β-Mn structures to the observed electron diffraction pattern [3] or by simulations of the crystallization of a monoatomic liquid [4]. One further aspect that makes the structure of the oQCs difficult to analyse is the occurrence of one approximant, and one approximant only, namely β-Mn. The structure of β-Mn is shown in Figure 1. In this figure we have chosen to highlight the rod-packing aspect of the structure, showing how it may be decomposed into three mutually perpendicular helices of face-sharing tetrahedra. This aspect of the structure has been analysed fully by previously [5,6].

Figure 1. The structure of β-Mn represented as a packing of three mutually perpendicular sets of tetrahelices. Each tetrahelix has a symmetry close to 8₃.

Figure 1. The structure of β-Mn represented as a packing of three mutually perpendicular sets of tetrahelices. Each tetrahelix has a symmetry close to 8₃.

This approximant is enigmatic since β-Mn is acentric, cubic (P4₁32). By lifting β-Mn to higher space, we may generate a structure where the three mutually perpendicular, pseudo 8-fold axes are truly 8-fold. An axial QC would be expected to be describable as a projection from a five-dimensional, hyperspace. As it turns out, however, a simple analysis shows that this cannot be done for β-Mn. As we attempt to show in this paper, this conundrum is resolved by recourse to a six-dimensional, tri-iso-octagonal orthogonal super space group that contains both the five dimensional super space group that projects onto the oQC and the three dimensional cubic space group P4₁32 as sub periodic groups. The principle is simple: In six dimensional space, it is possible to generate three mutually perpendicular 8 fold axes, and on projection to a five dimensional subspace, one of these may be preserved, while a projection to three-dimensional space may preserve only 4 fold axis. The procedure we are using owns a lot to that used by Lee et al. in a paper dealing with the unexpected occurrence of mutually perpendicular 5 fold axis in large cubic intermetallic structures [7].

2. Results and Discussion

The purpose of this paper is to show why a five-dimensional space description of the oQC approximant β-Mn is unsatisfactory and why a six dimensional description much better captures the nature of this structure. We will do this by considering the implications of five- and six-dimensional descriptions on this structure

2.1. Preliminary Considerations is Five Dimensional Space

An 8-fold axis in five-dimensional space is most easily described as the operation that permutes positive and negative axial direction with respect to one invariant axis. This is perfectly analogous to the 4-fold rotation in three-dimensional space. Using the notation introduced by Deonarine and Birman [8], where a permutation is simply given as a sequence of integers and a change of sign as a minus we may write the 4-fold rotation in 3 dimensions as

And the 8-fold rotation in five-dimensional space as

There are obviously 5 independent and mutually perpendicular axes in five-dimensional space, and we may chose any set of three to attempt to generate the point group that will project onto three-dimensional space as 432. Interestingly, this turns out to be impossible, as we show below.

Using two orthogonal 8-fold axes as generators induces a total of 1920 symmetry operators in five-dimensional space, a factor of 2 short of the five-dimensional hyper cubic holohedry 2⁵ × 5! = 3840. This means that all permutations of indices are realized and half of the permutations of sign (those with even parity):

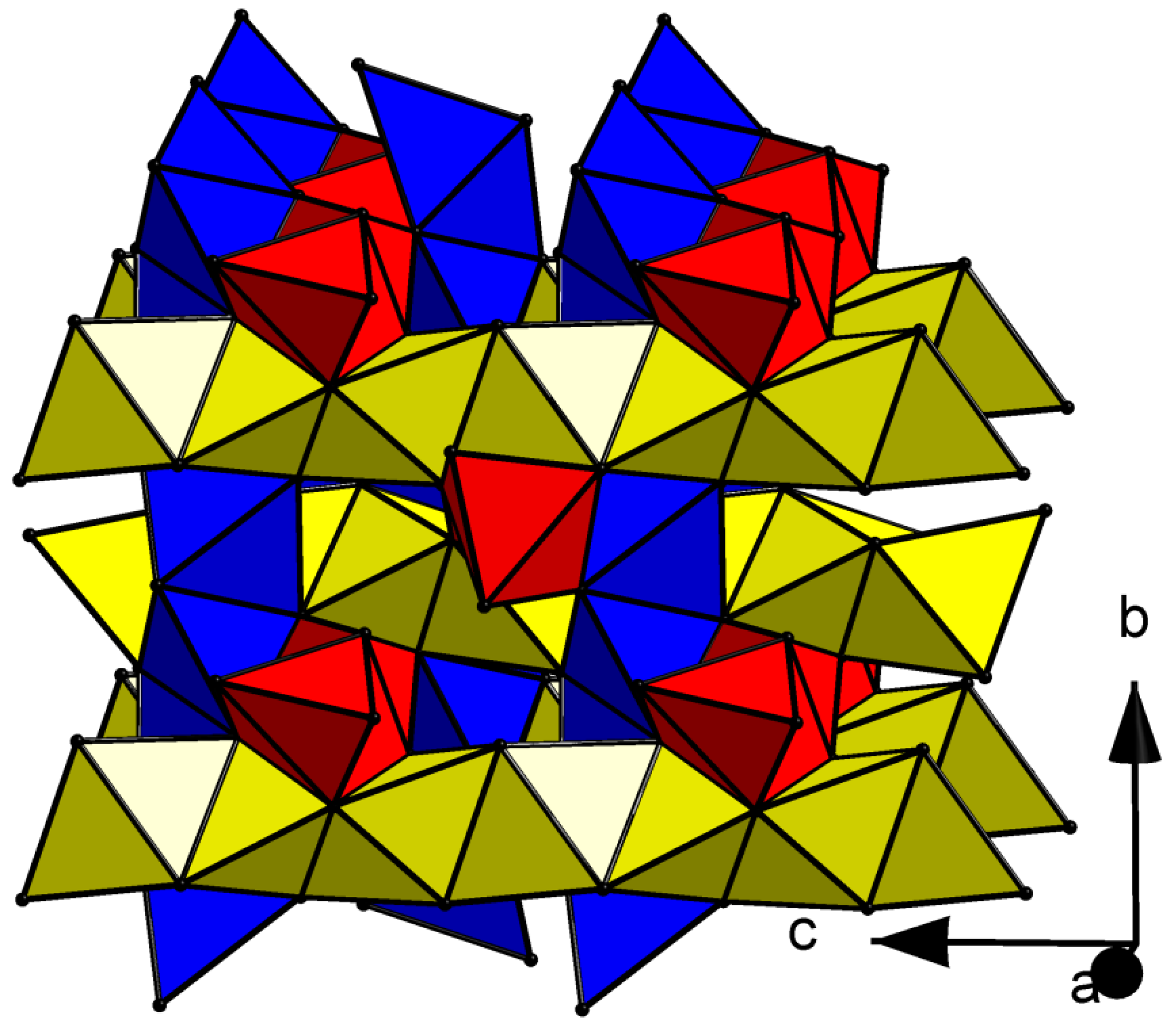
12345;

-1-2-3-45; -1-2-34-5; -1-23-4-5; -12-3-4-5; 1-2-3-4-5;

-1-2345; -12-345; -123-45; -1234-5; 1-2-345; 1-23-45; 1-234-5; 12-3-45; 12-34-5; 123-4-5;

Axial projection of these operators along any two axes will yield an inversion, e.g., dropping the last two indices yields:

123;

-1-2-3; -1-23; -12-3; 1-2-3;

-123; 1-23; 12-3;

and additionally some redundancies. Since all permutations in five-dimensional space are covered, the same will be true in three-dimensional space, and therefore the projection onto three-dimensional space of the five-dimensional superspace point group generated by two orthogonal 8-fold axes will be the cubic holohedry in three-dimensional space, m-3m. Thus we find that it is not possible to project the point group of β-Mn, 432 from a five-dimensional super space point group containing orthogonal 8-fold axes and hence not the three-dimensional space group P4₁32 from any five-dimensional super space group containing orthogonal 8-fold axes.

2.2. Preliminary Considerations is Six Dimensional Space

The holohedral hypercubic point group in six dimensional space is a bit of a monster with an order corresponding to the full set of permutations of positions and signs of all six indices, amounting to 2⁶ × 6! possible symmetry operations (=46080), a rather unwieldy number. Nevertheless, a full analysis of the character table for this group has been published [8].

The holohedral hypercubic six dimensional pointgroup B₆ contains five distinct sets of 8 fold operations. Basically these are quite similar. The 8-fold operation in six dimensional space is a hyper rotation that permutes four indices out of six, and changes the sign of one of those to produce an 8 fold operation. Simultaneously, the remaining two indices may be involved in another operation, creating a double rotation. The different possibilities are classified in the paper by Deonarine and Birman [8] as shown in Table 1.

Table 1. 8-fold hyper-rotations about the plane given by indices 1 and 2.

Class	43	45	47	49	51
Operation in12 plane	Invariant	Reflection in 1 or 2	C2 rotation perp 12	C2 rotation within 12	C4 rotation within 12
M1	1 2 4 5 6-3	1-2 4 5 6-3	-1-2 4 5 6-3	2 1 4 5 6-3	2-1 4 5 6-3
M2	1 2 5 6-3-4	1 2 5 6-3-4	1 2 5 6-3-4	1 2 5 6-3-4	-1-2 5 6-3-4
M3	1 2 6-3-4-5	1-2 6-3-4-5	-1-2 6-3-4-5	2 1 6-3-4-5	-2 1 6-3-4-5
M4	1 2-3-4-5-6	1 2-3-4-5-6	1 2-3-4-5-6	1 2-3-4-5-6	1 2-3-4-5-6
M5	1 2-4-5-6 3	1-2-4-5-6 3	-1-2-4-5-6 3	2 1-4-5-6 3	2-1-4-5-6 3
M6	1 2-5-6 3 4	1 2-5-6 3 4	1 2-5-6 3 4	1 2-5-6 3 4	-1-2-5-6 3 4
M7	1 2-6 3 4 5	1-2-6 3 4 5	-1-2-6 3 4 5	2 1-6 3 4 5	-2 1-6 3 4 5
M8	1 2 3 4 5 6	1 2 3 4 5 6	1 2 3 4 5 6	1 2 3 4 5 6	1 2 3 4 5 6

Table 1. 8-fold hyper-rotations about the plane given by indices 1 and 2.

Class	43	45	47	49	51
Operation in12 plane	Invariant	Reflection in 1 or 2	C2 rotation perp 12	C2 rotation within 12	C4 rotation within 12
M1	1 2 4 5 6-3	1-2 4 5 6-3	-1-2 4 5 6-3	2 1 4 5 6-3	2-1 4 5 6-3
M2	1 2 5 6-3-4	1 2 5 6-3-4	1 2 5 6-3-4	1 2 5 6-3-4	-1-2 5 6-3-4
M3	1 2 6-3-4-5	1-2 6-3-4-5	-1-2 6-3-4-5	2 1 6-3-4-5	-2 1 6-3-4-5
M4	1 2-3-4-5-6	1 2-3-4-5-6	1 2-3-4-5-6	1 2-3-4-5-6	1 2-3-4-5-6
M5	1 2-4-5-6 3	1-2-4-5-6 3	-1-2-4-5-6 3	2 1-4-5-6 3	2-1-4-5-6 3
M6	1 2-5-6 3 4	1 2-5-6 3 4	1 2-5-6 3 4	1 2-5-6 3 4	-1-2-5-6 3 4
M7	1 2-6 3 4 5	1-2-6 3 4 5	-1-2-6 3 4 5	2 1-6 3 4 5	-2 1-6 3 4 5
M8	1 2 3 4 5 6	1 2 3 4 5 6	1 2 3 4 5 6	1 2 3 4 5 6	1 2 3 4 5 6

Projecting these operations into five dimensional space and three dimensional space, respectively, making the operations axial may be achieved using the projection matrices:

Now it can be shown by direct computation that a basis set consisting of three mutually perpendicular 8 fold axes from class 43, that is, the set will generate a group of order 3840 that contains a hyper space inversion centre -1-2-3-4-5-6:

This is again incompatible with the point group 432. Since classes 45 and 47 generate the same inversion operation, all these cases may be discarded for our purposes. The remaining choices are class 49 and 51. The projection matrix P_6->5 should result in an axial 5 dimensional group with 8-fold rotational symmetry. For class 49 this requires that A + B = B + A, which is trivially true. For class 51, that requirement is instead A + B = B − A = − A − B = − B + A which is equally trivially incompatible with any other solution than A = B = 0, rendering the class 51 option unhelpful.

The only remaining choice for a point group is that generated by a set of three mutually perpendicular 8 fold axes of class 49:

Direct computation yields a point group with only 576 elements. This group contains no axes of 12- 10- or 5-fold symmetry. To generate the corresponding super space group that contains 8₃ operations as reported for the oQC, we simply add a translational part to the point group operations so that the three generators become

Again a direct computation shows that this yields a closed group with 576 elements. In the table below, the following information is given. The different classes of the rotational part of the super space group operations as defined by Deonarine and Birman, the general type of operation such as single rotation (C_x), double rotation (C_x, C_y), etc., the number of such operations in the group, the typical form from which the invariants are easily found, the translational part of the operations given as multiples of eighths along the six axes in super space, and finally a generation of the operation from the basic operations M₁, M₂, M₃ are all given in Table 2 below. The generating form is a sequence of basis operations needed to generate a particular operation. Example: Since the 3-fold double rotation that permutes the even indices and the odd indices simultaneously, (class 39) is generated by the sequence of operations M₂(M₁(M₁(M₃))), the generating form of that operation is given as 2113.

Table 2. Summary of the symmetry operators in the super space group.

Deonarine-Birman class	Type	Number	Typical form	Translational part (* 1/8)	Generating form M1, M2, M3
50	C4, C4	144	2-1 4 5 6 3	3 7 3 3 3 7	111111212
49	C8, C2	144	2 1 4 5 6-3	3 3 3 7 3 7	1
39	C3, C3	64	3 4 5 6 1 2	0 0 0 0 0 0	2113
35	C3, C2	48	1 4-3 6-5 2	4 0 4 0 0 0	2111
31	C3	16	1 4 3 6 5 2	0 0 0 0 0 0	112112112111
24	C2, C2 ,C2	36	-1-2 5 6 3 4	2 4 6 6 2 2	222113
22	C4, C2,	72	1-2-5 6 3 4	2 4 2 6 6 2	212111
20	C4, C4	36	1 2 5 6-3-4	6 6 2 2 2 4	11
5	C2,C2	9	1 2-3-4-5-6	4 4 4 6 0 2	1111
3	C2	6	1 2 3-4 5-6	0 4 0 6 0 2	21111121
1	C1	1	1 2 3 4 5 6	0 0 0 0 0 0	11111111

Table 2. Summary of the symmetry operators in the super space group.

Deonarine-Birman class	Type	Number	Typical form	Translational part (* 1/8)	Generating form M1, M2, M3
50	C4, C4	144	2-1 4 5 6 3	3 7 3 3 3 7	111111212
49	C8, C2	144	2 1 4 5 6-3	3 3 3 7 3 7	1
39	C3, C3	64	3 4 5 6 1 2	0 0 0 0 0 0	2113
35	C3, C2	48	1 4-3 6-5 2	4 0 4 0 0 0	2111
31	C3	16	1 4 3 6 5 2	0 0 0 0 0 0	112112112111
24	C2, C2 ,C2	36	-1-2 5 6 3 4	2 4 6 6 2 2	222113
22	C4, C2,	72	1-2-5 6 3 4	2 4 2 6 6 2	212111
20	C4, C4	36	1 2 5 6-3-4	6 6 2 2 2 4	11
5	C2,C2	9	1 2-3-4-5-6	4 4 4 6 0 2	1111
3	C2	6	1 2 3-4 5-6	0 4 0 6 0 2	21111121
1	C1	1	1 2 3 4 5 6	0 0 0 0 0 0	11111111

2.3. Projection to 3D

The general projection matrix to 3D is given by

And the simplest alternative is A = 1, B = 0. Allowing this projector to act on the different classes of the 6D point group we find that those generate the much reduced set given in Table 3 below.

Table 3. Projected symmetry operations in three-dimensional space.

Classes	Typical form	Translational part eights	3D symmetry
1,3,31	1 3 5	0 0 0	x y z
5,35	1-3-5	4 4 0	½ + x ½-y-z
20	1 5-3	6 2 2	¾ + x ¼ + z ¼-y
22	1-5 3	2 2 6	¼ + x ¼-z ¾ + y
24	-1 5 3	2 6 2	¼- x ¾ + z ¼ + y
39	3 5 1	0 0 0	y z x
49,50	2 4 6	3 3 3	Creation of a second independent position

Table 3. Projected symmetry operations in three-dimensional space.

Classes	Typical form	Translational part eights	3D symmetry
1,3,31	1 3 5	0 0 0	x y z
5,35	1-3-5	4 4 0	½ + x ½-y-z
20	1 5-3	6 2 2	¾ + x ¼ + z ¼-y
22	1-5 3	2 2 6	¼ + x ¼-z ¾ + y
24	-1 5 3	2 6 2	¼- x ¾ + z ¼ + y
39	3 5 1	0 0 0	y z x
49,50	2 4 6	3 3 3	Creation of a second independent position

The 3D space group may be easily identified directly from this as P4₁32. Each position in 6D space will generate two separate orbits depending on the values of the odd and even coordinates respectively.

For this case, it is trivial to determine the single position in 6D space that generates the β-Mn structure upon projection into 3D. The values of coordinates 1, 3 and 5 are given by the x, y and z coordinates of the first atomic position in β-Mn, i.e., (0.0635 0.0635 0.0635). The second position is generated by the action of the symmetry operator 2 1 4 5 6-3 + (3/8 3/8 3/8 7/8 3/8 7/8) on this position, and subsequent projection. The result of this procedure is 2 4 6 + (3/8 3/8 3/8), and since the second position in β-Mn is (0.125 0.20221 0.45221), we get immediately that values of coordinates 2, 4 and 6 must be (−0.25 −0.17579 0.075221), and that the single position in 6d space may be specified as (0.0635, −0.25, 0.0635, −0.17579, 0.0635, 0.07721). This is not a general (576 fold) position in the super space group, but a special (192 fold) position, of 3 fold degeneracy. Specifically the operations that leave this position invariant are those of class 31 that permute the odd indices, keeping the even indices invariant:

It is of course to be expected that the 3-fold degeneracy of position 8c in β-Mn must be generated by a 3-fold degenerate position in six-dimensional space.

2.4. Projection to 5D

To preserve the 8-fold nature of the unique axis, we need to fix the values A and B of the projection matrix:

Since the 8-fold rotation also permutes A and B, those must be equal, or the 8 fold axis will degenerate into two separate orbits. Putting A = B = 0.5 generates a projection according to Table 4.

Table 4. Preservation of the unique 8-fold axis upon projection into five-dimensional space.

Operation	Rotational part	Translational part	Projection rotation part	Projection transational part
M11	2 1 4 5 6-3	3 3 3 7 3 7	1' 4 5 6-3	3 3 7 3 7
M12	1 2 5 6-3-4	6 6 2 2 2 4	1' 5 6-3-4	6 2 2 2 4
M13	2 1 6-3-4-5	1 1 5 1 7 5	1' 6-3-4-5	1 5 1 7 5
M14	1 2-3-4-5-6	4 4 4 6 0 2	1' -3-4-5-6	4 4 6 0 2
M15	2 1-4-5-6 3	7 7 1 7 5 3	1' -4-5-6 3	7 1 7 5 3
M16	1 2-5-6 3 4	2 2 2 4 6 6	1' 2-5-6 3 4	2 2 4 6 6
M17	2 1-6 3 4 5	5 5 7 5 1 5	1'-6 3 4 5	5 7 5 1 5
M18	1 2 3 4 5 6	0 0 0 0 0 0	1' 3 4 5 6	0 0 0 0 0

Table 4. Preservation of the unique 8-fold axis upon projection into five-dimensional space.

Operation	Rotational part	Translational part	Projection rotation part	Projection transational part
M11	2 1 4 5 6-3	3 3 3 7 3 7	1' 4 5 6-3	3 3 7 3 7
M12	1 2 5 6-3-4	6 6 2 2 2 4	1' 5 6-3-4	6 2 2 2 4
M13	2 1 6-3-4-5	1 1 5 1 7 5	1' 6-3-4-5	1 5 1 7 5
M14	1 2-3-4-5-6	4 4 4 6 0 2	1' -3-4-5-6	4 4 6 0 2
M15	2 1-4-5-6 3	7 7 1 7 5 3	1' -4-5-6 3	7 1 7 5 3
M16	1 2-5-6 3 4	2 2 2 4 6 6	1' 2-5-6 3 4	2 2 4 6 6
M17	2 1-6 3 4 5	5 5 7 5 1 5	1'-6 3 4 5	5 7 5 1 5
M18	1 2 3 4 5 6	0 0 0 0 0 0	1' 3 4 5 6	0 0 0 0 0

This means that the 8₃ axis is preserved under the projection. Examining another 8-fold axis of rotation is enlightening. The orbit splits into 4 pairs of operations that leave the plane spanned by the basis vectors 3 and 4 invariant according to Table 5. It is notable that the translational part of the operations within that invariant plane is always ½ ½. Apart from this translational part, the operation contains an inversion of the other three indices. This means that the projection generates binary operations perpendicular to the unique axis in five-dimensional space.

3. Conclusions

Although the super space group of the oQC may be generated directly in five-dimensional space, without recourse to the procedure outlined above, we believe that it is useful to involve an analysis of the relationship between the octagonal QC and the structure of β-Mn in six-dimensional space if the cubic approximant is going to be used in the modelling of the structure of the oQC.

Table 5. Orbit splitting of an 8-fold axis upon projection into five-dimensional space.

Operation	Rotational part	Translational part	Projection rotation part	Projection translatinal part	New orbit
M21	2-5 4 3 6 1	3 7 3 3 3 7	1' 4 3 6 1	5 3 3 3 7	I
M22	-5-6 3 4 1 2	2 4 6 6 2 2	2' 3 4 1 2	3 6 6 2 2	II
M23	-6-1 4 3 2-5	7 5 1 1 5 1	3' 4 3 2-5	6 1 1 5 1	II
M24	-1-2 3 4-5-6	0 2 4 4 4 6	4' 3 4-5-6	1 4 4 4 6	IV
M25	-2 5 4 3-6-1	5 3 7 7 1 7	-1' 4 3-6-1	4 7 7 1 7	I
M26	5 6 3 4-1-2	6 6 2 2 2 4	-2' 3 4-1-2	6 2 2 2 4	II
M27	6 1 4 3-2 5	1 5 5 5 7 5	-3' 4 3-2 5	3 5 5 7 5	III
M28	1 2 3 4 5 6	0 0 0 0 0 0	-4' 3 4 5 6	0 0 0 0 0	IV

Table 5. Orbit splitting of an 8-fold axis upon projection into five-dimensional space.

Operation	Rotational part	Translational part	Projection rotation part	Projection translatinal part	New orbit
M21	2-5 4 3 6 1	3 7 3 3 3 7	1' 4 3 6 1	5 3 3 3 7	I
M22	-5-6 3 4 1 2	2 4 6 6 2 2	2' 3 4 1 2	3 6 6 2 2	II
M23	-6-1 4 3 2-5	7 5 1 1 5 1	3' 4 3 2-5	6 1 1 5 1	II
M24	-1-2 3 4-5-6	0 2 4 4 4 6	4' 3 4-5-6	1 4 4 4 6	IV
M25	-2 5 4 3-6-1	5 3 7 7 1 7	-1' 4 3-6-1	4 7 7 1 7	I
M26	5 6 3 4-1-2	6 6 2 2 2 4	-2' 3 4-1-2	6 2 2 2 4	II
M27	6 1 4 3-2 5	1 5 5 5 7 5	-3' 4 3-2 5	3 5 5 7 5	III
M28	1 2 3 4 5 6	0 0 0 0 0 0	-4' 3 4 5 6	0 0 0 0 0	IV