Flexibility of Hydrogen Bond and Lowering of Symmetry in Proton Conductor
Abstract
:1. Introduction
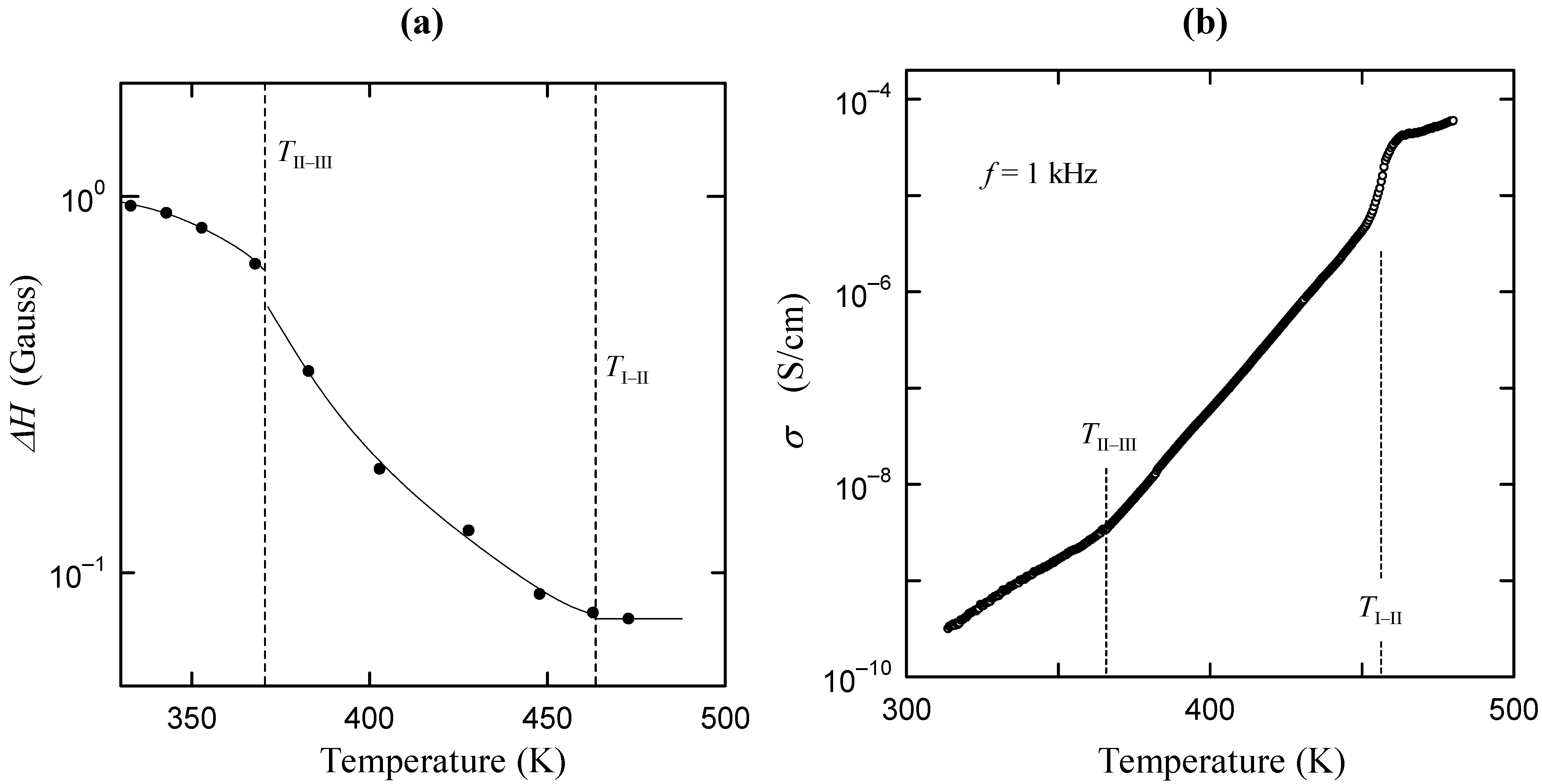
2. Experimental Procedure and Crystal Structure
2.1. Experimental Procedure
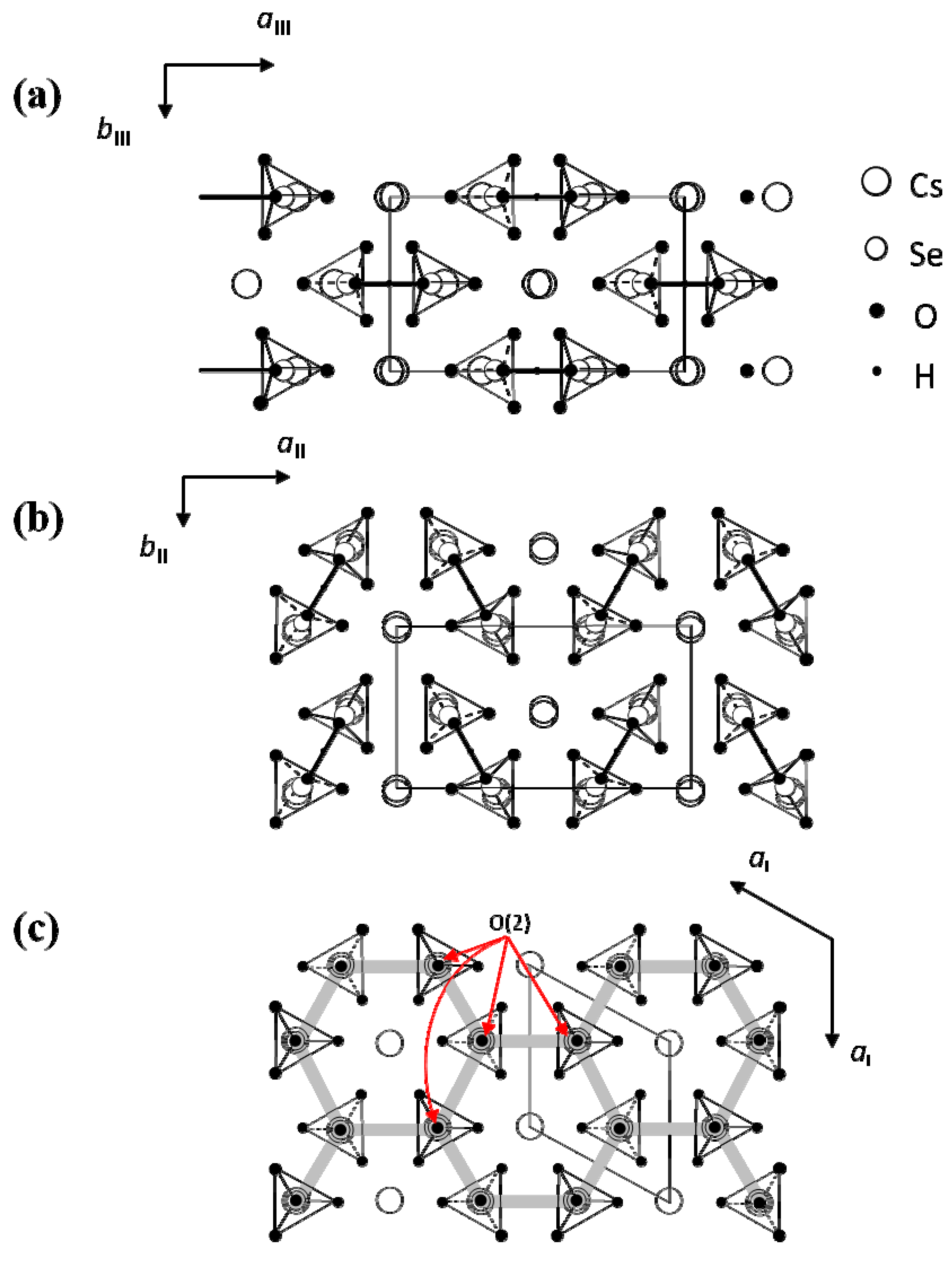
2.2. Crystal Structure
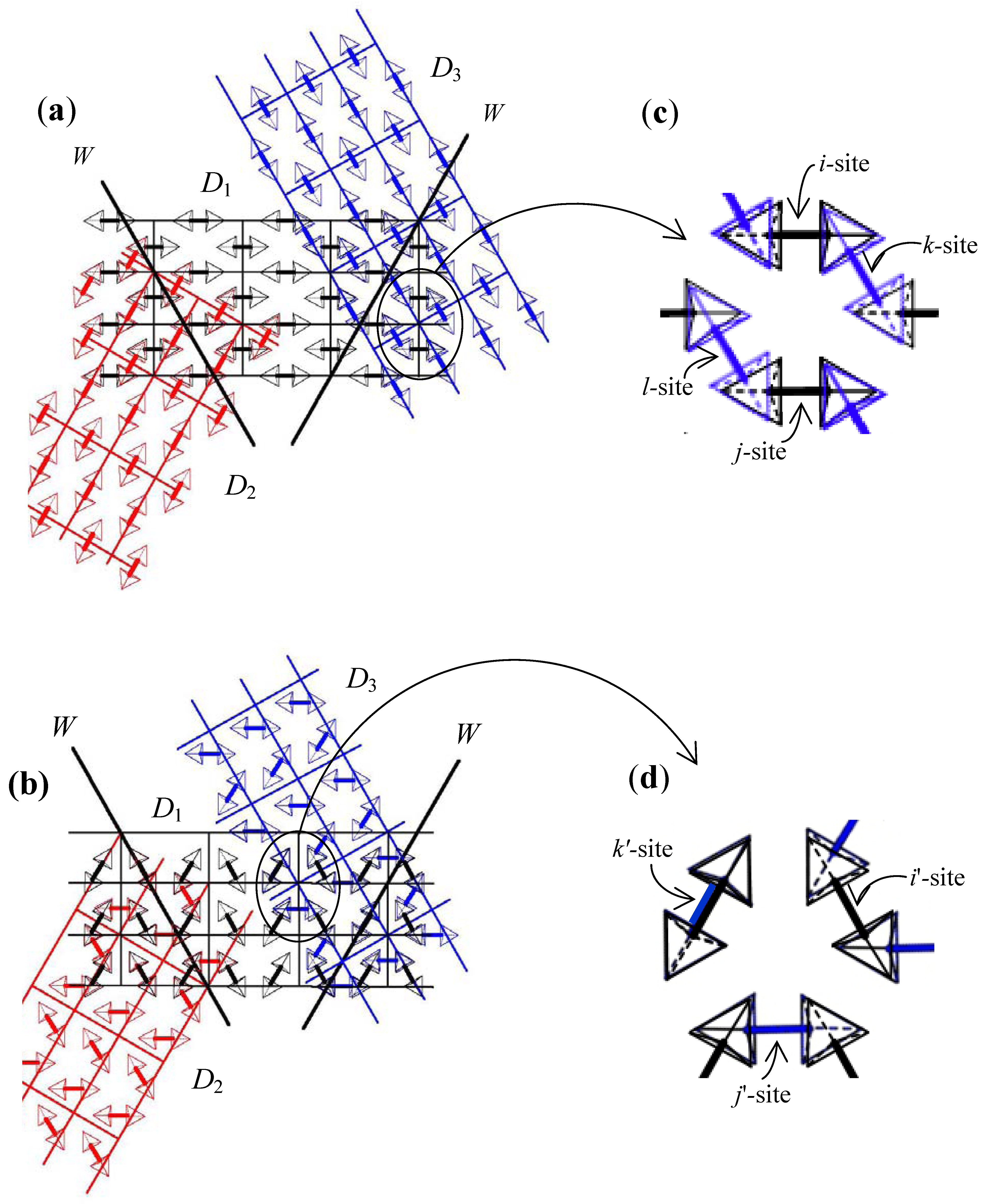
 direction, as shown in Figure 2b. In phase I, the Cs3H(SeO4)2 crystal belongs to a trigonal system with the space group
direction, as shown in Figure 2b. In phase I, the Cs3H(SeO4)2 crystal belongs to a trigonal system with the space group  . The lattice constants become aI = 6.4260(6) Å, cI = 23.447(2) Å, Z = 3 at 470 K [15]. As shown in Figure 2c, the distance between neighboring O(2) atoms is same in time-averaged structure. Considering that hydrogen bond is composed between O(2) atoms, three equivalent positions for a proton appear in phase I, and proton conductivity is realized in phase I. In this way, from the crystal structure, we can clearly see that the phase transitions of TII–III and TI–II are structural phase transition. Especially, it is interesting property that the orientation of the hydrogen bond by the phase transition of TII–III mainly changes. This result implies that the difference in the geometrical arrangement of hydrogen bond observed in phases III and II includes the information for the flexibility of proton motion and the lowering of crystal symmetry at TII–III phase transition.
. The lattice constants become aI = 6.4260(6) Å, cI = 23.447(2) Å, Z = 3 at 470 K [15]. As shown in Figure 2c, the distance between neighboring O(2) atoms is same in time-averaged structure. Considering that hydrogen bond is composed between O(2) atoms, three equivalent positions for a proton appear in phase I, and proton conductivity is realized in phase I. In this way, from the crystal structure, we can clearly see that the phase transitions of TII–III and TI–II are structural phase transition. Especially, it is interesting property that the orientation of the hydrogen bond by the phase transition of TII–III mainly changes. This result implies that the difference in the geometrical arrangement of hydrogen bond observed in phases III and II includes the information for the flexibility of proton motion and the lowering of crystal symmetry at TII–III phase transition. 3. Results and Discussion
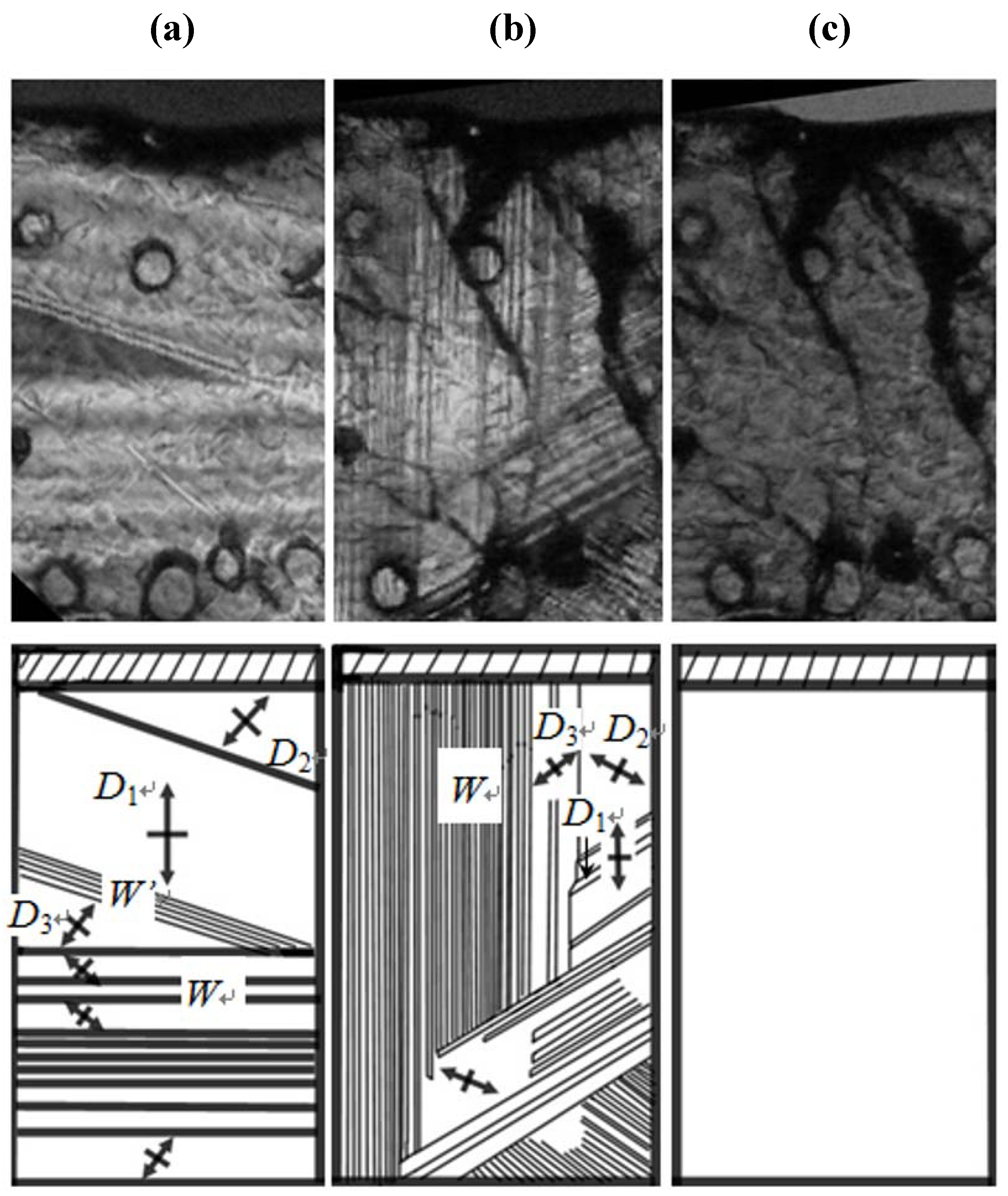
 . Considering that in the phase transition at TI–II domain boundaries vanish, the averaged structure of the crystal structure in all domains in phase II becomes crystal structure in phase I. That is, the crystal structure in phase I is obtained by averaging and superposing the crystal structure in all domains with the symmetry of domain boundary.
. Considering that in the phase transition at TI–II domain boundaries vanish, the averaged structure of the crystal structure in all domains in phase II becomes crystal structure in phase I. That is, the crystal structure in phase I is obtained by averaging and superposing the crystal structure in all domains with the symmetry of domain boundary. 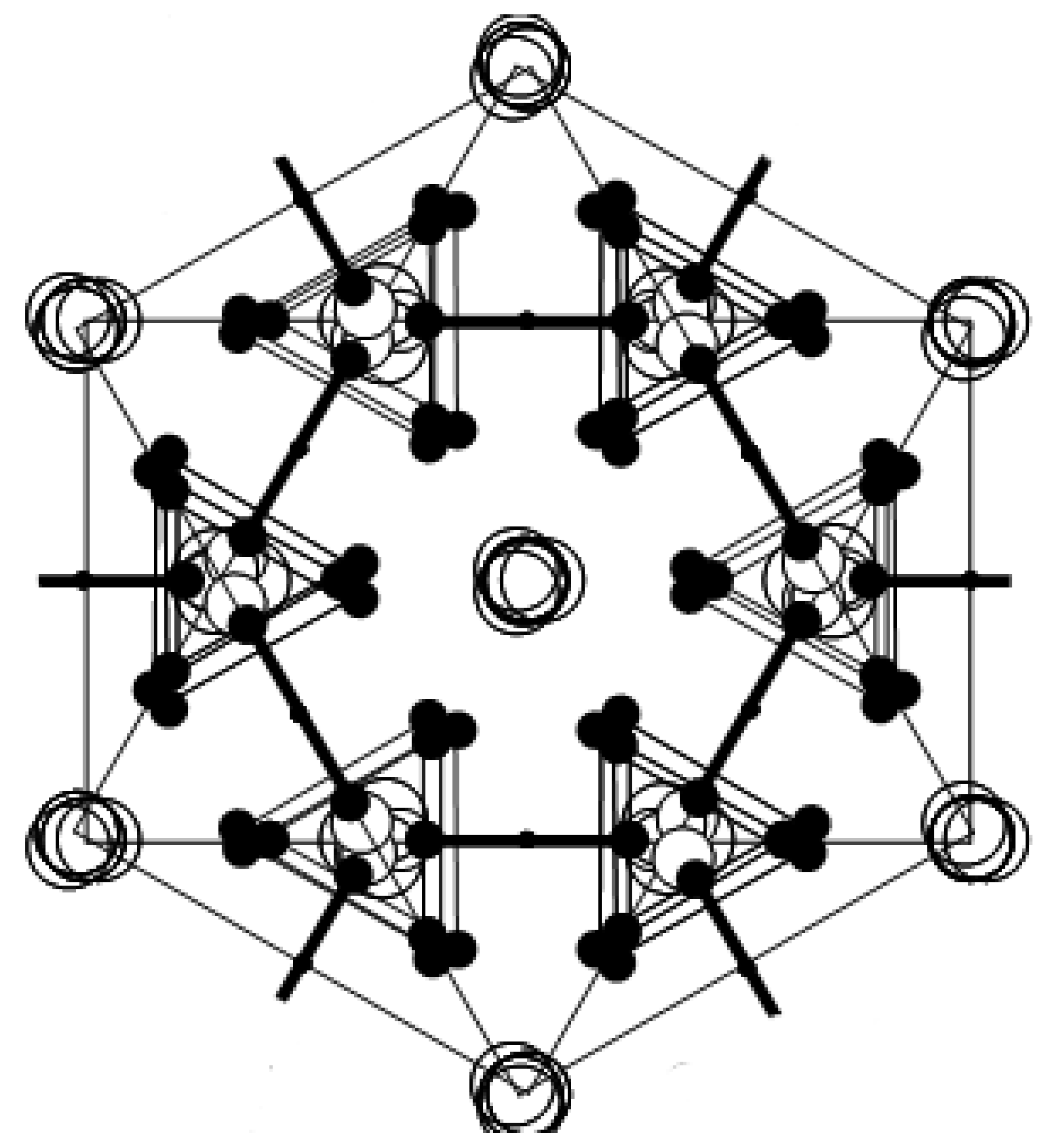
4. Conclusions
References
- Gesi, K. Dielectric properties and phase transitions in X3H(SO4)2 and X3D(SO4)2 crystals (X: K, Rb). J. Phys. Soc. Jpn. 1980, 48, 886–889. [Google Scholar] [CrossRef]
- Baranov, A.I. Crystals with disordered hydrogen-bond networks and superprotonic conductivity: Review. Crystallogr. Rep. 2003, 48, 1012–1037. [Google Scholar] [CrossRef]
- Pawlowski, A.; Pawlaczyk, C.; Hilzcer, B. Electric conductivity in crystal group Me3H(SeO4)2 (Me: NH+4, Rb+, Cs+). Solid State Ionics 1990, 44, 17–19. [Google Scholar] [CrossRef]
- Kamimura, H.; Watanabe, S. A novel approach to the mechanism of ionic conductivity below and at the ferroelastic phase transition in the zero-dimensional hydrogen-bonded crystal M3H(XO4)2 with M = Rb or Cs; X = S or Se. Phil. Mag. 2001, B81, 1011–1019. [Google Scholar] [CrossRef]
- Matsuo, Y.; Takahashi, K.; Ikehata, S. Evidence for proton conduction below superionic transition on Rb3H(SeO4)2. Solid State Commun. 2001, 119, 79–81. [Google Scholar] [CrossRef]
- Matsuo, Y.; Hatori, J.; Nakajima, Y.; Ikehata, S. Superprotonic and ferroelastic phase transition in K3H(SO4)2. Solid State Commun. 2004, 130, 269–274. [Google Scholar] [CrossRef]
- Kamimura, H.; Matsuo, Y.; Ikehata, S.; Ito, T.; Komukae, M.; Osaka, T. On the mechanism of superionic conduction in the zero-dimensional hydrogen-bonded crystals M3H(XO4)2 with M = K, Rb, Cs and X = S, Se. Phys. Status Solidi B 2004, 241, 61–68. [Google Scholar] [CrossRef]
- Matsuo, Y.; Hatori, J.; Yoshida, Y.; Saito, K.; Ikehata, S. Proton conductivity and spontaneous strain below superprotonic phase transition in Rb3H(SeO4)2. Solid State Ionics 2005, 176, 2461–2465. [Google Scholar] [CrossRef]
- Hatori, J.; Matsuo, Y.; Ikehata, S. The relation between elasticity and the superprotonic phase transition temperature for M3H(XO4)2. Solid State Commun. 2006, 140, 452–454. [Google Scholar] [CrossRef]
- Ishii, T. Superprotonic phase transition in M3H(XO4)2. Solid State Ionics 2007, 178, 667–670. [Google Scholar] [CrossRef]
- Matsuo, Y.; Tanaka, Y.; Hatori, J.; Ikehata, S. Effect of uniaxial stress in superprotonic phase transition in Cs3H(SeO4)2. Solid State Ionics 2008, 179, 1125–1127. [Google Scholar] [CrossRef]
- Komukae, M.; Osaka, T.; Kaneko, T.; Makita, Y. Dielectric study of phase transitions in Cs3H(SeO4)2 and its isotope effect. J. Phys. Soc. Jpn. 1985, 54, 3401–3405. [Google Scholar] [CrossRef]
- Baranov, A.I.; Tregubchenko, A.V.; Shuvalov, L.A.; Shchagina, N.M. Structural phase transitions and proton conductivity of Cs3H(SeO4)2 and (NH4)3H(SeO4)2 crystals. Sov. Solid State Phys. 1987, 29, 1448–1449. [Google Scholar]
- Merinov, B.V.; Baranov, A.I.; Shuvalov, L.A. Crystal structure of ferroelastic phase II of Cs3H(SeO4)2. Sov. Phys. Crystallogr. 1991, 36, 639–642. [Google Scholar]
- Merinov, B.V.; Baranov, A.I.; Shuvalov, L.A. Crystal structure and mechanism of protonic conductivity of the superionic phase of Cs3H(SeO4)2. Sov. Phys. Crystallogr. 1990, 35, 200. [Google Scholar]
- Merinov, B.V.; Bolotina, N.B.; Baranov, A.I.; Shuvalov, L.A. Crystal structure of Cs3H(SeO4)2 (T = 295 K) and its changes at the phase transitions. Sov. Phys. Crystallogr. 1988, 33, 824–827. [Google Scholar]
- Komukae, M.; Sakata, K.; Osaka, T.; Makita, Y. Optical and x-ray studies in ferroelastic Cs3H(SeO4)2. J. Phys. Soc. Jpn. 1994, 63, 1009–1017. [Google Scholar] [CrossRef]
- Matsuo, Y.; Tanaka, Y.; Hatori, J.; Ikehata, S. Proton activity and spontaneous strain of Cs3H(SeO4)2 in the phase transition at 369 K. Solid State Commun. 2005, 134, 361–365. [Google Scholar]
- Sapriel, J. Domain-wall orientation in ferroelastic. Phys. Rev. B 1975, 12, 5128–5140. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yoshida, Y.; Hatori, J.; Kawakami, H.; Matsuo, Y.; Ikehata, S. Flexibility of Hydrogen Bond and Lowering of Symmetry in Proton Conductor. Symmetry 2012, 4, 507-516. https://doi.org/10.3390/sym4030507
Yoshida Y, Hatori J, Kawakami H, Matsuo Y, Ikehata S. Flexibility of Hydrogen Bond and Lowering of Symmetry in Proton Conductor. Symmetry. 2012; 4(3):507-516. https://doi.org/10.3390/sym4030507
Chicago/Turabian StyleYoshida, Yukihiko, Junko Hatori, Hinako Kawakami, Yasumitsu Matsuo, and Seiichiro Ikehata. 2012. "Flexibility of Hydrogen Bond and Lowering of Symmetry in Proton Conductor" Symmetry 4, no. 3: 507-516. https://doi.org/10.3390/sym4030507



