1. Introduction
The study of
N =2 supersymmetric (SUSY) extensions of nonlinear evolution equations has been largely studied in the past [
1,
2,
3,
4,
5,
6,
7,
8] in terms of integrability conditions and solutions. Such extensions are given as a Grassmann-valued partial differential equation with one dependent variable
A(
x,
t;
θ1,
θ2)which is assumed to be bosonic to get nontrivial extensions. The independent variables are given as a set of even (commuting) space
x and time
t variables and a set of odd (anticommuting) variables variables
θ1,
θ2. Since the odd variables satisfy
![Symmetry 04 00441 i001]()
, the dependent variable
A admits the following finite Taylor expansion
where
u and
v are bosonic complex valued functions and
ξ1 and
ξ2 are fermionic complex valued functions. In this paper, we show that some of these extensions can be related to a linear partial differential equation (PDE) by assuming that
A is a chiral superfield [
9]. Proving the integrability of an equation by linearization has been largely studied in the classical case [
10,
11] and has found new developments in the
N=1 formalism [
12]. We propose a similar development in the
N=2 formalism. In
N=2 SUSY, we consider a pair of supercovariant derivatives defined as
which satisfy the anticommutation relations
![Symmetry 04 00441 i004]()
and {
D1,
D2} = 0. We consider also the complex supercovariant derivatives
which satisfy {
D±,
D±}=0 and
![Symmetry 04 00441 i006]()
. In terms of the complex Grassmann variables
![Symmetry 04 00441 i007]()
, the derivatives Equation (3) admits the following representation
and the superfield A given in Equation (1) writes
The fermionic complex valued functions
ρ± are defined as
![Symmetry 04 00441 i010]()
.
Chiral superfields are superfields of type Equation (5) satisfying D+A=0. In terms of components, we get
or equivalently ξ2 = iξ1 and v= -iux.
In the subsequent sections, we produce solutions of
N=2 SUSY extensions of the Korteweg–de Vries [
1] (SKdV
α), modified Korteweg–de Vries [
6] (SmKdV) and Burgers [
5] (SB) equations from a chiral superfield point of view. In this instance, the equations, in terms of the complex covariant derivatives Equation (3), reads, respectively, as
where [
X,
Y]=
XY -
YX is the commutator. In Equation (7),
α is an arbitrary parameter but we will consider only the integrable cases [
1] where
α = −2,1,4.
In this paper, we start by presenting a general reduction procedure of these equations using chiral superfields (
Section II). We thus treat SKdV
-2 and SmKdV together and construct classical
N super soliton solutions [
4,
7,
8,
13] and an infinite set of similarity solutions [
7]. In
Section IV, we demonstrate the existence of special
N super soliton solutions, called virtual solitons [
5], for the SUSY extensions of the KdV equation with
α=1,4 and the Burgers equation using a related linear partial differential equation. The last section is devoted to a
N=4 extension of the KdV equation [
6] in an attempt to construct a general
N super virtual soliton solution.
2. General Approach and Chiral Solutions
Here, we propose a general approach for the construction of chiral solutions of SUSY extensions. This approach avoids treating SUSY extensions in terms of components of the bosonic field A given in Equation (1). Assuming D+A = 0, we get the chiral property {D+,D-}A = D+D-A = Ax and the Equations (7–9) reduce to
Note that these equations may be evidently treated as classical [
14] PDE's, but remains SUSY extensions due to the Grassmannian dependence of the bosonic field
A.
The absence of the Grassmannian variables
θ+ and
θ- derivatives in Equations (10–12) indicates that the odd sectors of chiral solutions should be free from fermionic constraint. This property is in accordance with the integrability of these extensions due to arbitrary bosonization of the fermionic components [
15] of the bosonic superfield
A.
From the classical case, we know that the methods of resolution of all these equations are similar. The same could be said for the SUSY case. Indeed, if we assume the introduction of a potential à such that A = Ãx in Equation (10) and after one integration with respect to x, we get
where the constant of integration is set to zero. The same is done on Equation (12) and leads to
We thus observe that the Equations (11,13,14) are now on an equal footing,
i.e., the order of the equation in
x is equal to the number of appearance of ∂
x in the nonlinear terms. This is standard in Hirota formalism. The choice
α = -2 in Equation (13) gives, up to a slight change of variable, the SmKdV Equation (11). This means that the known [
7]
N super soliton solutions and similarity solutions of SKdV
-2 will lead to similar types of solutions for the SmKdV Equation (11).
Now setting
in Equation (13), we obtain
The above equation reduces to the linear dispersive equation [
14]
for the special and only values
α=1 with
β1=
i and
α=4 with
![Symmetry 04 00441 i023]()
. For
α=-2, Equation (16) writes
which does not linearize but can be bilinearized taking β-2=i. It is discussed in the next Section.
A similar change of variable as in Equation (15) but with
Ã=
βB log
HB and
![Symmetry 04 00441 i025]()
in Equation (14) is assumed and leads to the linear Schrödinger Equation
3. SKdV-2 and SmKdV Equations
It is well known [
13,
14,
15,
16,
17,
18,
19] that we can generate via the Hirota bilinear formalism
N soliton and similarity solutions in the classical case and in SUSY
N=1 extensions. Recently, the formalism was adapted to
N=2 extensions [
4,
7,
8] by splitting the equation into two
N=1 equations, one fermionic and one bosonic. Our approach consists of treating the equation as a
N=2 extension without splitting it, but imposing chirality conditions.
Equation (11) can be bilinearized using the Hirota derivative defined as
Indeed, we take
à as in Equation (15) with
β-2=
i and
![Symmetry 04 00441 i028]()
, where
![Symmetry 04 00441 i029]()
are bosonic chiral superfields for
i=1,2. Equation (11) leads to the set of bilinear equations
This set is analogous to the corresponding bilinear equations in the classical mKdV equation [
14] but we deal with superfields
τ1 and
τ2.
In order to get chiral solutions, we have to solve the set of bilinear equations with the additional chiral property
D+τi = 0 for
i=1,2. It will lead to new solutions of the SmKdV equation which are related to our recent contribution [
7].
3.1. N Super Soliton Solutions
The one soliton solution is easily retrieved. Indeed, we cast
where α1 is an even parameter. Ψ1 is a N=2 chiral bosonic superfield defined as
and never appears on this form in other approaches of N = 2 SUSY. The parameters κ1 and ξ1 are, respectively, even and odd. The τ-functions Equation (23) together with Equation (24) solve the set of bilinear Equations (21,22) and give rise to a one super soliton solution. Since D+Ψ1=0, the resulting traveling wave solution is chiral.
Since we exhibit the three super soliton solution of the SmKdV equation in
Figure 1 and
Figure 2, we give the general expressions of
τ1 and
τ2:
Where
![Symmetry 04 00441 i036]()
and the Ψ
i's are defined as in Equation (24). The functions
τ1 and
τ2 solves the bilinear Equations (21) and (22) and are such that
D+τi = 0 for
i=1,2. The generalization to a
N super soliton solution is direct using the
τ-functions expressed above. The forms of the
τ-functions given above are new representations of super soliton solutions and have never been introduced before.
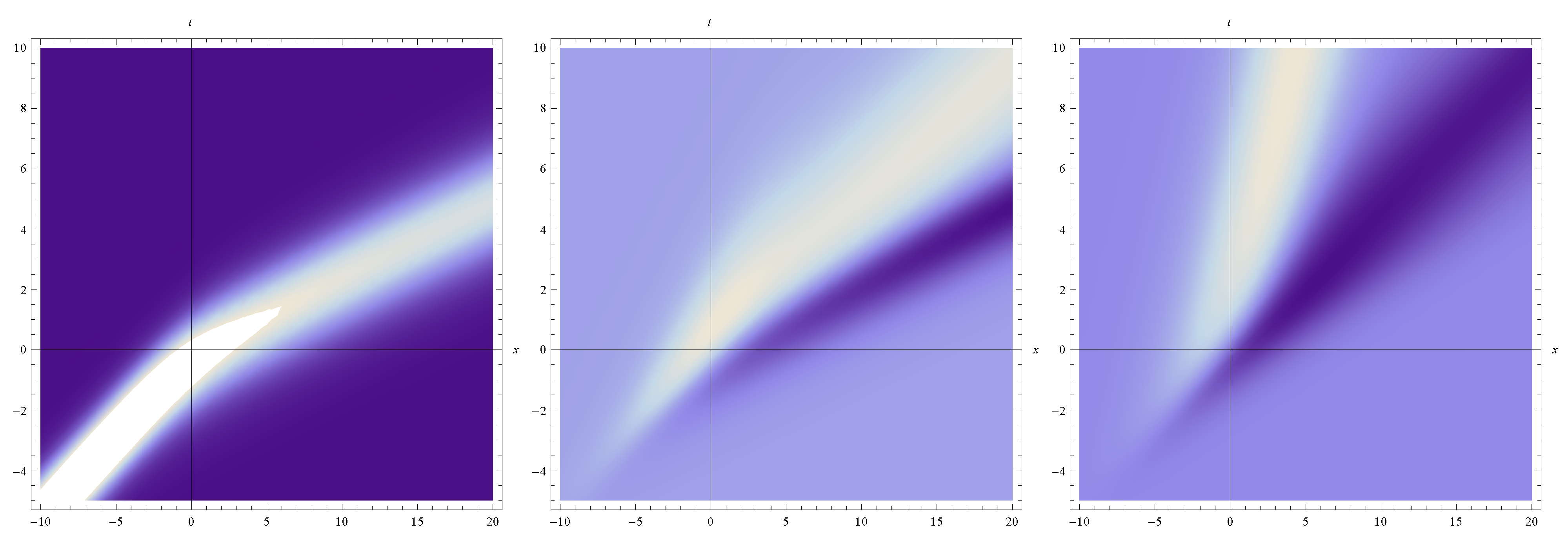
Figure 1.
The function Im(
v) of the three soliton solution of the SmKdV equation where
![Symmetry 04 00441 i037]()
and
t = -20,0,20
Figure 1.
The function Im(
v) of the three soliton solution of the SmKdV equation where
![Symmetry 04 00441 i037]()
and
t = -20,0,20
Figure 2.
The density plots of the functions
f1,
f2 and
f3, respectively from left to right, of the three soliton solution of the SmKdV equation where
![Symmetry 04 00441 i037]()
.
Figure 2.
The density plots of the functions
f1,
f2 and
f3, respectively from left to right, of the three soliton solution of the SmKdV equation where
![Symmetry 04 00441 i037]()
.
In
Figure 1, we may enjoy the three soliton solution Im(
v) of the SmKdV equation given by
as a function of
x, for the special values
![Symmetry 04 00441 i037]()
,
αi=
i in Equations (25) and (26) and
t=-20,0,20. In
Figure 2, we explore the behavior of the fermionic component
ρ- of the superfield
A for the same special values. To achieve this, we write
ρ- as
and trace out the bosonic functions f1, f2 and f3.
3.2. Similarity Solutions
In a recent paper [
7], we have proven the existence of an infinite set of rational similarity solutions of the SKdV
-2 using a SUSY version of the Yablonskii–Vorob'ev polynomials [
16,
17,
18]. We propose in this subsection to retrieve those solutions and find an infinite set of similarity solution for the SmKdV equation. To give us a hint into what change of variables we have to cast, we have used the symmetry reduction method associated to a dilatation invariance [
2].
Let us define the following
τ-functions [
7]
where
![Symmetry 04 00441 i041]()
and the functions
![Symmetry 04 00441 i042]()
are the Yablonskii–Vorob'ev polynomials defined by the recurrence relation
with
![Symmetry 04 00441 i044]()
and
![Symmetry 04 00441 i045]()
. We would like to insist that
![Symmetry 04 00441 i046]()
is a
N=2 bosonic superfield (as it is the case for the Ψ
i in the preceding subsection). Using the fact that the Yablonskii–Vorob'ev polynomials satisfy the following bilinear equations [
17]
we have that the pair of bilinear Equations (21) and (22) are such that [
7,
16,
17,
18]
From the choice of the variable
![Symmetry 04 00441 i046]()
, we also have
D+τi,n = 0 for all integers
n. Taking
τ2,n = τ1,n+1, we have an infinite set of similarity solutions of the SmKdV Equation given by
for all integers
n ≥ 0 and
τ1,n defined as in Equation (29). To get similarity solutions
An of the SKdV
-2, we use the above solution with
![Symmetry 04 00441 i052]()
. Plots of some similarity solutions are given in our recent contribution [
7].
4. SKdV1, SKdV4 and SB Equations and Virtual Solitons
In this section, we exhibit
N super soliton solutions, called
N super virtual solitons, for the three equations SKdV
1, SKdV
4 and SB. Virtual solitons are soliton-like solutions which exhibit no phase shifts in nonlinear interactions. In terms of classical
N soliton solutions [
3,
4,
5,
7,
14,
16,
19], this is equivalent to say that the interaction coefficients
Aij between soliton
i and soliton
j are zero,
![Symmetry 04 00441 i053]()
. They manifest as traveling wave solutions for negative time
t«0 and decrease spontaneously at time
t=0 to split into a
N soliton profile which exhibit no phase shifts. It is often said that the traveling wave solution was charged with
N-1 soliton, called virtual solitons [
5].
Using the change of variable Equation (15) for the unknown bosonic field Ã, we have seen that the bosonic field Hα must be a chiral superfield and solve the linear dispersive Equation (17) when α=1 and α=4. For the Burgers equation, the bosonic field HB had to be chiral and solves Equation (19).
It is easy to show that they admit the following solution
where the bosonic superfields Ψi are given as
The frequencies ω(κi) are such that ω(κi)= - κi3 for SKdVα and ω(κi)=- κi2 for SB. It looks like a typical KdV type soliton solution where all the interaction coefficients Aij are set to zero.
We see that the virtual soliton solutions of the SKdV1 and SKdV4 equations are completely similar due to the form of à which differs only by the constant value of βα. The expression of the original bosonic field is obtained from
where β=βα for the SKdVα equation and β=βB for the SB equation. Thus, we can give the explicit forms of the superfield components u and ρ-. Indeed, we have
where ηi=κix+ ω(κi)t and the bosonic functions fi(x,t) are defined as
In
Figure 3, we may enjoy the three virtual soliton solution Im(
u) of the SKdV
1 Equation for
![Symmetry 04 00441 i037]()
and
αi = 1 in Equation (36) and
t= 0,10,20. In
Figure 4, we observe the behavior of the function
v where
v = -
iux,
![Symmetry 04 00441 i037]()
and
αi=1 in Equation (36) and
t=20,0,20. For the same special values,
Figure 5 gives the density plots of the bosonic functions
f1,
f2 and
f3 as given in Equation (40).
Figure 3.
The function Im(
u) of the three virtual soliton solution of the SKdV
1 equation where
![Symmetry 04 00441 i037]()
and
t=0,10,20.
Figure 3.
The function Im(
u) of the three virtual soliton solution of the SKdV
1 equation where
![Symmetry 04 00441 i037]()
and
t=0,10,20.
Figure 4.
The function
v of the three virtual soliton solution of the SKdV
1 equation where
![Symmetry 04 00441 i037]()
and
t=20,0,20.
Figure 4.
The function
v of the three virtual soliton solution of the SKdV
1 equation where
![Symmetry 04 00441 i037]()
and
t=20,0,20.
Figure 5.
The density plots of the functions
f1,
f2 and
f3, respectively from left to right, of the three virtual soliton solution of the SKdV
1 equation where
![Symmetry 04 00441 i037]()
.
Figure 5.
The density plots of the functions
f1,
f2 and
f3, respectively from left to right, of the three virtual soliton solution of the SKdV
1 equation where
![Symmetry 04 00441 i037]()
.
5. SUSY N=4 KdV Equation and Virtual Solitons
The SUSY
N=4 KdV equation, as proposed by Popowicz in [
6], reads
where Г is a bosonic superfield and the complex supercovariant derivatives are defined as
where
![Symmetry 04 00441 i061]()
for
i=1,2,3,4. Using the relations {
Di,
Dj}=2
δij∂
x, where
δij is the Kronecker delta, we have that the supercovariant derivatives Equation (42) satisfy the anticommutation rules
where
μ,
v ∈ {+,-}. Equation (41) can easily be viewed as a generalization of a
N=2 equation. Indeed, setting
θ3=
θ4=0 and
![Symmetry 04 00441 i063]()
in Equation (41), we retrieve the SmKdV Equation (8).
To construct virtual solitons of N=2 SUSY extensions, we have considered chiral superfields. Here, we propose a generalization of this concept. Indeed, we impose the following constraints on the superfield Г
A bosonic superfield Ξ satisfying the chiral conditions Equation (44) has the following general form
where
u=u(
x,
t) and
w=w(
x,t) are complex valued bosonic functions and
ξ=
ξ(
x,t) and
η=
η(
x,t) are complex valued fermionic functions. The Grassmann variables in Equation (45) are defined as
![Symmetry 04 00441 i067]()
and
![Symmetry 04 00441 i068]()
. Now, using the chirality conditions Equation (44), we have
![Symmetry 04 00441 i069]()
and Equation (41) reduces to the classical nonlinear PDE
Equation (46) is, up to a slight change of variable, similar to Equation (13) for the integrable cases
α=1,4. Indeed, we retrieve Equation (13) for
α=1,4by casting
![Symmetry 04 00441 i071]()
in Equation (46).
The above equation can be linearized into the linear dispersive Equation (17) by the change of variable
Thus to obtain solutions of Equation (41), the superfield
![Symmetry 04 00441 i066]()
must satisfy the constraints
A solution to this system is
where φ is a N=4 chiral bosonic superfield of the form
with
![Symmetry 04 00441 i076]()
and
λ1 is an even constant. This result can thus be generalized to give a
N super virtual soliton solution of the SUSY
N=4 KdV Equation (41) by taking
where the superfields φi are defined as in Equation (50) for i=1,…,N.
It is interesting to note that by setting
![Symmetry 04 00441 i078]()
in Equation (50), one recovers the superfields Equation (24).
6. Concluding Remarks and Future Outlook
In this paper, we have studied special solutions of supersymmetric extensions of the Burgers, KdV and mKdV equations in a unified way and using a chirality of the superfield A.
We have recovered interacting super soliton solutions (often called KdV type solitons) and an infinite set of rational similarity solutions. To produce such rational solutions, we have used an SUSY extension of the Yablonskii–Vorob'ev polynomials. We have introduce a new representation of the τ-functions to solve the bilinear equations. These τ-functions are N=2 extensions of classical τ-functions of the mKdV equation. Till now, in the literature, only N=1 extensions of the τ-functions were given.
We have shown the existence of non-interacting super soliton solutions, called virtual solitons, for the Burgers and SKdV
α (
α=1,4). These special solutions are a direct generalization of the solutions obtained in a recent contribution [
5] where
N super virtual solitons have been found by setting to zero the fermionic contributions
ξ1 and
ξ2 in the bosonic superfield
A given as in Equation (1). We retrieve those solutions by setting
ςi= 0 in the exponent terms Equation (37). Thus the chirality property, exposed in this paper, has produced a nontrivial fermionic sector for a
N super virtual soliton. Furthermore, to obtain such solutions we have related the SUSY equations to linear PDE's showing the true origin of those special solutions.
A N=4 extension of the KdV equation has been shown to produce a N super virtual soliton solution. The study of N=4 extensions is quite new to us and we hope in the future to produce a N super soliton solution with interaction terms.
 , the dependent variable A admits the following finite Taylor expansion
, the dependent variable A admits the following finite Taylor expansion 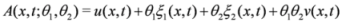
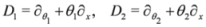
 and {D1,D2} = 0. We consider also the complex supercovariant derivatives
and {D1,D2} = 0. We consider also the complex supercovariant derivatives 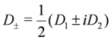
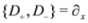 . In terms of the complex Grassmann variables
. In terms of the complex Grassmann variables 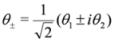 , the derivatives Equation (3) admits the following representation
, the derivatives Equation (3) admits the following representation 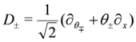
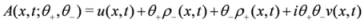
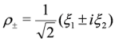 .
.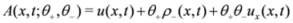
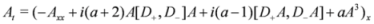
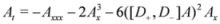
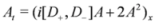
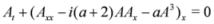
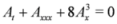
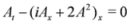
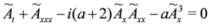
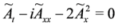
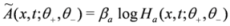
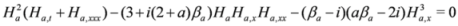
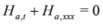
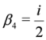 . For α=-2, Equation (16) writes
. For α=-2, Equation (16) writes 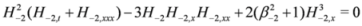
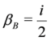 in Equation (14) is assumed and leads to the linear Schrödinger Equation
in Equation (14) is assumed and leads to the linear Schrödinger Equation 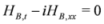
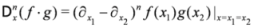
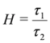 , where
, where 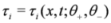 are bosonic chiral superfields for i=1,2. Equation (11) leads to the set of bilinear equations
are bosonic chiral superfields for i=1,2. Equation (11) leads to the set of bilinear equations 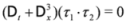
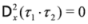
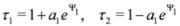
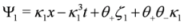
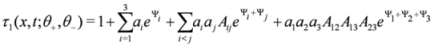
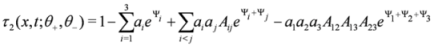
 and the Ψi's are defined as in Equation (24). The functions τ1 and τ2 solves the bilinear Equations (21) and (22) and are such that D+τi = 0 for i=1,2. The generalization to a N super soliton solution is direct using the τ-functions expressed above. The forms of the τ-functions given above are new representations of super soliton solutions and have never been introduced before.
and the Ψi's are defined as in Equation (24). The functions τ1 and τ2 solves the bilinear Equations (21) and (22) and are such that D+τi = 0 for i=1,2. The generalization to a N super soliton solution is direct using the τ-functions expressed above. The forms of the τ-functions given above are new representations of super soliton solutions and have never been introduced before.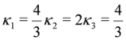 and t = -20,0,20
and t = -20,0,20
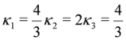 and t = -20,0,20
and t = -20,0,20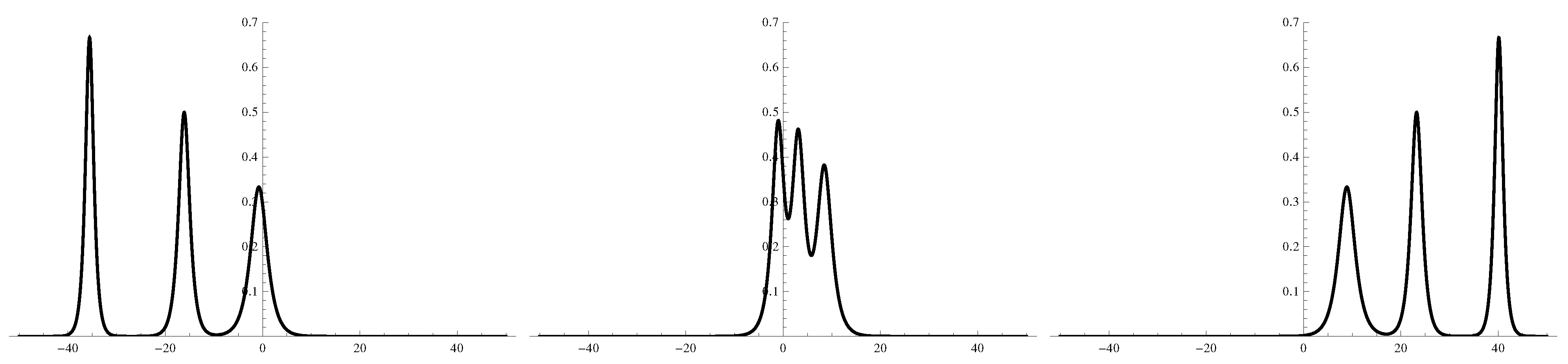
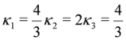 .
.
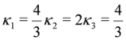 .
.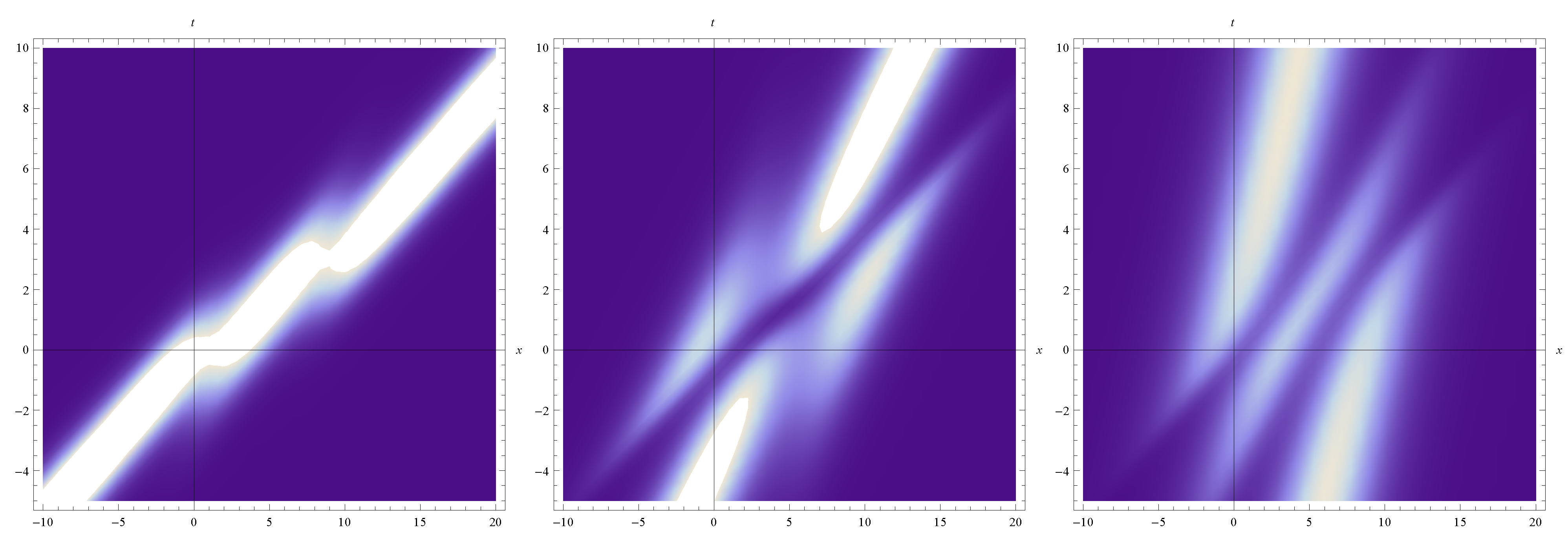
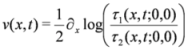
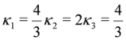 , αi=i in Equations (25) and (26) and t=-20,0,20. In Figure 2, we explore the behavior of the fermionic component ρ- of the superfield A for the same special values. To achieve this, we write ρ- as
, αi=i in Equations (25) and (26) and t=-20,0,20. In Figure 2, we explore the behavior of the fermionic component ρ- of the superfield A for the same special values. To achieve this, we write ρ- as 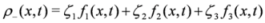
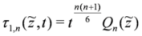
 and the functions
and the functions  are the Yablonskii–Vorob'ev polynomials defined by the recurrence relation
are the Yablonskii–Vorob'ev polynomials defined by the recurrence relation 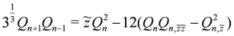
 and
and 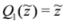 . We would like to insist that
. We would like to insist that  is a N=2 bosonic superfield (as it is the case for the Ψi in the preceding subsection). Using the fact that the Yablonskii–Vorob'ev polynomials satisfy the following bilinear equations [17]
is a N=2 bosonic superfield (as it is the case for the Ψi in the preceding subsection). Using the fact that the Yablonskii–Vorob'ev polynomials satisfy the following bilinear equations [17] 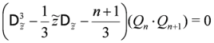
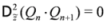
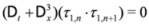
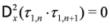
 , we also have D+τi,n = 0 for all integers n. Taking τ2,n = τ1,n+1, we have an infinite set of similarity solutions of the SmKdV Equation given by
, we also have D+τi,n = 0 for all integers n. Taking τ2,n = τ1,n+1, we have an infinite set of similarity solutions of the SmKdV Equation given by 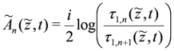
 . Plots of some similarity solutions are given in our recent contribution [7].
. Plots of some similarity solutions are given in our recent contribution [7]. . They manifest as traveling wave solutions for negative time t«0 and decrease spontaneously at time t=0 to split into a N soliton profile which exhibit no phase shifts. It is often said that the traveling wave solution was charged with N-1 soliton, called virtual solitons [5].
. They manifest as traveling wave solutions for negative time t«0 and decrease spontaneously at time t=0 to split into a N soliton profile which exhibit no phase shifts. It is often said that the traveling wave solution was charged with N-1 soliton, called virtual solitons [5].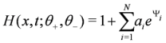
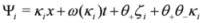
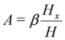

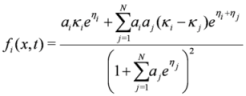
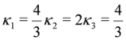 and αi = 1 in Equation (36) and t= 0,10,20. In Figure 4, we observe the behavior of the function v where v = - iux,
and αi = 1 in Equation (36) and t= 0,10,20. In Figure 4, we observe the behavior of the function v where v = - iux,  and αi=1 in Equation (36) and t=20,0,20. For the same special values, Figure 5 gives the density plots of the bosonic functions f1, f2 and f3 as given in Equation (40).
and αi=1 in Equation (36) and t=20,0,20. For the same special values, Figure 5 gives the density plots of the bosonic functions f1, f2 and f3 as given in Equation (40). and t=0,10,20.
and t=0,10,20.
 and t=0,10,20.
and t=0,10,20.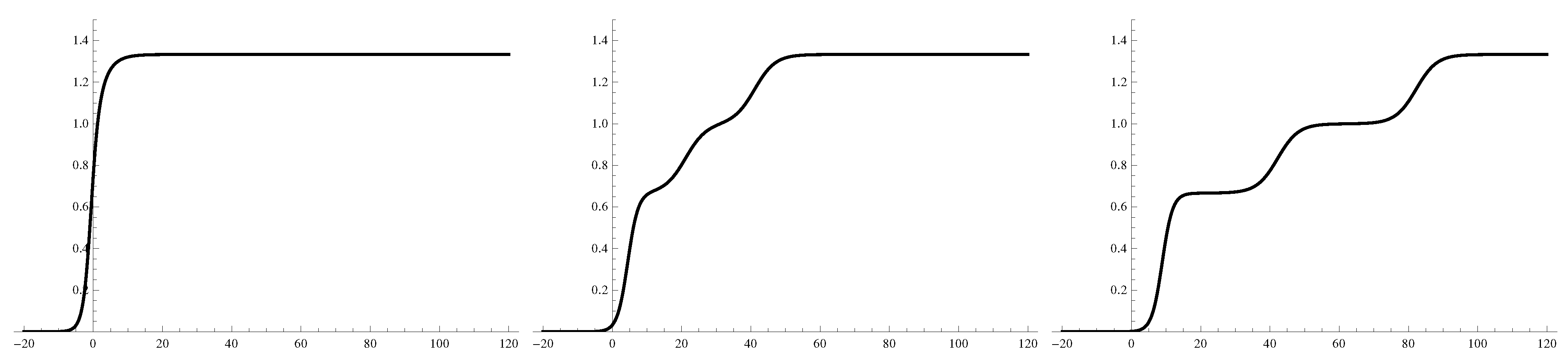
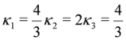 and t=20,0,20.
and t=20,0,20.
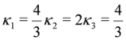 and t=20,0,20.
and t=20,0,20.
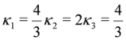 .
.
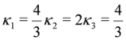 .
.
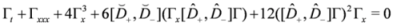
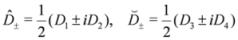
 for i=1,2,3,4. Using the relations {Di,Dj}=2δij∂x, where δij is the Kronecker delta, we have that the supercovariant derivatives Equation (42) satisfy the anticommutation rules
for i=1,2,3,4. Using the relations {Di,Dj}=2δij∂x, where δij is the Kronecker delta, we have that the supercovariant derivatives Equation (42) satisfy the anticommutation rules 
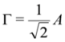 in Equation (41), we retrieve the SmKdV Equation (8).
in Equation (41), we retrieve the SmKdV Equation (8).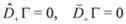
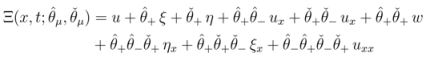
 and
and  . Now, using the chirality conditions Equation (44), we have
. Now, using the chirality conditions Equation (44), we have  and Equation (41) reduces to the classical nonlinear PDE
and Equation (41) reduces to the classical nonlinear PDE 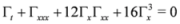
 in Equation (46).
in Equation (46).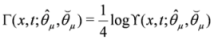
 must satisfy the constraints
must satisfy the constraints 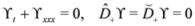
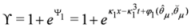
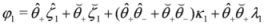
 and λ1 is an even constant. This result can thus be generalized to give a N super virtual soliton solution of the SUSY N=4 KdV Equation (41) by taking
and λ1 is an even constant. This result can thus be generalized to give a N super virtual soliton solution of the SUSY N=4 KdV Equation (41) by taking 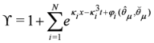
 in Equation (50), one recovers the superfields Equation (24).
in Equation (50), one recovers the superfields Equation (24).


