1. Introduction
Because of its intrinsic interest, the line graph transformation
G ↦
L(
G) of a graph
G has been widely studied. The impetus for much of this research was provided by Ore’s discussion of line graphs and problems associated with them [
1]. Line graphs are also interesting from a practical standpoint, since it has been shown that certain NP-complete problems for graphs are polynomial time problems for line graphs, e.g., [
2]. Because of their utility for recognizing non-isomorphic graphs, graph invariants have also been the object of intensive research, e.g., [
3].
In this paper, a new topological invariance associated with the line graph transformation is found using the natural relationship between a Krausz decomposition of L(G) and an abstract simplicial complex K. In particular, it is shown that, under the line graph transformation, an isomorphic copy of G is preserved as the nerve of K. As a consequence, the homology of G is isomorphic to that of K and an application of the Euler-Poincare formula yields the Euler characteristic of G as a line graph transformation invariant. This invariance also algebraically confirms several well-known graph theoretic properties of line graphs.
The remainder of this paper is organized as follows: The relevant definitions and terminology are summarized in the next section. Required preliminary lemmas are provided in
Section 3 and the main results are established in
Section 4. A simple illustrative example is presented in
Section 5. Closing remarks comprise the final section of this paper.
2. Definitions and Terminology
A graph G is a pair (V(G), E(G)), where V(G) is a finite non-empty set of vertices and E(G) is a set of doubleton subsets of V(G) called edges. G is a non-empty graph when V(G) ≠ Ø ≠ E(G) and G is a (p,q) graph if |V(G)| = p and |E(G)| = q. A (1,0) graph is a trivial graph. The number of edges incident to a vertex v is the valency of v. A vertex of valency zero is an isolated vertex (only graphs without isolated vertices are considered here). A component of G is a maximally connected subgraph of G. A complete graph Knon n vertices has every pair of vertices adjacent. When V(G) is partitioned into two sets V1 and V2 of cardinality m and n such that each vertex in V1 is adjacent to every vertex in V2, then G is the complete bipartite graph Km,n. If G is connected and has no cycles, then G is a tree. Graph G1 is isomorphic to graph G2 (denoted G1 ≅ G2) if there is an adjacency preserving bijective map 𝜑: V(G1) → V(G2).
Associate with any non-empty graph
G its
line graph L(
G) which has
E(
G) as its vertex set and has as its edge set those pairs in
E(
G) which are adjacent in
G. A collection
of subgraphs of a graph
F is a
Krausz decomposition of
F if (
i) each member of
is a complete graph; (
ii) every edge of
F is in exactly one member of
; and (
iii) every vertex of
F is in exactly two members of
. A nonempty graph is a line graph if, and only if, it has a Krausz decomposition and—provided that
G1 and
G2 are non-trivial connected graphs—
L(
G1) ≅
L(
G2) if, and only if,
G1 ≅
G2 or {
G1,
G2} is (up to isomorphism) the unordered pair {
K3,
K1,3} [
4].
A hypergraph is a pair (𝓝, 𝓔), where 𝓝 is a finite set of vertices and 𝓔 is a set of hyperedges which are non-empty subsets of 𝓝. A Krausz hypergraph 𝓗 of a line graph L(G) has V(L(G)) as its vertex set and the family of subsets of V(L(G)) that induce the members of as its hyperedges.
If S is a finite set, then the closure Cl(S) of S is the family of non-empty subsets of S. The closure Cl(𝓗) of 𝓗 is the union of the closures of its hyperedges, i.e., Cl(𝓗) = ⋃E ∈ 𝓔 C𝑙(E). The number of sets of cardinality k in Cl(𝓗) is hk and 𝝃 is the maximum k for which hk ≠ 0.
Let {a0,…, ak} be a set of geometrically independent points in ℝn. The k-simplex (or simplex) σk spanned by {a0,…, ak} is the set of points x ∈ ℝn for which there exist non-negative real numbers λ0,…,λk such that x = ∑0 ≤ i ≤ k λi ai and ∑0 ≤ i ≤ k λi = 1. In this case {a0,…, ak} is the vertex set of σ k. A face of σ k is any simplex spanned by a non-empty subset of {a0,…, ak}. A finite geometric simplicial complex (or complex) K is a finite union of simplices such that: (i) every face of a simplex of K is in K; and (ii) the non-empty intersection of any two simplices of K is a common face of each. Here it is assumed that all simplicial complexes are finite. Consequently, the dimension of K is the largest positive integer m such that K contains an m-simplex. The vertex scheme of K is the family of all vertex sets which span the simplices of K. The n-skeleton of K is the set of all simplices in K with dimension ≤n. K is connected if, and only if, its 1-skeleton is connected. If {Li} is a family of subcomplexes of K, then ⋃i Li and ⋂i Li ≠ Ø are subcomplexes of K.
A finite abstract simplicial complex (or abstract complex) is a finite family 𝓢 of finite non-empty sets such that if A is in 𝓢, then so is every non-empty subset of A. Thus, the vertex scheme of a complex is an abstract complex as are finite unions of set closures and finite intersections of set closures when they are non-empty.
Two abstract complexes 𝓢 and 𝓣 are isomorphic if there is a bijection φ from the vertex set of 𝓢 onto the vertex set of 𝓣 such that {a0,…, ak}∈ 𝓢 if, and only if, {φ(a0),…, φ(ak)} ∈ 𝓣. Every abstract complex 𝓢 is isomorphic to the vertex scheme of some geometric simplicial complex K—in which case K is the geometric realization of 𝓢 and is uniquely determined (up to linear isomorphism). An isomorphism between 𝓢 and the vertex scheme of K is denoted 𝓢 ≃ K.
To each simplicial complex K there corresponds a chain complex, i.e., abelian groups p(K) and homomorphisms ∂p+1 : p+1(K) → p(K), p ≥ 0. If K is finite and ηp(K) is the number of p-simplices in K, then the rank of p(K) is ηp(K) and p(K) is isomorphic to (here ≌ denotes both group and graph isomorphism) the direct sum of ηp(K) copies of the additive group of integers ℤ. The pth homology group of K is the quotient group Hp(K) ≡ ker ∂p/im ∂p+1 and its rank is the pth betti number bp(K). Complexes K and K ´ are homologically isomorphic when Hp(K) ≌ Hp(K ´), p ≥ 0, and K is homologically acyclic (or acyclic) if Hp(K) ≌ 0, p ≥ 1. The complex of a simplex is acyclic and if K is empty, then K is acyclic. The number of components of K is the betti number b0(K).
A cover of a simplicial complex K is a family of subcomplexes = {Lα : α ∈ A} with K = ⋃α Lα, where A is an index set. The family is an acyclic cover if each Lα and each finite intersection ⋂α Lα are acyclic. The nerve N() of is the simplicial complex having A as its vertex set with ∆ = {α0,…,αn} a simplex in N() if ⋂∆ Lα ≠ Ø.
3. Preliminary Lemmas
The following lemmas are required to prove the main results in the next section. The first four are well known and are stated without proof for completeness.
Lemma 1. [
5] (
Euler-Poincaré)
If K is a complex of dimension m, then ∑0 ≤ p ≤ m (−1)pηp(K) = ∑0 ≤ p ≤ m (−1)pbp(K) (1)
Lemma 2. [
6]
A non-empty connected graph G is a tree if, and only if, G is homologically acyclic and H0(
G) ≌ ℤ.
Lemma 3. [
7]
Let F be a graph. Then F ≌
L(
G)
for some graph G if, and only if, the vertices of G can be placed into one-to-one correspondence with the members of a Krausz decomposition of F such that two vertices of G are adjacent if, and only if, the corresponding members of have a common vertex. Lemma 4. [
8] (
Folkman-Leray)
If is an acyclic cover of a simplicial complex K, then K and N(
)
are homologically isomorphic. The closure operation C𝑙 is important for proving the main results of this paper. The required key properties of C𝑙 are provided by the next lemma. Since the proof is straight forward it is omitted.
Lemma 5. Let {Em : m ∈ I }be a collection of non-empty finite sets. Then the following statements are true:
Lemma 6. Let 𝓗 = (𝓝, 𝓔) be a Krausz hypergraph. Suppose 𝓢 = Cl(𝓗) = ⋃E ∈ 𝓔 C𝑙(E) is the abstract complex associated with 𝓗 and its geometric realization is the Krausz complex K. If Ei, Ej, Ek ∈ 𝓔 are distinct and the subcomplex Ki of K corresponds to the abstract complex Cl(Ei) of 𝓢, then
(1) | Ki ⋂ Kj | ≤ 1; and
(2) Ki ⋂ Kj ⋂ Kk = Ø.
Proof. Condition (1) follows since Ei and Ej are induced by a Krausz decomposition and have at most one vertex in common (apply (2) of Lemma 5 with A = Ei and B = Ej). Condition (2) follows since no three hyperedges of 𝓗 have a common vertex (apply (3) of Lemma 5 with A = Ei ⋂ Ej ⋂ Ek = Ø and then (1) of Lemma 5 with ⋂m Em = Ei ⋂ Ej ⋂ Ek).
4. Main Results
The terminology and results of the previous sections are now used to prove the following main results of this paper. In what follows, it is assumed that: (i) K is a Krausz complex associated with a Krausz hypergraph 𝓗 = (𝓝, 𝓔) of a graph F ≌ L(G); (ii) G is a non-trivial connected graph; (iii) G is not isomorphic to K3 or K1,3; and (iv) = {Ki ⊂ K : Ki ≌ C𝑙(Ei), Ei ∈ 𝓔}.
Theorem 1. G ≌ N().
Proof. By definition of , || = |𝓔|. Also, Ki ⋂ Kj ≠ Ø if, and only if, the corresponding pair of hyperedges in 𝓗 have a common vertex. Since F ≌ L(G), then Lemma 3 yields a correspondence between V(G) and 𝓔 such that u adjacent to v in G if, and only if, corresponding hyperedges have a vertex in common. Therefore, it follows from the definition of nerve that G ≌ N(). (Recall that here G is assumed to not be isomorphic to K3 or K1,3).
Lemma 7. is an acyclic cover of K.
Proof. By definition K = ⋃i Ki, where each Ki is the complex of a simplex. Thus, covers K. Since each Ki and (via Lemma 6) every finite intersection of the Ki’s is acyclic, then is an acyclic cover of K.
Theorem 2. Kand G are homologically isomorphic.
Proof. K and N() are homologically isomorphic (Lemma 7 and Lemma 4). Since G ≌ N() (Theorem 1), then K and G are also homologically isomorphic.
Corollary 1. If G is a (p,q) graph and F ≌ L(G), then
∑1 ≤ k ≤ 𝝃 (−1)k−1hk = p – q (2)
Proof. The left hand side of the Euler-Poincaré Formula (1), first for K = K and then for K = G, may be equated since, from Theorem 2, the corresponding right hand sides are equal. But when G =K, the left hand side of Equation (1) is p − q. Also, because of the one-to-one correspondence between the k − 1 dimensional simplices of K and the sets of size k in 𝓢 = Cl(𝓗) it is the case that the dimension of K is 𝝃 − 1 and 𝜼k−1(K) = hk. The validity of Equation (2) now follows from these observations and the appropriate K = K and K = G substitutions in the left hand side of Equation (1).
Corollary 2. The graph G and corresponding line graph L(G) have the same number of components.
Proof. From Theorem 2, b0(G) = b0(K) so that G and K have the same number of components. But L(G) and K also have an identical number of components since L(G) is isomorphic to the 1-skeleton of K. (This implies that L(G) is connected since it is assumed here that G is connected).
Corollary 3. Let L(G) be a connected line graph. Then G is a tree if, and only if,
∑1 ≤ k ≤ 𝝃 (−1)k−1hk = 1 (3)
Proof. Since L(G) is connected, an application of Corollary 2 shows that G is connected. A connected (p,q) graph G is a tree if, and only if, p − q = 1. The result follows from Equation (2).
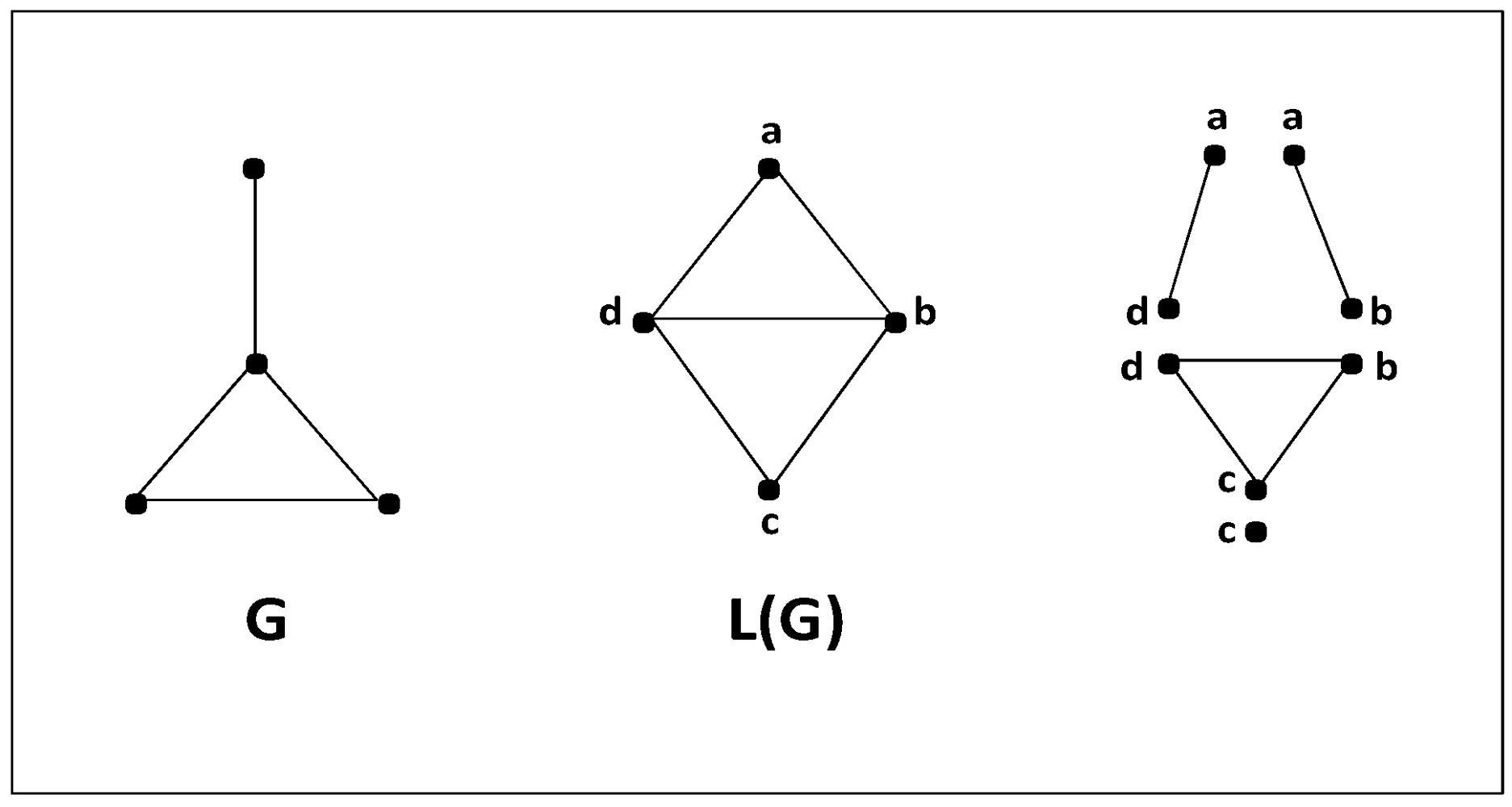
5. Example
In order to illustrate the theory developed above, consider the non-trivial connected (4,4) graph
G, its line graph
L(
G), and a Krausz decomposition of
L(
G) shown in
Figure 1. The associated Krausz hypergraph 𝓗 has the sets
E1 ={a,b},
E2 = {a,d},
E3 = {b,c,d}, and
E4 = {c} as it hyperedges. Their closures are
Cl(E1) = {{a,b},{a},{b}},
Cl(E2) = {{a,d},{a},{d}},
Cl(E3) = {{b,c,d},{b,c},{b,d},{c,d},{b},{c},{d}},
and
Cl(E4) = {{c}},
so that
= {Cl(E1),Cl(E2),Cl(E3),Cl(E4)}
and
Cl(𝓗) = {{b,c,d},{a,b},{a,d},{b,c},{b,d},{c,d},{a},{b},{c},{d}}.
It is clear that is an acyclic cover of the Krausz complex associated with Cl(𝓗).
Figure 1.
The line graph of a (4,4) graph and its Krausz decomposition.
Figure 1.
The line graph of a (4,4) graph and its Krausz decomposition.
The nerve N() of has the set {1,2,3,4} of 𝓗 hyperedge subscripts as its set of vertices. Since
Cl(E1) ⋂ Cl(E2) ≠ Ø, Cl(E1) ⋂ Cl(E3) ≠ Ø, Cl(E2) ⋂ Cl(E3) ≠ Ø, Cl(E3) ⋂ Cl(E4) ≠ Ø
and
Cl(E1) ⋂ Cl(E4) = Ø, Cl(E2) ⋂ Cl(E4) = Ø
then the doubleton subsets {1,2}, {1,3}, {2,3}, and {3,4} are
N(
) edges (see
Figure 2). It is obvious from
Figure 1 and
Figure 2 that − as required by Theorem 1 −
G ≅
N(
).
Figure 2.
The nerve of the acyclic cover of the Krausz complex associated with L(G).
Figure 2.
The nerve of the acyclic cover of the Krausz complex associated with L(G).
Since G is a p = 4 = q graph, then p − q = 0. It is also readily determined from Cl(𝓗) that h3 = 1, h2 = 5, h1 = 4, and 𝝃 = 3, so that − as required by Corollary 1−
∑1 ≤ k ≤ 3(-1)k-1hk = 4 − 5 + 1 = 0 = p – q
Acknowledgments
This work was supported by a grant from the Naval Surface Warfare Center Dahlgren Division’s In-house Laboratory Independent Research program.