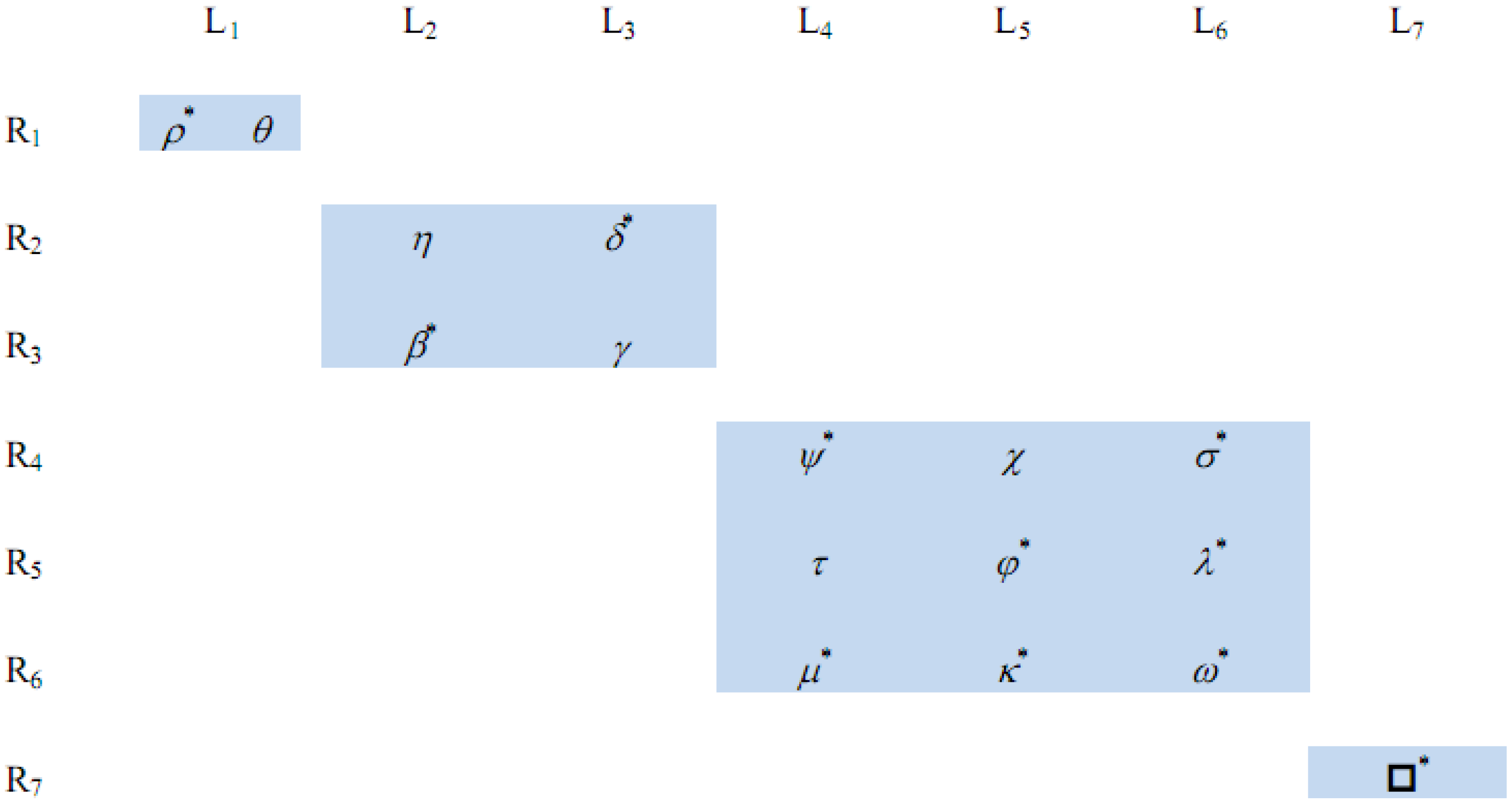Green’s Symmetries in Finite Digraphs

Abstract

The semigroup D_V of digraphs on a set V of n labeled vertices is defined. It is shown that D_V is faithfully represented by the semigroup B_n of n × n Boolean matrices and that the Green’s L, R, H, and D equivalence classifications of digraphs in D_V follow directly from the Green’s classifications already established for B_n. The new results found from this are: (i) L, R, and H equivalent digraphs contain sets of vertices with identical neighborhoods which remain invariant under certain one-sided semigroup multiplications that transform one digraph into another within the same equivalence class, i.e., these digraphs exhibit Green’s isoneighborhood symmetries; and (ii) D equivalent digraphs are characterized by isomorphic inclusion lattices that are generated by their out-neighborhoods and which are preserved under certain two-sided semigroup multiplications that transform digraphs within the same D equivalence class, i.e., these digraphs are characterized by Green’s isolattice symmetries. As a simple illustrative example, the Green’s classification of all digraphs on two vertices is presented and the associated Green’s symmetries are identified.

1. Introduction

The purpose of this paper is to discuss a semigroup-theoretic approach to digraph structural classification which uses the well known Green’s L, R, H, and D relations to provide rigorous classifications of digraphs. This approach yields the following new results: (i) L, R, and H equivalent digraphs exhibit isoneighborhood symmetries (i.e., they possess sets of vertices which have identical neighborhoods that remain invariant under certain special one-sided semigroup digraph multiplications which transform digraphs within an equivalence class); and (ii) D equivalent digraphs exhibit isolattice symmetries (i.e., they have isomorphic inclusion lattices generated by the closure under set union of their out-neighborhoods that are preserved under certain special two-sided semigroup digraph multiplications which transform digraphs within an equivalence class). These classifications are achieved in a direct manner by first defining the semigroup of digraphs on n labeled vertices and then by capitalizing upon the fact that this semigroup is faithfully represented by the semigroup of n × n Boolean matrices. The Green’s classification of digraphs follows immediately from the well established Green’s classification of the associated Boolean matrices.

The remainder of this paper is organized as follows: the next section briefly summarizes relevant topics in digraph and semigroup theory. The Green’s equivalence classifications of digraphs are established and isoneighborhood class and isolattice class structural invariants are identified in Section 3. Green’s symmetries are formally defined in section 4. Section 5 illustrates the theory developed in Section 3 and Section 4 by providing Green’s classifications of all digraphs on two vertices and identifying their Green’s symmetries. Concluding remarks comprise the final section of this paper.

2. Preliminaries

A digraph E is the pair (V,A) where V is a finite nonempty set of vertices and a binary relation A ⊆ V × V is the set of arcs. The order of E is card(V) and the size of E is card(A), where card(X) denotes the cardinality of set X. If (x,y) ∈ A, then x and y are adjacent in the direction from x to y; x is an in-neighbor of y; and y is an out-neighbor of x. The in-neighborhood of x ∈ V in E is the set I(E; x) of all in-neighbors of x and the out-neighborhood of x ∈ V in E is the set O(E;x) of all out-neighbors of x. The adjacency matrix of E is the card(V) × card(V) matrix α indexed by V with α_x,y = 1 when (x,y) ∈ A and α_x,y = 0 otherwise.

A semigroup S is a set and an associative binary operation called multiplication defined upon the set and denoted by juxtaposition. The one-sided right (one-sided left) [two-sided] multiplication of x ∈ S by y ∈ S is xy ∈ S (by y ∈ S is yx ∈ S) [by y,z ∈ S is yxz ∈ S]. An element x ∈ S is an idempotent if xx = x. The element e ∈ S is a left (right) identity if es = s (se = s) for s ∈ S and is a two-sided identity if it is both a left and a right identity. An identity e ∉ S can be adjoined to S be setting S¹ = S ⋃ {e} and defining se = es = s for s ∈ S¹. Let S = S¹ if S has an identity. Otherwise, let S¹ be the semigroup S with an identity adjoined.

The well known L, R, H, and D Green’s equivalence relations on S partition S into a highly organized “egg box” structure using relatively simple algebraic properties of the elements of S (see for example [1]). The equivalence relation L (R) on a semigroup S is defined by the rule that xLy (xRy) if and only if S¹x = S¹y (xS¹ = yS¹) for x, y ∈ S and the equivalence relation H = L ∩ R is similarly defined so that xHy if and only if xLy and xRy. The relations L and R commute under the composition “•” of binary relations and D ≡ L • R = R • L is the smallest equivalence relation containing L and R. For x ∈ S and X ∈ {L, R, H, D}, denote the X class containing x by X_x, where X = L, R, H, or D when X = L, R, H, or D, respectively. Thus, xXy if and only if X_x = X_y. Furthermore, if L_x = L_y (R_x = R_y) [D_x = D_y], then there are elements s and s′ (t and t′) [s,s′,t, and t′] in S¹ such that sx = y and s′y = x (xt = y and yt′ = x) [sxt = y and s′yt′ = x]. If an H class contains an idempotent, then the elements in that class form a group.

The semigroup B_n of Boolean matrices is the set of all n × n matrices over {0,1} with multiplication γ = αβ defined by the matrix expression

γ_ij = ⋁_k∈I (α_ik ⋀ β_kj)

Here, I = {1,2,3,…,n} is the matrix row and column index set, ⋀ denotes Boolean multiplication (i.e., 0 ⋀ 0 = 0 ⋀ 1 = 1 ⋀ 0 = 0, 1 ⋀ 1 = 1), and ⋁ denotes Boolean addition (i.e., 0 ⋁ 0 = 0, 0 ⋁ 1 = 1 ⋁ 0 = 1 ⋁ 1 = 1). The rows (columns) of any α ∈ B_n are Boolean row (column) n—vectors, i.e., row (column) n—tuples over {0,1}. Let 0 (1) denote either the zero (unit) row or zero (unit) column vector (the context in which 0 (1) is used defines whether it is a row or column vector). The matrix with 0 in every row – i.e., the zero matrix – is denoted by “□” and the matrix with 1 in every row is denoted by “ω”. The row (column) basis r(α) (c(α)) of α is the set of all row (column) vectors in α that are not Boolean sums of other row (column) vectors in α. The vector 0 is never a basis vector and the empty set Ø is the basis for the zero matrix. The row space R(α) of α is the set with 0 and all possible Boolean sums of one or more non-zero row vectors in α as its elements [2]. Let u_i be the i^th coordinate of u ∈ R(α). If v ∈ R(α), then u ⊑ v when u_i = 1 implies v_i = 1, 1 ≤ i ≤ n. The space R(α) is the lattice (R(α),⊑) under the partial order “⊑” [3].

The semigroup B_V of binary relations on V is the power set of V × V with multiplication Z = XY being the “composition of binary relations” defined by

Z = {(x,y) ∈ V×V:(x,z) ∈ X and (z,y) ∈ Y for some z ∈ V}

When card(V) = n and f:V → I is a bijective vertex indexing map, then B_V is isomorphic to B_n via the bijective map λ:B_V → B_n defined by λ(X) = χ, where χ_ij = 1 when (f ⁻¹(i),f ⁻¹(j)) ∈ X and χ_ij = 0 otherwise [4].

The following important lemma due to Plemmons and West [3] and Zaretskii [5] defines the properties of L, R, H, and D equivalent matrices in B_n and provides the foundation for the Green’s classifications of digraphs in D_V.

Lemma 2.1

Let α, β ∈ B_n.

(i)

L_α = L_β if and only if r(α) = r(β);

(ii)

R_α = R_β if and only if c(α) = c(β);

(iii)

H_α = H_β if and only if r(α) = r(β) and c(α) = c(β);

(iv)

D_α = D_β if and only if (R(α), ⊑) and (R(β), ⊑) are lattice isomorphic.

3. Green’s Equivalence Classifications of Digraphs

Let D_V be set of all digraphs on the finite vertex set V and define multiplication of digraphs by EF = G ≡ (V,Z), where E ≡ (V,X), F ≡ (V,Y), and

Z = {(x,y) ∈ V×V:(x,z) ∈ X and (z,y) ∈ Y for some z ∈ V}

Lemma 3.1

D_V is a semigroup that is isomorphic to B_V.

Proof.

It is obvious from the definition of D_V that (i) “multiplication of digraphs” is the same as “composition of binary relations” and (ii) the bijective map Φ:D_V → B_V defined by Φ(E) = X preserves this multiplication. Thus, Φ:D_V → B_V is a semigroup isomorphism.

The following lemma establishes the rationale for the approach used here to determine the Green’s equivalence classifications of digraphs.

Lemma 3.2

If V and I are equipotent finite sets, then B_n is a faithful semigroup representation of D_V where each digraph in D_V is represented by its adjacency matrix in B_n.

Proof. 

This is a consequence of the fact that B_V is isomorphic to B_n [4]. In particular, let λ: B_V → B_n be the required semigroup isomorphism. Since – from Lemma 3.1 – Φ:D_V → B_V is also a semigroup isomorphism, then there exists a semigroup isomorphism g : D_V → B_n which is the composition g = λΦ, where g(E) is – by definition – the adjacency matrix of E.

Assume that card(V) = n = card(I) and let f:V → I be the vertex indexing map associated with the isomorphism g: D_V → B_n of Lemma 3.2. Observe that if α_i* is the i^th Boolean row vector and α_*j is the j^th Boolean column vector in the adjacency matrix α = g(E) corresponding to digraph E, then α_i* encodes the out-neighbors of vertex f⁻¹(i) in digraph E according to

O(E;f⁻¹(i)) = {f⁻¹(k):α_ik = 1, k ∈ I}

and α_*j encodes the in-neighbors of vertex f⁻¹(j) in digraph E according to

I(E;f⁻¹(j)) = {f⁻¹(k):α_kj = 1, k ∈ I}

For the special cases that α_i* ∈ r(α) and α_*j ∈ c(α), then O_r(E;f⁻¹(i)) ≡ O(E;f⁻¹(i)) is a basis out-neighborhood and I_c(E;f⁻¹(j)) ≡ I(E;f⁻¹(j)) is a basis in-neighborhood for digraph E. Accordingly, a basis neighborhood in E is a non-empty neighborhood in E which is not the set union of other neighborhoods in E. Let O_r(E) be the set of basis out-neighborhoods and I_c(E) be the set of basis in-neighborhoods in digraph E.

Define the out-neighborhood space of E to be the set N(E) whose elements are the empty set and the sets generated by the closure under set union of the out-neighborhoods in E and let (N(E),⊆) be the poset ordered by the set inclusion relation “⊆”.

Lemma 3.3

(N(E),⊆) is a lattice that is isomorphic to (R(α),⊑).

Proof. 

Observe that each row vector v = (v₁,v₂,v₃,…,v_n) ∈ R(α) can be uniquely represented by the set of indices σ_v = {k ∈ I:v_k = 1}. Let S(α) = {σ_v:v ∈ R(α)} and θ:S(α) → R(α) be the associated bijection θ(σ_v) = v. The bijection f:V → I induces a map μ:N(E) → S(α) according to μ({x₁,x₂,x₃,…,x_m}) = {f(x₁),f(x₂),f(x₃),…,f(x_m)} with μ(Ø) = Ø. The map μ:N(E) → S(α) is bijective because it is onto and because μ(X) ≡ μ({x₁,x₂,x₃,…,x_l}) = σ_v = μ({y₁,y₂,y₃,…,y_l}) ≡ μ(Y) ⇒ X = Y since f is a bijection. Thus, there exists a bijection ψ:N(E) → R(α) given by the composition ψ = θμ and every row vector in R(α) has a vertex set as its unique ψ pre-image in N(E). It is also clear from this that for u, v ∈ R(α), u ⊑ v if and only if ψ⁻¹(u) ⊆ ψ⁻¹(v). Consequently, ψ⁻¹ preserves the partial order of (R(α),⊑) so that the Hasse diagram for (N(E), ⊆) is identical to that for (R(α), ⊑). Since (R(α),⊑) is a lattice, then so is (N(E),⊆). Thus, ψ is a lattice isomorphism since it preserves lattice joins and meets.

The following main theorem identifies the invariant structural features of L, R, H, and D equivalent digraphs.

Theorem 3.4

(Digraph Structural Invariants) Let α,β ∈ B_n with g⁻¹(α) = E and g⁻¹(β) = F.

(i)

L_E = L_F if and only if O_r(E) = O_r(F);

(ii)

R_E = R_F if and only if I_c(E) = I_c(F);

(iii)

H_E = H_F if and only if O_r(E) = O_r(F) and I_c(E) = I_c(F);

(iv)

D_E = D_F if and only if (N(E), ⊆) and (N(F), ⊆) are lattice isomorphic.

Proof. 

Items (i)–(iii) follow immediately from Lemma 2.1 and Lemma 3.2. Item (iv) is a direct consequence of Lemma 2.1, Lemma 3.2, and Lemma 3.3.

Thus, the Green’s L, R, and H equivalence classifications of the digraphs in D_V are based entirely upon their having (generally distinct) vertices with identical out-neighborhoods, identical in-neighborhoods, and both identical out-neighborhoods and identical in-neighborhoods, respectively. Accordingly, these digraph equivalence classes are called L, R, and H isoneighborhood classes and the associated sets of basis neighborhoods are structural invariants common to all digraphs within the respective isoneighborhood classes. Also, since Green’s D equivalence classification of digraphs in D_V is based solely upon their having isomorphic inclusion lattices, these digraph equivalence classes are called D isolattice classes. Here the unlabeled underlying Hasse diagram associated with the isomorphic inclusion lattices of an isolattice class is the structural invariant shared by the equivalent digraphs. Even though D equivalent digraphs generally have distinct vertex sets as lattice elements, their identical unlabeled Hasse diagrams express the fact that their generally distinct out-neighborhoods—which correspond to the atoms of the lattice—and the set unions thereof exhibit the same relative partial order.

4. Green’s Digraph Symmetries

Rosen [6] concisely defines symmetry as “immunity to a possible change”. Thus, in order to have a symmetry (a) “it must be possible to perform a change, although the change does not actually have to be performed” and (b) “some aspect of the situation would remain unchanged, if the change were performed”. Green’s equivalence classifications of finite digraphs clearly demonstrate that (b) is satisfied for finite digraphs since if a digraph were somehow to change into another equivalent digraph either the basis neighborhoods would remain unchanged for digraph changes occurring within an isoneighborhood class, or the associated underlying Hasse diagram would remain invariant for changes within an isolattice class. However, in order for these structural invariants to formally qualify as digraph symmetries —i.e., Green’s L, R, H, and D symmetries—it is necessary that condition (a) also be satisfied. As the next main theorem shows, satisfaction of condition (a) occurs within the semigroup D_V via the one- and two-sided multiplications by special transformation digraphs that are associated with the Green’s L, R, H, and D equivalence classes. Denote that digraph E changes—i.e., E transitions—into digraph F by E → F.

Theorem 4.1

(Green’s Digraph Symmetries) Let E ∈ D_V.

(i)

O_r(E) is a Green’s L symmetry;

(ii)

I_c(E) is a Green’s R symmetry;

(iii)

O_r(E) and I_c(E) are Green’s H symmetries;

(iv)

The underlying Hasse diagram for (N(E),⊆) is a Green’s D symmetry.

Proof. 

(i) O_r(E) is a structural invariant for every digraph in the same L isoneighborhood class as E (Theorem 3.4(i)). Also, for F ∈ D_V such that L_F = L_E semigroup theory guarantees the existence of a transformation digraph C ∈ D_V such that E → F according to CE = F; (ii) I_c(E) is a structural invariant for every digraph in the same R isoneighborhood class as E (Theorem 3.4(ii)). Also, for F ∈ D_V such that R_F = R_E semigroup theory guarantees the existence of a transformation digraph H ∈ D_V such that E → F according to EH = F; (iii) O_r(E) and I_c(E) are structural invariants for every digraph in the same H isoneighborhood class as E (Theorem 3.4(iii)). Also, for F ∈ D_V such that H_F = H_E semigroup theory guarantees the existence of transformation digraphs J,K ∈ D_V such that E → F according to JE = F and EK = F; (iv) The underlying Hasse diagram for (N(E), ⊆) is a structural invariant for every digraph in the same D isolattice class as E (Theorem 3.4(iv)). Also, for F ∈ D_V such that D_F = D_E semigroup theory guarantees the existence of transformation digraphs L, M ∈ D_V such that E → F according to LEM = F. Thus, (i)–(iv) satisfy conditions (a) and (b) and the associated structural invariants are formal Green’s symmetries.

5. Order Two Digraphs: An Example

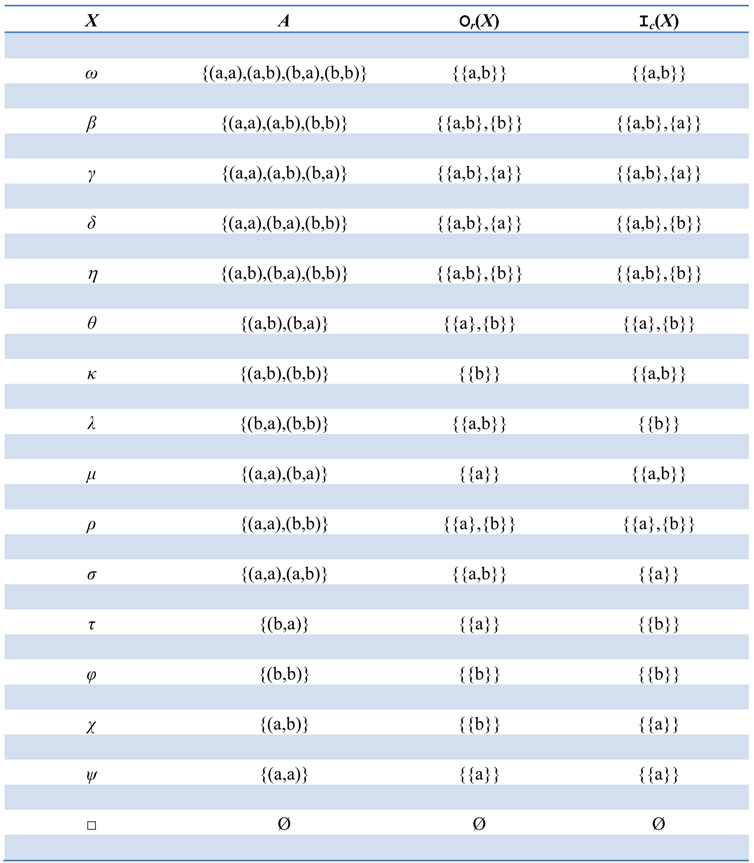
Table 1. The digraphs of D_{a,b} and their neighborhood basis sets.

lists and labels the sixteen order two digraphs on the vertex set V = {a,b} which form the semigroup D_{a,b}, along with their in-neighborhood and out-neighborhood basis sets. Note that here lower case Greek letters are used as digraph labels and that—rather than the pair (V,A)—only the arc set A is used to specify each digraph. Inspection of Table 1 using Theorem 3.4 yields the following L and R equivalence classes:

L₁ = {θ,ρ} with O_r(θ) = O_r(ρ) = {{a},{b}}

L₂ = {η,β} with O_r(η) = O_r(β) = {{a,b},{b}}

L₃ = {δ,γ} with O_r(δ) = O_r(γ) = {{a,b},{a}}

L₄ = {ψ,τ,μ} with O_r(ψ) = O_r(τ) = O_r(μ) = {{a}}

L₅ = {χ,φ,κ} with O_r(χ) = O_r(φ) = O_r(κ) = {{b}}

L₆ = {σ,λ,ω} with O_r(σ) = O_r(λ) = O_r(ω) = {{a,b}}

L₇ = {□} with O_r(□) = Ø

R₁ = {θ,ρ} with I_c(θ) = I_c(ρ) = {{a},{b}}

R₂ = {η,δ} with I_c(η) = I_c(δ) = {{a,b},{b}}

R₃ = {β,γ} with I_c(β) = I_c(γ) = {{a,b},{a}}

R₄ = {ψ,χ,σ} with I_c(ψ) = I_c(χ) = I_c(σ) = {{a}}

R₅ = {τ,φ,λ} with I_c(τ) = I_c(φ) = I_c(λ) = {{b}}

R₆ = {μ,κ,ω} with I_c(μ) = I_c(κ) = I_c(ω) = {{a,b}}

R₇ = {□} with I_c(□) = Ø.

Intersection of these L classes with these R classes generates the associated H classes—for example, H₁₁ = L₁ ∩ R₁ = {ρ,θ}, H₄₅ = L₄ ∩ R₅ = {τ}, and H₇₇ = L₇ ∩ R₇ = {□}. Note that the digraphs in each H class satisfy the neighborhood basis set requirements established by Theorem 3.4.

Using their out-neighborhoods as generators, the out-neighborhood spaces for these digraphs are readily found (e.g., N(η) = N(β) = {Ø,{b},{a,b}} and N(δ) = N(γ) = {Ø,{a},{a,b}}). Application of the set inclusion partial order “⊆” to each out-neighborhood space yields three lattice isomorphism (denoted by “~”) chains (e.g., (N(η),⊆) ~ (N(β),⊆ ) ~ (N(δ),⊆) ~ (N(γ),⊆)). These chains—in accordance with Theorem 3.4—define the following four D classes (there are four classes because the lattice (N(□),⊆) is isomorphic to itself):

D₁ = {θ,ρ}

D₂ = {η,β,δ,γ}

D₃ = {ψ,τ,μ,χ,φ,κ,σ,λ,ω}

D₄ = {□}.

The diamond “◊” is the underlying Hasse diagram h₁ that is the structural invariant for the digraphs in the D₁ isolattice class; and the undirected paths of length two, length one, and length 0 (i.e., •—•—•, •—•, and •) are the Hasse diagrams h₂, h₃, and h₄ that are the structural invariants for the digraphs in the D₂, D₃, and D₄ isolattice classes, respectively.

The above Green’s classification of the digraphs of D_{a,b} is compactly represented by the “egg box” structure for D_{a,b} given in Figure 1.

Note that the rows and columns in the “egg box” correspond to R classes and L classes, respectively, and their intersections are H classes. The shaded rectangular regions correspond to D classes. The asterisk superscripts denote that the associated digraph is an idempotent. Consequently, H₁₁ is a group isomorphic to the group Z₂ and H₃₂, H₂₃, H₄₄, H₆₄, H₅₅, H₆₅, H₄₆, H₅₆, H₆₆, and H₇₇ are all groups isomorphic to the trivial group.

The Green’s symmetries associated with D_{a,b} are easily determined from Theorem 4.1, Table 1, and Figure 1. For example: (i) the digraph transition ρ → θ is both a D₁ and an H₁₁ transition so that the Hasse diagram h₁ is the associated isolattice symmetry and the out-neighborhood set {{a},{b}} and the in-neighborhood set {{a},{b}} are the isoneighborhood symmetries; (ii) the transition τ → λ is both a D₃ transition – so that h₃ is its isolattice symmetry – and an R₅ transition—so that the in-neighborhood {{b}} is the isoneighborhood symmetry; (iii) κ → χ is a D₃ and an L₅ transition with h₃ and the out-neighborhood {{b}} as its isolattice and isoneighborhood symmetries; and (iv) the transition θ → τ has no guaranteed Green’s symmetries because the transition is neither a D-class, nor an L-class, nor an R-class transition.

6. Concluding Remarks

The classification of digraphs with finite vertex set V that is obtained from the application of Green’s equivalence relations to the digraph semigroup D_V has identified a new type of symmetry in digraphs—the Green’s isoneighborhood and isolattice symmetries. Not only are these new symmetries interesting from a purely graph theoretical perspective—they are also potentially useful to applied domains which employ digraph (or binary relation) models that are subject to change. For example, the Green’s symmetries associated with changing relationships between actors in a social network can provide insights into relationships that remain invariant (via isoneighborhood symmetries). These symmetries can also be applied to understanding the consequences of link reconfiguration in communication and sensor networks—as well as assisting in the classification and analysis of biological network data.