Generation of Stable Entanglement in an Optomechanical System with Dissipative Environment: Linear-and-Quadratic Couplings
Abstract
:1. Introduction
2. Description of the Model and Its Solution
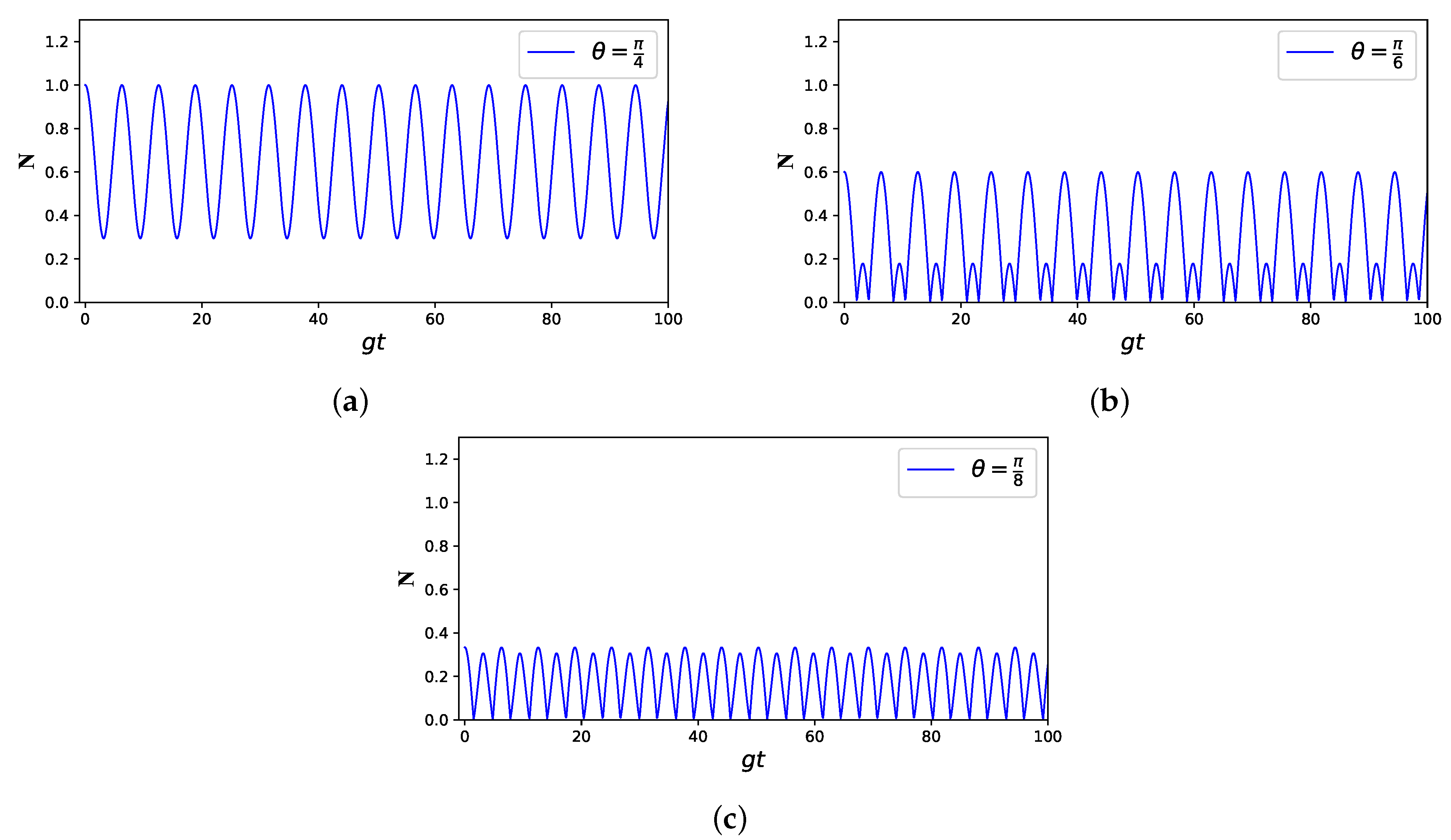
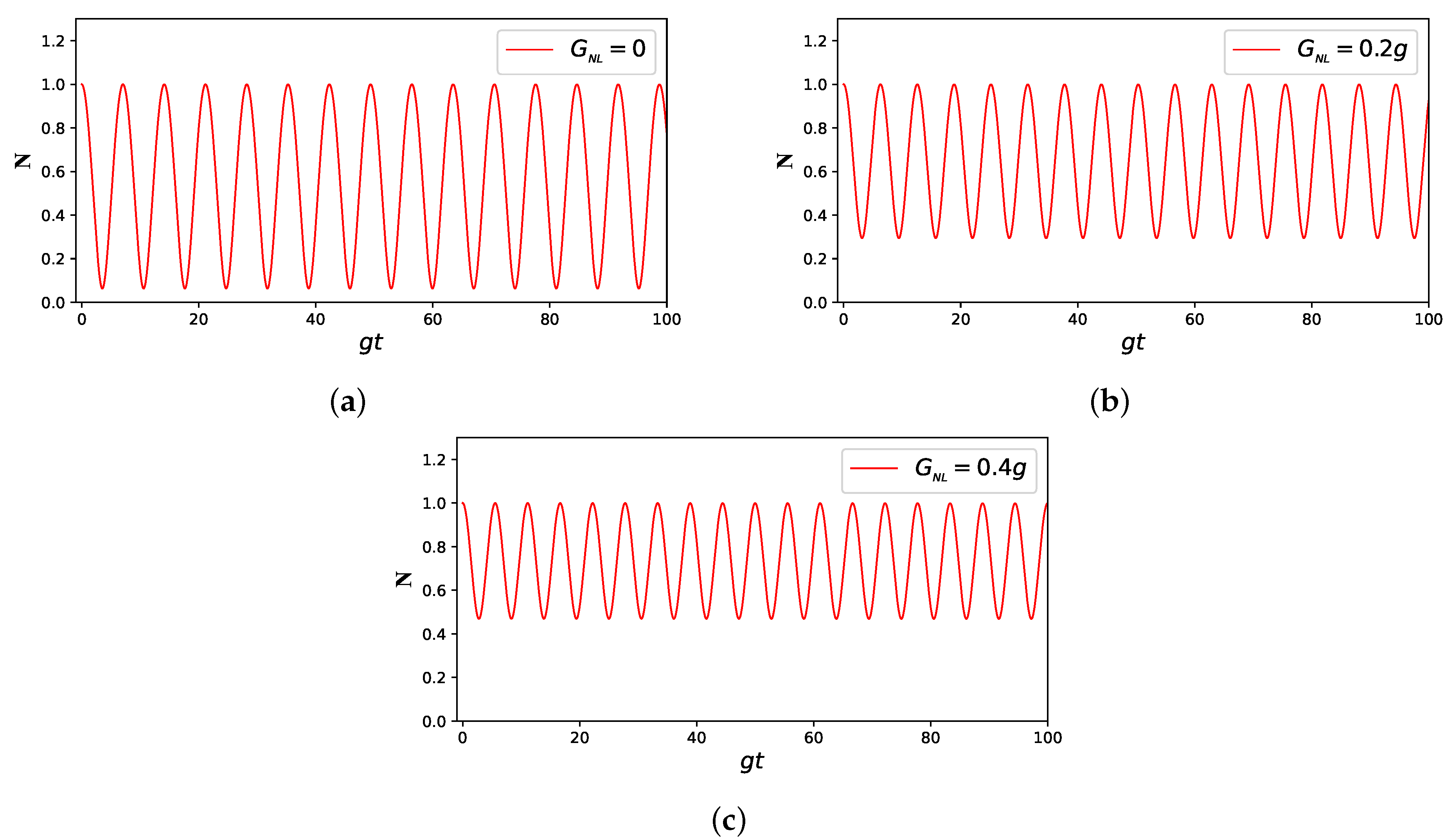
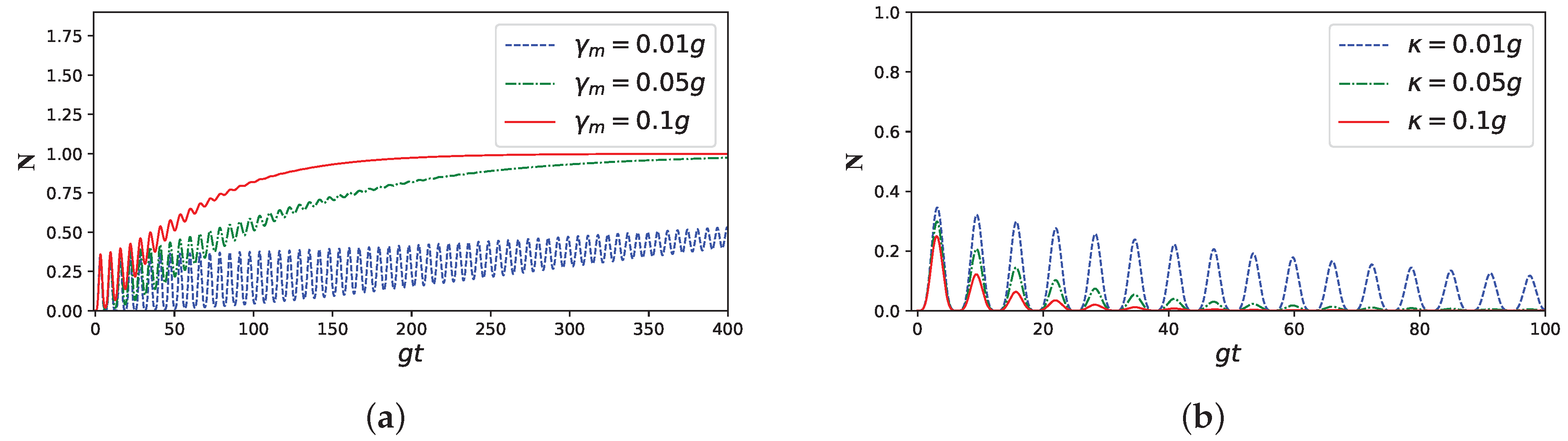
3. Results and Discussion: Atom–Atom Entanglement Dynamics
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Christopher, R.M.; Meekhof, D.M.; King, B.E.; Wineland, D.J. A “Schrödinger Cat” Superposition State of an Atom. Science 1996, 272, 1131. [Google Scholar]
- Nairz, M.A.O.; Andreae, J.V.; Keller, C.; Zouw, G.V.D.; Zeilinger, A. Wave–particle duality of C60 molecules. Nature 1999, 401, 680. [Google Scholar]
- Gerlich, S.; Eibenberger, S.; Tomandl, M.; Nimmrichter, S.; Hornberger, K.; Fagan, P.J.; Tuxen, J.; Mayor, M.; Arndt, M. Quantum interference of large organic molecules. Nat. Commun. 2011, 2, 263. [Google Scholar] [CrossRef] [PubMed]
- Franco, R.L.; Compagno, G. Quantum entanglement of identical particles by standard information-theoretic notions. Sci. Rep. 2016, 6, 20603. [Google Scholar] [CrossRef]
- Pan, J.W.; Gasparoni, S.; Ursin, R.; Weihs, G.; Zeilinger, A. Experimental entanglement purification of arbitrary unknown states. Nature 2003, 423, 417. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; Patron, R.G.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Cirac, J.I.; Gisin, N. Coherent eavesdropping strategies for the four state quantum cryptography protocol. Phys. Lett. A 1997, 229, 1–7. [Google Scholar] [CrossRef]
- Fuchs, C.A.; Gisin, N.; Griffiths, R.B.; Niu, C.; Peres, A. Optimal eavesdropping in quantum cryptography. I. Information bound and optimal strategy. Phys. Rev. A 1997, 56, 1163. [Google Scholar] [CrossRef]
- Salimian, S.; Tavassoly, M.K.; Sehati, N. Teleportation of the entangled state of two superconducting qubits. Europhys. Lett. 2021, 138, 55004. [Google Scholar] [CrossRef]
- Li, J.; Wallucks, A.; Benevides, R.; Fiaschi, N.; Hensen, B.; Alegre, T.P.M.; Groblacher, S. Proposal for optomechanical quantum teleportation. Phys. Rev. A 2020, 102, 032402. [Google Scholar] [CrossRef]
- Gyongyosi, L.; Imre, S. A Survey on quantum computing technology. Comput. Sci. Rev. 2019, 31, 51. [Google Scholar] [CrossRef]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, G.C. Scheme for implementing quantum dense coding in cavity QED. Phys. Rev. A 2005, 71, 034304. [Google Scholar]
- Mozes, S.; Reznik, B.; Oppenheim, J. Deterministic dense coding with partially entangled states. Phys. Rev. A 2005, 71, 012311. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Mattle, K.; Weinfurter, H.; Zeilinger, A.; Sergienko, A.; Shih, Y. New high-intensity source of polarization-entangled photon pairs. Phys. Lett. A 1995, 75, 4337. [Google Scholar] [CrossRef]
- Hagley, E.W.; Maitre, X.; Nogues, G.; Wunderlich, C.; Brune, M.; Raimond, J.M.; Haroche, S. Generation of Einstein-Podolsky-Rosen Pairs of Atoms. Phys. Rev. Lett. 1997, 79, 1. [Google Scholar] [CrossRef]
- Turchette, Q.A.; Wood, C.S.; King, B.E.; Myatt, C.J.; Leibfried, D.; Itano, W.M.; Monroe, C.R.; Wineland, D.J. Deterministic Entanglement of Two Trapped Ions. Phys. Rev. Lett. 1998, 81, 3631. [Google Scholar] [CrossRef]
- Rafeie, M.; Tavassoly, M.K.; Kheirabady, M.S. Macroscopic Mechanical Entanglement Stability in Two Distant Dissipative Optomechanical Systems. Ann. Phys. 2022, 534, 2100455. [Google Scholar] [CrossRef]
- Wu, Q.; Ma, P.C. Tunable double optomechanical induced transparency in an optomechanical system with Bose–Einstein condensate. J. Mod. Opt. 2017, 64, 685. [Google Scholar] [CrossRef]
- Yi, C.Q.; Yi, Z.; Gu, W.J.; Xu, D.H. Generating EPR-type entanglement of degenerate optomechanical parametric oscillators. J. Mod. Opt. 2017, 64, 2103. [Google Scholar] [CrossRef]
- Kong, C.; Li, S.; You, C.; Xiong, H.; Wu, Y. Two-color second-order sideband generation in an optomechanical system with a two-level system. Sci. Rep. 2018, 8, 1060. [Google Scholar] [CrossRef] [PubMed]
- Nadiki, M.H.; Tavassoly, M.K. The amplitude of the cavity pump field and dissipation effects on the entanglement dynamics and statistical properties of an optomechanical system. Opt. Commun. 2019, 452, 31. [Google Scholar] [CrossRef]
- Wang, K.; Gao, Y.P.; Jiao, R.; Wang, C. Recent progress on optomagnetic coupling and optical manipulation based on cavity-optomagnonics. Front. Phys. 2022, 17, 42201. [Google Scholar] [CrossRef]
- Ghasemi, M.; Tavassoly, M.K.; Nourmandipour, A. Dissipative entanglement swapping in the presence of detuning and Kerr medium: Bell state measurement method. Eur. Phys. J. Plus 2017, 132, 531. [Google Scholar] [CrossRef]
- Liu, N.; Li, J.Q.; Liang, J.Q. Entanglement in a Tripartite Cavity-Optomechanical System. Int. J. Theor. Phys. 2013, 52, 706. [Google Scholar] [CrossRef]
- Kippenberg, J.T.; Vahala, K.J. Cavity optomechanics: Back-action at the mesoscale. Science 2008, 321, 1172. [Google Scholar] [CrossRef] [PubMed]
- Aspelmeyer, M.; Meystre, P.; Schwab, K. Quantum optomechanics. Phys. Today 2012, 65, 29. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Gao, Y.P.; Cao, C.; Lu, P.F.; Wang, C. Phase-controlled photon blockade in optomechanical systems. Fundam. Res. 2023, 3, 30. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, H.Y. Photon antibunching in unconventional photon blockade with Kerr nonlinearities. J. Mod. Opt. 2017, 64, 1342. [Google Scholar] [CrossRef]
- Zhai, C.; Huang, R.; Jing, H.; Kuang, L.M. Mechanical switch of photon blockade and photon-induced tunneling. Opt. Express 2019, 27, 27649. [Google Scholar] [CrossRef]
- Yang, J.Y.; Jin, Z.; Liu, J.S.; Wang, H.F.; Zhu, A.D. Unconventional Phonon Blockade in a Tavis-Cummings Coupled Optomechanical System. Ann. Phys. 2020, 532, 2000299. [Google Scholar] [CrossRef]
- Wang, M.; Lu, X.Y.; Miranowicz, A.; Yi, T.S.; Wu, Y.; Nori, F. Unconventional phonon blockade via atom-photon-phonon interaction in hybrid optomechanical systems. Opt. Express 2022, 30, 10251. [Google Scholar] [CrossRef] [PubMed]
- Tan, H.T.; Li, G.X.; Meystre, P. Dissipation-driven two-mode mechanical squeezed states in optomechanical systems. Phys. Rev. A 2013, 87, 033829. [Google Scholar] [CrossRef]
- Sainadh, U.S.; Kumar, M.A. Squeezing of the mechanical motion and beating 3 dB limit using dispersive optomechanical interactions. J. Mod. Opt. 2016, 64, 1121. [Google Scholar] [CrossRef]
- Huang, S.; Chen, A. Mechanical squeezing in a dissipative optomechanical system with two driving tones. Phys. Rev. A 2021, 103, 023501. [Google Scholar] [CrossRef]
- Nunnenkamp, A.; Borkje, K.; Harris, J.G.E.; Girvin, S.M. Cooling and squeezing via quadratic optomechanical coupling. Phys. Rev. A 2010, 82, 021806. [Google Scholar] [CrossRef]
- SatyaSainadh, U.; Kumar, M.A. Effects of linear and quadratic dispersive couplings on optical squeezing in an optomechanical system. Phys. Rev. A 2015, 92, 033824. [Google Scholar]
- Gu, W.J.; Yi, Z.; Yan, Y.; Sun, L.H. Generation of Optical and Mechanical Squeezing in the Linear-and-Quadratic Optomechanics. Ann. Phys. 2019, 531, 1800399. [Google Scholar] [CrossRef]
- Liao, J.Q.; Nori, F. Photon blockade in quadratically coupled optomechanical systems. Phys. Rev. A 2013, 88, 023853. [Google Scholar] [CrossRef]
- Wan, K.; Gao, Y.P.; Pang, T.T.; Wang, T.; Wang, C. Enhanced photon blockade in quadratically coupled optomechanical system. EPL 2020, 131, 24003. [Google Scholar]
- Zhang, J.S.; Li, M.C.; Chen, A.X. Enhancing quadratic optomechanical coupling via a nonlinear medium and lasers. Phys. Rev. A 2019, 99, 013843. [Google Scholar] [CrossRef]
- Rabl, P. Photon blockade effect in optomechanical systems. Phys. Rev. Lett. 2011, 107, 063601. [Google Scholar] [CrossRef] [PubMed]
- Nunnenkamp, A.; Borkje, K.; Girvin, S.M. Single-photon optomechanics. Phys. Rev. Lett. 2011, 107, 063602. [Google Scholar] [CrossRef]
- Li, Z.Y.; Jin, G.R.; Yin, T.S.; Chen, A. Two-Phonon Blockade in Quadratically Coupled Optomechanical Systems. Photonics 2022, 9, 70. [Google Scholar] [CrossRef]
- Nadiki, M.H.; Tavassoly, M.K. Phonon blockade in a system consisting of two optomechanical cavities with quadratic cavity-membrane coupling and phonon hopping. Eur. Phys. J. Plus D 2022, 76, 58. [Google Scholar] [CrossRef]
- Xie, H.Y.; Liao, C.G.; Shang, X.; Ye, M.Y.; Lin, X. Phonon blockade in a quadratically coupled optomechanical system. Phys. Rev. A 2017, 96, 013861. [Google Scholar] [CrossRef]
- Zheng, L.L.; Yin, T.S.; Bin, Q.; Lu, X.U.; Wu, Y. Single-photon-induced phonon blockade in a hybrid spin-optomechanical system. Phys. Rev. A 2019, 99, 013804. [Google Scholar] [CrossRef]
- Rafeie, M.; Tavassoly, M.K. Quantum statistics and blockade of phonon and photon in a dissipative quadratically coupled optomechanical system. Eur. Phys. J. D 2023, 77, 63. [Google Scholar] [CrossRef]
- Vitali, D.; Gigan, S.; Ferreira, A.; Böhm, H.R.; Tombesi, P.; Guerreiro, A.; Vedral, V.; Zeilinger, A.; Aspelmeyer, M. Optomechanical entanglement between a movable mirror and a cavity field. Phys. Rev. Lett. 2007, 98, 030405. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhou, Y.H.; Guo, Y.Q.; Yi, X.X. Optomechanically induced transparency in optomechanics with both linear and quadratic coupling. Phys. Rev. A 2018, 98, 053802. [Google Scholar] [CrossRef]
- James, D.F.V.; Jerke, J. Effective Hamiltonian theory and its applications in quantum information. Can. J. Phys. 2007, 85, 625. [Google Scholar] [CrossRef]
- Carmichael, H.J. Statistical Methods in Quantum Optics 1; Springer: Berlin, Germany, 1999. [Google Scholar]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Hood, C.J.; Lynn, T.; Mabuchi, H.; Chapman, M.S.; Ye, J.; Kimble, H.J. Real-time cavity QED with single atoms. Phys. Rev. Lett. 1998, 80, 6. [Google Scholar] [CrossRef]
- Bose, S.; Jacobs, K.; Knight, P.L. A Quantum Optical Scheme to Probe the Decoherence of a Macroscopic Object. Phys. Rev. A 1999, 59, 3204. [Google Scholar] [CrossRef]
- Thompson, J.D.; Zwickl, B.M.; Jayich, A.M.; Marquardt, F.; Girvin, S.M.; Harris, J.G.E. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 2008, 452, 72. [Google Scholar] [CrossRef] [PubMed]
- Sankey, J.C.; Yang, C.; Zwickl, B.M.; Jayich, A.M.; Harris, J.G.E. Strong and tunable nonlinear optomechanical coupling in a low-loss system. Nature 2010, 6, 707. [Google Scholar] [CrossRef]
- NJacobs, E.F.; Hoch, S.W.; Sankey, J.; Kashkanova, A.; Jayich, A.M.; Deutsch, C.; Reichel, J.; Harris, J.G.E. Fiber-cavity-based optomechanical device. Appl. Phys. Lett. 2012, 101, 221109. [Google Scholar]
- Li, H.; Liu, Y.C.; Yi, X.; Zou, C.L.; Ren, X.; Xiao, Y.F. Proposal for a near-field optomechanical system with enhanced linear and quadratic coupling. Phys. Rev. A 2012, 85, 053832. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafeie, M.; Tavassoly, M.K. Generation of Stable Entanglement in an Optomechanical System with Dissipative Environment: Linear-and-Quadratic Couplings. Symmetry 2023, 15, 1770. https://doi.org/10.3390/sym15091770
Rafeie M, Tavassoly MK. Generation of Stable Entanglement in an Optomechanical System with Dissipative Environment: Linear-and-Quadratic Couplings. Symmetry. 2023; 15(9):1770. https://doi.org/10.3390/sym15091770
Chicago/Turabian StyleRafeie, Mehran, and Mohammad Kazem Tavassoly. 2023. "Generation of Stable Entanglement in an Optomechanical System with Dissipative Environment: Linear-and-Quadratic Couplings" Symmetry 15, no. 9: 1770. https://doi.org/10.3390/sym15091770





