A Proposed DEA Window Analysis for Assessing Efficiency from Asymmetry Dynamic Data

Abstract

Nowadays, one of the main challenges facing production management is how to enhance the performance of manufacturing processes by utilizing asymmetry input and output data. This research, therefore, developed a framework for window analysis in data envelopment analysis (DEA) for evaluating the overall technical efficiencies from asymmetry dynamic input and output data. The framework was applied to assess the technical (TE), managerial (PTE), and scale (SE) efficiencies of a blowing machine under three fuzzy input variables (planned production quantity, number of defectives, and idle time) and a fuzzy output variable (actual or target production quantity). The efficiency measures were then evaluated for all DMUs at low (L), middle (M), and high (H) data levels. The obtained optimal fuzzy efficiencies were then transformed into a single crisp optimal efficiency. The results showed that all seven DMUs of the blowing machine were technically inefficient. The input and output slacks were estimated and utilized to determine the necessary improvement actions. Improvement results revealed that the optimal TE, PTE, and SE were significantly improved, which may result in significant savings in production and quality costs. In conclusion, the proposed framework is effective in improving the efficiency of the blowing process and can be utilized for efficiency assessment in a wide range of applications.

1. Introduction

Industries across the globe rely on the efficiency evaluation of manufacturing processes to create quality products and save on expensive manufacturing and quality costs [1,2]. In practice, information asymmetries arise in the only collected data due to subjective judgments based on experience and historical data or variations, which may significantly affect the accuracy of the efficiency assessment results and the effectiveness of the improvement decisions [3]. Consequently, developing effective approaches for efficiency evaluation under asymmetry input and output has become a real challenge. This research, therefore, develops a framework for window analysis in data envelopment analysis (DEA) to evaluate efficiency from asymmetry input and output data for manufacturing processes.

Data envelopment analysis (DEA) is a mathematical programming-based non-parametric approach that is widely used for assessing the relative efficiency of homogeneous decision-making units (DMUs) [4]. In DEA, process engineers usually rely on multiple crisp inputs and crisp outputs for assessing process efficiency. In DEA models, a DMUs’ efficiency is defined by its relative distance from the production frontier [5,6]. Usually, two DEA techniques are used to evaluate the DMUs’ efficiency, including the Charnes–Cooper–Rhodes (CCR) [7] and Banker, Charnes, and Cooper (BCC) [8]. The CCR model measures technical efficiency (TE) by maximizing the output from a given set of inputs at an optimal scale of operation, or constant returns to scale (CRTS). To gain valuable information about the source of inefficiencies, TE is composed of two efficiencies: pure technical efficiency (PTE) and scale efficiency (SE). The BCC model assumes that a DMU is operating under variable returns to scale (VRS) and measures PTE by only comparing a DMU to a unit of a similar scale. PTE assesses the extent to which a DMU utilizes its sources in exogenous environments and evaluates managerial performance [9,10]. Finally, the scale efficiency (SE), calculated as TE divided by PTE, is used to evaluate the effect of the scale size on efficiency and enables management to select the optimal resource size to obtain the target production level. Inappropriate scale size causes technical inefficiency [11,12]. Scale inefficiency (SIE) is due to increasing returns-to-scale (IRTS) when the manufacturing process is too small for its scale of operations. SIE is due to decreasing returns-to-scale (DRTS) when the process is too large for its scale of operations. To reduce costs and maximize revenues, the process has to operate at the most productive scale, which is CRTS [13,14,15]. The traditional DEA models for evaluating DMUs relative efficiency in various business applications [16,17,18,19,20].

Nevertheless, for DEA models to avoid producing multiple efficient DMUs, the number of DMUs should be at least two times the sum of the number of inputs and outputs [6]. Fortunately, DEA window analysis was introduced to improve discriminating power by increasing the number of DMUs when using a limited number of DMUs [2]. DEA window analysis regards the same DMU in distinct periods, which are then treated as entirely different DMUs. The TE, PTE, and SE of a DMU in any period can then be estimated using the inputs and outputs of the same DMU in other periods as well as those of other DMUs. The window analysis was applied to evaluate process efficiency under crisp input and output data in a wide range of manufacturing and service applications [21,22,23,24,25]. In manufacturing systems, however, variations in process and measurement result in asymmetry data. As a result, the data available for efficiency analysis cannot be presented as crisp data. Consequently, window analysis should be developed to deal with asymmetry data, represent real-world problems more realistically, and obtain a reliable assessment of manufacturing processes.

In this context, this research proposes a DEA window analysis to assess the DMUs relative efficiency using asymmetry or fuzzy dynamic data. In this research, the relative efficiency is calculated for each element of the triangular fuzzy number of the input and output data. Then, the fuzzy efficiency is transformed into a crisp value. The efficiency evaluation for a blowing machine used to manufacture plastic products during the year 2020 is utilized to illustrate the developed fuzzy window analysis. The remainder of this paper, including the introduction section, is organized in the following sequence: Section 2 reviews the relevant background on fuzzy DEA techniques and applications. Section 3 presents this research methodology. Section 4 presents an application of the developed window analysis and research results. Section 5 summarizes the research conclusions.

2. Literature Review

The traditional DEA models were reported as powerful techniques for efficient evaluation of homogeneous DMUs from crisp input and output process data. In reality, however, production processes are usually volatile and complex, which makes it difficult to obtain accurate or precise input and output data. Therefore, significant research efforts were directed at developing DEA models that can evaluate the relative efficiency of DMUs for a manufacturing process from fuzzy input and output data. For example, Guo and Tanaka [26] proposed two fuzzy DEA models for evaluating the efficiencies of DMUs from fuzzy input and output data. The efficiencies were represented by fuzzy numbers to reflect the inherent fuzziness of evaluation problems. The fuzzy DEA models extended the CCR model to more general forms that can handle crisp, fuzzy, and hybrid data. Lertworasirikul et al. [27] transformed fuzzy DEA models into possibility DEA models by using possibility measures of fuzzy constraints. The fuzzy membership functions of fuzzy data were of the trapezoidal type. Liu and Chuang [28] proposed a DEA approach to determine the fuzzy efficiency measures embedded with the assurance region (AR) concept. The fuzzy DEA/AR model was transformed into a family of crisp DEA/AR models by calculating the lower and upper bounds of efficiency scores at a specific level. A study of twenty-four university libraries in Taiwan was employed to illustrate their model. Wen and Li [29] proposed a credibility measure in the fuzzy DEA model, followed by DMUs ranking. A hybrid algorithm combined with the fuzzy simulation and genetic algorithmgenetic algorithm was used to solve the model for trapezoidal or triangular fuzzy inputs and outputs. Puri and Yadav [30] proposed the concept of fuzzy input mix-efficiency and evaluated the fuzzy input mix-efficiency using the α-cut approach. A real case study from the State Bank of Patiala in the Punjab state of India, with districts, was provided for illustration. Wanke et al. [31] employed bootstrapped regressions and fuzzy-DEA (FDEA) models to capture vagueness in the input and output measurements obtained from Nigerian airports. Barak and Dahooei [32] proposed FDEA and fuzzy multi-attribute decision-making (F-MADM) for ranking the airlines’ safety. The FDEA was adopted to estimate criteria weights, which were then employed to rank each airline using MADM methods. Arana-Jiménez et al. [33] considered a slacks-based additive inefficiency measure and compared it with the existing fuzzy DEA methods. However, their model could not discriminate between efficient and weakly efficient DMUs. Khoshandam and Nematizadeh [34] proposed an inverse network DEA model for two-stage processes to evaluate the amount of change in one or more indicators of one stage of a process by changing indicators of another stage to preserve the level of efficiency in the presence of undesirable factors. The model was implemented in poultry farming. Mohanta et al. [35] developed an intuitionistic fuzzy DEA (IFDEA) model based on triangular intuitionistic fuzzy numbers (TIFNs). The weighted possibility means for TIFNs were then utilized to compare and rank the TIFNs.

Little research has been reported on using window analysis to assess efficiency when the input and output data are asymmetry and dynamic. For example, Wang et al. [36] combined DEA window analysis and fuzzy techniques for order of preference by similarity to the ideal solution to assess the capabilities of 42 countries in terms of renewable energy production potential. Three inputs (population, total energy consumption, and total renewable energy capacity) and two outputs (gross domestic product and total energy production) Peykani et al. [37] developed credibility-based fuzzy window analysis to evaluate the dynamic performance of hospitals during different periods of data ambiguity. The proposed approach was implemented on a real data set to evaluate the performance of hospitals in the USA. Al-Refaie [2] proposed a DEA window analysis and Malmquist productivity index under fuzzy data. The proposed window analysis was based on providing crisp efficiency scores by solving a single model.

This research provides an extension to ongoing research [38,39,40] by developing a framework for window analysis with asymmetry data. The collected input and output data are represented by triangular fuzzy numbers. Process efficiency is then calculated at three levels and transformed into a single, crisp optimal efficiency. The proposed DEA window analysis contributes to literature and practice by: (1) providing reliable assessments of process efficiency under asymmetry input and output data; (2) determining effective improvement actions based on slack analysis of inputs and outputs that lead to enhanced process performance; and (3) transforming the fuzzy efficiency into a crisp score that facilitates understanding and interpreting process efficiency.

3. Research Methodology

The developed framework for window analysis with asymmetry data are depicted in Figure 1.

The steps of the developed window analysis with asymmetry data are presented as follows:

Step 1: Specify the fuzzy input variables (planned production quantity, number of defectives, and idle time) and a single fuzzy output variable (actual production quantity) for the manufacturing process under consideration. Classify the variables into inputs and outputs for DEA window analysis, where input (output) variables are these variables to be minimized (maximized) [7]. Then, collect asymmetry data for those variables over a time horizon (T). It is assumed that the input and output data follow triangular fuzzy numbers (TFNs).

Step 2: Let the collected fuzzy input and output data of DEA variables at time t; t = 1, …, T, be denoted as ${\tilde{x}}_i^t$; i = 1,…, m, and ${\tilde{y}}_r^t$, r = 1, …, s, respectively. The time horizon, T, is then divided into n windows. Let z denote window width. Let w_j denote the jth window, which can be determined as follows: w₁: $t_1\to t_z{}_{}$, w₂: $t_2\to t_{z+1}{}_{}$, …, and so on. Finally, treat each window as a Decision-Making Unit (DMU).

Step 3.1: Evaluate the technical efficiency (TE) of each DMU_j (j = 1, …, n). Let ${\theta }_k^{{}^{}}$ be the efficiency of DMU_k ($k\in j$). Then, the objective of the optimization model aims to maximize ${\theta }_k^{{}^{}}$ [2, 9]. Generally,

$$\mathrm{Max} {\theta }_k^{{}^{}}=\frac{virtual output}{virtual input}=\frac{u_1{y}_{1k}+u_2{y}_{2k}+\mathrm{\dots }+u_s{y}_{sk}}{v_1{x}_{1k}+v_2{x}_{2k}+\mathrm{\dots }+v_m{x}_{mk}}$$

(1)

where u_r (r = 1,…, s) and v_m (i = 1,…, m) are the input and output weights. The ratio of the virtual output versus the virtual input of DMU_j cannot exceed one. Then, the following constraints are formulated [3, 8]:

$$\frac{u_1{y}_{1j}+u_2{y}_{2j}+\mathrm{\dots }+u_s{y}_{sj}}{v_1{x}_{1j}+v_2{x}_{2j}+\mathrm{\dots }+v_m{x}_{mj}}\le 1,\hspace{1em}\forall j$$

(2)

$$u_r\ge 0,\hspace{1em}\forall r$$

(3)

$$v_i\ge 0,\hspace{1em}\forall i$$

(4)

Let $s_i^{-}$ and $s_r^{+}$ denote the negative input and positive output slacks, respectively. The equivalent dual problem of the input-oriented fractional model (Formulas (1)–(4)) is formulated as [7]:

$$\mathrm{Min}{\theta }_k^{{}^{}}$$

(5)

Subject to:

$${\theta }_k^{{}^{}}{x}_{ik}-{\displaystyle \sum _{j=1}^n{\lambda }_j{x}_{ij}}-s_i^{-}=0,\hspace{1em}\forall i$$

(6)

$${\displaystyle \sum _{j=1}^n{\lambda }_j{y}_{rj}}-y_{rk}-s_r^{+}=0, \hspace{1em}\forall r$$

(7)

$${\lambda }_j\ge 0,\hspace{1em}\forall j$$

(8)

$$s_i^{-}\ge 0,\hspace{1em}\forall i$$

(9)

$$s_r^{+}\ge 0,\hspace{1em}\forall r$$

(10)

Let ${\theta }_k^{{}^{*}}$ denote the optimal efficiency of DMU_k. Then, DMU_k is identified as CCR-efficient if ${\theta }_k^{{}^{*}}$ is equal to one and all slacks are zeros. Otherwise, DMU_k is identified as CCR-inefficient.

Because the input and output ${\tilde{x}}_{ij}$ and ${\tilde{y}}_{rj}$ are fuzzy numbers, then ${\tilde{\theta }}_k^{{}^{*}}$ is a triangular fuzzy numbers [28]. Let ${\theta }_{qk}^{{}^{*L}}$, ${\theta }_{qk}^{{}^{*M}}$, and ${\theta }_{qk}^{{}^{*H}}$, denote the low, middle, and high levels of the optimal TE values, respectively. Let the fuzzy input ${\tilde{x}}_{itk}=(a_{itk},b_{itk},c_{itk})$, where a_itk, b_itk and c_itk denote the low (L), middle (M), and high (H) elements for fuzzy i^th input; i = 1,…, m, of DMU_k; $k\in j$. In addition, the fuzzy output ${\tilde{y}}_{rtk}=(d_{rtk},e_{rtk},f_{rtk})$, where d_rtk, e_rtk, and f_rtk represent the L, M, and H levels of fuzzy r^th output; r = 1,…, s, of DMU_k; $k\in j$. For illustration, the representation of the collected data for a window of six periods of DMU₁ is displayed in

Table 1. Representation of the fuzzy data for the six periods of DMU₁.

Inputs/Outputs of DMU1 (k = 1)	t = 1 ${\tilde{\mathit{x}}}_{\mathit{i}11}=({\mathit{a}}_{\mathit{i}11},{\mathit{b}}_{\mathit{i}11},{\mathit{c}}_{\mathit{i}11})$	…	t = 6 ${\tilde{\mathit{x}}}_{\mathit{i}61}=({\mathit{a}}_{\mathit{i}61},{\mathit{b}}_{\mathit{i}61},{\mathit{c}}_{\mathit{i}61})$
${\tilde{x}}_{it1}=(a_{it1},b_{it1},c_{it1})$	${\tilde{x}}_{111}=(a_{111},b_{111},c_{111})$	…	${\tilde{x}}_{161}=(a_{161},b_{161},c_{161})$
	${\tilde{x}}_{211}=(a_{211},b_{211},c_{211})$	…	${\tilde{x}}_{261}=(a_{261},b_{261},c_{261})$
	⋮	⋮	⋮
	${\tilde{x}}_{m11}=(a_{m11},b_{m11},c_{m11})$	…	${\tilde{x}}_{m61}=(a_{m61},b_{m61},c_{m61})$
${\tilde{y}}_{rt1}=(d_{rt1},e_{rt1},f_{rt1})$	${\tilde{y}}_{111}=(d_{111},e_{111},f_{111})$	…	${\tilde{y}}_{161}=(d_{161},e_{161},f_{161})$
	${\tilde{y}}_{211}=(d_{211},e_{211},f_{211})$	…	${\tilde{y}}_{261}=(d_{261},e_{261},f_{261})$
	⋮	⋮	⋮
	${\tilde{y}}_{s11}=(d_{s11},e_{s11},f_{s11})$	…	${\tilde{y}}_{s61}=(d_{s61},e_{s61},f_{s61})$

.

The optimal low TE, ${\theta }_{qk}^{{}^{*L}}$, of DMU_k at a specific time q; $q\in w_k$, in window k is estimated using the dual formulation of the CCR model as follows:

$$Min {\theta }_{qk}^L$$

(11)

Subject to:

$${\theta }_{qk}^L{}_{}{a}_{iqk}-{\displaystyle \sum _{t\in w_k}^{}{\lambda }_t{a}_{itk}-s_i^{-}=0,}\hspace{1em}\forall i$$

(12)

$${\displaystyle \sum _{t\in w_k}^{}{\lambda }_t{d}_{rtk}-d_{rqk}-s_r^{+}=0 , \hspace{1em}\forall }r$$

(13)

$$s_i^{-}\ge 0,\hspace{1em}\forall i$$

(14)

$$s_r^{+}\ge 0,\hspace{1em}\forall r$$

(15)

$${\lambda }_t\ge 0 , \hspace{1em}\forall t\in w_k$$

(16)

Table 2. The optimal TE and PTE values from low-level input and output data for DMU₁.

Inputs/Outputs of DMU1 (k = 1) at Low-Level Data	t = 1	…	t = 6	${\mathit{\theta }}_{\mathit{t}\mathit{k}}^{{}^{*\mathit{L}}}$	${\mathit{\delta }}_{\mathit{q}\mathit{k}}^{{}^{*\mathit{L}}}$
ait1	a111	…	a161	${\theta }_{11}^{{}^{*L}}$${\theta }_{21}^{{}^{*L}}$${\theta }_{31}^{{}^{*L}}$ ${\theta }_{41}^{{}^{*L}}$${\theta }_{51}^{{}^{*L}}$${\theta }_{61}^{{}^{*L}}$	${\delta }_{11}^{{}^{*L}}$${\delta }_{21}^{{}^{*L}}$${\delta }_{31}^{{}^{*L}}$ ${\delta }_{41}^{{}^{*L}}$${\delta }_{51}^{{}^{*L}}$${\delta }_{61}^{{}^{*L}}$
	a211	…	a261
	⋮	⋮	⋮
	am11	…	am61
drt1	d111	…	d161
	d211	…	d261
	⋮	⋮	⋮
	ds11	…	ds61
Averages of optimal TE and PTE at low-level data				${\theta }_1^{{}^{*L}}$	${\delta }_1^{{}^{*L}}$

displays the optimal TE and PTE efficiencies from low-level input and output data for DMU₁.

The middle and high optimal efficiencies ${\theta }_{tk}^{{}^{*L}}$ for the remaining periods in window k; $t\in w_k$ and t ≠ q, are estimated similarly. Repeat this step to obtain the optimal efficiencies ${\theta }_{tk}^{{}^{*M}}$ and ${\theta }_{tk}^{{}^{*H}}$ for all periods in window k; $t\in w_k$, of DMU_k. In a similar manner, obtain the optimal efficiencies ${\theta }_{tj}^{{}^{*M}}$ and ${\theta }_{tj}^{{}^{*H}}$ from the middle and high levels of input and output data.

Step 3.2: Evaluate the pure technical efficiency (PTE) of DMU_j. Let ${\delta }_{qk}^{{}^{*L}}$, ${\delta }_{qk}^{{}^{*M}}$, and ${\delta }_{qk}^{{}^{*H}}$, denote the low, middle, and high optimal PTE efficiencies, respectively. For illustration, the optimal PTE, ${\delta }_{qk}^{{}^{*L}}$, at the low data level DMU_k, is estimated using an input-oriented BCC model without slacks [2]. Mathematically,

$$Min {\delta }_{{}^{qk}}^L$$

(17)

Subject to:

$${\displaystyle \sum _{t\in w_k}^{}{\lambda }_t{d}_{rtk}-d_{rqk}\ge 0 , \hspace{1em}\forall }r$$

(18)

$${\delta }_{qk}^L{}_{}{a}_{iqk}-{\displaystyle \sum _{t\in w_k}^{}{\lambda }_t{a}_{itk}\ge } 0, \hspace{1em}\forall i$$

(19)

$${\displaystyle \sum _{j=1}^n{\lambda }_j=1}$$

(20)

$${\lambda }_t\ge 0 , \hspace{1em}\forall t\in w_k$$

(21)

The obtained optimal values of ${\tilde{\delta }}_{tk}^{{}^{*L}}$ are shown in Table 2. Similarly, the ${\tilde{\delta }}_{tk}^{{}^{*L}}$ values are calculated at the remaining periods (t ≠ q) of DMU_k. In a similar manner, the ${\delta }_{qj}^{{}^{*M}}$ and ${\delta }_{qj}^{{}^{*H}}$, are obtained at window periods of DMU_j (j ≠ k).

Table 3. Summary of the fuzzy optimal TE and PTE values.

DMUj	t = 1	t = 2	…	t = 6	t = 7		t = 11	t = 12	DMU Efficiency ${\mathit{\theta }}_{\mathit{j}}^{{}^{*}},{\mathit{\delta }}_{\mathit{j}}^{{}^{*}},{\mathit{\omega }}_{\mathit{j}}^{{}^{*}}$
DMU1	${\theta }_{11}^{{}^{*L}},{\theta }_{11}^{{}^{*M}},{\theta }_{11}^{{}^{*H}}$ ${\delta }_{11}^{{}^{*L}},{\delta }_{11}^{{}^{*M}},{\delta }_{11}^{{}^{*H}}$	${\theta }_{12}^{{}^{*L}},{\theta }_{12}^{{}^{*M}},{\theta }_{12}^{{}^{*H}}$ ${\delta }_{12}^{{}^{*L}},{\delta }_{12}^{{}^{*M}},{\delta }_{12}^{{}^{*H}}$	…	${\theta }_{61}^{{}^{*L}},{\theta }_{61}^{{}^{*M}},{\theta }_{61}^{{}^{*H}}$ ${\delta }_{61}^{{}^{*L}},{\delta }_{61}^{{}^{*M}},{\delta }_{61}^{{}^{*H}}$					${\theta }_1^{{}^{*}}, {\delta }_1^{{}^{*}}, {\omega }_1^{{}^{*}}$
DMU2		${\theta }_{22}^{{}^{*L}},{\theta }_{22}^{{}^{*M}},{\theta }_{22}^{{}^{*H}}$ ${\delta }_{22}^{{}^{*L}},{\delta }_{22}^{{}^{*M}},{\delta }_{22}^{{}^{*H}}$	…	${\theta }_{62}^{{}^{*L}},{\theta }_{62}^{{}^{*M}},{\theta }_{62}^{{}^{*H}}$ ${\delta }_{62}^{{}^{*L}},{\delta }_{62}^{{}^{*M}},{\delta }_{62}^{{}^{*H}}$	${\theta }_{72}^{{}^{*L}},{\theta }_{72}^{{}^{*M}},{\theta }_{72}^{{}^{*H}}$ ${\delta }_{72}^{{}^{*L}},{\delta }_{72}^{{}^{*M}},{\delta }_{72}^{{}^{*H}}$				${\theta }_2^{{}^{*}}, {\delta }_2^{{}^{*}}, {\omega }_2^{{}^{*}}$
⋮				⋮	⋮		⋮
DMU6				${\theta }_{66}^{{}^{*L}},{\theta }_{66}^{{}^{*M}},{\theta }_{66}^{{}^{*H}}$ ${\delta }_{66}^{{}^{*L}},{\delta }_{66}^{{}^{*M}},{\delta }_{66}^{{}^{*H}}$	${\theta }_{76}^{{}^{*L}},{\theta }_{76}^{{}^{*M}},{\theta }_{76}^{{}^{*H}}$ ${\delta }_{76}^{{}^{*L}},{\delta }_{76}^{{}^{*M}},{\delta }_{76}^{{}^{*H}}$	…	${\theta }_{11,6}^{{}^{*L}},{\theta }_{11,6}^{{}^{*M}},{\theta }_{11,6}^{{}^{*H}}$ ${\delta }_{11,6}^{{}^{*L}},{\delta }_{11,6}^{{}^{*M}},{\delta }_{11,6}^{{}^{*H}}$		${\theta }_6^{{}^{*}}, {\delta }_6^{{}^{*}}, {\omega }_6^{{}^{*}}$
DMU7					${\theta }_{77}^{{}^{*L}},{\theta }_{77}^{{}^{*M}},{\theta }_{77}^{{}^{*H}}$ ${\delta }_{77}^{{}^{*L}},{\delta }_{77}^{{}^{*M}},{\delta }_{77}^{{}^{*H}}$	…	${\theta }_{11,7}^{{}^{*L}},{\theta }_{11,7}^{{}^{*M}},{\theta }_{11,7}^{{}^{*H}}$ ${\delta }_{77}^{{}^{*L}},{\delta }_{77}^{{}^{*M}},{\delta }_{77}^{{}^{*H}}$	${\theta }_{12,7}^{{}^{*L}},{\theta }_{12,7}^{{}^{*M}},{\theta }_{12,7}^{{}^{*H}}$ ${\delta }_{77}^{{}^{*L}},{\delta }_{77}^{{}^{*M}},{\delta }_{77}^{{}^{*H}}$	${\theta }_7^{{}^{*}}, {\delta }_7^{{}^{*}}, {\omega }_7^{{}^{*}}$
Period efficiency	${\theta }_{}^{{}^{*1}}, {\delta }_{}^{{}^{*1}}, {\omega }_{}^{{}^{*1}}$	${\theta }_{}^{{}^{*2}}, {\delta }_{}^{{}^{*2}}, {\omega }_{}^{{}^{*2}}$		${\theta }_{}^{{}^{*6}}, {\delta }_{}^{{}^{*6}}, {\omega }_{}^{{}^{*6}}$	${\theta }_{}^{{}^{*7}}, {\delta }_{}^{{}^{*7}}, {\omega }_{}^{{}^{*7}}$		${\theta }_{}^{{}^{*11}}, {\delta }_{}^{{}^{*11}}, {\omega }_{}^{{}^{*11}}$	${\theta }_{}^{{}^{*12}}, {\delta }_{}^{{}^{*12}}, {\omega }_{}^{{}^{*12}}$

summarizes the calculated ${\theta }_{tj}^{{}^{*L}}, {\theta }_{tj}^{{}^{*M}}, {\theta }_{tj}^{{}^{*H}}$, ${\tilde{\delta }}_{tk}^{{}^{*L}}$, ${\delta }_{tk}^{{}^{*M}}$, and ${\delta }_{tk}^{{}^{*H}}$.

Step 3.3: Calculate the elements of the TE and PTE averages ${\tilde{\theta }}_j^{{}^{*}}({\theta }_j^{{}^{*L}},{\theta }_j^{{}^{*M}},{\theta }_j^{{}^{*H}})$ and ${\tilde{\delta }}_j^{{}^{*}}({\delta }_j^{{}^{*L}},{\delta }_j^{{}^{*M}},{\delta }_j^{{}^{*H}})$, respectively, of DMU_j; j = 1, …, n. For example, in Table 2, the low-level optimal efficiency of DMU₁, ${\theta }_1^{{}^{*}L}$, is the average of the period efficiencies ${\tilde{\theta }}_{11}^{{}^{*}}$, ${\tilde{\theta }}_{21}^{{}^{*}}$, …, and ${\tilde{\theta }}_{61}^{{}^{*}}$. Similarly, the low-level optimal PTE of DMU₁, ${\tilde{\delta }}_1^{{}^{*L}}$.

Step 4: To provide a more practical interpretation of the optimal fuzzy TE and PTE, the ${\tilde{\theta }}_j^{{}^{*}}({\theta }_j^{{}^{*L}},{\theta }_j^{{}^{*M}},{\theta }_j^{{}^{*H}})$ and ${\tilde{\delta }}_j^{{}^{*}}({\delta }_j^{{}^{*L}},{\delta }_j^{{}^{*M}},{\delta }_j^{{}^{*H}})$ are transformed into single crisp values. Let D denote the defuzzified optimal efficiency, which is calculated as follows [25]:

$$D=\frac{1}{3}(\left(U-L\right)+(M-L\left)\right)+L$$

(22)

where U, M, and L are the high, middle, and low of efficiency TFN, respectively. Use Equation (22) to calculate the optimal ${\theta }_j^{{}^{*}}$ and ${\delta }_j^{{}^{*}}$ of DMU_j; j = 1, …, n, respectively, as follows:

$${\theta }_j^{{}^{*}}=\frac{1}{3}(({\theta }_j^{{}^{*H}}-{\theta }_j^{{}^{*L}})+({\theta }_j^{{}^{*M}}-{\theta }_j^{{}^{*L}}))+{\theta }_j^{{}^{*L}}$$

(23)

$${\delta }_j^{{}^{*}}=\frac{1}{3}(({\delta }_j^{{}^{*H}}-{\delta }_j^{{}^{*L}})+({\delta }_j^{{}^{*M}}-{\delta }_j^{{}^{*L}}))+{\delta }_j^{{}^{*L}}$$

(24)

Step 5: Calculate the optimal SE, ${\omega }_j^{*}$, as follows:

$${\omega }_j^{*}=\frac{{\theta }_j^{{}^{*}}}{{\delta }_j^{{}^{*}}}$$

(25)

Table 3 also summarizes the values of ${\omega }_j^{*}$ for all DMUs.

Step 6: Let ${\theta }_{}^{{}^{*t}}$, ${\delta }_{}^{{}^{*t}}$, and ${\omega }_{}^{*t}$ denote the TE, PTE, and SE at period t, respectively. Obtain ${\tilde{\theta }}_{}^{{}^{*t}}$ and ${\tilde{\delta }}_{}^{{}^{*t}}$ as follows. Firstly, calculate the average period TE, ${\theta }_{}^{{}^{*tL}}$, at low-level data, from the values of ${\theta }_{tj}^{{}^{*L}}$ for the DMUs that include the period t in window j, as shown in Equation (26).

$${\theta }_{}^{{}^{*tL}}=\frac{{\displaystyle {\sum }_{j=1}^{n^{\prime }}{\theta }_{tj}^{{}^{*L}}}}{n^{\prime }}$$

(26)

where $n^{\prime }$ denotes the number of DMUs that include period t in window j. Similarly, calculate the ${\theta }_{}^{{}^{*tM}}$ and ${\theta }_{}^{{}^{*tH}}$ in a similar manner. Apply Equations (23) and (24) to calculate the crisp ${\theta }_{}^{{}^{*t}}$ and ${\delta }_{}^{{}^{*t}}$, respectively. Finally, calculate the values of ${\omega }_{}^{*t}$ using Equation (25). The results are shown in Table 3.

Step 7: Analyze the results for the DMUs and period fuzzy and crisp optimal efficiencies (TE, PTE, and SE). Determine and examine the input and output negative and positive slacks for all DMUs and periods. Recommend the required actions to improve process performance. Finally, validate the anticipated improvement.

4. Research Results

The efficiency evaluation of the blowing machine in the plastics industry was considered and is presented as follows. In steps 1 and 2, the relevant fuzzy input and output data for a blowing process were collected for 12 months; t = 1, …, 12, from the production reports. The planned production quantity (${\tilde{x}}_1$), number of defectives (${\tilde{x}}_2$), and idle time (${\tilde{x}}_3^{}$) were treated as the inputs, whereas the actual production quantity in production units ($\tilde{y}$) was set as the output for all periods in the DEA model as shown in

Table 4. DEA data (Units) for blowing machines.

Period t	Inputs			Output
	Planned Production ${\tilde{\mathit{x}}}_1^{\mathit{t}}$	Defectives ${\tilde{\mathit{x}}}_2^{\mathit{t}}$	Idle Time ${\tilde{\mathit{x}}}_3^{\mathit{t}}$	Production Quantity ${\tilde{\mathit{y}}}_{}^{\mathit{t}}$
1	(24150, 24192, 25100)	(179, 185, 192)	(1383,1426, 1483)	(21099, 22300, 23103)
2	(24100, 24192, 24300)	(91, 94, 97)	(7756, 7996, 8315)	(15550, 15731, 17832)
3	(24000, 24192, 25159)	(66, 69, 71)	(3054, 3149, 3274)	(20549, 21419, 22318)
4	(24000, 24192, 25000)	(94, 97, 100)	(6221, 6414, 6670)	(18231, 18359, 23721)
5	(20113, 20736,21565)	(170, 176, 183)	(1876, 1935, 2012)	(17128, 17221, 19762)
6	(26818, 27648, 28753)	(137, 142, 147)	(49, 51, 53)	(26810, 27620, 27640)
7	(23466, 24192, 25159)	(116, 120, 124)	(3317, 3420, 3556)	(18089, 19456, 22941)
8	(20113, 20736, 21565)	(51, 53, 55)	(2018, 2081, 2164)	(19012, 19616, 20000)
9	(13409, 13824, 14376)	(31, 32, 33)	(657, 678, 705)	(12984, 13500, 13561)
10	(10056, 10368, 10782)	(70, 73, 75)	(2769, 2855, 2969)	(8195, 8318, 9939)
11	(15085, 15552, 16174)	(111, 115, 119)	(2873, 2962, 3080)	(13294, 13350, 15230)
12	(21790, 22464, 23362)	(237, 245, 254)	(2268, 2339, 2432)	(20137, 20750, 22252)

. The length of each window consisted of six periods. Hence, seven DMUs; DMU₁ to DMU₇ for t₁–t₆, t₂–t₇, …, and t₇–t₁₂, respectively, were obtained.

In step 3.1, the input-oriented CCR model was employed to estimate the optimal TE; ${\theta }_{tj}^{{}^{*L}}$, ${\theta }_{tj}^{{}^{*M}}$, and ${\theta }_{tj}^{{}^{*H}}$, at the low, middle, and high levels respectively.

Table 5. Optimal technical efficiency.

DMU	Period t
j	1	2	3	4	5	6	7	8	9	10	11	12	${\theta }_j^{{}^{*}L}$	CV%
1	0.8739	0.7024	1.0000	0.8193	0.8518	1.0000							0.8746	13.01%
2		0.7024	1.0000	0.8193	0.8518	1.0000	0.7789						0.8587	14.01%
3			0.9015	0.7795	0.8518	1.0000	0.7738	1.0000					0.8844	11.45%
4				0.7702	0.8518	1.0000	0.7725	0.9737	1.0000				0.8947	12.31%
5					0.8518	1.0000	0.7725	0.9737	1.0000	0.8152			0.9022	11.21%
6						1.0000	0.7725	0.9737	1.0000	0.8152	0.8815		0.9072	10.90%
7							0.7961	0.9762	1.0000	0.8416	0.9101	0.9544	0.9131	8.77%
${\theta }_t^{{}^{*}L}$	0.8739	0.7024	0.9672	0.7971	0.8518	1.0000	0.7777	0.9795	1.0000	0.8240	0.8958	0.9544
CV%	0.00%	0.00%	5.88%	3.25%	0.00%	0.00%	1.20%	1.18%	0.00%	1.85%	2.26%	0.00%
j	1	2	3	4	5	6	7	8	9	10	11	12	${\theta }_j^{{}^{*M}}$	CV%
1	0.9227	0.6941	1.0000	0.8048	0.8313	1.0000							0.8755	13.81%
2		0.6941	1.0000	0.8048	0.8313	1.0000	0.8122						0.8571	14.08%
3			0.9299	0.7777	0.8313	1.0000	0.8080	1.0000					0.8912	11.06%
4				0.7665	0.8313	1.0000	0.8062	0.9668	1.0000				0.8951	11.79%
5					0.8313	1.0000	0.8062	0.9668	1.0000	0.8031			0.9012	10.80%
6						1.0000	0.8062	0.9668	1.0000	0.8031	0.8593		0.9059	10.37%
7							0.8235	0.9687	1.0000	0.8215	0.8790	0.9459	0.9064	8.41%
${\theta }_t^{{}^{*}M}$	0.9227	0.6941	0.9766	0.7885	0.8313	1.0000	0.8104	0.9738	1.0000	0.8092	0.8692	0.9459
CV%	0.00%	0.00%	4.14%	2.46%	0.00%	0.00%	0.84%	1.51%	0.00%	1.31%	1.60%	0.00%
j	1	2	3	4	5	6	7	8	9	10	11	12	${\theta }_j^{{}^{*}H}$	CV%
1	0.9575	0.7737	1.0000	1.0000	0.9533	1.0000							0.9474	9.28%
2		0.7737	1.0000	1.0000	0.9533	1.0000	0.9506						0.9463	9.27%
3			0.9524	1.0000	0.9533	1.0000	0.9506	1.0000					0.9761	2.69%
4				0.9944	0.9533	1.0000	0.9497	0.9815	1.0000				0.9798	2.35%
5					0.9533	1.0000	0.9497	0.9815	1.0000	0.9589			0.9739	2.37%
6						1.0000	0.9497	0.9815	1.0000	0.9589	0.9796		0.9783	2.12%
7							0.9638	0.9829	1.0000	0.9721	0.9925	1.0000	0.9852	1.52%
${\theta }_t^{{}^{*}H}$	0.9575	0.7737	0.9841	0.9986	0.9533	1.0000	0.9524	0.9855	1.0000	0.9633	0.9861	1.0000
CV%	0.00%	0.00%	2.79%	0.28%	0.00%	0.00%	0.59%	0.83%	0.00%	0.79%	0.93%	0.00%

displays the obtained optimal values of ${\theta }_{tj}^{{}^{*L}}$,${\theta }_{tj}^{{}^{*M}}$,${\theta }_{tj}^{{}^{*H}}$, and ${\theta }_j^{{}^{*L}}$.

From Table 5, the following remarks are obtained: Firstly, the estimated optimal TE listed at each period (column) reveals a stable performance because almost all the percentages of the coefficient of variation, CV%, are smaller than 0.05 for all columns. However, the CV percentages corresponding to the DMUs (rows) are greater than 0.05, which implies significant dispersion or trend in the TE scores of the same window. Secondly, the averages of ${\theta }_j^{{}^{*L}}$,${\theta }_j^{{}^{*M}}$, and ${\theta }_j^{{}^{*H}}$ are found to be smaller than one for all seven DMUs, and thereby it can be concluded that the blowing process was TE-inefficient at all data levels. Furthermore, the optimal TE values for each window period; ${\theta }_{}^{{}^{*tL}}, {\theta }_{}^{{}^{*tM}}$, and ${\theta }_{}^{{}^{*tH}}$ were estimated and found to be equal to one in two, two, and three out of twelve periods, respectively. In step 3.2, the optimal values of the pure technical efficiency; ${\delta }_{tj}^{{}^{*L}}$,${\delta }_{tj}^{{}^{*M}}$, and ${\delta }_{tj}^{{}^{*H}}$, were calculated at low, middle, and high data levels to explain the causes of the TE inefficiency (TIE) for all window periods.

Table 6. Optimal pure technical efficiency.

	Period t
DMUj	1	2	3	4	5	6	7	8	9	10	11	12	${\delta }_j^{{}^{*}L}$	CV%
1	0.9467	0.9624	1.0000	0.9620	1.0000	1.0000							0.9785	2.47%
2		0.9624	1.0000	0.9620	1.0000	1.0000	0.9520						0.9794	2.34%
3			1.0000	0.8380	1.0000	1.0000	0.8571	1.0000					0.9492	8.32%
4				0.7707	0.8665	1.0000	0.7824	1.0000	1.0000				0.9033	12.29%
5					0.8665	1.0000	0.7824	1.0000	1.0000	1.0000			0.9415	10.03%
6						1.0000	0.7824	1.0000	1.0000	1.0000	0.9088		0.9485	9.40%
7							0.8134	1.0000	1.0000	1.0000	0.9118	1.0000	0.9542	8.12%
${\delta }_{}^{{}^{*}tL}$	0.9467	0.9624	1.0000	0.8832	0.9466	1.0000	0.8283	1.0000	1.0000	1.0000	0.9103	1.0000
CV%	0	0.00%	0.00%	10.77%	7.72%	0.00%	8.13%	0.00%	0.00%	0.00%	0.23%	0.00%
DMUj	1	2	3	4	5	6	7	8	9	10	11	12	${\delta }_j^{{}^{*}M}$	CV%
1	0.9967	0.9703	1.0000	0.9669	1.0000	1.0000							0.9890	1.61%
2		0.9703	1.0000	0.9669	1.0000	1.0000	0.9413						0.9798	2.48%
3			1.0000	0.8571	1.0000	1.0000	0.8571	1.0000					0.9524	7.75%
4				0.7681	0.8424	1.0000	0.8125	1.0000	1.0000				0.9038	11.95%
5					0.8424	1.0000	0.8125	1.0000	1.0000	1.0000			0.9425	9.51%
6						1.0000	0.8125	1.0000	1.0000	1.0000	0.8825		0.9492	8.62%
7							0.8497	1.0000	1.0000	1.0000	0.8825	1.0000	0.9554	7.32%
${\delta }_{}^{{}^{*}tM}$	0.9967	0.9703	1.0000	0.8898	0.9370	1.0000	0.8476	1.0000	1.0000	1.0000	0.8825	1.0000
CV%	0	0.00%	0.00%	10.81%	9.21%	0.00%	5.92%	0.00%	0.00%	0.00%	0.00%	0.00%
DMUj	1	2	3	4	5	6	7	8	9	10	11	12	${\delta }_j^{{}^{*}H}$	CV%
1	0.9803	1.0000	1.0000	1.0000	1.0000	1.0000							0.9967	0.81%
2		1.0000	1.0000	1.0000	1.0000	1.0000	0.9832						0.9972	0.69%
3			1.0000	1.0000	1.0000	1.0000	0.9661	1.0000					0.9944	1.39%
4				1.0000	0.9603	1.0000	0.9521	1.0000	1.0000				0.9854	2.31%
5					0.9603	1.0000	0.9521	1.0000	1.0000	1.0000			0.9854	2.31%
6						1.0000	0.9521	1.0000	1.0000	1.0000	0.9942		0.9911	1.94%
7							1.0000	1.0000	1.0000	1.0000	0.9955	1.0000	0.9993	0.18%
${\delta }_t^{{}^{*}H}$	0.9803	1.0000	1.0000	1.0000	0.9841	1.0000	0.9676	1.0000	1.0000	1.0000	0.9949	1.0000
CV%	0	0.00%	0.00%	0.00%	2.21%	0.00%	2.08%	0.00%	0.00%	0.00%	0.09%	0.00%

displays the results of the optimal PTE, where it is found that: (1) the CV% indicates the existence of less dispersion in PTE scores than the TE scores of the same window for all DMUs. For example, the ${\delta }_1^{{}^{*L}}$(=0.9785) for DMU₁ implies that the same output level could be produced by 97.85% of the recourses. In other words, about 2.15% of recourses could be saved by enhancing the machine’s performance to the highest level, and (2) the averages of ${\delta }_j^{{}^{*L}}$,${\delta }_j^{{}^{*M}}$, and ${\delta }_j^{{}^{*H}}$ are smaller than one for all seven DMUs, and thereby the blowing machine is judged PTE-inefficient in all DMUs. Further, the optimal PTE at each window period; ${\delta }_{}^{{}^{*tL}}$,${\delta }_{}^{{}^{*tM}}$, and ${\delta }_{}^{{}^{*tH}}$) was calculated and found to be equal to one in six, six, and eight out of the twelve periods, respectively.

Table 7. Summary of optimal TE, PTE, and SE.

			TE		PTE				SE
DMUj	${\mathit{\theta }}_{\mathit{j}}^{{}^{*}\mathit{L}}$	${\mathit{\theta }}_{\mathit{j}}^{{}^{*\mathit{M}}}$	${\mathit{\theta }}_{\mathit{j}}^{{}^{*}\mathit{H}}$	${\mathit{\theta }}_{\mathit{j}}^{{}^{*}}$	${\mathit{\delta }}_{\mathit{j}}^{{}^{*}\mathit{L}}$	${\mathit{\delta }}_{\mathit{j}}^{{}^{*}\mathit{M}}$	${\mathit{\delta }}_{\mathit{j}}^{{}^{*}\mathit{H}}$	${\mathit{\delta }}_{\mathit{j}}^{{}^{*}}$	${\mathit{\omega }}_{\mathit{j}}^{*}$	${\Delta }_{\mathit{j}}^{}$$={\mathit{\delta }}_{\mathit{j}}^{{}^{*}}$$-{\mathit{\omega }}_{\mathit{j}}^{*}$
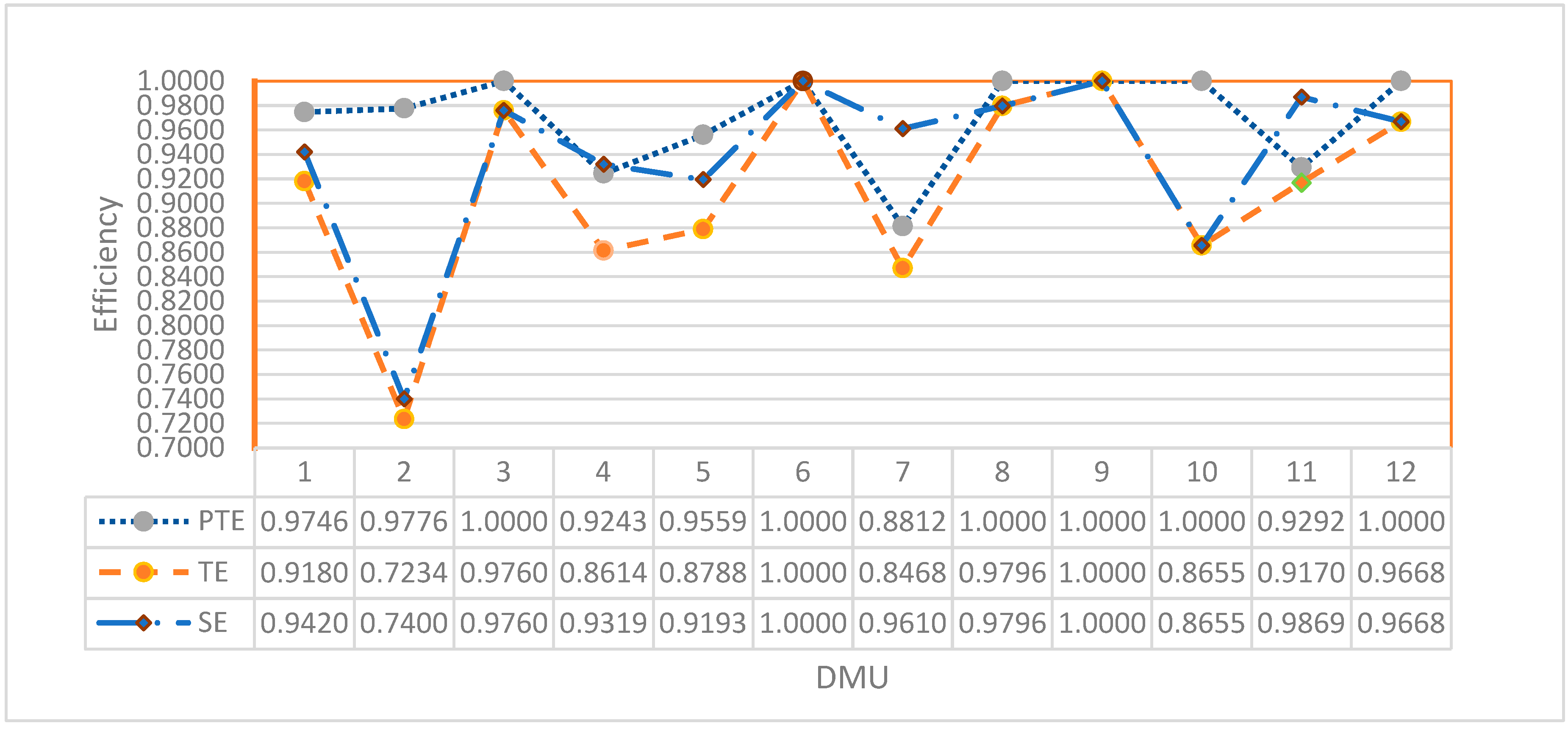
1	0.8746	0.8755	0.9474	0.8992	0.9785	0.989	0.9967	0.9881	0.9101	0.0780
2	0.8571	0.8587	0.9463	0.8874	0.9794	0.9798	0.9972	0.9855	0.9005	0.0850
3	0.8844	0.8912	0.9761	0.9172	0.9492	0.9524	0.9944	0.9653	0.9501	0.0152
4	0.8947	0.8951	0.9798	0.9232	0.9033	0.9038	0.9854	0.9308	0.9918	−0.0610
5	0.9012	0.9022	0.9739	0.9258	0.9415	0.9425	0.9854	0.9565	0.9679	−0.0115
6	0.9059	0.9072	0.9783	0.9305	0.9485	0.9492	0.9911	0.9629	0.9663	−0.0034
7	0.9064	0.9131	0.9852	0.9349	0.9542	0.9554	0.9993	0.9696	0.9642	0.0055
	Average			0.9169				0.9672	0.9501	0.0154

displays the estimated optimal fuzzy values of ${\theta }_j^{{}^{*}}$ and ${\delta }_j^{{}^{*}}$ for all DMUs. It is obvious in Table 7 that the existence of variations in the input and output data results in reasonable differences between the ${\theta }_j^{{}^{*}L}$, ${\theta }_j^{{}^{*M}}$, and ${\theta }_j^{{}^{*}H}$ values. A similar conclusion is obtained when comparing between ${\delta }_j^{{}^{*}L}$,${\delta }_j^{{}^{*M}}$, and ${\delta }_j^{{}^{*}H}$ values. Such differences may lead to erroneous improvement directions and complications in the decision-making process. Consequently, in step 4, the defuzzified values of the optimal TE and PTE, ${\theta }_j^{{}^{*}}$ and ${\delta }_j^{{}^{*}}$, respectively, were calculated using Equations (23) and (24), respectively. From Table 7, the optimal TE is found to be smaller than one for all DMUs. Hence, all DMUs can be characterized as TE-inefficient. Moreover, the optimal PTE is smaller than one for all DMUs, and consequently, the seven DMUs can be identified as PTE inefficient (PTIE). Step 5 follows to determine the optimal SE, ${\omega }_j^{*}$, values shown in Table 7. Figure 2 depicts the optimal TE, PTE, and SE for all DMUs, where the optimal PTE is found to be larger than the corresponding SE in four DMUs: DMU₁ to DMU₃ and DMU₇. Consequently, the reason behind the TIE for these DMUs was scale inefficiency. whereas the TIE was caused by managerial inefficiency for the remaining three DMUs, DMU₄ to DMU₆. The largest differences (${\Delta }_j^{}$ > 0.05) between PTE and SE correspond to DMU₁, DMU₂, and DMU₄. Further, the averages of optimal ${\theta }_j^{{}^{*}}$, ${\delta }_j^{{}^{*}}$, and ${\omega }_j^{*}$ were calculated from all DMUs and found 0.9169, 09672, and 0.9501, respectively. Consequently, it is concluded that TIE was caused by SIE.

The period averages of TE, PTE, and SE were analyzed in step 6 and then shown in Figure 3. It is noted that the TIE in months 1 to 3, 5, 8, 10, and 12 were caused by SIE, whereas the TIE was caused by PTE in months 4, 7, and 11. Finally, the process operated at an optimal TE in months 6 and 9.

Furthermore, the data projections resulting from the CCR and BCC models were calculated and then displayed in

Table 8. Slacks and projections.

	DMUj	PP			DQ			IT			PQ
Model		Data	Projection	Diff. (%)	Data	Projection	Diff. (%)	Data	Projection	Diff. (%)	Data	Projection	Diff. (%)
CCR	1	24,235.50	21,866.57	−9.77	125.7777	94.42027	−24.93	3471.387	1469.371	−57.67	20,728.33	20,728.33	0.00
	2	24,162.77	21,545.93	−10.83	114.9997	92.20273	−19.82	3801.447	1544.804	−59.36	20,384.87	20,384.87	0.00
	3	23,567.83	21,604.67	−8.33	108.2223	88.26153	−18.44	2822.163	1299.394	−53.96	20,889.97	20,889.97	0.00
	4	21,791.97	20,039.83	−8.04	102.2222	82.81483	−18.99	2413.11	366.3373	−84.82	19,562.93	19,562.93	0.00
	5	19,452.77	18,090.2	−7.00	98.16653	76.83613	−21.73	1823.943	295.734	−83.79	17,682.13	17,682.13	0.00
	6	18,594.60	17,402.13	−6.41	88.05557	73.32023	−16.73	1994.057	294.472	−85.23	17,004.37	17,004.37	0.00
	7	17,736.43	16,618.97	−6.30	105.1113	60.52847	−42.41	2372.777	957.104	−59.66	15,963.63	15,963.63	0.00
	Average			−8.10			−23.3			−69.21			0.00
BCC	1	24,235.5	23,862.77	−1.54	125.7767	120.9733	−3.82	3471.387	2509.017	−27.72	20,728.33	21,373.13	3.11
	2	24,162.77	23,811.93	−1.45	114.9967	113.49	−1.31	3801.447	2780.73	−26.85	20,384.87	21,140.6	3.71
	3	23,567.83	22,715.97	−3.61	108.2233	102.8267	−4.99	2822.163	2194.013	−22.26	20,889.97	20,945.23	0.26
	4	21,791.97	20,200.47	−7.30	102.22	76.3	−25.36	2413.11	1021.95	−57.65	19,562.93	19,562.93	0.00
	5	19,452.77	18,472.57	−5.04	98.16333	74.77667	−23.82	1823.943	1076.643	−40.97	17,682.13	17,682.13	0.00
	6	18,594.6	17,802.33	−4.26	88.05667	69.47333	−21.10	1994.057	1107.037	−44.48	17,004.37	17,004.37	0.00
	7	17,736.43	17,097.87	−3.60	105.1133	86.35333	−17.85	2372.777	1853.293	−21.89	15,963.63	15,963.63	0.00
	Average			−3.83			−14.04			−34.55			1.01

for all DMUs. It is found that the largest input excesses correspond to IT, followed by DQ for all DMUs. Thus, reductions in excess inputs should be made to become technically efficient. To illustrate, for DMU₁ to become CCR-efficient at the same PQ, the PP, DQ, and IT have to be reduced by 9.77%, 24.93%, and 57.67%, respectively. On the other hand, for DMU₁ to become BCC-efficient, the PP, DQ, and IT have to be reduced by 1.54%, 3.82%, and 27.72%, respectively, while the PQ should be increased by 3.11%. On average, for the blowing process to become CCR-efficient, the inputs PP, DQ, and IT should be reduced by 8.10, 23.3, and 69.21%, respectively. On the other hand, to become BCC-efficient, the inputs PP, DQ, and IT should be reduced by 3.83, 14.04, and 34.55%, respectively, while increasing the output by 1.01%.

In practice, the optimal SE and PTE obtained enable the identification of the causes of DMUs technical inefficiency: managerial or scale inefficiencies. Management actions, such as controlling resources to improve PTE, expanding/decreasing operational scale to boost overall technical efficiency, implementing effective quality control procedures to reduce defectives, increasing the sampling and testing scale to avoid producing defective outputs, and adopting efficient production scheduling and sequencing to reduce idle time (IT) and better utilize input resources and available production capacities, are needed.

Implementing these actions, the optimal TE, PTE, and SE, ${\theta }_j^{{}^{*}}$${\delta }_j^{{}^{*}}$, and ${\omega }_j^{*}$, respectively, were estimated and then displayed in

Table 9. Validation of TE, PTE, and SE.

DMUj	${\mathit{\theta }}_{\mathit{j}}^{{}^{*}\mathit{L}}$	${\mathit{\theta }}_{\mathit{j}}^{{}^{*\mathit{M}}}$	${\mathit{\theta }}_{\mathit{j}}^{{}^{*}\mathit{H}}$	${\mathit{\theta }}_{\mathit{j}}^{{}^{*}}$	${\mathit{\delta }}_{\mathit{j}}^{{}^{*}\mathit{L}}$	${\mathit{\delta }}_{\mathit{j}}^{{}^{*}\mathit{M}}$	${\mathit{\delta }}_{\mathit{j}}^{{}^{*}\mathit{H}}$	${\mathit{\delta }}_{\mathit{j}}^{{}^{*}}$	${\mathit{\omega }}_{\mathit{j}}^{*}$	${\Delta }_{\mathit{j}}^{}$$={\mathit{\delta }}_{\mathit{j}}^{{}^{*}}$$-{\mathit{\omega }}_{\mathit{j}}^{*}$
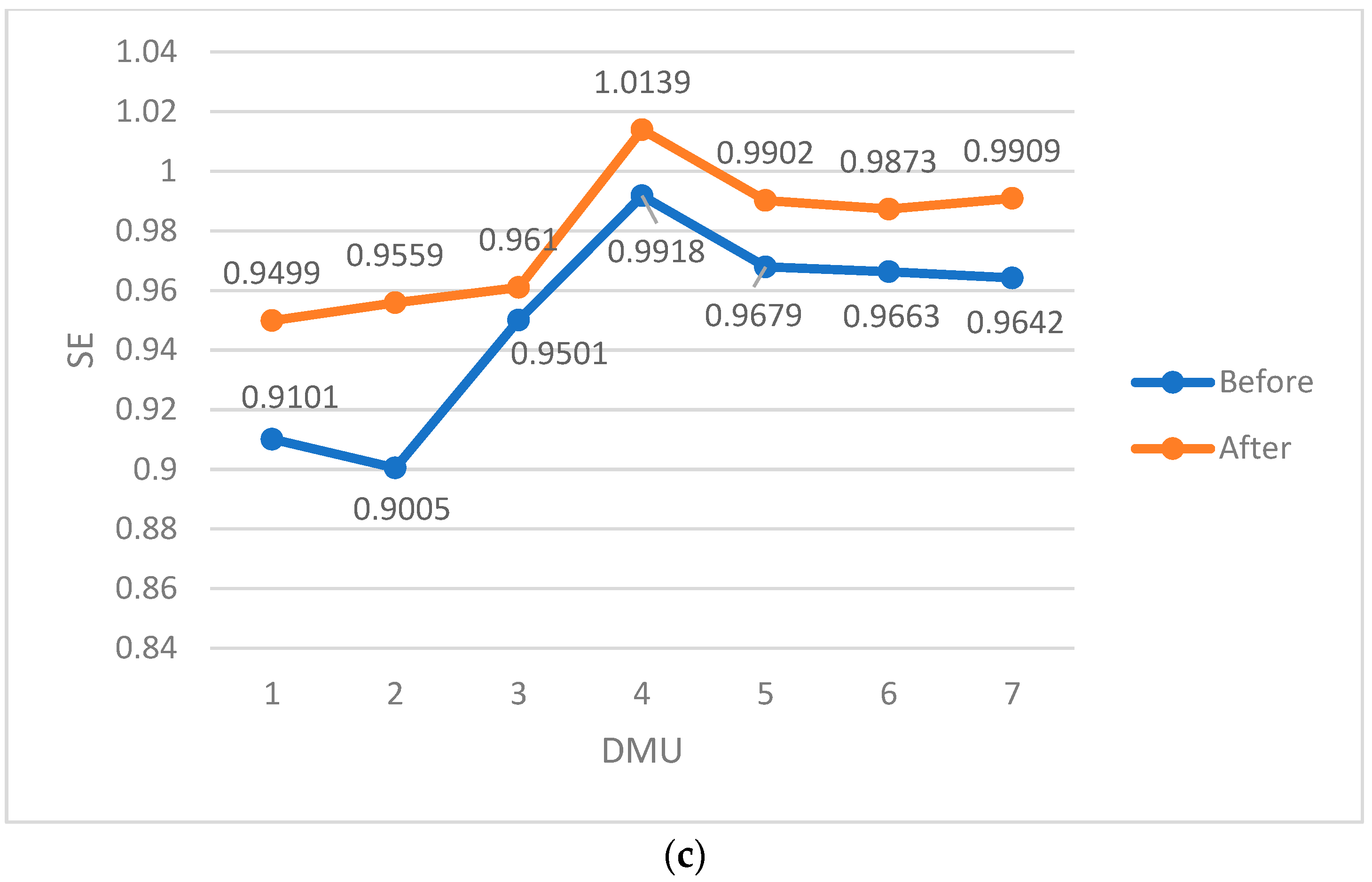
1	0.9183	0.9193	0.9465	0.9280	0.9429	0.9881	1.0000	0.9770	0.9499	0.0271
2	0.9251	0.9324	0.9553	0.9376	0.9538	0.9888	1.0000	0.9809	0.9559	0.0250
3	0.9286	0.9358	0.9545	0.9396	0.9614	0.9782	0.9938	0.9778	0.9610	0.0168
4	0.9394	0.9542	0.9633	0.9523	0.8873	0.9624	0.9679	0.9392	1.0139	−0.0747
5	0.9473	0.9635	0.9752	0.9620	0.9438	0.9709	1.0000	0.9716	0.9902	−0.0186
6	0.9356	0.9512	0.9654	0.9507	0.9363	0.9589	0.9938	0.9630	0.9873	−0.0243
7	0.9588	0.9654	0.9744	0.9662	0.9446	0.9806	1.0000	0.9751	0.9909	−0.0158
	Averages			0.9481				0.9692	0.9784

. It is noted after improvement that all the optimal TE, ${\theta }_j^{{}^{*}}$, values are less than one, which implies that the blowing process is still technically inefficient. Comparing the ${\theta }_j^{{}^{*}}$ values in Table 6 with the corresponding values in Table 9, it is obvious that the TE efficiency has improved for all DMUs. Moreover, the TIE is still caused by SIE in three DMUs (DMU₁ to DMU₃), while it is caused by PTIE in the remaining four DMUs. Nevertheless, all the differences are less than 0.05. The averages of ${\theta }_j^{{}^{*}}$, ${\delta }_j^{{}^{*}}$, and ${\omega }_j^{*}$ after improvement are 0.9481, 0.9692, and 0.9784, respectively. On average, the cause of the TIE is managerial inefficiency because improvement actions take longer to take effect. Despite that, these ${\theta }_j^{{}^{*}}$, ${\delta }_j^{{}^{*}}$, and ${\omega }_j^{*}$ averages are larger than their corresponding values in Table 4. Figure 4 compares the optimal TE, PTE, and SE before and after improvement actions.

From Figure 4, the following remarks are obtained: (a) the optimal TE after improvement is larger than its corresponding before-improvement TE for all DMUs; (b) the optimal PTE after improvement is larger than its corresponding PTE before improvement for almost all DMUs. The optimal PTE after improvement started to become larger than the corresponding before-improvement optimal PTE from DMU₃. The reason behind such a delay may be attributed to improving quality and production procedures that require time to take effect, and (c) the SE after improvement is larger than its corresponding before-improvement SE due to the improvement of the optimal technical efficiency for all DMUs.

The improvement analysis shows that the proposed DEA window analysis is effective in evaluating and enhancing the performance of the blowing process under asymmetry input and output data. Further, the improvement actions conducted based on the proposed efficiency analyses have resulted in significant improvements in the process’s technical efficiency and, thereby, savings in costly production and quality resources.

5. Conclusions

Efficiency assessment is a critical aspect of an improvement program that helps decision-makers optimize process resources to achieve maximum performance. This research, therefore, developed a framework for DEA window analysis to assess the efficiency of blowing machines in the plastic industry from asymmetry input and output data. The framework was implemented to evaluate the technical, pure technical, and scale efficiencies of the blowing process. Results showed that the blowing process was technically inefficient due to the inefficiencies in PTE and SE. Improvement actions were conducted to enhance scale and management efficiencies. The averages of ${\theta }_j^{{}^{*}}$, ${\delta }_j^{{}^{*}}$, and ${\omega }_j^{*}$ after (before) improvement are 0.9481 (0.9169), 0.9692 (0.9672), and 0.9784 (0.9501), respectively. An improvement analysis revealed that the actions taken have resulted in a significant improvement in the technical efficiency of the blowing process. In conclusion, the developed framework for fuzzy DEA window analysis can provide valuable feedback to production engineers on how to boost the technical efficiency of the blowing process under asymmetry data. In practice, the incorporation of fuzziness in the input and output data during efficiency evaluation provides reliable assessment and prediction results for process performance and helps implement effective improvement actions. Nevertheless, this framework requires significant computational effort and time, which can be solved by developing professional software in future research. Moreover, machine learning techniques can be utilized to predict process performance.