Design of Axially Symmetric Fluid–Spring Vibration Absorber with Five DOFs Based on Orthogonal Experiment
Abstract
:1. Introduction
2. Fluid–Spring Vibration Absorber
2.1. Mechanical Structure
2.2. Vibration Transmission
2.3. Vibration Absorption Method
- Vibration absorption in -direction: Under -directional vibration, there is relative motion between the dimethicone (4) in the box and the circular through-holes in the upper sieve plate (26), the middle sieve plate (12), and the lower sieve plate (8), which then generates fluid vibration absorption, and converts the mechanical vibration energy into thermal energy. In addition, the prestressed tension springs (29) can also reciprocate in the stretched balance position to assist reducing vibration while bearing weight.
- Vibration absorption in -direction: The excitation along the -direction is transmitted to the viscous parts with high vibration absorption (3); there is relative motion between the dimethicone (4) in the box and the circular through-holes in the outside sieve tube (7) and inner sieve tube (9), which converts the mechanical vibration energy into thermal energy to reduce the vibration along the .
- Vibration absorption in -direction: When the vibration in the -direction is transmitted, owing to the release of the -DOF by the spherical pairs (28,30), the viscous parts with high vibration absorption (3) vibrates around the in the box (20). There is mutual friction between the dimethicone (4) and the sieve plates distributed on the outside sieve tube (7), the inner sieve tube (9), the upper sieve plate (26), the middle sieve plate (12), and the lower sieve plate (8), which can consume energy.
- Vibration absorption in -direction: Due to the release of the -DOF by the spherical pairs (28,30), the viscous parts with high vibration absorption (3) vibrate around the in the box (20), and friction with the dimethicone (4) consumes energy.
- Vibration absorption in ()-direction: In a cylindrical coordinate system, the -direction and -direction are actually the same degrees of freedom; thus, this vibration absorber has five DOFs. The -direction and -direction are the same degreed of freedom. On the one hand, the vibration can be eliminated by the dimethicone (4) acting on the vertical sieve plate (32). On the other hand, the torsion spring (23) can also partially eliminate the vibration and prevent the platform (17) from drifting and rotating in the ()-direction.
3. Fluid Absorption Spring Coupling Damping Coefficient
3.1. Viscous Damping Coefficient of Vibration Absorber
3.2. Damping Coefficient of Springs
3.2.1. Tension Springs
3.2.2. Torsion Spring
4. Vibration Transmissibility
5. Orthogonal Experiment
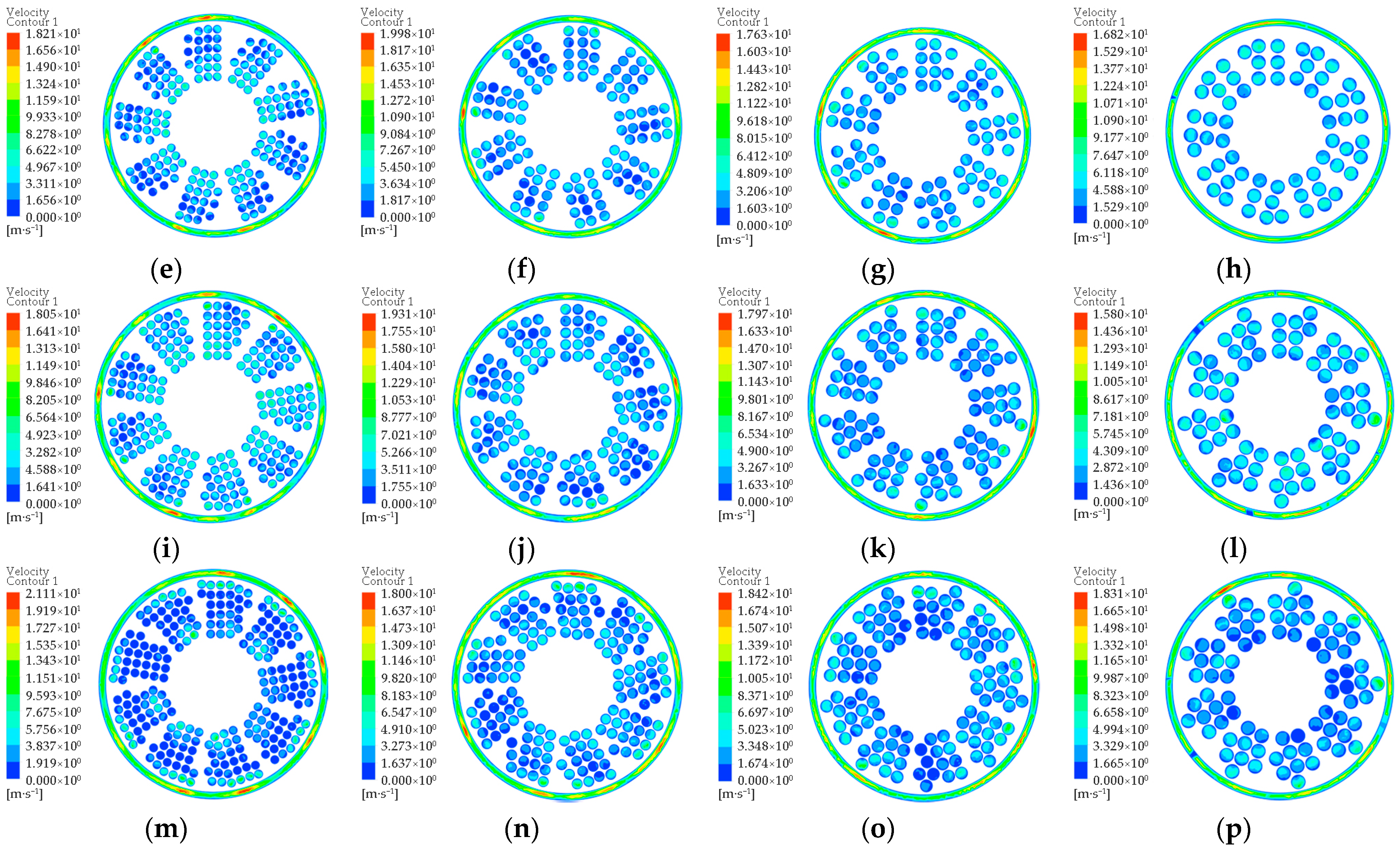
5.1. Simulation Analysis on Fluid
5.1.1. Boundary Conditions
5.1.2. Flow Field Analysis
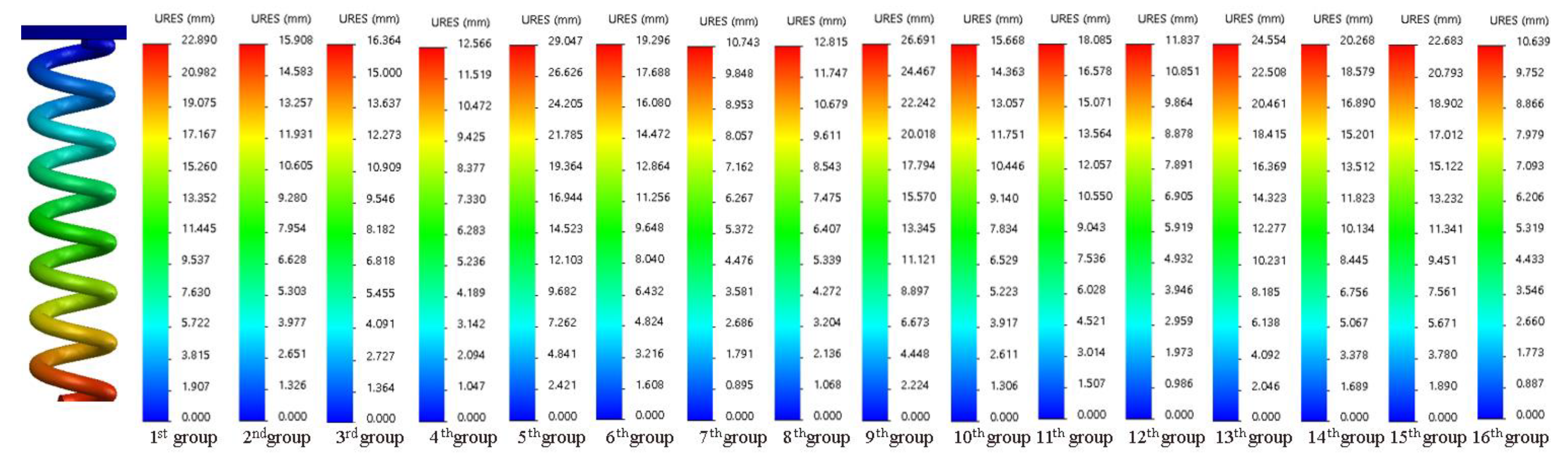
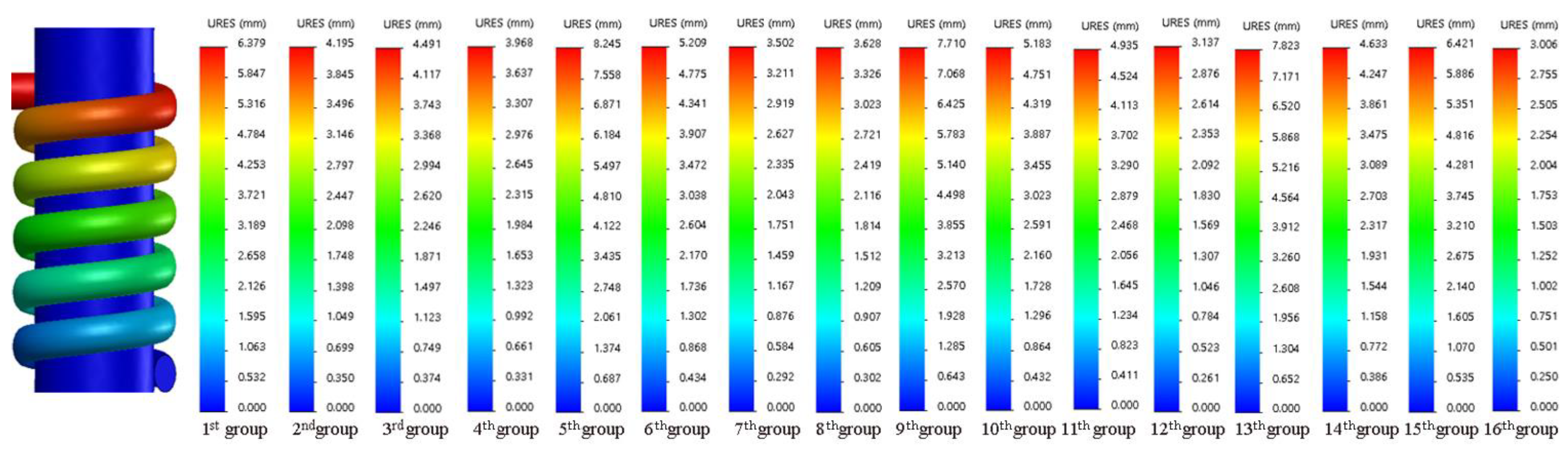
5.2. Dynamics Simulation on Springs
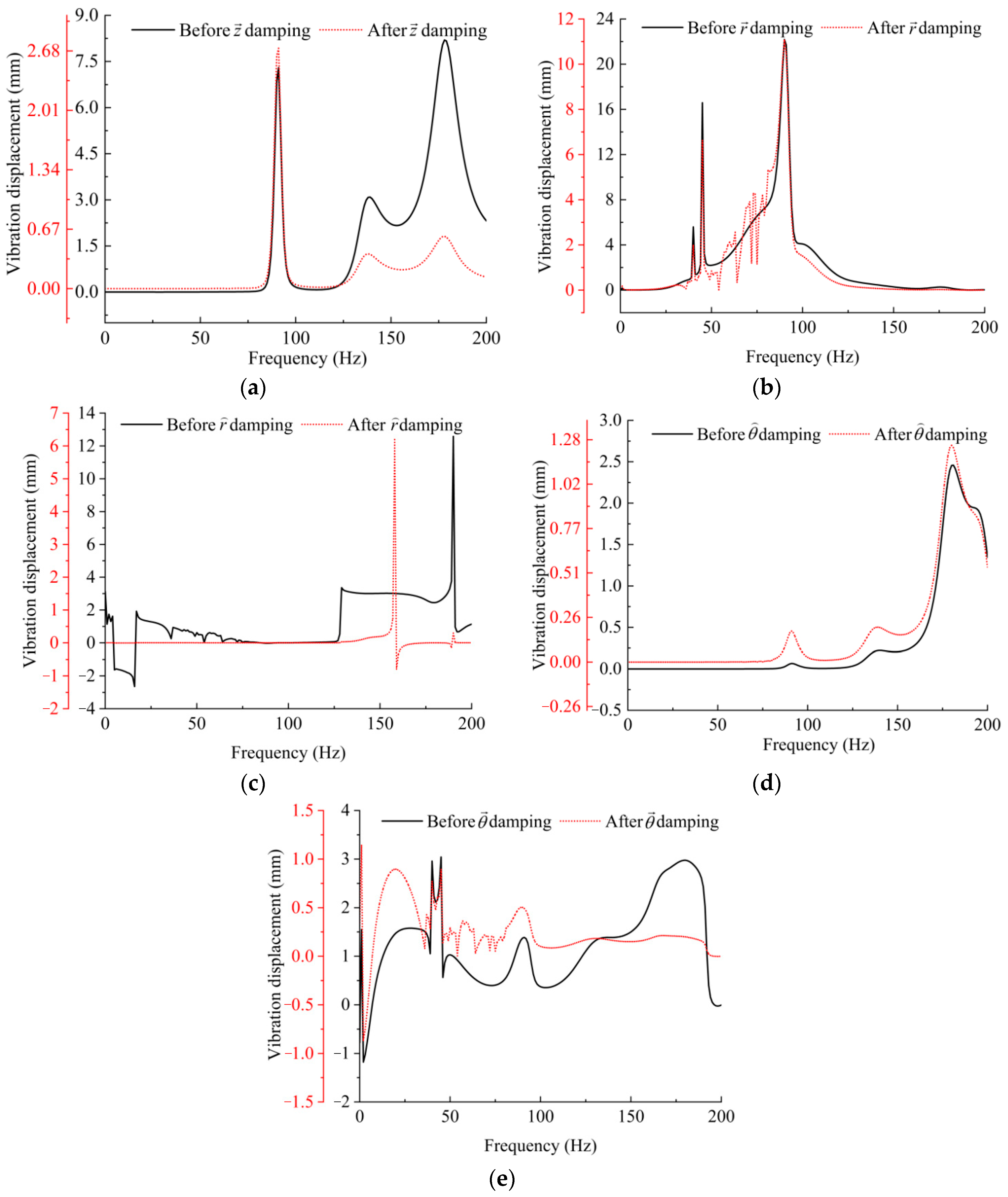
5.3. Fluid–Spring Coupling Vibration Absorption Response
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| -axis | |
| translational DOF along the -axis | |
| rotational DOF along the -axis | |
| polar angle (rad) | |
| translational DOF along | |
| rotational DOF along | |
| polar diameter (m) | |
| translational DOF along | |
| rotational DOF along | |
| pressure (Pa) | |
| inlet pressure of circular through-hole (Pa) | |
| outlet pressure of circular through-hole (Pa) | |
| gravitational acceleration (m/s2) | |
| current velocity (m·s−1) | |
| average current velocity at inlet of circular through-hole (m·s−1) | |
| average current velocity at outlet of circular through-hole (m·s−1) | |
| amending factors of kinetic energy for inlet | |
| amending factors of kinetic energy for outlet | |
| head loss (Pa) | |
| loss along the way (Pa) | |
| local loss (Pa) | |
| damping coefficient along the way | |
| thickness of vibration absorbing plate (mm) | |
| average current velocity of effective section (m·s−1) | |
| radius of circular through-hole (mm) | |
| excitation frequency (Hz) | |
| local resistance coefficient | |
| damping ratio of vibration system | |
| density (kg·m−3) | |
| mass flow | |
| area of circular through-hole (mm2) | |
| area ratio of circular circular through-holes to vibration-absorbing plate | |
| viscous damping ratio | |
| fluid–spring coupling damping coefficient (N·s·mm−1) | |
| viscous damping coefficient (N·s·mm−1) | |
| fluid–tension spring coupling damping coefficient (N·s·m−1) | |
| fluid–torsion spring coupling damping coefficient (N·s·mm−1) | |
| number of circular circular through-holes | |
| elastic coefficient of the tension spring (N·mm−1) | |
| rigidity modulus (N·mm−2) | |
| diameter of steel wire (mm) | |
| diameter of spring pitch (mm) | |
| Young’s modulus (Pa) | |
| number of active coils | |
| displacement of tension spring (mm) | |
| displacement of torsion spring (mm) | |
| damping force (N) | |
| force on springs (N) | |
| distance between the lower sieve plate (8) and pedestal (5) (mm) | |
| mass of attachment block of springs (kg) | |
| viscous vibration absorption constant | |
| speed of attachment block of springs (mm·s−1) | |
| acceleration of attachment block of springs (mm·s−2) | |
| elastic coefficient of torsion spring (g·mm·°−1) | |
| elastic coefficient of tension spring (N·mm−1) | |
| elastic modulus (N·mm−2) | |
| angular velocity (rad·s−1) | |
| vibration absorption torque (N·mm) | |
| diameter of axle sleeve (mm) | |
| diameter of column (mm) | |
| vibration transmissibility | |
| absolute amplitude (mm) | |
| amplitude of excitation(mm) | |
| frequency ratio, | |
| vibration frequency (Hz) | |
| natural frequency (Hz), | |
| vibration absorption ratio, | |
| system quality (kg) | |
| system stiffness (N·mm) |
References
- Huang, Z.X.; Yang, D.Q.; Jiang, S.P.; Zhang, Z.Y. Design and experiment of a mini isolator with fluid damping. J. Vib. Shock 2021, 40, 180–185. (In Chinese) [Google Scholar]
- Hou, C.Y.; Hsu, D.S.; Lee, Y.F.; Chen, H.Y.; Lee, J.D. Shear-thinning effects in annular-orifice viscous fluid dampers. J. Chin. Inst. Eng. 2007, 30, 275–287. [Google Scholar] [CrossRef]
- Makris, N.; Constantinou, M.C.; Reinhorn, A.M. Viscous Dampers: Testing, Modeling and Application in Vibration and Seismic Isolation; Buffalo: New York, NY, USA, 1990; pp. 67–78. [Google Scholar]
- Narkhede, D.I.; Sinha, R. Behavior of nonlinear fluid viscous dampers for control of shock vibrations. J. Sound Vib. 2014, 333, 80–98. [Google Scholar] [CrossRef]
- Ou, J.P.; Ding, J.H. Theory and performance experiment of viscous damper of clearance hydro cylinder. Earthq. Eng. Eng. Vib. 1999, 19, 82–89. [Google Scholar]
- Ding, J.H.; Ou, J.P. Theoretical study and performance experiment for cylinder with holes viscous damper. World Inf. Earthq. Eng 2001, 17, 30–35. [Google Scholar]
- Hou, C.Y. Behavior explanation and a new model for nonlinear viscous fluid dampers with a simple annular orifice. Arch. Appl. Mech. 2012, 82, 1–12. [Google Scholar] [CrossRef]
- Niwa, N.; Kobori, T.; Takahashi, M.; Hatada, T.; Kurino, H.; Tagami, J. Passive seismic response controlled high-rise building with high damping device. Earthq. Eng. Struct. Dyn. 1995, 24, 655–671. [Google Scholar] [CrossRef]
- Fu, W.Q.; Mao, L.I.; Tong, L.I.; Zhang, C.W. Design, performance test and structural wind vibration control analysis of multi-stage variable damping device. Eng. Mech. 2020, 37, 225–233. (In Chinese) [Google Scholar] [CrossRef]
- Ying, L.; Weiming, Y.; Jinbao, J. Performance analysis on viscous damper of variable clearance. Technol. Earthq. Disaster Prev. 2006, 1, 53–162. [Google Scholar]
- Symans, M.D.; Constantinou, M.C. Semi-active control systems for seismic protection of structures: A state-of-the-art review. Eng. Struct. 1999, 21, 469–487. [Google Scholar] [CrossRef]
- Hazaveh, N.K.; Rodgers, G.W.; Chase, J.G.; Pampanin, S. Experimental test and validation of a direction-and displacement-dependent viscous damper. J. Eng. Mech. 2017, 143, 04017132. [Google Scholar] [CrossRef]
- Khatibinia, M.; Gholami, H.; Kamgar, R. Optimal design of tuned mass dampers subjected to continuous stationary critical excitation. Int. J. Dyn. Control 2018, 6, 1094–1104. [Google Scholar] [CrossRef]
- Hrovat, D.; Barak, P.; Rabins, M. Semi-active versus passive or active tuned mass dampers for structural control. J. Eng. Mech. 1983, 109, 691–705. [Google Scholar] [CrossRef]
- Kamgar, R.; Samea, P.; Khatibinia, M. Optimizing parameters of tuned mass damper subjected to critical earthquake. Struct. Des. Tall Spec. Build. 2018, 27, e1460. [Google Scholar] [CrossRef]
- Dadkhah, M.; Kamgar, R.; Heidarzadeh, H.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Improvement of performance level of steel moment-resisting frames using tuned mass damper system. Appl. Sci. 2020, 10, 3403. [Google Scholar] [CrossRef]
- Salimi, M.; Kamgar, R.; Heidarzadeh, H. An evaluation of the advantages of friction TMD over conventional TMD. Innov. Infrastruct. Solut. 2021, 6, 95. [Google Scholar] [CrossRef]
- Kamgar, R.; Gholami, F.; Sanayei, H.R.Z.; Heidarzadeh, H. Modified tuned liquid dampers for seismic protection of buildings considering soil–structure interaction effects. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 339–354. [Google Scholar] [CrossRef]
- Kurino, H.; Tagami, J.; Shimizu, K.; Kobori, T. Switching oil damper with built-in controller for structural control. J. Struct. Eng. 2003, 129, 895–904. [Google Scholar] [CrossRef]
- Baldonedo, J.; López-Campos, J.A.; López, M.; Casarejos, E.; Fernández, J.R. Optimization of the Auxiliary-Beam System in Railway Bridge Vibration Mitigation Using FEM Simulation and Genetic Algorithms. Symmetry 2019, 11, 1089. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Ma, L.T.; Li, R.J.; Chen, B.; Guo, Y.C. Analysis of the Longitudinal-Bending-Torsional Coupled Vibration Mechanism of the Drilling of a Roof Bolter for Mine Support System. Math. Probl. Eng. 2022, 2022, 4279959. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Ma, L.T.; Yang, S.Y.; Yuan, L.; Chen, B. MTPA-and MSM-based Vibration Transfer of 6-DOF Manipulator for Anchor Drilling. Stroj. Vestn.-J. Mech. Eng. 2022, 68, 529–541. [Google Scholar] [CrossRef]
- Kazemi, A.; Padgett, D.A.; Callahan, S.; Stoddard, M.; Amini, A.A. Relative pressure estimation from 4D flow MRI using generalized Bernoulli equation in a phantom model of arterial stenosis. Magn. Reson. Mater. Physics. Biol. Med. 2022, 1–16. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; pp. 359–385. [Google Scholar]
- Wu, Y.; Guo, Y.S.; Hong, M. Performance simulation and parameter analysis of viscous fluid damper based on orthogonal design. Chin. J. Ship Res. 2021, 16, 164–169. (In Chinese) [Google Scholar] [CrossRef]
- Jee, J.; Kim, C.; Kim, Y. Design improvement of a viscous-spring damper for controlling torsional vibration in a propulsion shafting system with an engine acceleration problem. J. Mar. Sci. Eng. 2020, 8, 428. [Google Scholar] [CrossRef]
- Wu, X.J.; Zhu, S.J. Parameters optimization of shock isolator composed of ordinary components. J. Vib. Shock 2005, 5, 74–76. [Google Scholar]
- Dütsch, H.; Durst, F.; Melling, A. Fluid–structure interactions of a torsion spring pendulum at large initial amplitudes. J. Fluid Mech. 2002, 471, 219–238. [Google Scholar] [CrossRef]
- Nakamura, Y.; Nakayama, M.; Masuda, K.; Tanaka, K.; Yasuda, M.; Fujita, T. Development of active 6-DOF micro vibration control system using giant magneto strictive actuator. Smart Struct. Mater. Smart Syst. Bridges Struct. Highways. Spie 1999, 3671, 229–240. [Google Scholar] [CrossRef]
- Wei, Y.H.; Wu, R.X.; Zou, L.M.; Liu, N.N.; Xue, X. Vacuum Brazing Effect on the Interlayer Failure Behaviors of Elastic-Porous Sandwich Structure with Entangled Metallic Wire Mesh. Symmetry 2022, 14, 977. [Google Scholar] [CrossRef]
- Matsson, J.E. An Introduction to ANSYS Fluent; SDC Publications: Mission, KS, USA, 2021. [Google Scholar]
- Fu, L.; Guo, T.; Li, G. Investigation on damping performance of new type oscillator-liquid combined damper. Int. J. Mech. Sci. 2018, 135, 53–62. [Google Scholar] [CrossRef]
- Kurowski, P. Vibration Analysis with SolidWorks Simulation; SDC Publications: Mission, KS, USA, 2016. [Google Scholar]
- Sun, T.; Wang, H.; Zong, Z.; Zhang, G.Y.; Wang, A.; Xu, C. Splash formation and cavity dynamics of sphere entry through a viscous liquid resting on the water. Aip Adv. 2019, 9, 075211. [Google Scholar] [CrossRef]
- Supriyatna, Y.I.; Noviyana, R.; Suka, E.G.; Kambuna, B.N.H.; Sumardi, S. Influence of current density in Cu-Mn electroplating of AISI 1020 steel corrosion rate. Mater. Today Proc. 2021, 44, 3289–3295. [Google Scholar] [CrossRef]

| Levels | (%) | (mm) | (N·mm−1) | (g·mm·°−1) |
|---|---|---|---|---|
| 1 | 29 | 9 | 35 | 1107 |
| 2 | 33 | 11 | 37 | 1109 |
| 3 | 37 | 13 | 39 | 1111 |
| 4 | 41 | 15 | 41 | 1113 |
| Numbers | (%) | (mm) | (N·mm−1) | (g·mm·°−1) |
|---|---|---|---|---|
| 1 | 29% | 9 | 35 | 1107 |
| 2 | 29% | 11 | 37 | 1109 |
| 3 | 29% | 13 | 39 | 1111 |
| 4 | 29% | 15 | 41 | 1113 |
| 5 | 33% | 9 | 37 | 1111 |
| 6 | 33% | 11 | 35 | 1113 |
| 7 | 33% | 13 | 41 | 1107 |
| 8 | 33% | 15 | 39 | 1109 |
| 9 | 37% | 9 | 39 | 1113 |
| 10 | 37% | 11 | 41 | 1111 |
| 11 | 37% | 13 | 35 | 1109 |
| 12 | 37% | 15 | 37 | 1107 |
| 13 | 41% | 9 | 41 | 1109 |
| 14 | 41% | 11 | 39 | 1107 |
| 15 | 41% | 13 | 37 | 1113 |
| 16 | 41% | 15 | 35 | 1111 |
| Numbers | (Pa) | (m·s−1) | (N·s·mm−1) |
|---|---|---|---|
| 1 | −3.635 × 104 to 4.673 × 104 | 1.74 to 19.28 | 293.83 |
| 2 | −4.401 × 104 to 3.089 × 104 | 1.82 to 20.03 | 361.95 |
| 3 | −1.923 × 104 to 3.313 × 104 | 1.52 to 16.67 | 349.27 |
| 4 | −1.348 × 104 to 2.932 × 104 | 1.64 to 18.02 | 256.37 |
| 5 | −2.694 × 104 to 6.082 × 104 | 1.66 to 18.21 | 293.25 |
| 6 | −2.872 × 104 to 3.849 × 104 | 1.82 to 19.98 | 368.97 |
| 7 | −1.896 × 104 to 2.574 × 104 | 1.60 to 17.63 | 448.77 |
| 8 | −1.483 × 104 to 2.671 × 104 | 1.53 to 16.82 | 436.77 |
| 9 | −4.128 × 104 to 5.697 × 104 | 1.64 to 18.05 | 339.91 |
| 10 | −3.428 × 104 to 3.823 × 104 | 1.76 to 19.31 | 415.10 |
| 11 | −2.983 × 104 to 3.634 × 104 | 1.63 to 17.97 | 421.88 |
| 12 | −1.315 × 104 to 2.306 × 104 | 1.44 to 15.80 | 330.50 |
| 13 | −4.580 × 104 to 5.760 × 104 | 1.92 to 21.11 | 373.23 |
| 14 | −3.464 × 104 to 3.405 × 104 | 1.64 to 18.00 | 427.39 |
| 15 | −2.954 × 104 to 4.745 × 104 | 1.67 to 18.42 | 411.40 |
| 16 | −2.088 × 104 to 2.217 × 104 | 1.67 to 18.31 | 402.69 |
| Numbers | (mm) | |
|---|---|---|
| 1 | 22.89 | 6.38 |
| 2 | 15.91 | 4.20 |
| 3 | 16.36 | 4.49 |
| 4 | 12.57 | 3.97 |
| 5 | 29.05 | 8.25 |
| 6 | 19.30 | 5.21 |
| 7 | 10.74 | 3.50 |
| 8 | 12.82 | 3.63 |
| 9 | 26.69 | 7.71 |
| 10 | 15.67 | 5.18 |
| 11 | 18.09 | 4.94 |
| 12 | 11.84 | 3.14 |
| 13 | 24.56 | 7.82 |
| 14 | 20.27 | 4.63 |
| 15 | 22.68 | 6.42 |
| 16 | 10.64 | 3.01 |
| Numbers | (N·mm−1) | (g·mm·°−1) | (N·s·mm−1) | (N·s·mm−1) |
|---|---|---|---|---|
| 1 | 35 | 1107 | 293.83 | 417.97 |
| 2 | 37 | 1109 | 361.95 | 402.64 |
| 3 | 39 | 1111 | 349.27 | 415.26 |
| 4 | 41 | 1113 | 256.37 | 432.19 |
| 5 | 37 | 1111 | 293.25 | 424.60 |
| 6 | 35 | 1113 | 368.97 | 409.82 |
| 7 | 41 | 1107 | 448.77 | 424.53 |
| 8 | 39 | 1109 | 436.77 | 410.98 |
| 9 | 39 | 1113 | 339.91 | 425.64 |
| 10 | 41 | 1111 | 415.10 | 432.70 |
| 11 | 35 | 1109 | 421.88 | 410.58 |
| 12 | 37 | 1107 | 330.50 | 407.67 |
| 13 | 41 | 1109 | 373.23 | 432.66 |
| 14 | 39 | 1107 | 427.39 | 389.81 |
| 15 | 37 | 1113 | 411.40 | 419.12 |
| 16 | 35 | 1111 | 402.69 | 404.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Fang, Z.; Ma, L.; Tao, W.; Wang, P.; Wang, Z. Design of Axially Symmetric Fluid–Spring Vibration Absorber with Five DOFs Based on Orthogonal Experiment. Symmetry 2023, 15, 980. https://doi.org/10.3390/sym15050980
Liu Y, Fang Z, Ma L, Tao W, Wang P, Wang Z. Design of Axially Symmetric Fluid–Spring Vibration Absorber with Five DOFs Based on Orthogonal Experiment. Symmetry. 2023; 15(5):980. https://doi.org/10.3390/sym15050980
Chicago/Turabian StyleLiu, Youyu, Zhao Fang, Liteng Ma, Wanbao Tao, Peng Wang, and Zhijia Wang. 2023. "Design of Axially Symmetric Fluid–Spring Vibration Absorber with Five DOFs Based on Orthogonal Experiment" Symmetry 15, no. 5: 980. https://doi.org/10.3390/sym15050980





