Dynamical Structures of Multi-Solitons and Interaction of Solitons to the Higher-Order KdV-5 Equation
Abstract
:1. Introduction
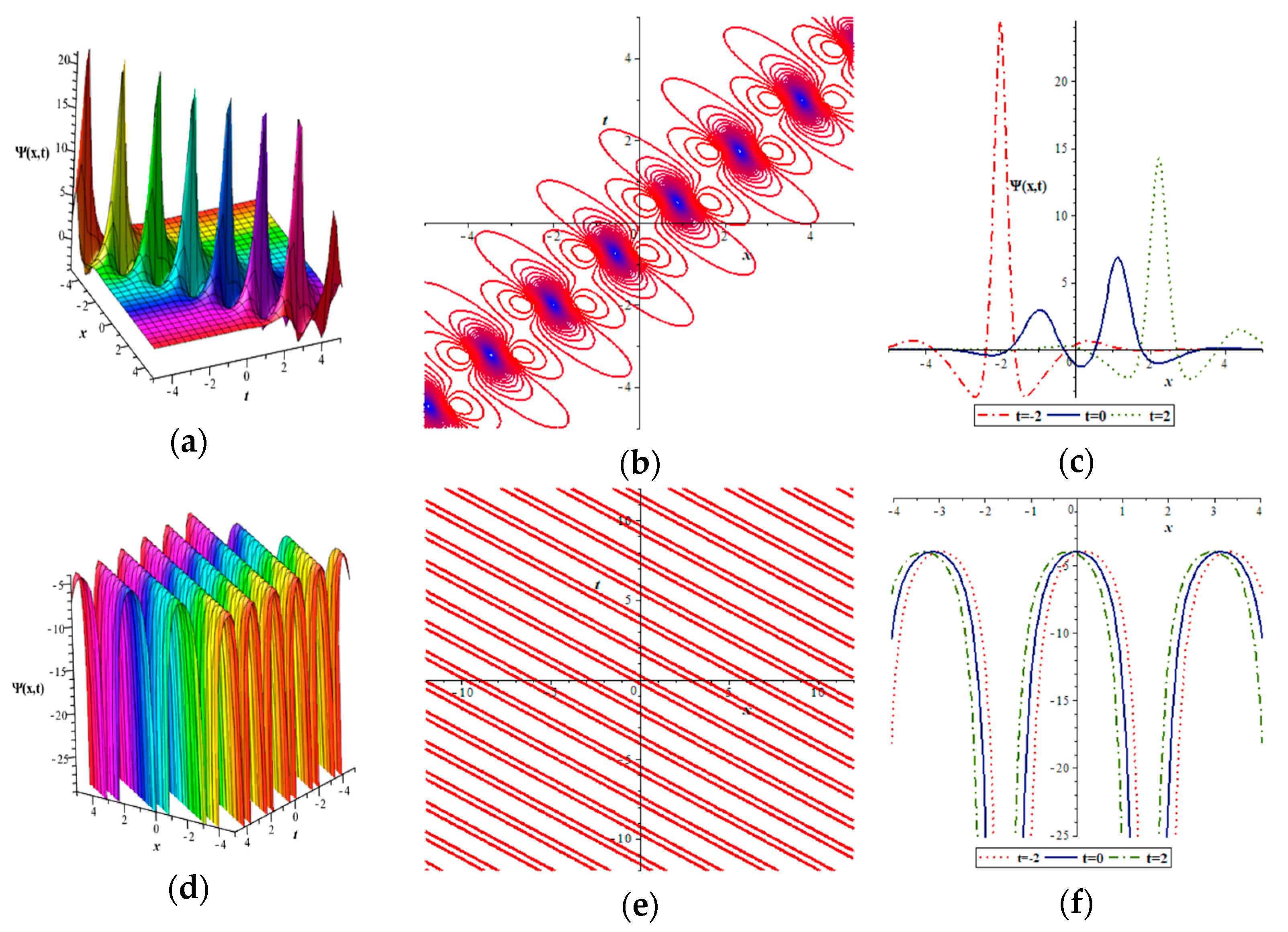
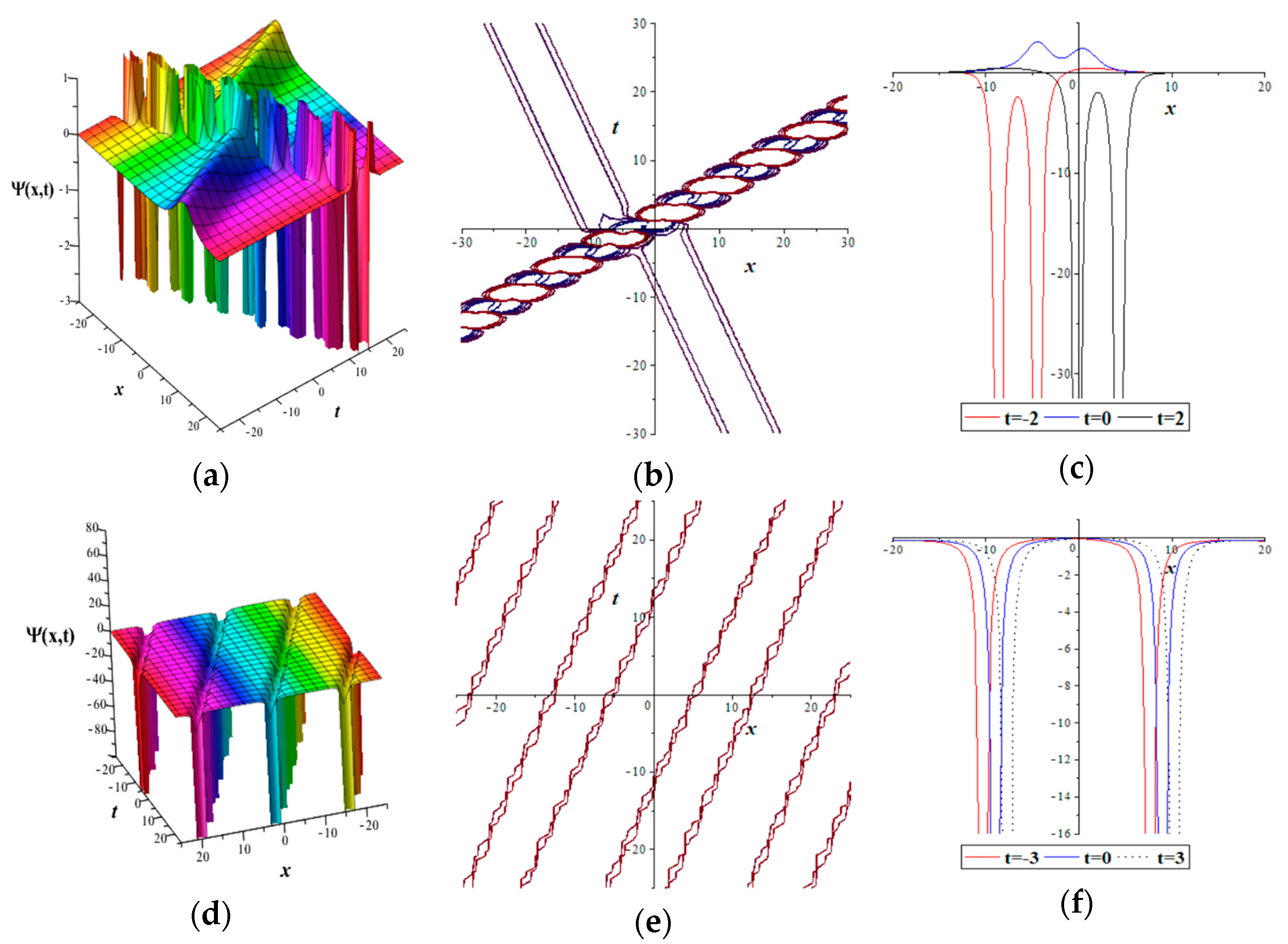
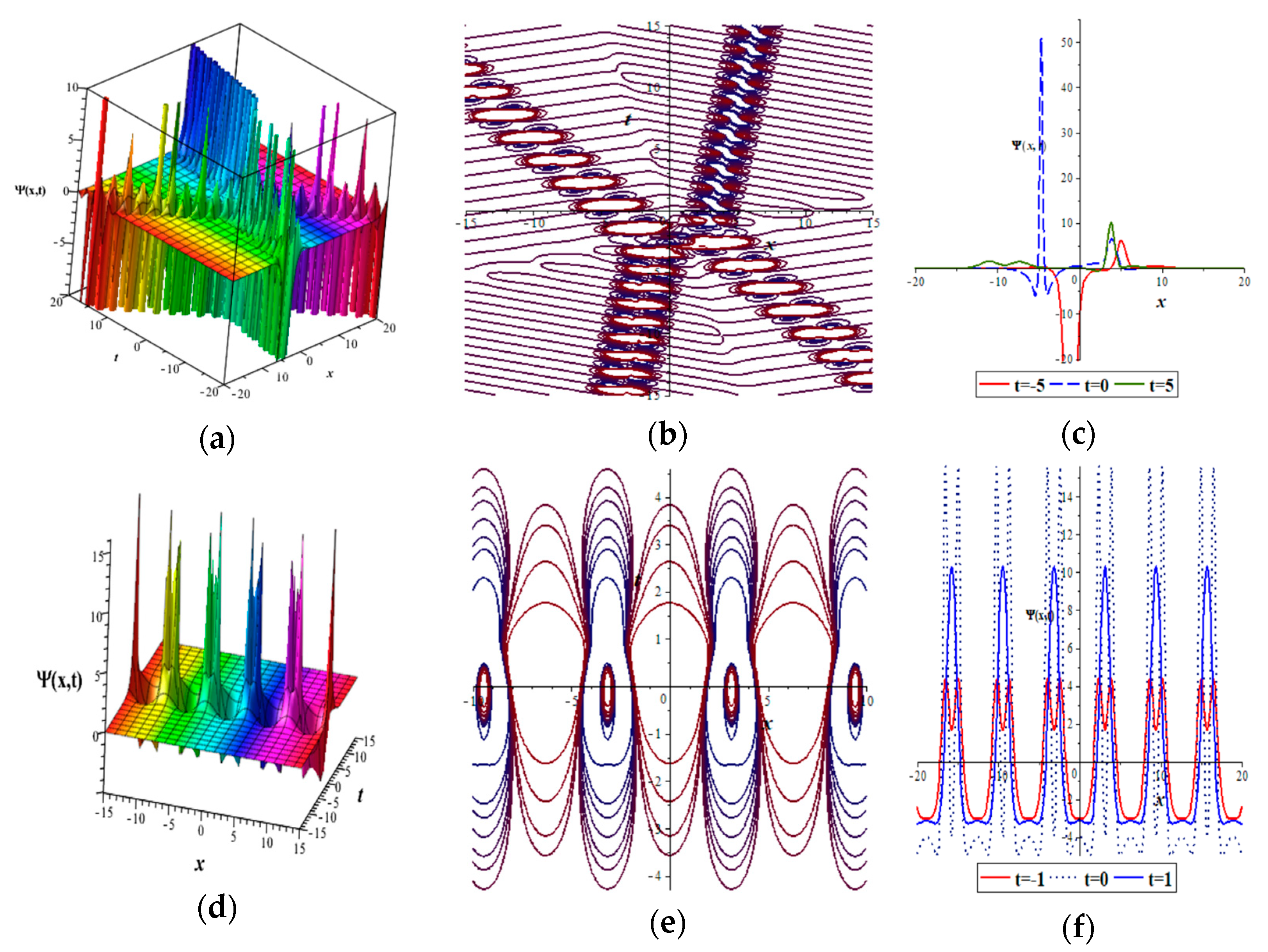
2. The Extended Higher-Order KdV-5 Equations
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ullah, M.S.; Roshid, H.O.; Ali, M.Z.; Noor, N.F.M. Novel dynamics of wave solutions for Cahn-Allen and diffusive predator-prey models using MSE scheme. Partial. Differ. Equ. Appl. Math. 2021, 3, 100017. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef] [Green Version]
- Allahyani, S.A.; Rehman, H.U.; Awan, A.U.; ElDin, E.M.T.; Hassan, M.U. Diverse Variety of Exact Solutions for Nonlinear Gilson–Pickering Equation. Symmetry 2022, 14, 2151. [Google Scholar] [CrossRef]
- Isah, M.A.; Yokus, A. The investigation of several soliton solutions to the complex Ginzburg-Landau model with Kerr law nonlinearity. Math. Model. Numer. Simul. Appl. 2022, 2, 147–163. [Google Scholar] [CrossRef]
- Ullah, M.S.; Abdeljabbar, A.; Roshid, H.O.; Ali., M.Z. Application of the unified method to solve the Biswas–Arshed model. Results Phys. 2022, 42, 105946. [Google Scholar]
- Ma, W.X.; Huang, T.; Zhang, Y. A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 2010, 82, 065003. [Google Scholar] [CrossRef]
- Sulaiman, T.; Yusuf, A.; Abdeljabbar, A.; Alquran, M. Dynamics of lump collision phenomena to the (3 + 1)-dimensional nonlinear evolution equation. J. Geom. Phys. 2021, 169, 104347. [Google Scholar] [CrossRef]
- Ullah, M.S.; Roshid, H.O.; Ali, M.Z.; Rahman, Z. Novel exact solitary wave solutions for the time fractional generalized Hirota–Satsuma coupled KdV model through the generalized Kudryshov method. Contem. Math. 2019, 1, 25–32. [Google Scholar]
- Manakov, S.V.; Zakharov, V.E.; Bordag, L.A.; Its, A.R.; Matveev, V.B. Two-dimensional solitons of the Kadomstev-Petviashvili equation and their interaction. Phys. Lett. A 1977, 63, 205–206. [Google Scholar] [CrossRef]
- Draper, L. Freak wave. Mar. Obs. 1965, 35, 193–195. [Google Scholar]
- Rehman, H.U.; Awan, A.U.; ElDin, E.M.T.; Alhazmi, S.E.; Yassen, M.F.; Haider, R. Extended hyperbolic function method for the (2 +1)-dimensional nonlinear soliton equation. Results Phys. 2022, 40, 105802. [Google Scholar] [CrossRef]
- Yokus, A.; Isah, M.A. Investigation of internal dynamics of soliton with the help of traveling wave soliton solution of Hamilton amplitude equation. Opt. Quantum Electron. 2022, 54, 528. [Google Scholar] [CrossRef]
- Nandi, D.C.; Ullah, M.S.; Roshid, H.O.; Ali, M.Z. Application of the unified method to solve the ion sound and Langmuir waves model. Heliyon 2022, 8, e10924. [Google Scholar] [CrossRef]
- Ullah, M.S.; Roshid, H.O.; Ali, M.Z.; Biswas, A.; Ekici, M.; Khan, S.; Moraru, L.; Alzahrani, A.K.; Belic, M.R. Optical soliton polarization with Lakshamanan-Porsezian-Daniel model by unified approach. Results Phys. 2021, 22, 103958. [Google Scholar] [CrossRef]
- Malfliet, W.; Hereman, W. The tanh method: I. Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 1996, 54, 563–568. [Google Scholar] [CrossRef]
- Roshid, H.O.; Rahman, M.A. The exp (−Φ(η))-expansion method with application in the (1+1)-dimensional classical Boussinesq equation. Results Phys. 2014, 4, 150–155. [Google Scholar] [CrossRef] [Green Version]
- Feng, Z. The first integral method to study the Burgers-Korteweg-de Vries equation. J. Phys. A Math. Gen. 2002, 35, 343–349. [Google Scholar] [CrossRef]
- Yusuf, A.; Sulaiman, T.; Abdeljabbar, A.; Alquran, M. Breather waves, analytical solutions and conservation laws using Lie–Bäcklund symmetries to the (2 + 1)-dimensional Chaffee–Infante equation. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Matveev, V.B.; Salle, M.A. Darboux Transformation and Solitons; Springer: Berlin, Germany, 1991. [Google Scholar]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Yokus, A.; Isah, M.A. Stability analysis and solutions of (2 + 1)-Kadomtsev–Petviashvili equation by homoclinic technique based on Hirota bilinear form. Nonlinear Dyn. 2022, 109, 3029–3040. [Google Scholar] [CrossRef]
- Ullah, M.S.; Ahmed, O.; Mahbub, M.A. Collision phenomena between lump and kink wave solutions to a (3+1)-dimensional Jimbo-Miwa-like model. Partial. Differ. Equ. Appl. Math. 2022, 5, 100324. [Google Scholar] [CrossRef]
- Ullah, M.S.; Ali, M.Z.; Roshid, H.O.; Hoque, M.F. Collision phenomena among lump, periodic and stripe soliton solutions to a (2 + 1)-dimensional Benjamin-Bona-Mahony-Burgers model. Eur. Phys. J. Plus. 2021, 136, 370. [Google Scholar] [CrossRef]
- Ullah, M.S.; Roshid, H.O.; Alshammari, F.S.; Ali, M.Z. Collision phenomena among the solitons, periodic and Jacobi elliptic functions to a (3+1)-dimensional Sharma-Tasso-Olver-like model. Results Phys. 2022, 35, 103958. [Google Scholar] [CrossRef]
- Ullah, M.S.; Ali, M.Z.; Roshid, H.O.; Seadawy, A.R.; Baleanu, D. Collision phenomena among lump, periodic and soliton solutions to a (2 + 1)-dimensional Bogoyavlenskii’s breaking soliton model. Phys. Lett. A 2021, 397, 127263. [Google Scholar] [CrossRef]
- Rahman, Z.; Ali, M.Z.; Roshid, H.O.; Ullah, M.S. Dynamical structures of interaction wave solutions for the two extended higher-order KdV equations. Pramana J. Phys. 2021, 95, 134. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A new generalized fifth-order nonlinear integrable equation. Phys. Scr. 2011, 83, 35003–35021. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Wen, X.Y.; Wang, D.S. The N-soliton solution and localized wave interaction solutions of the (2+1)-dimensional generalized Hirota-Satsuma-Ito equation. Comput. Math. Appl. 2019, 77, 947–966. [Google Scholar] [CrossRef]
- Peng, Y.Z. A new (2 + 1) dimensional KdV equation and its localized structures. Commun. Theor. Phys. 2010, 54, 863–865. [Google Scholar] [CrossRef]
- Ullah, M.S.; Roshid, H.O.; Ma, W.X.; Ali, M.Z.; Rahman, Z. Interaction phenomena among lump, periodic and kink wave solutions to a (3 + 1)-dimensional Sharma-Tasso-Olver-like equation. Chin. J. Phys. 2020, 68, 699–711. [Google Scholar] [CrossRef]
- Kirane, M.; Abdeljabbar, A. Non-existence of global solutions of systems of time-fractional differential equations posed on the Heisenberg group. Math. Methods Appl. Sci. 2022, 45, 7336–7345. [Google Scholar] [CrossRef]
- Abdeljabbar, A. New double Wronskian solutions for a generalized (2 + 1)-dimensional Boussinesq system with variable coefficients. Partial. Differ. Equ. Appl. Math. 2021, 3, 100022. [Google Scholar] [CrossRef]
- Abdeljabbar, A.; Roshid, H.O.; Aldurayhim, A. Bright, dark and rogue wave soliton solutions of thequadratic nonlinear Klein-Gordon equation. Symmetry 2022, 14, 1223. [Google Scholar] [CrossRef]
- Abdeljabbar, A.; Tran, T.D. Pfaffian solutions to a generalized KP system with variable coefficients. Appl. Math. Sci. 2016, 10, 2351–2368. [Google Scholar] [CrossRef]
- Marchant, T.R.; Smyth, N.F. Soliton interaction for the extended Korteweg-de Vries equation. IMA J. Appl. Math. 1996, 56, 157–176. [Google Scholar] [CrossRef] [Green Version]
- Marchant, T.R.; Smyth, N.F. The extended Korteweg–de Vries equation and the resonant flow of a fluid over topography. J. Fluid Mech. 1990, 221, 263–288. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y. Bell polynomials approach for two higher-order KdV-type equations in fluid. Nonlinear Anal. Real World Appl. 2016, 31, 533–551. [Google Scholar] [CrossRef] [Green Version]
- Dullin, H.R.; Gottwald, G.A.; Holm, D. On asymptotically equivalent shallow water wave equations. Phys. D 2004, 190, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.H.; Chen, Y. The integrability of an extended fifth orderKdV equation with Riccati-type pseudo-potential. Pramana J. Phys. 2013, 81, 737–746. [Google Scholar] [CrossRef]
- Dullin, H.R.; Gottwald, G.A.; Holm, D. Camassa–Holm, Korteweg–de Vries-5 and other asymptotically equivalent equations for shallow water waves. Fluid Dyn. Res. 2003, 33, 73–95. [Google Scholar] [CrossRef]
- Asjad, M.I.; Rehman, H.U.; Ishfaq, Z.; Awrejcewicz, J.; Akgul, A.; Riaz, M.B. On Soliton Solutions of Perturbed Boussinesq and KdV-Caudery-Dodd-Gibbon Equations. Coatings 2021, 11, 1429. [Google Scholar] [CrossRef]
- Bouhali, K.; Moumen, A.; Tajer, K.W.; Taha, K.O.; Altayeb, Y. Spatial Analyticity of Solutions to Korteweg–de Vries Type Equations. Math. Comput. Appl. 2021, 26, 75. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, F.S.; Rahman, Z.; Roshid, H.-O.; Ullah, M.S.; Aldurayhim, A.; Ali, M.Z. Dynamical Structures of Multi-Solitons and Interaction of Solitons to the Higher-Order KdV-5 Equation. Symmetry 2023, 15, 626. https://doi.org/10.3390/sym15030626
Alshammari FS, Rahman Z, Roshid H-O, Ullah MS, Aldurayhim A, Ali MZ. Dynamical Structures of Multi-Solitons and Interaction of Solitons to the Higher-Order KdV-5 Equation. Symmetry. 2023; 15(3):626. https://doi.org/10.3390/sym15030626
Chicago/Turabian StyleAlshammari, Fahad Sameer, Zillur Rahman, Harun-Or Roshid, Mohammad Safi Ullah, Abdullah Aldurayhim, and M. Zulfikar Ali. 2023. "Dynamical Structures of Multi-Solitons and Interaction of Solitons to the Higher-Order KdV-5 Equation" Symmetry 15, no. 3: 626. https://doi.org/10.3390/sym15030626






