Labeling Circulant Graphs: Distance Two Condition

Abstract

Given $n\ge 6$, $D=\{1,2,\dots ,\lfloor \frac{n}{2}\rfloor \}$, and a generating set $S\subseteq D$, the circulant graph $C_n\left(S\right)$ has ${\mathbb{Z}}_n$ as a vertex set in which two distinct vertices i and j are adjacent if and only if ${|i-j|}_n\in S$, where ${\left|x\right|}_n=min\left(\right|x|,n-\left|x\right|)$ is the circular distance modulo n. In this paper, we determine the $L(2,1)$-labeling number of $C_n(D\setminus X)$, referred to as $\lambda \left(C_n(D\setminus X)\right)$, for $X=\left\{\lfloor \frac{n}{2}\rfloor \right\}$, $X=\left\{a\right\}$, $X=\{a,b\}$, and in the general case when $\left|X\right|<\lfloor \frac{n}{2}\rfloor -\lceil \frac{n}{4}\rceil$, where $a,b\in D$. Furthermore, we demonstrate that for all $n\ge 6$ and any given set S, $\lambda \left(C_n\left(S\right)\right)=n+gcd(n,\overline{S})-2$ if and only if $gcd(n,\overline{S})\ge 2$, and $\lambda \left(C_n\left(S\right)\right)\le n-1$ if and only if $gcd(n,\overline{S})=1$. Additionally, we establish that when the diameter of $C_n\left(S\right)$ equals 2, $\lambda \left(C_n\left(S\right)\right)=n-1$. This observation motivated us to investigate the properties of S that lead to a diameter of $C_n\left(S\right)$ equal to 2. Then, we introduce a highly distinctive family, denoted as $A_n$, that generates a large number of generating sets. For each value of n, we acquire a circulant graph $C_n\left(A_n\right)$ with a diameter of 2, $\lambda \left(C_n\left(A_n\right)\right)=n-1$, and various additional interesting properties.

1. Introduction and Preliminary

The frequency assignment problem (FAP) is an optimization challenge encountered in telecommunications, radio spectrum management, wireless network planning, and satellite communication. Its main goal is to allocate frequencies to transmitters or communication links in a manner that minimizes interference and maximizes system performance. In wireless communication, using different frequencies for distinct transmitters is essential to prevent interference, a task that becomes increasingly intricate when faced with multiple transmitters and limited frequency resources. Solving the FAP entails finding an optimal assignment that adheres to constraints such as frequency separation, power limits, and interference avoidance.

Distance-constrained graph labeling has emerged as a general model for the FAP. This approach assumes that the distance of transmitters can be modeled by a graph and that the distance of the transmitters influences possible interference in such a way that the closer two transmitters are, the farther apart their frequencies must be. In a formal sense, an assignment of non-negative integers to the vertices of a graph G is an $L(c_1,\dots ,c_t)$-labeling if, for any two vertices with a distance of at most $i\le t$, the difference between their assigned integers (labels) is at least $c_i$. Here, $t\ge 1$ denotes the depth at which distance constraints are applied, while integers $c_1\ge c_2\ge \dots \ge c_t$ act as parameters for the problem. Again, the goal is to minimize the maximum label used.

Due to its difficulty, many particular cases of this general problem have been studied. Among them is the radio k-labeling problem, initially introduced by Chartrand et al. [1,2]. This problem can be regarded as a particular case of the $L(c_1,\dots ,c_t)$-labeling problem, with constraints defined by $c_i=k+1-i$, where $k\ge 1$ is an integer. Formally, a radio k-labeling of G is a function f that assigns each vertex of G a value from the set $\{0,1,2,\dots ,r{n}_k\left(f\right)\}$, subject to the condition $\left|f\right(x)-f(y\left)\right|\ge k+1-d(x,y)$, where $d(x,y)$ is the distance between the vertices x and y in G. The term $r{n}_k\left(f\right)$ denotes the span of f. Consequently, the radio k-labeling number $r{n}_k\left(G\right)$ of G corresponds to the minimum span among all radio k-labelings of G. The task of determining the radio k-labeling number appears to be challenging, even when dealing with particular graphs. Kchikech et al. [3] introduced a classical approach to establish a lower bound for $r{n}_k\left(G\right)$ in a given graph G. To accomplish this, they employed a distinct graph parameter known as the upper traceable number [4], denoted as $t^{+}$:

Theorem 1 

([3]). Let G be a graph of order n, then for any positive integer k,

$$r{n}_k\left(G\right)\ge (n-1)(k+1)-t^{+}\left(G\right);$$

Moreover, if $k\ge 2diam\left(G\right)-2$, then

$$r{n}_k\left(G\right)=(n-1)(k+1)-t^{+}\left(G\right).$$

For a graph G of order n and for a linear ordering s: $(x_0,x_1,\dots ,x_{n-1})$ of its vertices, let $d\left(s\right)={\sum }_{i=0}^{n-2}d(x_i,x_{i+1})$. The upper traceable number $t^{+}\left(G\right)$ of G is defined by $t^{+}\left(G\right)=maxd\left(s\right)$, where the maximum is taken over all linear orderings s of vertices of $G.$ Kràl et al. [5] showed that the problem of determining the upper traceable number of a given graph is an NP-hard problem.

The radio k-labelings extend certain well-known graph labelings, as presented in

Table 1. Radio k-labelings for $k=1,2$, $diam\left(G\right)-1$, $diam\left(G\right)$.

k	Radio k-Labeling	Radio k-Labeling Number, ${\mathit{rn}}_{\mathit{k}}\left(\mathit{G}\right)$
1	Vertex coloring	Chromatic number, $\chi \left(G\right)$
2	$L(2,1)$-labeling	Lambda number, $\lambda \left(G\right)$
$diam\left(G\right)-1$	Antipodal labeling	Radio antipodal number, $ac\left(G\right)$
$diam\left(G\right)$	Radio labeling	Radio number, $rn\left(G\right)$

. Each row in the table provides the more commonly used terminology for a given value of k, with $diam\left(G\right)$ representing the diameter of graph G.

Our focus lies on $L(2,1)$-labelings, which were introduced by Griggs and Yeh in 1992 [6]. Since then, this problem has been extensively studied [7,8,9]. Formally, an $L(2,1)$-labeling of a graph G is an assignment f: $V\left(G\right)\to {\mathbb{Z}}^{+}\cup \left\{0\right\}$ such that

$$|f\left(x\right)-f\left(y\right)|\ge \left\{\begin{array}{cc}2,\hfill & \mathrm{if}d(x,y)=1,\hfill \\ 1,\hfill & \mathrm{if}d(x,y)=2.\hfill \end{array}\right.$$

The span, $\lambda \left(f\right)$, of an $L(2,1)$-labeling f is the difference between the largest and the smallest label used by f. For simplicity, we assume the label zero corresponds to the smallest value, thereby making the span equivalent to the highest assigned label. Consequently, the $L(2,1)$-labeling number $\lambda \left(G\right)$ of G corresponds to the minimum span among all $L(2,1)$-labelings of G.

Griggs and Yeh [6] employed the greedy algorithm to demonstrate that $\lambda \left(G\right)\le {\mathsf{\Delta }}^2+2\mathsf{\Delta }$ for any graph G, where $\mathsf{\Delta }$ denotes the maximum degree of G. This upper bound was later enhanced by Gonçalves [10] to ${\mathsf{\Delta }}^2+2\mathsf{\Delta }-2$, which is currently the best upper bound known for $\lambda \left(G\right)$ in terms of the maximum degree across graphs in general. Griggs and Yeh [6] proposed the ${\mathsf{\Delta }}^2$-conjecture, suggesting that $\lambda \left(G\right)\le {\mathsf{\Delta }}^2$ for any graph G with $\mathsf{\Delta }\ge 2$. Although the conjecture has been verified for specific families of graphs, including paths, cycles, wheels [6], trees [11,12], Cartesian products, compositions of graphs [13], generalized Petersen graphs [14], and chordal graphs [15], its general validity remains unproven. For only a limited number of graph classes, such as paths, cycles, wheels, trees, and generalized Petersen graphs, the efficient computation of $\lambda \left(G\right)$ is possible. However, for a vast array of graph families, it remains unknown whether calculating $\lambda \left(G\right)$ is NP-complete or can be solved in polynomial time. Therefore, our research has been directed towards determining bounds for the $\lambda$-number of graphs, with a particular focus on utilizing the following result, which is a specific case of Theorem 1 when $k=2$.

Corollary 1. 

Let G be a graph of order n

$$\lambda \left(G\right)\ge 3(n-1)-t^{+}\left(G\right);$$

Moreover, if $diam\left(G\right)\le 2$, then

$$\lambda \left(G\right)=3(n-1)-t^{+}\left(G\right).$$

This paper centers its attention on circulant graphs, a subset of the more general family of Cayley graphs. Specifically, circulant graphs are Cayley graphs over the simplest family of groups, namely the cyclic groups. Given $n\ge 6$, $D=\{1,2,\dots ,\lfloor \frac{n}{2}\rfloor \}$ and a generating set $S\subseteq D$. The circulant graph $C_n\left(S\right)=(V\left(C_n\left(S\right)\right),E\left(C_n\left(S\right)\right))$ has ${\mathbb{Z}}_n$ as a vertex set in which two distinct vertices i and j are adjacent if and only if ${|i-j|}_n\in S$, where ${\left|x\right|}_n=min\left(\right|x|,n-\left|x\right|)$ is the circular distance modulo n. For example, $C_n\left(\left\{1\right\}\right)$ is the cycle $C_n$, while $C_n\left(D\right)$ is the complete graph $K_n$. 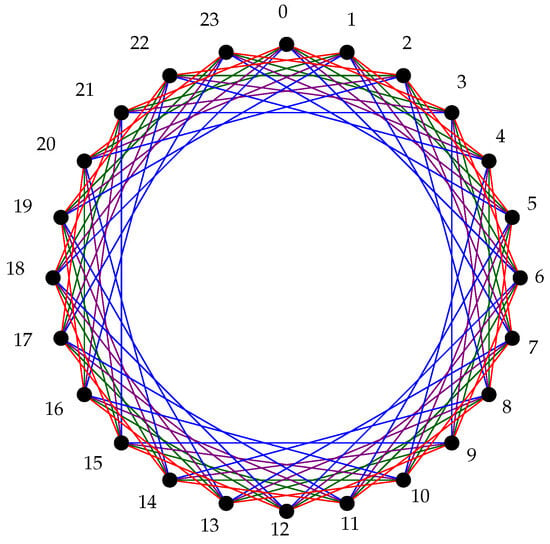The circulant graph $C_{24}\left(\{3,4,5,6\}\right)$ is illustrated in Figure 1.

Circulant graphs are regular and vertex-transitive. Their symmetry has consistently captivated mathematicians. Applications have been found for these graphs in various domains, including the modeling of data connection networks [16,17] and the theory of designs and error-correcting codes [18].

• Observations 

• Since circulants belong to the family of Cayley graphs, any undirected circulant graph is vertex-transitive. As a result, for any pair of vertices x and y within $C_n\left(S\right)$, $d(x,y)=d(0,z)$, where $z=\left\{\begin{array}{cc}y-x,\hfill & \mathit{if}x<y,\hfill \\ n-x+y,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$
• The complementary of $C_n\left(S\right)$ is $\overline{C_n\left(S\right)}=C_n\left(\overline{S}\right)$, where $\overline{S}=D\setminus S$.

In this paper, we delve into the $L(2,1)$-labeling of circulant graphs. The initial investigation into this problem was conducted by Mitra and Bhoumik [19]. They presented upper bounds for the span of the $L(2,1)$-labeling for circulant graphs with generating sets $D\setminus \left\{\frac{n}{2}\right\}$ (for even n), $D\setminus \left\{a\right\}$, and $D\setminus \{a,\frac{n}{2}\}$ (for n even and $a\in D$). Expanding upon their research, we commence by providing precise span values of the $L(2,1)$-labeling for circulants with generating sets $D\setminus \left\{\lfloor \frac{n}{2}\rfloor \right\}$ (for all n), $D\setminus \left\{a\right\}$, and $D\setminus \{a,b\}$, where $a,b\in D$. Subsequently, we generalize these results to any set $X\subset D$, by introducing conditions related to the cardinality of X, ensuring that the graph $C_n(D\setminus X)$ possesses an exact span value of the $L(2,1)$-labeling.

Furthermore, we demonstrate that for all $n\ge 6$ and any given set S, the $L(2,1)$-labeling number of $C_n\left(S\right)$ assumes two distinct values: $\lambda \left(C_n\left(S\right)\right)=n+gcd(n,\overline{S})-2$ if and only if $gcd(n,\overline{S})\ge 2$, and $\lambda \left(C_n\left(S\right)\right)\le n-1$ if and only if $gcd(n,\overline{S})=1$, where $gcd(n,\overline{S})$ denotes the greatest common divisor of n and the elements belonging to $\overline{S}$. Our research also seeks to give a precise value for $\lambda \left(C_n\left(S\right)\right)$ when $gcd(n,\overline{S})=1$, which leads us to find that $\lambda \left(C_n\left(S\right)\right)=n-1$ when $diam\left(C_n\left(S\right)\right)=2$. This discovery led us to explore the characteristics of S such that $diam\left(C_n\left(S\right)\right)=2$.

Then, we introduce a highly distinctive family, denoted as $A_n$, that generates a large number of generating sets. For each value of n, we acquire a circulant graph $C_n\left(A_n\right)$ with a diameter of 2, $\lambda \left(C_n\left(A_n\right)\right)=n-1$, and various additional interesting properties.

2. Main Results

Mitra and Bhoumik [19] determined the upper bound for $\lambda \left(C_n\left(S\right)\right)$ when $S=D\setminus \left\{\frac{n}{2}\right\}$. Specifically, for even values of n, they showed that $\lambda \left(C_n\left(S\right)\right)\le \frac{3n}{2}-2$. Expanding upon this discovery, we proceed to provide the exact value for the span of the $L(2,1)$-labeling of $C_n\left(S\right)$, for all n.

Theorem 2. 

For any generating set $S=D\setminus \left\{\lfloor \frac{n}{2}\rfloor \right\}$, where $n\ge 6$,

$$\lambda \left(C_n\left(S\right)\right)=\left\{\begin{array}{cc}n-1,\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \\ \frac{3n}{2}-2,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}.\hfill \end{array}\right.$$

Proof. 

Let $n\ge 6$, and let $S=D\setminus \left\{\lfloor \frac{n}{2}\rfloor \right\}$. According to Corollary 1, if $diam\left(C_n\left(S\right)\right)=2$, then we can establish that $\lambda \left(C_n\left(S\right)\right)=3(n-1)-t^{+}\left(C_n\left(S\right)\right)$. □

Claim 1. 

For each integer $n\ge 6$, $diam\left(C_n\left(S\right)\right)=2$.

Proof. 

If $i\in S$, then ${|0-i|}_n=min(i,n-i)=i\in S$. Thus, $(0,i)\in E\left(C_n\left(S\right)\right)$ and $d(0,i)=1$. If $i=\lfloor \frac{n}{2}\rfloor$, then ${|0-i|}_n=i\notin S$. Thus, $d(0,i)\ge 2$. However, $2\le d(0,i)\le d(0,i-1)+d(i-1,i)\le d(0,i-1)+1$. Moreover, ${|0-(i-1)|}_n=i-1\in S$, i.e., $d(0,i-1)=1$. Thus, $d(0,i)=2$. Hence, for all $i\in \{1,2,\dots ,\lfloor \frac{n}{2}\rfloor \}$, $d(0,i)\le 2$. Consequently, $diam\left(C_n\left(S\right)\right)=2$. □

Now, the current task is to precisely determine the value of the parameter $t^{+}\left(C_n\left(S\right)\right)$.

Claim 2. 

For each integer $n\ge 6$, $t^{+}\left(C_n\left(S\right)\right)=\left\{\begin{array}{cc}2(n-1),\hfill & \mathit{if}n\mathit{is}\mathit{odd},\hfill \\ \frac{3n}{2}-1,\hfill & \mathit{if}n\mathit{is}\mathit{even}.\hfill \end{array}\right.$

Proof. 

Let $n=2p+1$ with $p\ge 2$, we provide the permutation $\{x_0,x_1,\dots ,x_{n-1}\}$ to the set of vertices $V\left(C_n\left(S\right)\right)$ such that,

$$\left\{\begin{array}{cc}{x}_{2j}=j,\hfill & \mathrm{for}j\in \{0,1,\dots ,p\},\hfill \\ x_{2j+1}=p+j+1,\hfill & \mathrm{for}j\in \{0,1,\dots ,p-1\}.\hfill \end{array}\right.$$

For all $j\in \{0,1,\dots ,p\},$ $|x_{2j}-x_{2j+1}{|}_n=p\notin S$. So, for all $j\in \{0,1,\dots ,p\},$ $d(x_{2j},x_{2j+1})=2$. Thus, $t^{+}\left(C_n\left(S\right)\right)\ge {\sum }_{i=0}^{n-2}d(x_i,x_{i+1})\ge 2(n-1).$ Moreover, we know that $t^{+}\left(C_n\left(S\right)\right)\le diam\left(C_n\left(S\right)\right)(n-1)$. As $diam\left(C_n\left(S\right)\right)=2$, we conclude that $t^{+}\left(C_n\left(S\right)\right)=2(n-1)$.

Let $n=2p$, where $p\ge 3$, and $i\in \{0,1,\dots ,\frac{n}{2}\}$. Assuming that there exist $j,k\in \{0,1,\dots ,\frac{n}{2}\}$ such that $j\neg \equiv k(modn)$, $j\neg \equiv i(modn)$, and $i\neg \equiv k(modn)$, while satisfying $d(i,j)=2$ and $d(i,k)=2$. So, ${|i-j|}_n\notin S$ and ${|i-k|}_n\notin S$. It follows that ${|i-j|}_n={|i-k|}_n=\frac{n}{2}$. Hence, $|i-j|=|i-k|=\frac{n}{2}$, implying $i-j=i-k=\frac{n}{2}$ or $i-j=k-i=\frac{n}{2}$.

From which, $j=k$ or $i-j+k-i=n$. Thus, $j=k(modn)$ or $k=j+n\equiv j(modn).$ However, this leads to a contradiction as $j\neg \equiv k(modn)$. Hence, for each vertex $i\in \{0,1,\dots ,\frac{n}{2}\}$, there exists a unique vertex $j\in \{0,1,\dots ,\frac{n}{2}\},$ such that $d(i,j)=2$. Let $\{x_0,x_1,\dots ,x_{n-1}\}$ be a permutation of $V\left(C_n\left(S\right)\right)$. Without loss of generality, assuming that $d(x_0,x_1)=2$, it follows that $d(x_1,x_2)=1$ and $d(x_2,x_3)=2$. Consequently, given $d(x_2,x_3)=2$, we can deduce that $d(x_3,x_4)=1$, and so on. To formally represent this permutation of $V\left(C_n\left(S\right)\right)$, we present the following:

$$\left\{\begin{array}{cc}d(x_{2p},x_{2p+1})=2,\hfill & \mathrm{for}p\in \{0,1,\dots ,\frac{n}{2}-1\},\hfill \\ d(x_{2p+1},x_{2p+2})=1,\hfill & \mathrm{for}p\in \{0,1,\dots ,\frac{n}{2}-2\}.\hfill \end{array}\right.$$

(1)

Hence,

$$\begin{array}{cc}\hfill t^{+}\left(C_n\left(S\right)\right)& \ge \sum _{p=0}^{\frac{n}{2}-1}d(x_{2p},x_{2p+1})+\sum _{p=0}^{\frac{n}{2}-2}d(x_{2p+1},x_{2p+2})\hfill \\ \hfill & =\frac{n}{2}\times 2+(\frac{n}{2}-1)\times 1\hfill \\ \hfill & =\frac{3n}{2}-1.\hfill \end{array}$$

Let $Q=\{x_0,x_1,\dots ,x_{n-1}\}$ be the permutation of $V\left(C_n\left(S\right)\right)$, such that $t^{+}\left(C_n\left(S\right)\right)={\sum }_{i=0}^{n-2}d(x_i,x_{i+1})$. Let $\{0,1,\dots ,n-1\}=I\cup J\cup \{n-2,n-1\}$ where, $I=\{i\in \{0,1,\dots ,n-3\}:d(x_i,x_{i+1})=2\}$ and $J=\{i\in \{0,1,\dots ,n-3\}:d(x_i,x_{i+1})=1\}$. It is evident that $I\cap J=\varnothing$ and $\left|I\right|+\left|J\right|=n-2$, where $\left|I\right|$ and $\left|J\right|$ denoted the cardinality of set I and J, respectively. Since $diam\left(C_n\left(S\right)\right)=2$, $d(x_i,x_{i+1})\in \{1,2\}$. It is imperative that $d(x_{n-2},x_{n-1})=2$. Otherwise, $t^{+}\left(C_n\left(S\right)\right)$ would fail to attain its maximum. Furthermore, as previously established in this proof, if $i\in I$, then $i+1\in J$. Thus, $\left|I\right|\le \left|J\right|$. If $\left|I\right|=\left|J\right|$ we obtain,

$$\begin{array}{cc}\hfill t^{+}\left(C_n\left(S\right)\right)& =\sum _{i\in I}d(x_i,x_{i+1})+\sum _{i\in J}d(x_i,x_{i+1})+2\hfill \\ \hfill & =2\left|I\right|+\left|J\right|+2\hfill \\ \hfill & =3\left|I\right|+2.\hfill \end{array}$$

Nevertheless, given that $\left|I\right|+\left|J\right|=n-2$, it follows that $\left|I\right|=\frac{n-2}{2}$. Therefore, $t^{+}\left(C_n\left(S\right)\right)=3\times \frac{n-2}{2}+2=\frac{3n}{2}-1$.

If $\left|I\right|<\left|J\right|$, then there exists $ϵ>0$, such that $\left|I\right|+ϵ=\left|J\right|$. Furthermore, considering that the sum $\left|I\right|+\left|J\right|=n-2$ is an even number, it implies that $ϵ$ is even, specifically $ϵ\ge 2$. Thus,

$$\begin{array}{cc}\hfill t^{+}\left(C_n\left(S\right)\right)& =\sum _{i\in I}d(x_i,x_{i+1})+\sum _{i\in J}d(x_i,x_{i+1})+2\hfill \\ \hfill & =2\left|I\right|+\left|J\right|+2\hfill \\ \hfill & =2\left(\right|J|-ϵ)+\left|J\right|+2\hfill \\ \hfill & =3\left|J\right|-2ϵ+2.\hfill \end{array}$$

Since $\left|I\right|+\left|J\right|=n-2$, we obtain $\left|J\right|=\frac{n-2}{2}+\frac{ϵ}{2}$. Therefore,

$$\begin{array}{cc}\hfill t^{+}\left(C_n\left(S\right)\right)& =3\left|J\right|-2ϵ+2\hfill \\ \hfill & =3(\frac{n-2}{2}+\frac{ϵ}{2})-2ϵ+2\hfill \\ \hfill & =(\frac{3n}{2}-1)-ϵ(2-\frac{3}{2})\hfill \\ \hfill & <\frac{3n}{2}-1.\hfill \end{array}$$

This leads to a contradiction with the fact that $t^{+}\left(C_n\left(S\right)\right)\ge \frac{3n}{2}-1$. Hence, $\left|I\right|=\left|J\right|$ and $t^{+}\left(C_n\left(S\right)\right)=\frac{3n}{2}-1$. □

An alternative approach to determine the exact span value for the $L(2,1)$-labeling of circulant graphs involves introducing another parameter known as path coverings. Specifically, the path covering number $c\left(G\right)$ of a graph G denotes the minimum number of vertex-disjoint paths required to cover all vertices within the graph G. In the following discussion, we provide a large study, presenting necessary and sufficient conditions that provide exact values for $\lambda \left(C_n\left(S\right)\right)$, involving the parameter $c\left(C_n\left(\overline{S}\right)\right)$, inspired by the work of Georges and Mauro [20].

We will commence our investigation by directing our attention to the case where $c\left(C_n\left(\overline{S}\right)\right)\ge 2$. Throughout the entirety of this paper, unless explicitly indicated otherwise, we shall refer to the generating set as $S=\{s_1,s_2,\dots ,s_t\}$, where $s_1,s_2,\dots ,s_t\in D$ represent integers arranged in ascending order ($1\le s_1<s_2<\dots <s_t\le \lfloor \frac{n}{2}\rfloor$). To enhance the clarity and coherence of our discussions, we opt to use the notation $gcd(n,S)$ in place of $gcd(n,s_1,s_2,\dots ,s_t)$.

Lemma 1. 

For any generating set S, $c\left(C_n\left(S\right)\right)=gcd(n,S)$. 

Proof. 

If $gcd(n,S)=1$, then $C_n\left(S\right)$ is Hamiltonian [21], thereby implying that $c\left(C_n\left(S\right)\right)=1$. Let us consider $S=\{s_1,s_2,\dots ,s_t\}$. If $gcd(n,S)\ge 2$, then $C_n\left(S\right)$ consists of exactly $gcd(n,S)$ connected circulant graphs $C_{\frac{n}{gcd(n,S)}}^i(\frac{s_1}{gcd(n,S)},\frac{s_2}{gcd(n,S)},\dots ,\frac{s_t}{gcd(n,S)})$ [22]. Notably, it follows that

$$c\left(C_n\left(S\right)\right)\le \sum _{i=0}^{gcd(n,S)-1}c\left(C_{\frac{n}{gcd(n,S)}}^i(\frac{s_1}{gcd(n,S)},\dots ,\frac{s_t}{gcd(n,S)})\right)=gcd(n,S).$$

Let us assume, without loss of generality, that $c\left(C_n\left(S\right)\right)=gcd(n,S)-1$, meaning that there exists a path containing vertices from two of the $gcd(n,S)$ connected circulant graphs. Nevertheless, since $gcd(n,S)\ge 2$, the graph $C_n\left(S\right)$ is not connected [23]. Therefore, we deduce that $c\left(C_n\left(S\right)\right)=gcd(n,S).$ □

Theorem 3. 

For any generating set S,

$$\lambda \left(C_n\left(S\right)\right)=n+gcd(n,\overline{S})-2\mathit{if}\mathit{and}\mathit{only}\mathit{if}gcd(n,\overline{S})\ge 2.$$

Proof. 

Georges and Mauro [20] showed that for any graph G, $\lambda \left(G\right)=n+c\left(\overline{G}\right)-2$ if and only if $c\left(\overline{G}\right)\ge 2.$ Utilizing Lemma 1, we can establish that $c\left(C_n\left(\overline{S}\right)\right)=gcd(n,\overline{S})$, which then leads us to the desired result. □

Let $a\in D$. Mitra and Bhoumik [19] presented the upper bound for $\lambda \left(C_n\left(S\right)\right)$ when $S=D\setminus \left\{a\right\}$. Specifically, when $gcd(n,a)\ge 2$, they showed that $\lambda \left(C_n\left(S\right)\right)\le n+gcd(n,a)-2$. By applying Theorem 3, we provide the exact value:

Proposition 1. 

For any generating set $S=D\setminus \left\{a\right\}$,

$$\lambda \left(C_n\left(S\right)\right)=n+gcd(n,a)-2\mathit{if}\mathit{and}\mathit{only}\mathit{if}gcd(n,a)\ge 2.$$

Let $a\in D$. When $gcd(n,a,\frac{n}{2})\ge 2,$ Mitra and Bhoumik [19] established that $\lambda (C_n(D\setminus \{a,$ $\frac{n}{2}\left\}\right))\le n+gcd(n,a,\frac{n}{2})-2$ (for even n). In the following, we generalize their findings by presenting the precise value for $\lambda \left(C_n(D\setminus \{a,b\})\right)$ for every value of n and each pair of values a and b within the set D.

Proposition 2. 

For any generating set $S=D\setminus \{a,b\}$,

$$\lambda \left(C_n\left(S\right)\right)=n+gcd(n,a,b)-2\mathit{if}\mathit{and}\mathit{only}\mathit{if}gcd(n,a,b)\ge 2.$$

Let us shift our focus to the situation in which $c\left(C_n\left(\overline{S}\right)\right)=1$ (i.e., $gcd(n,\overline{S})=1$). Our starting point involves introducing the following upper bound for $\lambda \left(C_n\left(S\right)\right)$.

Corollary 2. 

$\lambda \left(C_n\left(S\right)\right)\le n-1\mathit{if}\mathit{and}\mathit{only}\mathit{if}gcd(n,\overline{S})=1.$ 

Proof. 

Georges and Mauro proved in [20] that for any graph G, $\lambda \left(G\right)\le n-1$ if and only if $c\left(\overline{G}\right)=1.$ Utilizing Lemma 1, we can establish the desired result. □

As our objective is to determine the precise value for the span of $L(2,1)$-labeling in circulant graphs, our investigation revolves around identifying necessary and sufficient conditions within circulant graphs where the upper bound in Corollary 2 is satisfied as an equality. In light of our research, we have obtained the following result.

Theorem 4. 

Let $C_n\left(S\right)$ be a circulant graph of diameter 2.

$$\lambda \left(C_n\left(S\right)\right)=n-1\mathit{if}\mathit{and}\mathit{only}\mathit{if}gcd(n,\overline{S})=1.$$

Before proceeding with the proof of Theorem 4, it is essential to introduce an additional result that will play a crucial role in establishing the proof of this theorem.

Lemma 2. 

Let G be a graph of order n and diameter 2.

$$t^{+}\left(G\right)=2(n-1)\mathit{if}\mathit{and}\mathit{only}\mathit{if}\overline{G}\mathit{contains}\mathit{an}\mathit{Hamiltonian}\mathit{path}.$$

Proof. 

Assuming that $\overline{G}=(E_{\overline{G}},V_{\overline{G}})$ contains an Hamiltonian path $x_0,x_1,\dots ,$ $x_{n-1}$, for all $i\in \{0,1,\dots ,n-1\}$, we observe that $(x_i,x_{i+1})\in E_{\overline{G}}$, which implies $(x_i,x_{i+1})\notin E_G$ and yields $d_G(x_i,x_{i+1})=2$. Thus, $t^{+}\left(G\right)\ge 2(n-1)$. Moreover, we know that $t^{+}\left(G\right)\le diam\left(G\right)(n-1)$. As a result, $t^{+}\left(G\right)=2(n-1)$.

If $t^{+}\left(G\right)=2(n-1)$, it implies the existence of a vertex permutation $\{x_0,x_1,\dots ,$ $x_{n-1}\}$ such that ${\sum }_{i=0}^{n-2}{d}_G(x_i,x_{i+1})=2(n-1)$. Now, let us assume that there exists $i_0\in V_G$ such that $(x_{i_0},x_{i_0+1})\in E_G$. In this case, $d_G(x_{i_0},x_{i_0+1})=1$, leading to $t^{+}\left(G\right)<2(n-1)$, which contradicts our previous finding. Therefore, for all $i\in V_G$, $(x_i,x_{i+1})\notin E_G$ and subsequently, for all $i\in V_{\overline{G}}$, $(x_i,x_{i+1})\in E_{\overline{G}}.$ Consequently, $\overline{G}$ contains an Hamiltonian path. □

Proof of Theorem 4. 

If $\lambda \left(C_n\left(S\right)\right)=n-1$, then according to Corollary 2, $gcd(n,\overline{S}))=1$. On the other hand, if $gcd(n,\overline{S}))=1$, it follows that $C_n\left(\overline{S}\right)$ is Hamiltonian [21], implying that $C_n\left(\overline{S}\right)$ contains an Hamiltonian path. Consequently, with the aid of Lemma 2, we ascertain that $t^{+}\left(C_n\left(S\right)\right)=2(n-1)$. Furthermore, given that $diam\left(C_n\left(S\right)\right)=2$, we deduce from Corollary 1 that $\lambda \left(C_n\left(S\right)\right)=3(n-1)-t^{+}\left(C_n\left(S\right)\right)=n-1$. □

Proposition 3. 

For any generating set $S=D\setminus \left\{a\right\}$,

$$\lambda \left(C_n\left(S\right)\right)=n-1\mathit{if}\mathit{and}\mathit{only}\mathit{if}gcd(n,a)=1.$$

Proof. 

Given that $\overline{S}=\left\{a\right\}$, if $\lambda \left(C_n\left(S\right)\right)=n-1$, then according to Corollary 2, $gcd(n,a)=1$. Moreover, if $gcd(n,a)=1$, then by applying Theorem 4, $\lambda \left(C_n\left(S\right)\right)=n-1$ under the condition that the diameter of $C_n\left(S\right)$ is 2. This is the statement that will be established in the upcoming claim. □

Claim 3. 

For each integer $n\ge 6,$ $diam\left(C_n\left(S\right)\right)=2.$

Proof. 

• If $i\in S$, then ${|0-i|}_n=i\in S$. Thus, $(0,i)\in E\left(C_n\left(S\right)\right)$ and $d(0,i)=1$.
• If $i=a=1$, then ${|0-1|}_n=1\notin S$, which implies that $d(0,1)\ge 2$. However, we have $2\le d(0,1)\le d(0,\lfloor \frac{n}{2}\rfloor -1)+d(\lfloor \frac{n}{2}\rfloor -1,1)\le 2$. In fact, since $\lfloor \frac{n}{2}\rfloor -1\in S$, we have $d(0,\lfloor \frac{n}{2}\rfloor -1)=1$. Furthermore, $|(\lfloor \frac{n}{2}\rfloor -1){-1|}_n=\lfloor \frac{n}{2}\rfloor -2\in S$, resulting that $d((\lfloor \frac{n}{2}\rfloor -1)-1,1)=1$. Consequently, $d(0,1)=2$.
• If $i=a>1$, then ${|0-a|}_n=a\notin S$. However, $2\le d(0,a)\le d(0,a-1)+d(a-1,a)\le d(0,a-1)+1$. Moreover, ${|0-(a-1)|}_n=a-1\in S$, which implies that $d(0,a-1)=1$. Thus, $d(0,a)=2$.

Hence, for all $i\in \{1,2,\dots ,\frac{n}{2}\}$, $d(0,i)\le 2$. Consequently, $diam\left(C_n\left(S\right)\right)=2.$ □

Proposition 4. 

For any generating set $S=D\setminus \{a,b\}$,

$$\lambda \left(C_n\left(S\right)\right)=n-1\mathit{if}\mathit{and}\mathit{only}\mathit{if}gcd(n,a,b)=1.$$

Proof. 

Given that $\overline{S}=\{a,b\}$, if $\lambda \left(C_n\left(S\right)\right)=n-1$, then according to Corollary 2, it follows that $gcd(n,a,b)=1$. Moreover, if $gcd(n,a,b)=1$, then by applying Theorem 4, $\lambda \left(C_n\left(S\right)\right)=n-1$ under the condition that the diameter of $C_n\left(S\right)$ is 2, which is the assertion that will be proved in the following claim. □

Claim 4. 

For each integer $n\ge 10,$ $diam\left(C_n\left(S\right)\right)=2.$

Proof. 

Without loss of generality, we assume that $a<b$. We discuss the following cases:

Case 1. 

$a>1$

When $i=a$, we have $d(0,a)\ge 2$. Given that $a\ne 1$, it follows that $1,a-1\in S$, which implies that $d(0,a-1)=d(a-1,a)=1$. Thus, $2\le d(0,a)\le d(0,a-1)+d(a-1,a)\le 2$. Consequently, $d(0,a)=2$. When $i=b$, we discuss the following cases:

• If $i=b<\lfloor \frac{n}{2}\rfloor$, we observe that $2\le d(0,b)\le d(0,b+1)+d(b+1,b)\le 2$. Indeed, considering that ${|0-(b+1)|}_n=b+1\in S$, it follows that $d(0,b+1)=1$. Furthermore, due to the fact that $1\in S$, we can also establish that $d(b+1,b)=1$.
• If $i=b=\lfloor \frac{n}{2}\rfloor$ and $a\ne b-1$, then $2\le d(0,b)\le d(0,1)+d(1,b)\le 2$. In fact, since $1\in S$, we obtain $d(0,1)=1$. Moreover, given that $a\ne b-1$, it follows that ${|1-b|}_n=b-1\in S$, which implies that $d(1,b)=1$.
• If $i=b=\lfloor \frac{n}{2}\rfloor$ and $a=b-1$, then $2\le d(0,b)\le d(0,b-2)+d(b-2,b)\le 2$. Indeed, given that $b-2\ne a$, we obtain ${|0-(b-2)|}_n=b-2\in S$, which implies that $d(0,b-2)=1$. Moreover, since $n\ge 10$, we have $a\ge 4$ and $b\ge 5$. Thus, $2\in S$. Hence, $d(b-2,b)=1$.

Case 2. 

$a=1$ and $b\ge 4$ 

• In this case, we have $2,3\in S$. Thus, $d(0,3)=d(3,a)=1$. Hence, if $i=a=1$, then $2\le d(0,a)\le d(0,3)+d(3,a)\le 2$.
• If $i=b$, we chose $2\le d(0,b)\le d(0,b-2)+d(b-2,b)\le 2$. In fact, given that $a=1$ and $b\ge 4$, it follows that $b-2\in S$. Thus, $d(0,b-2)=1$. Moreover, since $2\in S$, then $d(b-2,b)=1$.

Case 3. 

$a=1$ and $2\le b\le 3$ 

• If $i=a=1$, we have $2\le d(0,1)\le d(0,5)+d(5,1)\le 2$. In fact, since $n\ge 10$ and $2\le b\le 3$, we obtain $4,5\in S$.
• If $i=b=2$, similarly we chose $2\le d(0,2)\le d(0,5)+d(5,2)\le 2$ ($3,5\in S$).
• If $i=b=3$, we have $2\le d(0,3)\le d(0,5)+d(5,3)\le 2$ ($2,5\in S$).

Hence, for all $i\in \{1,2,\dots ,\frac{n}{2}\}$, $d(0,i)\le 2$. Consequently, $diam\left(C_n\left(S\right)\right)=2.$ □

In summary, based on the findings we have established thus far in this paper, it becomes evident that when $gcd(n,\overline{S})\ge 2$, we can derive an exact value for the span of $L(2,1)$-labeling, which is given by $\lambda \left(C_n\left(S\right)\right)=n+gcd(n,\overline{S})-2$. In the alternate case when $gcd(n,\overline{S})=1$, we proved that $\lambda \left(C_n\left(S\right)\right)\le n-1$. Afterwords, we observed that $\lambda \left(C_n\left(S\right)\right)=n-1$ when $diam\left(C_n\left(S\right)\right)=2$. Consequently, the remainder of this section is dedicated to examining the characteristics of S such that $diam\left(C_n\left(S\right)\right)=2$.

Notation 1. 

1.

Let i be a vertex of $C_n\left(S\right)$, and let α and β be integers in $\mathbb{Z}$. For any $s,s^{\prime }\in S$, the expression $i=\alpha s+\beta s^{\prime }$ indicates the presence of a path leading from the vertex 0 to the vertex i in $C_n\left(S\right)$ with a length equal to $\left|\alpha \right|+\left|\beta \right|$. This path traverses through the chord s in the clockwise (+) direction α times if $\alpha \ge 0$, or in the counterclockwise (−) direction α times if $\alpha \le 0$. Similarly, the path walks through the chord $s^{\prime }$ in the clockwise (+) direction β times if $\beta \ge 0$, or in the counterclockwise (−) direction β times if $\beta \le 0$. 

2.

In $C_n\left(S\right)$, we represent the connection between two vertices, denoted as i and j, linked by a chord $s\in S$, either in the clockwise $(+)$ or counterclockwise $(-)$ direction, as follows: $i{⇝}^{s^{\pm }}j$. 

Example 1. 

Consider the graph $C_{24}\left(\{3,4,5,6\}\right)$ represented in Figure 1. If we select an arbitrary vertex, such as vertex 9, there are multiple paths that lead from 0 to 9. We provide a few examples in

Table 2. Examples of paths leading from the vertex 0 to the vertex 9 in $C_{24}\left(\{3,4,5,6\}\right)$.

Expressions of the Vertex 9	Representation	Length
$9=(1\times 4)+(1\times 5)$	$0{⇝}^{4^{+}}4{⇝}^{5^{+}}9$	2
$9=(2\times 6)+\left(\right(-1)\times 3)$	$0{⇝}^{6^{+}}6{⇝}^{6^{+}}12{⇝}^{3^{-}}9$	3
$9=3\times 3$	$0{⇝}^{3^{+}}3{⇝}^{3^{+}}6{⇝}^{3^{+}}9$	3

. 

Lemma 3. 

Let $\alpha ,\beta \in \mathbb{Z}$, such that $\left|\alpha \right|+\left|\beta \right|\le 2$, $diam\left(C_n\left(S\right)\right)=2\mathit{if\; and\; only\; if},$ $\mathit{for\; all}$ $i\in \{1,\dots ,\lfloor \frac{n}{2}\rfloor \},i=\alpha s+\beta s^{\prime },$ where $s,s^{\prime }\in S$. 

Proof. 

The sufficient condition is evident. We will now proceed to assume that $diam\left(C_n\left(S\right)\right)=2$. Let $i\in \{1,\dots ,\lfloor \frac{n}{2}\rfloor \}$. If $i\in S$, then there exists $s^{\prime \prime }\in S$ such that $i=s^{\prime \prime }$. Otherwise, if $i\notin S$, then there exist $k\in \{1,\dots ,\lfloor \frac{n}{2}\rfloor \}$, with $i\ne k$, such that $(0,k)$ and $(k,i)$ are in $E\left(C_n\left(S\right)\right)$. Moreover, since $(0,k)\in E\left(C_n\left(S\right)\right)$, then ${|0-k|}_n\in S$, which implies the existence of $s^{\prime }\in S$ and $\beta \in \{-1,1\}$ such that $k=\beta s^{\prime }$. Similarly, given that $(k,i)\in E\left(C_n\left(S\right)\right)$, it follows that ${|i-k|}_n\in S$. Thus, there exists $s\in S$ and $\alpha \in \{-1,1\}$ such that $i-k=\alpha s$. Hence, $i=\alpha s+\beta s^{\prime }$. This conclude the proof. □

Example 2. 

Consider the graph $C_{24}\left(\{3,4,5,6\}\right)$ represented in Figure 1. For example, we have $\begin{array}{ll}1=(1\times 4)+\left(\right(-1)\times 3);& 7=(1\times 3)+(1\times 4);\\ 2=(1\times 5)+\left(\right(-1)\times 3);& 8=(1\times 3)+(1\times 5);\\ 3=1\times 3;& 9=(1\times 3)+(1\times 6);\\ 4=1\times 4;& 10=2\times 5;\\ 5=1\times 5;& 11=(1\times 5)+(1\times 6);\\ 6=1\times 6;& 12=2\times 6;\end{array}$

Thus, for all $i\in \{1,\dots ,12\},i=\alpha s+\beta s^{\prime },$ where $s,s^{\prime }\in \{3,4,5,6\}$ with $\left|\alpha \right|+\left|\beta \right|\le 2$. Consequently, $diam\left(C_{24}\left(\{3,4,5,6\}\right)\right)$ $=2$. 

Lemma 4. 

If $diam\left(C_n\left(S\right)\right)=2$, then for all generating sets $S^{\prime }$ such that $S^{\prime }\supset S$, we have $diam\left(C_n\left(S^{\prime }\right)\right)=2$. 

Proof. 

Let $i\in V\left(C_n\left(S^{\prime }\right)\right)$. Since $diam\left(C_n\left(S\right)\right)=2$, by applying Lemma 3, $i=\alpha s+\beta s^{\prime }$ where, $s,s^{\prime }\in S$ and $\alpha ,\beta \in \mathbb{Z}$, such that $\left|\alpha \right|+\left|\beta \right|\le 2$. However, $S^{\prime }\supset S$. Thus, $s,s^{\prime }\in S^{\prime }$. Consequently, $i=\alpha s+\beta s^{\prime }$ where, $s,s^{\prime }\in S^{\prime }$ and $\alpha ,\beta \in \mathbb{Z}$, such that $\left|\alpha \right|+\left|\beta \right|\le 2$. By applying Lemma 3, we conclude that $diam\left(C_n\left(S^{\prime }\right)\right)=2$. □

Proposition 5. 

If $diam\left(C_n\left(\overline{S}\right)\right)\ge 3$, then $diam\left(C_n\left(S\right)\right)=2$. 

Proof. 

Let $x,y\in V\left(C_n\left(S\right)\right)$. If $(x,y)\in E\left(C_n\left(S\right)\right)$, then $d_{C_n\left(S\right)}(x,y)=1$. Otherwise, if $(x,y)\notin E\left(C_n\left(S\right)\right)$ then $(x,y)\in E\left(C_n\left(\overline{S}\right)\right)$. Since the graph $C_n\left(\overline{S}\right)$ is vertex-transitive such that $diam\left(C_n\left(\overline{S}\right)\right)\ge 3$, there exists $z\in V\left(C_n\left(\overline{S}\right)\right)$, with $z\ne y$, such that $d_{C_n\left(\overline{S}\right)}(x,z)\ge 3$, i.e., $(x,z)\notin E\left(C_n\left(\overline{S}\right)\right)$. Hence, $(x,z)\in E\left(C_n\left(S\right)\right)$. Similarly, $(y,z)\notin E\left(C_n\left(\overline{S}\right)\right)$ because otherwise, $d_{C_n\left(\overline{S}\right)}(x,z)\le d_{C_n\left(\overline{S}\right)}(x,y)+d_{C_n\left(\overline{S}\right)}(x,y)=2$, a contradiction. So, $(y,z)\in E\left(C_n\left(S\right)\right)$. Hence, $d_{C_n\left(S\right)}(x,y)=2$. Consequently, $diam\left(C_n\left(S\right)\right)=2$. □

Theorem 5. 

For all $n\ge 6$, if $\left|S\right|>\lceil \frac{n}{4}\rceil$, then $diam\left(C_n\left(S\right)\right)=2$. 

Proof. 

Let S be a generating set such that $\left|S\right|>\lceil \frac{n}{4}\rceil$. Note that $C_n\left(S\right)$ is r-regular with

$r=\left\{\begin{array}{cc}2\left|S\right|-1,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}\mathrm{and}\frac{n}{2}\in S,\hfill \\ 2\left|S\right|,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$

Let i and j be two non-adjacent vertices of $C_n\left(S\right)$ such that $N\left(i\right)\cap N\left(j\right)=\varnothing$. We have $V\supset \{i,j\}\cup N\left(i\right)\cup N\left(j\right)$. Thus, $n=\left|V\right|\ge 2+\left|N\right(i\left)\right|+\left|N\right(j\left)\right|$.

If n is even and $\frac{n}{2}\in S$, then $\left|N\right(i\left)\right|=\left|N\right(j\left)\right|=2\left|S\right|-1$. So, $n\ge 2+2\left(2\right|S|-1)$. Hence, $n\ge 4\left|S\right|>4\lceil \frac{n}{4}\rceil \ge n$, a contradiction.

Otherwise, if n is odd, then $\left|N\right(i\left)\right|=\left|N\right(j\left)\right|=2\left|S\right|$. Thus, $n\ge 2+4\left|S\right|>2+4\lceil \frac{n}{4}\rceil$. So, $n>2+n$, a contradiction.

Therefore, for any two non-adjacent vertices i and j in $C_n\left(S\right)$, there exists a vertex k in $C_n\left(S\right)$, such that $(i,k)$ and $(k,j)$ are in $E\left(C_n\left(S\right)\right)$. Consequently, $diam\left(C_n\left(S\right)\right)=2$. □

By combining all the previous results, we present the following theorem, which describes the characteristics that S must possess in order for us to obtain a precise value for the $L(2,1)$-labeling number of $C_n\left(S\right)$ when $gcd(n,\overline{S})=1$.

Proposition 6. 

For each $n\ge 6$,

1.

if $\left|S\right|>\lceil \frac{n}{4}\rceil$ and $gcd(n,\overline{S})=1$, then $\lambda \left(C_n\left(S\right)\right)=n-1$. 

2.

if $diam\left(C_n\left(\overline{S}\right)\right)\ge 3$ and $gcd(n,\overline{S})=1$, then $\lambda \left(C_n\left(S\right)\right)=n-1$. 

• Observations 

The greatest common divisor of two integers can be calculated by a simple algorithm, yet there are situations (as mentioned below) where it is straightforward to establish that $gcd(n,\overline{S})=1$.

• If n is a prime number, then $gcd(n,\overline{S})=1$.
• If $1\notin S$, then $gcd(n,\overline{S})=1$.
• Consider a generating set $S=\{s_1,s_2,\dots ,s_t\}$. If there exists $i_0\in \{1,2,\dots ,t\}$, such that $s_{i_0+1}-s_{i_0}\ge 3$, then $gcd(n,\overline{S})=1$.

Subsequently, we investigate the case in which $\left|S\right|<\lceil \frac{n}{4}\rceil$.

Proposition 7. 

For all $n\ge 6$, if $\left|S\right|<\lceil \frac{n}{4}\rceil$, then $\lambda \left(C_n\left(S\right)\right)\le n-1$. 

Proof. 

Note that $C_n\left(S\right)$ is r-regular with $r=\left\{\begin{array}{cc}2\left|S\right|-1,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}\mathrm{and}\frac{n}{2}\in S,\hfill \\ 2\left|S\right|,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$ We discuss the following cases:

• If n is even and $\frac{n}{2}\in S$, then $\frac{n}{2}\notin \overline{S}$. Thus, the minimum degree of the graph $C_n\left(\overline{S}\right)$, denoted by $\delta \left(C_n\left(\overline{S}\right)\right)$, is equal to $2|\overline{S}|$. Given that $\left|S\right|+|\overline{S}|=\lfloor \frac{n}{2}\rfloor$, it follows that $\delta \left(C_n\left(\overline{S}\right)\right)=n-2\left|S\right|>n-2\lceil \frac{n}{4}\rceil \ge \frac{n}{2}.$ According to Dirac’s theorem [24], we conclude that $C_n\left(\overline{S}\right)$ is Hamiltonian, which implies that $c\left(C_n\left(\overline{S}\right)\right)=1$. Hence, with Lemma 1 and Corollary 2, we deduce that $\lambda \left(C_n\left(S\right)\right)\le n-1$.
• If n is even and $\frac{n}{2}\notin S$, then $\frac{n}{2}\in \overline{S}$. Thus, $\delta \left(C_n\left(\overline{S}\right)\right)=2\left|\overline{S}\right|-1$. Given that $\left|S\right|+|\overline{S}|=\lfloor \frac{n}{2}\rfloor$, it follows that $\delta \left(C_n\left(\overline{S}\right)\right)=n-2\left|S\right|-1>n-2\lceil \frac{n}{4}\rceil -1\ge \frac{n}{2}-1.$ Similarly, with Dirac’s theorem [24], we conclude that $\lambda \left(C_n\left(S\right)\right)\le n-1$.
• If n is odd, then $\delta \left(C_n\left(\overline{S}\right)\right)=2|\overline{S}|=n-2|S|-1>\frac{n}{2}-1.$ Thus, $\lambda \left(C_n\left(S\right)\right)\le n-1$.

□

At the outset of this section, we initiated by providing precise span values for circulants with generating sets $D\setminus \left\{\lfloor \frac{n}{2}\rfloor \right\}$ (for all n), $D\setminus \left\{a\right\}$, and $D\setminus \{a,b\}$, where $a,b\in D$. Our aim is to determine the maximum number of elements we can remove from D while still achieving an exact span value. In the subsequent result, we generalize these results to any set $X\subset D$, by introducing conditions related to the cardinality of X, ensuring that the graph $C_n(D\setminus X)$ possesses an exact span value.

Proposition 8. 

Let $n\ge 6$ and $X\subset D$. If $\left|X\right|<\lfloor \frac{n}{2}\rfloor -\lceil \frac{n}{4}\rceil$ and $gcd(n,X)=1$, then $\lambda \left(C_n(D\setminus X)\right)=n-1$. 

Proof. 

Let $S=D\setminus X$. Given that $\left|D\right|=\lfloor \frac{n}{2}\rfloor$ and $\left|X\right|<\lfloor \frac{n}{2}\rfloor -\lceil \frac{n}{4}\rceil$, it follows that $\left|S\right|=\left|D\right|-\left|X\right|>\lfloor \frac{n}{2}\rfloor -(\lfloor \frac{n}{2}\rfloor -\lceil \frac{n}{4}\rceil )$. Thus, $\left|S\right|>\lceil \frac{n}{4}\rceil$. With Theorem 5, we conclude that $diam\left(C_n\left(S\right)\right)=2$. Moreover, given that $gcd(n,X)=1$, it follows from Theorem 4 that $\lambda \left(C_n\left(S\right)\right)=n-1$. □

Next, we present an illustrative example, where we introduce a highly distinctive family, denoted as $A_n$, that generates a large number of generating sets. For each value of n, we acquire a circulant graph $C_n\left(A_n\right)$ such that $\lambda \left(C_n\left(A_n\right)\right)=n-1$, and various additional interesting properties.

Theorem 6. 

For each integer $n\ge 10$, there exists a family $A_n=\{\lceil \frac{m}{2}\rceil ,\dots ,m\}$, where $m=\lceil \frac{\lfloor \frac{n}{2}\rfloor }{2}\rceil$, such that the following assertions are verified:

1.

$C_n\left(A_n\right)$ is not a self-complementary graph. 

2.

$C_n\left(A_n\right)$ and $C_n\left(\overline{A_n}\right)$ are Hamiltonian. (i.e., $c\left(C_n\left(A_n\right)\right)=c\left(C_n\left(\overline{A_n}\right)\right)=1$) 

3.

$diam\left(C_n\left(A_n\right)\right)=diam\left(C_n\left(\overline{A_n}\right)\right)=2$. 

4.

$\lambda \left(C_n\left(A_n\right)\right)=\lambda \left(C_n\left(\overline{A_n}\right)\right)=n-1$. 

5.

$\lambda \left(C_n\left(A_n\right)\right)+\lambda \left(C_n\left(\overline{A_n}\right)\right)=2n-2$ (Nordhaus–Gaddum’s upper bound is reached [25]). 

Proof. 

For each integer $n\ge 10$, let $A_n=\{\lceil \frac{m}{2}\rceil ,\dots ,m\}$ be a family of integers where $m=\lceil \frac{\lfloor \frac{n}{2}\rfloor }{2}\rceil$.

• It is evident that $|A_n|\ne |\overline{A_n}|$. Consequently, $C_n\left(A_n\right)$ and $C_n\left(\overline{A_n}\right)$ cannot be isomorphic. Therefore, $C_n\left(A_n\right)$ is not a self-complementary graph.
• As $gcd(n,A_n)=1$, it follows that $C_n\left(A_n\right)$ is Hamiltonian [21]. Indeed, as $n\ge 10$, we observe that $1\notin A_n$, implying that $1\in \overline{A_n}$. Therefore, $gcd(n,\overline{A_n})=1$. Consequently, $C_n\left(A_n\right)$ and $C_n\left(\overline{A_n}\right)$ are Hamiltonian [21].
• Through a straightforward calculation, considering the parity of n, it becomes evident to see that $|\overline{A_n}|>\lceil \frac{n}{4}\rceil$. Hence, with Theorem 5, we deduce that $diam\left(C_n\left(\overline{A_n}\right)\right)=2$. In the case of the set $A_n$, we employ Lemma 3 to demonstrate that $diam\left(C_n\left(A_n\right)\right)=2$. Specifically, we find suitable $\alpha ,\beta \in \mathbb{Z}$ with $\left|\alpha \right|+\left|\beta \right|\le 2$, such that for all $i\in \{1,2,\dots ,\lfloor \frac{n}{2}\rfloor \}$, $i=\alpha s+\beta s^{\prime }$, where $s,s^{\prime }\in A_n$. To accomplish this, we examine the following cases:

  Case 1. 

  $n=4p$ or $n=4p+1$, with $p\ge 3$ 

  In this case, we have $\lfloor \frac{n}{2}\rfloor =2p$ and $m=p$. If p is odd, we obtain $A_n=\{\frac{p+1}{2},\dots ,p\}$. The proof’s concept involves partitioning the set $\{1,2,\dots ,2p\}$ into four distinct subsets. In this particular case, these subsets are as follows: $V_1=\{1,2,\dots ,\frac{p+1}{2}-1\}$, $V_2=\{\frac{p+1}{2},\frac{p+1}{2}+1,\dots ,p\}$, $V_3=\{p+1,p+2,\dots ,p+\frac{p+1}{2}\}$ and $V_4=\{p+\frac{p+1}{2}+1,p+\frac{p+1}{2}+2,\dots ,2p\}$.
  • If $i\in V_1$, then i can be expressed as $i=\frac{p+1}{2}+i-\frac{p+1}{2}$. Thus, $i=\alpha s+\beta s^{\prime }$, where $s=\frac{p+1}{2}+i\in A_n$ and $s^{\prime }=\frac{p+1}{2}\in A_n$, $\alpha =1$, and $\beta =-1$.
  • If $i\in V_2=A_n$, we have $i=s\in A_n$.
  • If $i\in V_3$, then i can be written as $i=p+j=\frac{p+1}{2}+(\frac{p+1}{2}-1+j)$ with $j\in \{1,\dots ,\frac{p+1}{2}\}$. So, $i=s+s^{\prime }$, where $s=\frac{p+1}{2}\in A_n$ and $s^{\prime }=\frac{p+1}{2}-1+j\in A_n$.
  • If $i\in V_4$, we have $i=p+(\frac{p+1}{2}+j)$, with $j\in \{1,\dots ,\frac{p+1}{2}-1\}=s+s^{\prime }$, where $s=p\in A_n$ and $s^{\prime }=\frac{p+1}{2}+j\in A_n$.
  If p is even, then $A_n=\{\frac{p}{2},\dots ,p\}$. In this case, we have $\{1,2,\dots ,2p\}=V_1\cup V_2\cup V_3\cup V_4$, where $V_1=\{1,2,\dots ,\frac{p}{2}-1\}$, $V_2=\{\frac{p}{2},\frac{p}{2}+1,\dots ,p\}$, $V_3=\{p+1,p+2,\dots ,p+\frac{p}{2}\}$ and $V_4=\{p+\frac{p}{2}+1,p+\frac{p}{2}+2,\dots ,2p\}$.
  • If $i\in V_1$, then $i=\frac{p}{2}+i-\frac{p}{2}$. Thus, $i=\alpha s+\beta s^{\prime }$, where $s=\frac{p}{2}+i\in A_n$ and $s^{\prime }=\frac{p}{2}\in A_n$, $\alpha =1$, and $\beta =-1$.
  • If $i\in V_2=A_n$, it is evident.
  • If $i\in V_3$, then $i=p+j=\frac{p}{2}+(\frac{p}{2}+j)$ with $j\in \{1,\dots ,\frac{p}{2}\}$. So, $i=s+s^{\prime }$, where $s=\frac{p}{2}\in A_n$ and $s^{\prime }=\frac{p}{2}+j\in A_n$.
  • If $i\in V_4$, we have $i=p+\frac{p}{2}+j$, with $j\in \{1,\dots ,\frac{p}{2}\}$. So, $i=s+s^{\prime }$, where $s=p\in A_n$ and $s^{\prime }=\frac{p}{2}+j\in A_n$.

  Case 2. 

  $n=4p+2$ or $n=4p+3$, with $p\ge 3$ 

  In this case, we have $\lfloor \frac{n}{2}\rfloor =2p+1$ and $m=p+1$. We employ the same technique as for Case 1 but with a distinct partition of $\{1,2,\dots ,2p+1\}$. If p is odd, then $A_n=\{\frac{p+1}{2},\dots ,p+1\}$. The new partition is defined as follows: $V_1=\{1,2,\dots ,\frac{p+1}{2}-1\}$, $V_2=\{\frac{p+1}{2},\frac{p+1}{2}+1,\dots ,p+1\}$, $V_3=\{p+2,p+3,\dots ,p+1+\frac{p+1}{2}\}$ and $V_4=\{p+1+\frac{p+1}{2}+1,p+1+\frac{p+1}{2}+2,\dots ,2p+1\}$.
  Otherwise, if p is even, then $A_n=\{\frac{p+2}{2},\dots ,p+1\}$. The subsets are as follows: $V_1=\{1,2,\dots ,\frac{p+2}{2}-1\}$, $V_2=\{\frac{p+2}{2},\frac{p+2}{2}+1,\dots ,p+1\}$, $V_3=\{p+2,p+3,\dots ,p+1+\frac{p+2}{2}\}$ and $V_4=\{p+1+\frac{p+2}{2}+1,p+1+\frac{p+2}{2}+2,\dots ,2p+1\}$.
  For example, consider the graph $C_{24}\left(\{3,4,5,6\}\right)$ represented in Figure 1. In this case, we have $\lfloor \frac{24}{2}\rfloor =12$, $m=6$ and $A_{24}=\{3,4,5,6\}$. Since $p=6$ is even, the set $\{1,2,\dots ,12\}=V_1\cup V_2\cup V_3\cup V_4$, where $V_1=\{1,2\}$, $V_2=A_{24}=\{3,4,5,6\}$, $V_3=\{7,8,9\}$ and $V_4=\{10,11,12\}$.
  • If $i\in V_1$, we have $1=4-3$ and $2=5-3$.
  • If $i\in V_2=A_{24}$, it is evident.
  • If $i\in V_3$, then $7=3+4$, $8=3+5$, and $9=3+6$.
  • If $i\in V_4$, we have $10=6+4$, $11=6+5$, and $12=6+6$.
  Thus, for all $i\in \{1,\dots ,12\},d(0,i)\le 2$.
• With assertion 2, Lemma 1, and assertion 3, we observe that the conditions mentioned in Theorem 4 are satisfied for both graphs $C_n\left(A_n\right)$ and $C_n\left(\overline{A_n}\right)$. Thus, $\lambda \left(C_n\left(A_n\right)\right)=\lambda (C_n\left(\overline{A_n}\right)=n-1$. In this context, it becomes evident that the upper bound set by Nordhaus–Gaddum [25] has been achieved: $\lambda \left(C_n\left(A_n\right)\right)+\lambda (C_n\left(\overline{A_n}\right)=2n-2$.

□

Remark 1. 

In 1985, Harary and Robinson [26] established a significant result stating that every nontrivial self-complementary graph G has a diameter equal to 2 or 3. In the previous theorem, the class of graphs $C_n\left(A_n\right)$ that we have identified possess a diameter of 2, although they are not self-complementary. Thus, it becomes evident that the family $A_n$ is of a distinct nature. Remarkably, this family has the capability to generate a substantial number of generating sets that satisfy the conditions presented in the previous theorem. Moreover, based on the result mentioned in Lemma 4, we can generate even more generating sets $S\supset A_n$ that will also fulfill the conditions laid out in Theorem 6. 

3. Conclusions and Future Explorations

For this paper, we have undertaken a comprehensive study of the $L(2,1)$-labeling for circulant graphs with large generating sets. We have extended Mitra and Bhoumik’s results, for any set $X\subset D$, by introducing conditions related to the cardinality of X, ensuring that the graph $C_n(D\setminus X)$ possesses exact span values of the $L(2,1)$-labeling.

When $gcd(n,\overline{S})\ge 2$, we have successfully derived the exact span value for the $L(2,1)$-labeling, given by $\lambda \left(C_n\left(S\right)\right)=n+gcd(n,\overline{S})-2$. In the other case when $gcd(n,\overline{S})=1$, we have established that $\lambda \left(C_n\left(S\right)\right)=n-1$ if and only if $diam\left(C_n\left(S\right)\right)=2$. This discovery led us to provide the characteristics of S such that $diam\left(C_n\left(S\right)\right)=2$.

Our current research opens up various avenues for future exploration. For instance, it is possible to determine the necessary and sufficient conditions on S to guarantee that $C_n\left(S\right)$ has a diameter of 2. Additionally, one can verify whether, in the case of $\lambda \left(C_n\left(S\right)\right)=n-1$, $diam\left(C_n\left(S\right)\right)=2$.

It is worth noting that as $\mathsf{\Delta }=2\left|S\right|$ and $\left|S\right|\le \frac{n}{2}$, the conjecture of Griggs and Yeh [6] ($\lambda \left(G\right)\le {\mathsf{\Delta }}^2$ for any graph G) simplifies, in the context of circulant graphs, to $\lambda \left(C_n\left(S\right)\right)\le \mathcal{O}\left(n^2\right)$. Nevertheless, based on the entirety of the results we have established in this paper, it is evident that $\lambda \left(C_n\left(S\right)\right)\le \mathcal{O}\left(n\right)$. Therefore, this conjecture is verified for any circulant graph.