Exact Solutions for the Generalized Atangana-Baleanu-Riemann Fractional (3 + 1)-Dimensional Kadomtsev–Petviashvili Equation
Abstract
:1. Introduction
2. Summary of the Generalized Jacobi Elliptic Functions Expansion Method
3. Exact Solutions to the Fractional (3 + 1)-Dimensional KP Equation
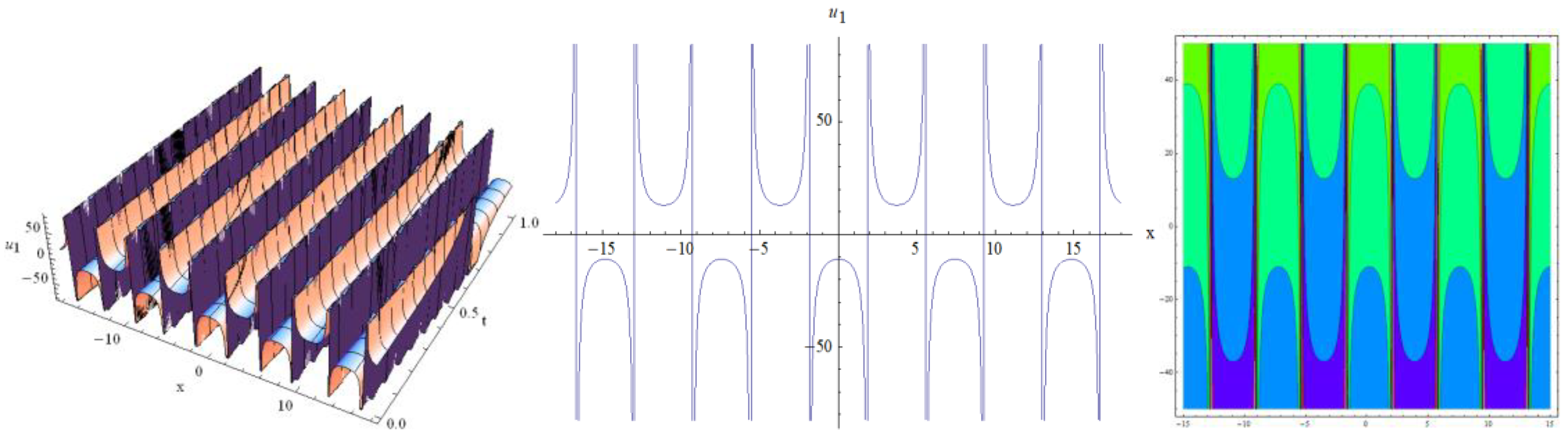
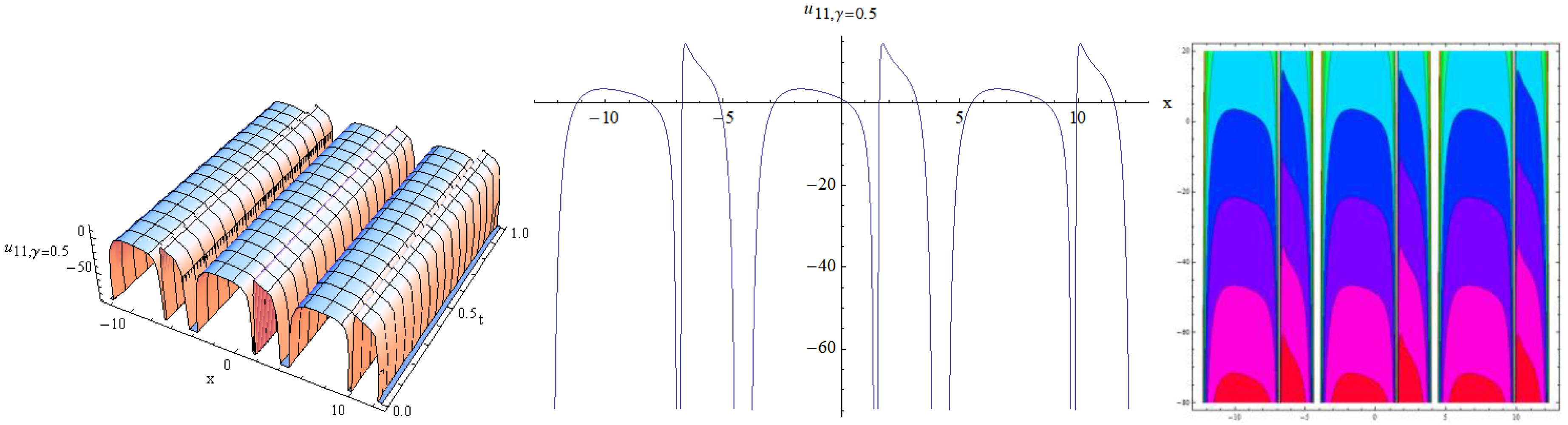
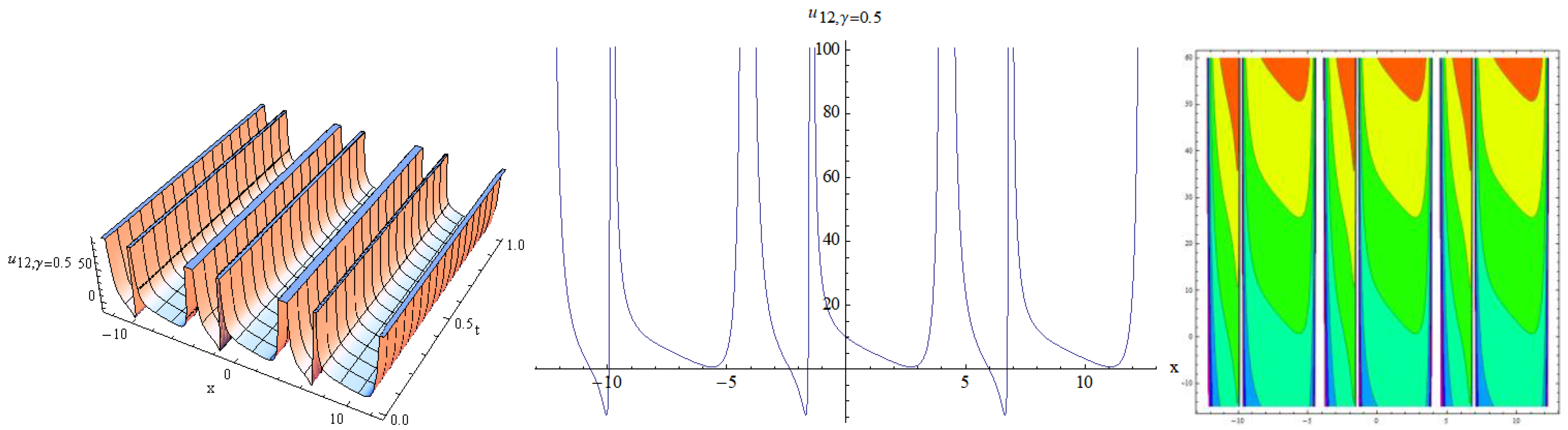
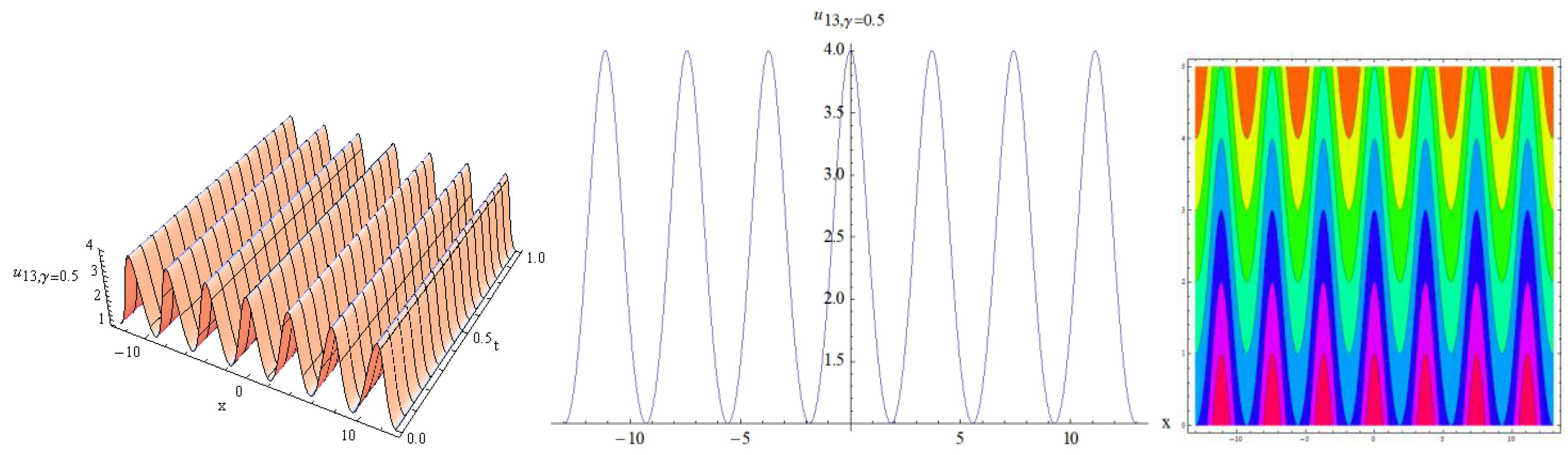
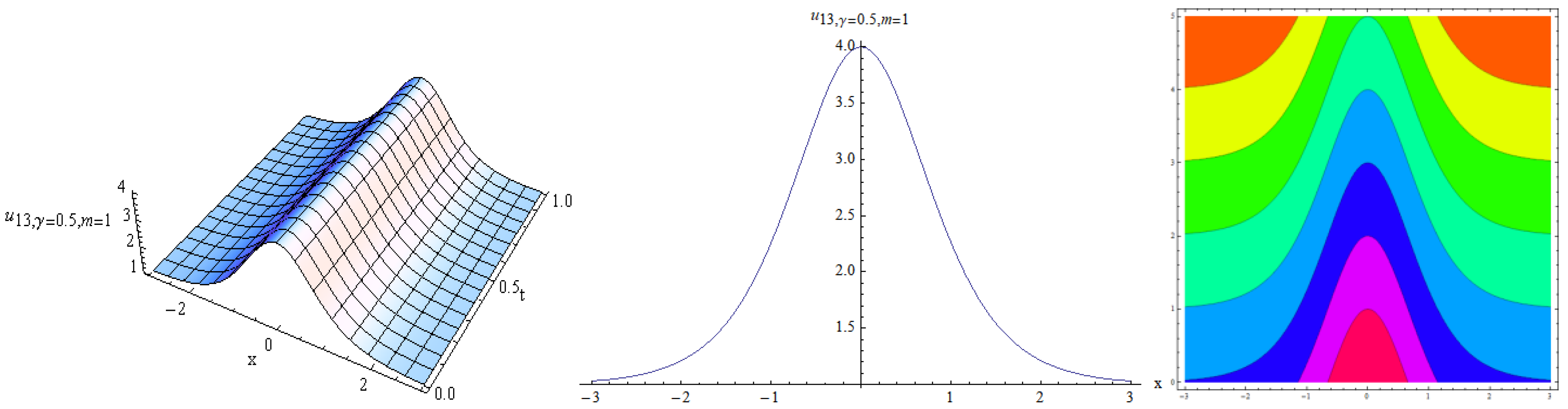
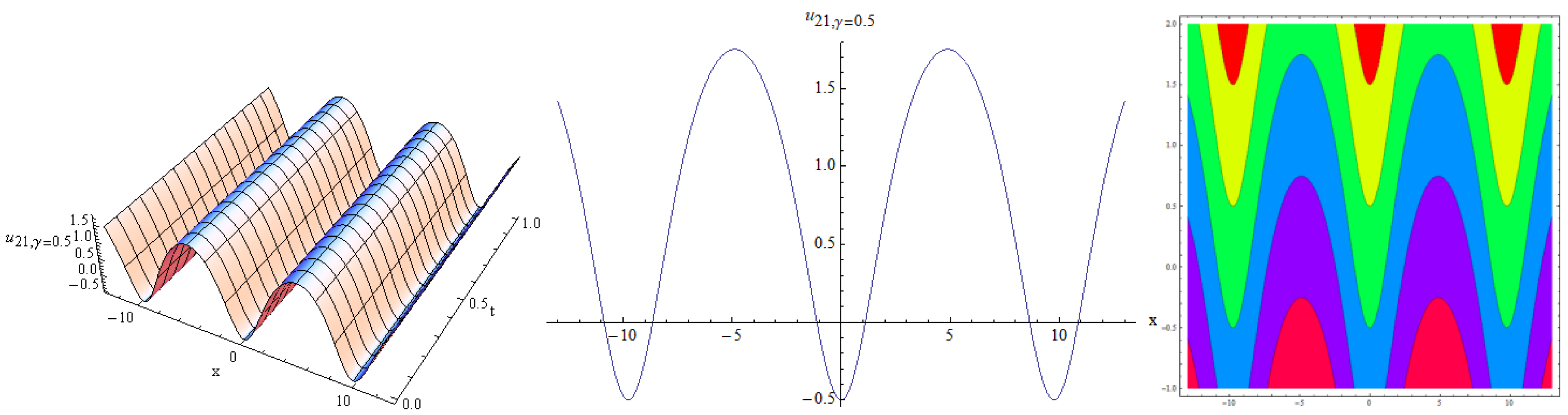
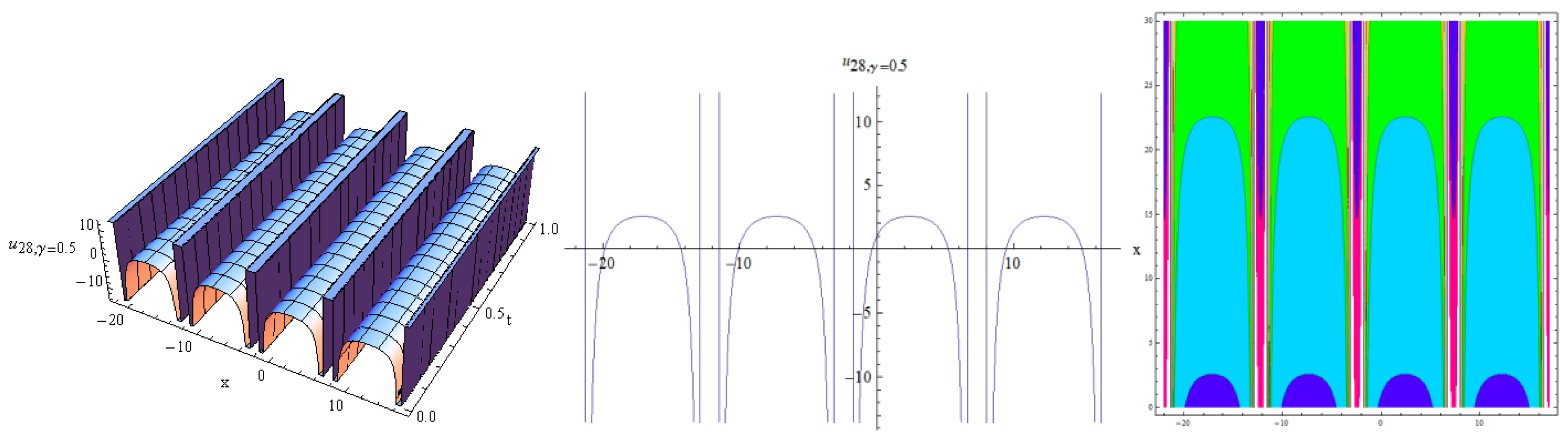
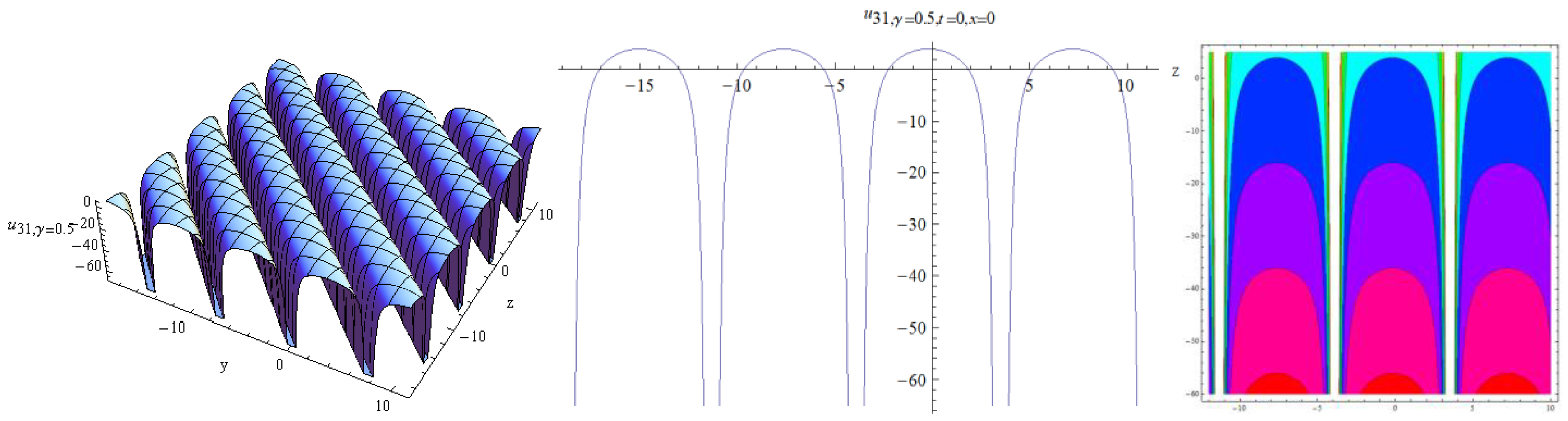
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, R.F.; Bilige, S. Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gBKP equation. Nonlinear Dyn. 2019, 95, 3041–3048. [Google Scholar] [CrossRef]
- Almutairi, A.; El-Metwally, H.; Sohaly, M.A.; Elbaz, I.M. Lyapunov stability analysis for nonlinear delay systems under random effects and stochastic perturbations with applications in finance and ecology. Adv. Differ. Equ. 2021, 2021, 186. [Google Scholar] [CrossRef]
- He, J.H. Seeing with a single scale is always unbelieving: From magic to two-scale fractal. Therm. Sci. 2021, 25, 1217–1219. [Google Scholar] [CrossRef]
- Yokus, A.; Baskonus, H.M. Dynamics of traveling wave solutions arising in fiber optic communication of some nonlinear models. Soft Comput. 2022, 26, 13605–13614. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M.; Jafari, S.; Bolouki, S.; Siami, M. Some applications of fractional calculus in suppression of chaotic oscillations. IEEE Trans. Ind. Electron. 2008, 55, 4094–4101. [Google Scholar] [CrossRef]
- Korn, P. A Regularity-Aware algorithm for variational data assimilation of an idealized coupled Atmosphere-Ocean Model. J. Sci. Comput. 2018, 79, 748–786. [Google Scholar] [CrossRef] [Green Version]
- Radu, C.C.; Eugene, C.E.; Cicero, L.F.; Jerome, A.G. Fractional telegraph equations. J. Math. Anal. Appl. 2002, 276, 145–159. [Google Scholar]
- Abdelwahed, H.G.; El-Shewy, E.K.; Abdelrahman, M.A.; Alsarhana, A.F. On the physical nonlinear (n + 1)-dimensional Schrödinger equation applications. Results Phys. 2021, 21, 103798. [Google Scholar] [CrossRef]
- Samei, M.E.; Karimi, L.; Kaabar, M.K.A. To investigate a class of multi-singular pointwise defined fractional q–integro-differential equation with applications. AIMS Math. 2022, 7, 7781–7816. [Google Scholar] [CrossRef]
- Yousef, F.; Alquran, M.; Jaradat, I.; Momani, S.; Baleanu, D. New Fractional Analytical Study of Three-Dimensional Evolution Equation Equipped With Three Memory Indices. J. Comput. Nonlinear Dyn. 2019, 14, 111008. [Google Scholar] [CrossRef]
- Yousef, F.; Alquran, M.; Jaradat, I.; Momani, S.; Baleanu, D. Ternary-fractional differential transform schema: Theory and application. Adv. Differ. Equ. 2019, 2019, 197. [Google Scholar] [CrossRef]
- Lu, D.C.; Hong, B.J. Bäcklund transformation and n-soliton-like solutions to the combined KdV-Burgers equation with variable coefficients. Int. J. Nonlinear Sci. 2006, 1, 3–10. [Google Scholar]
- Matveev, V.A.; Salle, M.A. Darboux Transformations and Solitons; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Hu, X.B.; Ma, W.X. Application of Hirotas bilinear formalism to the Toeplitz lattice-some special soliton-like solutions. Phys. Lett. A 2002, 293, 161–165. [Google Scholar] [CrossRef]
- Bashar, M.H.; Islam, S.M.R. Exact solutions to the (2 + 1)-Dimensional Heisenberg ferromagnetic spin chain equation by using modified simple equation and improve F-expansion methods. Phys. Open 2020, 5, 100027. [Google Scholar] [CrossRef]
- Kundu, P.R.; Fahim MR, A.; Islam, M.E.; Akbar, M.A. The sine-Gordon expansion method for higher-dimensional NLEEs and parametric analysis. Heliyon 2021, 7, e06459. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.C.; Hong, B.J.; Tian, L.X. New explicit exact solutions for the generalized coupled Hirota-Satsuma KdV system. Comput. Math. Appl. 2007, 53, 1181–1190. [Google Scholar] [CrossRef] [Green Version]
- Mohanty, S.K.; Kravchenko, O.V.; Dev, A.N. Exact traveling wave solutions of the Schamel Burgers equation by using generalized-improved and generalized (G’/G) expansion methods. Results Phys. 2022, 33, 105124. [Google Scholar] [CrossRef]
- Siddique, I.; Jaradat, M.M.; Zafar, A.; Mehdi, K.B.; Osman, M.S. Exact traveling wave solutions for two prolific conformable M-Fractional differential equations via three diverse approaches. Results Phys. 2021, 33, 105216. [Google Scholar] [CrossRef]
- Ismael, H.F.; Bulut, H.; Baskonus, H.M. Optical soliton solutions to the Fokas–Lenells equation via sine-Gordon expansion method and (m + (G’/G))-expansion method. Pramana 2020, 94, 35. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Bibi, S. Exact solutions for nonlinear fractional differential equations using G′/G2-expansion method. Alex. Eng. J. 2018, 57, 1003–1008. [Google Scholar] [CrossRef]
- Ma, W.-X.; Osman, M.; Arshed, S.; Raza, N.; Srivastava, H. Practical analytical approaches for finding novel optical solitons in the single-mode fibers. Chin. J. Phys. 2021, 72, 475–486. [Google Scholar] [CrossRef]
- Shakeel, M.; Attaullah; Alaoui, M.K.; Zidan, A.M.; Shah, N.A.; Weera, W. Closed-Form solutions in a Magneto-Electro-Elastic circular rod via generalized Exp-function method. Mathematics 2022, 10, 3400. [Google Scholar] [CrossRef]
- Rani, A.; Shakeel, M.; Kbiri Alaoui, M.; Zidan, A.M.; Shah, N.A.; Junsawang, P. Application of the Exp(−φ(ξ))-expansion method to find the soliton solutions in biomembranes and nerves. Mathematics 2022, 10, 3372. [Google Scholar] [CrossRef]
- Nass, A.M. Lie symmetry analysis and exact solutions of fractional ordinary differential equations with neutral delay. Appl. Math. Comput. 2019, 347, 370–380. [Google Scholar] [CrossRef]
- Yue, C.; Lu, D.; Khater, M.M.A.; Abdel-Aty, A.-H.; Alharbi, W.; Attia, R.A.M. On explicit wave solutions of the fractional nonlinear DSW system via the modified Khater method. Fractals 2020, 28, 2040034. [Google Scholar] [CrossRef]
- He, J.H.; Elagan, S.K.; Li, Z.B. Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 2012, 376, 257–259. [Google Scholar] [CrossRef]
- He, J.H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Ghanbari, B.; Inc, M.; Yusuf, A.; Baleanu, D.; Bayram, M. Families of exact solutions of Biswas-Milovic equation by an exponential rational function method. Tbil. Math. J. 2020, 13, 39–65. [Google Scholar] [CrossRef]
- Hong, B.J. Exact solutions for the conformable fractional coupled nonlinear Schrödinger equations with variable coefficients. J. Low Freq. Noise Vib. Act. Control 2022, 41, 1–14. [Google Scholar] [CrossRef]
- Yu, F.; Yu, Q.; Chen, H.; Kong, X.; Mokbel, A.A.M.; Cai, S.; Du, S. Dynamic analysis and audio encryption application in IoT of a multi-scroll fractional-order hopfield neural network. Fractal Fract. 2022, 6, 370. [Google Scholar] [CrossRef]
- Hong, B.J.; Lu, D.C.; Chen, W. Exact and approximate solutions for the fractional Schrödinger equation with variable coefficients. Adv. Differ. Equ. 2019, 2019, 370. [Google Scholar] [CrossRef]
- Shah, N.A.; Agarwal, P.; Chung, J.D.; El-Zahar, E.R.; Hamed, Y.S. Analysis of Optical Solitons for Nonlinear Schrödinger Equation with Detuning Term by Iterative Transform Method. Symmetry 2020, 12, 1850. [Google Scholar] [CrossRef]
- Alquran, M.; Yousef, F.; Alquran, F.; Sulaiman, T.A.; Yusuf, A. Dual-wave solutions for the quadratic–cubic conformable-Caputo time-fractional Klein–Fock–Gordon equation. Math. Comput. Simul. 2021, 185, 62–76. [Google Scholar] [CrossRef]
- Singh, J.; Secer, A.; Swroop, R.; Kumar, D. A reliable analytical approach for a fractional model of advection-dispersion equation. Nonlinear Eng. 2019, 8, 107–116. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.-D.; Shah, R.; Khan, A. A Comparative Analysis of Fractional-Order Kaup–Kupershmidt Equation within Different Operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Haq, A. Partial-approximate controllability of semi-linear systems involving two Riemann-Liouville fractional derivatives. Chaos Solitons Fractals 2022, 157, 111923. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent: Part II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Guner, O.; Atik, H.; Kayyrzhanovich, A.A. New exact solution for space-time fractional differential equations via (G’/G)-expansion method. Optik 2017, 130, 696–701. [Google Scholar] [CrossRef]
- He, J.H. A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Yao, S.-W.; Manzoor, R.; Zafar, A.; Inc, M.; Abbagari, S.; Houwe, A. Exact soliton solutions to the Cahn-Allen equation and Predator-Prey model with truncated M-fractional derivative. Results Phys. 2022, 37, 105455. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical investigation of Fractional-Order Korteweg–De-Vries-Type equations under Atangana–Baleanu–Caputo operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar] [CrossRef]
- Hashemi, M.S. A novel approach to find exact solutions of fractional evolution equations with non-singular kernel derivative. Chaos Solitons Fractals 2021, 152, 111367. [Google Scholar] [CrossRef]
- Tajadodi, H. A Numerical approach of fractional advection-diffusion equation with Atangana-Baleanu derivative. Chaos Solitons Fractals 2020, 130, 109527. [Google Scholar] [CrossRef]
- Yusuf, A.; Inc, M.; Aliyu, A.I.; Baleanu, D. Optical solitons possessing beta derivative of the Chen-Lee-Liu equation in optical fibers. Front. Phys. 2019, 7, 00034. [Google Scholar] [CrossRef] [Green Version]
- Khater, M.M.A.; Ghanbari, B.; Nisar, K.S.; Kumar, D. Novel exact solutions of the fractional Bogoyavlensky–Konopelchenko equation involving the Atangana-Baleanu-Riemann derivative. Alex. Eng. J. 2020, 59, 2957–2967. [Google Scholar] [CrossRef]
- Shafiq, M.; Abbas, M.; Abdullah, F.A.; Majeed, A.; Abdeljawad, T.; Alqudah, M.A. Numerical solutions of time fractional Burgers’ equation involving Atangana-Baleanu derivative via cubic B-spline functions. Results Phys. 2022, 34, 105244. [Google Scholar] [CrossRef]
- Sarwar, S. New Rational Solutions of fractional-order Sharma-Tasso-Olever equation with Atangana-Baleanu derivative arising in physical sciences. Results Phys. 2020, 19, 103621. [Google Scholar] [CrossRef]
- Elboree, M.K. Lump solitons, rogue wave solutions and lump-stripe interaction phenomena to an extended (3 + 1)-dimensional KP equation. Chin. J. Phys. 2020, 63, 290–303. [Google Scholar] [CrossRef]
- Mohammed, K. New exact traveling wave solutions of the (3 + 1)-dimensional Kadomtsev-Petviashvili (KP) equation. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1169–1175. [Google Scholar]
- Ma, W.X.; Zhu, Z.N. Solving the (3 + 1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl. Math. Comput. 2012, 218, 11871–11879. [Google Scholar] [CrossRef]
- Hussain, A.; Anjum, A.; Junaid-U-Rehman, M.; Khan, I.; Sameh, M.A.; Al-Johani, A.S. Symmetries, optimal system, exact and soliton solutions of (3 + 1)-dimensional Gardner-KP equation. J. Ocean. Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Hao, X.Z.; Liu, Y.P.; Li, Z.B.; Ma, W.X. Painlevé analysis, soliton solutions and lump-type solutions of the (3 + 1)-dimensional generalized KP equation. Comput. Math. Appl. 2019, 77, 724–730. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple-soliton solutions for a (3 + 1)-dimensional generalized KP equation. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 491–495. [Google Scholar] [CrossRef]
- Elboree, M.K. Soliton molecules and exp(−Φ(ζ)) expansion method for the new (3 + 1)-dimensional kadomtsev-Petviashvili (KP) equation. Chin. J. Phys. 2021, 71, 623–633. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; El-Tantawy, S.A. A new (3 + 1)-dimensional generalized Kadomtsev–Petviashvili equation. Nonlinear Dyn. 2016, 84, 1107–1112. [Google Scholar] [CrossRef]
- Hong, B.J. New Jacobi elliptic functions solutions for the variable-coeffiffifficient mKdV equation. Appl. Math. Comput. 2009, 215, 2908–2913. [Google Scholar]
- Hong, B.J. New exact Jacobi elliptic functions solutions for the generalized coupled Hirota-Satsuma KdV system. Appl. Math. Comput. 2010, 217, 472–479. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, B.; Wang, J. Exact Solutions for the Generalized Atangana-Baleanu-Riemann Fractional (3 + 1)-Dimensional Kadomtsev–Petviashvili Equation. Symmetry 2023, 15, 3. https://doi.org/10.3390/sym15010003
Hong B, Wang J. Exact Solutions for the Generalized Atangana-Baleanu-Riemann Fractional (3 + 1)-Dimensional Kadomtsev–Petviashvili Equation. Symmetry. 2023; 15(1):3. https://doi.org/10.3390/sym15010003
Chicago/Turabian StyleHong, Baojian, and Jinghan Wang. 2023. "Exact Solutions for the Generalized Atangana-Baleanu-Riemann Fractional (3 + 1)-Dimensional Kadomtsev–Petviashvili Equation" Symmetry 15, no. 1: 3. https://doi.org/10.3390/sym15010003





