New Analytical Solutions for Coupled Stochastic Korteweg–de Vries Equations via Generalized Derivatives
Abstract
:1. Introduction
2. Preliminaries
3. An Algorithm for Solving Conformable SPDEs
4. Applications to the Stochastic CNKdV
4.1. Deterministic Solutions of Equation (17)
4.2. Stochastic Solutions of Equation (17)
4.3. Stochastic Wave Solutions of a Periodic Kind
4.4. Stochastic Wave Solutions of a Soliton Kind
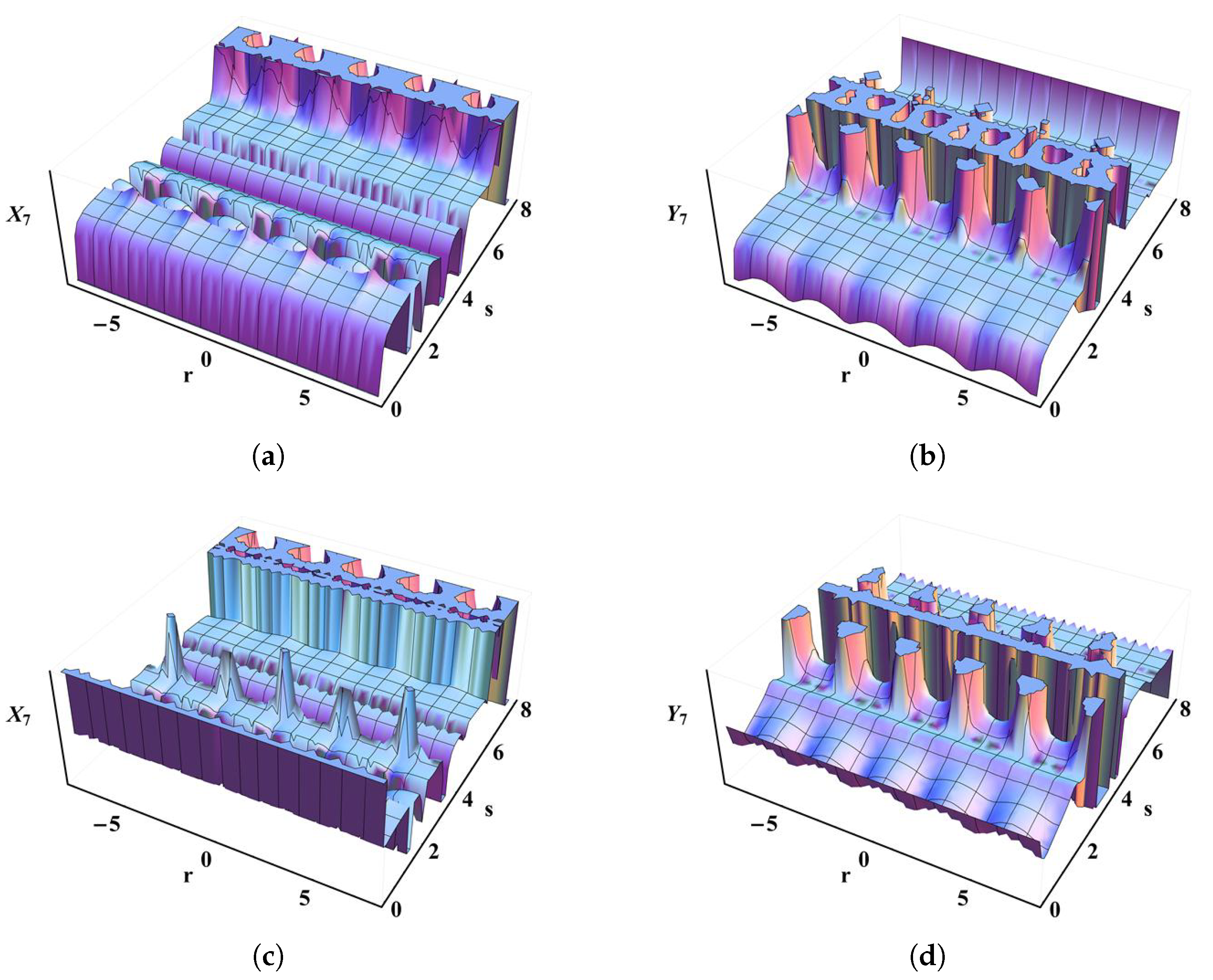
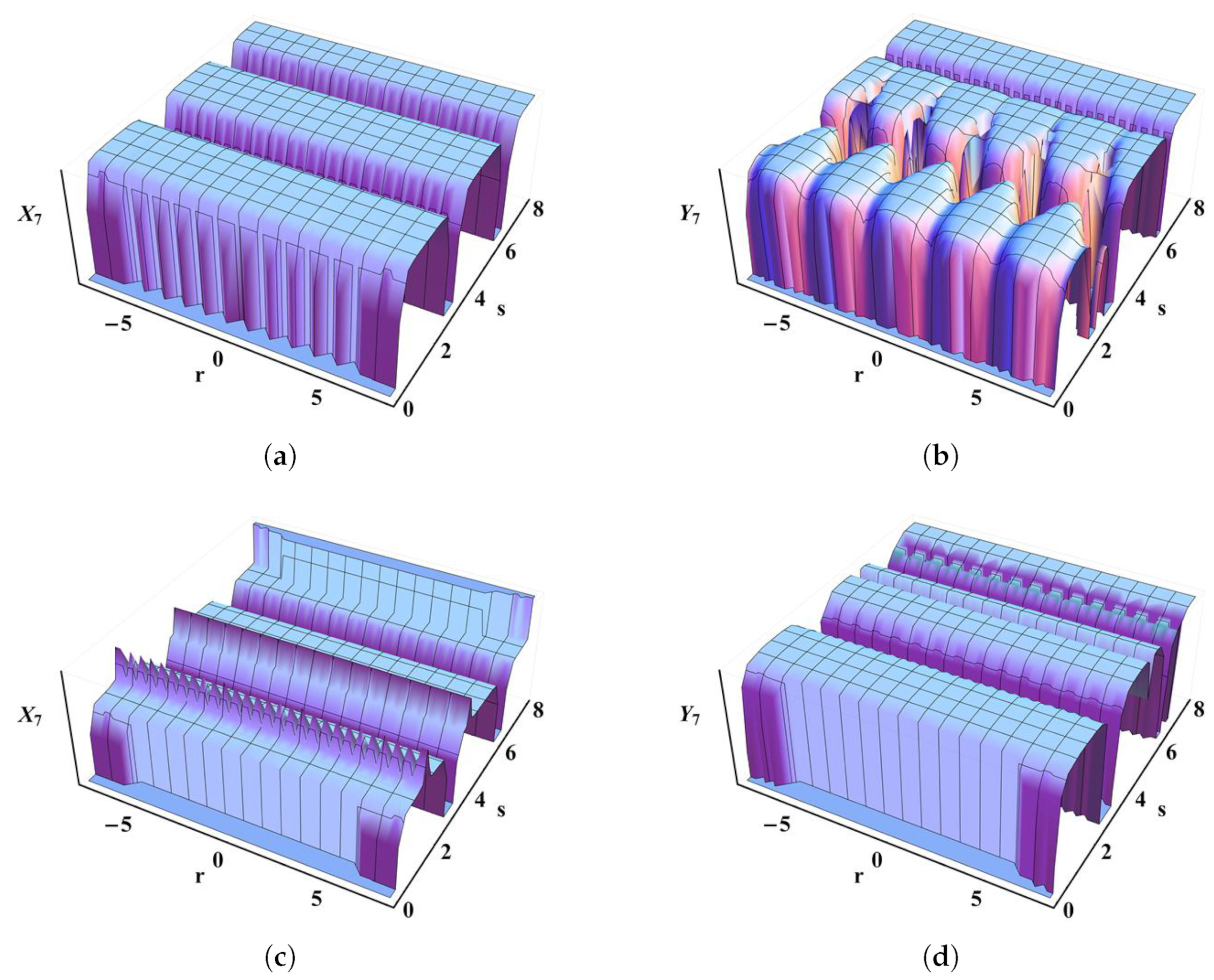
5. Graphical Interpretation and Ultimate Remarks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Abdelsalam, S.I. Editorial: Recent Trends in Computational Fluid Dynamics. Front. Phys. 2020, 8, 593111. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Sohaly, M.A.; Alharbi, A. The new exact solutions for the deterministic and stochastic(2+1)-dimensional equations in natural sciences. J. Taibah Univ. Sci. 2019, 13, 834–843. [Google Scholar] [CrossRef]
- Korpinar, Z.; Inc, M.; Bayram, M. Theory and application for the system of fractional Burger equations with Mittag leffler kernel. Appl. Math. Comp. 2020, 367, 124781. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The Size-Dependent Thermoelastic Vibrations of Nanobeams Subjected to Harmonic Excitation and Rectified Sine Wave Heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equation; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Anastassiou, G.A. Generalized Fractional Calculus: New Advancements and Applications; Springer: Cham, Swiztherland, 2021. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Zhao, D.; Luo, M. General conformable fractional derivative and its physical interpretation. Calcolo 2017, 54, 903–917. [Google Scholar] [CrossRef]
- Zhao, D.; Pan, X.; Luo, M. A new framework for multivariate general conformable fractional calculus and potential applications. Phys. A 2018, 510, 271–280. [Google Scholar] [CrossRef]
- Hyder, A.; Soliman, A.H. A new generalized θ-conformable calculus and its applications in mathematical physics. Phys. Scr. 2020, 96, 015208. [Google Scholar] [CrossRef]
- Hereman, W. Shallow Water Waves and Solitary Waves. In Mathematics of Complexity and Dynamical Systems; Meyers, R.G., Ed.; Springer: New York, NY, USA, 2012; pp. 1520–1532. [Google Scholar]
- Khismatullin, D.B.; Akhatov, I.S. Sound-ultrasound interaction in bubbly fluids: Theory and possible applications. Phys. Fluids 2001, 13, 3582–3598. [Google Scholar] [CrossRef]
- Crighton, D.G. Applications of KdV. In KdV ’95; Hazewinkel, M., Capel, H.W., de Jager, E.M., Eds.; Springer: Dordrecht, The Netherlands, 1995; pp. 39–67. [Google Scholar]
- Dodd, R.K.; Eilbeck, J.C.; Gibbon, J.D.; Morris, H.C. Solitons and Nonlinear Wave Equations; MR 696935; Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers]: London, UK; New York, NY, USA, 1982. [Google Scholar]
- Drazin, P.G.; Johnson, R.S. Solitons: An introduction, Cambridge Texts in Applied Mathematics; MR 985322; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Newell, A.C. Solitons in Mathematics and Physics; CBMS-NSF Regional Conference Series in Applied Mathematics, MR 847245; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1985; Volume 48. [Google Scholar]
- Wazwaz, A. A two-mode modified KdV equation with multiple soliton solutions. Appl. Math. Lett. 2017, 70, 1–6. [Google Scholar] [CrossRef]
- Korsunsky, S.V. Soliton solutions for a second-order KdV equation. Phys. Lett. A 1994, 185, 174–176. [Google Scholar] [CrossRef]
- Hirota, R.; Satsuma, J. Soliton solutions of a coupled Korteweg-de Vries equation. Phys. Lett. A 1981, 85, 407–408. [Google Scholar] [CrossRef]
- Bouard, A.; Debussche, A. On the Stochastic Korteweg–de Vries Equation. J. Funct. Anal. 1998, 154, 215–251. [Google Scholar] [CrossRef]
- Hyder, A.; Barakat, M.A. General improved Kudryashov method for exact solutions of nonlinear evolution equations in mathematical physics. Phys. Scr. 2020, 95, 045212. [Google Scholar] [CrossRef]
- Hyder, A. White noise theory and general improved Kudryashov method for stochastic nonlinear evolution equations with conformable derivatives. Adv. Differ. Equ. 2020, 2020, 236. [Google Scholar] [CrossRef]
- Hyder, A.; Soliman, A.H. An extended Kudryashov technique for solving stochastic nonlinear models with generalized conformable derivatives. Commun. Nonlinear Sci. Numer. Simul. 2021, 97, 105730. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H. A generalized F-expansion method to find abundant families of Jacobi elliptic function solutions of the (2+1)-dimensional Nizhnik-Novikov-Veselov equation. Chaos Solitons Fract. 2006, 27, 959–979. [Google Scholar] [CrossRef]
- Dai, C.; Zhang, J. Jacobian elliptic function method for nonlinear differential difference equations. Chaos Solitons Fractals 2006, 27, 1042–1049. [Google Scholar] [CrossRef]
- Fan, E.; Zhang, J. Applications of the Jacobi elliptic function method to special-type nonlinear equations. Phys. Lett. A 2002, 305, 383–392. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, J.; Li, X. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolutions equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Özkan, E.M.; Özkan, A. On exact solutions of some important nonlinear conformable time-fractional differential equations. SeMA J. 2022, 1–16. [Google Scholar] [CrossRef]
- Behera, S.; Aljahdaly, N.H.; Virdi, J.P.S. On the modified (G′/G2)-expansion method for finding some analytical solutions of the traveling waves. J. Ocean Eng. Sci. 2022, 7, 313–320. [Google Scholar] [CrossRef]
- Ferdous, F.; Hafez, M.; Biswas, A.; Ekicid, M.; Zhoue, Q.; Alfirasf, M.; Moshokoac, S.P.; Belic, M. Oblique resonant optical solitons with Kerr and parabolic law nonlinearities and fractional temporal evolution by generalized exp(ϕ(ξ))-expansion. Optik 2019, 178, 439–448. [Google Scholar] [CrossRef]
- Ferdous, F.; Hafez, M. Nonlinear time fractional Kortewegde Vries equations for the interaction of wave phenomena in fluid-filled elastic tubes. Eur. Phys. J. Plus 2018, 133, 384. [Google Scholar] [CrossRef]
- Ferdous, F.; Hafez, M. Oblique closed form solutions of some important fractional evolution equations via the modified Kudryashov method arising in physical problems. J. Ocean Eng. Sci. 2018, 3, 244–252. [Google Scholar] [CrossRef]
- Akkurt, A.; Yildirim, M.E.; Yildirim, H. A new generalized fractional derivative and integral Konuralp. Konuralp J. Math. 2017, 5, 248–259. [Google Scholar]
- Aljahdaly, N.H. Some applications of the modified (G′/G2)-expansion method in mathematical physics. Results Phys. 2019, 13, 102272. [Google Scholar] [CrossRef]
- Das, P.K. New multi–hump exact solitons of a coupled Korteweg–de–Vries system with conformable derivative describing shallow water waves via RCAM. Phys. Scr. 2020, 95, 105212. [Google Scholar] [CrossRef]
- Grimshaw, R. Coupled Korteweg–de Vries equations. In Without Bounds: A Scientific Canvas of Nonlinearity and Complex Dynamics; Springer: Heidelberg, Germany, 2013; pp. 317–333. [Google Scholar]
- Holden, H.; sendal, B.; Ubøe, J.; Zhang, T. Stochastic Partial Differential Equations; Springer Science Media, LLC: New York, NY, USA, 2010. [Google Scholar]
- Allen, J.E.; Frantzeskakis, D.J.; Karachalios, N.I.; Kevrekidis, P.G.; Koukouloyannis, V. Solitary and periodic waves in collisionless plasmas: The Adlam-Allen model revisited. Phys. Rev. E 2020, 102, 013209. [Google Scholar] [CrossRef]
- Churilov, A.N. Orbital stability of periodic solutions of an impulsive system with a linear continuous-time part. AIMS Math. 2020, 5, 96–110. [Google Scholar] [CrossRef]
- Vidal-Henriquez, E.; Zykov, V.; Bodenschatz, E.; Gholami, A. Convective instability and boundary driven oscillations in a reaction-diffusion-advection model. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 103110. [Google Scholar] [CrossRef] [PubMed]
- Melchert, O.; Demircan, A.; Yulin, A. Multi-frequency radiation of dissipative solitons in optical fiber cavities. Sci. Rep. 2020, 10, 8849. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Yang, K.; Gu, H.; Guan, F.; Kara, A.H. A (2+1)-dimensional sine-Gordon and sinh-Gordon equations with symmetries and kink wave solutions. Nucl. Phys. B 2020, 953, 114956. [Google Scholar] [CrossRef]
- Xie, Y. Exact solutions for Wick-type stochastic coupled KdV equations. Phys. Lett. A 2004, 327, 174–179. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyder, A.-A.; Barakat, M.A.; Soliman, A.H.; Almoneef, A.A.; Cesarano, C. New Analytical Solutions for Coupled Stochastic Korteweg–de Vries Equations via Generalized Derivatives. Symmetry 2022, 14, 1770. https://doi.org/10.3390/sym14091770
Hyder A-A, Barakat MA, Soliman AH, Almoneef AA, Cesarano C. New Analytical Solutions for Coupled Stochastic Korteweg–de Vries Equations via Generalized Derivatives. Symmetry. 2022; 14(9):1770. https://doi.org/10.3390/sym14091770
Chicago/Turabian StyleHyder, Abd-Allah, Mohamed A. Barakat, Ahmed H. Soliman, Areej A. Almoneef, and Clemente Cesarano. 2022. "New Analytical Solutions for Coupled Stochastic Korteweg–de Vries Equations via Generalized Derivatives" Symmetry 14, no. 9: 1770. https://doi.org/10.3390/sym14091770