Multiplicative Brownian Motion Stabilizes the Exact Stochastic Solutions of the Davey–Stewartson Equations
Abstract
:1. Introduction
2. Wave Equation for SDSEs
3. The Analytical Solutions of the SDSEs
3.1. Method Description
| Case | ||||
|---|---|---|---|---|
| 1 | 1 | |||
| 2 | 2 | |||
| 3 | 2 | |||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | 2 | 0 | 0 | |
| 13 | 0 | 1 | 0 |
3.2. Solutions of SDSEs
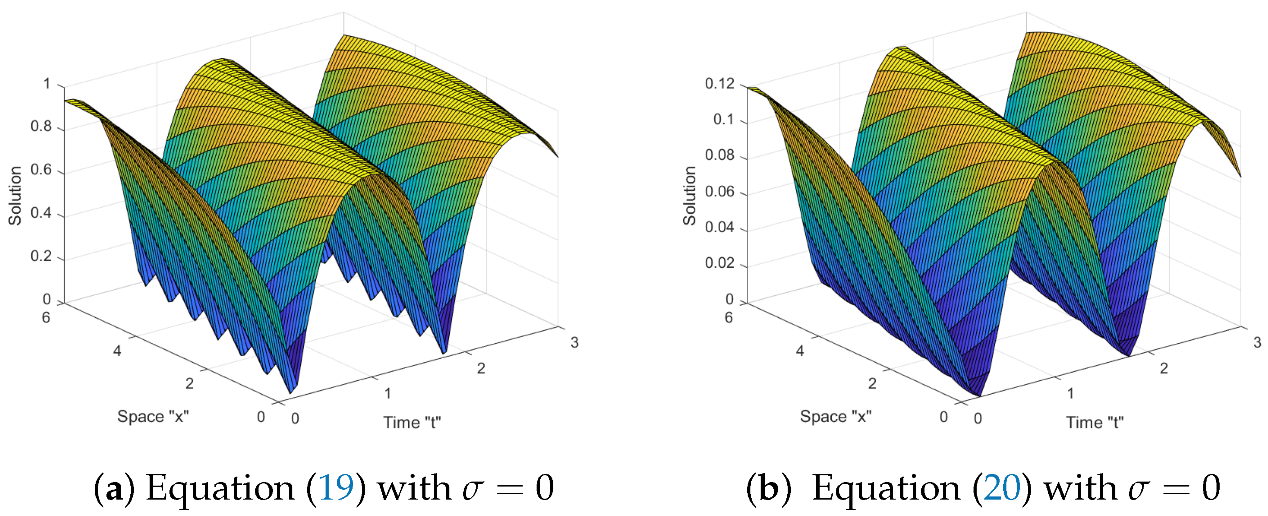
4. The Impact of Noise on the SDSE Solutions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wazwaz, A.M. The tanh method: Exact solutions of the Sine–Gordon and Sinh–Gordon equations. Appl. Math. Comput. 2005, 167, 1196–1210. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Alshammari, M.; Cesarano, C.; El-Morshedy, M. Brownian Motion Effects on the Stabilization of Stochastic Solutions to Fractional Diffusion Equations with Polynomials. Mathematics 2022, 10, 1458. [Google Scholar] [CrossRef]
- Al-Askar, E.M.; Mohammed, W.W.; Albalahi, A.M.; El-Morshedy, M. The Impact of the Wiener process on the analytical solutions of the stochastic (2+1)-dimensional breaking soliton equation by using tanh–coth method. Mathematics 2022, 10, 817. [Google Scholar] [CrossRef]
- Zaman, U.H.M.; Arefin, M.A.; Akbar, M.A.; Uddin, M.H. Analytical behavior of soliton solutions to the couple type fractional-order nonlinear evolution equations utilizing a novel technique. Alex. Eng. J. 2022, 61, 11947–11958. [Google Scholar] [CrossRef]
- Khatun, M.A.; Arefin, M.A.; Islam, M.Z.; Akbar, M.A.; Uddin, M.H. New dynamical soliton propagation of fractional type couple modified equal-width and Boussinesq equations. Alex. Eng. J. 2022, 61, 9949–9963. [Google Scholar] [CrossRef]
- Wazwaz, A.M. An analytic study of compactons structures in a class of nonlinear dispersive equations. Math. Comput. Simul. 2003, 63, 35–44. [Google Scholar] [CrossRef]
- Wen-Xiu, M.; Sumayah, B. A binary darboux transformation for multicomponent NLS equations and their reductions. Anal. Math. Phys. 2021, 11, 44. [Google Scholar]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fract. 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Fan, E.; Zhang, J. Applications of the Jacobi elliptic function method to special-type nonlinear equations. Phys. Lett. A 2002, 305, 383–392. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Yan, C. A simple transformation for nonlinear waves. Phys. Lett. A 1996, 224, 77–84. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The (G’/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Zhang, H. New application of the (G’/G)-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(−(ς))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Mohammed, W.W.; Blömker, D. Fast-Diffusion Limit with Large Noise for Systems of Stochastic Reaction-Diffusion Equations. Stoch. Anal. Appl. 2016, 34, 961–978. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, W.W.; Blömker, D. Fast-diffusion limit for reaction-diffusion equations with multiplicative noise. J. Math. Anal. Appl. 2021, 496, 124808. [Google Scholar] [CrossRef]
- Elbrolosy, M.E.; Elmandouh, A.A. Dynamical behaviour of nondissipative double dispersive microstrain wave in the microstructured solids. Eur. Phys. J. 2021, 136, 955. [Google Scholar] [CrossRef]
- Elmandouha, A.A.; Ibrahim, A.G. Bifurcation and travelling wave solutions for a (2+1)-dimensional KdV equation. J. Taibah Univ. Sci. 2020, 14, 139–147. [Google Scholar] [CrossRef] [Green Version]
- Elmandouha, A.A. Bifurcation and new traveling wave solutions for the 2D Ginzburg–Landau equation. Eur. Phys. Plus 2020, 135, 1–13. [Google Scholar]
- Elbrolosy, M.E.; Elmandouh, A.A. Construction of new traveling wave solutions for the (2+1) dimensional extended kadomtsev-petviashvili equation. J. Appl. Anal. Comput. 2022, 12, 533–550. [Google Scholar] [CrossRef]
- Elmandouh, A.A.; Elbrolosy, M.E. New traveling wave solutions for Gilson–Pickering equation in plasma via bifurcation analysis and direct method. Math. Methods Appl. Sci. 2022, accepted. [Google Scholar] [CrossRef]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Diff. Equa. 2015, 1, 117–133. [Google Scholar] [CrossRef]
- Filiz, A.; Ekici, M. Sonmezoglu A. F-expansion method and new exact solutions of the Schrödinger-KdV equation. Sci. World J. 2014, 2014, 14. [Google Scholar] [CrossRef] [Green Version]
- Arnold, L. Random Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Weinan, E.; Li, X.; Vanden-Eijnden, E. Some recent progress in multiscale modeling. In Multiscale Modeling and Simulation; Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2004; Volume 39, pp. 3–21. [Google Scholar]
- Mohammed, W.W. Amplitude equation with quintic nonlinearities for the generalized Swift-Hohenberg equation with additive degenerate noise. Adv. Differ. Equ. 2016, 2016, 84. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, W.W.; Iqbal, N.; Botmart, T. Additive noise effects on the stabilization of fractional-space diffusion equation solutions. Mathematics 2020, 10, 130. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: New York, NY, USA, 1995. [Google Scholar]
- Davey, A.; Stewartson, K. On three-dimensional packets of surface waves. Proc. Royal. Soc. Lond. Ser. A 1974, 338, 101–110. [Google Scholar]
- Bhrawy, A.H.; Abdelkawy, M.A.; Biswas, A. Cnoidal and snoidal wave solutions to coupled nonlinear wave equations by the extended Jacobi’s elliptic function method. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 915–925. [Google Scholar] [CrossRef]
- Jafari, H.; Sooraki, A.; Talebi, Y.; Biswas, A. The first integral method and traveling wave solutions to Davey–Stewartson equation. Nonlinear Anal. Model. Control 2012, 17, 182–193. [Google Scholar] [CrossRef] [Green Version]
- Mirzazadeh, M. Soliton solutions of Davey–Stewartson equation by trial equation method and ansatz approach. Nonlinear Dyn. 2015, 82, 1775–1780. [Google Scholar] [CrossRef]
- El Achab, A. Constructing new wave solutions to the (2+1)-dimensional Davey–Stewartson equation (DSE) which arises in fluid dynamics. JMST Adv. 2019, 1, 227–232. [Google Scholar] [CrossRef] [Green Version]
- Fu, H.M.; Dai, Z.D. Double exp-function method and application. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 927–933. [Google Scholar] [CrossRef]
- Abdelaziz, M.A.M.; Moussa, A.E.; Alrahal, D.M. Exact Solutions for the nonlinear (2+1)-dimensional Davey-Stewartson equation using the generalized (G’/G)-expansion method. J. Math. Res. 2014, 6, 91–99. [Google Scholar] [CrossRef] [Green Version]
- Ebadi, G.; Biswas, A. The (G’/G) method and 1-soliton solution of the Davey–Stewartson equation. Math. Comput. Model. 2011, 53, 694–698. [Google Scholar] [CrossRef]
- Zedan, H.A.; Monaquel, S.J. The sine-cosine method for the Davey-Stewartson equations. Appl. Math. E-Notes 2010, 10, 103–111. [Google Scholar]
- Peng, Y.Z. Exact solutions for some nonlinear partial differential equations. Phys. Lett. A 2003, 314, 401–408. [Google Scholar] [CrossRef]
- Caraballo, T.; Langa, J.A.; Valero, J. Stabilisation of differential inclusions and PDEs without uniqueness by noise. Commun. Pure Appl. Anal. 2008, 7, 1375–1392. [Google Scholar] [CrossRef]
- Caraballo, T.; Robinson, J.C. Stabilisation of linear PDEs by Stratonovich noise. Syst. Control. Lett. 2004, 53, 41–50. [Google Scholar] [CrossRef] [Green Version]
- Mackey, M.C.; Longtin, A.; Lasota, A. Noise-induced global asymptotic stability. J. Stat. Phys. 1990, 60, 735–751. [Google Scholar] [CrossRef]
- Blömker, D.; Fu, H. The impact of multiplicative noise in SPDEs close to bifurcation via amplitude equations. Nonlinearity 2020, 33, 3905. [Google Scholar] [CrossRef]
- Caraballo, T.; Kloeden, P.E. Stabilization of evolution equations by noise. Interdiscip. Math. Sci. 2009, 8, 43–66. [Google Scholar]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Multiplicative Brownian Motion Stabilizes the Exact Stochastic Solutions of the Davey–Stewartson Equations. Symmetry 2022, 14, 2176. https://doi.org/10.3390/sym14102176
Al-Askar FM, Cesarano C, Mohammed WW. Multiplicative Brownian Motion Stabilizes the Exact Stochastic Solutions of the Davey–Stewartson Equations. Symmetry. 2022; 14(10):2176. https://doi.org/10.3390/sym14102176
Chicago/Turabian StyleAl-Askar, Farah M., Clemente Cesarano, and Wael W. Mohammed. 2022. "Multiplicative Brownian Motion Stabilizes the Exact Stochastic Solutions of the Davey–Stewartson Equations" Symmetry 14, no. 10: 2176. https://doi.org/10.3390/sym14102176