Study on a Surrounding Rock Pressure Calculation Method for Super-Large Section Highway Tunnels

Abstract

This paper presents new correlations for estimating the surrounding rock pressure of symmetrically shaped tunnels based on a symmetrical numerical model. Surrounding rock pressure is defined as the load acting on the support structure due to the deformation of the surrounding rock after tunnel excavation. Surrounding rock pressure is directly related to the selection of the lining structure and the determination of support parameters. The main challenge in designing and proceeding with the construction process is choosing a calculation method for the surrounding rock pressure for super-large sections, and this has been the focus of research among the tunnel research community. The excavation area of Liantang tunnel of Shenzhen Eastern Transit Expressway (China) is over 400 m², making it the largest highway tunnel in the world so far. Based on this project, this paper analyses the applicability of various traditional methods of calculating the surrounding rock pressure for super-large section tunnels. In addition, based on the Tunneling Quality Index (Q), the factor of span is introduced into the method of calculating the surrounding rock pressure using the numerical simulation results of super-large symmetrical tunnels with different values of Q and different spans. Additionally, calculated correlations that could quickly estimate the surrounding rock pressure of tunnels are obtained. The comparison of surrounding rock pressures between the estimated and monitoring results of Liantang tunnel and more than 30 projects around the world effectively proves the rationality and universal applicability of the proposed correlations. This method could provide engineers and designers with a quick way to predict the surrounding rock pressure of deep super-large section underground structures during their design and construction stage.

1. Introduction

With the rapid development of the economy, logistics and automobile industry, the traffic flow and comfort standards of highway traffic are significantly improving. Traditional two-lane and three-lane highway tunnels struggle to meet the needs of modern traffic development.

According to the standard recommended by Japan Tunnel Association [1], the tunnel sections can be defined in accordance with

Table 1. Classification standard of tunnel sections.

Section Size	Excavation Area/m2	Remark
Standard section	70~80	Two-lane highway tunnel
Large section	100~140	Two-lane highway tunnel with crosswalk
Super-large section	> 140	Highway tunnels with three or more lanes

, which means the standard two-lane tunnel section is less than 100 m² and the super-large section tunnel is over 140 m². According to some statistics, up till now, there are 51 highway tunnels with a maximum area of more than 200 m² excavated by drilling and blasting methods in China and abroad. The construction situation of some super-large section tunnels is shown in

Table 2. Construction situation of super-large section tunnels.

Tunnel	Span/m	Tunnel Height/m	Height-Span Ratio	Excavation Area/m2	Tunnel Type	Completion Time
Qingdao Jiaozhou Bay	28.3	18.64	0.66	411.9	Branch	June 2011
Dalian Hanjialing	21.2	15.52	0.731	230	Single Four-lane	April 2003
Guangzhou Longtoushan	24.5	13.56	0.63	230	Twin Eight-lane	October 2008
Shenzhen Henglongshan	29.2	-	-	304	Branch	October 2008
Shenzhen Yabao	20.9	13.48	0.645	220	Twin Eight-lane	January 2007
Fuzhou Jinjishan	41.4	13.2	-	171 × 2	Twin-arch	May 2009
Sang-Lim, Korea	18.77	10.48	0.56	170	Single Four-lane	2005
Dongming, Japan	16.53	8.4	0.51	170~200	Single Three-lane	1989
Toshikazu, Japan	20	13.5	0.67	225	Water diversion	1989
The Channel, Europe	21.2	15.4	0.73	252	-	-
Second, Japan	24	-	-	240	-	-
Kobylish Metro, Czech	20.35	13.75	0.68	220	Single	2006

.

Due to the peculiar nature of super-large section structural design and irregular design shape, the mechanical characteristics of surrounding rock are difficult to predict. Furthermore, due to the large section and low flat ratio of tunnels, the self-bearing capacity of surrounding rock cannot be fully utilized, and safety accidents such as block falls and collapses can occur during construction. Therefore, super-large sections are very complex in terms of structural design and technological challenges for its construction. There are still many key technical problems to be solved in this field. Among them, the mode of action and the calculation method of surrounding rock pressure for super-large sections are the key to solving other technical problems and have been researched a lot by the academic and engineering communities in recent years, using numerical simulations, theoretical analysis, on-site monitoring and other ways.

Yan et al. [2] analyzed and discussed the influence of stress path on surrounding rock pressure of super-large section tunnels by introducing a process load influence coefficient and combining it with numerical results. Liu et al. [3] discussed the vertical distribution characteristics of surrounding rock pressure of large-span highway tunnel in combination with the experimental values of surrounding rock pressure of Longtoushan large-span tunnel in Guangzhou (China). The authors also considered the effect of double-sided tunnel construction method on the release of vertical surrounding rock pressure. Based on the summarized types and main influencing factors of tunnel surrounding rock pressure, Li et al. [4] studied the distribution characteristics of tunnel surrounding rock pressure and its relationship with surrounding rock grade and tunnel burial depth through statistical analysis of surrounding rock pressure of 91 monitoring sections of 44 tunnels. The authors also studied the basic law of rock pressure time-history and put forward three stages including rapid growth, slowly growth, settle out. Based on the monitoring and measurement of surrounding rock and supporting structure during the construction of a large-span and high-sidewall underground cavern, Zhao et al. [5] analyzed the applicability of various numerical techniques to the calculation of surrounding rock pressure of the underground cavern, and summarized some suitable numerical methods for surrounding rock pressure of large-span and high-sidewall deep-buried cavern in hard stratum. Jiang et al. [6] discussed the applicability and unification of various pressure correlations relying on large-span tunnels. Jiang [7], Wang [8], Jiang [9] have conducted a lot of research on the surrounding rock pressure and the stability of large-scale underground hydropower stations using numerical simulations and on-site monitoring. Chee-nan [10] investigated the development of ground arching using stress redistribution during tunneling and established a three-dimensional numerical model of the tunnel to gain more insight into the adjustment of tunneling stress. They also proposed a method to determine the area of pressure arch above the tunnel and concluded that the stress adjustment above the tunnel roof during the tunneling process increases significantly for the lateral earth pressure coefficient (K > 1.5). Regarding the distance from the inflection point of tangential stress above the arch top to the arch top as an indirect index, which is used to evaluate the stability of surrounding rock in tunnel excavations, Kong [11] analyzed the influence of Geological Strength Index (GSI from 20 to 80), the overburden depth (H from 40 m to 420 m), in-situ stress ratio (k₀ from 0.8 to 3) and excavation roof rise-to-span ratio on the surrounding rock pressure. Based on the block theory, Prasad et al. [12] proposed a calculation method for surrounding rock pressure. Scussel et al. [13] proposed a new approach to obtain tunnel support pressure for polyaxial state of stress. The proposed method incorporates the intermediate principal stress in the analysis and has a wide applicability to many available software. These research results provide abundant references for calculating the surrounding rock pressure of large section tunnels. However, due to the complexity of geological conditions and construction processes, studies focusing on the surrounding rock pressure of super-large section highway tunnels with excavation area exceeding 400 m² are scarce in literature.

Based on the Liantang tunnel (China) large-span project of the Shenzhen Eastern Transit Expressway, this paper analyses the applicability of various traditional surrounding rock pressure calculation methods in super-large section tunnels. By comparing and analyzing the numerical simulation results of super-large section tunnels under different values of Q and spans, the span term is introduced into the method of calculating surrounding rock pressure based on Q system; Based upon this strategy, a method that can quickly estimate the surrounding rock pressure of tunnels is proposed. A comparison of surrounding rock pressures between estimated and monitored values of more than 30 projects around the world effectively proves the rationality and universal applicability of the correlations. This method can not only provide calculation basis for engineering designers and on-site staff, but can also serve as a theoretical reference for researchers in this field.

2. Project Overview

The Shenzhen Eastern Transit Expressway is a key project in Guangdong Province, and consists of a road starting from Luosha road, that connects to the Highway Network of Hong Kong through ports and ends at Huishan Expressway (Figure 1). The project is designed to be a two-way 8-lane road with a total length of 32.5 km and an investment of 5.792 billion yuan. The longest tunnel in the whole line is the Liantang tunnel, with a total length of 1435 m. The Liantang tunnel passes through low mountains and hills with relatively complete topography. The strata mainly consists of Carboniferous metamorphic sandstone and Jurassic rhyolite with well-developed rock fissures and weakened development in the depth direction.

At present, China mainly adopts the Basic Quality Index of Rock Mass ([BQ]) in the “Code for Engineering Rock Mass Quality Classification” [14], while rest of the countries have adopted the Q system. The [BQ] classification system considers that the classification of surrounding rock should be determined by two factors: rock hardness and rock integrity. The corresponding correlation is given by Equation (1):

$$[BQ]=90+3R_c+250K_v$$

(1)

where R_c—Uniaxial compressive strength of rocks; K_ν—Integrity index of the rock mass. The Tunneling Quality Index (Q) system [15] was proposed by the Norwegian scholar Barton to estimate the surrounding rock pressure that can reflect the influence of multiple factors. The corresponding correlation is given by Equation (2):

$$Q=\frac{RQD}{J_n}\times \frac{J_r}{J_a}\times \frac{J_w}{SRF}$$

(2)

where RQD—Rock quality index; J_n—Joint group coefficient; J_r—Joint roughness coefficient; J_a—Joint alteration value; J_w—Water cut reduction coefficient of joints; SRF—Initial stress reduction coefficient. The surrounding rock classification is based on the [BQ] value or the Q value.

Table 3. Relationship between the [BQ] system and the Q system.

Value	Class I (Very Good)	Class II (Good)	Class III (Fair)	Class IV (Poor)	Class V (Very Poor)
[BQ]	>550	451~550	351~450	251~350	<250
Q	>40	10~40	4~10	1~4	<1

[16] shows the simplified relationship between the two systems.

In accordance with the principle that the friction angle of the equivalent of rock mass is equivalent to the deformation modulus, Xu [17] used the correlations of Rock Mass Rating (RMR) system and Q system proposed by Bieniawski [18], and proposed that the improved correlation for conversion between the [BQ] and the Q system (see Equation (3)):

$$[BQ]=150\ln \frac{15+0.24(9\ln Q+44)}{5.7-0.06(9\ln Q+44)}$$

(3)

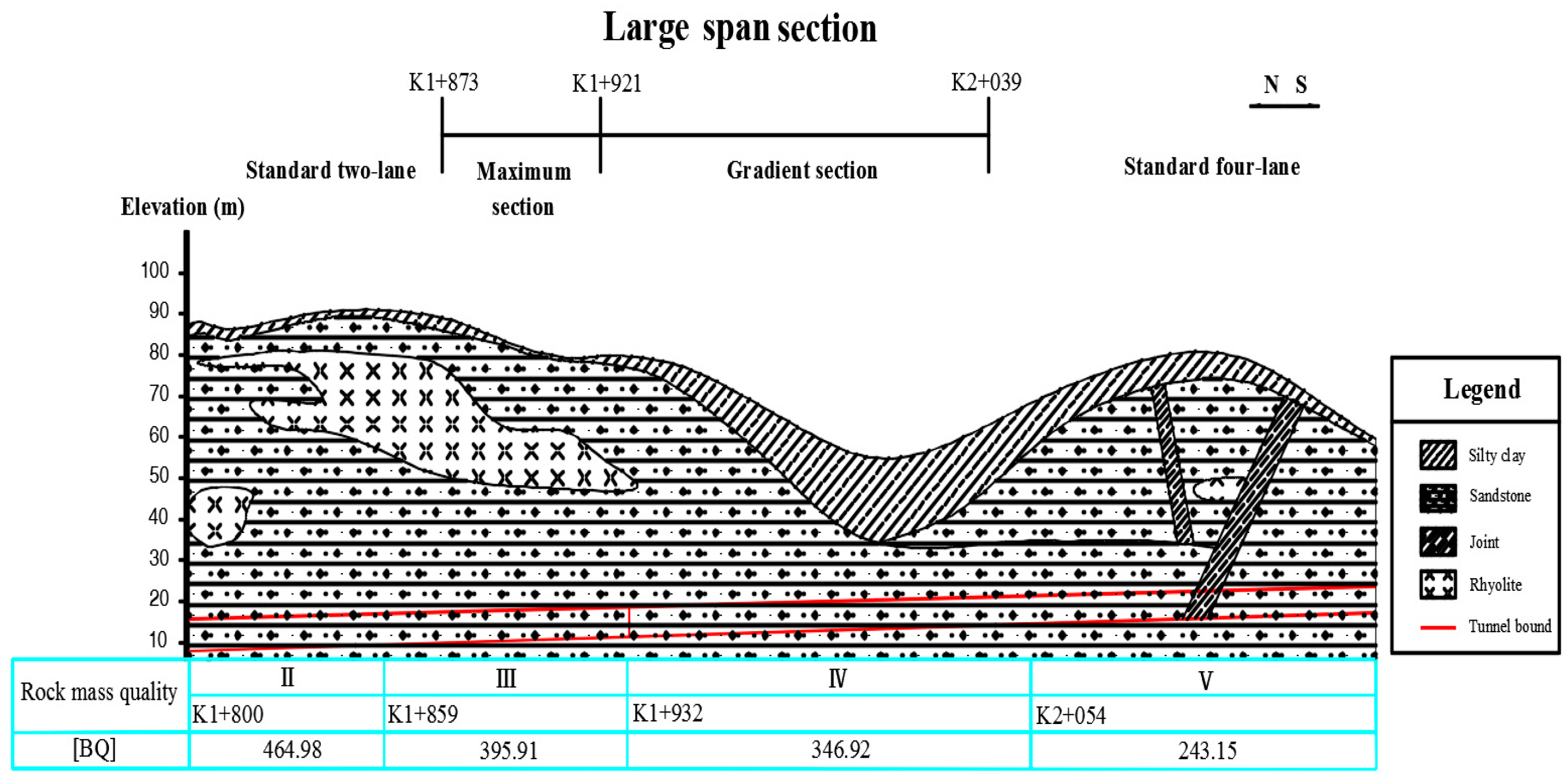
The tunnel consists of medium and slightly-weathered rocks, and the surrounding rock level is Class II–V, which have satisfactory stability. The entrance and exit mainly consist of strong-weathered rock with the V level of surrounding rock, which has a poor stability of excavation with high risk to collapse. Figure 2 shows some parts of the geological sections.

Table 4. Index conversion for Liantang tunnel.

Number	Section Size	Value of [BQ]	Value of Q	Evaluation of Q	Classification of Surrounding Rock
1	Standard two-lane	464.98	19.97	Good	II
2	Maximum section	395.91	5.92	Fair	III
3	Gradient section	395.91	5.92	Fair	III
4	Gradient section	346.92	2.02	Poor	IV
5	Standard four-lane	346.92	2.02	Poor	IV
6	Standard four-lane	243.15	0.86	Very poor	V

shows results of Liantang tunnel with [BQ] indicators converted to the values of corresponding Q system.

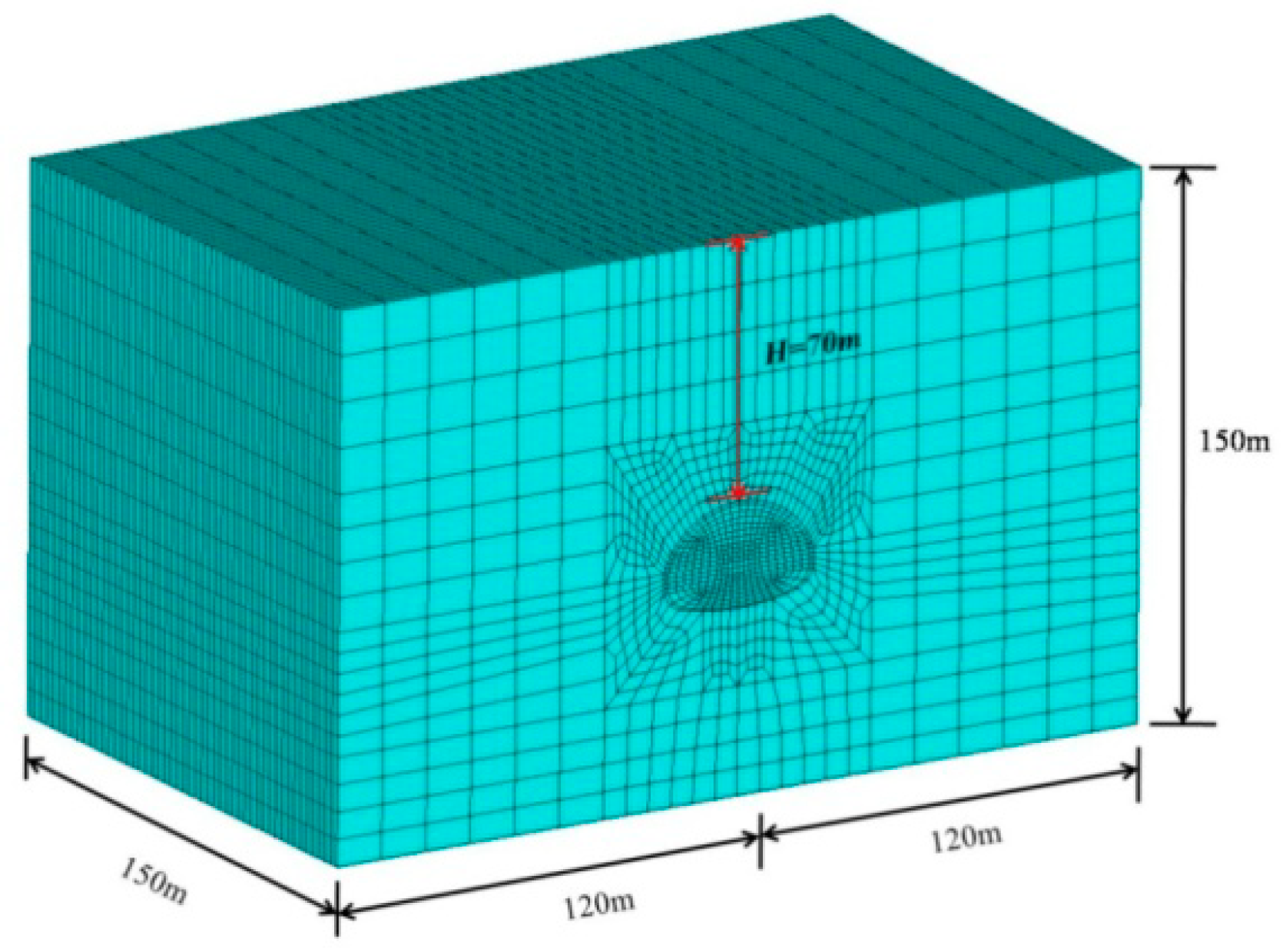
Large-span section of Liantang tunnel is located at the intersection of main line section and the municipal section at the entrance of tunnel. The section is at a depth of 70 m, while the maximum profile is 27.45 m × 16 m (width × height). Furthermore, the excavation section of unlined tunnel is 30.01 m ×18.4 m (width × height). The excavation volume is 428.5 m³/m. It is the largest highway tunnel in the world (Figure 3). Since this excavation span is very rare and there are only a few analogous projects, reasonable calculation of the surrounding rock pressure of the super-large section deep-buried underground structure becomes the key to the structural design and safe construction of the Liantang tunnel (China).

3. Applicability Analysis of Various Traditional Methods of Calculating the Surrounding Rock Pressure for Super-Large Section Tunnel

At present, the most commonly used calculation methods for surrounding rock pressure are as follows:

1)

Traditional theories: including Protodyakonov’s theory, Terzaghi theory, and the Caquot correlation.

2)

Industry recommended standards: Code for Design of Railway Tunnel (TB10003-2016), Guidelines for Design of Highway Tunnel (JTG D70-2010) and Specification for design of hydraulic tunnel (DLT_5195-2004).

3)

Surrounding rock pressure correlations based on rock mass classification system: including correlations based on the Q system proposed by Grimstad and Barton [15] and by Bhasin and Grimstad [19]. Geol [20] proposed a correlation based on rock mass number N, while Unal [21] proposed a correlation based on RMR classification system.

3.1. Comparison of the Common-Applied Calculation Methods for Surrounding Rock Pressure

The geometric size of each block in rock mass is very small compared to the whole stratum. Protodyakonov’s theory [22] assumes that the rock mass around the cavern can be regarded as a large bulk mass with no cohesion. Terzaghi theory [23] assumes that the rock mass is granular with a certain amount of cohesion. According to the statistical results for the loosening range of surrounding rock as reflected by the collapse data of 1046 tunnels presented in the Code for Design of Railway Tunnel of China [14], an empirical correlation for estimating the surrounding rock’s loosening pressure is obtained. The Caquot correlation [24] is based on a circular-sized cavern with the assumption that the plastic zone is separated from the elastic zone and that the surrounding rock pressure is the gravity of rock mass in the plastic zone. Grimstad and Barton [15] used statistical data for the surrounding rock pressure of hundreds of tunnels and put forward a correlation for surrounding rock pressure based on the Q system. Bhasin and Grimstad [19] improved the correlations proposed by the former. Geol put forward the concept of rock mass number N and proposed the correlation of surrounding rock pressure. Unal proposed a correlation for calculating the surrounding rock pressure based on the RMR and different spans. These correlations are summarized in

Table 5. Different correlations for calculating surrounding rock pressure.

Number	Correlation	Proposer
1	$P=\gamma h_1$	Protodyakonov [22]
2	$P=\frac{\gamma d_1-c}{\lambda \tan \phi }$, $d_1=0.5d+h\tan ({45}^{°}-0.5\phi )$	Karl Terzaghi [23]
3	$P=\gamma h^{*}$, $h^{*}=h\left\{0.45\times 2^{s-1}\times \left[1+i\left(B-5\right)\right]\right\}$	TB10003-2016 of China [14]
4	$P=k_1\gamma r-k_{2}c$	Caquot [24]
5	$P_1=\left(\frac{200}{J_r}\right)Q^{-\frac{1}{3}}$, $P_2=\frac{200J_n^{\frac{1}{2}}{Q}^{-\frac{1}{3}}}{3J_r}$	Barton [15]
6	$P=\left(\frac{\alpha }{30}\right){10}^{\frac{H^{0.6}{r}^{0.1}}{50N^{0.33}}+3}$	Bhasin and Grimstad [19]
7	$P=\frac{40}{J_r}d{Q}^{-\frac{1}{3}}$	Geol [20]
8	$P=\frac{100-RM{R}_{76}}{100}\rho d$	Unal [21]

.

Notation:

• γ—Rock mass bulk density; h₁ = d₁/f; d₁ = 0.5d + htan(45°–0.5ϕ); d—Tunnel span; h—Tunnel height; ϕ—Internal friction; f—Rigidity coefficient.
• c—Cohesion; λ—Lateral pressure coefficient. The other parameters are the same as above.
• h* = h{0.45×2^s−1×[1+i(B−5)]}; S—Surrounding rock grade; B—Tunnel span; i—Surrounding rock pressure change rate. The other parameters are the same as above.
• k₁ and k₂, calculation coefficients; r—Approximate radius. The other parameters are the same as above.
• $Q=\frac{RQD}{J_n}\times \frac{J_r}{J_a}\times \frac{J_w}{SRF}$; RQD—Rock quality index; J_n—Joint group coefficient; J_r—Joint roughness coefficient; J_a—Joint alteration value; J_w—Water cut reduction coefficient of joints; SRF—Initial stress reduction coefficient. P₁ is the same as P₂ when J_n = 9, P₁ is greater than P₂ when J_n < 9 and P₁ is less than P₂ when J_n > 9.
• $N=\frac{RQD}{J_n}\times \frac{J_r}{J_a}\times J_w$. α is a correction factor, usually 0.5~2.0. The other parameters are the same as above.
• The parameters are the same as in Correlation 5
• RMR₇₆ is the hierarchical value of the RMR system.

3.2. Analysis of Different Surrounding Rock Pressure Calculation Methods for the Large-Span Section of the Liantang Tunnel

According to the core obtained by drilling the large span central mileage K1 + 895, the surrounding rock of the large-span section consists of slightly weathered blue-grey sandstone with developed joints and fissures. Furthermore, the rock mass is fragmented, showing a fragmented mosaic structure. The parameters required for calculating the surrounding rock pressure using different correlations can be obtained through the results of laboratory experiments and the geological survey reports.

Table 6. Calculation parameters.

Item	Q	ρ (kg/m3)	ϕ	c(kPa)	λ	h(m)	d(m)
Value	5.92	2500	45°	700	2	18.4	30
Item	H(m)	Jn	Jr	RMR	k1	k2
Value	0	9	1	60.01	0.249	0.261

shows these calculation parameters.

Table 7. Calculation results.

Correlation Number	1	2	3	4	5	6	7	8
Result/kPa	503.31	194.97	157.52	52.37	155.78	50.20	756	326.10

shows the calculation results of the surrounding rock pressure of the large-span section of Liantang tunnel based on the parameters provided in Table 6. Figure 4 shows the comparison between the calculated results and measured values.

3.3. Influence of Span on the Calculation Methods of Surrounding Rock Pressure

In order to better analyze the effect of span term on different surrounding rock pressure correlations, the geological conditions of Liantang tunnel were used and height-to-span ratio was kept the same as that of single arch and large span (0.6).

As can be seen from Figure 5, the pressure curves of surrounding rock turn to diverge from dense overlap with the increase in span. This indicates that, when the span exceeds a certain value, some of the correlations are no longer applicable. The curves of Correlations 1, 2, 3, 4, 7 and 8 increase in a linear way. The curve from Correlation 6 increases nonlinearly, however the rate of increase decreases gradually. The curve from Correlation 5 does not change with the increase in span, which was due to the introduction of N parameter. Braton believes that the pressure of surrounding rock is only related to the quality of surrounding rock, and not to the span.

4. Study on Surrounding Rock Pressure under Different Spans and Different Q Values

According to the comparison of different correlations for calculating the pressure of surrounding rock, there are two main factors affecting the pressure of surrounding rock. One is the geological condition, while the other is the span of excavation structure. Based on these two factors, a single-arch deep-buried large-span structural model with different Q values and spans is established to simulate the variation of surrounding rock pressure.

4.1. Numerical Model

According to geological exploration reports, in the tunnel crossing area, located in a low mountain foothill area, the tectonic stress is not obvious, and the in-situ stress is mainly gravity stress. The three-dimensional finite element model of Liantang tunnel’s large-span section was established using the ANSYS software. The model in Figure 6 is symmetrical in structure.

The boundary conditions of the model are that the left and right boundaries are constrained horizontally in corresponding directions, the lower boundary is constrained vertically, and the upper one a free surface boundary. The overburden depth H is the vertical distance from the ground to the top of tunnel. The solid elements are used to simulate the surrounding rock and the lining. The total number of elements used for the mesh is 109,400. Some simplifications and assumptions are made as follows: (1) the surrounding rock mass is considered as a homogeneous and elastic-plastic continuum following the Mohr-Coulomb failure criterion and the associated flow rule; (2) the initial in-situ stress is uniformly distributed within the computational domain.

4.2. Selection of Parameters and Calculation Conditions

Based on the geological longitudinal section of the Liantang tunnel and the classification table of the Q system, the Q values are set to be 0.86, 2.02, 5.92 and 19.97 to represent four different geological conditions. Higher the Q value, better are the geological conditions. Other calculation parameters corresponding to different Q values are obtained through geological exploration reports and field tests.

Table 8. Calculation parameters for the rock mass.

Number	Value of Q	E(GPa)	ρ(kg/m3)	ν	ϕ	c (kPa)
1	0.86	1.3	2500	0.3	22	100
2	2.02	3	2500	0.3	33	500
3	5.92	10	2500	0.3	45	700
4	19.97	27	2500	0.3	50	2100

shows the specific results.

The span ranges from 5 to 45 m, with a total of nine spans. This means that a numerical model is established for each span plus 5 m. The models adopt the single-arch and large-span form of Liantang tunnel with a depth of 70 m and a height-to-span ratio of 0.6. The excavation methods are selected based on the geological conditions and the size of excavation section. The detailed selection method is presented in

Table 9. The selection of the excavation method.

Span/m	Q = 0.86	Q = 2.02	Q = 5.92	Q = 19.97
5	Two-bench excavation	Two-bench excavation	Full face excavation	Full face excavation
10	Two-bench excavation	Two-bench excavation	Two-bench excavation	Two-bench excavation
15	Three-bench seven-step excavation	Three-bench excavation	Three-bench excavation	Three-bench excavation
20	Three-bench seven-step excavation	Three-bench excavation	Three-bench excavation	Three-bench excavation
25	Three-bench seven-step excavation	Three-bench seven-step excavation	Three-bench seven-step excavation	Three-bench seven-step excavation
30	Oneside-wallheading excavation	Oneside-wall headingexcavation	One side-wall heading excavation	Three-bench seven-Step excavation
35	Doubleside-wall headingexcavation	Double side-wall heading excavation	Doubleside-wallheading excavation	One side-wall heading excavation
40	Doubleside-wallheading excavation	Doubleside-wallheading excavation	Doubleside-wallheading excavation	Double side-wall heading excavation

and model diagrams of the excavation method are shown in Figure 7.

4.3. Analysis of the Calculated Results

After the excavation process of each model is completed, the surrounding rock pressure at the vault of the section at the longitudinal depth of 10 m is selected as the research object. The results are shown in Figure 8.

The results presented in

Table 10. Fitted equations and the correlation coefficients.

Value of Q	Slope	Fitted Equations	Correlative Coefficients R2
0.86	3.763	$P=3.763d+106.10$	0.9477
2.02	3.223	$P=3.223d+93.68$	0.9717
5.92	1.974	$P=1.974d+86.04$	0.7976
19.97	1.425	$P=1.425d+63.54$	0.8394

show that the changes in surrounding rock pressure hold the following characteristics:

1)

Under the same span, the surrounding rock pressure decreases with the increase in Q value.

2)

Under the same Q value, the pressure increases with the increase in tunnel span. However, as the Q value increases, the increase in pressure gradually decreases.

The distribution of surrounding rock pressure varies with span for the same Q value. Furthermore, the corresponding correlation is presented in Table 10.

5. Estimation of the Surrounding Rock Pressure Based on Q System and Span

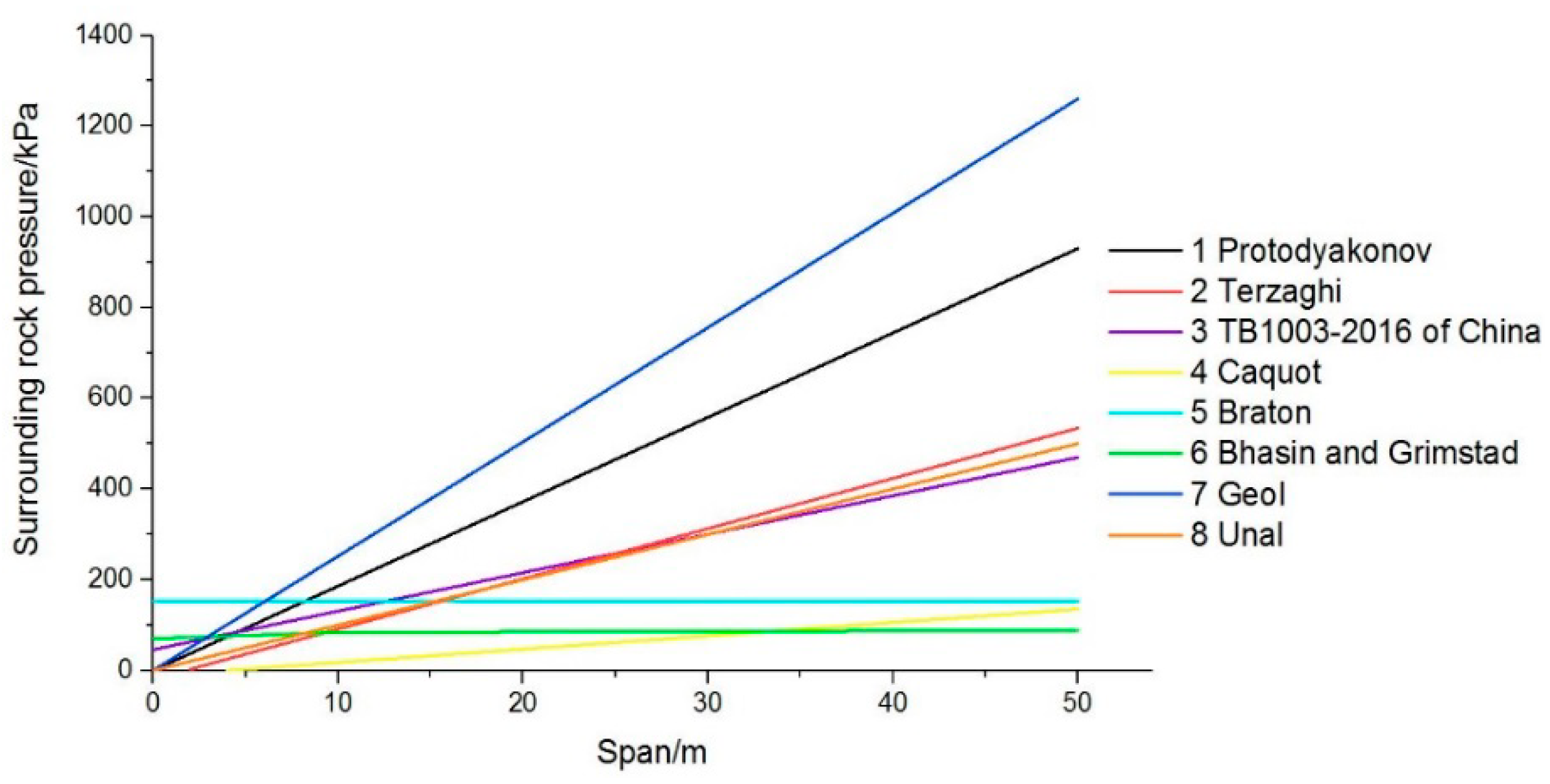
Figure 5 shows that when the tunnel span is larger than the conventional tunnel diameter, there is a big difference between the calculated results of Protodyakonov’s theory, Terzaghi theory, Code for Design of Railway Tunnel of China and Unal and the actual situation. When the buried depth of cavern exceeds a certain range, the calculated results of the surrounding rock pressure correlation, proposed by Bhasin, will not be reasonable. When the radius of cavern becomes smaller, the calculated results of the Caquot correlation will produce tensile stress, which does not accord with engineering practice. The results of Barton’s correlation are always within the proper limits though it does not change with the change in span. Therefore, on the basis of the correlation, the estimation correlation of surrounding rock pressure of large-span deep-buried underground structure based on Q system would be obtained by combining the numerical analysis and introducing the span-correction method.

5.1. Establishment of the Estimation Correlation

(1) The correlation for surrounding rock pressure based on Q system

The correlations for calculating the surrounding rock pressure based on Q system consist of empirical correlations proposed by Barton on the basis of statistical analysis of different engineering practices:

$$P_{roof1}=\left(\frac{200}{J_r}\right)Q^{-\frac{1}{3}}$$

(4)

$$P_{roof2}=\frac{200J_n^{\frac{1}{2}}{Q}^{-\frac{1}{3}}}{3J_r}$$

(5)

The units of the correlation is kPa and each parameter is shown in Notation 4. Screening the engineering cases selected by Barton [15], the statistical results of surrounding rock pressure of underground structures with span greater than 10 m are shown in Figure 9.

It can be seen from Figure 9 that the span corresponding to the statistical surrounding rock pressure is concentrated in a certain region. The statistical analysis for the item of span is conducted to determine this region more accurately.

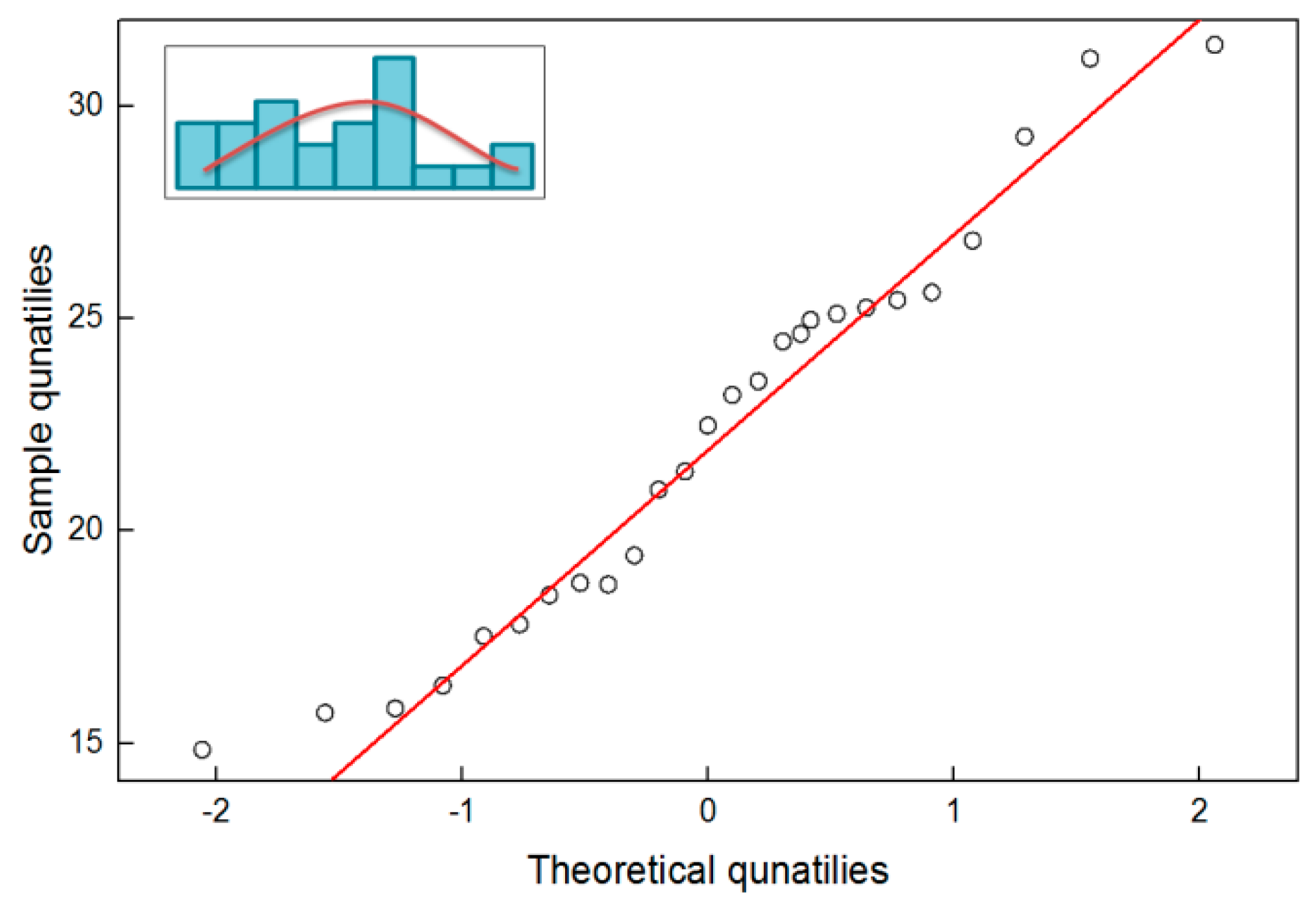
Data for the distribution of span is in accordance with the normal distribution having a mean value of 22.20 and a variance of 4.79 through the Q-Q test of residuals (the main function of the Q-Q test of residuals is to judge whether the sample is approximate to normal distribution. The normal distribution hypothesis of the sample would be acceptable, if each point of the graph is close to the reference line.). Therefore, Correlations (4) and (5) can be considered to produce the corresponding surrounding rock pressure with a span of 22 m. The corresponding results are shown in Figure 10.

(2) Relationship between the Q value and the fitting linear correlation

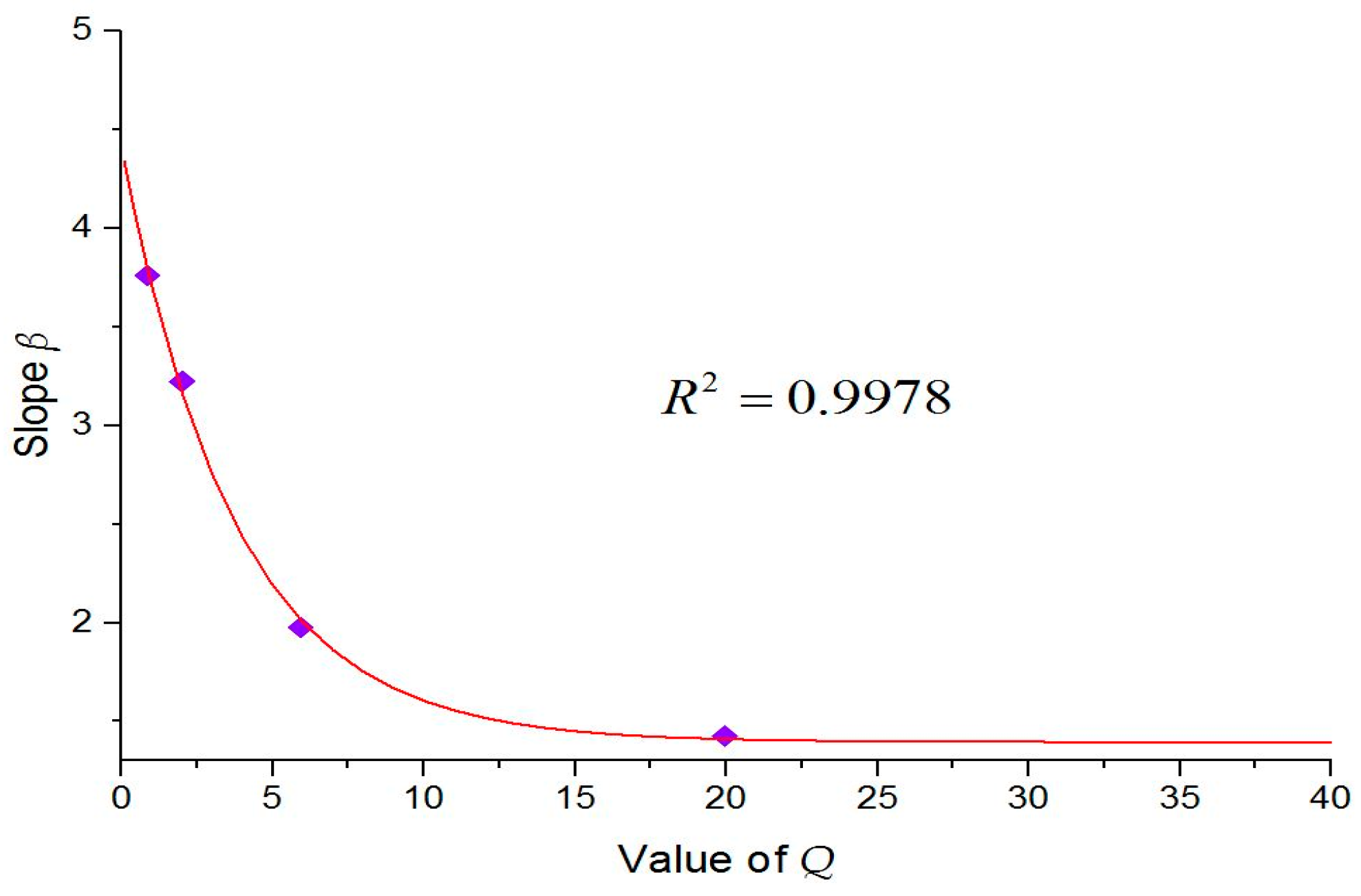
The slope β corresponds to different Q values and is plotted in the coordinate system, as shown in Figure 11. The fitting correlation and the correlation coefficient are represented by Equation (6).

$$\beta =3.025\times e^{(-0.2672Q)}+1.395$$

(6)

(3) Derivation process of the correlation estimation

The results show that the surrounding rock pressure values have a certain linear relationship with span under different Q values. The corresponding pressure values are given by Correlations (4) and (5) for the relationship between the Q value and the slope. Assuming that the intercept of the linear correlation between Q values and span d is given by B, the following correlations are established:

$$P_{roof}=\beta d+B$$

(7)

With the assumption that d = 22, B could be obtained by substituting Correlations (4)–(6) into (7):

$$B=\left(\frac{200}{J_r}\right)Q^{-\frac{1}{3}}-22\times (3.025\times e^{-0.2672Q}+1.395)$$

(8)

$$B=\frac{200J_n^{\frac{1}{2}}{Q}^{-\frac{1}{3}}}{3J_r}-22\times (3.025\times e^{-0.2672Q}+1.395)$$

(9)

Equations (8) and (9) are introduced into Equation (7) to obtain Equations (10) and (11):

$$P_{roof1}=(3.025\times e^{-0.2672Q}+1.395)\times (d-22)+\left(\frac{200}{J_r}\right)Q^{-\frac{1}{3}}$$

(10)

$$P_{roof2}=(3.025\times e^{-0.2672Q}+1.395)\times (d-22)+\frac{200J_n^{\frac{1}{2}}{Q}^{-\frac{1}{3}}}{3J_r}$$

(11)

When a parameter α is introduced, Equation (12) is obtained:

$$\alpha =3.025\times e^{-0.2672Q}+1.395$$

(12)

The units of α are kN/m³. Therefore, the estimation correlation for surrounding rock pressure based on Q value and span d is obtained as follows (see Equations (13) and (14)):

$$P_{roof1}=\alpha (d-22)+\left(\frac{200}{J_r}\right)Q^{-\frac{1}{3}}$$

(13)

$$P_{roof2}=\alpha (d-22)+\frac{200J_n^{\frac{1}{2}}{Q}^{-\frac{1}{3}}}{3J_r}$$

(14)

The units of P_roof1 and P_roof2 in Equations (11) and (12) are kPa, while those of d are m. J_n—Joint group coefficient; J_r—Joint roughness coefficient. P_roof1 = P_roof2 when J_n = 9; P_roof1 > P_roof2 when J < 9; P_roof1 < P_roof2 when J_n > 9.

Assuming J_n = 9 and J_r = 1, the relationship between the surrounding rock pressure and Q values under different spans is calculated, and the corresponding results are shown in Figure 12.

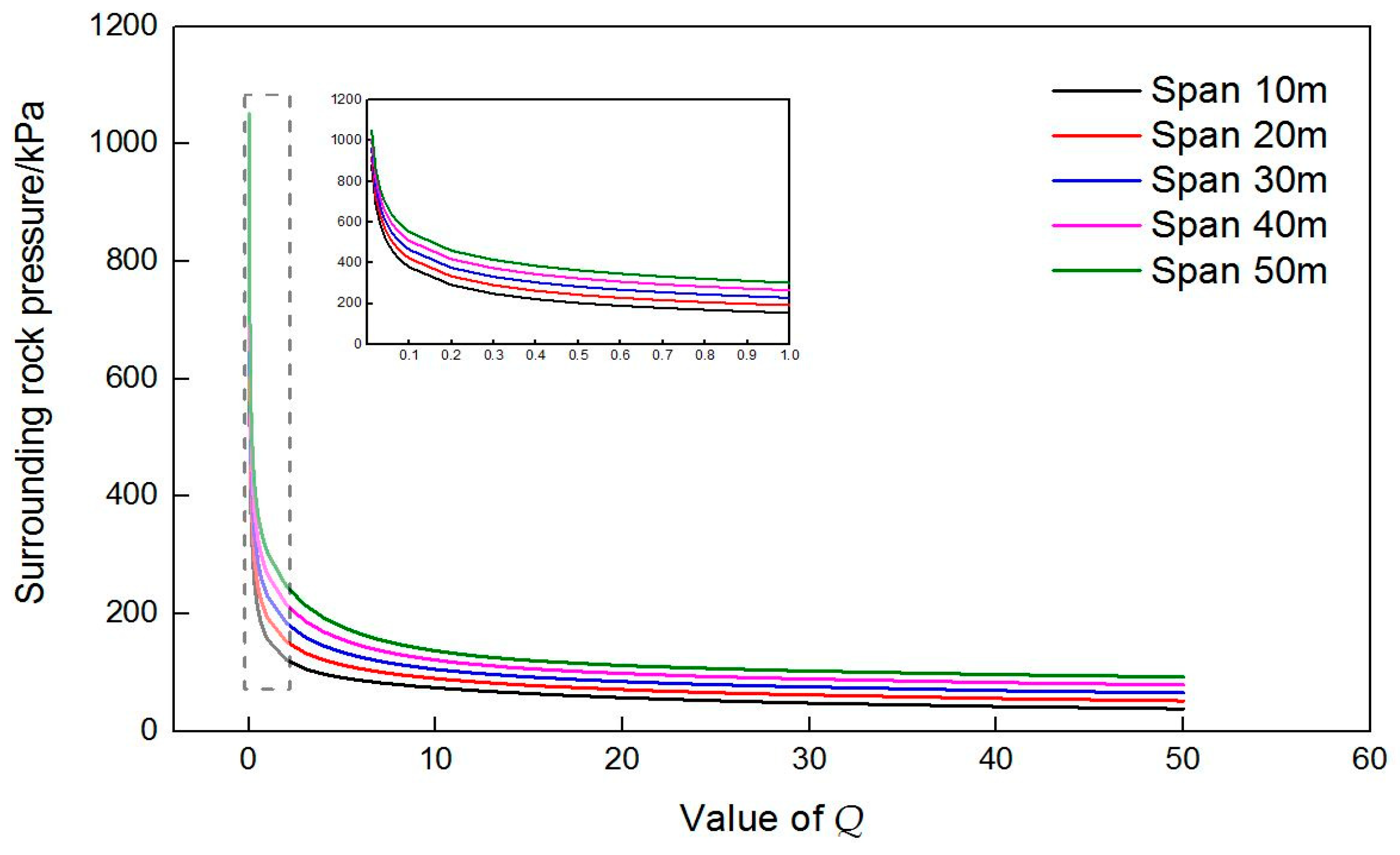
1)

Under the same span, with the increase in Q value, the quality of surrounding rock increases. Furthermore, the surrounding rock pressure of the vault gradually decreases and tends to stabilize.

2)

Under the same Q value, as the span increases, the surrounding rock pressure of the vault gradually becomes larger.

3)

According to the local graph, when Q value is between 0 and 1, the slope of surrounding rock pressure curve increases rapidly with the decrease in Q value for the same span. This means a worse quality of surrounding rock results in a greater increase in the surrounding rock pressure.

4)

As shown in the local graph, smaller the Q value, worse is the quality of surrounding rock, and more obvious is the influence of span on the surrounding rock pressure.

(4) Applicable conditions

1)

The relationship between the slope β and Q value is based on the calculation model of lateral pressure coefficient λ = 2 and height-to-span ratio of 0.6. Therefore, the correlations are applicable to caverns, whose product of the lateral pressure coefficient and height-to-span ratio is close to 1.

2)

The correlations are derived on the basis of Q system, so they are similar to the correlation based on Q system. They represent the calculation of surrounding rock pressure under deep burial conditions.

3)

The surrounding rock pressure of underground structure with a span greater than 10 m is analyzed statistically in the process of deriving the correlation. Therefore, the calculation correlations for the surrounding rock pressure are more suitable for underground structures with large span.

5.2. Comparison between the Results of Correlations and the Measured Values

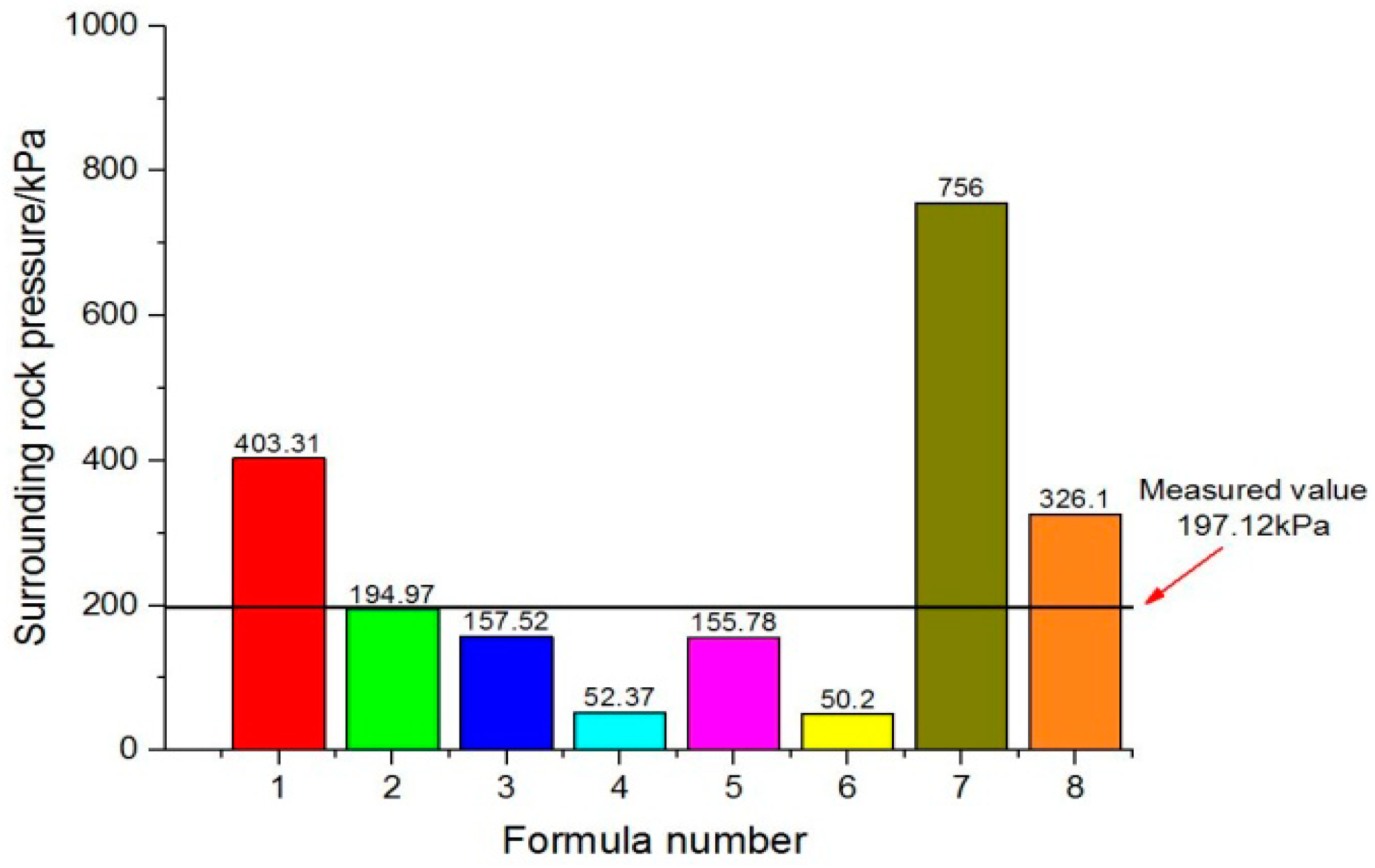
In order to better understand the variation of surrounding rock pressure during the construction of super-large section tunnel and verify the applicability of the estimation correlations, the contact pressure between the surrounding rock and the initial support of Liantang tunnel is monitored in-situ. The monitoring section mileage is K1 + 890, and the surrounding rock grade is III. The monitoring instruments are shown in Figure 13.

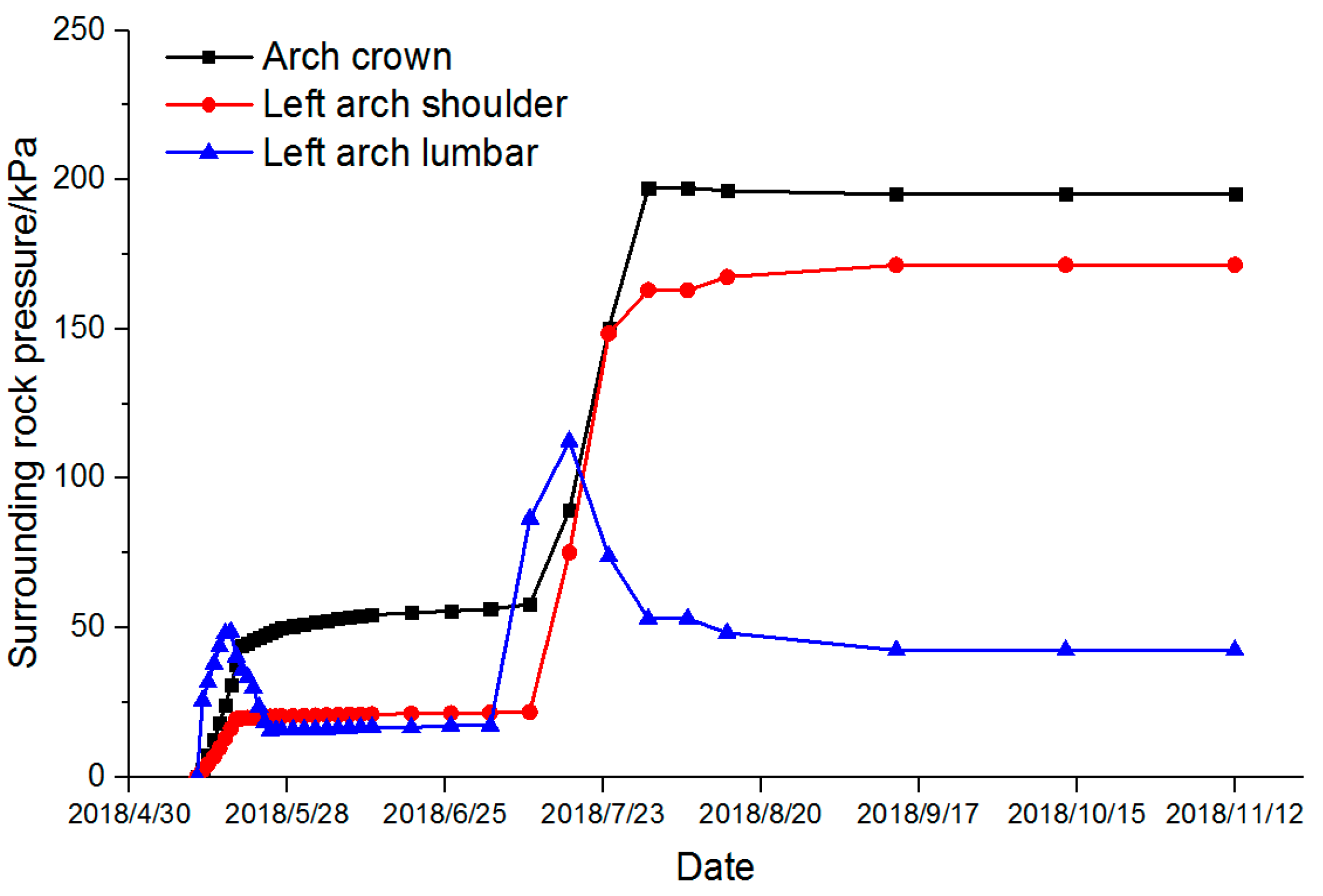
Up until 24 November 2018, the variation of surrounding rock pressure in Section K1 + 890 is shown in Figure 14. The pressure stability value of the vault surrounding rock at Section K1 + 890 is 197.12 kPa.

In addition, data for 34 engineering cases around the world were collected through literature and engineering data [20,25,26,27,28,29]. The detailed engineering conditions and the measured values for the surrounding rock pressure are presented in

Table 11. Engineering examples.

Number	Engineering Name	Span/m	Measured Value (kPa)	Estimated Value(kPa)	Value of Q	Jn	Jr
1	Liantang Tunnel	30	197.12	183.19	5.92	1	9
2	Jiaozhou Bay Tunnel	28.3	245.12	224.47	0.83	1	8
3	Longtoushan Tunnel	18	143.7	123.40	0.89	1.5	9
4	Xiangshan Tunne	9.1	320	293.95	0.19	1	9
5	Zhongnanshan Tunnel	12.5	148	149.22	2.18	1	12
6	Huangyanzi Tunnel	15.8	56	74.54	7.39	1.2	9
7	Maozhan Ridge Tunnel	16.82	160	140.39	0.89	1.5	12
8	Heluoshan Tunnel	19.65	70	60.25	31.33	1	9
9	Wushaoling tunnel	7.95	373	481.19	0.11	1	15
10	Bajiaoqing Tunnel	11	150	164.18	0.51	1.2	9
11	Banzhulin Tunne	12.5	277	295.88	0.26	1.2	15
12	Zhengyang Tunnel	12	41	38.10	7.39	1.5	6
13	Alatan Tunnel	10	110	63.88	2.43	1	4
14	Chhibro-Khodri	3	310	335.97	0.05	1.5	12
15	Chhibro-Khodri	3	320	308.48	0.02	1.2	4
16	Giri-Bata	4.6	200	156.55	0.37	1	6
17	Giri-Bata	4.6	170	194.89	0.12	1	4
18	Maneri Stage-I	5.8	200	232.59	0.17	1.2	9
19	Maneri Stage-III	7	290	226.96	0.19	1.2	9
20	Noonidih Colliery	7	150	137.21	0.57	1	6
21	Tala Hydro	6.9	940	1203.33	0.01	1	15
22	Tala HRT	7.2	800	1204.65	0.01	1	15
23	Kaligandaki	9.7	900	791.00	0.03	1	15
24	Kaligandaki	9.7	1270	855.89	0.02	1	15
25	Kaligandaki	9.7	1000	791.00	0.03	1	15
26	Kaligandaki	9.7	1020	925.78	0.02	1	15
27	Nathpa Jhakri	11	260	224.21	0.41	1	9
28	Nathpa Jhakri	11	320	244.23	0.33	1	9
29	Nathpa Jhakri	11	350	244.23	0.33	1	9
30	Nathpa Jhakri	11	380	265.96	0.26	1	9
31	Nathpa Jhakri	11	990	582.53	0.03	1	9
32	Udhampur rail	6.5	300	321.45	0.06	1.5	12
33	Chenani-Nashri	6	100	70.00	2.18	1.5	12
34	Chenani-Nashri	6	100	67.47	2.43	1.5	12
35	Chenani-Nashri	6	100	63.07	3.04	1.5	12

.

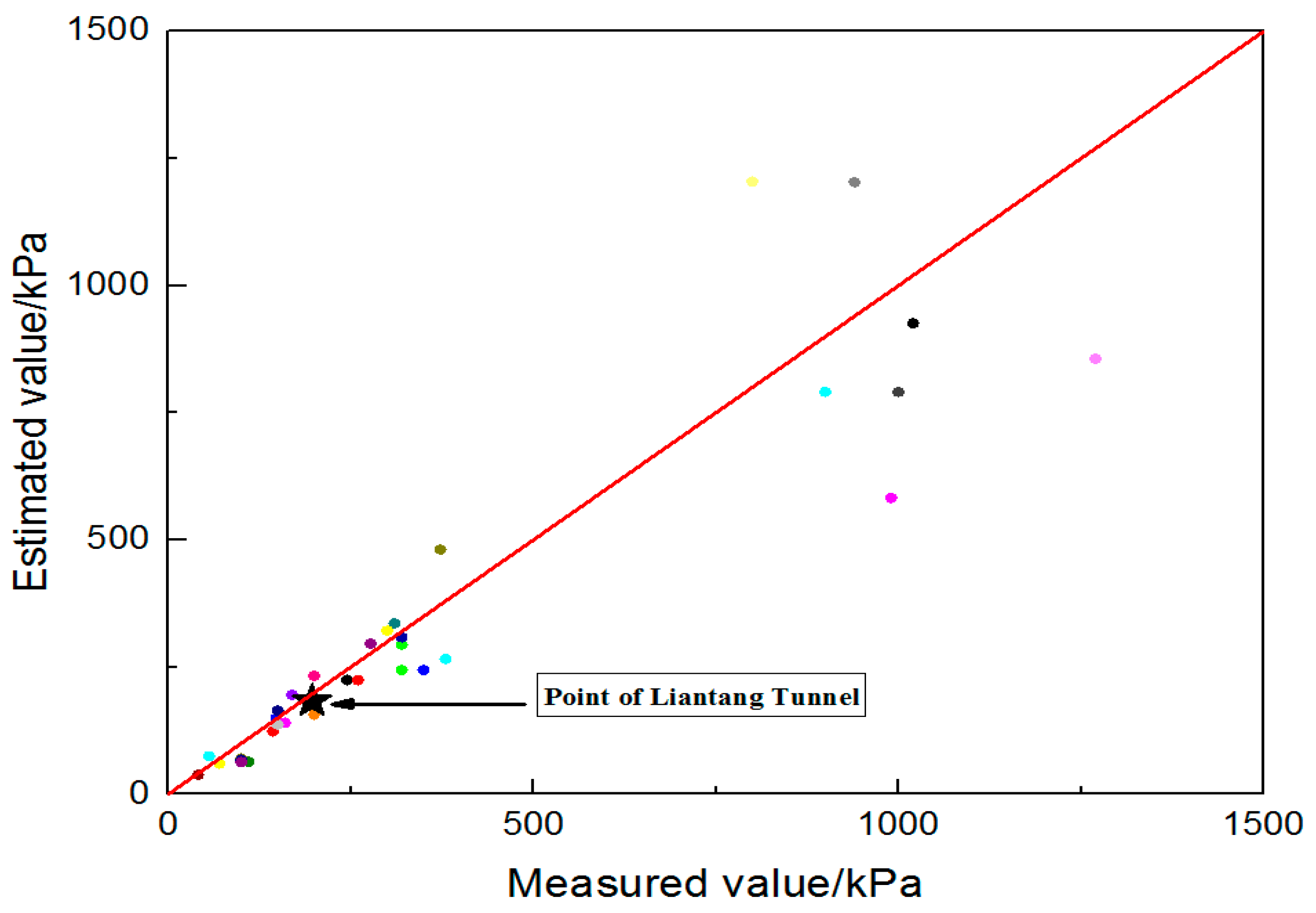
Figure 15 is a comparison chart between the measured and calculated surrounding rock pressures. The diagonal is represented as the isoline. It can be seen that the contrast values are basically distributed near the isoline, which shows that the estimation correlations have good applicability. The correlations can be used to rapidly estimate the surrounding rock pressure of deep-buried tunnels with conventional span or super-large section similar to Liantang tunnel.

5.3. Discussion

According to Figure 15, the contrast values are basically distributed near the isoline, which indicates that the correlations meet the needs of engineering stability analysis. The correlations are derived on the basis of Q system and statistical results of surrounding rock pressure for underground structures with a span greater than 10 m. Therefore, the correlations are applicable to large span underground structures under deep burial conditions. Further improvement is required for the correlations since the influence of construction methods on surrounding rock pressure in the process of derivation has not been focused on efficiently. In addition, the calculation of the side pressure will be the focus of the follow-up work.

6. Conclusions

(1) Based on the Liantang tunnel’s large-span project, the surrounding rock pressure of the single-arch super-large section tunnel is calculated using different correlations for the surrounding rock pressure. Additionally, the applicability and the characteristics of these traditional correlations are analyzed.

(2) The excavation simulation is carried out by using a single arch deep buried large-span structural model with different Q values and different spans to study the variation in surrounding rock pressure. The corresponding variation pattern is obtained, which shows that the surrounding rock pressure decreases with the increase in Q value for the same span. Furthermore, the surrounding rock pressure increases with the increase in tunnel span for the same Q value. However, the increase in surrounding rock pressure gradually decreases with the increase in Q value. With the increase in Q value, the rate of increase of surrounding rock pressure gradually decreases.

(3) New correlations for estimating the surrounding rock pressure are proposed after improving the correlation based on Q system and introducing the span term. The correlations are validated by the data collected from Liantang tunnel large-span and the surrounding rock pressure from more than 30 projects around the world. The validation results show that the correlations can provide a reference for the stability analysis of the surrounding rock of deep-buried super-large section structures.