Application-Level Packet Loss Rate Measurement Based on Improved L-Rex Model
Abstract
1. Introduction
2. L-Rex Model
2.1. Model Description
- (a)
- The recv() will be triggered and return a typical number of bytes as soon as data are available;
- (b)
- During a burst, the time interval between two consecutive recv() is very small;
- (c)
- The “silence period” between two consecutive bursts is usually smaller than Round Trip Time (RTT).
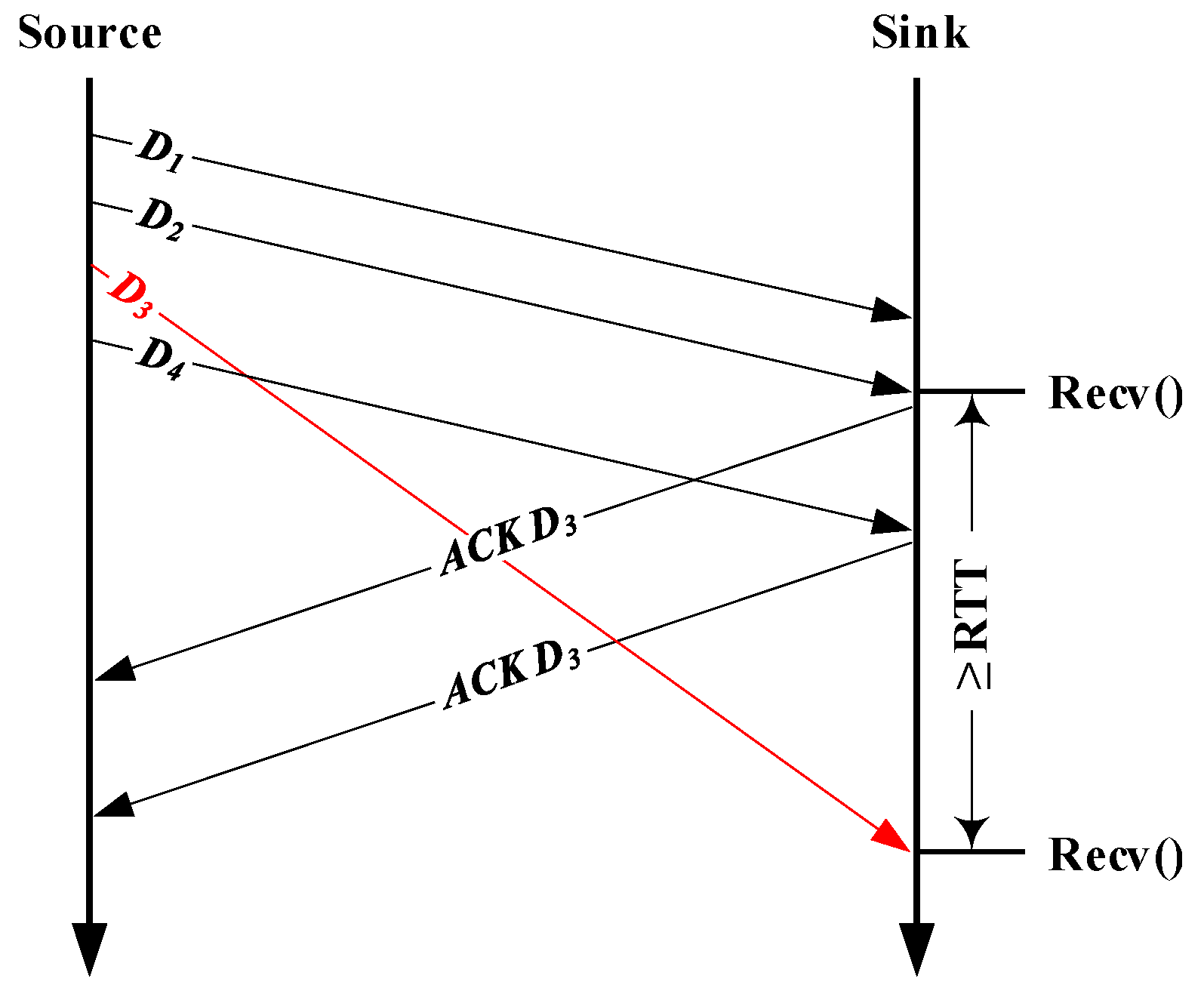
- (A)
- The recv() is blocked due to packet loss, which makes the silence period longer; in the best case (i.e., fast retransmission), an additional RTT is needed to re-trigger recv();
- (B)
- When the lost packet(s) are repaired, a large and non-typical number of bytes will be returned to userspace.
- (i)
- The time elapsed since the previous recv() is greater than H · RTT;
- (ii)
- The number of received bytes is greater than 1 MSS and less frequent than K;
2.2. Limitations of L-Rex
3. IM-L-Rex
3.1. Self-Clocking Mechanism
3.2. Methodology
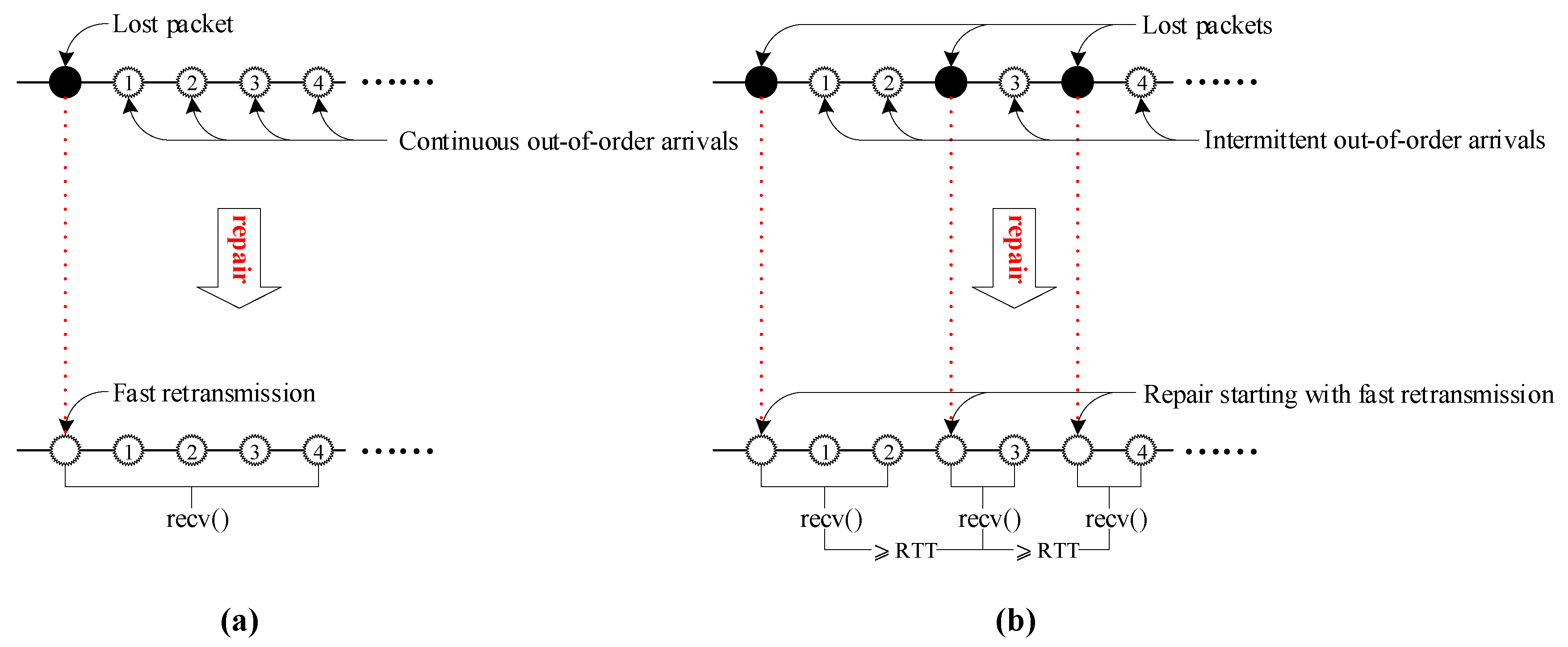
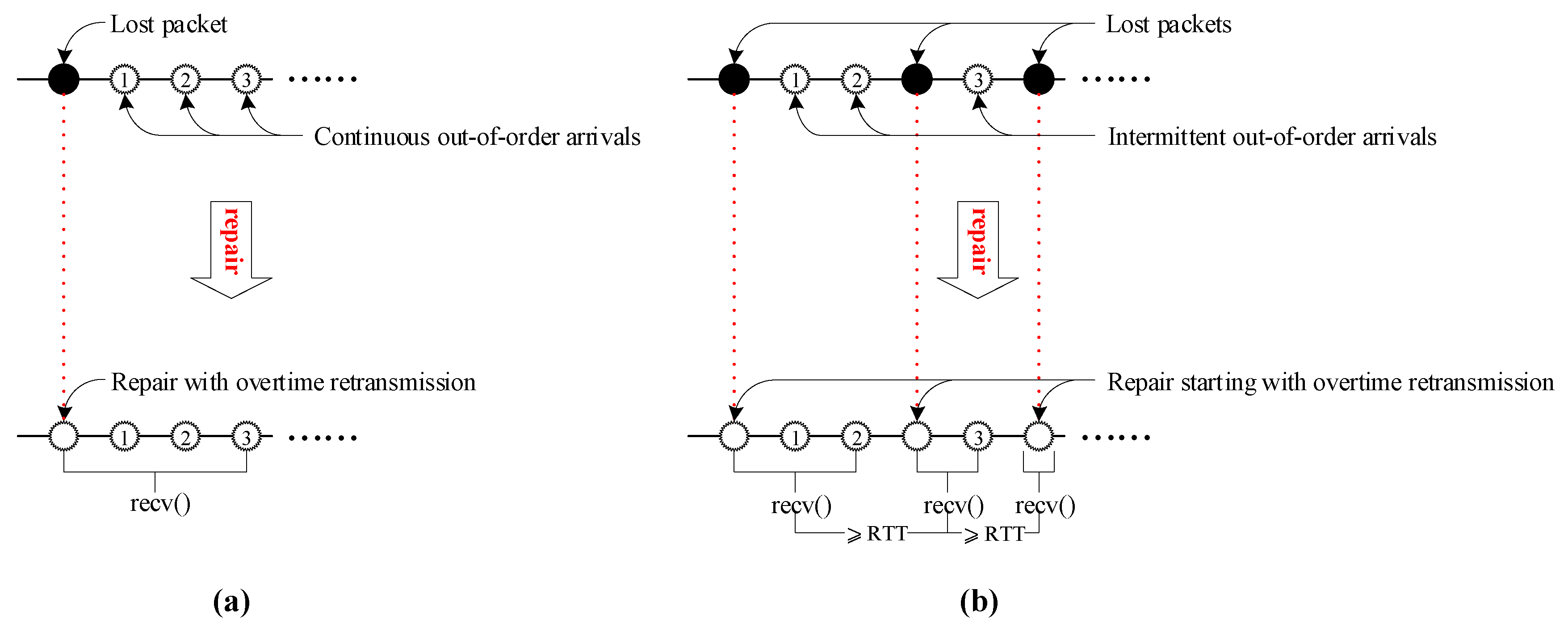
- Form 1: The out-of-order arrivals are continuous and can be returned by recv() at one time. For instance, in Figure 3a, the four continuous out-of-order arrivals result in recv() returning to userspace at least five segments at a time (i.e., the fast retransmission used for repairing the lost packet plus the four continuous out-of-order segments that arrived while recv() was blocked).
- Form 2: The out-of-order arrivals are intermittent (discontinuous) and need at least two recv()s to be returned to userspace; the first recv() is triggered by a fast retransmission, while the time interval between the subsequent recv() and the previous recv() is greater than RTT. For instance, in Figure 3b, the four out-of-order arrivals triggering fast retransmission require calling recv() three times to return to user space. In this case, the recv () triggered by the first fast retransmission returns a fast retransmission and the first two out-of-order arrivals; after RTT, the recv() triggered by the second retransmission returns a retransmission and the third out-of-order arrival; after another RTT, recv() triggered by the third retransmission returns a retransmission and the fourth out-of-order arrival.
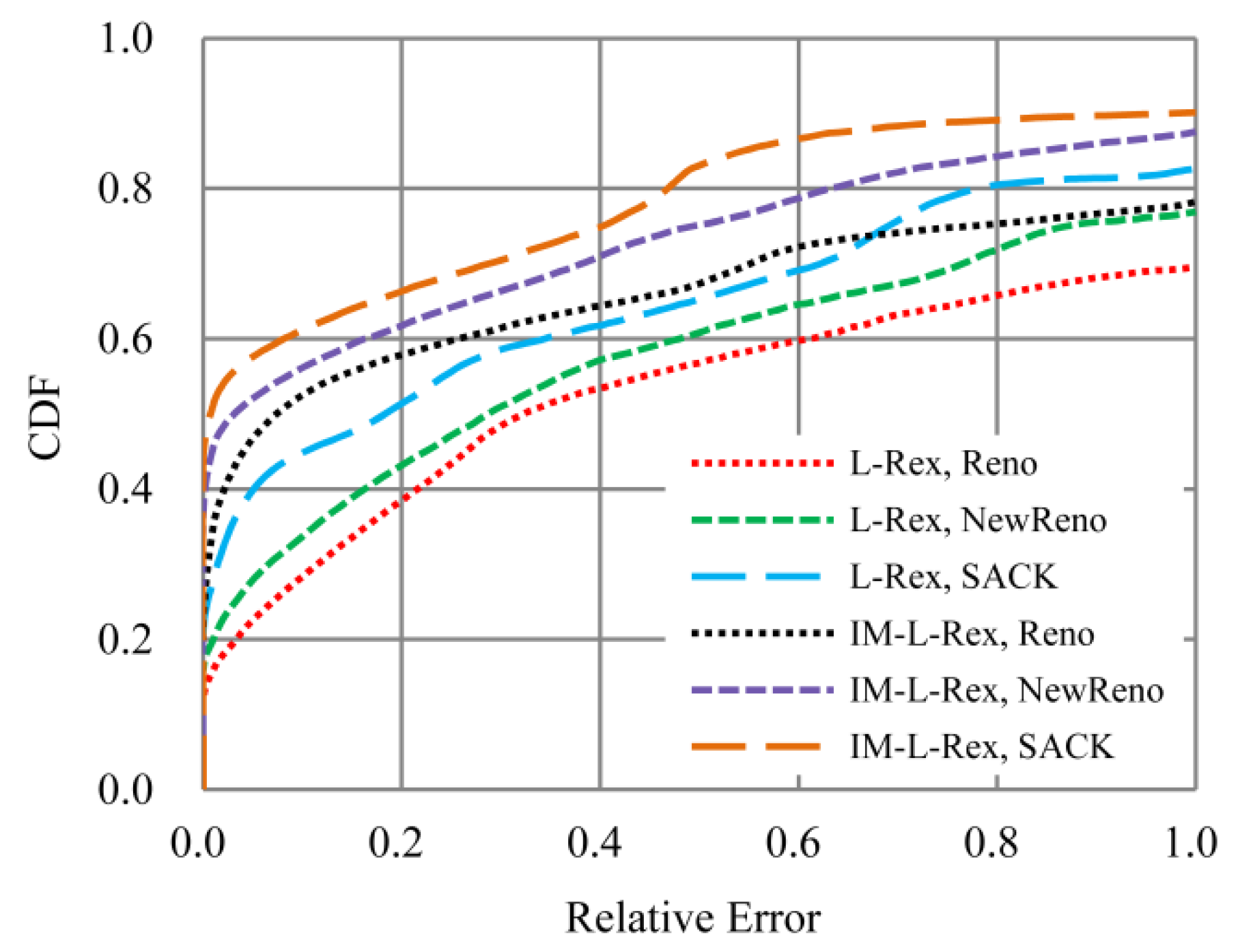
3.3. TCP Variants
- Reno: According to RFC 2581 [24], it cooperates with TCP’s basic congestion control mechanisms (e.g., slow start, congestion avoidance, fast recovery, etc.) to repair packet losses with overtime retransmissions and fast retransmissions.
- NewReno: This version, described in RFC 2582 [25], is an extension to the Reno. It mainly improves TCP’s fast recovery algorithm to avoid multiple retransmission timeouts in Reno’s fast recovery phase.
- SACK: It uses the Selective Acknowledgment (SACK) blocks to acknowledge out-of-order segments that arrived at the receiver and were not covered by the acknowledgement number. The SACK combines with a selective retransmission policy at the sender-side to repair packet losses and reduce spurious retransmissions. More details about SACK are available from RFC 2018 [26].
3.4. Summary
- (1)
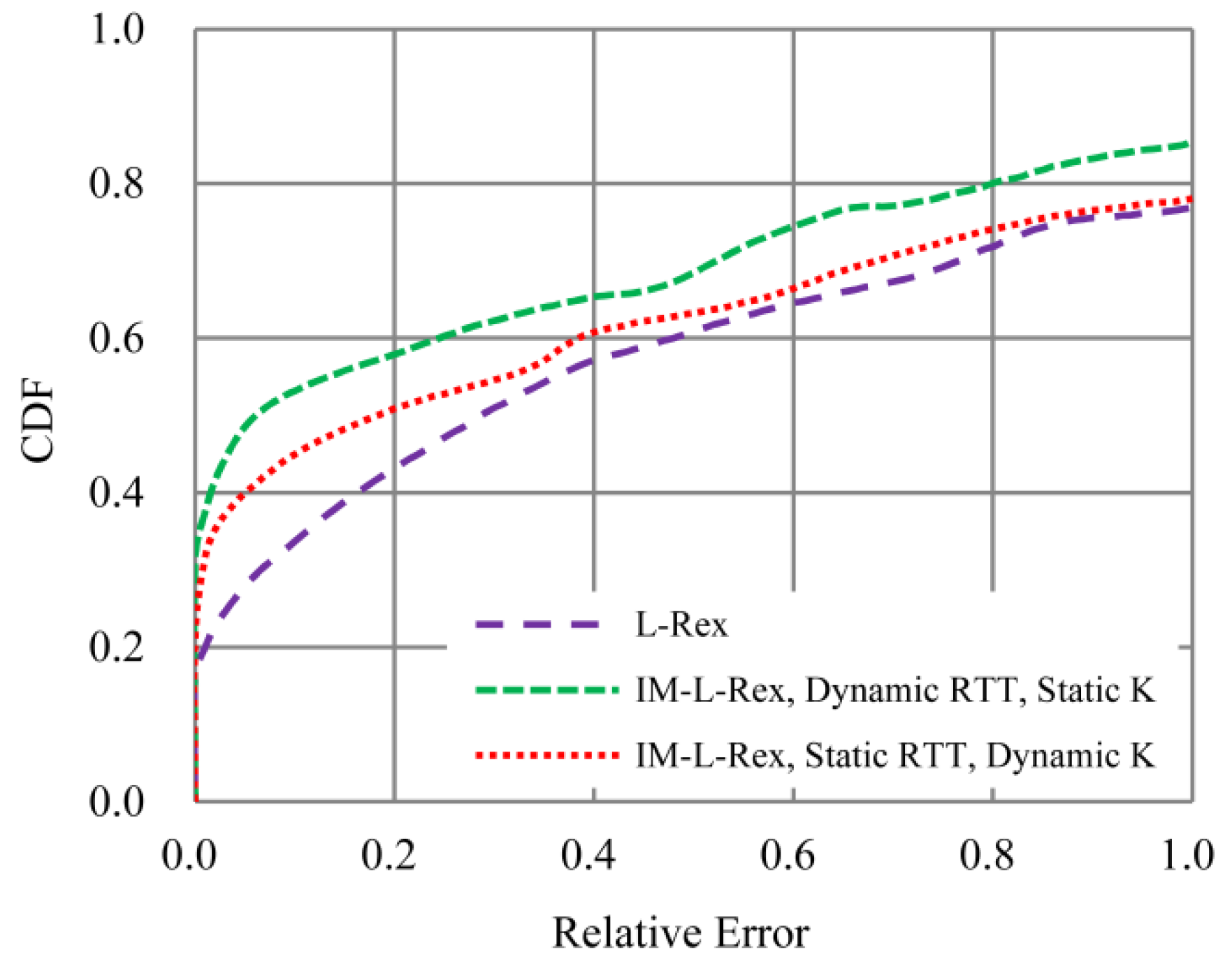
- As the key parameters, RTT, H and K are all static in L-Rex, i.e., RTT is the time required for the connect() system call to complete, while the parameters H and K were optimized from repeated experiments on Asymmetric Digital Subscriber Lime (ADSL) and fast Ethernet, with values of 0.7 and 1%, respectively. On the contrary, the parameters RTT and K are dynamically estimated in IM-L-Rex by leveraging the TCP’s self-clocking mechanism. Moreover, the parameter H used for smoothing RTT is no longer needed in IM-L-Rex due to the dynamically estimated RTT.
- (2)
- Compared with L-Rex, IM-L-Rex is also committed to excluding the adverse effect of packet reordering by refining overtime retransmissions and fast retransmissions.
4. Implementation
| Algorithm 1: IM-L-Rex |
| 01. //Preprocessing stage 02. Total_num = Loss_num = Nqst = EPLR = 0 03. Intvl = 500 04. Frctn = 1/4 05. Crltn = 0.75 06. S = null 07. for Recvdata returned by each recv() 08. //Form data sequence 09. Recvdata.addArray(S) 10. Total_num += Recvdata.getPktnum() 11. end for 12. for Recvdata in S 13. //Count application level traffic losses 14. if Recvdata.isRexmit(S, Intvl, Nqst, Frctn, Crltn) 15. if Recvdata.isFast(S, Intvl, Nqst, Frctn, Crltn) 16. Loss_num+=1 17. else if Recvdata.isFast(S, Intvl, Nqst, Frctn, Crltn) 18. Loss_num+=1 19. else 20. continue 21. else 22. continue 23. end for 24. EPLR = Loss_num / Total_num |
5. Experiments
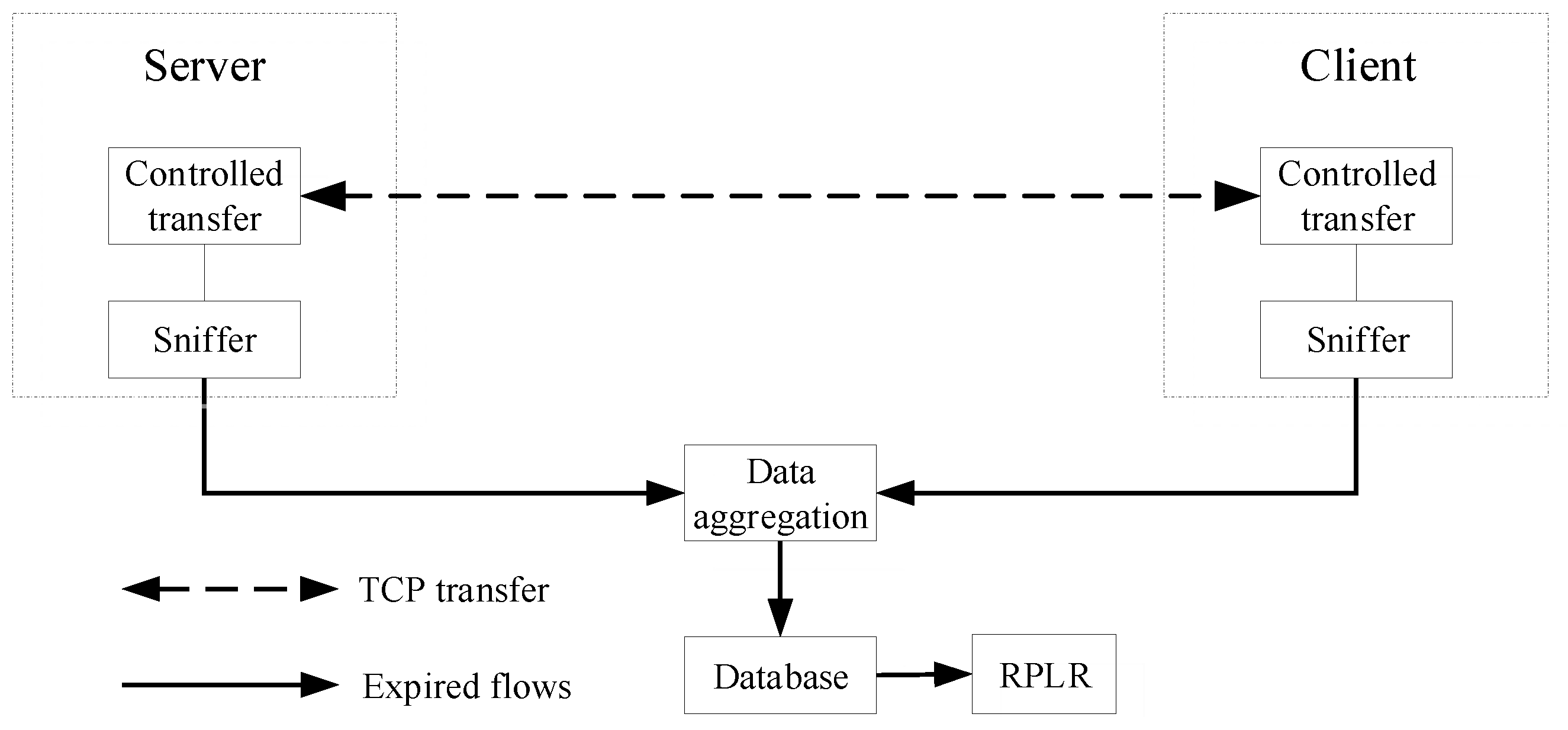
5.1. Controlled TCP Transfers
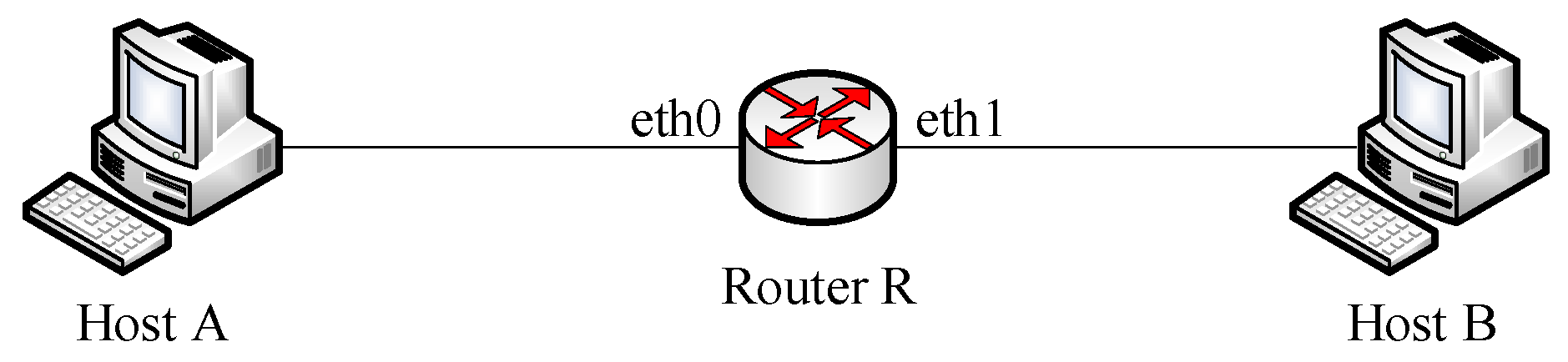
5.2. Testbed
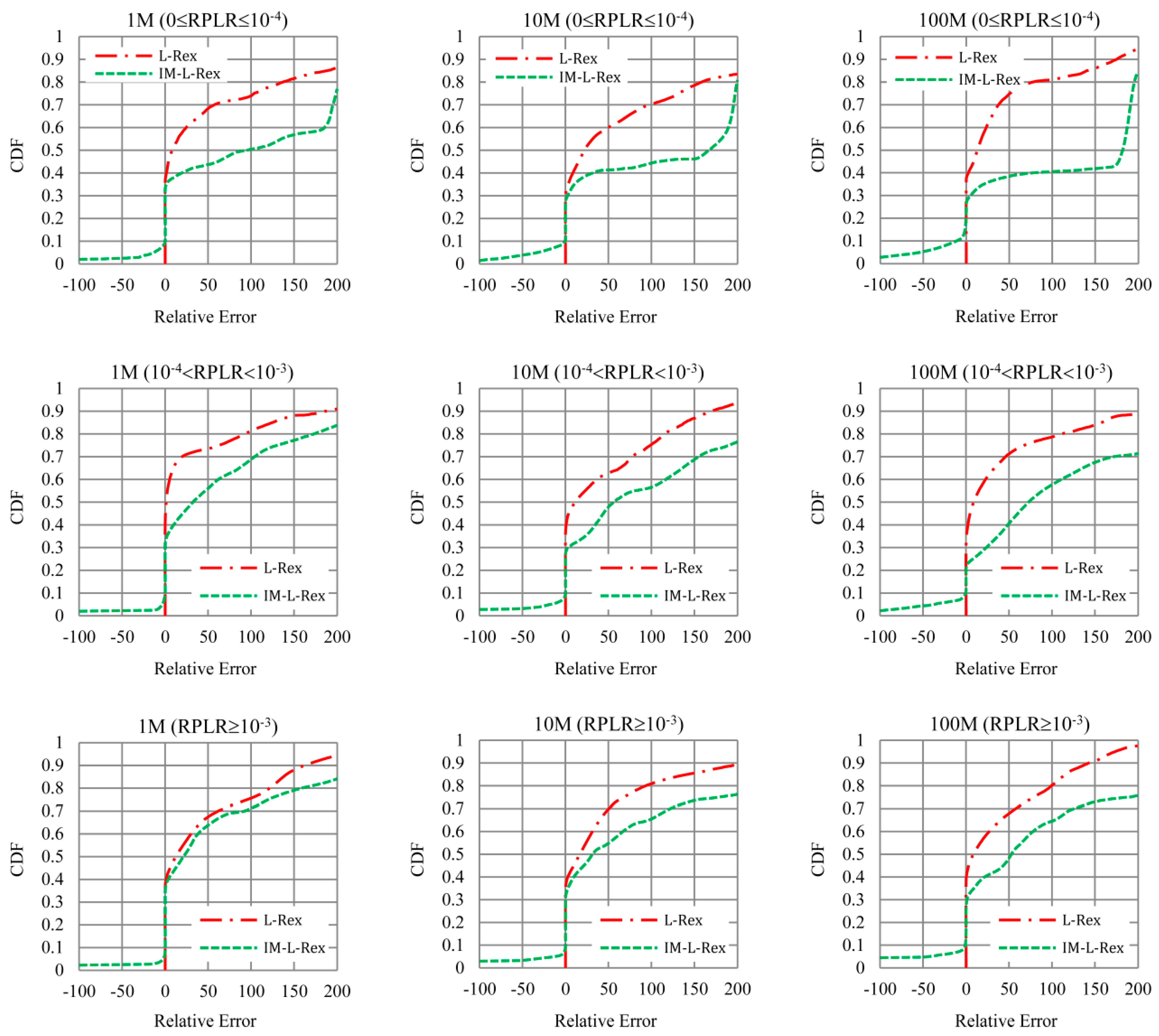
5.2.1. Impact of Packet Reordering
5.2.2. Impact of TCP Variants
5.2.3. Impact of Parameters RTT and K
6. Conclusion and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Antonopoulos, A.; Kartsakli, E.; Perillo, C.; Verikoukis, C. Shedding light on the Internet: Stakeholders and network neutrality. IEEE Commun. Mag. 2017, 55, 216–223. [Google Scholar] [CrossRef]
- Peitz, M.; Schuett, F. Net neutrality and inflation of traffic. Int. J. Ind. Organ. 2016, 46, 16–62. [Google Scholar] [CrossRef]
- Bauer, J.M.; Knieps, G. Complementary innovation and network neutrality. Telecommun. Policy 2018, 42, 172–183. [Google Scholar] [CrossRef]
- Dustdar, S.; Duarte, E.P. Network Neutrality and Its Impact on Innovation. IEEE Internet Comput. 2018, 22, 5–7. [Google Scholar] [CrossRef]
- Schulzrinne, H. Network Neutrality Is About Money, Not Packets. IEEE Internet Comput. 2018, 22, 8–17. [Google Scholar] [CrossRef]
- Statovci-Halimi, B.; Franzl, G. QoS differentiation and Internet neutrality. Telecommun. Syst. 2013, 52, 1605–1614. [Google Scholar] [CrossRef]
- Basso, S.; Meo, M.; Servetti, A.; De Martin, J.C. Estimating packet loss rate in the access through application-level measurements. In Proceedings of the ACM SIGCOMM workshop on Measurements up the stack, Helsinki, Finland, 17 August 2012; pp. 7–12. [Google Scholar]
- Basso, S.; Meo, M.; De Martin, J.C. Strengthening measurements from the edges: Application-level packet loss rate estimation. ACM SIGCOMM Comput. Commun. Rev. 2013, 43, 45–51. [Google Scholar] [CrossRef]
- Ellis, M.; Pezaros, D.P.; Kypraios, T.; Perkins, C. A two-level Markova model for packet loss in UDP/IP-based real-time video applications targeting residential users. Comput. Netw. 2014, 70, 384–399. [Google Scholar] [CrossRef]
- Baglietto, M.; Battistelli, G.; Tesi, P. Packet loss detection in networked control systems via process measurements. In Proceedings of the IEEE Conference on Decision and Control, Miami Beach, FL, USA, 17–19 December 2018; pp. 4849–4854. [Google Scholar]
- Mittag, G.; Möller, S. Single-ended packet loss rate estimation of transmitted speech signals. In Proceedings of the IEEE Global Conference on Signal and Information Processing, Anaheim, CA, USA, 26–29 November 2018; pp. 226–230. [Google Scholar]
- Lan, H.; Ding, W.; Gong, J. Useful Traffic Loss Rate Estimation Based on Network Layer Measurement. IEEE Access 2019, 7, 33289–33303. [Google Scholar] [CrossRef]
- Carra, D.; Avrachenkov, K.; Alouf, S.; Blanc, A.; Nain, P.; Post, G. Passive online RTT estimation for flow-aware routers using one-way traffic. In Proceedings of the 9th International IFIP TC 6 Networking Conference, Chennai, India, 11–15 May 2010; pp. 109–121. [Google Scholar]
- Allman, M.; Eddy, W.M.; Ostermann, S. Estimating loss rates with TCP. ACM SIGMETRICS Perform. val. Rev. 2003, 31, 12–24. [Google Scholar] [CrossRef]
- Priya, S.; Murugan, K. Improving TCP performance in wireless networks by detection and avoidance of spurious retransmission timeouts. J. Inf. Sci. Eng. 2015, 31, 711–726. [Google Scholar]
- Anelli, P.; Lochin, E.; Harivelo, F.; Lopez, D.M. Transport congestion events detection (TCED): Towards decorrelating congestion detection from TCP. In Proceedings of the ACM Symposium on Applied Computing, Sierre, Switzerland, 22–26 March 2010; pp. 663–669. [Google Scholar]
- Zhani, M.F.; Elbiaze, H.; Aly, W.H.F. TCP based estimation method for loss control in OBS networks. In Proceedings of the IEEE GLOBECOM, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Ullah, S.; Ullah, I.; Qureshi, H.K.; Haw, R.; Jang, S.; Hong, C.S. Passive packet loss detection in Wi-Fi networks and its effect on HTTP traffic characteristics. In Proceedings of the International Conference on Information Networking, Phuket, Thailand, 10–12 February 2014; pp. 428–432. [Google Scholar]
- Hagos, D.H.; Engelstad, P.E.; Yazidi, A.; Kure, Ø. A machine learning approach to TCP state monitoring from passive measurements. In Proceedings of the IEEE Wireless Days, Dubai, UAE, 3–5 April 2018; pp. 164–171. [Google Scholar]
- Laghari, A.A.; He, H.; Channa, M.I. Measuring effect of packet reordering on quality of experience (QoE) in video streaming. 3D Research 2018, 9, 30. [Google Scholar] [CrossRef]
- Veal, B.; Li, K.; Lowenthal, D. New methods for passive estimation of TCP round-trip times. In International Workshop on Passive and Active Network Measurement; Springer: Berlin/Heidelberg, Germany, 2005; pp. 121–134. [Google Scholar]
- Mirkovic, D.; Armitage, G.; Branch, P. A survey of round trip time prediction systems. IEEE Commun. Surv. Tutor. 2015, 20, 1758–1776. [Google Scholar] [CrossRef]
- Paxson, V.; Allman, M.; Chu, J.; Sargent, M. Computing TCP’s retransmission timer. RFC 6298. 2011. [Google Scholar] [CrossRef]
- Allman, M.; Paxson, V.; Stevens, W. TCP Congestion Control, RFC 2581. 1999. [Google Scholar] [CrossRef]
- Floyd, S.; Henderson, T. The NewReno Modification to TCP's Fast Recovery Algorithm, RFC 2582. 1999. [Google Scholar] [CrossRef]
- Mathis, M.; Mahdavi, J.; Floyd, S.; Romanow, A. TCP Selective Acknowledgment Options, RFC 2018. [CrossRef]
- Lan, H.; Ding, W.; Zhang, Y. Passive overall packet loss estimation at the border of an ISP. KSII T. Internet. Inf. 2018, 12, 3150–3171. [Google Scholar]
- Stevens, W.R. TCP/IP Illustrated, Volume 1: The protocols, 1st ed.; Addison-Wesley Publisher: Boston, MA, USA, 1994; pp. 136–139. [Google Scholar]
- Nguyen, H.X.; Roughan, M. Rigorous statistical analysis of internet loss measurements. IEEE/ACM Trans. Netw. 2013, 21, 734–745. [Google Scholar] [CrossRef]





| Server-ID | IP Address | Port Number | RAM | ROM |
|---|---|---|---|---|
| 1 | 211.65.*.31 | 1313 | 512 MB | 8 GB |
| 2 | 211.65.*.32 | 1313 | 512 MB | 8 GB |
| 3 | 211.65.*.33 | 1313 | 512 MB | 8 GB |
| 4 | 211.65.*.34 | 80 | 512 MB | 8 GB |
| RPLR | 1 MB | 10 MB | 100 MB |
|---|---|---|---|
| [10−3, ∞) | 57 (19%) | 68 (26%) | 57 (35%) |
| (10−4, 10−3) | 111 (37%) | 109 (42%) | 111 (44%) |
| [0, 10−4) | 132 (44%) | 83 (32%) | 132 (21%) |
| ID | Parameter | Parameter Description |
|---|---|---|
| 1 | Protocol | NewReno |
| 2 | Proportion delay | 10 ms |
| 3 | File size | 10-second random-data TCP download |
| 4 | Link bandwidth | 10 Mbps |
| 5 | Packet size | uniformly distributed between 0.2 and 1 Kbytes |
| 6 | Loss rate | gradually from 0 to 5% |
| 7 | Reordering proportion | 5% and 10% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, H.; Ding, W.; Deng, L. Application-Level Packet Loss Rate Measurement Based on Improved L-Rex Model. Symmetry 2019, 11, 442. https://doi.org/10.3390/sym11040442
Lan H, Ding W, Deng L. Application-Level Packet Loss Rate Measurement Based on Improved L-Rex Model. Symmetry. 2019; 11(4):442. https://doi.org/10.3390/sym11040442
Chicago/Turabian StyleLan, Haoliang, Wei Ding, and Lu Deng. 2019. "Application-Level Packet Loss Rate Measurement Based on Improved L-Rex Model" Symmetry 11, no. 4: 442. https://doi.org/10.3390/sym11040442
APA StyleLan, H., Ding, W., & Deng, L. (2019). Application-Level Packet Loss Rate Measurement Based on Improved L-Rex Model. Symmetry, 11(4), 442. https://doi.org/10.3390/sym11040442





