Hysteretic Loops in Correlation with the Maximum Dissipated Energy, for Linear Dynamic Systems
Abstract
:1. Introduction
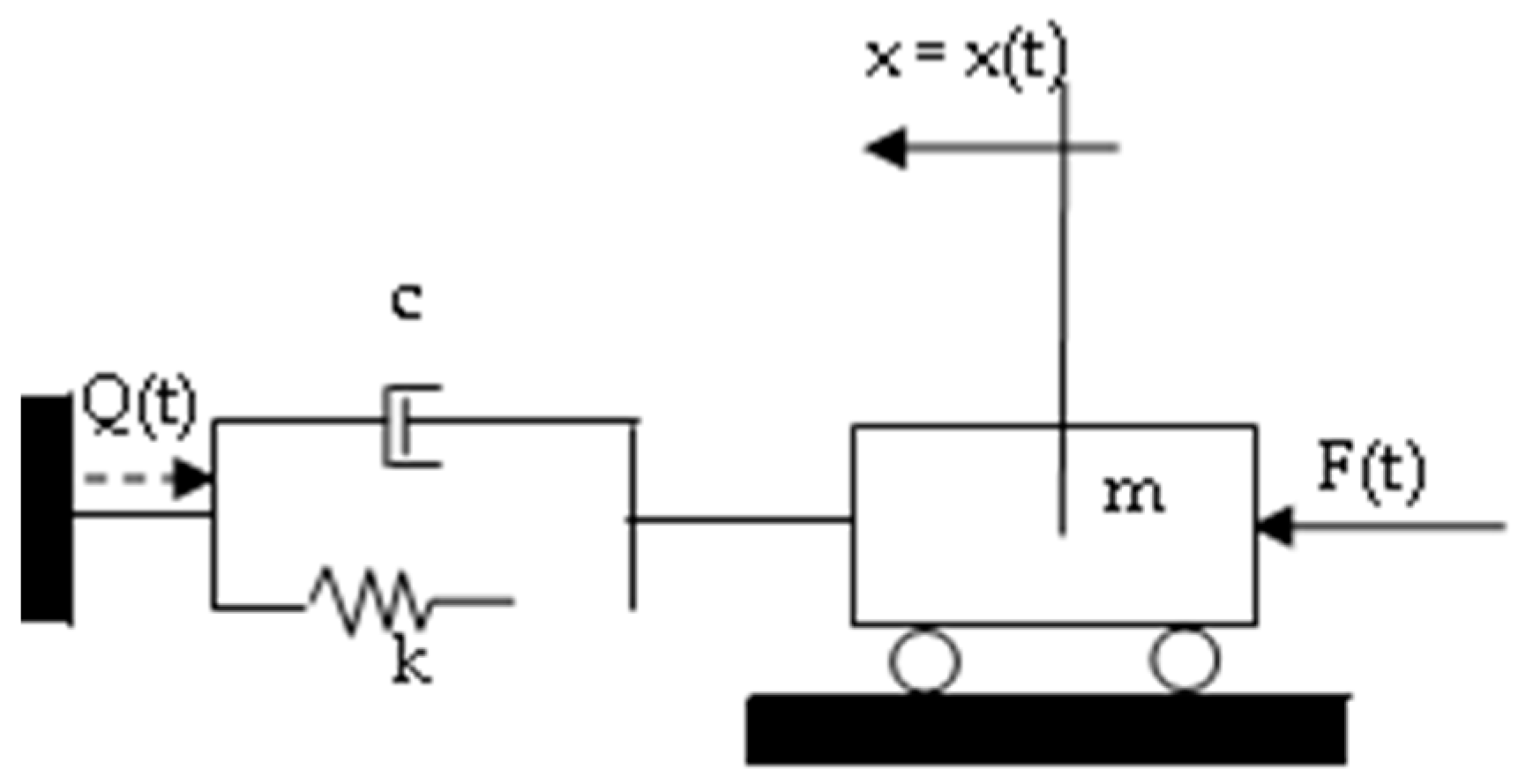
2. Parameter Analysis
2.1. Amplitude of Displacement
2.2. De-Phasing between Force and Displacement
2.3. Dissipated Energy
2.4. Equation of the F–x Elliptic Hysteretic Loop
- (a)
- For the ante-resonance regime at , obtainingor
- (b)
- For the post-resonance regime at the following is obtained:orwhereor
2.5. Equation of the Hysteretic Loop Q–x
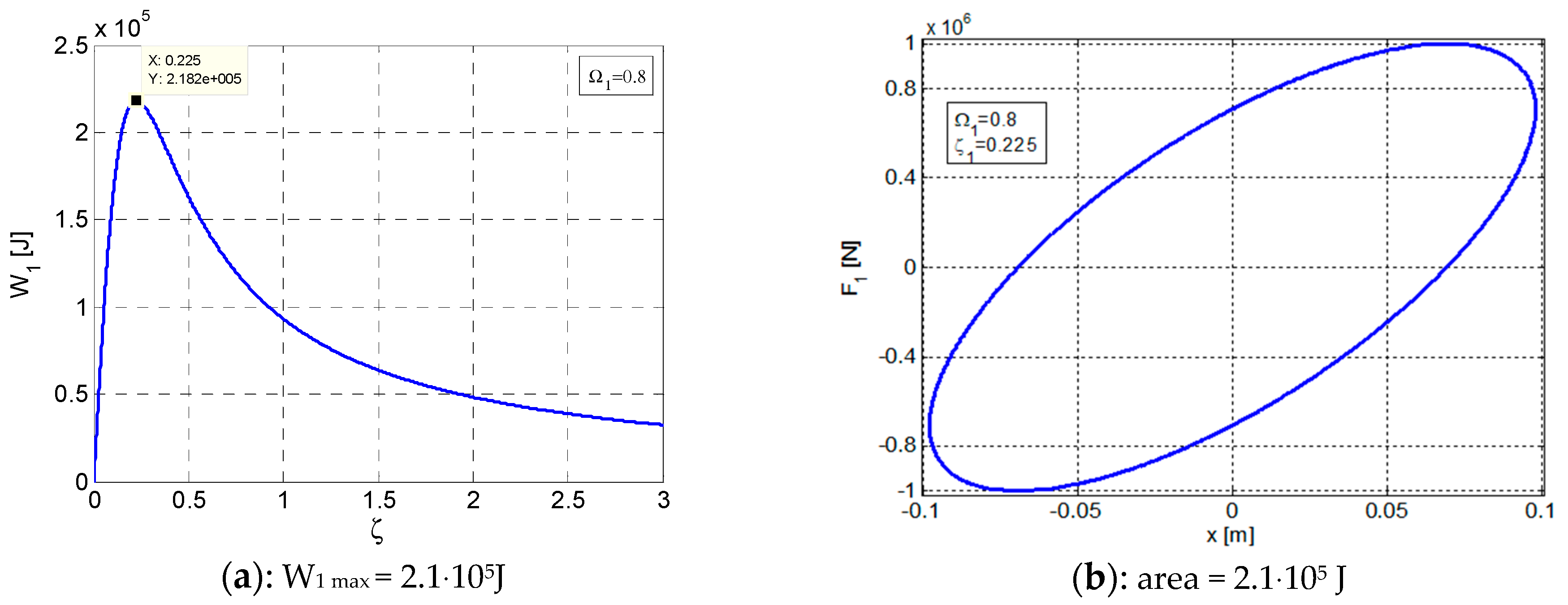
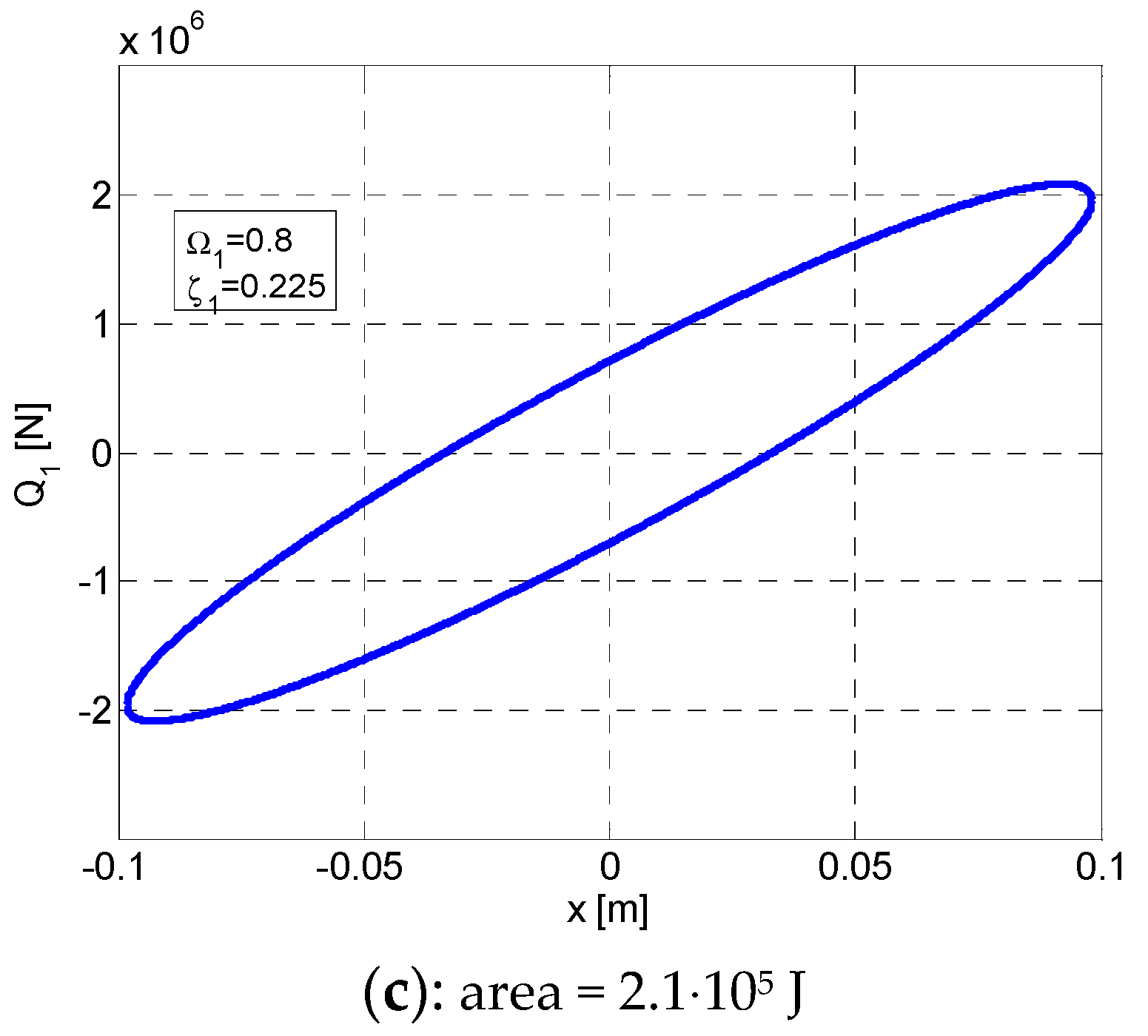
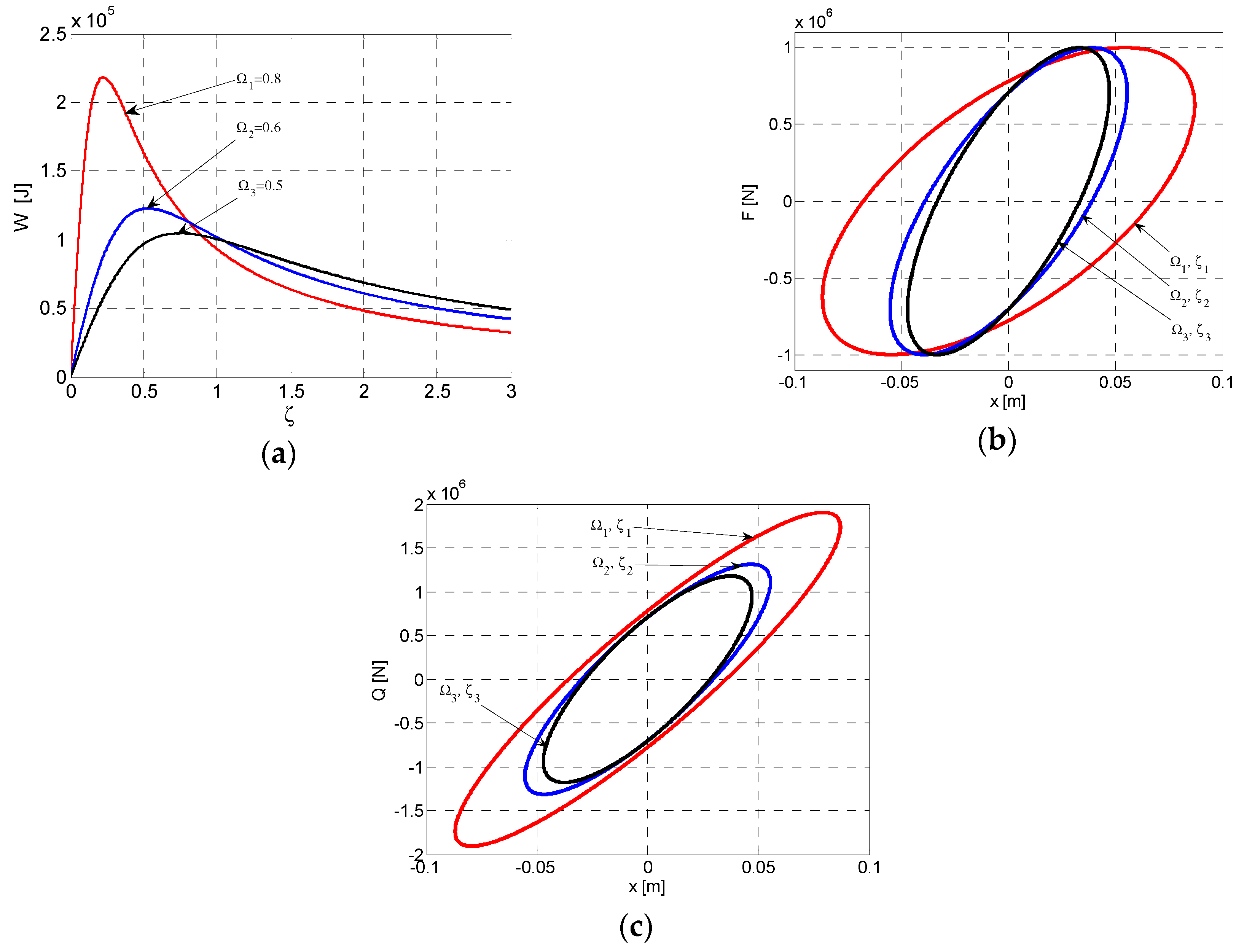
3. Elliptic Hysteretic Loops for the Ante-Resonance Regime ()
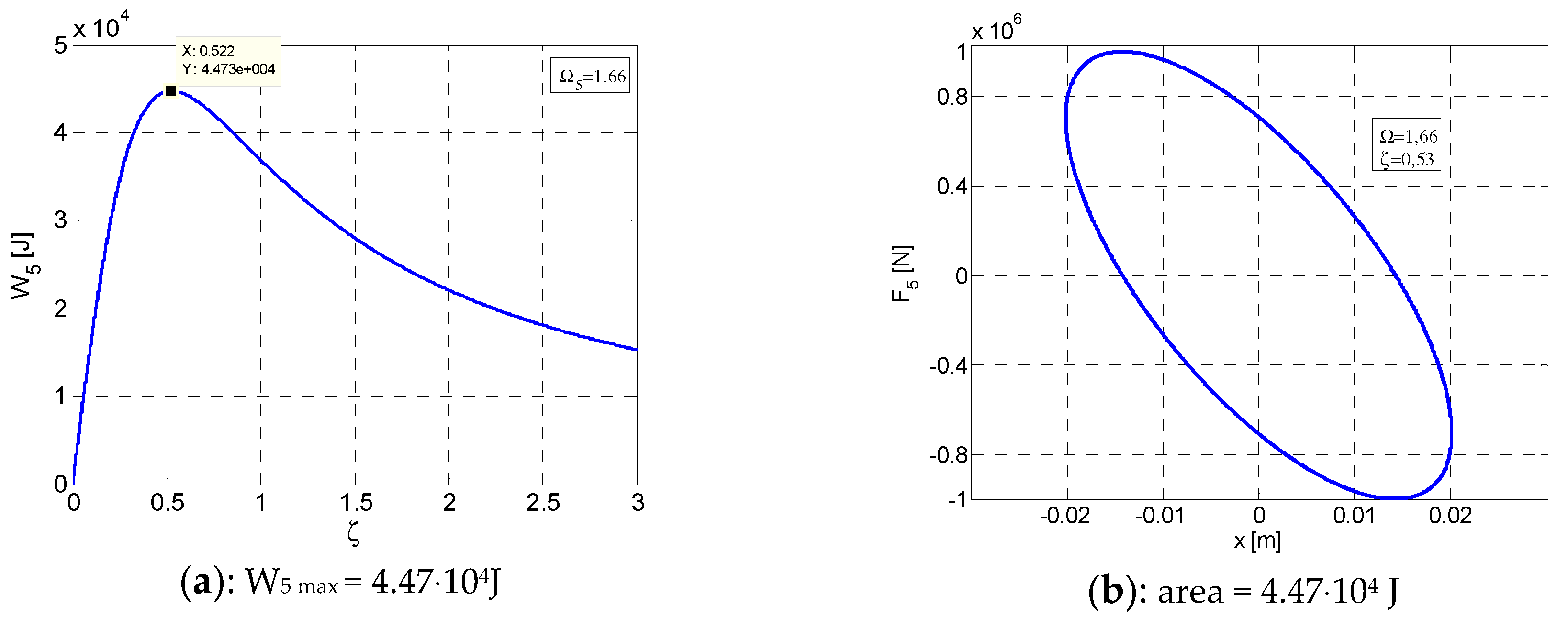
4. Elliptic Hysteretic Loops for the Post-Resonance Regime ()
5. Conclusions
- (a)
- For this, there are established the functional relations of the perturbatory force F = F(x) in relation with the instantaneous displacement x = x(t), of the viscoelastic force Q = Q(t) in relation with x = x(t), of the viscoelastic force Q = Q(x) in relation with x = x(t), and of the dissipated energy in relation with the variation of the viscous dumping , namely Wd = W(ζ);
- (b)
- In this context, based on the graphical representations, it was possible to emphasize the fact that the ellipses F–x are rotating in relation to the origin of the axis system, according to the dynamic regime or . The axis of the ellipse F–x rotation is caused by the inertial effect that is produced by the presence of the factor in the expression of the function F = F(x);
- (c)
- The representation of the function Q = Q(x) highlights the that it constantly maintains an angle of inclination of the ellipse Q–x, axis, with a positive slope;
- (d)
- It can be noticed that the areas of the hysteretic loops F–x and Q–x are equal between them and equal with the maximum value of the dissipated energy Wmax () for .
- (e)
- The effective critical dumping depends both on the value of as well as on the relative pulsation , for ante-resonance or , for post-resonance. In the case of the resonance regime, for , then is a sole situation that enables the assessment of the fraction from the optimal critical amortization .
Funding
Conflicts of Interest
References
- Dobrescu, C. The Rheological Behaviour of Stabilized Bioactive Soils During the Vibration Compaction Process for Road Structures. In Proceedings of the 22th International Congress on Sound and Vibration, Florence, Italy, 12–16 July 2015. [Google Scholar]
- Mitu, A.M.; Sireteanu, T.; Ghita, G. Passive and semi-active bracing systems for seismic protection: A comparative study. Rom. J. Acoust. Vib. 2015, 12, 49–56. [Google Scholar]
- Sireteanu, T. Smart suspension systems. Rom. J. Acoust. Vib. 2016, 13, 2. [Google Scholar]
- Conveney, V.V.; Johnson, D.E.; Kulak, R.F. Modelling the Free Oscillation of Building Suported on High Damping Rubber Isolators. In Proceedings of the Seismic Engineering 2000, The 2000 ASME Pressure Vessels and Piping Conference, Seattle, WA, USA, 23–27 July 2000; Volume 1. [Google Scholar]
- Lin, S.B. Theoretical and Experimental Study of High Damping Rubber Bearing and Lead Extrusion Damper. Master’s Thesis, Feng Chia University, Taichung, Taiwan, 2000. [Google Scholar]
- Chen, B.J.; Lin, S.B.; Tsai, C.S. Theoretical and Experimental Study of High Damping Rubber Bearings. In Proceedings of the Seismic Engineering 2001, The 2000 ASME Pressure Vessels and Piping Conference, Seattle, WA, USA, 23–27 July; Volume 2.
- Dolce, M.; Ponzo, F.C.; Di Cesare, A.; Arlego, G. Progetto di Edifici con Isolamento Sismico; IUSS Press: Pavia, Italy, 2010. [Google Scholar]
- Marioni, A. Sisitemi di Isplamento Sismico Innovetivi Prodotti dalla Societa ALGA. In Moderni Sistemi e Tecnologie Antisismici. Una Guida per il Progettista; 21mo Secolo: Milano, Italy, 2008. [Google Scholar]
- Bratu, P. Vibration Transmissivity in Mechanical Systems with Rubber Elements Using Viscoelastic Models. In Proceedings of the 5th European Rheology Conference, Ljubljana, Slovenia, 6–11 September 1998. [Google Scholar]
- Delfosse, C.G. Étude des vibrations linéaires d’un systeme mecanique complexe par méthode des mates normaux. Ann. l’ITBTP 1976, 336, 122–136. [Google Scholar]
- Giacchetti, R. Fondamente di Dinamica delle Strutture e di Ingineria Sismica; EPC Libri: Roma, Italy, 2004. [Google Scholar]
- Bratu, P. Analyze Insulator Rubber Elements Subjected to Actual Dynamic Regime. In Proceedings of the 9th International Congress Sound and Vibration, Orlando, FL, USA, 8–11 July 2002. [Google Scholar]
- Bratu, P. Experimental evaluation of the antivibrating damping capacity in case of elastomers used for tram railway supportins. Mater. Plast. 2009, 46, 127–130. [Google Scholar]
- Bratu, P. Rheological model of the neopren elements used for base isolation against seismic actions. Mater. Plast. 2009, 46, 288–294. [Google Scholar]
- Jennings, P. Equivalent viscous damping for yelding structures. J. Eng. Mech. Division 1968, 94, 103–116. [Google Scholar]
- Rao, M. Mechanical Vibrations; Addison-Wesley Pub. Co.: Boston, MA, USA, 2011. [Google Scholar]
- Sireteanu, T.; Giuclea, M.; Mitu, A.M. An analitical approach for approximation of exxperimental hysteretic by Bouc.-Wen model. Procc. Rom. Acad. Ser. A 2009, 10, 4354. [Google Scholar]
- Sireteanu, T.; Giuclea, M.; Mitu, A.M. Identification of an extended Bouc.-Wen model with application to seismic protection through hysteretic devices. Comput. Mech. 2010, 45, 5. [Google Scholar] [CrossRef]
- Le Tallec, P. Introduction à la Dynamique des Structures; Cépaduès: Toulouse, France, 2000. [Google Scholar]
- Trigili, G. Introduzione alla Dinamica delle Strutture e Spettri di Progeto; Laccorio: Palermo, Italy, 2010. [Google Scholar]
- Dolce, M.; Mortelli, A.; Panza, G. Proteggersi dal Terremoto; 21/mo Secolo: Milano, Italy, 2004. [Google Scholar]
- Mortelli, A.; Sannino, U.; Parducci, A.; Braga, F. Moderni Sistemi e Tecnologie Antisismici Una Guida per il Progettista; 21mo Secolo: Milano, Italy, 2008. [Google Scholar]
- Radeș, M. Mechanical Vibrationes; Ed. Printech: București, Romania, 2006. [Google Scholar]
- Johnson, E.A.; Ramallo, J.C.; Spencer, B.F., Jr.; Sain, M.K. Intelligent Base Isolation Systems. In Proceedings of the 2nd World Conference on Structural Control, Kyoto, Japan, 28 June–1 July 1998. [Google Scholar]
- Wang, Y.-P. Fundamentals of Seismic Base Isolation. In International Training Programs for Seismic Design of Building Structures; National Certer of Research on Earthquake Engineering: Taipei, Taiwan, 2016. [Google Scholar]
- Stanescu, N.D. Vibrations of a shell with clearances, neo-Hookean stiffness, and harmonic excitations. Rom. J. Acoust. Vib. 2016, 13, 104–111. [Google Scholar]
- Vasile, O. Active vibration control for viscoelastic damping systems under the action of inertial forces. Rom. J. Acoust. Vib. 2017, 14, 54–58. [Google Scholar]
- Inman, D. Vibration with Control; John Wiley & Sons Ltd.: London, UK, 2007. [Google Scholar]
- Najari, S. Identification par Analyse Harmonique des Structures en Géniè Civil; INSA: Toulouse, France, 1981. [Google Scholar]

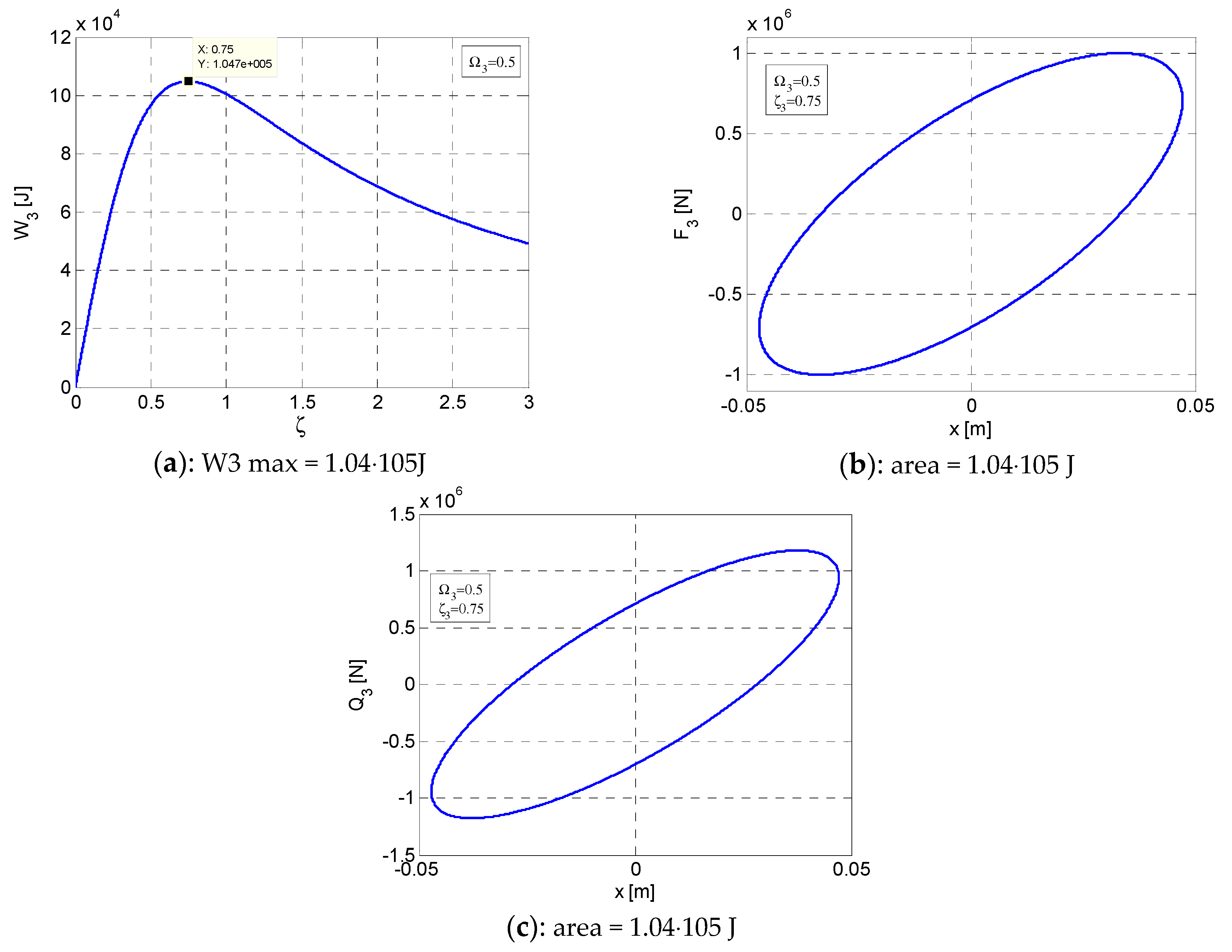
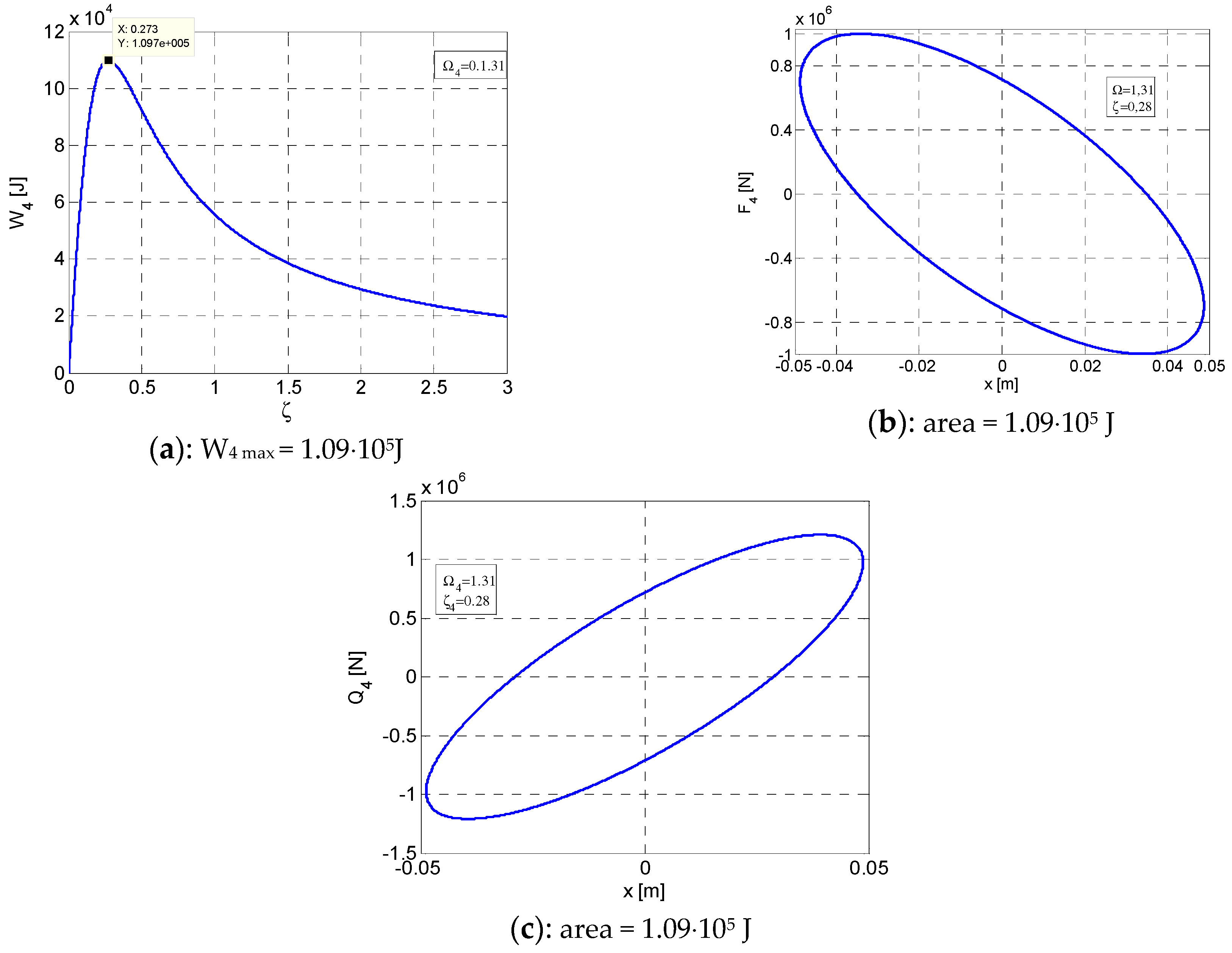

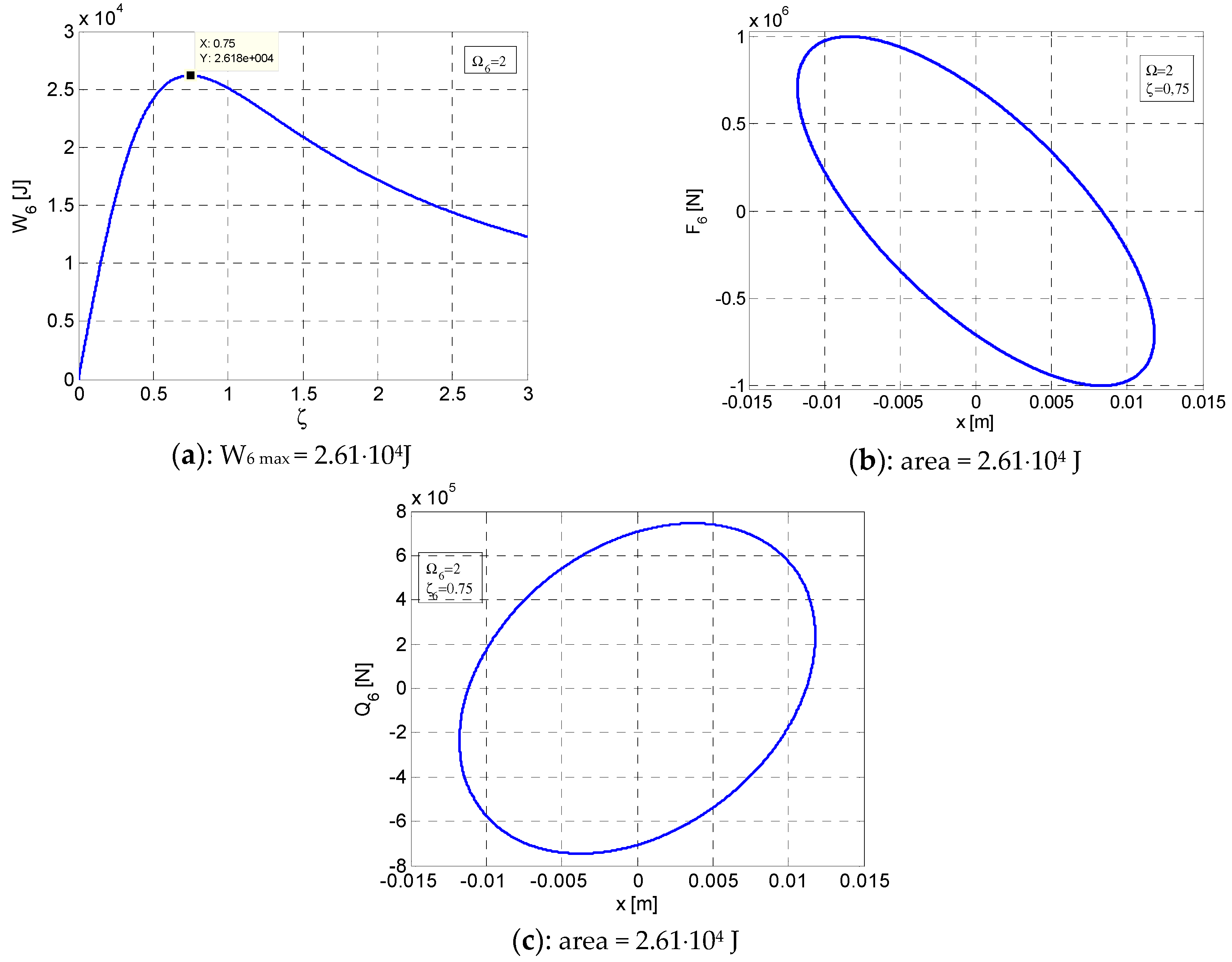
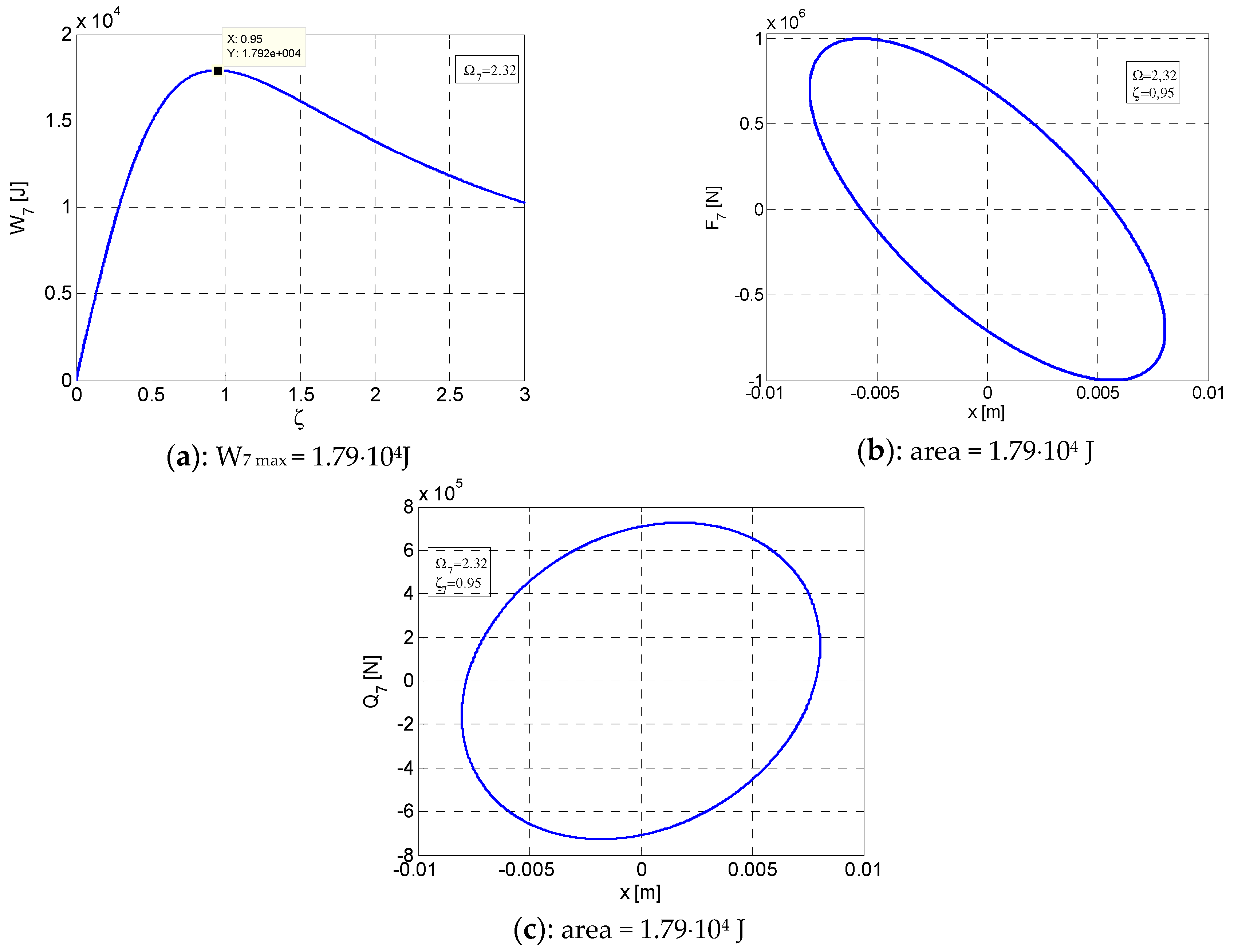

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bratu, P. Hysteretic Loops in Correlation with the Maximum Dissipated Energy, for Linear Dynamic Systems. Symmetry 2019, 11, 315. https://doi.org/10.3390/sym11030315
Bratu P. Hysteretic Loops in Correlation with the Maximum Dissipated Energy, for Linear Dynamic Systems. Symmetry. 2019; 11(3):315. https://doi.org/10.3390/sym11030315
Chicago/Turabian StyleBratu, Polidor. 2019. "Hysteretic Loops in Correlation with the Maximum Dissipated Energy, for Linear Dynamic Systems" Symmetry 11, no. 3: 315. https://doi.org/10.3390/sym11030315



