Face Recognition with Symmetrical Face Training Samples Based on Local Binary Patterns and the Gabor Filter
Abstract
1. Introduction
2. Literature Review
3. Preprocessing Methods
3.1. Wavelet Transforms
3.2. Gaussian Low-Pass Filter (GLPF)
3.3. Difference of Gaussians (DoG)
4. Feature Extraction Methods
4.1. Feature Extraction Using GLCM
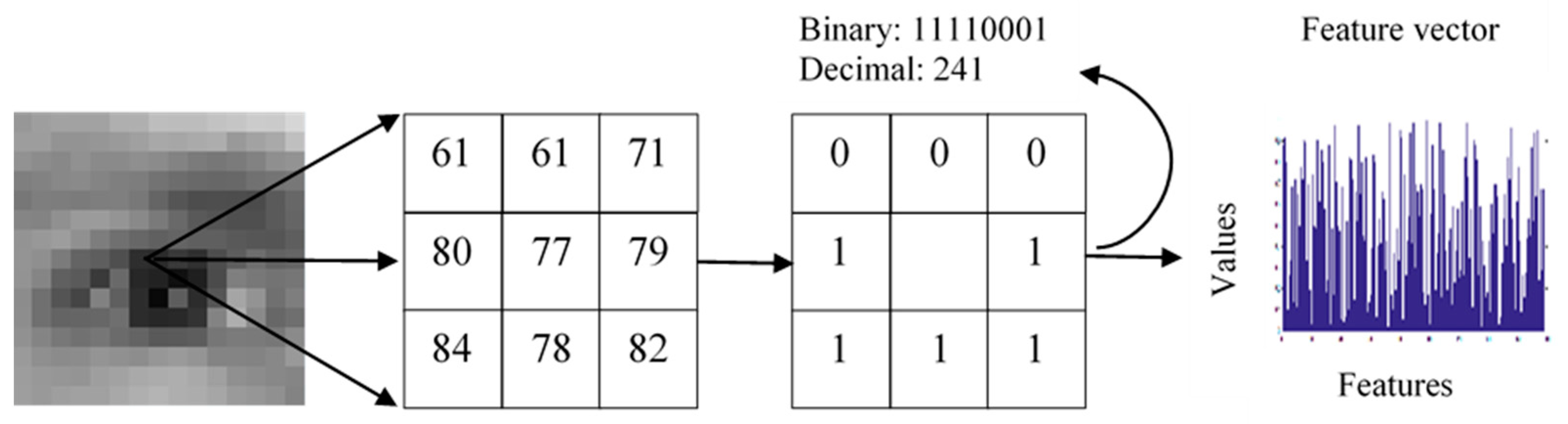
4.2. Feature Extraction Using LBP
4.3. Feature Extraction Using the Gabor Filter
5. Classification
5.1. Euclidean Distance
6. Dataset
6.1. The ORL Dataset
6.2. The Yale Dataset
7. Experiments and Results
7.1. Generating New Images
7.2. Experiments on the ORL Dataset
7.3. Experiments on Symmetrical ORL Dataset
7.4. Using a Preprocessing Stage
7.5. The GLCM Method
7.6. Combining Feature Extraction Methods
7.7. The Gabor Filter Method
7.8. Other Experiments
7.9. Experiments on the Yale Dataset
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahonen, T.; Hadid, A.; Pietikainen, M. Face description with local binary patterns: Application to face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 2037–2041. [Google Scholar] [CrossRef] [PubMed]
- Tan, X.; Chen, S.; Zhou, Z.-H.; Zhang, F. Face recognition from a single image per person: A survey. Pattern Recognit. 2006, 39, 1725–1745. [Google Scholar] [CrossRef]
- Liu, Z.; Pu, J.; Wu, Q.; Zhao, X. Using the original and symmetrical face training samples to perform collaborative representation for face recognition. Optik 2016, 127, 1900–1904. [Google Scholar] [CrossRef]
- Liu, L.; Fieguth, P.; Guo, Y.; Wang, X.; Pietikäinen, M. Local binary features for texture classification: Taxonomy and experimental study. Pattern Recognit. 2017, 62, 135–160. [Google Scholar] [CrossRef]
- Julsing, B. Face Recognition with Local Binary Patterns; Research No. SAS008-07; University of Twente: Enschede, The Netherlands, 2007. [Google Scholar]
- Ahonen, T.; Hadid, A.; Pietikäinen, M. Face recognition with local binary patterns. In Computer Vision-Eccv 2004, 2nd ed.; Springer: Berlin, Germany, 2004; pp. 469–481. [Google Scholar]
- Yang, P.; Yang, G. Feature extraction using dual-tree complex wavelet transform and gray level co-occurrence matrix. Neurocomputing 2016, 197, 212–220. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, J. Facial Expression Recognition by Fusing Gabor and Local Binary Pattern Features. In Proceedings of the International Conference on Multimedia Modeling, Reykjavik, Iceland, 4–6 January 2017; pp. 209–220. [Google Scholar]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Arabi, P.M.; Joshi, G.; Deepa, N.V. Performance evaluation of glcm and pixel intensity matrix for skin texture analysis. Perspect. Sci. 2016, 8, 203–206. [Google Scholar] [CrossRef]
- Li, W.; Mao, K.; Zhang, H.; Chai, T. Designing compact gabor filter banks for efficient texture feature extraction. In Proceedings of the 2010 11th International Conference on Control Automation Robotics & Vision, Singapore, 7–10 December 2010; pp. 1193–1197. [Google Scholar]
- Tan, X.; Triggs, B. Fusing gabor and lbp feature sets for kernel-based face recognition. In Proceedings of the International Workshop on Analysis and Modeling of Faces and Gestures, Rio de Janeiro, Brazil, 20 October 2007; pp. 235–249. [Google Scholar]
- Makandar, A.; Halalli, B. Image enhancement techniques using highpass and lowpass filters. Int. J. Comput. Appl. 2015, 109, 21–27. [Google Scholar] [CrossRef]
- Anila, S.; Devarajan, N. Preprocessing technique for face recognition applications under varying illumination conditions. Glob. J. Comput. Sci. Technol. 2012, 12, 12–18. [Google Scholar]
- Jadhav, D.V.; Holambe, R.S. Feature extraction using radon and wavelet transforms with application to face recognition. Neurocomputing 2009, 72, 1951–1959. [Google Scholar] [CrossRef]
- Samaria, F.S.; Harter, A.C. Parameterisation of a stochastic model for human face identification. In Proceedings of the Second IEEE Workshop on Applications of Computer Vision, Sarasota, FL, USA, 5–7 December 1994; pp. 138–142. [Google Scholar]
- Georghiades, A.; Belhumeur, P.; Kriegman, D. Yale Face Database. Center for Computational Vision and Control at Yale University, 1997. Available online: http://cvc.cs.yale.edu/cvc/projects/yalefaces/yalefaces.html (accessed on 31 October 2016).
- Azeem, A.; Sharif, M.; Raza, M.; Murtaza, M. A survey: Face recognition techniques under partial occlusion. Int. Arab J. Inf. Technol. 2014, 11, 1–10. [Google Scholar]
- Mehta, G.; Vatta, S. An introduction to a face recognition system using pca, flda and artificial neural networks. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 1418–1420. [Google Scholar]
- Zhao, W.; Chellappa, R.; Phillips, P.J.; Rosenfeld, A. Face recognition: A literature survey. ACM Comput. Surv. (CSUR) 2003, 35, 399–458. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Zhang, L. Gabor feature based sparse representation for face recognition with gabor occlusion dictionary. In Computer Vision–Eccv 2010; Springer: Berlin, Germany, 2010; pp. 448–461. [Google Scholar]
- Mairal, J.; Ponce, J.; Sapiro, G.; Zisserman, A.; Bach, F.R. Supervised dictionary learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 1033–1040. [Google Scholar]
- He, X.; Yan, S.; Hu, Y.; Niyogi, P.; Zhang, H.-J. Face recognition using laplacianfaces. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 328–340. [Google Scholar] [PubMed]
- Belhumeur, P.N.; Hespanha, J.P.; Kriegman, D.J. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 711–720. [Google Scholar] [CrossRef]
- Turk, M.A.; Pentland, A.P. Face recognition using eigenfaces. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Maui, HI, USA, 3 June 1991; pp. 586–591. [Google Scholar]
- Tunç, B.; Gökmen, M. Manifold learning for face recognition under changing illumination. Telecommun. Syst. 2011, 47, 185–195. [Google Scholar] [CrossRef]
- Tran, C.K.; Tseng, C.D.; Lee, T.F. In Improving the face recognition accuracy under varying illumination conditions for local binary patterns and local ternary patterns based on weber-face and singular value decomposition. In Proceedings of the 2016 3rd International Conference on Green Technology and Sustainable Development (GTSD), Kaohsiung, Taiwan, 24–25 November 2016; pp. 5–9. [Google Scholar]
- Wiskott, L.; Fellous, J.-M.; Kuiger, N.; Von Der Malsburg, C. Face recognition by elastic bunch graph matching. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 775–779. [Google Scholar] [CrossRef]
- Georghiades, A.S.; Belhumeur, P.N.; Kriegman, D.J. From few to many: Illumination cone models for face recognition under variable lighting and pose. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 643–660. [Google Scholar] [CrossRef]
- Shashua, A.; Riklin-Raviv, T. The quotient image: Class-based re-rendering and recognition with varying illuminations. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 129–139. [Google Scholar] [CrossRef]
- Zhou, S.; Chellappa, R. Rank constrained recognition under unknown illuminations. In Proceedings of the IEEE International Workshop on Analysis and Modeling of Faces and Gestures, Nice, France, 17 October 2003; pp. 11–18. [Google Scholar]
- Zhang, L.; Samaras, D. Face recognition from a single training image under arbitrary unknown lighting using spherical harmonics. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 351–363. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Zhang, L. Face recognition algorithm based on discriminative dictionary learning and sparse representation. Neurocomputing 2016, 174, 749–755. [Google Scholar] [CrossRef]
- Kim, T.-K.; Kittler, J. Locally linear discriminant analysis for multimodally distributed classes for face recognition with a single model image. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 318–327. [Google Scholar] [PubMed]
- Jaiswal, S. Comparison between face recognition algorithm-eigenfaces, fisherfaces and elastic bunch graph matching. Int. J. Glob. Res. Comput. Sci. 2011, 2, 187–193. [Google Scholar]
- Pentland, A.; Moghaddam, B.; Starner, T. View-based and modular eigenspaces for face recognition. In Proceedings of the 1994 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 84–91. [Google Scholar]
- Gross, R.; Matthews, I.; Baker, S. Eigen light-fields and face recognition across pose. In Proceedings of the Fifth IEEE International Conference on Automatic Face and Gesture Recognition, Washington, DC, USA, 21 May 2002; pp. 1–7. [Google Scholar]
- Zhou, S.K.; Chellappa, R. Illuminating light field: Image-based face recognition across illuminations and poses. In Proceedings of the Sixth IEEE International Conference on Automatic Face and Gesture Recognition, Seoul, Korea, 17–19 May 2004; pp. 229–234. [Google Scholar]
- Blanz, V.; Vetter, T. Face recognition based on fitting a 3d morphable model. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1063–1074. [Google Scholar] [CrossRef]
- Basri, R.; Jacobs, D.W. Lambertian reflectance and linear subspaces. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 218–233. [Google Scholar] [CrossRef]
- Ramamoorthi, R. Analytic pca construction for theoretical analysis of lighting variability in images of a lambertian object. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1322–1333. [Google Scholar] [CrossRef]
- Vasilescu, M.A.O.; Terzopoulos, D. Multilinear subspace analysis of image ensembles. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 16–22 June 2003. [Google Scholar]
- Wang, R.; Shan, S.; Chen, X.; Gao, W. Manifold-manifold distance with application to face recognition based on image set. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Shin, D.; Lee, H.-S.; Kim, D. Illumination-robust face recognition using ridge regressive bilinear models. Pattern Recognit. Lett. 2008, 29, 49–58. [Google Scholar] [CrossRef]
- Prince, S.J.; Warrell, J.; Elder, J.H.; Felisberti, F.M. Tied factor analysis for face recognition across large pose differences. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 970–984. [Google Scholar] [CrossRef] [PubMed]
- Davis, T.A.; Ramanujacharyulu, C. Statistical analysis of bilateral symmetry in plant organs. Sankhyā Indian J. Stat. Ser. B 1971, 33, 259–290. [Google Scholar]
- Endress, P.K. Symmetry in flowers: Diversity and evolution. Int. J. Plant Sci. 1999, 160, S3–S23. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Flynn, P.J.; Bowyer, K.W. Fully automated facial symmetry axis detection in frontal color images. In Proceedings of the Fourth IEEE Workshop on Automatic Identification Advanced Technologies, Buffalo, NY, USA, 16–18 October 2005; pp. 106–111. [Google Scholar]
- Zhao, W.Y.; Chellappa, R. Illumination-insensitive face recognition using symmetric shape-from-shading. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, SC, USA, 15 June 2000; pp. 286–293. [Google Scholar]
- Pan, G.; Wu, Z. 3d face recognition from range data. Int. J. Image Graph. 2005, 5, 573–593. [Google Scholar] [CrossRef]
- Farin, G.; Femiani, J.; Bae, M.; Lockwood, C. 3D face authentication and recognition based on bilateral symmetry analysis. Vis. Comput. 2005, 22, 43–55. [Google Scholar]
- Saha, S.; Bandyopadhyay, S. A symmetry based face detection technique. In Proceedings of the IEEE WIE National Symposium on Emerging Technologies, Kolkata, India, 29–30 June 2007; pp. 1–4. [Google Scholar]
- Peng, Y.; Li, L.; Liu, S.; Lei, T.; Wu, J. A new virtual samples-based crc method for face recognition. Neural Proc. Lett. 2018, 48, 313–327. [Google Scholar] [CrossRef]
- Swarnalatha, S.; Satyanarayana, P.; Babu, B.S. Wavelet transforms, contourlet transforms and block matching transforms for denoising of corrupted images via bi-shrink filter. Indian J. Sci. Technol. 2016, 9. [Google Scholar] [CrossRef]
- Dalali, S.; Suresh, L. Daubechives wavelet based face recognition using modified lbp. Procedia Comput. Sci. 2016, 93, 344–350. [Google Scholar] [CrossRef]
- Woods, G. Digital Image Processing, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Liu, D.-H.; Lam, K.-M.; Shen, L.-S. Illumination invariant face recognition. Pattern Recognit. 2005, 38, 1705–1716. [Google Scholar] [CrossRef]
- Winnemöller, H.; Kyprianidis, J.E.; Olsen, S.C. Xdog: An extended difference-of-gaussians compendium including advanced image stylization. Comput. Graph. 2012, 36, 740–753. [Google Scholar] [CrossRef]
- Davidson, M.W.; Abramowitz, M. Molecular Expressions Microscopy Primer: Digital Image Processing-Difference of Gaussians Edge Enhancement Algorithm; Olympus America Inc.; Florida State University: Miami, FL, USA, 2006. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Nikisins, O.; Greitans, M. Local binary patterns and neural network based technique for robust face detection and localization. In Proceedings of the 2012 BIOSIG International Conference of Biometrics Special Interest Group (BIOSIG), Darmstadt, Germany, 6–7 September 2012; pp. 1–6. [Google Scholar]
- Thomas, L.L.; Gopakumar, C.; Thomas, A.A. Face recognition based on gabor wavelet and backpropagation neural network. J. Sci. Eng. Res. 2013, 4, 2114–2119. [Google Scholar]
- Dobrisek, S.; Struc, V.; Krizaj, J.; Mihelic, F. Face recognition in the wild with the probabilistic gabor-fisher classifier. In Proceedings of the 2015 11th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (FG), Ljubljana, Slovenia, 4–8 May 2015. [Google Scholar]
- Haghighat, M.; Zonouz, S.; Abdel-Mottaleb, M. Identification using encrypted biometrics. In Proceedings of the International Conference on Computer Analysis of Images and Patterns, York, UK, 27–29 August 2013; pp. 440–448. [Google Scholar]
- Kamarainen, J.-K.; Kyrki, V.; Kalviainen, H. Invariance properties of gabor filter-based features-overview and applications. IEEE Trans. Image Proc. 2006, 15, 1088–1099. [Google Scholar] [CrossRef]
- Meshgini, S.; Aghagolzadeh, A.; Seyedarabi, H. Face recognition using gabor-based direct linear discriminant analysis and support vector machine. Comput. Electr. Eng. 2013, 39, 727–745. [Google Scholar] [CrossRef]
- Rahma, A.S.; Bisono, E.F.; Arifin, A.Z.; Navastara, D.A.; Indraswari, R. Generating automatic marker based on combined directional images from frequency domain for dental panoramic radiograph segmentation. In Proceedings of the 2017 Second International Conference on Informatics and Computing (ICIC), Papua, Indonesia, 2 November 2017; pp. 1–6. [Google Scholar]
- Dixon, S.J.; Brereton, R.G. Comparison of performance of five common classifiers represented as boundary methods: Euclidean distance to centroids, linear discriminant analysis, quadratic discriminant analysis, learning vector quantization and support vector machines, as dependent on data structure. Chemom. Intell. Lab. Syst. 2009, 95, 1–17. [Google Scholar]
- Nicolini, C.A.; Vakula, S. From Neural Networks and Biomolecular Engineering to Bioelectronics; Plenum Press: New York, NY, USA, 2013. [Google Scholar]
- Xiang, Z.; Tan, H.; Ye, W. The excellent properties of a dense grid-based hog feature on face recognition compared to gabor and lbp. IEEE Access 2018, 6, 29306–29319. [Google Scholar] [CrossRef]
- Ravat, C.; Solanki, S.A. Survey on different methods to improve accuracy of the facial expression recognition using artificial neural networks. Int. J. Sci. Res. Sci. Eng. Technol. 2018, 4, 151–158. [Google Scholar]
- Zhang, L.; Yang, M.; Feng, X. Sparse representation or collaborative representation: Which helps face recognition? In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 471–478. [Google Scholar]



















| Preprocessing Method | Feature Extraction Method | No. of Training Images | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| Recognition Rate % | |||||||||||
| No | LBP | OTS | 62.5 | 75 | 82.5 | 82.5 | 90 | 90 | 92.5 | 92.5 | 92.5 |
| OSTS | 67.5 | 77.5 | 87.5 | 87.5 | 92.5 | 95 | 95 | 95 | 95 | ||
| DWT | LBP | OTS | 70 | 80 | 90 | 92.5 | 95 | 95 | 95 | 97.5 | 97.5 |
| OSTS | 72.5 | 82.5 | 92.5 | 95 | 97.5 | 97.5 | 97.5 | 97.5 | 97.5 | ||
| GLPF | LBP | OTS | 72.5 | 80 | 87.5 | 92.5 | 95 | 95 | 97.5 | 97.5 | 97.5 |
| OSTS | 75 | 87.5 | 90 | 97.5 | 97.5 | 97.5 | 97.5 | 100 | 100 | ||
| DoG | LBP | OTS | 50 | 55 | 62.5 | 62.5 | 65 | 65 | 65 | 67.5 | 70 |
| OSTS | 52.5 | 60 | 62.5 | 67.5 | 67.5 | 67.5 | 67.5 | 72.5 | 72.5 | ||
| No | GLCM | OTS | 55 | 65 | 77.5 | 77.5 | 80 | 87.5 | 87.5 | 87.5 | 90 |
| OSTS | 60 | 67.5 | 85 | 85 | 87.5 | 90 | 90 | 90 | 90 | ||
| DWT | GLCM | OTS | 50 | 55 | 60 | 60 | 62.5 | 62.5 | 62.5 | 65 | 62.5 |
| OSTS | 57.5 | 70 | 70 | 80 | 77.5 | 75 | 80 | 80 | 82.5 | ||
| DoG | GLCM | OTS | 37.5 | 40 | 40 | 40 | 42.5 | 42.5 | 45 | 45 | 45 |
| OSTS | 40 | 42.5 | 50 | 50 | 50 | 50 | 50 | 52.5 | 55 | ||
| GLPF | GLCM | OTS | 57.5 | 67.5 | 80 | 80 | 80 | 82.5 | 82.5 | 82.5 | 82.5 |
| OSTS | 57.5 | 75 | 82.5 | 82.5 | 87.5 | 90 | 90 | 90 | 90 | ||
| No | LBP–GLCM | OTS | 70 | 82.5 | 87.5 | 92.5 | 92.5 | 95 | 95 | 95 | 95 |
| OSTS | 72.5 | 85 | 90 | 95 | 95 | 97.5 | 97.5 | 100 | 100 | ||
| No | Gabor | OTS | 87.5 | 95 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| OSTS | 90 | 97.5 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||
| No | PCA | OTS | 69 | 79 | 84 | 87 | 89 | 95 | 96 | 96 | 95 |
| No | CRC | OTS | 72 | 84 | 86 | 91 | 91 | 94 | 93 | 94 | 93 |
| No | SRC | OTS | 76 | 89 | 90 | 94 | 94 | 94 | 95 | 96 | 95 |
| No | SCRC | OSTS | 76 | 90 | 92 | 94 | 94 | 95 | 96 | 96 | 95 |
| Preprocessing Method | Feature Extraction Method | No. of Training Images | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Recognition Rate % | ||||||||||||
| No | LBP | OTS | 90 | 93 | 96 | 98 | 100 | 100 | 100 | 100 | 100 | 100 |
| OSTS | 95 | 98 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||
| No | GLCM | OTS | 70 | 75 | 87 | 87 | 87 | 87 | 87 | 87 | 87 | 87 |
| OSTS | 75 | 80 | 93 | 93 | 93 | 93 | 93 | 93 | 93 | 93 | ||
| DWT | GLCM | OTS | 12 | 15 | 18 | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| OSTS | 20 | 23 | 27 | 30 | 33 | 33 | 33 | 33 | 33 | 33 | ||
| DoG | GLCM | OTS | 60 | 60 | 73 | 73 | 73 | 73 | 80 | 80 | 80 | 80 |
| OSTS | 65 | 67 | 87 | 87 | 87 | 87 | 87 | 87 | 87 | 87 | ||
| GLPF | GLCM | OTS | 80 | 85 | 87 | 87 | 87 | 87 | 87 | 87 | 87 | 87 |
| OSTS | 80 | 93 | 93 | 93 | 93 | 93 | 93 | 93 | 93 | 93 | ||
| No | Gabor | OTS | 95 | 97 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| OSTS | 97 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||
| No | PCA | OTS | 69 | 89 | 89 | 93 | 87 | 87 | 98 | 95 | 96 | 100 |
| No | CRC | OTS | 87 | 93 | 94 | 99 | 98 | 96 | 98 | 95 | 96 | 100 |
| No | SRC | OTS | 87 | 90 | 90 | 98 | 92 | 92 | 98 | 100 | 100 | 100 |
| No | SCRC | OSTS | 88 | 95 | 97 | 99 | 100 | 100 | 100 | 100 | 100 | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allagwail, S.; Gedik, O.S.; Rahebi, J. Face Recognition with Symmetrical Face Training Samples Based on Local Binary Patterns and the Gabor Filter. Symmetry 2019, 11, 157. https://doi.org/10.3390/sym11020157
Allagwail S, Gedik OS, Rahebi J. Face Recognition with Symmetrical Face Training Samples Based on Local Binary Patterns and the Gabor Filter. Symmetry. 2019; 11(2):157. https://doi.org/10.3390/sym11020157
Chicago/Turabian StyleAllagwail, Saad, Osman Serdar Gedik, and Javad Rahebi. 2019. "Face Recognition with Symmetrical Face Training Samples Based on Local Binary Patterns and the Gabor Filter" Symmetry 11, no. 2: 157. https://doi.org/10.3390/sym11020157
APA StyleAllagwail, S., Gedik, O. S., & Rahebi, J. (2019). Face Recognition with Symmetrical Face Training Samples Based on Local Binary Patterns and the Gabor Filter. Symmetry, 11(2), 157. https://doi.org/10.3390/sym11020157




