Lossless and Efficient Polynomial-Based Secret Image Sharing with Reduced Shadow Size

Abstract

Thien-and-Lin’s polynomial-based secret image sharing (PSIS) is utilized as the basic method to achieve PSISs with better performances, such as meaningful shares, two-in-one property and shares with different priorities. However, this $(k,n)$ threshold PSIS cannot achieve lossless recovery for pixel values more than 250. Furthermore, current solutions to lossless recovery for PSIS have several natural drawbacks, such as large computational costs and random pixel expansion. In this paper, a lossless and efficient $(k,n)$ threshold PSIS scheme with reduced shadow size is presented. For lossless recovery and efficiency, two adjacent pixels are specified as a secret value, the prime in the sharing polynomial is replaced with 65,537, and then the additional screening operation can ensure each shared value in the range $[0,\mathrm{65,535}]$. To reduce shadows size and improve security, only the first $k-1$ coefficients are embedded with secret values and the last coefficient is assigned randomly. To prevent the leakage of secrets, generalized Arnold permutation with special key generating strategy is performed on the secret image prior to sharing process without key distribution. Both theoretical analyses and experiments are conducted to demonstrate the effectiveness of the proposed scheme.

1. Introduction

In a secret image sharing (SIS) scheme, the secret image is divided into several shadow images (or shares) without any secret information leakage, and it can be recovered only when a sufficient number of shadow images are combined together. In comparison with other cryptographic techniques, such as symmetric cryptography, asymmetric encryption and information hiding, SIS have a unique property, namely loss-tolerance, which means the secret information can still be recovered even though parts of shares are lost or destroyed. Therefore, it is beneficial in certain application scenarios, such as access control, distributed storage system, communications in unreliable public channels and electronic voting.

Currently, there are two main categories in the field of SIS: visual cryptography scheme (VCS) [1,2,3] and polynomial-based SIS (PSIS). The best advantage of VCS is the stack-to-see property, which means the secret information can be visually recognized by human visual system (HVS) just with sufficient shares stacking. This natural property of VCS is based on OR operation, so it has several drawbacks, such as lossy recovery and low visual quality of recovered images. In comparison with VCS, PSIS is more suitable for digital images, which can achieve secret image recovery with high visual quality.

In 1979, Shamir [4] first proposed a $(k,n)$ threshold polynomial-based secret sharing (PSS) scheme on number field. In the scheme, the secret is divided into n shares, any k or more of them can reveal the original secret, while any less than k shares can obtain nothing about the secret. Although the scheme is secure in theory, each participant requires relatively large storage space for the reason that the size of each share is equal to that of the secret [5]. Therefore, when using the scheme to share image or video at the pixel level, huge communication burden will be introduced.

In 2002, Thien and Lin [6] first introduced polynomial-based secret image sharing based on Shamir’s $(k,n)$ threshold PSS scheme. In the scheme, firstly, a $k-1$ degree polynomial is generated by setting the k coefficients to grayscale values of the permuted secret image. Then, the corresponding shadow image according to the polynomial is computed. The main difference between their scheme and Shamir’s scheme is that they do not use random coefficients, thus their scheme can reduce the size of each shadow image to $\frac{1}{k}$ of the secret image’s. The small shadow size is a good property in practice. From then on, plenty of PSIS schemes based on Thien-and-Lin’s scheme have been emerged to achieve more interesting performances, such as meaningful shares [7,8,9], two-in-one recovery [10,11] and shares with different priorities [12,13,14,15,16,17]. However, there exists a disadvantage in Thien-and-Lin’s PSIS scheme that it cannot actually recover a lossless secret image, which is described in detail in Section 2.

Lossless recovery is one of the most significant properties in the field of SS [18,19,20]; many researchers attempted to design SS or SIS schemes with both lossless recovery and other properties. Based on PSIS, there exist several solutions to lossless recovery for PSIS [21,22], and three primary lossless solutions are discussed in detail as follows. In Thien-and-Lin’s scheme with lossless recovery [6], they divided pixel values more than 250 into two parts, and then shared two parts with respective sharing phases. Yang et al. [23] utilized polynomial-based operations on Galois Field GF($2^8$) instead of integer computations in the finite field. In Ding and coworkers’ scheme [24], pixel values more than 250 also need to be divided, but then both parts are embedded into another two coefficients of the constructed polynomial during one single sharing phase. However, these solutions bring in some other negative effects, such as random shape changes, large shadow size and high computational complexity.

In this paper, a lossless and efficient $(k,n)$ threshold PSIS scheme with reduced shadow size is presented. In our method, we firstly utilize two adjacent pixel values to form a secret value which can be represented as a 16-bit integer from 0 to 65,535, and then specify 65,537 as the prime in the sharing polynomial with the help of a screening operation, to avoid generating share values larger than 65,535 which is the maximum of a 16-bit integer. These operations guarantee to achieve lossless recovery and high efficiency in our scheme. Subsequently, $k-1$ secret values are embedded into $k-1$ out of k coefficients of the sharing polynomial, so that it can achieve reduced shadow size. Besides, generalized Arnold permutation with special key generating strategy is performed on the secret image prior to sharing to prevent the leakage of secret information and key distribution. Theoretical analyses and experiments are conducted to show the effectiveness of the proposed scheme.

The rest of the paper is organized as follows. Some basic background and preliminary techniques are introduced in Section 2. The proposed PSIS is explicitly presented in Section 3. Furthermore, theoretical analyses of its performance are given in Section 4. The experiments and comparisons are shown in Section 5. Finally, we conclude our contributions in Section 6.

2. Preliminaries

2.1. Polynomial-Based Secret Image Sharing

Based on $k-1$ degree polynomial as shown in Equation (1), Shamir [4] proposed $(k,n)$ threshold PSS, which has been widely used in various practical applications. In Equation (1), the modulus p must be a prime to guarantee the recoverability. Furthermore, the coefficient $a_0$ is utilized to embed the secret value, while the other $k-1$ coefficients including $a_1,a_2,\cdots ,a_{k-1}$ are randomly assigned during each sharing phase. Therefore, the function value $f\left(x\right)$ is unrelated to $a_0$, which is the shared value corresponding to one certain serial number x. With n different serial numbers, n shared values $f\left(x_1\right),\cdots ,f\left(x_n\right)$ are generated for distribution. When obtaining any k shared values, the secret value $a_0$ will be precisely decrypted by the Lagrange interpolation.

$$f\left(x\right)=(a_0+a_{1}x+a_2{x}^2+\cdots +a_{k-1}{x}^{k-1})modp$$

(1)

Shamir’s PSS scheme can be directly utilized for the encryption of images, where the prime p is generally 251. Experimental results of $(3,4)$ threshold PSIS based on Shamir’s proposed PSS are given in Figure 1. Secret image S is shown in Figure 1a. One out of four shadow images $S{C}_1$ (Figure 1b) reveals nothing secret, as well as the recovered image $S_{t=2}^{\prime }$ with insufficient shares, where $S_{t=2}^{\prime }$ denotes recovery with any 2 shares. Images $S_{t=3}^{\prime }$ and $S_{t=4}^{\prime }$, which are similar to the original one, can be recovered with any 3 or more shares.

However, there exist some errors in the recovered images, as shown in Figure 1d,e, e.g., the top right surface of the left object and the top surface of the right object should be recovered to white as the original secret image, but they are wrongly restored into black. Since $p=251$, all the values in Equation (1), such as $x,f\left(x\right),a_0,a_1,\cdots ,a_{k-1}$, are limited in the range $[0,250]$. However, the grayscale image includes 256 gray levels from 0 to 255. As a result, some pixel values more than 250 cannot be processed, so classic PSISs are lossy recovery. Currently, many researchers ignore this kind of error in PSIS by truncating values more than 250 to 250. Although the recovered images by this technique look similar to the secret image, they cannot satisfy the requirement of lossless recovery in certain application scenarios.

Thien and Lin [6] proposed $(k,n)$ threshold PSIS with reduced shadow size based on Shamir’s PSS in 2002, which is more beneficial for storage and transmission of shares. In Thien-and-Lin’s scheme, all the coefficients $a_0,a_1,\cdots ,a_{k-1}$ in Equation (1) are used to embed secret values, so k times more secret information is processed than that of Shamir’s scheme during a sharing phase. Therefore, the size of the generated shadow images is $\frac{1}{k}$ times that of the secret image. However, parts of secret information will reveal in these reduced shadow size without pre-encryption for the secret image, as shown in Figure 2b–f. Due to the lack of randomness during each sharing phase, k secret values $a_0,a_1,\cdots ,a_{k-1}$ as a whole group have a one-to-one mapping to shared values $f\left(x_1\right),f\left(x_2\right),\cdots ,f\left(x_n\right)$. Therefore, adjacent shared values in each shadow image change a little, while pixel values in the secret image have a little changes. As a result, outlines of the secret image leak out in shares and recovered images with insufficient shares. Currently, pre-encryption needs to be done for security before the sharing process, so Thien-and-Lin’s scheme must be an integrated scheme which is a combination of PSIS and encryption.

2.2. PSIS with Lossless Recovery

Currently, there are three typical solutions to PSIS with lossless recovery, while some integrated schemes [22,25] with lossless recovery are not mentioned due to much larger costs.

In Thien-and-Lin’s scheme with lossless recovery [6], secret values equal to and more than 250 are divided into two parts, including 250 and the remainder modulo 250. Then, two parts are shared with two sharing phases separately. During recovery, if the first recovered value $s_1^{\prime }$ is 250, the second value $s_2^{\prime }$ also needs to be recovered. The original secret value $s^{\prime }$ is equal to $s_1^{\prime }+s_2^{\prime }$. By this technique, lossless recovery is achieved, but there exists an obvious drawback that it results in random pixel expansion of shadow images due to the random number of secret pixel values in $[250,255]$, so shares should be treated as data rather than images.

Yang et al. [23] proposed a solution based on Galois Field GF($2^8$), where the basic polynomial is changed into Equation (2). In Yang and coworkers’ scheme, all computations of integers are replaced with operations of polynomials in GF($2^8$), and there are 256 polynomials in corresponding to integers from 0 to 255. Therefore, lossless property can be achieved in this scheme. Afterwards, several researchers [11,26] referred Yang’s proposed PSIS with lossless recovery to build schemes with other properties. However, its detailed algorithm is not given yet, and further a proof for its effectiveness does not exist. More importantly, the sharing and recovery phases based on Galois Field have much larger costs than classic PSIS schemes.

$$f\left(x\right)=(a_0+a_{1}x+a_2{x}^2+\cdots +a_{k-1}{x}^{k-1})mod(2^8)$$

(2)

Ding et al. [24] introduced a new solution to lossless recovery. Similar to Thien-and-Lin’s scheme, integers from 250 to 255 are divided into two parts, but both parts are shared during one sharing phase. For example, in $(2,2)$ threshold scheme, $a_0$ and $a_1$ are utilized to embed 250 and the remainder, respectively. To guarantee the security, it needs a technique to increase the randomness: $a_1$ should be random integer multiples of the remainder r, which is no more than 250. Therefore, the secret value can be recovered with k shared values after recombination. However, the size of shadow images is equal to that of the secret image, as shown in Figure 3.

2.3. Generalized Arnold Permutation

Arnold map was proposed by Russian mathematician Vladimir I. Arnold in 1968. Generalized Arnold map, which is shown in Equation (3), is the generalization of Arnold map. $\alpha$ and $\beta$ are integers, N is the dimension of an image matrix, and $(x,y)$ is the original position that is mapped to the new position $(x^{\prime },y^{\prime })$. This permutation randomizes the original order of pixels or bits in an image. However, after sufficient iterations, the original image is reconstructed. Inverse mapping using Equation (4) is a phase in decryption process to transform the shuffled image into the input image. The number of iterations in the permutation step must be equal to that of the inverse transformation.

$$\mathsf{\Gamma }:\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& \alpha \\ \beta & \alpha \beta +1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]modN$$

(3)

$${\mathsf{\Gamma }}^{\prime }:\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}\alpha \beta +1& -\alpha \\ -\beta & 1\end{array}\right]\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]modN$$

(4)

If M denotes the conversion matrix and $\theta$ denotes the number of iterations, it can be proven that $\theta$ iterations of Arnold permutation using the matrix M is equivalent to one single iteration of Arnold permutation using the matrix $M^{\theta }$ [27]. The three parameters $\alpha$, $\beta$, and $\theta$ can serve as the key of encryption and decryption.

3. The Proposed Scheme

3.1. Design Concept

In the classic PSIS, one pixel, which can be represented as 8 bits or a byte, is specified as a secret value or shared value. Our method specifies two adjacent pixel values to form a secret value or shared value, which can be represented as a 16-bit integer from 0 to 65,535. Therefore, the number of secret values is decreased by half. As a result, the total number of sharing phases or recovery phases will be decreased, and the efficiency of sharing and recovery will be improved.

In the classic PSIS, 251, the largest prime less than 255, is specified as the prime p, so all generated shared values are limited in $[0,250]$, which cannot cover 256 gray levels. In our scheme, when the secret values are 16-bit integers, 65,537, the smallest prime more than 65,535, can be selected as p. Most importantly, when the shared value is equal to the only integer 65,536 which cannot be represented as 16 bits in shadow image, a screening operation can be performed to give up the value and redoing the sharing phase to guarantee all shared values can be represented as 16 bits. As a result, all secret values in $[0,\mathrm{65,535}]$ can be processed by the new sharing polynomial as Equation (5), and the secret pixel values from 0 to 255 can be recovered losslessly.

$$f\left(x\right)=(a_0+a_{1}x+a_2{x}^2+\cdots +a_{k-1}{x}^{k-1})mod\mathrm{65,537}$$

(5)

In Thien-and-Lin’s PSIS, all coefficients are used to embed the secret values. As mentioned in Section 2, the lack of randomness causes the leakage of secret information, so pre-encryption is necessary to guarantee the security. Our method is to utilize the first $k-1$ coefficients in Equation (5) to embed secret values while randomly selecting the last coefficient $a_{k-1}$ in $[0,\mathrm{65,537}]$ to increase the randomness and thus security. As a result, the size of each shadow images is only $\frac{1}{k-1}$ of the secret image($k=2,3,\cdots ,n$), at the same time the one-to-one mapping between secret values and shared values are destroyed by $a_{k-1}$, and then no secret information will be leaked out in shares. However, some recovered images with insufficient shares may still leak secret information by specific strategy. Therefore, to increase the security, we also permute the secret image before doing sharing process by generalized Arnold permutation without key distributing separately.

In Thien-and-Lin’s PSIS, to permute the pixels of secret image, a permutation sequence is generated by a key. The key is kept by the system owner or shared among the owners of shadows, which indicates it is fixed or needs to be distributed extra. The key of generalized Arnold permutation is a set of three parameters including $\alpha$, $\beta$ and $\theta$, as mentioned in Section 2.3. In our scheme, the parameters are generated based on the statistical feature of all pixel values in the secret image. We first count the numbers of each grayscale pixel value and sort them in ascending order. Then, we select three small numbers represented as $l_1$, $l_2$ and $l_3$ ($l_1\le l_2\le l_3$) and three large numbers represented as $h_1$, $h_2$ and $h_3$ ($h_1\ge h_2\ge h_3$) according to a certain formula. For example, $l_1$, $l_2$ and $l_3$ can be the numbers at the position of $5\%$, $10\%$ and $15\%$ in the order, while $h_1$, $h_2$ and $h_3$ can be the three largest numbers. Thus, we can get the parameters as Equation (6). The modular operations make the generated parameters not too large, which can decrease computational costs of permutation to the acceptable range. Besides, the generated parameters depended on the secret image need no extra distribution.

$$\begin{array}{c}\hfill \theta =h_{1}mod{l}_1\\ \hfill \alpha =h_{2}mod{l}_2\\ \hfill \beta =h_{3}mod{l}_3\end{array}$$

(6)

3.2. The Permutation Process

The permutation process includes two phases, one is the permutation phase to permute the original secret image and obtain the permuted secret image before the sharing process, and the other is the inverse permutation phase after the recovery process. Suppose that we want to permute an image I with size of $N\times N$, the permutation process is given in Algorithm 1. We remark that:

• In Step 2, the formula to select the six numbers is fixed in advance.
• In Step 4, if in permutation phase before the sharing process, we evaluate M as Equation (7); else, in inverse permutation after the recovery process phase, we evaluate M as Equation (8).

  $$M={\left[\begin{array}{cc}1& \alpha \\ \beta & \alpha \beta +1\end{array}\right]}^{\theta }modN$$

  (7)

  $$M={\left[\begin{array}{cc}\alpha \beta +1& -\alpha \\ -\beta & 1\end{array}\right]}^{\theta }modN$$

  (8)

  $$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=M\left[\begin{array}{c}x\\ y\end{array}\right]modN$$

  (9)

Algorithm 1 The permutation process

Input: An image I with size of $N\times N$.

Output: A permuted image $\widehat{I}$ with size of $N\times N$

Step 1. Count the numbers of each grayscale pixel value in the image I and sort them in ascending order.

Step 2. Select three small numbers $l_1$, $l_2$, $l_3$ ($l_1\le l_2\le l_3$) and three large numbers $h_1$, $h_2$, $h_3$ ($h_1\ge h_2\ge h_3$) from the order according to a certain formula.

Step 3. Generate the three parameters $\alpha$, $\beta$ and $\theta$ as Equation (6).

Step 4. Evaluate the conversion matrix M as Equation (7) or Equation (8).

Step 5. For each pixel P with the position $(x,y)$ in the image I, map P to a new position $(x^{\prime },y^{\prime })$ according to Equation (9).

Step 6. Output the permuted image $\widehat{I}$.

3.3. The Sharing Process

Suppose that we want to divide a permuted secret image $\widehat{S}$ with size of $N\times N$ into n shadow images $S{C}_1,S{C}_2,\cdots ,S{C}_n$, the sharing process of our $(k,n)$ threshold PSIS scheme is given in Algorithm 2. We remark that.

• In Step 1, each section consists of $2(k-1)$ pixels due to the first $k-1$ coefficients in Equation (5) are utilized to embed secret values in Step 2 and each value consists of two adjacent pixel values in Step 3. Besides, to guarantee all pixels can be processed, the width of the image, N, should be an integer multiple of $2(k-1)$.
• In Step 4, the last coefficient $a_{k-1}$ is randomly assigned to improve the security.
• In Steps 5–7, we evaluate n shared values of each section. The screening operation occurs in Step 7 to guarantee none of the shared values is larger than 65,535.
• In Step 8, we obtain $2n$ shared pixels of each section.
• A sharing phase consists of Steps 3–8. In total, there are $N\times \frac{N}{2(k-1)}$ sharing phases, and $N\times \frac{N}{k-1}$ shared pixels for each shadow image are generated.

To illustrate the sharing phase of our method more intuitively, we give Example 1 as follows.

Example 1.

Given four grayscale pixels $\{99,56,138,235\}$ as a section of a permuted secret image, threshold parameters $(3,4)$ and serial numbers $\{1,2,3,4\}$.

Firstly, we assign the coefficients $a_0=99\times 256+56=\mathrm{25,400}$ and $a_1=138\times 256+235=\mathrm{35,563}$. Secondly, coefficient $a_2$ is generated randomly, we suppose that $a_2=4573$. Then, shared values $f\left(1\right)$, $f\left(2\right)$, $f\left(3\right)$ and $f\left(4\right)$ can be evaluated. Because $f\left(1\right)=\mathrm{25,400}+\mathrm{35,563}+4573mod\mathrm{65,537}=\mathrm{65,537}>\mathrm{65,535}$, so we re-generate another random integer, supposing that it is 17,386. Thus,

$f\left(1\right)=\mathrm{25,400}+\mathrm{35,563}+\mathrm{17,386}mod\mathrm{65,537}=\mathrm{12,812}$,

$f\left(2\right)=\mathrm{25,400}+\mathrm{35,563}\times 2+\mathrm{17,386}\times 2^{2}mod\mathrm{65,537}=\mathrm{34,996}$,

$f\left(3\right)=\mathrm{25,400}+\mathrm{35,563}\times 3+\mathrm{17,386}\times 3^{2}mod\mathrm{65,537}=\mathrm{26,415}$,

$f\left(4\right)=\mathrm{25,400}+\mathrm{35,563}\times 4+\mathrm{17,386}\times 4^{2}mod\mathrm{65,537}=\mathrm{53,606}$.

Finally, we obtain four pairs of shared pixels in $S{C}_1$, $S{C}_2$, $S{C}_3$ and $S{C}_4$ at positions $(1,1)$ and $(1,2)$, which are

$S{C}_1(1,1)=\mathrm{12,812}/256=50$, $S{C}_1(1,2)=\mathrm{12,812}mod256=12$,

$S{C}_2(1,1)=\mathrm{34,996}/256=136$, $S{C}_1(1,2)=\mathrm{34,996}mod256=180$,

$S{C}_3(1,1)=\mathrm{26,415}/256=103$, $S{C}_1(1,2)=\mathrm{26,415}mod256=47$,

$S{C}_4(1,1)=\mathrm{53,606}/256=209$, $S{C}_1(1,2)=\mathrm{53,606}mod256=102$.

Algorithm 2 The proposed $(k,n)$ threshold PSIS scheme

Input: A permuted secret image $\widehat{S}$ with size of $N\times N$; Threshold parameters $(k,n)$; n different serial numbers $x_1,x_2,\cdots ,x_n$.

Output:n shadow images $S{C}_1,S{C}_2,\cdots ,S{C}_n$.

Step 1. Divide the image S into $N\times \frac{N}{2(k-1)}$ non-overlapping sections, each of which consists of $2(k-1)$ adjacent pixels.

Step 2. For each $2(k-1)$-pixel section $Sec(i,j)=\{P_m(i,j)|m\in \left[1,2(k-1)\right]\}$, $i\in \left[1,N\right]$, $j\in \left[1,\frac{N}{2(k-1)}\right]$, repeat Steps 3–8 until all sections have been processed.

Step 3. Assign the coefficients $a_0,a_1,\cdots ,a_{k-2}$ as follows. $$\begin{array}{cc}{a}_0=& P_1(i,j)\times 256+P_2(i,j)\hfill \\ a_1=& P_3(i,j)\times 256+P_4(i,j)\hfill \\ & \cdots \hfill \\ a_{k-2}=& P_{2(k-2)+1}(i,j)\times 256+P_{2(k-2)+2}(i,j)\hfill \end{array}$$

Step 4. Generate a random integer from $[0,\mathrm{65,536}]$ as the coefficient $a_{k-1}$.

Step 5. For each serial number $x_t$, $t\in \left[1,n\right]$, repeat Steps 6–7 until all n shared values have been evaluated.

Step 6. Evaluate the shared value $f\left(x_t\right)$ as follows. $$f\left(x_t\right)=(a_0+a_1{x}_t+a_2{x}_t^2+\cdots +a_{k-1}{x}_t^{k-1})mod\mathrm{65,537}$$

Step 7. If $f\left(x_t\right)>\mathrm{65,535}$, return to Step 4 and redo Steps 4–7. Else continue.

Step 8. For each shared value $f\left(x_t\right)$, $t\in \left[1,n\right]$, generate two adjacent pixels in shadow image $S{C}_t$ as follows. $$\begin{array}{c}\hfill S{C}_t(i,2j-1)=f(x_t)/256\\ \hfill S{C}_t(i,2j)=f\left(x_t\right)mod256\end{array}$$

Step 9. Output n shadow images $S{C}_1,S{C}_2,\cdots ,S{C}_n$.

3.4. The Recovery Process

Without loss of generality, suppose that we want to reconstruct a permuted secret image $\widehat{S_r}$ with k shadow images $S{C}_1,S{C}_2,\cdots ,S{C}_k$, the recovery process is described in Algorithm 3. We remark that:

• In Step 1, we take the first two non-used adjacent pixels from each of the k shadow images, to form a set with k pairs of shared pixels. The number of all sets is $N\times \frac{N}{2(k-1)}$.
• Steps 2, 3 and 4 are the inverse operations of Steps 8, 6 and 3 in Algorithm 2, respectively.
• A recovery phase consists of Steps 2–4. In each recovery phase, we retrieve a $2(k-1)$-pixel section of the permuted secret image as mentioned in Algorithm 2. In total, there are $N\times \frac{N}{2(k-1)}$ recovery phases.

Here, we also give Example 2 to illustrate how to retrieve a $2(k-1)$-pixel section.

Example 2.

Given three pairs of pixels $\{50,12\}$, $\{136,180\}$ and $\{103,47\}$ at positions $(1,1)$ and $(1,2)$ in each of three shadow images, threshold parameters $(3,4)$ and serial numbers $\{1,2,3\}$.

Firstly, we evaluate the three shared values $shar{e}_1(1,1)=50\times 256+12=\mathrm{12,812}$, $shar{e}_2(1,1)=136\times 256+180=\mathrm{34,996}$ and $shar{e}_3(1,1)=103\times 256+47=\mathrm{26,415}$. Thus, three polynomials can be constructed as follows.

$$\left\{\begin{array}{c}{a}_0+a_1\times 1+\cdots +a_{k-1}\times 1=\mathrm{12,812}mod\mathrm{65,537}\hfill \\ a_0+a_1\times 2+\cdots +a_{k-1}\times 2^2=\mathrm{34,996}mod\mathrm{65,537}\hfill \\ a_0+a_1\times 3+\cdots +a_{k-1}\times 3^2=\mathrm{26,415}mod\mathrm{65,537}\hfill \end{array}\right.$$

Then, we solve the equations to obtain $a_0=\mathrm{25,400}$, $a_1=\mathrm{35,563}$. Finally, we retrieve a 4-pixel section $\{99,56,138,235\}$ corresponding to $a_0$ and $a_1$.

$$\left\{\begin{array}{c}{a}_0+a_1\times x_1+\cdots +a_{k-1}\times x_1^{k-1}=shar{e}_1(i,j)mod\mathrm{65,537}\hfill \\ a_0+a_1\times x_2+\cdots +a_{k-1}\times x_2^{k-1}=shar{e}_2(i,j)mod\mathrm{65,537}\hfill \\ \cdots \hfill \\ a_0+a_1\times x_k+\cdots +a_{k-1}\times x_k^{k-1}=shar{e}_k(i,j)mod\mathrm{65,537}\hfill \end{array}\right.$$

(10)

Algorithm 3 Secret image recovery of the proposed scheme

Input:k shadow images $S{C}_1,S{C}_2,\cdots ,S{C}_k$ with size of $N\times \frac{N}{k-1}$; Threshold parameters $(k,n)$; k different serial numbers $x_1,x_2,\cdots ,x_k$.

Output: A reconstructed permuted secret image $\widehat{S_r}$.

Step 1. For each two non-overlapping adjacent pixels $S{C}_t(i,2j-1)$ and $S{C}_t(i,2j)$ in each shadow image $S{C}_t$, $i\in \left[1,N\right]$, $j\in \left[1,\frac{N}{2(k-1)}\right]$, $t\in \left[1,k\right]$, repeat Steps 2–4 until all pairs pixels of the k shadow images have been processed.

Step 2. Evaluate the k shared values $shar{e}_t(i,j)$, $t\in \left[1,k\right]$, as follows. $$shar{e}_t(i,j)=S{C}_t(i,2j-1)\times 256+S{C}_t(i,2j)$$

Step 3. Use the k serial numbers, k shared values and the Lagrange’s interpolation to obtain the $k-1$ coefficients $a_0,a_1,\cdots ,a_{k-2}$ in the the linear equations as Equation (10).

Step 4. Obtain the $2(k-1)$ pixels $\{P_m(i,j)|m\in \left[1,2(k-1)\right]\}$ corresponding to $a_0,a_1,\cdots ,a_{k-2}$ as follows. $$\begin{array}{cc}{P}_1(i,j)& =a_0/256\hfill \\ P_2(i,j)& =a_{0}mod256\hfill \\ & \cdots \hfill \\ P_{2(k-1)-1}(i,j)& =a_{k-2}/256\hfill \\ P_{2(k-1)}(i,j)& =a_{k-2}mod256\hfill \end{array}$$

Step 5. Obtain all $N\times N$ pixels and reconstruct the permuted secret image $\widehat{S_r}$.

Step 6. Output $\widehat{S_r}$.

4. Performance Analyses

This section introduces the performances of the proposed scheme by theoretically analyzing the image quality, valid threshold construction and security.

4.1. Lossless Recovery Analysis

In a sharing phase, a secret value is represented as two adjacent pixel values, thus the range of a secret value is $[0,\mathrm{65,535}]$. In Equation (5), $k-1$ secret values are utilized as coefficients $a_0,a_1,\cdots ,a_{k-2}$, while the last coefficients $a_{k-1}$ is randomly assigned in $[0,\mathrm{65,537}]$ during one sharing phase. Therefore, with a certain serial number x, the shared value $f\left(x\right)$ is generated in $[0,\mathrm{65,537}]$, and there might exist a certain value of $a_{k-1}$ that makes $f\left(x\right)$ equal to 65,536. When $f\left(x\right)$ is equal to 65,536, the screening operation will assign another value to $a_{k-1}$, and the value of $f\left(x\right)$ will be changed too. Thus, each shared value can be limited in $[0,\mathrm{65,535}]$ and represented as two adjacent shared pixel values.

In a recovery phase, with k shared values, the linear equations as Equation (10) can be constructed. By solving the linear equations, the k coefficients $a_0,a_1,\cdots ,a_{k-1}$ are uniquely determined. Among them, $a_0,a_1,\cdots ,a_{k-2}$ are the $k-1$ secret values, each of which is represented as two adjacent secret pixel values. Hence, the secret value is recovered losslessly and the proposed scheme is a lossless scheme. Furthermore, we can conclude that any k or more shared values can reveal the $k-1$ secret values losslessly. Therefore, it is easy to conclude that any k or more shadow images can disclose the secret image losslessly.

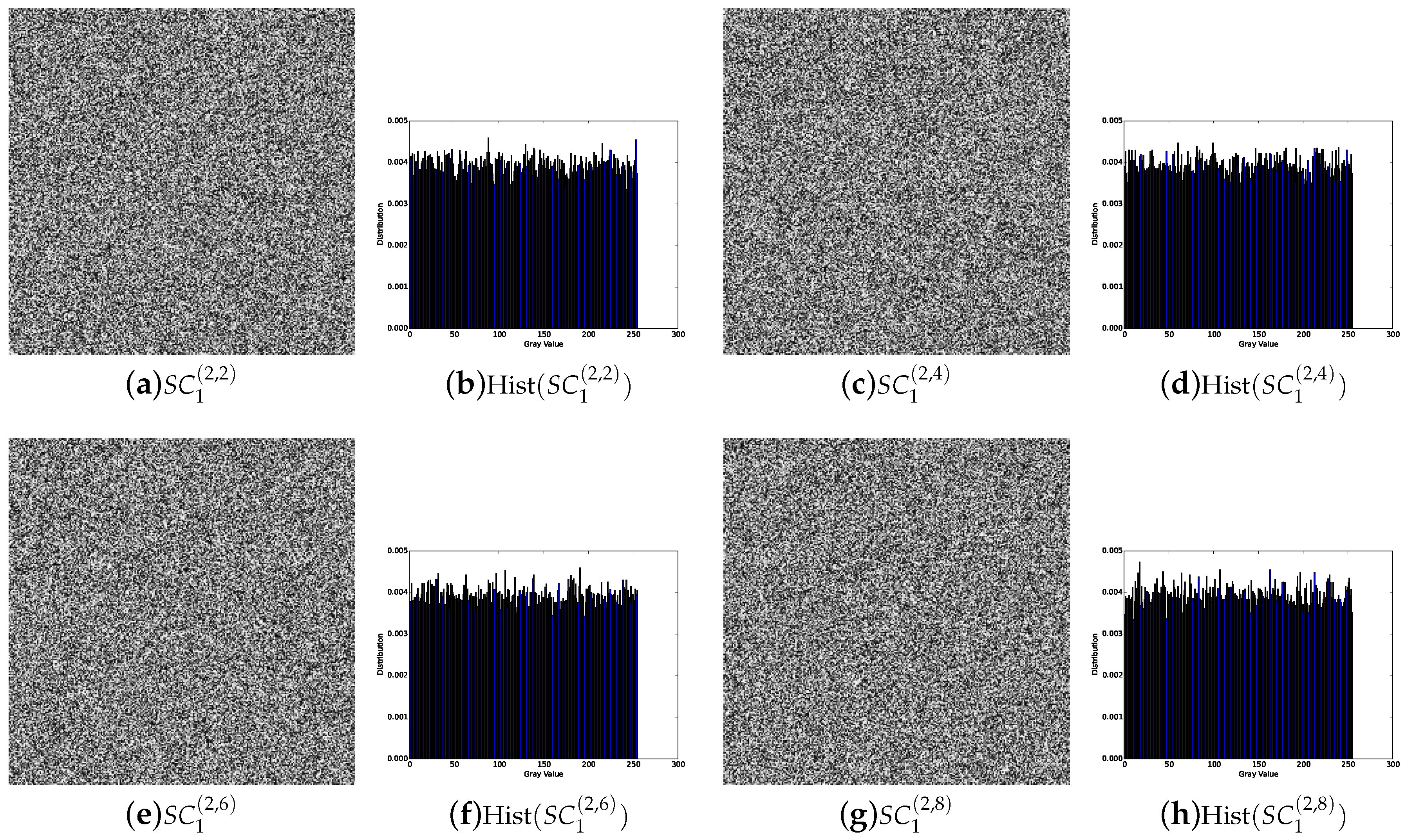
4.2. Threshold Analysis

Without losing of generality, suppose that only $k-1$ shared values are given. From Equation (5), we can construct only $k-1$ polynomials as Equation (11). To solve for k unknowns using these $k-1$ equations, there are 65,537 possible solution sets. The possibility of guessing the secret values is only about $\frac{1}{\mathrm{65,537}}$, and we cannot uniquely determine them. It indicates that any $k-1$ or less shared values cannot reveal the secret values. Therefore, it is easy to conclude that any $k-1$ or less shadow images cannot get sufficient information to reveal the secret image. Furthermore, as analyzed in Section 4.1, we have concluded that any k or more shadow images can disclose the secret image losslessly.

$$\left\{\begin{array}{c}{a}_0+a_1\times x_1+\cdots +a_{k-1}\times x_1^{k-1}=shar{e}_1(i,j)mod\mathrm{65,537}\hfill \\ a_0+a_1\times x_2+\cdots +a_{k-1}\times x_2^{k-1}=shar{e}_2(i,j)mod\mathrm{65,537}\hfill \\ \cdots \hfill \\ a_0+a_1\times x_{k-1}+\cdots +a_{k-1}\times x_{k-1}^{k-1}=shar{e}_{k-1}(i,j)mod\mathrm{65,537}\hfill \end{array}\right.$$

(11)

Given the above discussion, it can be concluded that the proposed scheme is a $(k,n)$ threshold PSIS scheme.

4.3. Security Analysis

For the proposed $(k,n)$ threshold PSIS, there are totally ${\mathrm{65,537}}^k$ sets of shared values before screening, and further there are 65,537 sets of shared values corresponding to every set of $k-1$ secret values from 0 to 65,536. If $k-1$ secret values are given, the last coefficient $a_{k-1}$ is randomly assigned in $[0,\mathrm{65,537}]$, so there must exist a certain value of $a_{k-1}$ which makes $f\left(x_i\right)$ equal to 65,536. Furthermore, there are totally ${\mathrm{65,537}}^{k-1}$ sets of $a_0,\cdots ,a_{k-1}$ which make $f(x_i)$ equal to 65,536. For n shares, there are at most $n\times {\mathrm{65,537}}^{k-1}$ sets of shared values, which include one or more 65,536 that need to be deleted during the sharing process. Considering that several shared values may be equal to 65,536 at the same time, the sum of deleted sets $Su{m}_{screening}$ is less than ${\mathrm{65,537}}^{k-1}$. Besides, secret values belong to the range from 0 to 65,535 for two adjacent pixel values in 8-bit grayscale image, so ${\mathrm{65,537}}^{k-1}$ sets including the secret value 65,536 need to be deleted from the final sets. Therefore, there are at least $Su{m}_{sharing}={\mathrm{65,537}}^k-Su{m}_{screening}-{\mathrm{65,537}}^{k-1}=(\mathrm{65,537}-n-1)\times {\mathrm{65,537}}^{k-1}$ sets for sharing. There are ${\mathrm{65,537}}^{k-1}$ sets of $k-1$ secret values, so there are at least $\frac{Su{m}_{sharing}}{{\mathrm{65,536}}^{k-1}}=(\mathrm{65,537}-n-1)\times \frac{{\mathrm{65,537}}^{k-1}}{{\mathrm{65,536}}^{k-1}}\approx \mathrm{65,537}-n-1$ sets corresponding to each set of $k-1$ secret values. In other words, there are at most $n+1$ sets screened by the screening operation, so that the randomness of sharing remains to guarantee the security and effectiveness of the proposed PSIS.

Moreover, before sharing process, the secret image will be permuted by generalized Arnold permutation; therefore, there is no correlation between polynomials. In other words, the lack of information cannot be supplied from the image property, as the neighboring pixels are usually similar. In addition, note that the parameters of generalized Arnold permutation is generated based on the feature of secret image, which will increase the randomness of key; thus, the security of the scheme is further enhanced.

5. Experiments and Comparisons

In this section, experiments and comparisons are presented to evaluate the effectiveness of the proposed scheme.

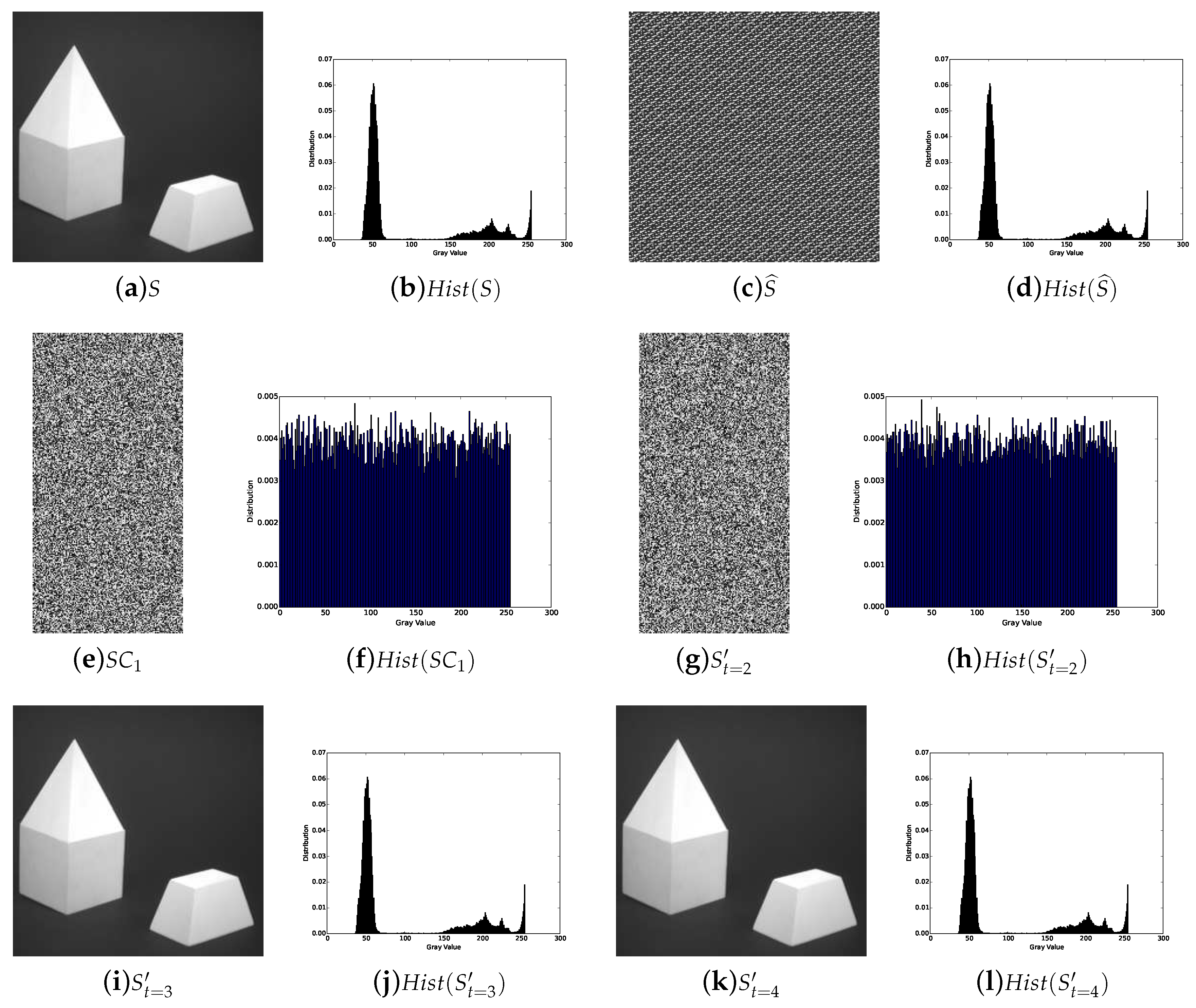
5.1. Image Illustration

Figure 4 is an experimental result of our proposed $(k,n)$ threshold PSIS, where $k=3$ and $n=4$. Figure 4a is the original secret image and Figure 4c is the permuted image, and their statistical histograms of each pixel value are drawn in Figure 4b,d respectively. Figure 4e is the first one out of four shadow images $S{C}_1$ without any secret information revealed; its size is $\frac{1}{2}$ of the secret image, that its histogram follows the uniform distribution providing effective proof of its security. Note that, for the recovery process, the sharing polynomials are reconstructed based on the number of collected shares t if $t<k$, as shown in Equation (12). Therefore, when $t(t<k)$ shares are collected in $(k,n)$ threshold scheme, the recovered image is $t-1$ times the shadow images, e.g., $S_{t=2}^{\prime }$, as shown in Figure 4g, has the same size of $S{C}_1$. There is no leakage of secret information in $S_{t=2}^{\prime }$, which is noise-like similar to $S{C}_1$. With k or more shadow images, the secret image can be reconstructed losslessly, as shown in Figure 4i,k.

$$f\left(x\right)=(a_0+a_1\times x+\cdots +a_{t-1}\times x^{t-1})mod\mathrm{65,537}$$

(12)

Figure 5 shows a further experimental result of our proposed $(k,n)$ threshold PSIS. As mentioned in Section 4, there are at least $\mathrm{65,537}-n-1$ sets of shared values for each set of $k-1$ secret values. Therefore, the security of the proposed PSIS decreases with the increase of the number of shares n. To prove whether the decrease of the security will result in the leakage of secret information, four shadow images of $(2,n)$ threshold PSIS with different n and their statistical histograms of each pixel value are provided in Figure 5. Obviously, all these shares are noise-like, and their histograms follow the uniform distribution. As a result, it is considered that the proposed $(k,n)$ threshold PSIS scheme is secure when n is not too large.

From experimental results above, the properties of the proposed PSIS are concluded as follows:

• Lossless recovery: The secret image can be reconstructed losslessly with k or more shadow images.
• Security: The shadow images are noisy-like, thus every single shadow is secure. Furthermore, there is no leakage of secret information from recovered images with less than k shadow images, which shows security of our scheme.
• Reduced shadow size: In the proposed $(k,n)$ threshold PSIS, the size of each shadow image is $\frac{1}{k-1}$ of that of the secret image.

In addition, when we skip the permutation process but do sharing process directly, the experimental result is shown in Figure 6. Similar to experimental result in Figure 4, the four shadow images $S{C}_1$, $S{C}_2$, $S{C}_3$, and $S{C}_4$ are noisy; and no leakage of secret information in $S_{t=2}^{\prime }$ exists, which is noise-like similar to $S{C}_1$; the secret image can be losslessly reconstructed with k or more shadow images, as shown in Figure 4g,h. In fact, when sharing natural secret image or secret data, we can also use our $(k,n)$ threshold PSIS without permutation in general application scenarios.

5.2. Comparisons with Related Works

Herein, we provide some comparisons between our proposed scheme and other related typical schemes [4,6,23,24].

According to experimental results shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 6, we can distinguish differences between our proposed scheme and other schemes intuitively, such as lossless recovery, reduced shadow size and security. Meanwhile, more comparisons of significant properties are shown in

Table 1. Comparisons of significant properties.

Schemes	Lossless Recovery	Shadow Size	Random Pixel Expansion	Pre-Encryption and Decryption	Computational Complexity
Shamir et al. [4]	No	1	No	No	$O\left(k{log}^{2}k\right)$
Thien-and-Lin (lossy) [6]	No	$\frac{1}{k}$	No	Yes	$O\left(k^3\right)$
Thien-and-Lin (lossless) [6]	Yes	$\ge \frac{1}{k}$	Yes	Yes	$O\left(k^3\right)$
Yang et al. [23]	Yes	1	No	No	High
Ding et al. [24]	Yes	1	No	No	$O\left(k^3\right)$
Our PSIS	Yes	$\frac{1}{k-1}$	No	Yes	$O\left(k^3\right)$
Our PSIS (without permutation)	Yes	$\frac{1}{k-1}$	No	No	$O\left(k^3\right)$

, including random pixel expansion, pre-encryption before sharing for security, and computational complexity. Comparisons of these properties are discussed in detail as follows.

• Lossless recovery: Classic PSISs can only achieve lossy recovery, while several other PSISs including our scheme with different solutions can achieve lossless recovery.
• Shadow size: Except Thien-and-Lin’s and Our proposed PSISs, shadow size generated by other PSISs are the same or more than that of the secret image. The size of our PSIS is a little larger than that of Thien-and-Lin’s, but the security and lossless recovery can be guaranteed. Furthermore, we can also utilize partial bits of the coefficient $a_{k-1}$ to embed more secret values and assign remainder bits randomly, to further reduce the shadow size as well as to improve the efficiency.
• Random pixel expansion: Random pixel expansion may occur in Thien-and-Lin’s lossless PSIS, so its generated shares can only be stored as data rather than images. In our scheme, n noise-like shares with size of $\frac{1}{k-1}$ of that of the secret image are generated, which can be still stored as images.
• Pre-encryption and decryption: Thien-and-Lin’s PSIS needs extra pre-encryption to avoid the leakage of secret information, so it results in more costs. Our scheme needs no extra permutation if there is no higher level of security requirement in general application scenarios.
• Computational complexity: In some PSISs, there is extra recombination or decryption after the recovery process, so only the complexity of secret recovery process is calculated here. Only the constant coefficient needs to be calculated by the Lagrange interpolation as the secret value in Shamir’s PSISs, while two or more coefficients as secret values in Thien-and-Lin’s, Ding and coworkers’ and Our PSISs should be computed by solving equations. Therefore, the complexity of the latter PSISs is larger than that of the former PSISs. Yang and coworkers’ PSIS is based on Galois Field GF($2^8$), which lacks the theoretical calculation of computational complexity. However, the complexity of computations based on Galois Field GF($2^8$) is much larger than that of computations based on integers.

In addition, in our scheme, two adjacent pixel values are specified as a secret value; thus, the total number of secret values is decreased by half, and the total number of sharing phases or recovery phases will also be decreased. It can be inferred that the efficiency of our scheme will be improved. However, it is difficult to give the theoretical proof of this inference because efficiency could be influenced by many other factors. Thus, to evaluate the efficiency of the proposed scheme, we set up additional experiments with the $512\times 512$ grayscale image “Cameraman” as shown in Figure 7. The algorithms of Shamir’s, Thien-and-Lin’s, Ding and coworkers’ and our PSISs are implemented using Python on a virtual machine with 32-bit Windows XP OS, Core i5 CPU, and 1 GB installed RAM.

Table 2. Comparisons of running time.

Schemes	Sharing Time (s)	Recovery Time (s)
Shamir et al. [4]	7.721	7.831
Thien and Lin (lossy) [6]	1.792	2.764
Ding et al. [24]	138.219	10.585
Our PSIS	2.213	2.694
Our PSIS (without permutation)	1.732	2.424
Our PSIS (mod 257)	2.714	3.205

presents the average running time for sharing and recovery in $(3,4)$ threshold PSIS. According to experimental results, comparisons are given as follows.

• The running time of our scheme is much shorter than that of Shamir’s and Ding and coworkers’ schemes, which indicates our scheme is more efficient than Shamir’s and Ding and coworkers’ schemes.
• The running time of our scheme is little longer than Thien-and-Lin’s scheme. However, if the permutation process is removed in our scheme, the running time is approximately equal to or even slightly shorter than that of Thien-and-Lin’s scheme. In fact, our scheme without permutation is sufficient to ensure security in general application scenarios.
• We can modify our scheme, specifying one pixel value as a secret value and 257 as the prime, with the same principle. As a result, the running time becomes longer than our original scheme’s. Therefore, to a certain degree, decreasing the number of secret values has improved the efficiency of sharing and recovery.

In other words, according to the experimental results and analyses above, it can be conclude that the proposed scheme has the feature of efficiency.

6. Conclusions

A lossless and efficient $(k,n)$ threshold PSIS scheme with reduced shadow size is proposed in this paper. For lossless recovery and efficiency, two adjacent pixel values are specified as a secret value, 65,537 is selected as the prime in the sharing polynomial, and then the additional screening operation can ensure each of shared values in the range $[0,\mathrm{65,535}]$; furthermore, the first $k-1$ coefficients are embedded with secret values to achieve reduced shadow size, while the last coefficient is assigned randomly to improve security. To prevent the leakage of secret information, generalized Arnold permutation is used before sharing processes. In comparison with other solutions to lossless recovery, the proposed scheme is achieved with no side effects, such as large computational costs and random pixel expansion. By theoretical analyses and experiments, the security, efficiency and effectiveness of our scheme are proven. Our future work is to utilize the proposed scheme to achieve PSIS with other interesting properties.