On the Convolution Quadrature Rule for Integral Transforms with Oscillatory Bessel Kernels
Abstract
:1. Introduction
2. Convergence of the Convolution Quadrature Rule
- is analytic in the region
- there exist constants M and such that
- is analytic and without zeros in a neighbourhood of the closed unit disc with the exception of a zero at
- for for some
- for some
- Modified convolution quadrature rule for (1) of the first kind (MCQ1).
3. Application to a Volterra Equation
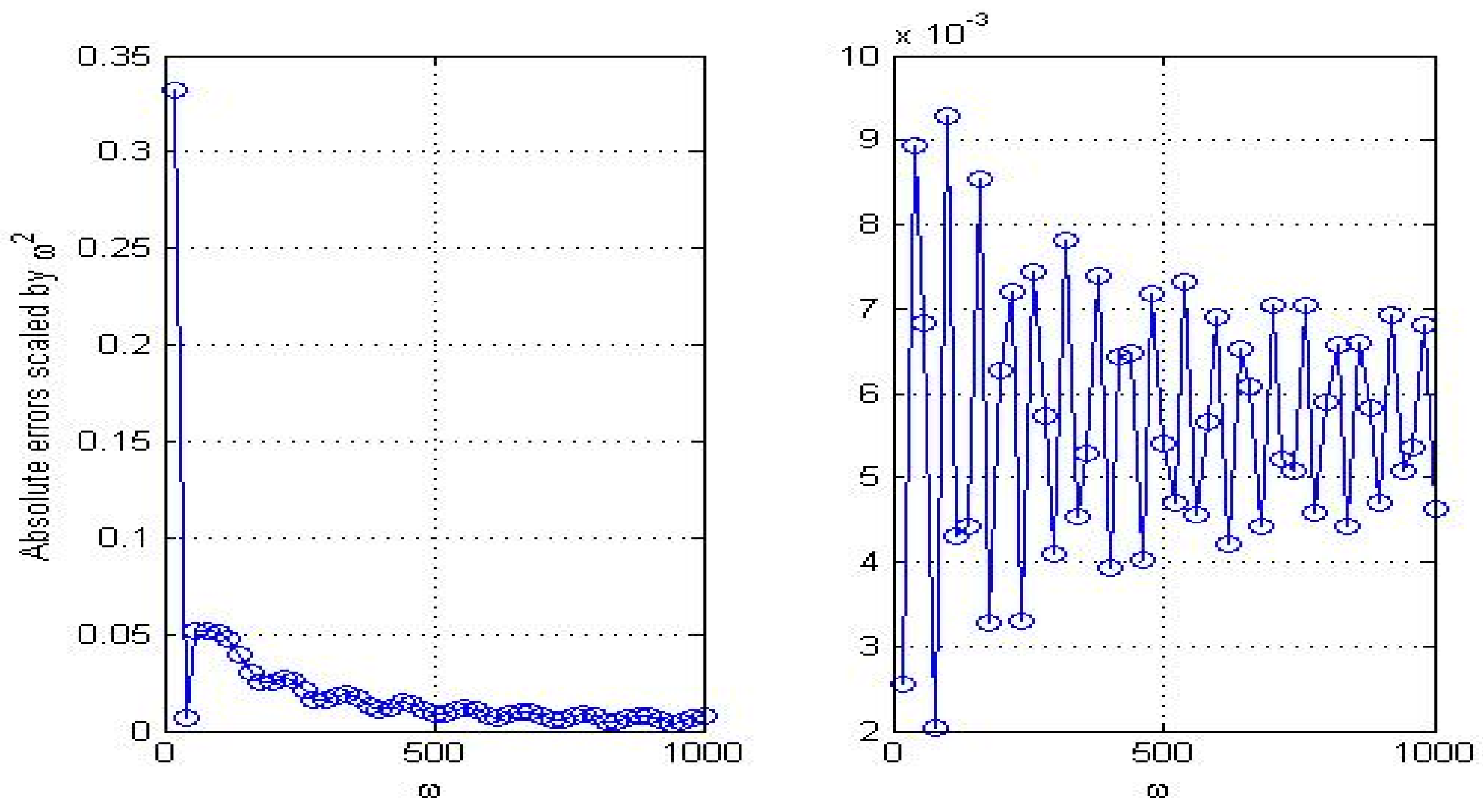
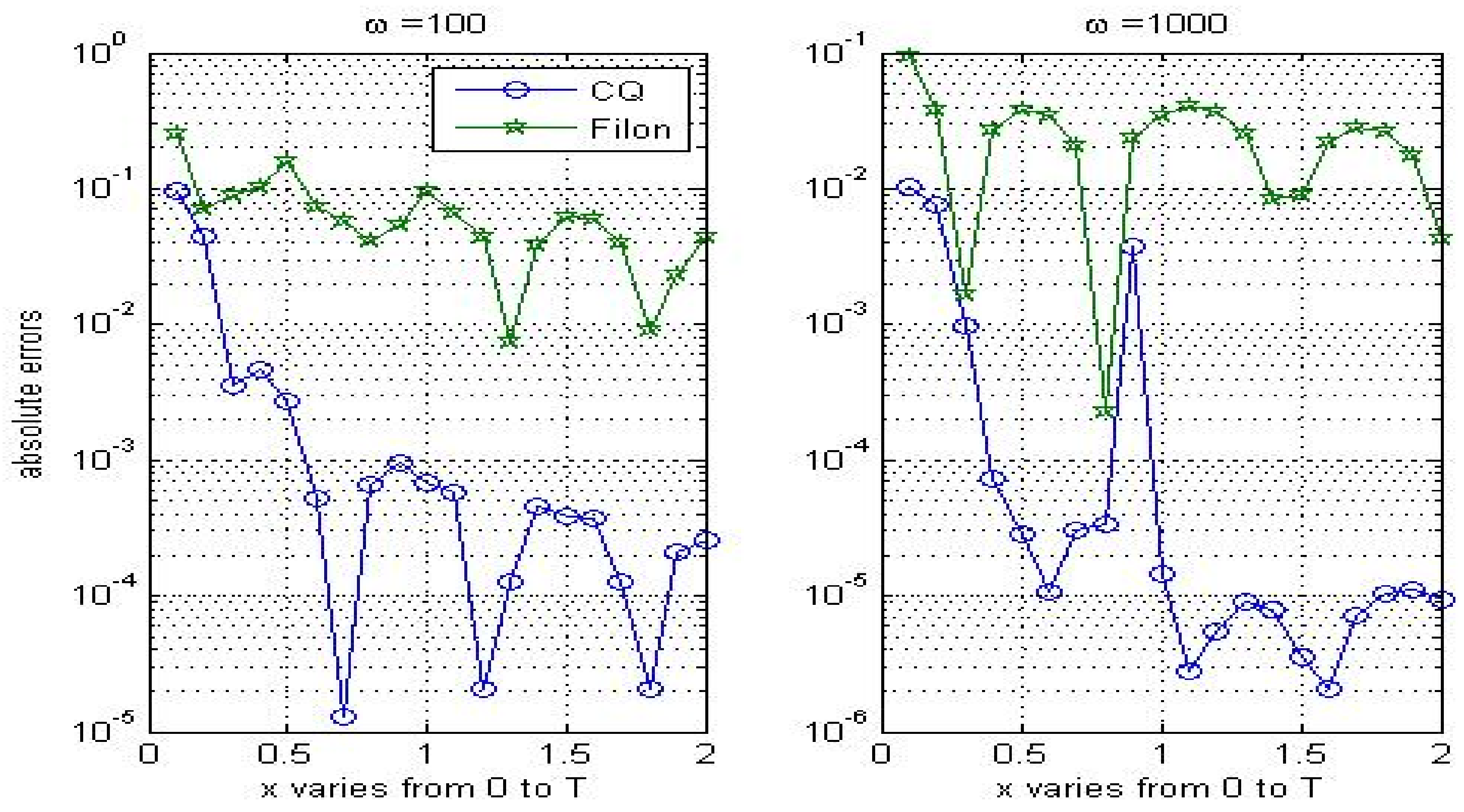
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BDF | backward differentiation formula |
| CQ | convolution quadrature rule |
| FFT | fast Fourier transform |
| GMRES | generalized minimal residual method |
| HOI | highly oscillatory integral |
| HOP | highly oscillatory problem |
| ODE | ordinary differential equation |
| HOVIE | highly oscillatory Volterra integral equation |
| MCQ1 | modified convolution quadrature of the first kind |
| MCQ2 | modified convolution quadrature of the second kind |
References
- Michalski, K. Extrapolation methods for sommerfeld integral tails. IEEE Trans. Antennas Propag. 1998, 46, 1405–1418. [Google Scholar] [CrossRef]
- Rakov, V.; Uman, M. Review and evaluation of lightning return stroke models including some aspects of their application. IEEE Trans. Electromagn. C 1998, 40, 403–426. [Google Scholar] [CrossRef]
- Theodoulidis, T. Exact solution of Pollaczek’s integral for evaluation of earth-return impedane for underground conductors. IEEE Trans. Electromagn. C 2012, 54, 806–814. [Google Scholar] [CrossRef]
- Ma, J. Fast and high-precision calculation of earth return mutual impedance between conductors over a multilayered soil. COMPEL 2018, 37, 1214–1227. [Google Scholar] [CrossRef]
- Iserles, A. On the numerical quadrature of highly-oscillating integrals I: Fourier transforms. IMA J. Numer. Anal. 2004, 24, 365–391. [Google Scholar] [CrossRef] [Green Version]
- Filon, L.N.G. On a quadrature formula for trigonometric integrals. Proc. R. Soc. Edinb. 1928, 49, 38–47. [Google Scholar] [CrossRef]
- Iserles, A.; Nørsett, S.P. Efficient quadrature of highly oscillatory integrals using derivatives. Proc. R. Soc. A 2005, 461, 1383–1399. [Google Scholar] [CrossRef] [Green Version]
- Domínguez, V.; Graham, I.G.; Smyshlyaev, V.P. Stability and error estimates for Filon-Clenshaw-Curtis rules for highly-oscillatory integrals. IMA J. Numer. Anal. 2011, 31, 1253–1280. [Google Scholar] [CrossRef]
- Xiang, S.; Cho, Y.; Wang, H.; Brunner, H. Clenshaw-Curtis-Filon-type methods for highly oscillatory Bessel transforms and applications. IMA J. Numer. Anal. 2011, 31, 1281–1314. [Google Scholar] [CrossRef]
- Milovanovíc, G. Numerical calculation of integrals involving oscillatory and singular kernels and some applications of quadratures. Comput. Math. Appl. 1998, 36, 19–39. [Google Scholar] [CrossRef]
- Huybrechs, D.; Vandewalle, S. On the evaluation of highly oscillatory integrals by analytic continuation. SIAM J. Numer. Anal. 2006, 44, 1026–1048. [Google Scholar] [CrossRef]
- Majidian, H. Numerical approximation of highly oscillatory integrals on semi-finite intervals by steepest descent method. Numer. Algorithms 2013, 63, 537–548. [Google Scholar] [CrossRef]
- Ma, J. Implementing the complex integral method with the transformed Clenshaw-Curtis quadrature. Appl. Math. Comput. 2015, 250, 792–797. [Google Scholar] [CrossRef]
- Levin, D. Procedures for computing one- and two-dimensional integrals of functions with rapid irregular oscillations. Math. Comput. 1982, 38, 531–538. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Wang, T. A universal solution to one-dimensional highly oscillatory integrals. Sci. China 2008, 10, 1614–1622. [Google Scholar]
- Olver, S. Shifted GMRES for oscillatory integrals. Numer. Math. 2010, 114, 607–628. [Google Scholar] [CrossRef]
- Ma, J.; Liu, H. A well-conditioned Levin method for calculation of highly oscillatory integrals and its application. J. Comput. Appl. Math. 2018, 342, 451–462. [Google Scholar] [CrossRef]
- Chen, R.; Xiang, S. Note on the homotopy perturbation method for multivariate vector-value oscillatory integrals. Appl. Math. Comput. 2009, 215, 78–84. [Google Scholar] [CrossRef]
- Evans, G.A.; Chung, K.C. Some theoretical aspects of generalised quadrature rules. J. Complex. 2003, 19, 272–285. [Google Scholar] [CrossRef]
- Sidi, A. Extrapolation method for oscillatory infinite integrals. Math. Comput. 1988, 51, 249–266. [Google Scholar] [CrossRef]
- Lubich, C. Convolution quadrature and discretized operational calculus. I. Numer. Math. 1988, 52, 129–145. [Google Scholar] [CrossRef]
- Lubich, C. Convolution quadrature and discretized operational calculus. II. Numer. Math. 1988, 52, 413–425. [Google Scholar] [CrossRef]
- Lubich, C. On convolution quadrature and Hille-Phillips operational calculus. Appl. Numer. Math. 1992, 9, 187–199. [Google Scholar] [CrossRef]
- Xiang, S.; Brunner, H. Efficient methods for Volterra integral equations with highly oscillatory Bessel kernels. BIT Numer. Math. 2013, 53, 241–263. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, H. Fast integration of highly oscillatory integrals with exotic oscillators. Math. Comput. 2010, 79, 829–844. [Google Scholar] [CrossRef]
- Ma, J.; Xiang, S.; Kang, H. On the convergence rates of Filon methods for the solution of a Volterra integral equation with a highly oscillatory Bessel kernel. Appl. Math. Lett. 2013, 26, 699–705. [Google Scholar] [CrossRef]
- Stein, M.S.; Shakarchi, R. Complex Analysis; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Davis, P.; Duncan, D. Convolution spline approximations for time domain boundary integral equations. J. Integral Equ. Appl. 2014, 26, 369–410. [Google Scholar] [CrossRef] [Green Version]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: Mineola, NY, USA, 1964. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Kauthen, J.P. A survey of singularly perturbed Volterra equations. Appl. Numer. Math. 1997, 24, 95–114. [Google Scholar] [CrossRef]
- Davis, P.; Duncan, D. Stability and convergence of collocation schemes for retarded potential integral equations. SIAM J. Numer. Anal. 2004, 42, 1167–1188. [Google Scholar] [CrossRef]
- Olver, F.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Wang, H.; Xiang, S. Asymptotic expansion and Filon-type methods for a Volterra integral equation with a highly oscillatory kernel. IMA J. Numer. Anal. 2011, 31, 469–490. [Google Scholar] [CrossRef]
- Banjai, L.; Lubich, C.; Melenk, J.M. Runge-Kutta convolution quadrature for operators arising in wave propagation. Numer. Math. 2011, 119, 1–20. [Google Scholar] [CrossRef]
- Xu, K.; Austin, A.P.; Wei, K. A Fast Algorithm for the Convolution of Functions with Compact Support Using Fourier Extensions. SIAM J. Sci. Comput. 2017, 39, A3089–A3106. [Google Scholar] [CrossRef]


| Scheme | Initial Basis () | Recurrence for Basis Functions () |
|---|---|---|
| BDF1 | ||
| BDF2 | ||
| BDF3 | ||
| BDF4 |
| 20 | 100 | 200 | 400 | 600 | 800 | 1000 | |
|---|---|---|---|---|---|---|---|
| CQ | |||||||
| MCQ1 | |||||||
| MCQ2 |
| 20 | 100 | 200 | 400 | 600 | 800 | 1000 | |
|---|---|---|---|---|---|---|---|
| CQ | |||||||
| MCQ1 | |||||||
| MCQ2 |
| 10 | |||||||
| 100 | |||||||
| 200 | |||||||
| 500 | |||||||
| 1000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Liu, H. On the Convolution Quadrature Rule for Integral Transforms with Oscillatory Bessel Kernels. Symmetry 2018, 10, 239. https://doi.org/10.3390/sym10070239
Ma J, Liu H. On the Convolution Quadrature Rule for Integral Transforms with Oscillatory Bessel Kernels. Symmetry. 2018; 10(7):239. https://doi.org/10.3390/sym10070239
Chicago/Turabian StyleMa, Junjie, and Huilan Liu. 2018. "On the Convolution Quadrature Rule for Integral Transforms with Oscillatory Bessel Kernels" Symmetry 10, no. 7: 239. https://doi.org/10.3390/sym10070239




