Optimum Geometric Transformation and Bipartite Graph-Based Approach to Sweat Pore Matching for Biometric Identification
Abstract
:1. Introduction
2. Technical Background
2.1. Live-Scan Fingerprint Image
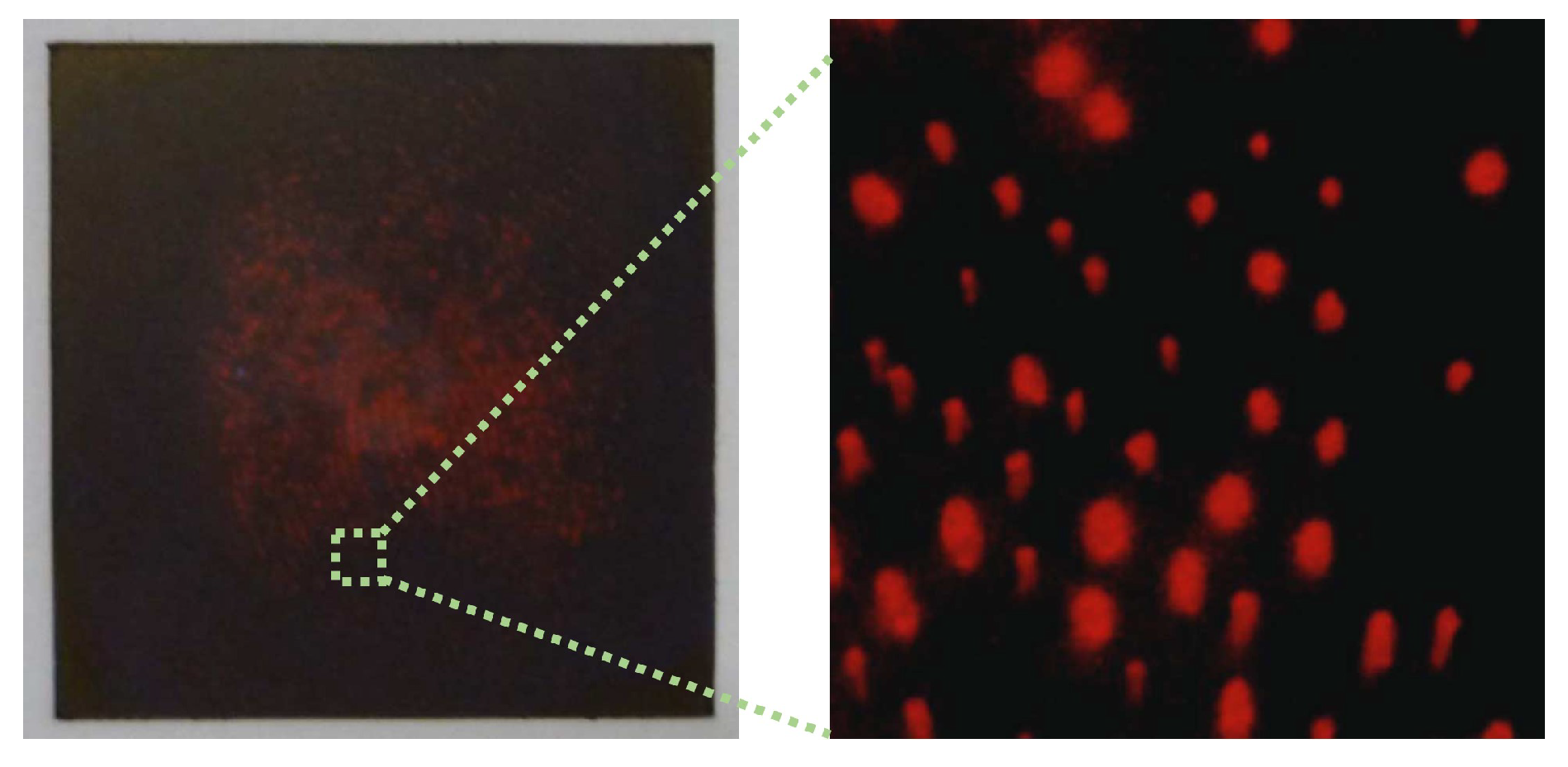
2.2. Pore-Based Fingerprint Image
3. Geometric Transformation and Bipartite Graph-Based Approach to Sweat Pore Matching
3.1. Problem Statement
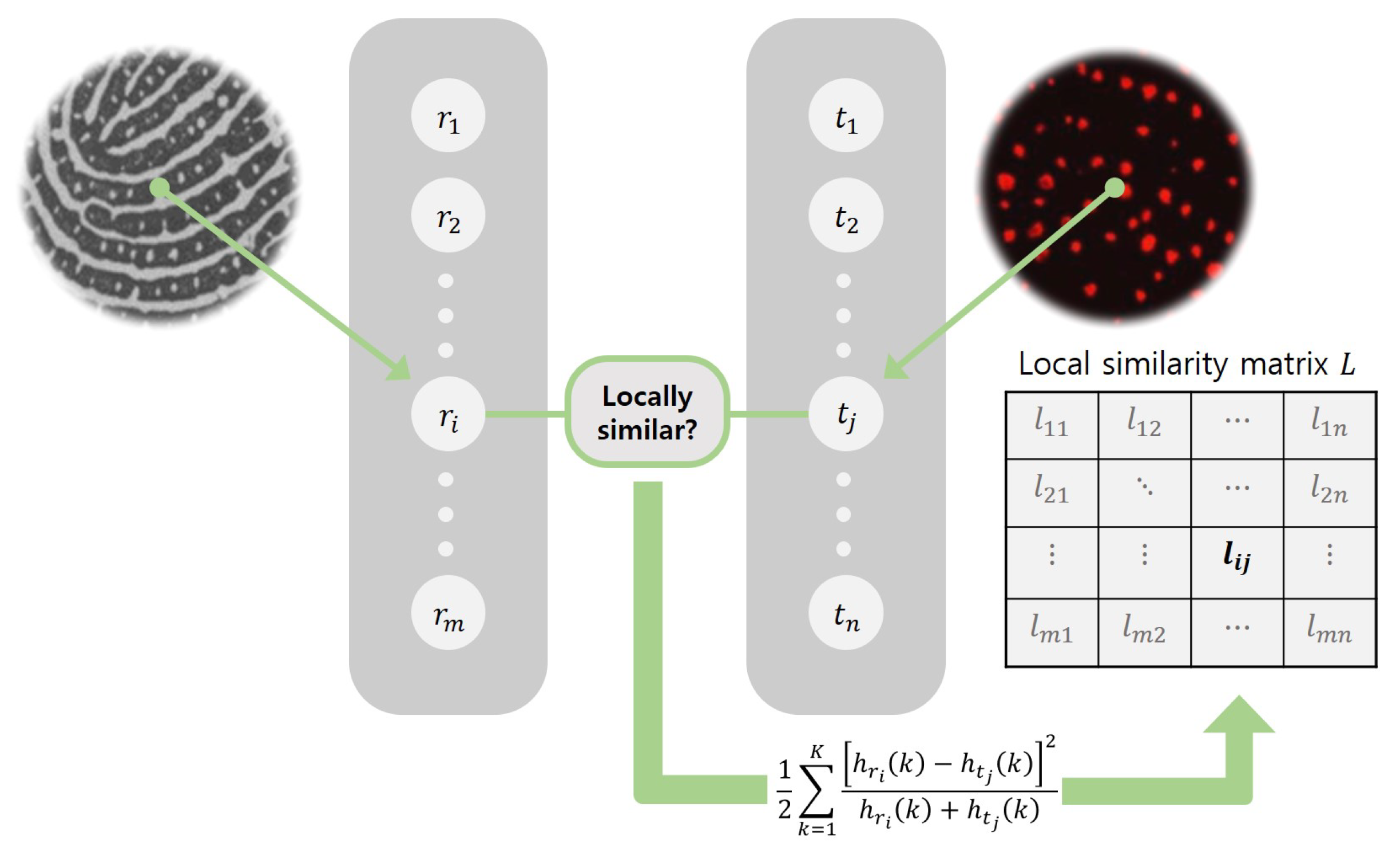
- Local similarity: If two pores and are mated each other in the final matching state, they would have the similar distribution patterns of neighboring pores.
- Global similarity: There is a certain geometric relationship between two pore sets, consistently in the entire picture.
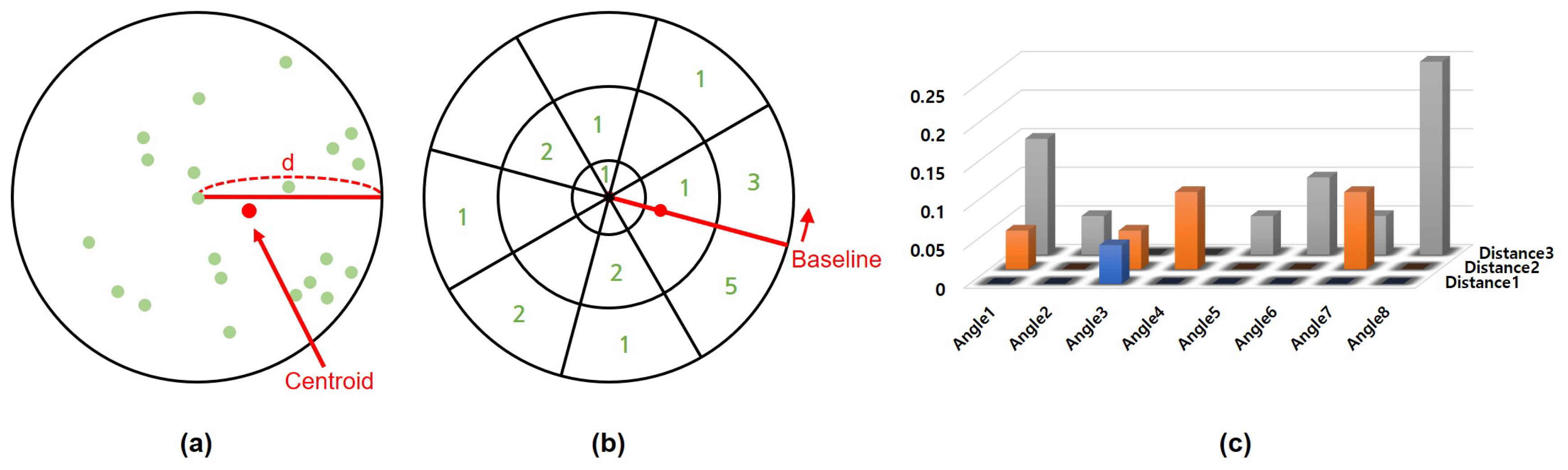
3.2. Local Correspondence
3.3. Global Correspondence
3.4. Stable Pore Matching
| Algorithm 1: Stable pore matching |
 |
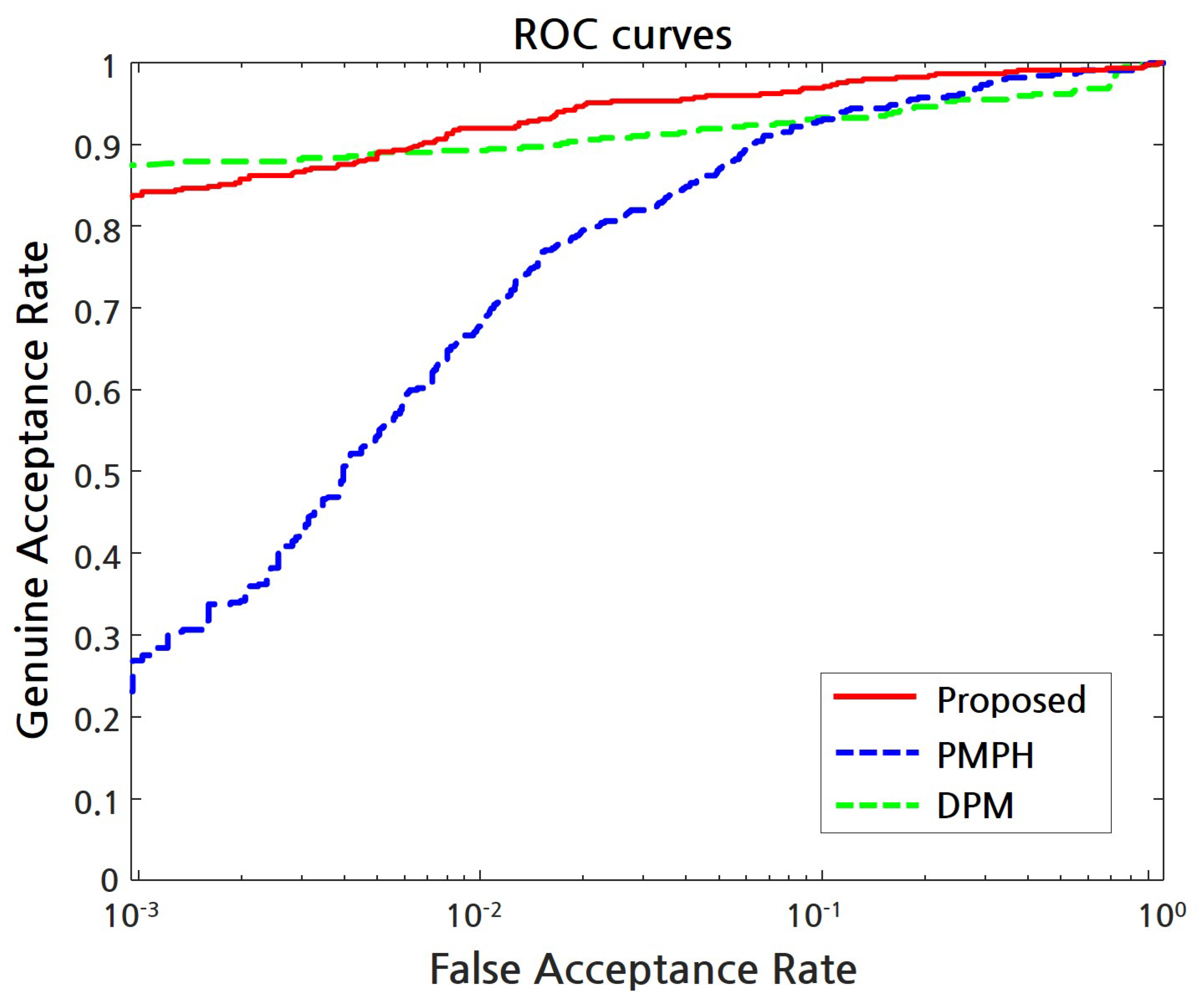
4. Experimental Results
4.1. PolyU HRF Database
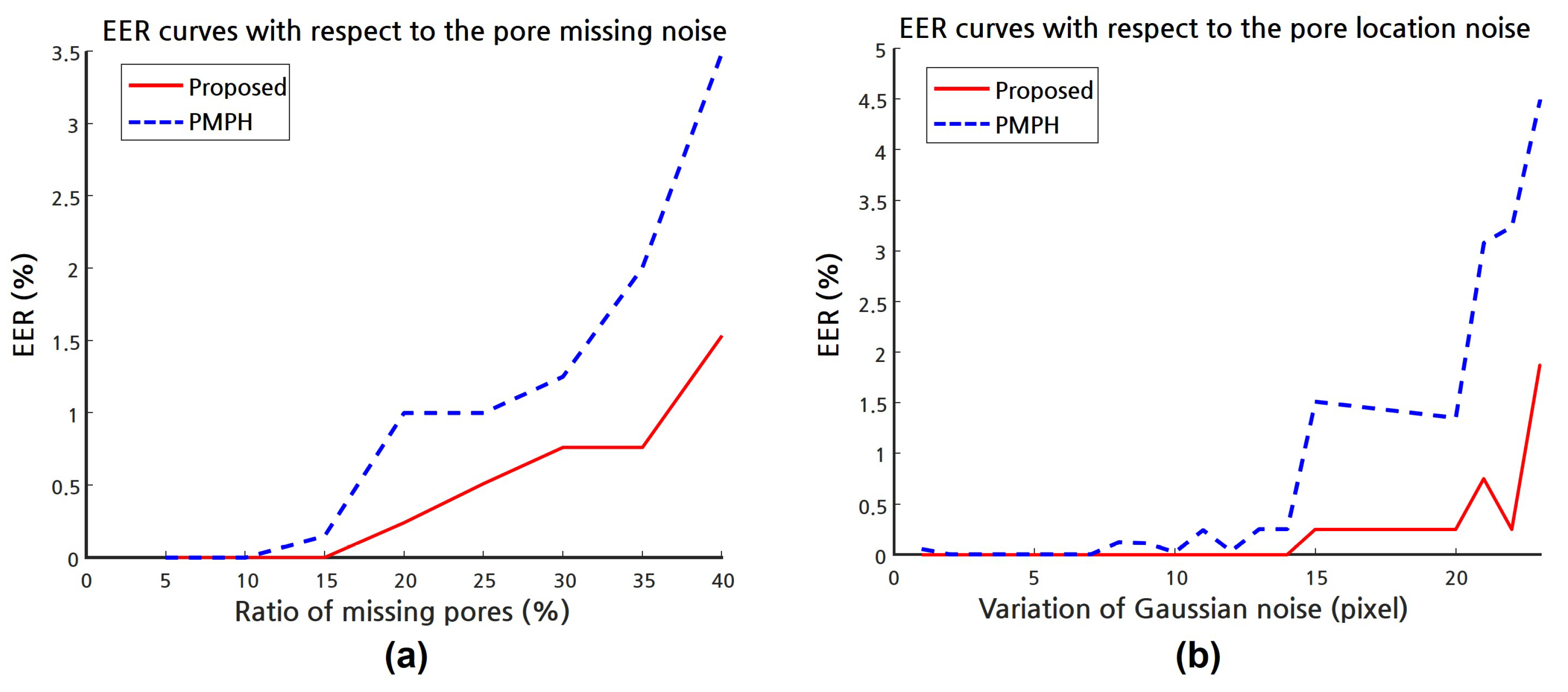
4.2. Synthetic Database
4.3. Pore-Based Fingerprint Image
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Maltoni, D.; Maio, D.; Jain, A.; Prabhakar, S. Handbook of Fingerprint Recognition; Springer Science & Business Media: Heidelberg/Berlin, Germany, 2009. [Google Scholar]
- Ratha, N.; Bolle, R. Automatic Fingerprint Recognition Systems; Springer Science & Business Media: Heidelberg/Berlin, Germany, 2007. [Google Scholar]
- Pankanti, S.; Prabhakar, S.; Jain, A.K. On the individuality of fingerprints. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1010–1025. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, F.; Zhao, Q.; Lu, G.; Luo, N. Selecting a reference high resolution for fingerprint recognition using minutiae and pores. IEEE Trans. Instrum. Meas. 2011, 60, 863–871. [Google Scholar] [CrossRef]
- Jain, A.K.; Chen, Y.; Demirkus, M. Pores and ridges: High-resolution fingerprint matching using Level 3 features. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Ashbaugh, D. Poroscopy. Identif. News 1982, 32, 3–8. [Google Scholar]
- Zhao, Q.; Jain, A.K. On the utility of extended fingerprint features: a study on pores. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition-Workshops, San Francisco, CA, USA, 13–18 June 2010; pp. 9–16. [Google Scholar]
- Roddy, A.R.; Stosz, J.D. Fingerprint features-statistical analysis and system performance estimates. Proc. IEEE 1997, 85, 1390–1421. [Google Scholar] [CrossRef]
- Lee, J.; Pyo, M.; Lee, S.H.; Kim, J.; Ra, M.; Kim, W.Y.; Park, B.J.; Lee, C.W.; Kim, J.M. Hydrochromic conjugated polymers for human sweat pore mapping. Nat. Commun. 2014, 5, 3736. [Google Scholar] [CrossRef] [PubMed]
- Elsner, C.; Abel, B. Ultrafast High-Resolution Mass Spectrometric Finger Pore Imaging in Latent Finger Prints. Sci. Rep. 2014, 4, 6905. [Google Scholar] [CrossRef] [PubMed]
- Stosz, J.D.; Alyea, L.A. Automatic Systems for the Identification and Inspection of Humans; International Society for Optics and Photonics: Bellingham, WA, USA, 1994; Volume 2277, pp. 210–224. [Google Scholar]
- Kryszczuk, K.; Drygajlo, A.; Morier, P. Extraction of Level 2 and Level 3 Features for Fragmentary Fingerprint Comparison; Speech Processing and Biometrics Group, Signal Pro-cessing Institute, Swiss Federal Institute of Technology Lausanne: Lausanne, Switzerland, 2004. [Google Scholar]
- Zhao, Q.; Zhang, L.; Zhang, D.; Luo, N. Direct Pore Matching for Fingerprint Recognition; Springer: Heidelberg/Berlin, Germany, 2009; pp. 597–606. [Google Scholar]
- Liu, F.; Zhao, Q.; Zhang, L.; Zhang, D. Fingerprint Pore Matching Based on Sparse Representation; Indian Council of Philosophical Research: New Delhi, India, 2010; pp. 1630–1633. [Google Scholar]
- Cui, J.; Ra, M.S.; Kim, W.Y. Fingerprint pore matching method using polar histogram. In Proceedings of the 18th IEEE International Symposium on Consumer Electronics (ISCE 2014), JeJu Island, Korea, 22–25 June 2014; pp. 1–2. [Google Scholar]
- PolyU HRF Database. Available online: http://www4.comp.polyu.edu.hk/~biometrics/ (accessed on 19 May 2018).
- Ray, M.; Meenen, P.; Adhami, R. A novel approach to fingerprint pore extraction. In Proceedings of the Thirty-Seventh Southeastern Symposium on System Theory, Tuskegee, AL, USA, 20–22 March 2005; pp. 282–286. [Google Scholar]
- Zhao, Q.; Zhang, D.; Zhang, L.; Luo, N. Adaptive fingerprint pore modeling and extraction. Pattern Recognit. 2010, 43, 2833–2844. [Google Scholar] [CrossRef]
- Cui, J.; Ra, M.; Kim, W.Y. Fingerprint Pore Extraction Method using 1D Gaussian Model. J. Inst. Electr. Inf. Eng. 2015, 52, 135–144. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Moré, J.J. the Levenberg-Marquardt algorithm: implementation and theory. In Numerical Analysis; Springer: Heidelberg/Berlin, Germany, 1978; pp. 105–116. [Google Scholar]
- Pujol, J. the solution of nonlinear inverse problems and the Levenberg-Marquardt method. Geophysics 2007, 72, W1–W16. [Google Scholar] [CrossRef]
- Gusfield, D.; Irving, R.W. The Stable Marriage Problem: Structure and Algorithms; MIT Press: Cambridge, UK, 1989. [Google Scholar]
- Manlove, D.F.; Irving, R.W.; Iwama, K.; Miyazaki, S.; Morita, Y. Hard variants of stable marriage. Theor. Comput. Sci. 2002, 276, 261–279. [Google Scholar] [CrossRef]
- Iwama, K.; Miyazaki, S. A survey of the stable marriage problem and its variants. In Proceedings of the 2008 International Conference on Informatics Education and Research for Knowledge-Circulating Society, Kyoto, Japan, 17 January 2008; pp. 131–136. [Google Scholar]











| Name | Projective Transformation |
|---|---|
| Matrix (M) | |
| Parameter (m) | |
| Jacobian (J) | |
| Degree-of-freedom | 8 |
| Method | DPM | PMPH | Proposed |
|---|---|---|---|
| EER | |||
| FMR1000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-j.; Kim, W.-Y.; Paik, J. Optimum Geometric Transformation and Bipartite Graph-Based Approach to Sweat Pore Matching for Biometric Identification. Symmetry 2018, 10, 175. https://doi.org/10.3390/sym10050175
Kim M-j, Kim W-Y, Paik J. Optimum Geometric Transformation and Bipartite Graph-Based Approach to Sweat Pore Matching for Biometric Identification. Symmetry. 2018; 10(5):175. https://doi.org/10.3390/sym10050175
Chicago/Turabian StyleKim, Min-jae, Whoi-Yul Kim, and Joonki Paik. 2018. "Optimum Geometric Transformation and Bipartite Graph-Based Approach to Sweat Pore Matching for Biometric Identification" Symmetry 10, no. 5: 175. https://doi.org/10.3390/sym10050175
APA StyleKim, M.-j., Kim, W.-Y., & Paik, J. (2018). Optimum Geometric Transformation and Bipartite Graph-Based Approach to Sweat Pore Matching for Biometric Identification. Symmetry, 10(5), 175. https://doi.org/10.3390/sym10050175






