1. Introduction
For solving many problems involving uncertainty and vagueness in engineering, social sciences, economics, computers sciences and in several other areas, our traditional classical methods are not always absolutely effective. These traditional and conventional mechanism of reasoning, modeling and computing are usually crisp and deterministic. Zadeh introduced a successful tool known as fuzzy sets [
1], based on the membership function. The situations concerning with the vagueness and uncertainty were also been tackled by the effective tool of probability. However, this tool is valuable only when the occurrence of event is totally determined by the chance. In contrast with fuzzy set theory and probability theory, some other theories like rough set theory, soft set theory, neutrosophic set theory and an amalgamation of these theories have been studied ([
1,
2,
3,
4,
5,
6,
7], and the references therein) to deal with uncertainty.
In 1982, Pawlak [
3] introduced the concept of rough sets as a mathematical tool for imprecise and uncertain data. The basic advantage of this theory is that it does not involve any additional information about the data like the membership in fuzzy sets. The rough sets theory defined by Pawlak is based on partition or an equivalence relation. Many applications of rough set theory, probability theory, and rough set theory can be seen in the followings [
4,
5,
8,
9,
10,
11,
12,
13], these include applications in data mining, machine learning, pattern recognition and knowledge discovery. The blending of rough sets with fuzzy sets and referring them to graphs with concepts of fuzzy sets or rough sets can be seen in [
14,
15,
16,
17]. The above said theories have different approaches to tackle vagueness, imprecision and uncertainty. Each said theory has its own limitations and restrictions. While dealing with such theories, a question arises, how to handle multi-attributes? Molodtsov [
18] introduced a novel concept of soft sets as a powerful mathematical tool for dealing multi-attribute uncertainty. This newer concept has enough parameters, which make it free from those difficulties which the contemporary theories have and that makes it popular among the experts and researchers working in different fields of research like operation research, probability theory, smoothness of functions and many more. Later on the theory has been modified in some aspects to handle many problems [
19,
20,
21]. A number of applications were established and used regarding decision making problems and multi-attributes modeling using soft sets, [
22,
23,
24,
25,
26,
27].
Feng et al. [
28] introduced the concept of soft rough sets which is a blend of soft and rough sets. Clearly, in a rough set model, an equivalence relation is used to form the granulation structure of the universe while a soft set can be used to form the granulation structure of the universe in soft rough model. Huge number of applications, presented by many researchers in data labeling problems, data mining, attributes reduction problems, knowledge based systems, some can be seen in [
23,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42].
A graph can be used to represent many real life problems in computer science especially, which are otherwise abstract. Euler, known as father of graph theory, was universally credited when he settled a famous Kōnigsberg Bridge problem [
43] in 1736. After that, many mathematicians applied graph theory in finite fields, for details readers are referred to ([
44], and the references therein).
The concept of soft graphs and their basic operations are defined in [
45], which were required to handle multi-attributes problems related with graph theory. A number of generalizations of soft graphs are available in [
46,
47,
48]. Soft sets and rough sets are different approaches that provide efficient tools for modeling the problems involving uncertainty and granularity in information system. Graphs are another powerful tool for representing the information by means of diagrams, matrices or relations. Particularly soft graphs serve this purpose fruitfully. Apparently no direct link exists between above said theories. However an effort is made by [
49] to establish some kind of linkage and to discuss the uncertainty in soft graphs. He introduced the concept of soft rough graphs, where instead of equivalence classes, parameterized subsets of vertices and edges serve the aim of finding the lower and upper approximations. In such process, some unusual situations may occur like the upper approximation of a non-empty vertex/edge set may be empty. Upper approximation of a subset K of vertices or edges may not contain K. In our present article we endeavour to search a positive answer to above unusual situations and shortcomings. To strengthen the concept of soft rough graphs, a tgeneralized approach is presented, called modified soft rough graphs (
-graphs), whose lower and upper vertex and edge approximations are different from those of Noor [
49] but the elemental concepts are closely akin. It is shown that the
-graphs are more precise and finer than soft rough graphs. Uncertainty measurement is an important issue in the field of rough set theory. There are many approaches available in literature for reasoning with uncertainty. We have discussed uncertainty measures associated with
-graphs such as information entropy and rough entropy. The notion of information granules is an important topic in rough set theory, which gives an idea about the objects which are indistinguishable from each other. Here the concept of granularity measures for
-graphs has been introduced. The layout of this paper is as follows.
In
Section 2, some basic concepts are revised.
Section 3, is devoted to present the concept of modified soft rough graphs (
-graphs, lower, upper
-vertex approximations, lower, upper
-edge approximations and the roughness membership function for modified soft rough graphs. Moreover, the notion of
-equal relations is proposed and the related properties are explored.
Section 4 is about uncertainty measurements associated with modified soft rough graphs and it is shown how these are linked.
Section 5 is concerned about the application of
-graphs. An algorithm is developed in a realistic way to compute the effectiveness of some diseases among colleagues working in same office. Vertices are denoted by the 20 colleagues and the interaction of these colleagues are presented by the edges. Measure of optimality
and possibly measure of optimality
are defined with the help of lower and upper
-vertex approximations of the given graph and using marginal fuzzy sets as weights corresponding to each person, the persons at high risk for having given diseases are found. Computations are made using MATLAB program. Results are shown in tables. Conclusion of the paper is presented in
Section 6.
3. Modified Soft Rough Graphs
In this section, based on the properties and usefulness of both rough sets and soft sets, we introduce the notion of Modified Soft Rough Graphs (-graphs). Basic properties and results of such graphs are investigated and discussed which enable us to put these graphs to more effective practical use.
Definition 9. Let be a soft graph. Let be a map such that Denote by and call it Modified soft rough vertex (-vertex)approximation space. Based on , we define two sets, called the lower -vertex approximation and the upper -vertex approximation respectively as follows:and If then X is called -vertex definable set and the graph
is called -vertex definable graph otherwise X is called -vertex set and is called -vertex graph. Define and denote the lower and upper -vertex approximations of byandfor any Definition 10. Let be a -vertex graph. Then the vertex roughness membership function of is denoted and defined as It can be seen that if then So the graph is -vertex definable graph. i.e., there is no roughness.
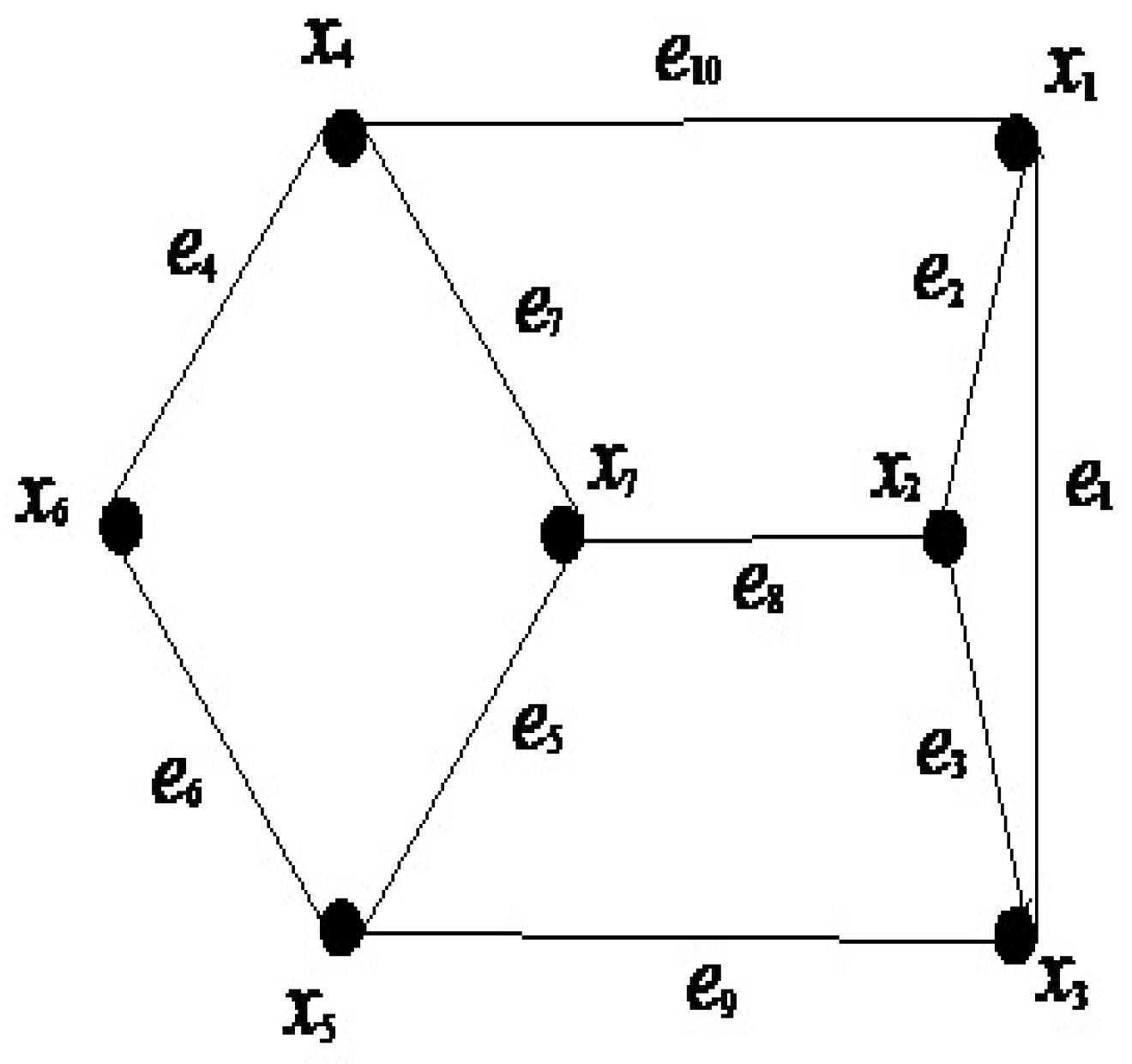
Example 1. Let be a soft graph over a simple graph where and as shown in Figure 1. Let be a soft set over V with as the set of parameters such that , as shown in Table 1. Let Let be a map such that So and Here and
Thereforeandshowing that , so is -vertex graph, whereand Furthermore,
Definition 11. Let be a soft graph. Let be a map such that Denote by and call it Modified soft rough edge approximation space. Based on , we define two sets, called the lower -edge approximation and the upper -edge approximation respectively as follows:and If then Y is called -edge definable set and the graph is called -edge definable graph otherwise Y is called -edge set and is called -edge graph. Define and denote the lower and upper -edge approximations of byandfor any Definition 12. Let be a -edge graph. Then the edge roughness membership function of is denoted and defined as It can be seen that if then So the graph is -edge definable graph. i.e., there is no roughness.
Example 2. From Example 1, let be a soft sets over E as shown in Table 2. Let thenand Clearly for So Y is -edge definable set and the graph
is -edge definable graph. Also That is, there is no roughness.
Definition 13. The roughness membership function of any subgraph graph can be found by Definition 14. A soft graph is called -definable if
- (1)
X is -vertex definable i.e., and
- (2)
Y is -edge definable i.e.,
Definition 15. A soft graph is called -graph if
- (1)
X is -vertex set i.e.,
- (2)
Y is -edge set i.e.,
A -graph is denoted by
Definition 16. By a lower and upper approximations of the -graph , we mean and respectively, for any and
Proposition 1. Let be a soft graph such that and represents respectively, the -vertex approximation space and -edge approximation space, then
- (i)
- (ii)
- (iii)
If then and
- (iv)
- (v)
- (vi)
- (vii)
where and are subgraphs of .
Proof. and directly follows from the definitions of -vertex/edge approximations.
Let so or and Let such that and That is, with for all and with for all Since and , so with for all and with for all Thus and showing that Hence implies Similarly one can show if then
Since is contained in both and so by and Therefore
Since and so by and . Hence Now for reverse inclusion, we suppose Which implies and such that and So with for all and with for all implies with for all . Which shows with for all , so . Similarly we can show . So Thus Hence
Since and so by and Hence
It is easy to show, by using that Conversely suppose that then and Which implies with for some and with for some So with for some or with for some Both these conditions shows or . So . Similarly, it can be shown that Thus or Which means or That is, Thus □
Remark 1. In the proof of Proposition 1, we have proved . If we want to prove this result by the approach used by [49], we have to employ a strong condition on soft sets and to be intersection complete. However in our approach, no such condition is required. Now in the following, we define some relations associated with modified soft rough graphs.
Definition 17. Let a soft graph be Then for two -graphs and , we define
- (i)
if and only if
- (ii)
if and only if
- (iii)
if and only if and
The above relations to are respectively called, the lower -equal relation, the upper -equal relation and the -equal relation.
Proposition 2. The relations ≂ and ≈ defined on -graphs are equivalence relations.
Proposition 3. Suppose is soft graph defined on simple graph . Then for two -graphs and , the following hold:
- (i)
if and only if
- (ii)
If and then
- (iii)
If then ,
- (iv)
If and , then .
Proof. Let then However, from Proposition 1, which implies that , so and showing that . Conversely suppose that . Since ≂ is an equivalence relation, so it is transitive. Thus,
The proof is similar to the proof of (i).
Suppose then Then by Proposition 1 Therefore
Suppose and , then by definition which implies . So However, shows Hence or equivalently □
Proposition 4. Suppose is soft graph. Then for two -graphs and , the following hold:
- (i)
if and only if
- (ii)
and then
- (iii)
If then , where is a simple graph.
- (iv)
If and , then .
Proof. Proof follows from Proposition 1 and 3. □
Remark 2. In order to show the similar results in Propositions 2 and 3, in case of soft rough graphs of proposed in [49], the soft sets and must be intersection complete but in case of our proposed model of modified soft rough graphs, no such condition is required on and . Proposition 5. Suppose be a -graph and be a soft rough graph then
Proof. To prove we have to prove only and , where and
Let then for which shows and Suppose on contrary, Then for some Since so which implies However, so Which is a contradiction because So Hence Similarly if then we can show Hence we conclude that □
Remark 3. From above Proposition , it is clear that granules of information in -graph are finer than soft rough graph Thus -graph are more robust than soft rough graph.
4. Uncertainty Measurement in Modified Soft Rough Graphs
Different membership functions for reasoning with uncertainty has been proposed in literature [
50,
51,
52,
53]. In this section, some uncertainty measurements such as information entropy, naive granularity measure, elementary entropy and rough entropy of modified soft rough graphs are proposed. Further, some theoretical properties are obtained and investigated.
Definition 18. Let be -vertex approximation space and , then the set is called the soft association of parameter
Definition 19. Let be -vertex approximation space and Then the soft neighborhood of α is denoted and is defined as .
Definition 20. Let and be two -vertex approximation spaces with
- (i)
For all there exists such that and
- (ii)
For all there exists such that Then we say is finer than and denote it by .
Note that a similar definition can be made for -edge approximation spaces.
Proposition 6. Let and be two -vertex approximation spaces such that . Then .
Proof. Suppose . Then for any By Definition for any there exists such that Hence for any Thus, Consequently, □
Proposition 7. Let and be two -edge approximation spaces such that . Then .
Proof. The proof is similar to the proof of Proposition 6. □
Note: From now onwards, will represent a -graph with and as -vertex approximation space and -edge approximation space, respectively unless stated otherwise.
Definition 21. Let be a -graph. Then the neighborhood information entropy of is defined Proposition 8. Suppose and are two -graphs such that and Then
Proof. From Propositions 6 and 7, we have
and
Which implies
□
Remark 4. The neighborhood information entropy attains the maximum value when and achieves the minimum values 0 when and for
Definition 22. Let be a -graph. Then the naive granularity measure of is defined Proposition 9. Suppose and are two -graphs such that and Then
Proof. The proof is similar to the proof of Proposition 8. □
Remark 5. The granularity measure achieves the maximum value 2 when and and attains the minimum values when for .
Proposition 10. Let be a -graph. Then
Definition 23. Let be a -graph. Then the neighborhood elementary entropy of is defined Proposition 11. Suppose and are two -graphs such that and Then
Proof. From Propositions 6 and 7, we have
and
for
Which shows
□
Remark 6. The neighborhood granularity measure achieves the maximum value when and attains the minimum values 0 when and for .
Definition 24. be a -graph. Then the neighborhood rough entropy of is defined Proposition 12. Suppose and are two -graphs such that and Then
Proof. The proof is similar to the proof of Proposition 11 by using Proposition 6, Proposition 7 and Definition 24 □
Remark 7. The neighborhood rough entropy achieves the maximum value when and Also attains the minimum values 0 when for any
Proposition 13. Suppose be a -graph. Then
5. Application of Modified Soft Rough Graphs
In this section, an algorithm is formulated for decision making problems based on modified soft rough graphs. To show the application of modified soft rough graphs in decision making, an example is constructed. Suppose
be the set of
n objects
and
be the set of
m parameters
. Let
be a simple graph whose vertex set is
V and edge set is
Let
and
be two soft sets over
V and
E respectively such that for each
i,
is a subgraph of
showing that
is a soft graph. Where
For basic evaluation, let
be the set of
r experts and let
be a soft set over
V. Let
be
-vertex approximation space then
and
can be calculated by
Now we compute the fuzzy functions
and
given by
where
and
are a kind of indicator functions, defined by
Now the marginal weights for each
, can be computed by;
where
is an indicator function on
defined by
Finally, we calculate the evaluation function given by
The person is at high risk if One can apply this algorithms in other related problems.
5.1. Pseudo Code
Step 1: Input is the soft graph .
Step 2: Find -vertex approximation space .
Step 3: Find lower -vertex approximation according to Definition 9.
Step 4: Find upper -vertex approximation according to Definition 9.
Step 5: Compute the fuzzy functions
and
given by
Step 6: Apply the marginal function
for all vertices
given by
Step 7: Apply the evaluation function
for all vertices
given by
The vertex is optimal if
5.2. Example
Suppose during the annual medical checkup of persons working in an office, five viral diseases found in a group of 20 people , through different sources such as body fluids contaminated with a virus, having sex with an infected person, eating contaminated food, breathing air polluted by a virus and insect bite. The above process of infection results in a diversity of symptoms that vary in severity and character, depending upon the individual factor and the kind of viral infection. Suppose be the set of parameters such that represents “ body fluids contaminated with a virus”, represents “entering of virus in human body through having sex with an infected person”, represents “entering of virus in human body through eating contaminated food”, represents “entering of virus in human body through breathing air polluted by a virus” and represents “entering of virus in human body through insect bite”. It is also assumed that a person may have more than one viral disease. Suppose be a simple digraph having vertex set V of 20 persons and edge set E.
Let
be a soft set over
V as shown in
Table 3 such that
Let
be a soft set over
E such that
Let
be a map such that
Then
and
Let
be the soft set (can be seen in
Table 4) which shows whether a staff member is at high risk or not, giving the values 1 or 0 respectively. Where
S is the set of 3 expert doctors .i.e.,
A MATLAB code is developed to perform all the calculations. Let
be
-vertex approximation space. If we consider the technique proposed in [
49] then we have the following lower and upper approximations as
From these lower and upper approximations, we get no information with uncertainty about the patients from experts. Now we apply lower and upper approximations of our proposed model.
It can be seen that
for
That is, the properties of Pawlak [
3] rough sets have been translated into the proposed model whereas it cease to happen in model proposed in [
49]. Now we compute the fuzzy functions
and
given by
Clearly
is a soft graph. The interaction of all persons with each other and the marginal fuzzy sets for rows and columns are given in
Table 5.
Now we calculate the evaluation function given by
By simple calculations, it is found that
For a threshold it can be seen that the all person are at optimum for all in which The person is at high risk if So by calculations, the person is best optimal.
6. Conclusions
A possible fusion of three concepts rough sets, soft sets and graphs, known as soft rough graphs, is introduced by [
49]. During this attempt, some shortcomings become the part of the theory. In order to remove these shortcomings, a new approach is being introduced to study the roughness of soft graphs and the resulting graphs are called modified soft rough graphs. The theory of approximation of a soft graph is also investigated to obtain
-vertex graph and
-edge graph. The related properties of both soft rough graphs and modified soft rough graphs are surveyed. It is shown that the
-graphs are more precise and finer than soft rough graphs. Different uncertainty measures like information entropy and granularity measures are discussed for
-graphs. A real life example of decision making problem is formulated to optimized the diagnosis process of some diseases in an office where we have compared the robustness of the proposed model with soft rough graphs proposed by Noor in [
49]. An algorithm is developed in a realistic way to compute the effectiveness of diseases among colleagues working in same office. The set of edges has been used to describe the interaction between the persons. This interaction may cause the spreadness of diseases among the staff members. Using the concepts of lower/upper
-vertex approximations, the fuzzy sets
and
are introduced, while the marginal fuzzy sets
and
are used to find the measure of interaction of any staff member
with
and vice versa. Finally, the evaluation function has pointed out the optimal carriers of diseases. All the calculations are made on MATLAB program.
We hope that our results in this article would constitute a base for DM problems of real life based on soft rough graphs. In future work it is also under consideration, how the upper and lower -edge approximations can be used to optimized the algorithm.
References and Notes