How to Make a Barranco: Modeling Erosion and Land-Use in Mediterranean Landscapes
Abstract
:1. Introduction
| Experiment Number | Number of People | Land Tenure Type |
|---|---|---|
| 1 | 30 | Satisfice |
| 2 | 30 | Maximize |
| 3 | 60 | Satisfice |
| 4 | 60 | Maximize |
| 5 | 120 | Satisfice |
| 6 | 120 | Maximize |
2. MedLanD Modeling Laboratory (MML)
2.1. Surface Process Model
2.2. Human Land-Use Model
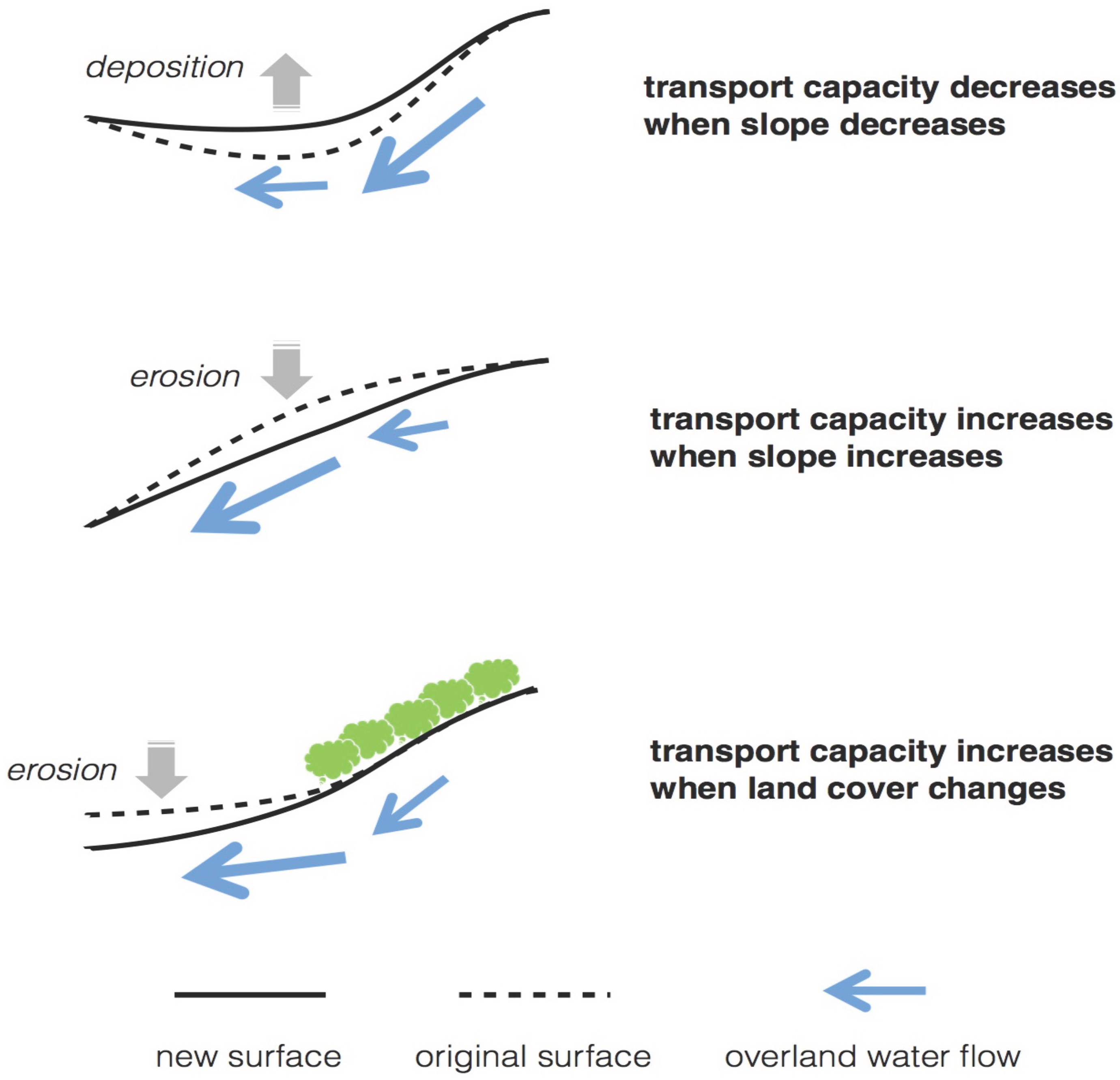
3. Modeling Experiment Design
3.1. Creating the Digital Landscape
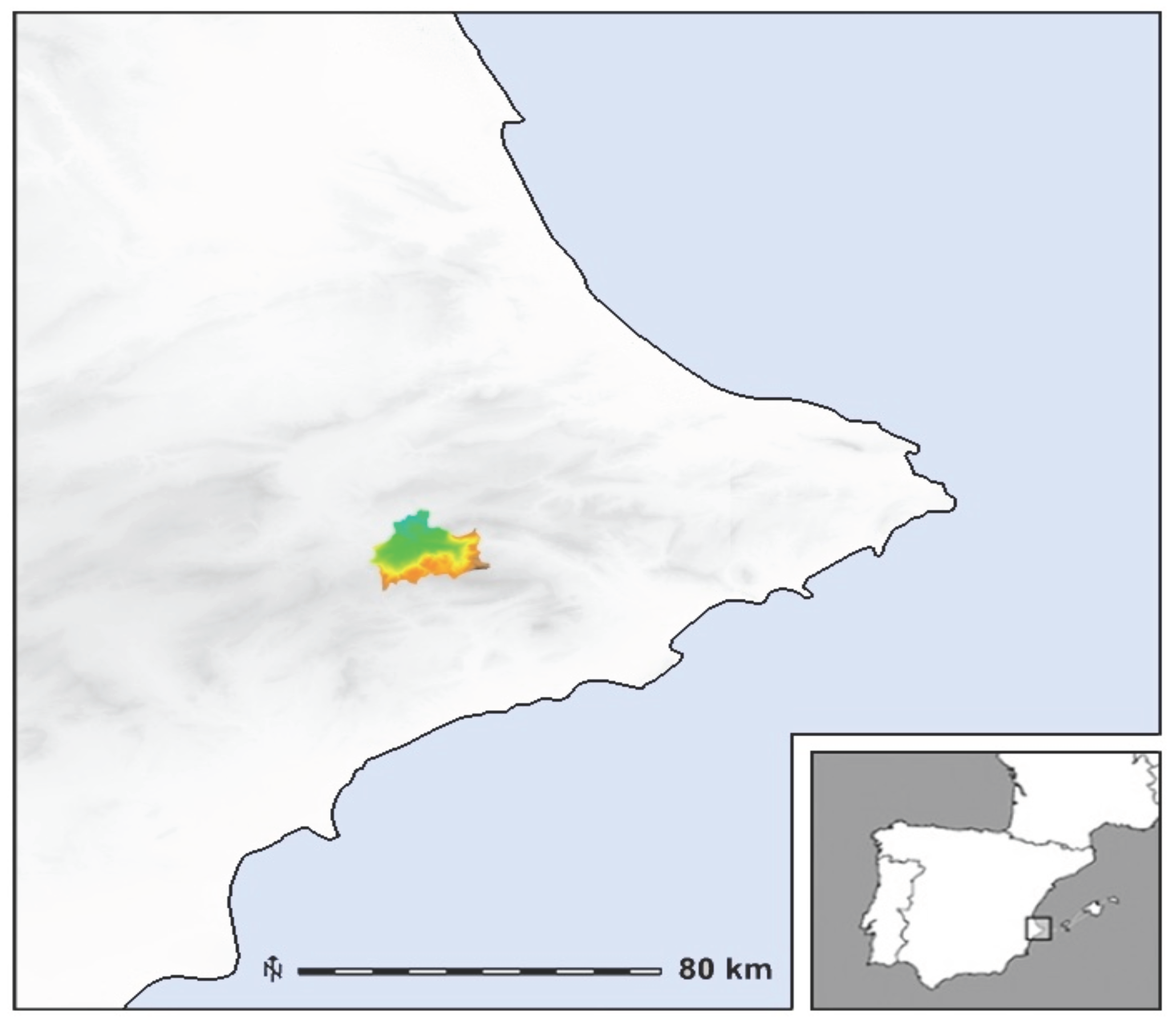

3.2. Modeling Past Climate

3.3. Modeling Land-Use
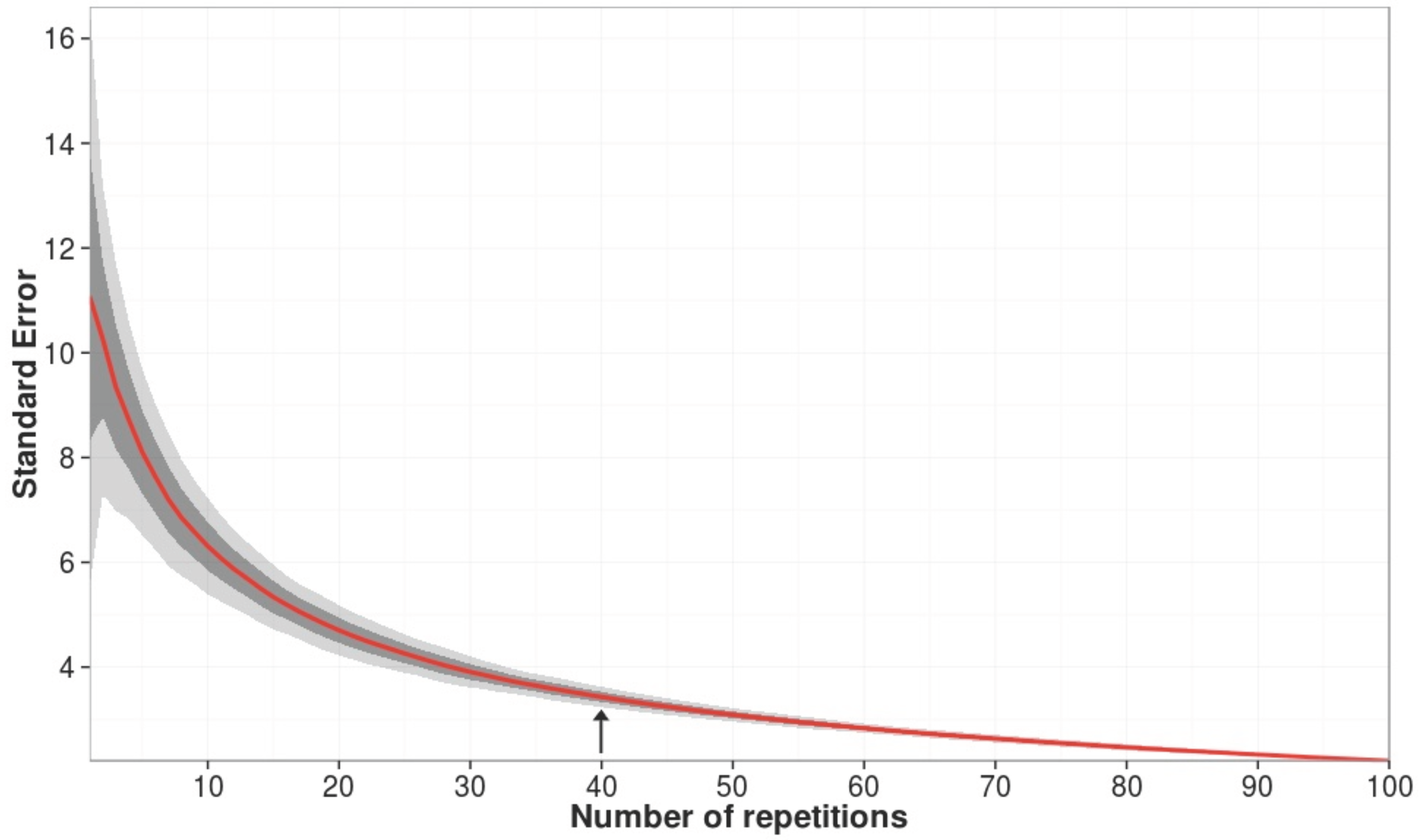
3.4. Sensitivity Testing and Experiment Repetition
4. Simulation Results
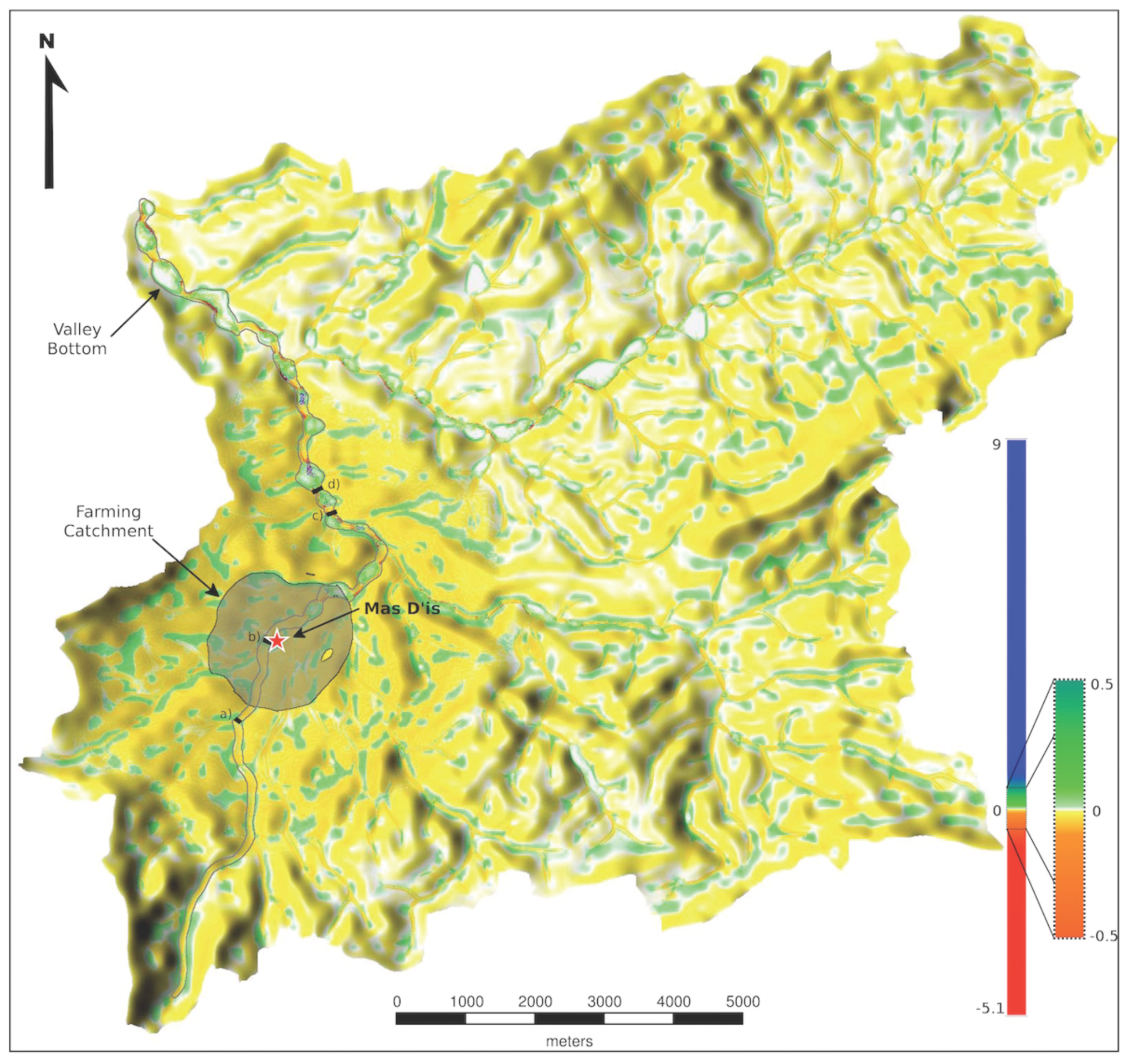
4.1. Erosion and Deposition in Barrancos
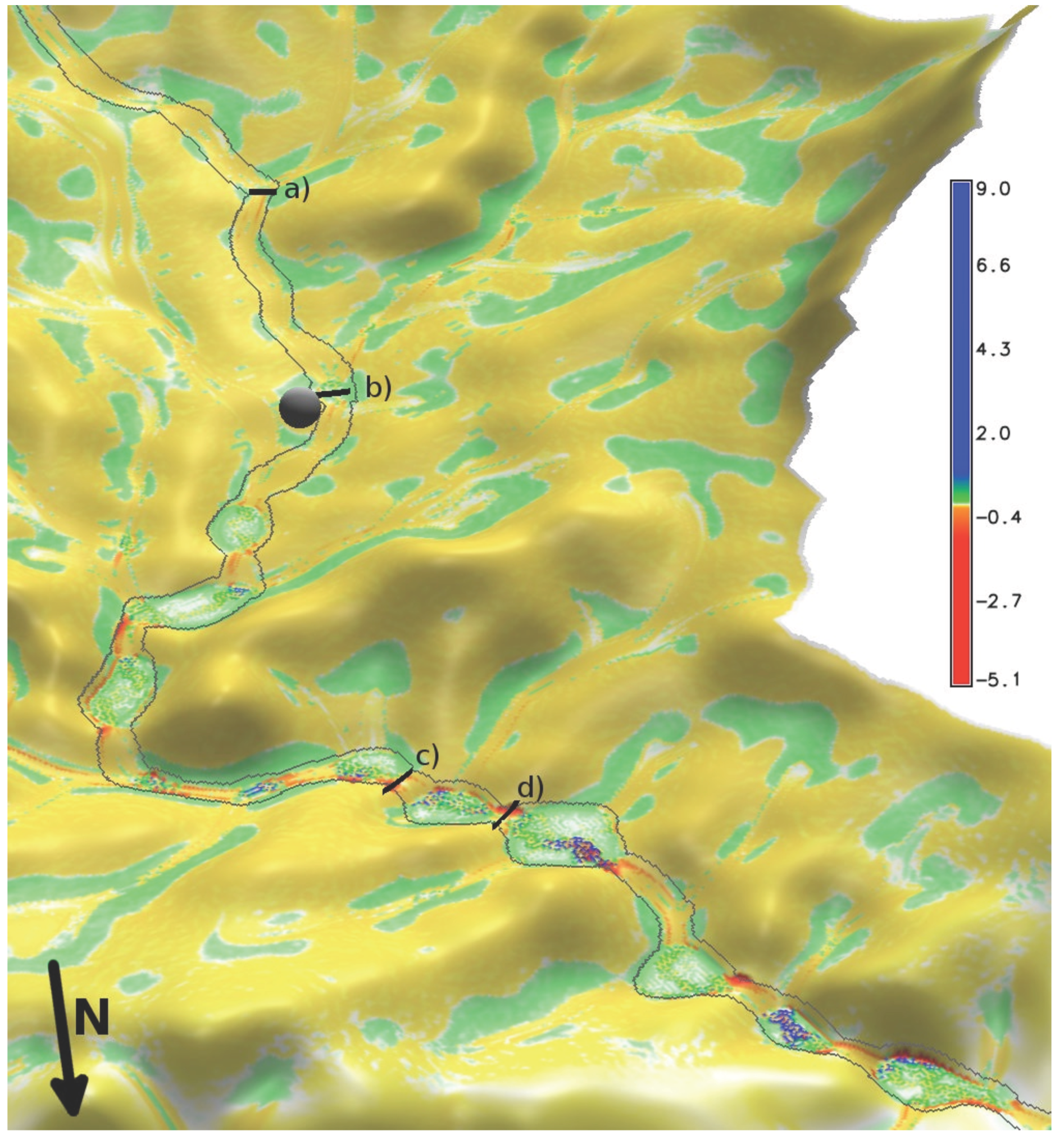
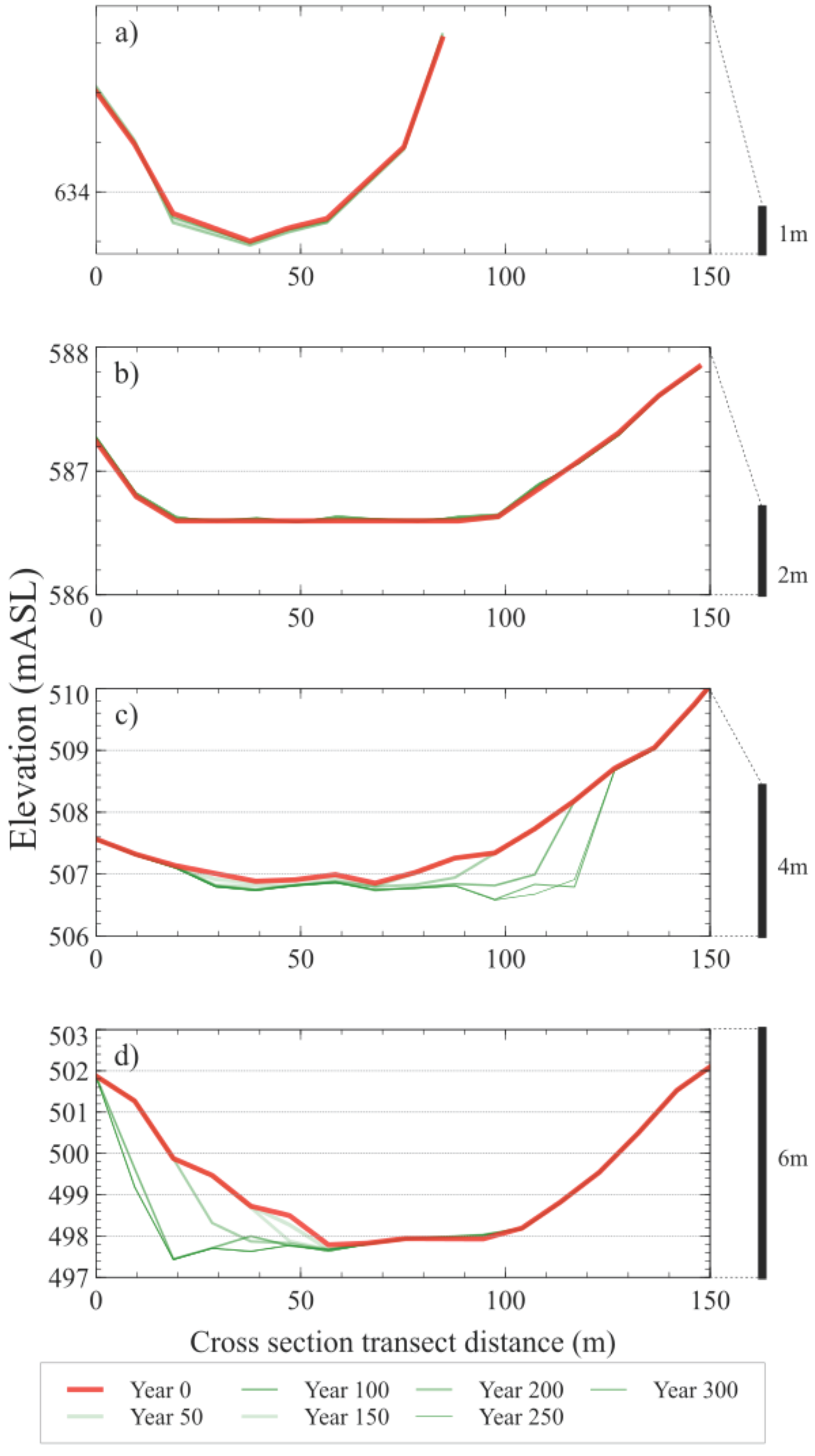
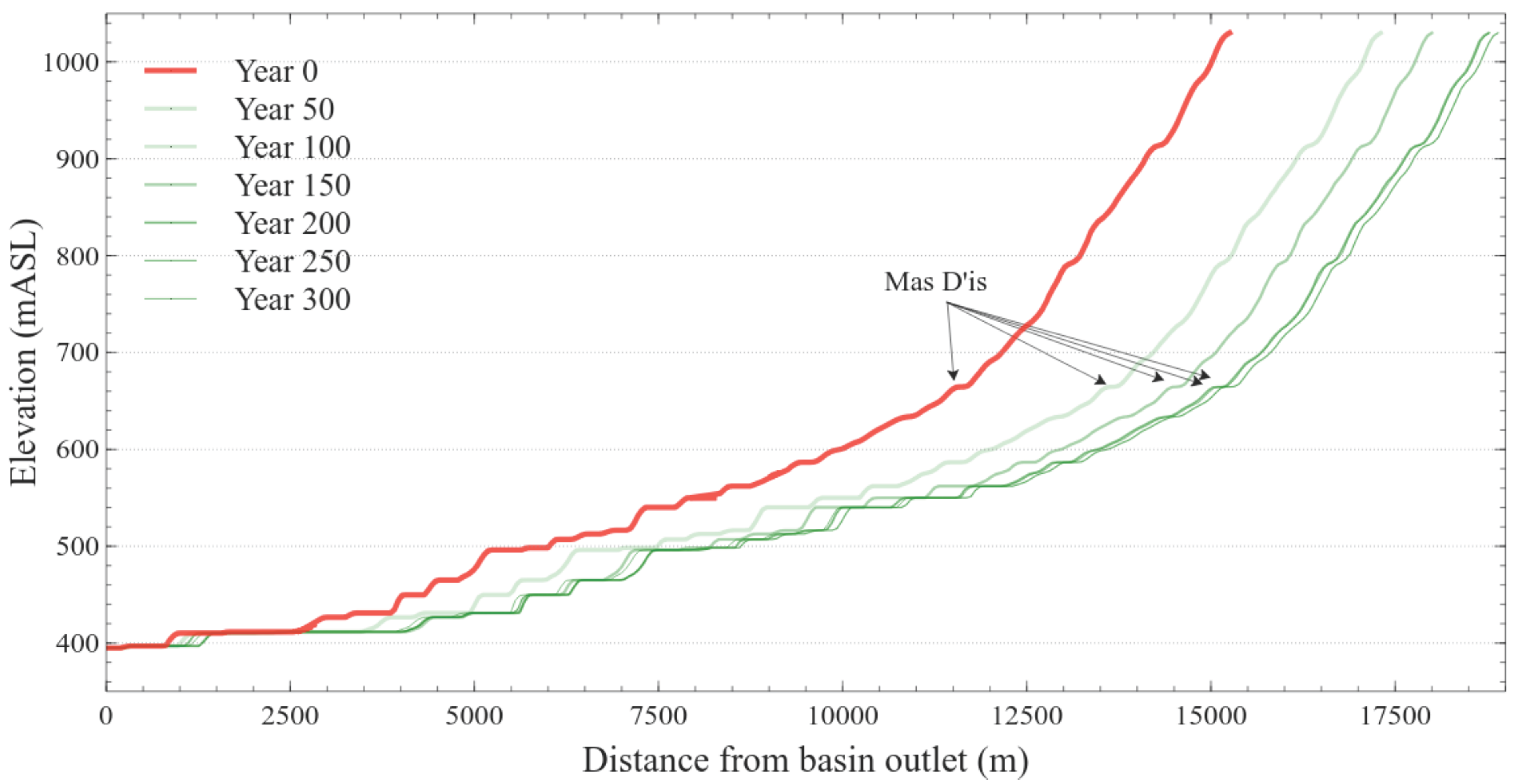
4.2. Effects of Land-Use on Barranco Incision

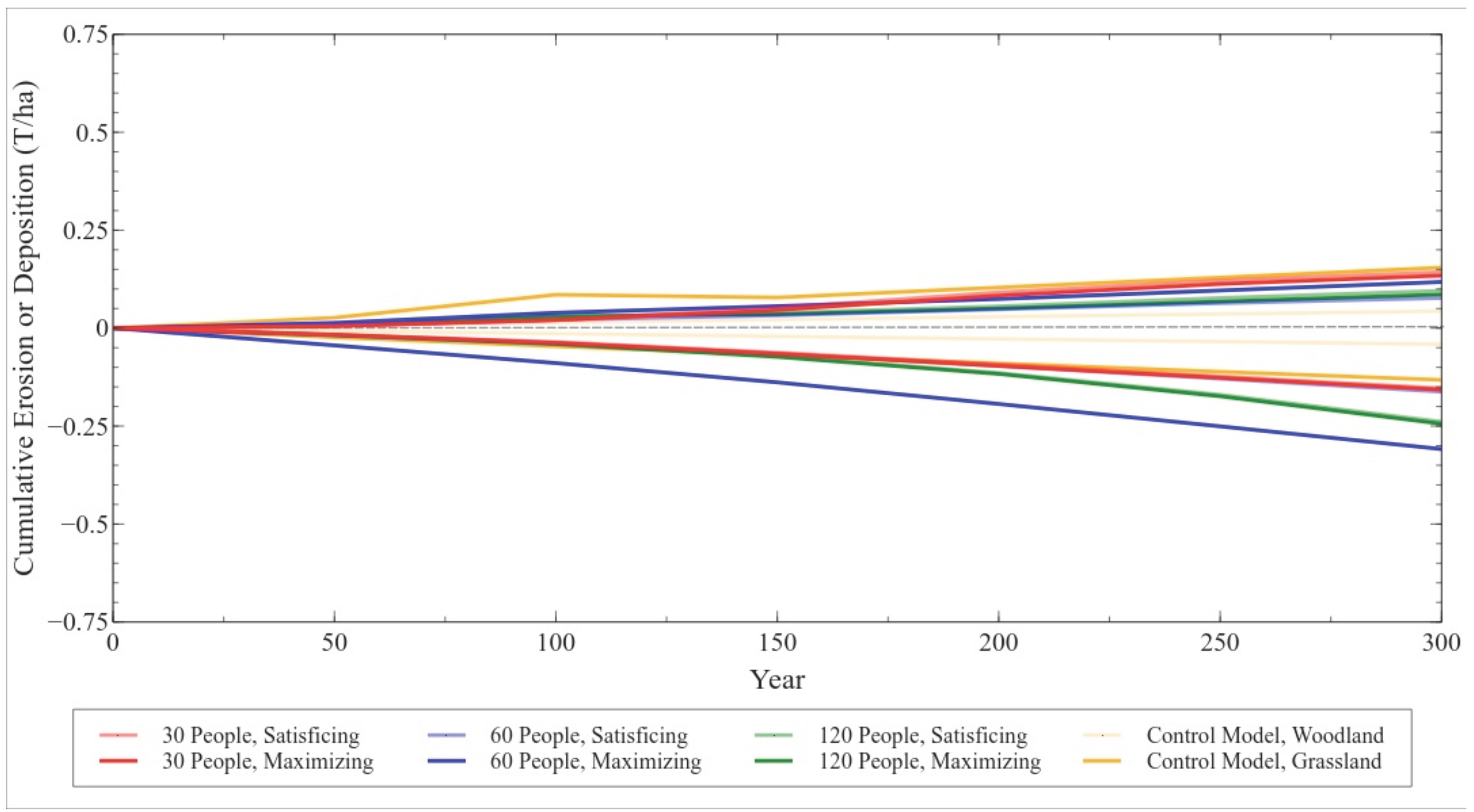
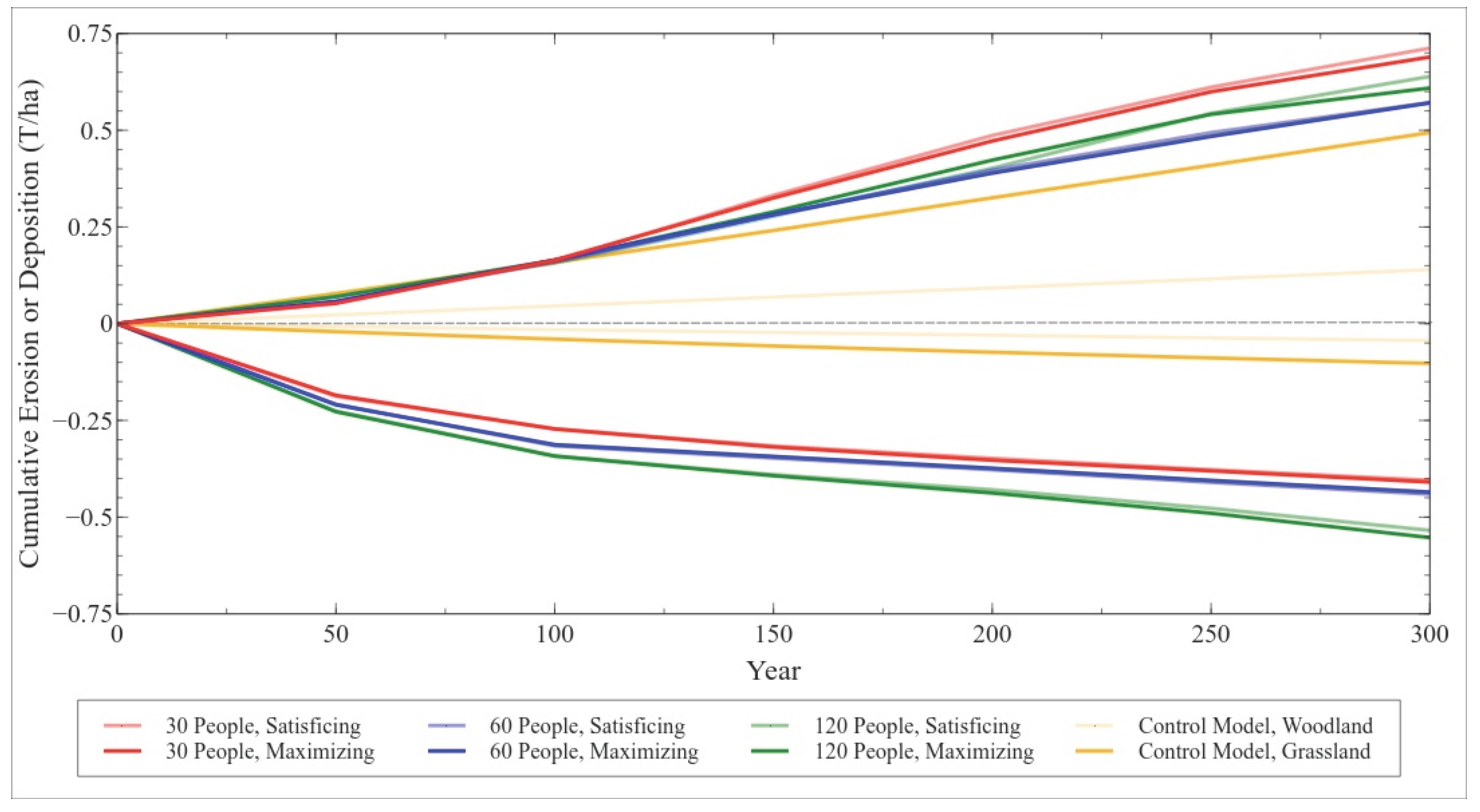
5. Conclusions
Acknowledgments
Author Contributions
Appendix
| Landscape Evolution Parameter | Typical Range of Values | Units | Value(s) Used in This Paper | Explanation |
|---|---|---|---|---|
| USPED K-factor | 0.01–0.75 | ((T·ha·hr)/(ha·MJ·mm)) | 0.42 | Soil erodibility index from RUSLE. |
| USPED R-factor | 0–50 | ((MJ·mm)/(ha·hr·yr)) | 4.54 | Rainfall factor from RUSLE. |
| USPED C-factor | 0.005–0.5 | unitless | 0.005–0.5 | Vegetation cover factor from RUSLE. |
| Kt | 0.001–0.000001 | unitless | 0.0001 | Stream transport efficiency variable (erodibility of stream substrate). |
| Sediment load exponent | 1.5,2.5 | unitless | 1.5 | Stream transport type variable (1.5 for mainly bedload transport, 2.5 for mainly suspended load transport). |
| Manning's N | 0.01–0.16 | s/m1/3 | 0.05 | Average value of Manning's surface roughness coefficient value for channelized flow in the drainage. |
| Flow speed | 0-3 | m/s | 1.4 | Average velocity of flowing water in the drainage. |
| Soil density | 0-3 | T/m3 | 1.2184 | Soil density map or constant for conversion from mass to volume. |
| Transition point | 10–500 | number of raster cells | 100 | Flow accumulation breakpoint value for shift from hillslopes to stream flow. |
| Per-storm precipitation totals | 0–10,000 | mm | 20.61 | Precipitation totals for the average storm. |
| Number of storms | 0–300 | storms/yr | 25 | Average number of storms per year. |
| Storm length | 0–72 | hr | 24 | Length of the average storm. |
| Village Subsistence Characteristic | Typical Range of Values | Units | Value(s) Used in This Paper | Explanation | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| General Village Characteristics | ||||||||||
| Number of people in the village | 0–1000 | number of individuals | 30, 60, 120 | The “target” number of people to be fed every year. Stays constant throughout the simulation. | ||||||
| Length of village “memory” | 0–59 | yr | 5 | Length of the “memory” of the agent in years. The agent will use the mean surplus/deficit information from this many of the most recent previous years when making a subsistence plan for the current year. | ||||||
| Amount of agricultural labor available | 0–365 | person-days | 300 | The amount of agricultural labor an average person of the village can do in a year. | ||||||
| Required amount of cereals | 300–500 | kg | 370 | Amount of cereals that would be required per person per year if cereals were the only food item being consumed. | ||||||
| Required number of animals | 40–100 | number of individuals | 60 | Number of herd animals that would be needed per person per year if pastoral products were the only food item being consumed. | ||||||
| Required amount of animal fodder | 500–1000 | kg | 680 | Amount of fodder required per herd animal per year. | ||||||
| Agropastoral Ratio | 0–1 | unitless ratio | 0.2 | Actual ratio of agricultural to pastoral foods in the diet, where 0 = 100% agricultural and 1 = 100% pastoral. | ||||||
| Village Farming Characteristics | ||||||||||
| Agricultural mix | 0–1 | unitless ratio | 0.25 | The wheat/barley ratio (e.g., 0.0 for all wheat, 1.0 for all barley, 0.5 for an equal mix). | ||||||
| Field dimensions | 5–100 | m | 20, 50 | North-South and East-West dimensions of agricultural fields. | ||||||
| Labor per field | 5–100 | person-days | 50 | Number of person-days required to till, sow, weed, and harvest one farm field in a year. | ||||||
| Field landcover value | 0–50 | succession stage | 5 | The landcover value for farmed fields (corresponds to an appropriate value from the landcover regrowth scheme). | ||||||
| Farming impact | 0–10 (0–5) | % of maximum fertility | 3 (2) | The mean and standard deviation of the amount to which farming a patch decreases its fertility (in percentage points of maximum fertility). Fertility impact values of individual farm plots is randomly chosen from a gaussian distribution that has this mean and standard deviation. | ||||||
| Maximum wheat | 3000–4000 | kg/ha | 3500 | Maximum amount of wheat that can be grown. | ||||||
| Maximum barley | 2000–3000 | kg/ha | 2500 | Maximum amount of barley that can be grown. | ||||||
| Satisficing farming strategy | Y/N | boolean | Both Y and N | Land is never dropped, only added if needed. | ||||||
| Maximizing Farming strategy | Y/N | boolean | Both Y and N | Land is dropped if below a previously defined threshold in productivity. | ||||||
| Productivity threshold | 0–1 | unitless ratio | 0.2 | Threshold for dropping land out of tenure with a maximizing strategy, interpreted as a percentage below the yearly average yield of all farm cells. | ||||||
| Fertility regain rate | 0–100 (0–100) | % of maximum fertility | 2 (0.5) | The mean and standard deviation of the natural fertility recovery rate (percentage by which soil fertility increases per year if not farmed). Fertility recovery values of individual landscape patches will be randomly chosen from a gaussian distribution that has this mean and standard deviation. | ||||||
| Village Grazing Characteristics | ||||||||||
| Minimum grazability | 0–50 | succession stage | 2 | Minimum amount of vegetation on a cell for it to be considered grazable by ovicaprines (corresponds to an appropriate value from the landcover regrowth scheme). | ||||||
| Grazing spatiality coefficient | 0–200 | m | 50 | Spatial dependency of the grazing pattern in map units. This value determines how “clumped” grazing patches will be. A value close to 0 will produce a perfectly randomized grazing pattern with patch size equal to raster cell resolution, and larger values will produce increasingly clumped grazing patterns, with the size of the patches corresponding to the value given. | ||||||
| Grazing patchiness coefficient | 0–1 | unitless | 1 | Coefficient that, along with the spatiality coefficient, determines the patchiness of the grazing pattern. Value must be non-zero, and usually will be ≤1.0. Values close to 0 will create a patchy grazing pattern, values close to 1 will create a "smooth" grazing pattern. Actual grazing patches will be sized to the resolution of the input landcover map. | ||||||
| Maximum grazing impact | 0–50 | succession stage | 3 | Maximum impact of grazing in units of “landcover succession” per annual grazing event. Grazing impact values of individual patches will be chosen from a gaussian distribution between 1 and this maximum value (i.e., most values will be between 1 and this value). Value must be ≥1. | ||||||
| Manuring rate | 0–100 | % of maximum fertility | 0.2 | Base rate that animal dung contributes to fertility increase on a grazed patch in units of percentage of maximum fertility regained per increment of grazing impact. Actual fertility regain values are thus calculated as “manuring rate x grazing impact”, so this variable interacts with the grazing impact settings. | ||||||
| Avoid grazing in agricultural catchment | Y/N | boolean | N | If turned on, ovicaprines will not graze in unused portions of the agricultural catchment (i.e., do not graze on "fallowed" fields, and thus no “manuring” of those fields will occur). | ||||||
| Avoid grazing on field stubbles | Y/N | boolean | N | If turned on, ovicaprines will not do any “stubble grazing” on harvested fields (and thus no “manuring” of fields). | ||||||
Conflicts of Interest
References
- Nogueras, P.; Burjachs, F.; Gallart, F.; Puigdefàbregas, J. Recent gully erosion in the El Cautivo badlands (Tabernas, SE Spain). Catena 2000, 40, 203–215. [Google Scholar] [CrossRef]
- Casalı́, J.; López, J.J.; Giráldez, J.V. Ephemeral gully erosion in southern Navarra (Spain). Catena 1999, 36, 65–84. [Google Scholar] [CrossRef]
- Valcárcel, M.; Taboada, M.T.; Paz, A.; Dafonte, J. Ephemeral gully erosion in northwestern Spain. Catena 2003, 50, 199–216. [Google Scholar] [CrossRef]
- Gutiérrez, Á.G.; Schnabel, S.; Contador, F.L. Gully erosion, land use and topographical thresholds during the last 60 years in a small rangeland catchment in SW Spain. Land Degrad. Dev. 2009, 20, 535–550. [Google Scholar] [CrossRef]
- Marzolff, I.; Ries, J.B.; Poesen, J. Short-term versus medium-term monitoring for detecting gully-erosion variability in a Mediterranean environment. Earth Surf. Process. Landf. 2011, 36, 1604–1623. [Google Scholar] [CrossRef]
- Hooke, J.M. Human impacts on fluvial systems in the Mediterranean region. Geomorphology 2006, 79, 311–335. [Google Scholar] [CrossRef]
- Van Andel, T.H.; Zanagger, E. Landscape stability and destabilization in the prehistory of Greece. In Man’s Role in the Shaping of the Eastern Mediterranean Landscape; Bottema, S., Entjes-Nieborg, G., van Zeist, W., Eds.; A.A. Balkema: Rotterdam, The Netherlands, 1990; pp. 139–157. [Google Scholar]
- Bintliff, J. Time, process and catastrophism in the study of Mediterranean alluvial history: A review. World Archaeol. 2002, 33, 417–435. [Google Scholar] [CrossRef]
- Redman, C.L.; Fish, P.R.; James, S.R.; Rogers, J.D. The Archaeology of Global Change: The Impact of Humans on Their Environment; Smithsonian Books: Washington, DC, USA, 2004. [Google Scholar]
- Perevolotsky, A.; Seligman, N.G. Role of grazing in Mediterranean rangeland ecosystems. BioScience 1998, 48, 1007–1017. [Google Scholar] [CrossRef]
- Barton, C.M.; Bernabeu Auban, J.; Garcia Puchol, O.; Schmich, S.; Molina Balaguer, L. Long-term socioecology and contingent landscapes. J. Archaeol. Method Theory 2004, 11, 253–295. [Google Scholar] [CrossRef]
- Fumanal Garcia, M.P. Dinámica sedimentaria Holocena en valles de cabecera del País Valenciano. Cuatern. Geomorfol. 1990, 4, 93–106. [Google Scholar]
- Hill, J.B. Land use and an archaeological perspective on socio-natural studies in the Wadi Al-Hasa, West-Central Jordan. Am. Antiq. 2004, 69, 389–412. [Google Scholar] [CrossRef]
- García-Ruiz, J.M. The effects of land uses on soil erosion in Spain: A review. Catena 2010, 81, 1–11. [Google Scholar] [CrossRef]
- Martı́nez-Casasnovas, J.A. A spatial information technology approach for the mapping and quantification of gully erosion. Catena 2003, 50, 293–308. [Google Scholar] [CrossRef]
- Vandekerckhove, L.; Poesen, J.; Govers, G. Medium-term gully headcut retreat rates in Southeast Spain determined from aerial photographs and ground measurements. Catena 2003, 50, 329–352. [Google Scholar] [CrossRef]
- Hill, J.B. What difference does environmental degradation make? In The Archaeology of Environmental Change; Fisher, C.T., Hill, J.B., Feinman, G.M., Eds.; The University of Arizona Press: Tucson, AZ, USA, 2009; pp. 160–173. [Google Scholar]
- Clevis, Q.; Tucker, G.E.; Lock, G.; Lancaster, S.T.; Gasparini, N.; Desitter, A.; Bras, R.L. Geoarchaeological simulation of meandering river deposits and settlement distributions: A three-dimensional approach. Geoarchaeology 2006, 21, 843–874. [Google Scholar] [CrossRef]
- Mitasova, H.; Barton, C.M.; Ullah, I.I.T.; Hofierka, J.; Harmon, R.S. GIS-based soil erosion modeling. In Treatise in Geomorphology: Vol. 3 Remote Sensing and GI Science in Geomorphology; Shroder, J., Bishop, M., Eds.; Academic Press: San Diego, CA, USA, 2013; pp. 228–258. [Google Scholar]
- Wainwright, J. Can modelling enable us to understand the rôle of humans in landscape evolution? Geoforum 2008, 39, 659–674. [Google Scholar] [CrossRef]
- Barton, C.M.; Ullah, I.I.T.; Bergin, S.M.; Mitasova, H.; Sarjoughian, H. Looking for the future in the past: Long-term change in socioecological systems. Ecol. Model. 2012, 241, 42–53. [Google Scholar] [CrossRef]
- Barton, C.M.; Ullah, I.I.T.; Mitasova, H. Computational modeling and Neolithic socioecological dynamics: A case study from Southwest Asia. Am. Antiq. 2010, 75, 364–386. [Google Scholar] [CrossRef]
- Mayer, G.R.; Sarjoughian, H.S. Composable cellular automata. Simulation 2009, 85, 735–749. [Google Scholar] [CrossRef]
- Mayer, G.R.; Sarjoughian, H.S.; Allen, E.K.; Falconer, S.E.; Barton, C.M. Simulation modeling for human community and agricultural landuse. In Agent-Directed Simulation, Proceedings of the Agent-Directed Simulation Multi-Conference, Huntsville, AL, USA, 2–6 April 2005; Society for Computer Simulation International: San Diego, CA, USA, 2006; pp. 65–72. [Google Scholar]
- Ullah, I.I. T.; Bergin, S. Modeling the consequences of village site location: Least cost path modeling in a coupled GIS and agent-based model of village agropastoralism in eastern Spain. In Least Cost Analysis of Social Landscapes: Archaeological Case Studies; White, D.A., Surface-Evans, S.L., Eds.; University of Utah Press: Salt Lake City, UT, USA, 2012; pp. 155–173. [Google Scholar]
- Barton, C.M.; Ullah, I.I.; Mayer, G.R.; Bergin, S.M.; Sarjoughian, H.S.; Mitasova, H. MedLanD Modeling Laboratory v.1. CoMSES Computational Model Library. Available online: https://www.openabm.org/model/4609/version/1 (accessed on 23 April 2015).
- Bernabeu Auban, J.; Orozco Köhler, T.; Diez Castillo, A.; Gomez Puche, M. Mas d’Is (Penàguila, Alicante): Aldeas y recintos monumentales del Neolítico Antiguo en el Valle del Serpis. Trab. Prehist. 2003, 60, 39–59. [Google Scholar]
- Bernabeu, J.; García Puchol, O.; Pardo, S.; Barton, M.; McClure, S.B. AEA 2012 Conference reading: Socioecological dynamics at the time of Neolithic transition in Iberia. Environ. Archaeol. 2014, 19, 214–225. [Google Scholar] [CrossRef]
- Mitas, L.; Mitasova, H. Distributed soil erosion simulation for effective erosion prevention. Water Resour. Res. 1998, 34, 505–516. [Google Scholar] [CrossRef]
- Mitasova, H.; Hofierka, J.; Zlocha, M.; Iverson, R. Modeling topographic potential for erosion and deposition using GIS. Int J. Geogr. Inf. Syst. 1996, 10, 629–641. [Google Scholar] [CrossRef]
- Moore, I.D.; Burch, G.J. Physical basis of the length-slope factor in the Universal Soil Loss Equation. Soil Sci. Soc. Am. J. 1986, 50, 1294–1298. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised Universal Soil Loss Equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting soil erosion by water: A guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE). In Agriculture Handbook; US Department of Agriculture: Washington, DC, USA, 1997; Volume 703, pp. 1–251. [Google Scholar]
- Onori, F.; de Bonis, P.; Grauso, S. Soil erosion prediction at the basin scale using the Revised Universal Soil Loss Equation (RUSLE) in a catchment of Sicily (southern Italy). Environ. Geol. 2006, 50, 1129–1140. [Google Scholar] [CrossRef]
- Barton, C.M.; Ullah, I.I.; Bergin, S. Land use, water and Mediterranean landscapes: Modelling long-term dynamics of complex socio-ecological systems. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2010, 368, 5275–5297. [Google Scholar] [CrossRef] [PubMed]
- Ullah, I.I.T. A GIS method for assessing the zone of human-environmental impact around archaeological sites: A test case from the Late Neolithic of Wadi Ziqlâb, Jordan. J. Archaeol. Sci. 2011, 38, 623–632. [Google Scholar] [CrossRef]
- Koriat, A.; Goldsmith, M.; Pansky, A. Toward a psychology of memory accuracy. Annu. Rev. Psychol. 2000, 51, 481–537. [Google Scholar] [CrossRef] [PubMed]
- Schacter, D.L. The seven sins of memory: Insights from psychology and cognitive neuroscience. Am. Psychol. 1999, 54, 182–203. [Google Scholar] [CrossRef] [PubMed]
- Quiroga, A.; Funaro, D.; Noellemeyer, E.; Peinemann, N. Barley yield response to soil organic matter and texture in the Pampas of Argentina. Soil Tillage Res. 2006, 90, 63–68. [Google Scholar] [CrossRef]
- Araus, J.L.; Febrero, A.; Buxó, R.; Camalich, M.D.; Martin, D.; Molina, F.; Rodriguez-Ariza, M.; Romagosa, I. Changes in carbon isotope discrimination in grain cereals from different regions of the western Mediterranean Basin during the past seven millennia. Palaeoenvironmental evidence of a differential change in aridity during the late Holocene. Glob. Change Biol. 1997, 3, 107–118. [Google Scholar] [CrossRef]
- Araus, J.L.; Amaro, T.; Zuhair, Y.; Nachit, M.M. Effect of leaf structure and water status on carbon isotope discrimination in field-grown durum wheat. Plant Cell Environ. 1997, 20, 1484–1494. [Google Scholar] [CrossRef]
- Barzegar, A.R.; Yousefi, A.; Daryashenas, A. The effect of addition of different amounts and types of organic materials on soil physical properties and yield of wheat. Plant Soil 2002, 247, 295–301. [Google Scholar] [CrossRef]
- Carter, D.L.; Berg, R.D.; Sanders, B.J. The effect of furrow irrigation erosion on crop productivity. Soil Sci. Soc. Am. J. 1985, 49, 207–211. [Google Scholar] [CrossRef]
- Pswarayi, A.; van Eeuwijk, F.A.; Ceccarelli, S.; Grando, S.; Comadran, J.; Russell, J.R.; Francia, E.; Pecchioni, N.; Li Destri, O.; Akar, T.; et al. Barley adaptation and improvement in the Mediterranean basin. Plant Breed. 2008, 127, 554–560. [Google Scholar] [CrossRef]
- Sadras, V.O.; Calvino, P.A. Quantification of grain yield response to soil depth in soybean, maize, sunflower, and wheat. Agron. J. 2001, 93, 577. [Google Scholar] [CrossRef]
- Araus, J.L.; Slafer, G.A.; Romagosa, I.; Molist, M. FOCUS: Estimated wheat yields during the emergence of agriculture based on the carbon isotope discrimination of grains: Evidence from a 10th millennium BP site on the Euphrates. J. Archaeol. Sci. 2001, 28, 341–350. [Google Scholar] [CrossRef]
- Wong, M.T.F.; Asseng, S. Yield and environmental benefits of ameliorating subsoil constraints under variable rainfall in a Mediterranean environment. Plant Soil 2007, 297, 29–42. [Google Scholar] [CrossRef]
- Slafer, G.A.; Romagosa, I.; Araus, J.L. Durum wheat and barley yields in antiquity estimated from 13C discrimination of archaeological grains: A case study from the western Mediterranean Basin. Funct. Plant Biol. 1999, 26, 345–352. [Google Scholar] [CrossRef]
- Adler, P.; Raff, D.; Lauenroth, W. The effect of grazing on the spatial heterogeneity of vegetation. Oecologia 2001, 128, 465–479. [Google Scholar] [CrossRef]
- Alados, C.L.; ElAich, A.; Papanastasis, V.P.; Ozbek, H.; Navarro, T.; Freitas, H.; Vrahnakis, M.; Larrosi, D.; Cabezudo, B. Change in plant spatial patterns and diversity along the successional gradient of Mediterranean grazing ecosystems. Ecol. Model. 2004, 180, 523–535. [Google Scholar] [CrossRef]
- Alados, C.L.; Pueyo, Y.; Barrantes, O.; Escós, J.; Giner, L.; Robles, A.B. Variations in landscape patterns and vegetation cover between 1957 and 1994 in a semiarid Mediterranean ecosystem. Landsc. Ecol. 2004, 19, 543–559. [Google Scholar] [CrossRef]
- Al-Jaloudy, M.A. Country Pasture/Forage Resource Profiles: JORDAN; Food and Agriculture Organization of the United Nations: Rome, Italy, 2006. [Google Scholar]
- Gulelat, W. Household Herd Size among Pastoralists in Relation to Overstocking and Rangeland Degradation (Sesfontein, Namibia). Master’s Thesis, International Institute for Geo-Information Science and Earth Observations, Enschede, The Netherlands, 2002. [Google Scholar]
- Lubbering, J.M.; Stuth, J.W.; Mungall, E.C.; Sheffield, W.J. An approach for strategic planning of stocking rates for exotic and native ungulates. Appl. Anim. Behav. Sci. 1991, 29, 483–488. [Google Scholar] [CrossRef]
- Nablusi, H.; Ali, J.M.; Abu Nahleh, J. Sheep and Goat Management Systems in Jordan: Traditional and Feedlot—A Case Study; Task Force Documents; Amman, Jordan, 1993. [Google Scholar]
- Ngwa, A.T.; Pone, D.K.; Mafeni, J.M. Feed selection and dietary preferences of forage by small ruminants grazing natural pastures in the Sahelian zone of Cameroon. Anim. Feed Sci. Technol. 2000, 88, 253–266. [Google Scholar] [CrossRef]
- Hocking, D.; Mattick, A. Dynamic Carrying Capacity Analysis as Tool for Conceptualising and Planning Range Management Improvements, with a Case Study from India; Overseas Development Institute, Pastoral Development Network: London, UK, 1993. [Google Scholar]
- Stuth, J.W.; Sheffield, W.J. Determining carrying capacity for combinations of livestock, white-tailed deer and exotic ungulates. In Wildlife Managagement Handbook; Texas A&M University: College Station, TX, USA, 2001; pp. 5–12. [Google Scholar]
- Stuth, J.W.; Kamau, P.N. Influence of woody plant cover on dietary selection by goats in an Acacia senegal savanna of East Africa. Small Rumin. Res. 1990, 3, 211–225. [Google Scholar] [CrossRef]
- Degen, A.A. Sheep and goat milk in pastoral societies. Small Rumin. Res. 2007, 68, 7–19. [Google Scholar] [CrossRef]
- Haenlein, G.F. W. The Nutritional Value of Sheep Milk. Available online: http://www.smallstock.info/issues/sheepmilk.htm (accessed on 21 October 2010).
- Maltz, E.; Shkolnik, A. Milk production in the desert: Lactation and water economy in the black Bedouin goat. Physiol. Zool. 1980, 53, 12–18. [Google Scholar]
- Meged’, S.S.; Torkaev, A.N.; Egorov, S.V.; Storozhuk, S.I. Milk productivity of breeding sheep of the Altai finewool breed. Russ. Agric. Sci. 2008, 34, 52–54. [Google Scholar] [CrossRef]
- Thomson, E.F.; Bahhady, F.; Termanini, A.; Mokbel, M. Availability of home-produced wheat, milk products and meat to sheep-owning families at the cultivated margin of the NW Syrian steppe. Ecol. Food Nutr. 1986, 19, 113–121. [Google Scholar] [CrossRef]
- Harris, F. Management of manure in farming systems in semi-arid West Africa. Exp. Agric. 2002, 38, 131–148. [Google Scholar] [CrossRef]
- Bernabeu Auban, J.; Molina Balaguer, L.; Orozco Köhler, T.; Díaz Castillo, A.; Barton, C.M. Early Neolithic at the Serpis Valley, Alicante, Spain. In The Early Neolithic in the Iberian Peninsula. Regional and Transregional Components, Proceedings of the XV World Congress, Lisbon, Portugal, 4–9 September 2006; Diniz, M., Ed.; BAR International Series: Oxford, UK, 2008; pp. 53–59. [Google Scholar]
- Bryson, R.A.; Bryson, R.U. High resolution simulations of regional Holocene climate: North Africa and the Near East. In Third Millennium BC Climate Change and Old World Collapse; Nato ASI Series I: Global Environmental Change; Nüzhet Dalfes, H., Kukla, G., Eds.; Springer Verlag: Berlin, Germany, 1996; Volume 49, pp. 565–593. [Google Scholar]
- Ruter, A.; Arzt, J.; Vavrus, S.; Bryson, R.A.; Kutzbach, J.E. Climate and environment of the subtropical and tropical Americas (NH) in the mid-Holocene: Comparison of observations with climate model simulations. Quat. Sci. Rev. 2004, 23, 663–679. [Google Scholar] [CrossRef]
- Arıkan, B. Macrophysical climate modeling, economy, and social organization in Early Bronze Age Anatolia. J. Archaeol. Sci. 2014, 43, 38–54. [Google Scholar] [CrossRef]
- Ullah, I. The Consequences of Human Land-Use Strategies during the PPNB-LN Transition: A Simulation Modeling Approach. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2013. [Google Scholar]
- Bogaard, A. “Garden agriculture” and the nature of early farming in Europe and the Near East. World Archaeol. 2005, 37, 177–196. [Google Scholar] [CrossRef]
- Conolly, J.; Colledge, S.; Shennan, S. Founder effect, drift, and adaptive change in domestic crop use in early Neolithic Europe. J. Archaeol. Sci. 2008, 35, 2797–2804. [Google Scholar] [CrossRef]
- Colledge, S.; Conolly, J.; Shennan, S. The evolution of Neolithic farming from SW Asian origins to NW European limits. Eur. J. Archaeol. 2005, 8, 137–156. [Google Scholar] [CrossRef]
- Halstead, P. Traditional and ancient rural economy in Mediterranean Europe: Plus ça change? J. Hell. Stud. 1987, 107, 77–87. [Google Scholar] [CrossRef]
- Butzer, K.W. Archaeology as Human Ecology; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- McClure, S.B.; Barton, C.M.; Jochim, M.A. Human behavioral ecology and climate change during the transition to agriculture in Valencia, eastern Spain. J. Anthropol. Res. 2009, 65, 253–269. [Google Scholar] [CrossRef]
- McClure, S.; Jochim, M.A.; Barton, C.M. Behavioral ecology, domestic animals, and land use during the transition to agriculture in Valencia, eastern Spain. In Foraging Theory and the Transition to Agriculture; Kennett, D., Winterhalder, B., Eds.; Smithsonian Institution Press: Washington, DC, USA, 2006; pp. 197–216. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barton, C.M.; Ullah, I.; Heimsath, A. How to Make a Barranco: Modeling Erosion and Land-Use in Mediterranean Landscapes. Land 2015, 4, 578-606. https://doi.org/10.3390/land4030578
Barton CM, Ullah I, Heimsath A. How to Make a Barranco: Modeling Erosion and Land-Use in Mediterranean Landscapes. Land. 2015; 4(3):578-606. https://doi.org/10.3390/land4030578
Chicago/Turabian StyleBarton, C. Michael, Isaac Ullah, and Arjun Heimsath. 2015. "How to Make a Barranco: Modeling Erosion and Land-Use in Mediterranean Landscapes" Land 4, no. 3: 578-606. https://doi.org/10.3390/land4030578





