Surface and Tropospheric Water Vapor Variability and Decadal Trends at Two Supersites of CO-PDD (Cézeaux and Puy de Dôme) in Central France
Abstract
:1. Introduction
2. Data Sets
2.1. CO-PDD, the Cézeaux, Opme, and Puy de Dôme Sites
2.1.1. Scientific Context, Networks, and Geographical Location
- The temporal variations of the properties of the gases, aerosols, and clouds on the medium and long-term and their vertical distribution in the troposphere.
- The processes linking these different atmospheric components (gas, aerosol, cloud).
- The impact of anthropogenic changes on the composition of the troposphere, and their consequences in terms of climate (cloud, radiation) and meteorology (precipitation).
2.1.2. Meteorological Stations
2.1.3. Spectrometer
2.1.4. GPS Ground Receivers
2.1.5. Raman Lidar
- a 400 mm Cassegrain telescope, equipped with a field stops set from 1 mm to 4 mm,
- a detection box dedicated to the splitting of the collected photons with respect to their wavelength
- LICEL photomultiplier modules equipped with R7400 Hamamatsu PMT tubes for each different channel.
2.2. Satellite Observations
2.2.1. AIRS/AQUA
2.2.2. COSMIC/FORMOSAT
3. Methodology and Numerical Tools
3.1. ECMWF ERA-Interim
3.2. Long Term Trend Estimation
3.3. Determination of the Influence of Geophysical Forcings on Water Vapor Variations
- North Atlantic Oscillation (NAO).
- East Atlantic Pattern (EA).
- East Atlantic-West Russia Pattern (EA-WR).
4. Seasonal Cycle and Short Time Variability of Water Vapor
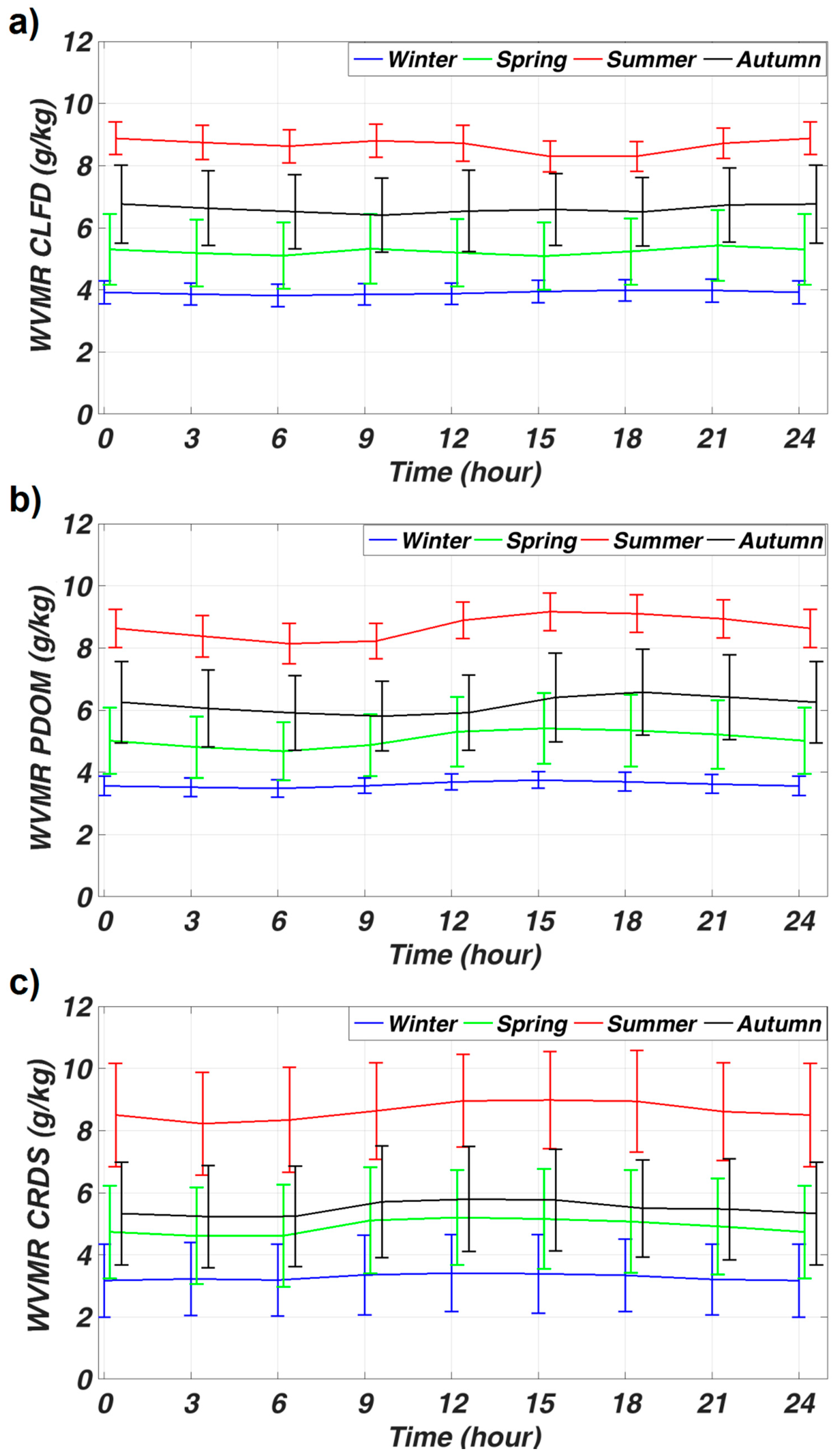
4.1. Surface Water Vapor
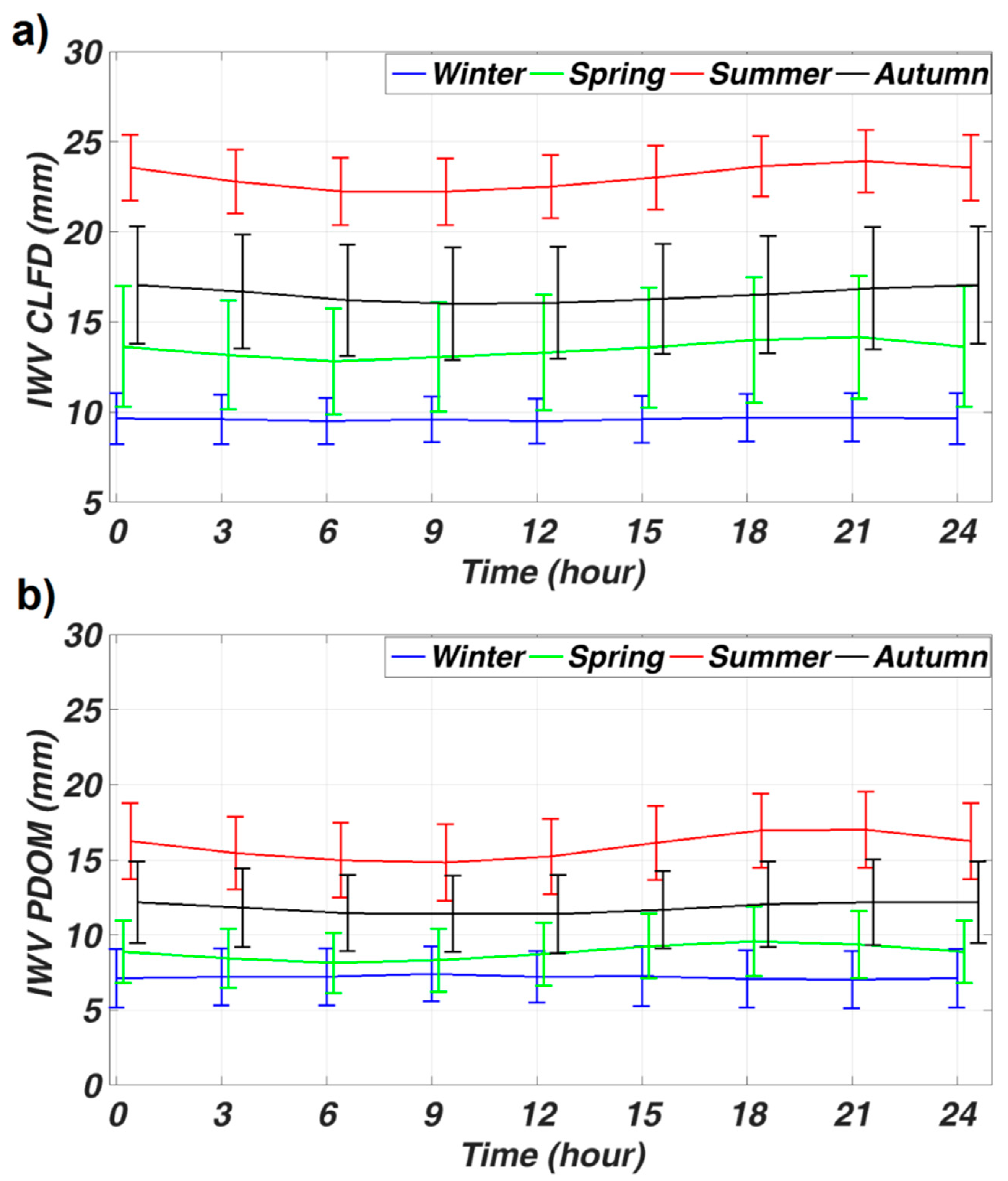
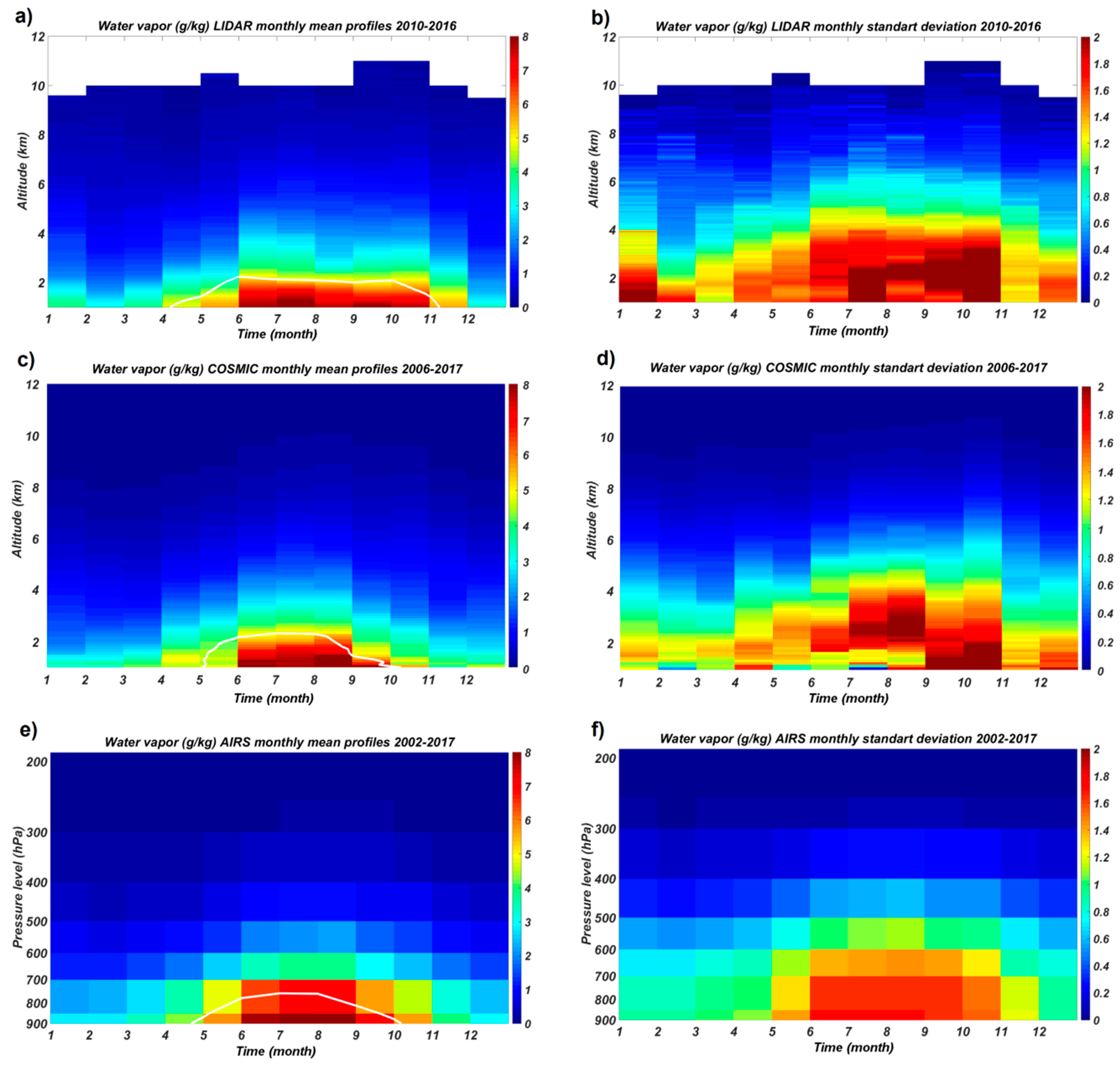
4.2. Vertical Columns and Profiles
5. Geophysical Forcing Contributions
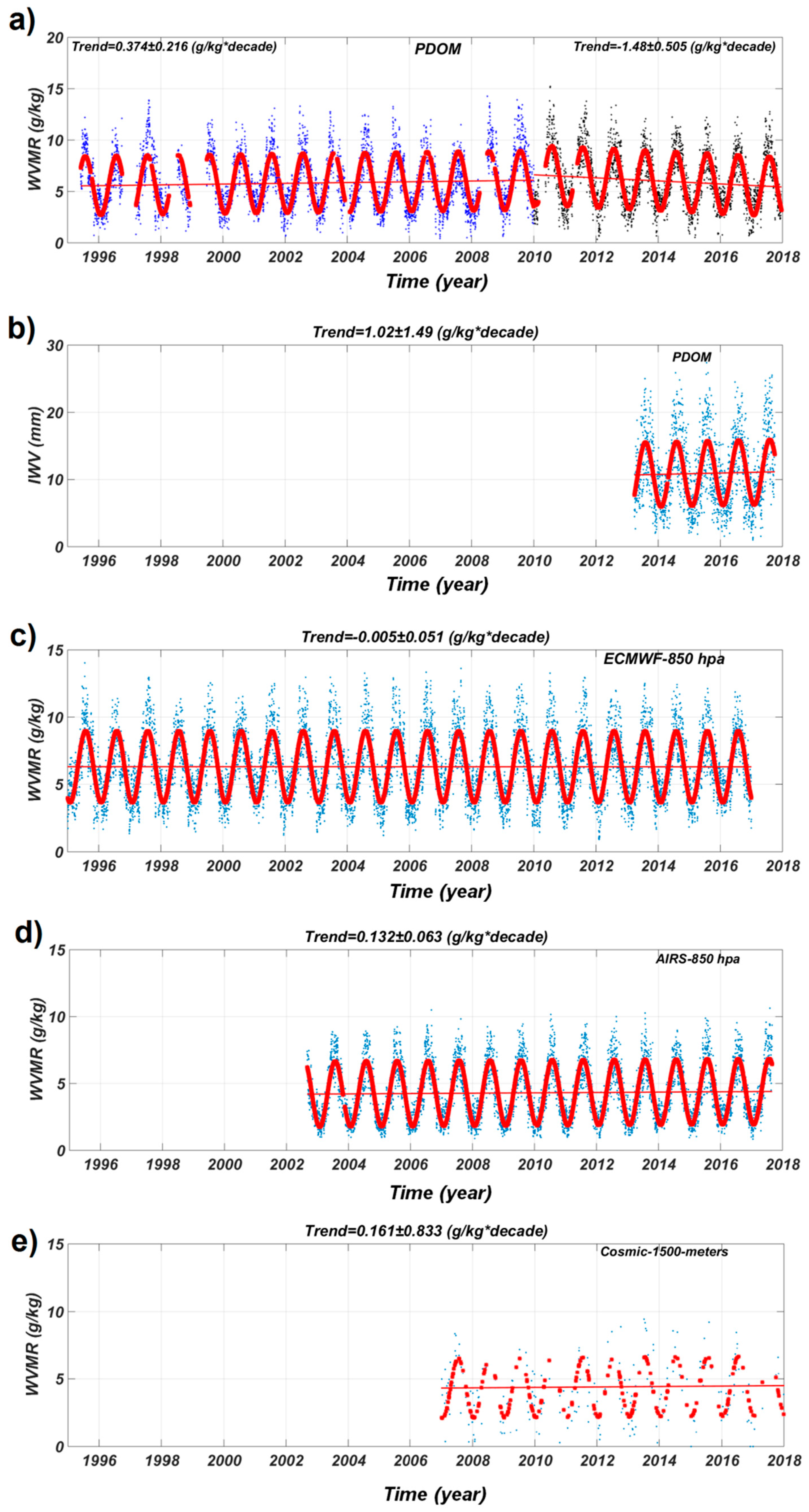
6. Decadal Trends from Long Time Series of Water Vapor
- At the Cezeaux site, the trend of IWV (2007–2017) is positive but not significant and the trend of WVMR (2003–2017) is negative.
- At the puy de Dôme site, the trends are difficult to analyze because the series are temporally short or inhomogeneous.
- Trends of IWV and specific humidity of ECMWF ERA-Interim are weaker than trends calculated from observation series.
- AIRS WVMR trends are in disagreement with ECMWF and the meteorological sensor WVMR trends, probably due to the low vertical resolution of AIRS.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Twomey, S. Aerosols, clouds and radiation. Atmos. Environ. 1991, 25, 2435–2442. [Google Scholar] [CrossRef]
- Lawson, R.P.; Angus, L.J.; Heymsfield, A.J. Cloud Particle Measurements in Thunderstorm Anvils and Possible Weather Threat to Aviation. J. Aircr. 1998, 35, 113–121. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Trenberth, K.E.; Stepaniak, D.P. Seamless Poleward Atmospheric Energy Transports and Implications for the Hadley Circulation. J. Clim. 2003, 16, 3706–3722. [Google Scholar] [CrossRef]
- D’Aulerio, P.; Fierli, F.; Congeduti, F.; Redaelli, G. Analysis of water vapor LIDAR measurements during the MAP campaign: Evidence of sub-structures of stratospheric intrusions. Atmos. Chem. Phys. 2005, 5, 1301–1310. [Google Scholar] [CrossRef]
- Baray, J.-L.; Pointin, Y.; van Baelen, J.; Lothon, M.; Campistron, B.; Cammas, J.-P.; Masson, O.; Colomb, A.; Hervier, C.; Bezombes, Y.; et al. Case study and climatological analysis of upper tropospheric jet stream and stratosphere-troposphere exchanges using VHF profilers and radionuclide measurements in France. J. Appl. Meteorol. Climatol. 2017, 56, 3081–3097. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The Concept of Essential Climate Variables in Support of Climate Research, Applications, and Policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef] [Green Version]
- Wulfmeyer, V.; Hardesty, R.M.; Turner, D.D.; Behrendt, A.; Cadeddu, M.P.; di Girolamo, P.; Schlüssel, P.; van Baelen, J.; Zus, F. A review of the remote sensing of lower tropospheric thermodynamic profiles and its indispensable role for the understanding and the simulation of water and energy cycles. Rev. Geophys. 2015, 53, 819–895. [Google Scholar] [CrossRef] [Green Version]
- Noh, Y.-C.; Sohn, B.-J.; Kim, Y.; Joo, S.; Bell, W. Evaluation of Temperature and Humidity Profiles of Unified Model and ECMWF Analyses Using GRUAN Radiosonde Observations. Atmosphere 2016, 7, 94. [Google Scholar] [CrossRef]
- Colomb, A.; Baray, J.L.; Sellegri, K.; Freney, E.; Deguillaume, L.; Pichon, J.M.; Ribeiro, M.; Bouvier, L.; Picard, D.; Van Baelen, J.; et al. The instrumented station Cézeaux-Opme-Puy De Dôme (CO-PDD): 20 years of measurement to document the atmospheric composition and climate change. 2018. to be submitted. [Google Scholar]
- Zhao, P.; Yin, Y.; Xiao, H.; Zhou, Y.; Liu, J. Role of water vapor content in the effects of aerosol on the electrification of thunderstorms: A numerical study. Atmosphere 2016, 7, 137. [Google Scholar] [CrossRef]
- Available online: http://wwwobs.univ-bpclermont.fr/SO/mesures/index.php (accessed on 31 July 2018).
- Available online: https://www.vaisala.com/sites/default/files/documents/HMP45AD-User-Guide-U274EN.pdf (accessed on 31 July 2018).
- Hyland, R.W.; Wexler, A. Formulations for the Thermodynamic Properties of the saturated Phases of H2O from 173.15K to 473.15K. ASHRAE Trans. 1983, 89, 500–519. [Google Scholar]
- Todd, M.W.; Provencal, R.A.; Owano, T.G.; Paldus, B.A.; Kachanov, A.; Vodopyanoy, K.L.; Hunter, M.; Coy, S.L.; Arnold, J.T. Application of mid-infrared cavity-ringdown spectroscopy to trace explosives vapor detection using a btoadly tunable (6–8 µm) optical parametric oscillator. Appl. Phys. B 2002, 75, 367–376. [Google Scholar] [CrossRef]
- Winderlich, J.; Chen, H.; Gerbig, C.; Seifert, T.; Kolle, O.; Lavric, J.V.; Kaiser, C.; Höfer, A.; Heimann, M. Continuous low-maintenance CO2/CH4/H2O measurements at the Zotino Tall Tower Observatory (ZOTTO) in Central Siberia. Atmos. Meas. Tech. 2010, 3, 1113–1128. [Google Scholar] [CrossRef]
- Rella, C.W.; Chen, H.; Andrews, A.E.; Filges, A.; Gerbig, C.; Hatakka, J.; Karion, A.; Miles, N.L.; Richardson, S.J.; Steinbacher, M.; et al. High accuracy measurements of dry mole fractions of carbon dioxide and methane in humid air. Atmos. Meas. Tech. 2013, 6, 837–860. [Google Scholar] [CrossRef]
- Available online: http://rgp.ign.fr (accessed on 31 July 2018).
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Petit, G.; Luzum, B. IERS Conventions. IERS Technical, Note No. 36, 2010, ISSN 1019-4568. Available online: http://www.iers.org/TN36/ (accessed on 31 July 2018).
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394. [Google Scholar] [CrossRef]
- Bertiger, W.; Desai, S.D.; Haines, B.; Harvey, N.; Moore, A.W.; Owen, S.; Weiss, J.P. Single receiver phase ambiguity resolution with GPS data. J. Geod. 2010, 84, 327. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Bosser, P.; Bock, O.; Thom, C.; Pelon, J.; Willis, P. A case study of using Raman lidar measurements in high-accuracy GPS applications. J. Geod. 2010, 84, 251. [Google Scholar] [CrossRef]
- Bock, O.; Bosser, P.; Bourcy, T.; David, L.; Goutail, F.; Hoareau, C.; Keckhut, P.; Legain, D.; Pazmino, A.; Pelon, J.; et al. Accuracy assessment of water vapor measurements from in situ and remote sensing techniques during the DEMEVAP 2011 campaign at OHP. Atmos. Meas. Tech. 2013, 6, 2777–2802. [Google Scholar] [CrossRef] [Green Version]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Fréville, P.; Montoux, N.; Baray, J.-L.; Chauvigné, A.; Réveret, F.; Hervo, M.; Dionisi, D.; Payen, G.; Sellegri, K. Lidar developments at Clermont-Ferrand—France for atmospheric observation. Sensors 2015, 15, 3041–3069. [Google Scholar] [CrossRef] [PubMed]
- Parkinson, C.L. Aqua: An Earth-Observing Satellite Mission to Examine Water and Other Climate Variables. IEEE Trans. Geosci. Remote Sens. 2003, 41, 173–183. [Google Scholar] [CrossRef]
- Available online: http://docserver.gesdisc.eosdis.nasa.gov/repository/Mission/AIRS/3.3_ScienceDataProductDocumentation/3.3.4_ProductGenerationAlgorithms/V6_L2_Product_User_Guide.pdf (accessed on 31 July 2018).
- Kursinski, E.R.; Hajj, G.A.; Hardy, K.R.; Schofield, J.T.; Linfield, R. Observing Earth’s atmosphere with radio occultation measurements. J. Geophys. Res. 1997, 102, 429–465. [Google Scholar] [CrossRef]
- Anthes, R.A.; Bernhardt, P.A.; Chen, Y.; Cucurull, L.; Dymond, K.F.; Ector, D.; Healy, S.B.; Ho, S.; Hunt, D.C.; Kuo, Y.; et al. The COSMIC/FORMOSAT-3 Mission: Early Results. Bull. Am. Meteor. Soc. 2008, 89, 313–334. [Google Scholar] [CrossRef] [Green Version]
- Isioye, O.A.; Combrinck, L.; Botai, J.O.; Munghemezulu, C. The Potential for Observing African Weather with GNSS Remote Sensing. Adv. Meteorol. 2015, 723071. [Google Scholar] [CrossRef]
- Ho, S.-P.; Peng, L.; Anthes, R.A.; Kuo, Y.-H.; Lin, H.-C. Marine Boundary Layer Heights and Their Longitudinal, Diurnal, and Interseasonal Variability in the Southeastern Pacific Using COSMIC, CALIOP, and Radiosonde Data. J. Clim. 2015, 28, 2856–2872. [Google Scholar] [CrossRef]
- Davis, N.A.; Birner, T. Seasonal to multidecadal variability of the width of the tropical belt. J. Geophys. Res. 2013, 118, 7773–7787. [Google Scholar] [CrossRef] [Green Version]
- Gettelman, A.; Wang, T. Structural diagnostics of the tropopause inversion layer and its evolution. J. Geophys. Res. 2015, 120, 46–62. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Bechtold, P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Available online: http://apps.ecmwf.int/datasets/data/interim-full-daily (accessed on 31 July 2018).
- Mastenbrook, H.J. The variability of water vapor in the stratosphere. J. Atmos. Sci. 1971, 28, 1495–1501. [Google Scholar] [CrossRef]
- Available online: ftp://ftp.cpc.ncep.noaa.gov/wd52dg/data/indices/tele_index.nh (accessed on 31 July 2018).
- Lamb, P.J.; Peppler, R.A. North Atlantic Oscillation: Concept and application. Bull. Am. Meteorol. Soc. 1987, 68, 1218–1225. [Google Scholar] [CrossRef]
- Hurrell, J.W.; van Loon, H. Decadal variations in climate associated with the North Atlantic Oscillation. Clim. Chang. 1997, 36, 301–326. [Google Scholar] [CrossRef]
- Wibig, J. Precipitation in Europe in relation to circulation patterns at the 500 hPa level. Int. J. Climatol. 1999, 19, 253–269. [Google Scholar] [CrossRef] [Green Version]
- Jerez, S.; Jimenez-Guerrero, P.; Montávez, J.P.; Trigo, R.M. Impact of the North Atlantic Oscillation on European aerosol ground levels through local processes: A seasonal model-based assessment using fixed anthropogenic emissions. Atmos. Chem. Phys. 2013, 13, 11195–11207. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Comas-Bru, L.; McDermott, F. Impacts of the EA and SCA patterns on the European twentieth century NAO–winter climate relationship. Q. J. R. Meteorol. Soc. 2014, 140, 354–363. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, Seasonality and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef] [Green Version]
- Krichak, S.O.; Alpert, P. Decadal trends in the east Atlantic–west Russia pattern and Mediterranean precipitation. Int. J. Climatol. 2005, 25, 183–192. [Google Scholar] [CrossRef]
- Ionita, M. The Impact of the East Atlantic/Western Russia Pattern on the Hydroclimatology of Europe from Mid-Winter to Late Spring. Climate 2014, 2, 296–309. [Google Scholar] [CrossRef] [Green Version]
- Beaufils, D.; Richoux, H.; Pagnol, L.M. Régression linéaire et incertitudes expérimentales. Bull. Union Phys. 1997, 796, 1361–1376. [Google Scholar]
- Keckhut, P.; Hauchecorne, A.; Chanin, M.L. Midlatitude long-term variability of the middle atmosphere: Trends and cyclic and episodic changes. J. Geophys. Res. 1995, 100, 18887–18897. [Google Scholar] [CrossRef]
- Bègue, N.; Bencherif, H.; Sivakumar, V.; Kirgis, G.; Mzé, N.; Leclair de Bellevue, J. Temperature variability and trends in the UT-LS over a subtropical site: Reunion (20.8° S, 55.5° E). Atmos. Chem. Phys. 2010, 10, 8563–8574. [Google Scholar] [CrossRef] [Green Version]
- Toihir, A.M.; Portafaix, T.; Sivakumar, V.; Bencherif, H.; Pazmiño, A.; Bègue, N. Variability and trend in ozone over the southern tropics and subtropics. Ann. Geophys. 2018, 36, 381–404. [Google Scholar] [CrossRef] [Green Version]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Goldsmith, J.E.M.; Bisson, S.E.; Ferrare, R.A.; Evans, K.D.; Whiteman, D.N.; Melfi, S.H. Raman lidar profiling of atmospheric water vapor: Simultaneous measurements with two collocated systems. Bull. Am. Meteorol. Soc. 1994, 75, 975–982. [Google Scholar] [CrossRef]
- Ferrare, R.A.; Melfi, S.H.; Whiteman, D.N.; Evans, K.D.; Schmidlin, F.J.; Starr, D.O. A Comparison of Water Vapor Measurements Made by Raman Lidar and Radiosondes. J. Atmos. Ocean. Technol. 1995, 12, 1177–1195. [Google Scholar] [CrossRef] [Green Version]
- Hoareau, C.; Keckhut, P.; Baray, J.-L.; Robert, L.; Courcoux, Y.; Porteneuve, J.; Vömel, H.; Morel, B. A Raman lidar at La Reunion (20.8° S, 55.5° E) for monitoring water vapour and cirrus distributions in the subtropical upper troposphere: Preliminary analyses and description of a future system. Atmos. Meas. Tech. 2012, 5, 1333–1348. [Google Scholar] [CrossRef] [Green Version]
- Deguillaume, L.; Charbouillot, T.; Joly, M.; Vaïtilingom, M.; Parazols, M.; Marinoni, A.; Amato, P.; Delort, A.-M.; Vinatier, V.; Flossmann, A.I.; et al. Classification of clouds sampled at the puy de Dôme (France) based on 10 yr of monitoring of their physicochemical properties. Atmos. Chem. Phys. 2014, 14, 1485–1506. [Google Scholar] [CrossRef] [Green Version]
- Seluchi, M.E.; Norte, F.A.; Satyamurty, P.; Chou, S.C. Analysis of three situations of the foehn effect over the Andes (zonda wind) using the Eta–CPTEC regional model. Weather Forecast. 2003, 18, 481–501. [Google Scholar] [CrossRef]
- Dione, C.; Lohou, F.; Chiriaco, M.; Lothon, M.; Bastin, S.; Baray, J.-L.; Yiou, P.; Colomb, A. The influence of synoptic circulations and local processes on temperature anomalies at three French observatories. J. Atmos. Ocean. Technol. 2017, 56, 141–158. [Google Scholar] [CrossRef]
- Morland, J.; Mätzler, C. Spatial interpolation of GPS integrated water vapour measurements made in the Swiss Alps. Meteorol. Appl. 2007, 14, 15–26. [Google Scholar] [CrossRef]
- Vogelmann, H.; Sussmann, R.; Trickl, T.; Reichert, A. Spatiotemporal variability of water vapor investigated using lidar and FTIR vertical soundings above the Zugspitze. Atmos. Chem. Phys. 2015, 15, 3135–3148. [Google Scholar] [CrossRef] [Green Version]
- Kalinnikov, V.V.; Khutorova, O.G. Diurnal variations in integrated water vapor derived from a GPS ground network in the Volga–Ural region of Russia. Ann. Geophys. 2017, 35, 453–464. [Google Scholar] [CrossRef] [Green Version]
- Farah, A.; Freney, E.; Chauvigné, A.; Baray, J.-L.; Rose, C.; Picard, D.; Colomb, A.; Hadad, D.; Abboud, M.; Farah, W.; et al. Seasonal variation of aerosol size distribution data at the Puy de Dôme station with emphasis on the boundary layer/free troposphere segregation. Atmosphere 2018, 9, 244. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Kushnir, Y.; Ottersen, G.; Visbeck, M. An overview of the North Atlantic oscillation. N. Atl. Oscil. Clim. Signif. Environ. Impact 2003, 134. [Google Scholar] [CrossRef]
- Pope, R.J.; Chipperfield, M.P.; Arnold, S.R.; Glatthor, N.; Feng, W.; Dhomse, S.S.; Kerridge, B.J.; Latter, B.G.; Siddans, R. Influence of the wintertime North Atlantic Oscillation on European tropospheric composition: An observational and modelling study. Atmos. Chem. Phys. 2018, 18, 8389–8408. [Google Scholar] [CrossRef]
- Wypych, A.; Bochenek, B.; Różycki, M. Atmospheric Moisture Content over Europe and the Northern Atlantic. Atmosphere 2018, 9, 18. [Google Scholar] [CrossRef]
- Sussmann, R.; Borsdorff, T.; Rettinger, M.; Camy-Peyret, C.; Demoulin, P.; Duchatelet, P.; Mahieu, E.; Servais, C. Harmonized retrieval of column-integrated atmospheric water vapor from the FTIR network–first examples for long-term records and station trends. Atmos. Chem. Phys. 2009, 9, 8987–8999. [Google Scholar] [CrossRef]
- Ning, T.; Wickert, J.; Deng, Z.; Heise, S.; Dick, G.; Vey, S.; Schöne, T. Homogenized time series of the atmospheric water vapor content obtained from the GNSS reprocessed data. J. Clim. 2016, 29, 2443–2456. [Google Scholar] [CrossRef]
- Nilsson, T.; Elgered, G. Long-term trends in the atmospheric water vapor content estimated from ground-based GPS data. J. Geophys. Res. 2008, 113, D19101. [Google Scholar] [CrossRef]
- Haas, R.; Ning, T.; Elgered, G. Long-term trends in the amount of atmospheric water vapour derived from space geodetic and remote sensing techniques. In Proceedings of the 3rd International Colloquium–Scientific and Fundamental Aspects of the Galileo Programme, Copenhagen, Denmark, 31 August–2 September 2011. [Google Scholar]
- Thao, S.; Eymard, L.; Obligis, E.; Picard, B. Trend and variability of the atmospheric water vapor: A mean sea level issue. J. Atmos. Ocean. Technol. 2014, 31, 1881–1901. [Google Scholar] [CrossRef]


| Technique | Location | Variable | Availability | Temporal Resolution | Vertical Resolution |
|---|---|---|---|---|---|
| GPS 1 | Cézeaux | IWV 2 | 2006–2017 | 5 min | Vertical column |
| GPS | puy de Dôme | IWV | 2013–2017 | 5 min | Vertical column |
| Meteorol station | Cézeaux | WVMR 3 | 2003–2017 | 5 min | Single point |
| Meteorol station | puy de Dôme | WVMR | 1995–2017 | 5 min 4 | Single point |
| CRDS 5 | puy de Dôme | WVMR | 2016–2018 | 1 h | Single point |
| Lidar | Cézeaux | WVMR | 2009–2016 | 2 min | Very high |
| AIRS 6 | Radius of 100 km around Cézeaux | WVMR | 2002–2017 | Few minutes | Low |
| COSMIC 7 | Radius of 100 km around Cézeaux | WVMR | 2006–2017 | Few days | High |
| ECMWF 8 | 45.75° N, 3.125° E | WVMR | 1978–2017 | 6 h | High |
| ECMWF | 45.75° N, 3.125° E | IWV | 1978–2017 | 3 h | Vertical column |
| Station | Summer | Autumn | Spring | Winter |
|---|---|---|---|---|
| CLFD | 8.9 ± 0.6 | 6.8 ± 1.2 | 5.4 ± 1.1 | 3.9 ± 0.3 |
| PDOM | 8.7 ± 0.6 | 6.6 ± 1.3 | 5.1 ± 1.0 | 3.6 ± 0.3 |
| CRDS | 8.6 ± 1.7 | 5.5 ± 1.7 | 4.9 ± 1.6 | 3.3 ± 1.2 |
| Data Series | Semi Annual Cycle (%) | Annual Cycle (%) | EA (%) | EA-WR (%) | NAO (%) | R2 (%) |
|---|---|---|---|---|---|---|
| PDOM WVMR (2011–2017) | 6.6 ± 2.6 | 57.4 ± 2.9 | 12 ± 7.2 | 12 ± 5.2 | 4.7 ± 5.5 | 92.7 |
| CLFD WVMR (2004–2017) | 5.7 ± 1.7 | 62.0 ± 1.8 | 11.5 ± 4.5 | 12.4 ± 4.0 | 1.2 ± 3.6 | 92.8 |
| CLFD GPS IWV (2009–2016) | 8.1 ± 1.4 | 62.7 ± 1.4 | 12.7 ± 3.8 | 10.9 ± 3.1 | 0.5 ± 2.9 | 94.9 |
| AIRS WVMR (2003–2016) | 8.1 ± 1.02 | 65.6 ± 1.0 | 12.7 ± 4.2 | -5.1 ± 4.0 | 4.6 ± 3.6 | 96.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadad, D.; Baray, J.-L.; Montoux, N.; Van Baelen, J.; Fréville, P.; Pichon, J.-M.; Bosser, P.; Ramonet, M.; Yver Kwok, C.; Bègue, N.; et al. Surface and Tropospheric Water Vapor Variability and Decadal Trends at Two Supersites of CO-PDD (Cézeaux and Puy de Dôme) in Central France. Atmosphere 2018, 9, 302. https://doi.org/10.3390/atmos9080302
Hadad D, Baray J-L, Montoux N, Van Baelen J, Fréville P, Pichon J-M, Bosser P, Ramonet M, Yver Kwok C, Bègue N, et al. Surface and Tropospheric Water Vapor Variability and Decadal Trends at Two Supersites of CO-PDD (Cézeaux and Puy de Dôme) in Central France. Atmosphere. 2018; 9(8):302. https://doi.org/10.3390/atmos9080302
Chicago/Turabian StyleHadad, Dani, Jean-Luc Baray, Nadège Montoux, Joël Van Baelen, Patrick Fréville, Jean-Marc Pichon, Pierre Bosser, Michel Ramonet, Camille Yver Kwok, Nelson Bègue, and et al. 2018. "Surface and Tropospheric Water Vapor Variability and Decadal Trends at Two Supersites of CO-PDD (Cézeaux and Puy de Dôme) in Central France" Atmosphere 9, no. 8: 302. https://doi.org/10.3390/atmos9080302





