A Robust Non-Gaussian Data Assimilation Method for Highly Non-Linear Models
Abstract
:1. Introduction
2. Preliminaries
2.1. Ensemble Kalman Filters Based on Modified Cholesky Decomposition
2.2. Gaussian Mixture Models Based Filters
3. Proposed Method
3.1. Estimation of Hyper-Parameters—EM Method
3.2. Sampling Method—Approaching the Posterior
- Step 1
- Let , set , go to step 2.
- Step 2
- Set .
- Step 3
- Linearize about and compute the direction (18b).
- Step 4
- Compute via Equation (19).
- Step 5
- Set according to Equation (20).
- Step 6
- If set and go to step 3, set and go to step 7 otherwise.
- Step 7
- If go to step 1, go to step 8 otherwise.
- Step 8
- The posterior mode approximations read .
3.3. Building the Posterior Ensemble
3.4. Computational Complexity
- During the E-Step, the computations of weights (14a) depend on the calculation:From this step, given the special structure of , can be computed with no more than long computations where denotes the maximum number of non-zero elements across all rows in with . Likewise, the number of long computations in order to obtain is bounded by since is diagonal. Thus, since there are K clusters, each E-step has the following operation counting:
- During the M-step, updating the centroids (15b) can be performed with no more than since has only n components different from zero (the diagonal ones), the least square solution of (15c) is bounded by calculations since there are n model components, and the cost of (15e) is bounded by since the multiplication of coefficients and model components is constrained to the neighbourhood of each model component. The computational effort of this method is then estimated as follows:
- During the sampling procedure, the gradient (18b) can be efficiently computed as follows:Given the special structure of , and can be computed with no more than , the computations in are bounded by since is diagonal. Thus, since this sampling method is performed v times, the computational effort of the sampling procedure reads,
- The posterior ensemble can be built (Section 3.3 [19]) with no more thanlong computations.
3.5. Comparison of GM-EnKF-MCMC with Other Sampling Methods
4. Experimental Settings
- Starting with an initial random solution, a 4th order Runge Kutta method is employed in order to integrate it over a long time period from which initial condition is obtained.
- A perturbed background solution is formed at time by drawing a sample from the Normal distribution,This solution is then integrated for 10 time units (equivalent to 70 days) in order to obtain a background solution consistent with the dynamics of the numerical model.
- An initial perturbed ensemble is built about the background state by taking samples from the distribution,In order to make them consistent with the model dynamics, the ensemble members are propagated for 10 time units, from which the initial ensemble members are obtained. We create the initial pool of members. The actual solution is integrated over 20 more time units in order to place it at the beginning of the assimilation window.
- Two assimilation windows are proposed for the tests, both of them consist of observations. In the first assimilation window, observations are taken every 16 h (time step of 0.1 time units) while in the last one, observations are available every 50 h (time step of 0.3 time units). We denote by the elapsed time between two observations.
- The observational errors are described by the probability distribution,where the standard deviations of observational errors , and ℓ should be interpreted as time index. Random observation networks are formed at the different assimilation cycles. The space between observations will depend on the step size, for instance, in the first step size observations are available every 0.1 time units (16 h) while in the last one, observations are taken every 0.3 time units (50 h).
- We consider the non-linear observation operator [32]:where j denotes the j-th observed component from the model state. .
- We consider two percentages of observed components s from the model state .
- The radius of influence is set to while the inflation factor is set to 1.02 (a typical value).
- We propose two ensemble sizes for the benchmark . These members are randomly chosen from the pool for different experiments in order to form the initial ensemble for the assimilation window. Evidently, .
- The norm of errors are utilized as a measure of accuracy at the assimilation step ℓ,where and are the reference and the analysis solutions, respectively. The analysis state is obtained by a weighted combination of posterior centroids via the likelihood ratio (21b) in lieu of the posterior mean.
- The Root-Mean-Square-Error (RMSE) is used as a measure of performance. On average, on a given assimilation window,
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hoar, T.; Anderson, J.; Collins, N.; Kershaw, H.; Hendricks, J.; Raeder, K.; Mizzi, A.; Barré, J.; Gaubert, B.; Madaus, L.; et al. DART: A Community Facility Providing State-Of-The-Art, Efficient Ensemble Data Assimilation for Large (Coupled) Geophysical Models; AGU: Washington, DC, USA, 2016. [Google Scholar]
- Clayton, A.; Lorenc, A.C.; Barker, D.M. Operational implementation of a hybrid ensemble/4D-Var global data assimilation system at the Met Office. Q. J. R. Meteorol. Soc. 2013, 139, 1445–1461. [Google Scholar] [CrossRef]
- Fairbairn, D.; Pring, S.; Lorenc, A.; Roulstone, I. A comparison of 4DVar with ensemble data assimilation methods. Q. J. R. Meteorol. Soc. 2014, 140, 281–294. [Google Scholar] [CrossRef]
- Reynolds, D. Gaussian mixture models. Encycl. Biom. 2015, 827–832. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Wu, Q.J.; Zhang, H. Bounded generalized Gaussian mixture model. Pattern Recogn. 2014, 47, 3132–3142. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Mandel, M.I.; Weiss, R.J.; Ellis, D.P. Model-based expectation-maximization source separation and localization. IEEE Trans. Audio Speech Lang. Proc. 2010, 18, 382–394. [Google Scholar] [CrossRef]
- Vila, J.P.; Schniter, P. Expectation-maximization Gaussian-mixture approximate message passing. IEEE Trans. Signal Process. 2013, 61, 4658–4672. [Google Scholar] [CrossRef]
- Dovera, L.; Della Rossa, E. Multimodal ensemble Kalman filtering using Gaussian mixture models. Comput. Geosci. 2011, 15, 307–323. [Google Scholar] [CrossRef]
- Evensen, G. Data Assimilation: The Ensemble Kalman Filter; Springer: Secaucus, NJ, USA, 2006. [Google Scholar]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Greybush, S.J.; Kalnay, E.; Miyoshi, T.; Ide, K.; Hunt, B.R. Balance and ensemble Kalman filter localization techniques. Mon. Weather Rev. 2011, 139, 511–522. [Google Scholar] [CrossRef]
- Buehner, M. Evaluation of a Spatial/Spectral Covariance Localization Approach for Atmospheric Data Assimilation. Mon. Weather Rev. 2011, 140, 617–636. [Google Scholar] [CrossRef]
- Anderson, J.L. Localization and Sampling Error Correction in Ensemble Kalman Filter Data Assimilation. Mon. Weather Rev. 2012, 140, 2359–2371. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Sandu, A. Efficient parallel implementation of DDDAS inference using an ensemble Kalman filter with shrinkage covariance matrix estimation. Clust. Comput. 2017, 1–11. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Sandu, A.; Deng, X. A parallel implementation of the ensemble Kalman filter based on modified Cholesky decomposition. J. Comput. Sci. 2017, in press. [Google Scholar] [CrossRef]
- Bickel, P.J.; Levina, E. Regularized estimation of large covariance matrices. Ann. Statist. 2008, 36, 199–227. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Mancilla, A.; Calabria, J.C. A Posterior Ensemble Kalman Filter Based on A Modified Cholesky Decomposition. Procedia Comput. Sci. 2017, 108, 2049–2058. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D. A Matrix-Free Posterior Ensemble Kalman Filter Implementation Based on a Modified Cholesky Decomposition. Atmosphere 2017, 8, 125. [Google Scholar] [CrossRef]
- Attia, A.; Sandu, A. A hybrid Monte Carlo sampling filter for non-gaussian data assimilation. AIMS Geosci. 2015, 1, 41–78. [Google Scholar] [CrossRef]
- Attia, A.; Moosavi, A.; Sandu, A. Cluster Sampling Filters for Non-Gaussian Data Assimilation. arXiv, 2016; arXiv:1607.03592. [Google Scholar]
- Kotecha, J.H.; Djuric, P.M. Gaussian sum particle filtering. IEEE Trans. Signal Process. 2003, 51, 2602–2612. [Google Scholar] [CrossRef]
- Rings, J.; Vrugt, J.A.; Schoups, G.; Huisman, J.A.; Vereecken, H. Bayesian model averaging using particle filtering and Gaussian mixture modeling: Theory, concepts, and simulation experiments. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Moon, T.K. The expectation-maximization algorithm. IEEE Signal Process. Mag. 1996, 13, 47–60. [Google Scholar] [CrossRef]
- Alspach, D.; Sorenson, H. Nonlinear Bayesian estimation using Gaussian sum approximations. IEEE Trans. Autom. Control 1972, 17, 439–448. [Google Scholar] [CrossRef]
- Frei, M.; Künsch, H.R. Mixture ensemble Kalman filters. Comput. Stat. Data Anal. 2013, 58, 127–138. [Google Scholar] [CrossRef]
- Tagade, P.; Seybold, H.; Ravela, S. Mixture Ensembles for Data Assimilation in Dynamic Data-driven Environmental Systems1. Procedia Comput. Sci. 2014, 29, 1266–1276. [Google Scholar] [CrossRef]
- Sondergaard, T.; Lermusiaux, P.F. Data assimilation with Gaussian mixture models using the dynamically orthogonal field equations. Part I: Theory and scheme. Mon. Weather Rev. 2013, 141, 1737–1760. [Google Scholar] [CrossRef]
- Smith, K.W. Cluster ensemble Kalman filter. Tellus A 2007, 59, 749–757. [Google Scholar] [CrossRef]
- Hansen, P.R. A Winner’s Curse for Econometric Models: On the Joint Distribution of In-Sample Fit and Out-Of-Sample Fit and Its Implications for Model Selection; Research Paper; Stanford University: Stanford, CA, USA, 2010; pp. 1–39. [Google Scholar]
- Vrieze, S.I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 2012, 17, 228. [Google Scholar] [CrossRef] [PubMed]
- Van Leeuwen, P.J.; Cheng, Y.; Reich, S. Nonlinear Data Assimilation; Springer: Cham, Switzerland, 2015; Volume 2. [Google Scholar]
- Bannister, R. A review of operational methods of variational and ensemble-variational data assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 607–633. [Google Scholar] [CrossRef]
- Snyder, C.; Bengtsson, T.; Bickel, P.; Anderson, J. Obstacles to high-dimensional particle filtering. Mon. Weather Rev. 2008, 136, 4629–4640. [Google Scholar] [CrossRef]
- Rebeschini, P.; Van Handel, R. Can local particle filters beat the curse of dimensionality? Ann. Appl. Probab. 2015, 25, 2809–2866. [Google Scholar] [CrossRef]
- Moré, J.J.; Sorensen, D.C. Computing a trust region step. SIAM J. Sci. Stat. Comput. 1983, 4, 553–572. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.; Toint, P.L. Trust Region Methods; SIAM: Philadelphia, PA, USA, 2000; Volume 1. [Google Scholar]
- Nino-Ruiz, E.D. Implicit Surrogate Models for Trust Region Based Methods. J. Comput. Sci. 2018, in press. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Grippo, L.; Lampariello, F.; Lucidi, S. A nonmonotone line search technique for Newton’s method. SIAM J. Numer. Anal. 1986, 23, 707–716. [Google Scholar] [CrossRef]
- Kramer, O.; Ciaurri, D.E.; Koziel, S. Derivative-free optimization. In Computational Optimization, Methods and Algorithms; Springer: Berlin/Heidelberg, Germany, 2011; pp. 61–83. [Google Scholar]
- Conn, A.R.; Scheinberg, K.; Vicente, L.N. Introduction to Derivative-Free Optimization; SIAM: Philadelphia, PA, USA, 2009; Volume 8. [Google Scholar]
- Rios, L.M.; Sahinidis, N.V. Derivative-free optimization: A review of algorithms and comparison of software implementations. J. Glob. Optim. 2013, 56, 1247–1293. [Google Scholar] [CrossRef]
- Jang, J.S.R. Derivative-Free Optimization. In Neuro-Fuzzy Soft Computing; Prentice Hall: Englewood Cliffs, NJ, USA, 1997; pp. 173–196. [Google Scholar]
- Nino-Ruiz, E.D.; Ardila, C.; Capacho, R. Local search methods for the solution of implicit inverse problems. In Soft Computing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–14. [Google Scholar]
- Anderson, J.L.; Anderson, S.L. A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts. Mon. Weather Rev. 1999, 127, 2741–2758. [Google Scholar] [CrossRef]
- Grubmüller, H.; Heller, H.; Windemuth, A.; Schulten, K. Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions. Mol. Simul. 1991, 6, 121–142. [Google Scholar] [CrossRef]
- Van Gunsteren, W.F.; Berendsen, H. A leap-frog algorithm for stochastic dynamics. Mol. Simul. 1988, 1, 173–185. [Google Scholar] [CrossRef]
- Koontz, W.L.; Fukunaga, K. A nonparametric valley-seeking technique for cluster analysis. IEEE Trans. Comput. 1972, 100, 171–178. [Google Scholar] [CrossRef]
- Lorenz, E.N. Designing Chaotic Models. J. Atmos. Sci. 2005, 62, 1574–1587. [Google Scholar] [CrossRef]
- Fertig, E.J.; Harlim, J.; Hunt, B.R. A comparative study of 4D-VAR and a 4D ensemble Kalman filter: Perfect model simulations with Lorenz-96. Tellus A 2007, 59, 96–100. [Google Scholar] [CrossRef]
- Karimi, A.; Paul, M.R. Extensive chaos in the Lorenz-96 model. Chaos 2010, 20, 043105. [Google Scholar] [CrossRef] [PubMed]
- Gottwald, G.A.; Melbourne, I. Testing for chaos in deterministic systems with noise. Physica D 2005, 212, 100–110. [Google Scholar] [CrossRef]
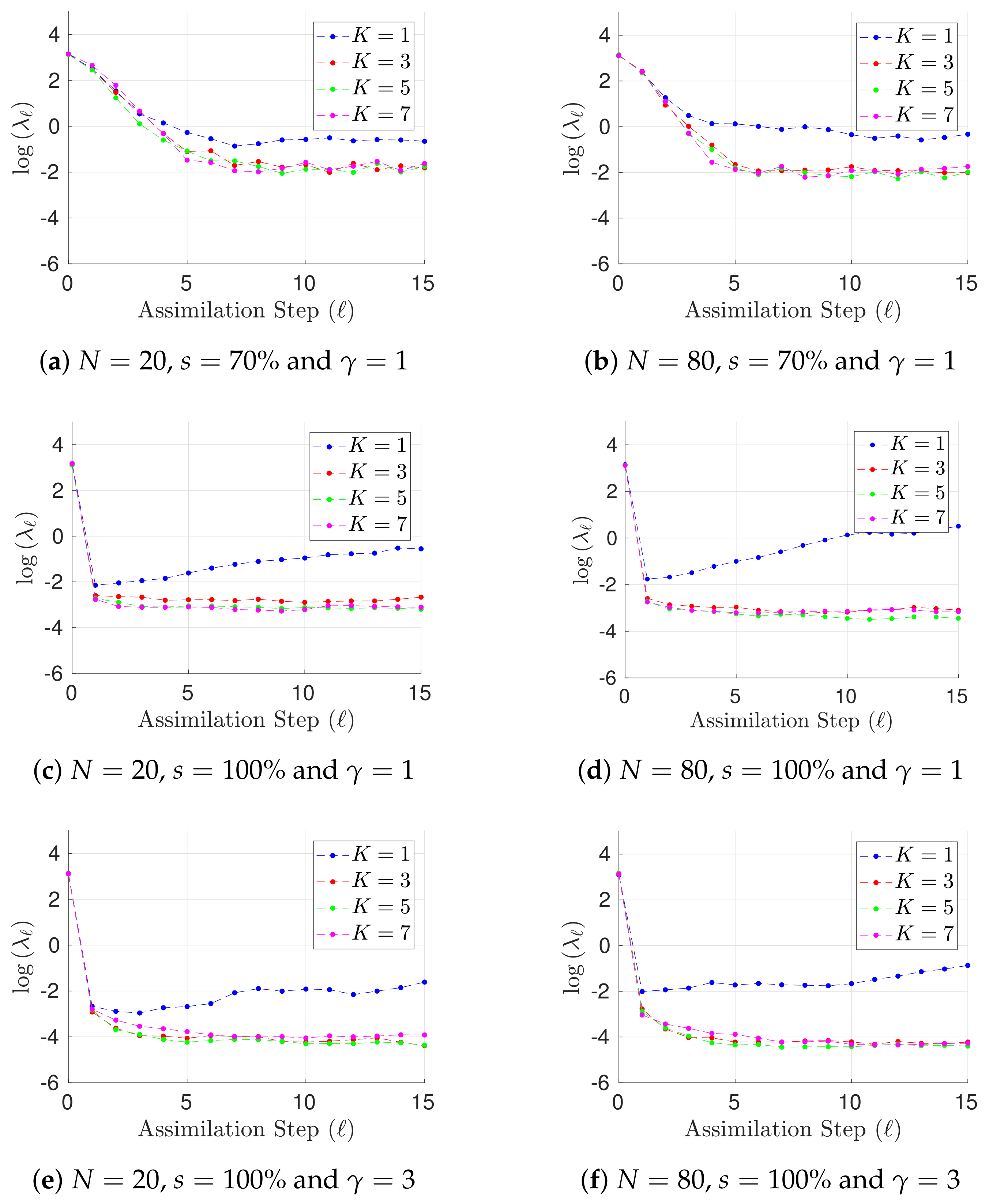
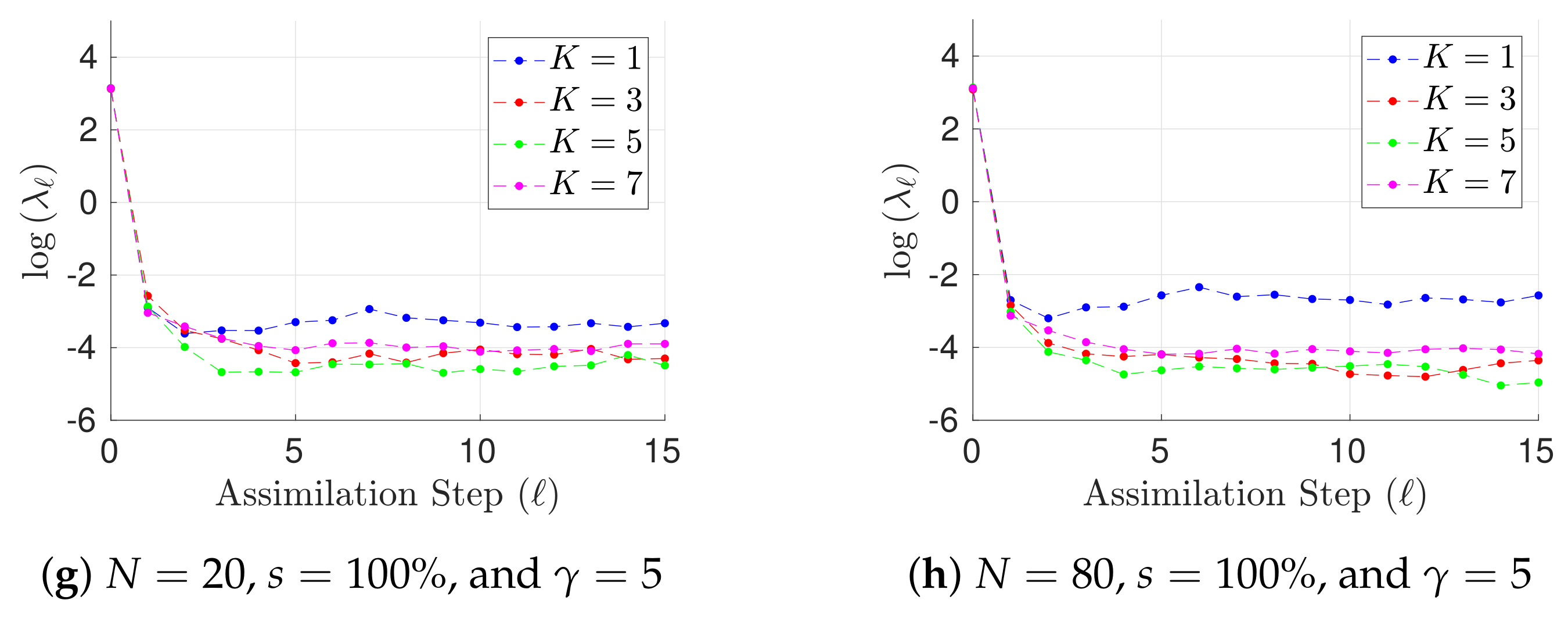

| 70% | 16 h |  |  |  |
| 50 h |  |  |  | |
| 100% | 16 h |  |  |  |
| 50 h |  |  |  |
| s | ||||
|---|---|---|---|---|
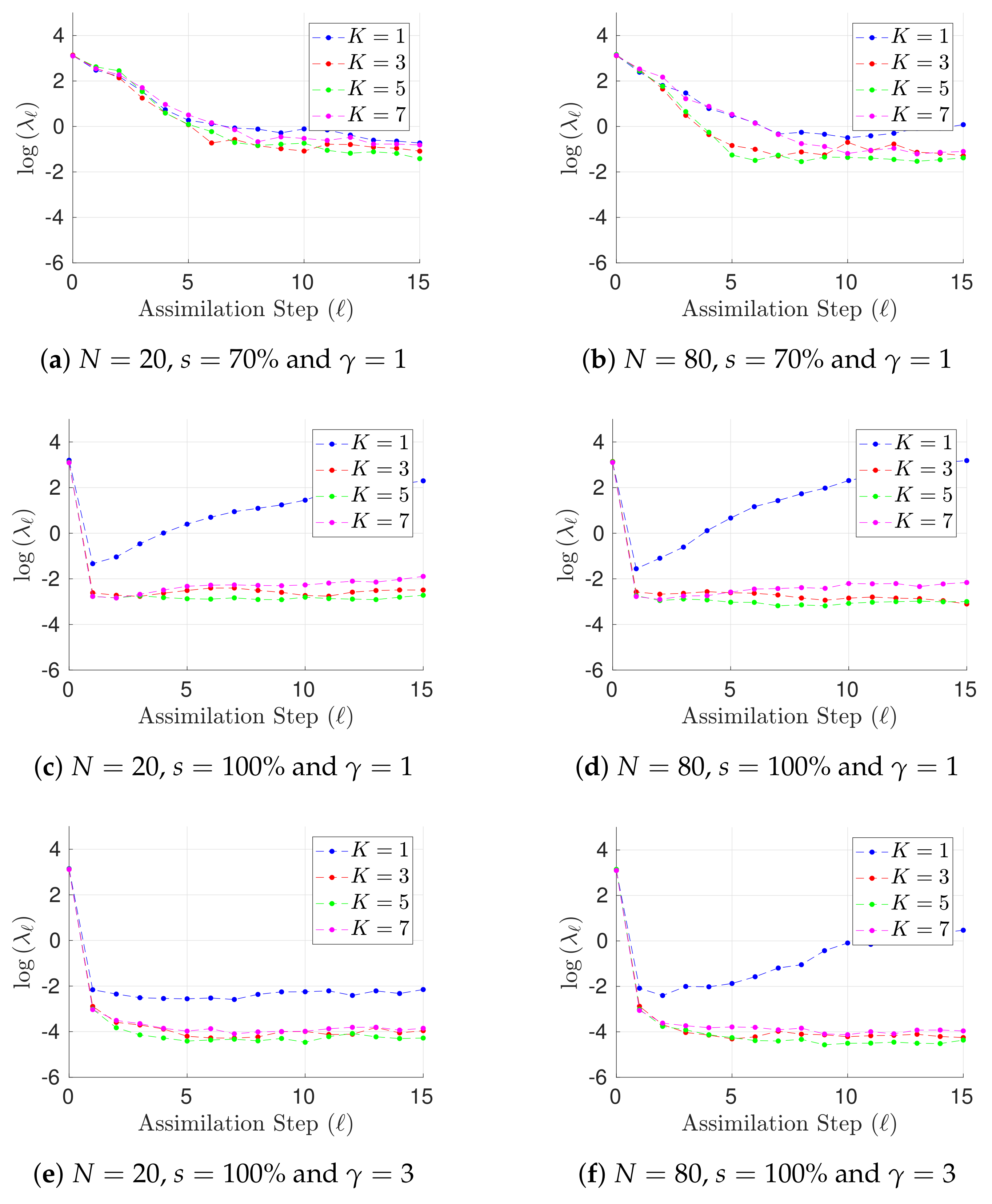
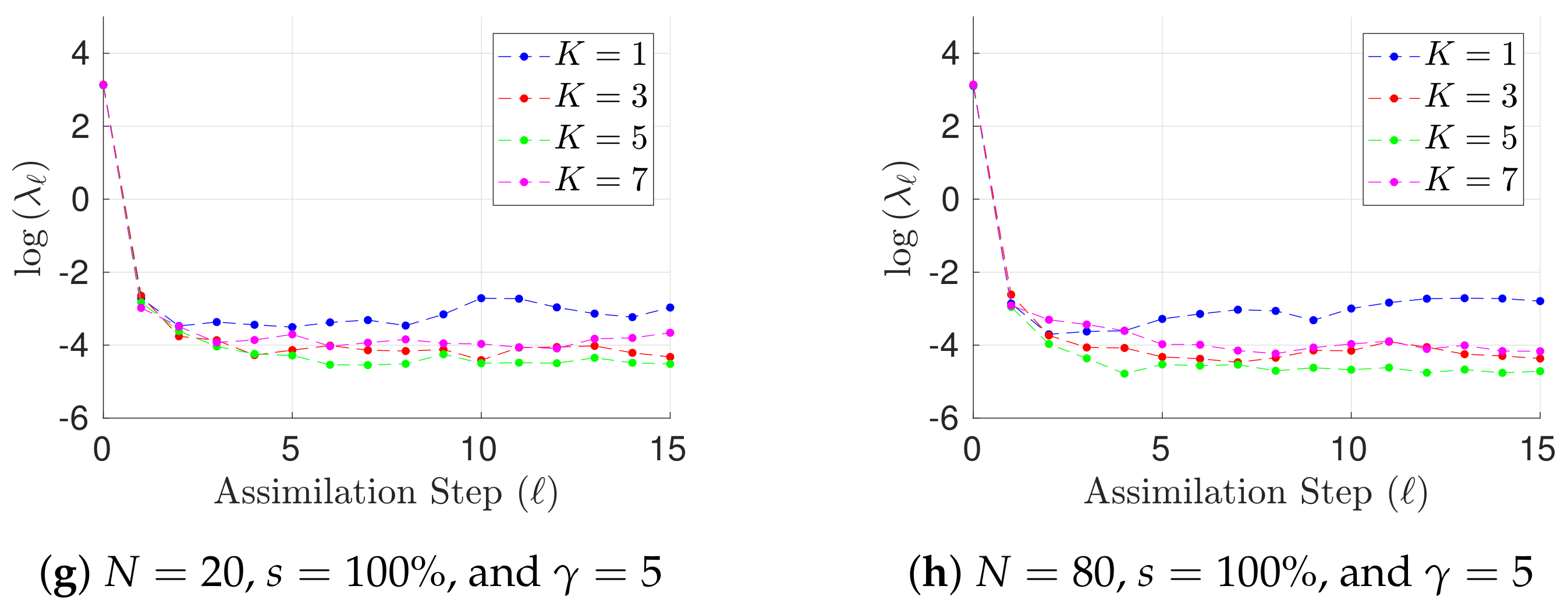
| 70% | 16 h |  |  |  |
| 50 h |  |  |  | |
| 100% | 16 h |  |  |  |
| 50 h |  |  |  |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nino-Ruiz, E.D.; Cheng, H.; Beltran, R. A Robust Non-Gaussian Data Assimilation Method for Highly Non-Linear Models. Atmosphere 2018, 9, 126. https://doi.org/10.3390/atmos9040126
Nino-Ruiz ED, Cheng H, Beltran R. A Robust Non-Gaussian Data Assimilation Method for Highly Non-Linear Models. Atmosphere. 2018; 9(4):126. https://doi.org/10.3390/atmos9040126
Chicago/Turabian StyleNino-Ruiz, Elias D., Haiyan Cheng, and Rolando Beltran. 2018. "A Robust Non-Gaussian Data Assimilation Method for Highly Non-Linear Models" Atmosphere 9, no. 4: 126. https://doi.org/10.3390/atmos9040126





