Next Article in Journal
Assessing the Impact of Surface and Upper-Air Observations on the Forecast Skill of the ACCESS Numerical Weather Prediction Model over Australia
Previous Article in Journal
Exposure to Black Carbon during Bicycle Commuting–Alternative Route Selection
 
Search for Articles:
Title / Keyword
Author / Affiliation
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
Journals
Atmosphere
Volume 9
Issue 1
10.3390/atmos9010027
atmosphere-logo
Submit to this Journal Review for this Journal Edit a Special Issue
► Article Menu

Article Menu

share announcement thumb_up
...
textsms
...
Open AccessArticle

The Dynamic Character of Northern Hemisphere Flow Regimes in a Near-Term Climate Change Projection

by
Andrew D. Jensen
1,
Mirseid G. Akperov
2,
Igor I. Mokhov
2,3,
Anthony R. Lupo
4,5,* and
Fengpeng Sun
6
1
Department of Mathematics and Meteorology, Northland College, Ashland, WI 54806, USA
2
A.M Obukhov Institute of Atmospheric Physics, Russian Academy of Sciences, Moscow 119017, Russia
3
Department of Physics, Lomonosov Moscow State University, Moscow 119991, Russia
4
Atmospheric Science Program, University of Missouri, Columbia, MO 65202, USA
5
Department of Natural Resources Management and Land Cadastre, Belgorod State University, Belgorod 308015, Russia
6
Department of Geosciences, University of Missouri—Kansas City, Kansas City, MO 64110, USA
*
Author to whom correspondence should be addressed.
Atmosphere 2018, 9(1), 27; https://doi.org/10.3390/atmos9010027
Received: 16 December 2017 / Revised: 11 January 2018 / Accepted: 11 January 2018 / Published: 16 January 2018
(This article belongs to the Section Meteorology)
Download PDF
Browse Figures

Abstract

The dynamic character of an enstrophy-based diagnostic, previously used in the study of atmospheric blocking, is examined here, in near-term future simulations from the Institut Pierre Simon Laplace Climate Model version 4 (IPSL-CM4) and version 5 (IPSL-CM5) climate models of the Northern Hemisphere flow for moderate climate change scenarios. Previous research has shown that integrated regional enstrophy (IE) increases during blocking onset and decay, which is a reflection of planetary-scale instability. In addition, IE has been shown previously to increase during flow regime transitions in general, even those not associated with blocking events. Here, a 31-year IE diagnostic time series is examined for changes in short term (5–40 days) planetary-scale variability that may correspond flow regime changes in an increased carbon dioxide environment. The time-series analysis herein indicates that the IE diagnostic provides evidence for approximately 30–35 atmospheric flow regime transitions per year in a warmer climate, which is similar to that of the control run and the latest 30-year observed climate, as derived from re-analyses. This result has implications regarding the predictability of weather in a warmer world.
Keywords: regime transition; blocking; climate change; climate model; enstrophy regime transition; blocking; climate change; climate model; enstrophy

1. Introduction

The idea that Earth’s atmosphere has preferred states or that certain states are persistent, at least in a qualitative sense, has been noted in the atmospheric science literature for more than 75 years [1]. Later research found correlations between the large-scale flow pattern over the north Pacific and the eastern U.S. [2,3]. At the same time, researchers identified persistent positive pressure anomalies that occurred in preferred regions of the Northern Hemisphere (e.g., [4]), called blocking anticyclones. Then, the work of [5] demonstrated, using a low-order primitive equation model for convection in a closed hydrodynamic system, that two flows which are initially similar may evolve very differently over time, or that predictability beyond a certain time frame for a system like the atmosphere is essentially impossible using the primitive equations. The solutions to the low-order model in [5] could be represented in phase space as two basins of attraction, which gave rise to the idea that the hemispheric scale flow might be represented by two stable states, characterized as flow regimes.
The work of [6,7] attempted to demonstrate, through statistical analysis, that the Northern Hemisphere flow could be characterized by two basins of attraction (a more meridional or amplified state and a more zonal state), represented as a bi-modal distribution of filtered winter-season 500 hPa height fields. Their research decomposed the 500 hPa height fields into wave numbers, and then created and analyzed a wave amplitude index, derived from wave numbers two to four. They [6,7] defined wave numbers two to four as the planetary-scale. These studies also demonstrated that a particular Northern Hemisphere flow regime type persists for about 11 days. However, dynamic studies from the same era and later [8,9,10,11] determined that there is evidence for multiple flow regimes that exist in the hemispheric flow, including those that represent persistent or blocking flows (e.g., [8]).
At the same time, [12] defined teleconnection indexes for various regions of the Northern Hemisphere, using correlation analysis to show that 500 hPa height anomalies may be positively or negatively correlated over long distances, or that the large-scale flow has preferred states locally. One example is the Pacific North American Pattern (PNA), which can be characterized by four alternating negative and positive height anomalies (or positive and negative height anomalies) [12], dominating the weather from the central Pacific to the Southeast United States. Since then, several studies have quantitatively or qualitatively identified multiple persistent flow regimes regionally—for example, in the Atlantic basin (e.g., [13,14]). Studies [13,14] have shown that some local flow regimes and flow regime transitions are preferred, while others are less likely, and that certain precursors, such as breaking Rossby waves (e.g., [15]), could be associated with regime transitions. Other studies have used potential vorticity to identify flow regimes or persistent states in the East Asian and Pacific sector [16], as well as the preferred flow regime transition paths in that region. Similar studies have identified analogous multiple persistent regimes in the Southern Hemisphere (e.g., Pacific South American Pattern (PSA) [17,18] and references therein).
Studies using simplified models also demonstrate that large-scale flows may have two or more preferred states. For example, [19] used a two-layer, quasi-geostrophic mid-latitude channel type model with a flat bottom (but inhomogeneous, in order to simulate land–sea differences similar to the Atlantic), and found two preferred states for the zonal mean flow. This study [19] called these the high-latitude and low-latitude states, and they demonstrated that the synoptic scale eddies were important in explaining the relative persistence of each mode. The work of [20,21] used an even simpler analytic channel-type model to explore the phase transitions of a pattern similar to the North Atlantic Oscillation (NAO). They imposed a low-frequency planetary-scale wave with a period of about two to three weeks on a zonal flow, as well as a synoptic-scale perturbation of about three days in length, to describe the transitions between the positive and negative phases of the NAO. The model was extended by [22] to show the interactions among the mean flow, planetary waves, and synoptic eddies, and a new mechanism was proposed to explain the onset or destruction of blocking regimes. Other studies examine the impact of climate change (in a warmer, higher CO2 world) on preferred modes or flow regimes in general circulation models [23,24,25].
Additionally, [26] showed that the occurrence of observed blocking increased across the Northern Hemisphere during the first part of the 21st century, a result that was somewhat sensitive to the three blocking criteria used in their study. This same paper used the Institut Pierre Simon Laplace Climate Model version 4 (IPSL-CM4) general circulation model (GCM) [27], and demonstrated that frequency and duration of blocking would increase during the early part of the 21st century, under a business-as-usual scenario (Special Report Emission Scenarios (SRES-A2) [28]) and a more moderate increased CO2 environment (SRES-A1B). Another study [29], however, shows that by the end of the 21st century, the frequency, duration, and intensity of blocking will be similar to that of the current era (1976–2005) for the entire Northern Hemisphere annually, and during the summer and winter seasons. This study used the Institut Pierre Simon Laplace Climate Model version 5 (IPSL-CM5) climate model for the control, a low-emission (representative concentration pathways (RCP) 2.6 [28]), and more extreme (RCP 8.5) anthropogenic emissions scenarios. However, [26] notes increased inter-annual variability in their projected blocking climatologies. Additionally, a comparison of [30] and the model studies cited here demonstrates the well-known tendency for the underrepresentation of blocking in climate models.
In [31] and references therein, integrated enstrophy (IE) first published by [32] is demonstrated to be useful in identifying the onset and decay period for blocking. However, [33] states that this diagnostic may not be unambiguously associated only with blocking regime transitions, but is likely associated flow regime transitions in general. Also, [34] used IE to identify seasonal flow regime transitions in their study, and showed that the behavior of the IE diagnostic on the seasonal time scale is similar to that of the index in [6,7].
Then, the characteristics of the IE diagnostic in climate model simulations for the period 2020–2050 were obtained from simulations in the IPSL-CM4 and IPSL-CM5 models. In particular, hemispheric-scale flow regime transitions were identified in the 5–40 day range, which is consistent with the time period for these types of transitions (e.g., [6,7]). The IE diagnostic used to identify flow regime transition is related also to finite-time instability [32,35]. While these methods have been applied previously to past blocking events, here an important objective is to apply the methodology (time-series analysis of IE) to a reanalysis data set and climate model simulations, in order to study flow regime transition. The authors are not aware of published studies that perform a similar analysis with IE. The results of time-series analysis indicate that the IE diagnostic supports approximately 30–35 large-scale flow regime transitions (not necessarily blocking as discussed above) per year in the current and in a warmer climate. The paper is organized as follows. The relevant theory is described in section two, where the methods developed in [32,36] are outlined. Section three contains our findings, and section four includes a discussion of the results and conclusions.

2. Data and Methods

2.1. Model and Reanalysis Data

Simulations from the coupled ocean–atmosphere general circulation models, the IPSL-CM4 [27], with horizontal resolution 2.5° × 3.75° (lat/lon) under the SRES-A1B, and the IPSL-CM5-LR [37] with horizontal resolution 1.875° × 3.75° under a present-day control scenario (from IPSL-CM5) and the RCP 4.5 (intermediate emission) scenario, were the models and scenarios used here. The near-future scenarios covered the 31-year period from 2020 to 2050. The model was chosen because the data were available readily, and because this model is part of the Coupled Model Intercomparison Project (CMIP) suite [37]. Also, the IPSL-CM5 model featured improvements, including those in the boundary layer physics, an improved ocean model, and air–sea ice interaction scheme, as well as improvements in the atmospheric chemistry. A complete review of improvements can be found in [37]. Since the intermediate scenario was chosen as a mid-range scenario, it may be representative of the range of scenarios produced by [28]. The variable used to calculate the IE diagnostic from each model and scenario were the Northern Hemisphere 500 hPa height (m).
In order to calculate the spectral characteristics of the daily IE field, obtained from the Northern Hemisphere 500 hPa heights for the years 2020–2050 from both versions of the IPSL model, a Fast Fourier Transform (FFT) was applied to the daily IE time series. A bandpass filter with was employed to isolate periods of approximately 5–40 days in the IE time series, which correspond to the general time-scale of planetary-scale flows. Additionally, [38] and references therein demonstrate that the planetary scale using spatial filtering techniques corresponds to low wave numbers, up to four or five, which have a time-scale of about six days as inferred from [39,40] or others. For the wavelet analysis, the Morlet wavelet was used as the wave basis, and this has been used in published climatological studies [41,42,43]. The data were smoothed, using a moving average to remove seasonality, and the linear trend was subtracted before obtaining the power spectrum. The spectral density was calculated at the 95% confidence level. IE was also calculated from the set of Northern Hemisphere re-analyses, as well for comparison to the model output. The 500 hPa heights were obtained from the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) re-analyses, which were archived on a 2.5° × 2.5° latitude/longitude grid from 1981 to 2010.

2.2. Methods

Here the IE diagnostic of [32] is introduced. Local Lyapunov exponents from the barotropic vorticity equation are defined in [27] as λ i ( ξ 0 ,   T )   = 1 2 n log ν i for initial vorticity ξ0 and time T = n Δt. The νi are the eigenvalues of M n * M n , where M n = ∏ k = − n k = n B ( k Δ t ) , and B(t) is the Jacobian operator, and n is a multiple of the time increment Δt, and k an index in the product of M*M. The study of [32] also showed that the sum of the positive local Lyapunov exponents is highly correlated with the integral of enstrophy. This integral may be used as a stability indicator, and is defined as in [36]:
Integrated   Enstrophy   ( IE )   ≡ ∫ ξ 2 d A .
In (1), A is the area and ξ is the relative vorticity; detailed explanations and derivations of this quantity can be found in [32,44]. Briefly, the relative vorticity was calculated as the geostrophic value using the height field and second order finite differencing. Height fields were used, since they have less error than wind fields. This value can be integrated over the entire NH [32].
The IE diagnostic is based on the premise that changes in the stability in the Northern Hemisphere flow have been shown to coincide with large-scale flow regime transition as in [45]. The time series of IE can be interpreted as follows: (a) peaks (local maxima or minima) in the IE time series are associated with a change in sign of the time derivative of IE as in [46]. The authors of [46] also showed that the change in the sign of the time derivative of this quantity from positive to negative, associated with an IE maximum, indicated a local maximum in instability. Based on previous research ([33,36]), instability is expected at or near block onset and decay ([45,46]). The study of [45] argued that blocking existed within a large-scale flow regime. In their statistical analysis, they argued that the minimum in the probability density distribution between two large-scale flow regimes represented instability associated with regime change. This is consistent with the view of [46] and here.
Additionally, [46] provided an explanation for the reason large-scale flow and blocking regime changes are correlated with extrema in the IE time series. They showed that enstrophy can be written as:
1 2 ξ 2 =   ∇ h 2 ϕ −   f ξ   +   β u +   1 2 σ 2
In (2) f, φ, β, σ, and u are the Coriolis parameter, geopotential height, the “Beta” effect (meridional change in Coriolis parameter), deformation (shearing and stretching), and the zonal wind, respectively. In other words, extrema in the geopotential height (the horizontal Laplacian term), as well as relative vorticity, zonal wind, and resultant deformation, all contribute to the enstrophy budget. For example, local maxima in the geopotential height field within a ridge or blocking event decrease the enstrophy. Then, with the changes in geopotential height as the large-scale flow regime breaks down, or when a blocking event decays, enstrophy is increased. The fields of westerlies and relative vorticity are known also to be different in higher-amplitude flows versus zonal flows. The study of [46] also showed that fluxes of enstrophy across a fluid boundary are balanced by the time rate of change of deformation, which leads to changes in the enstrophy as shown by:
∂ ∂ t ∫ σ 2 d A =   − ∮ C ξ 2 v h · n d s
In Equation (3), C, vh, n, and ds are the fluid boundary, the horizontal wind (flow), the unit normal, and the change in position on C, respectively.

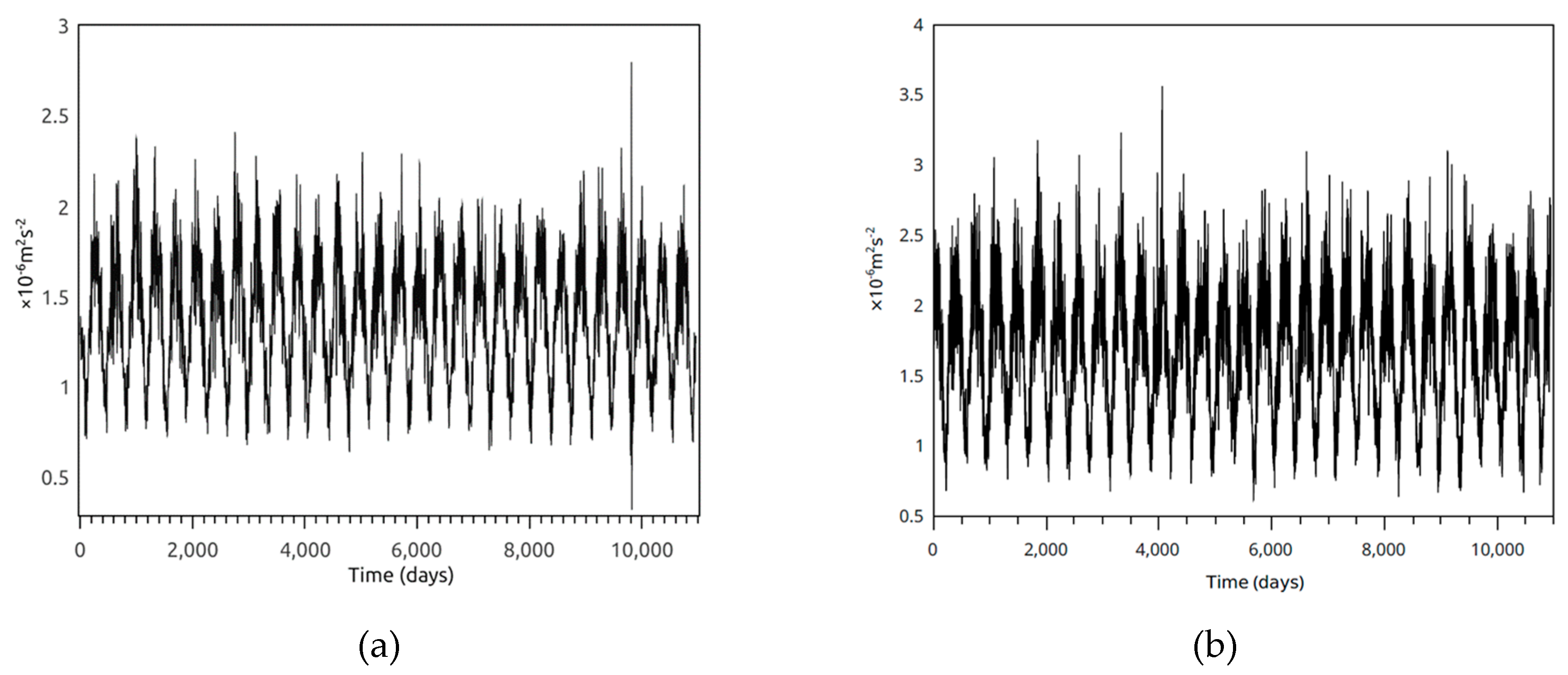
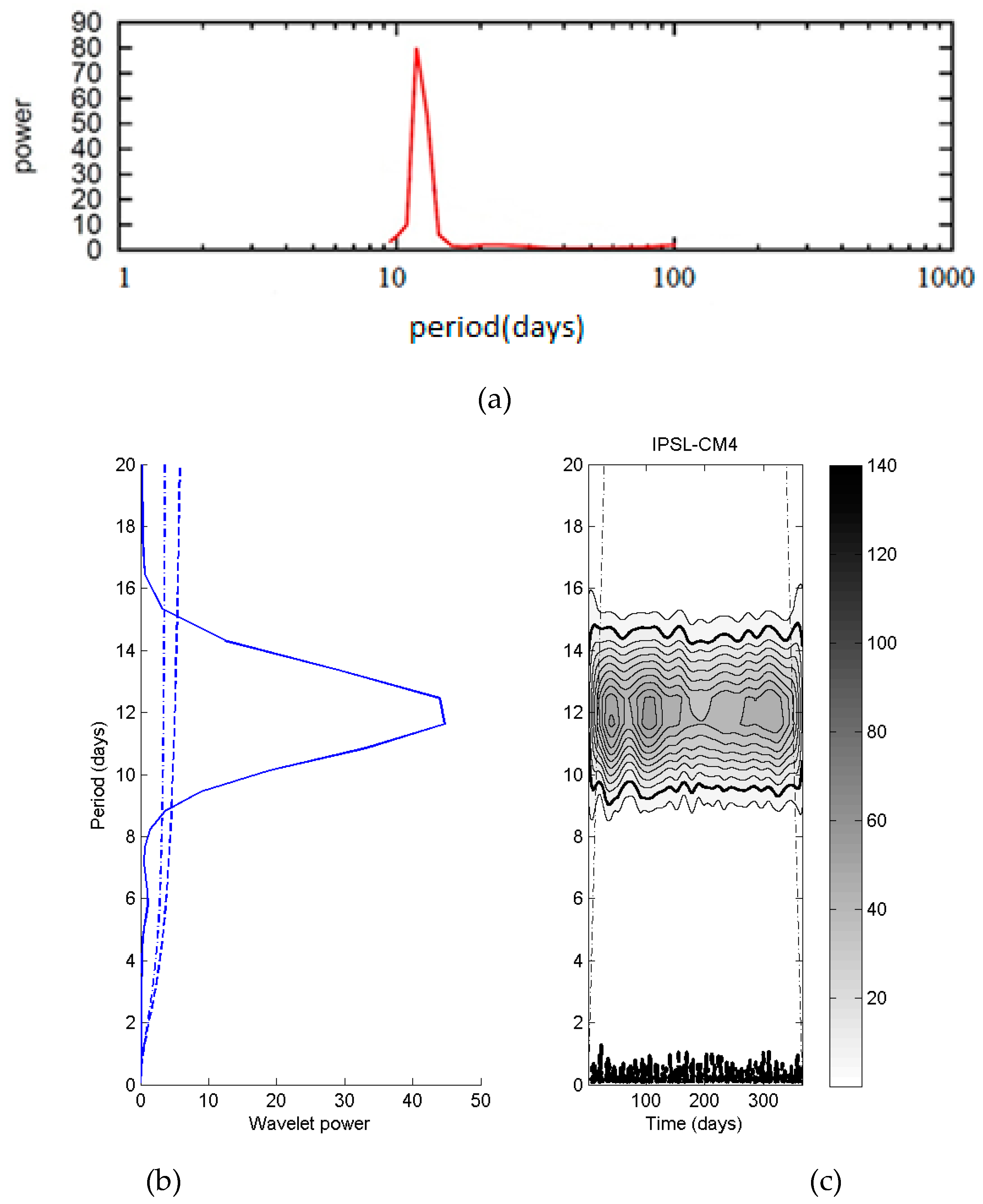
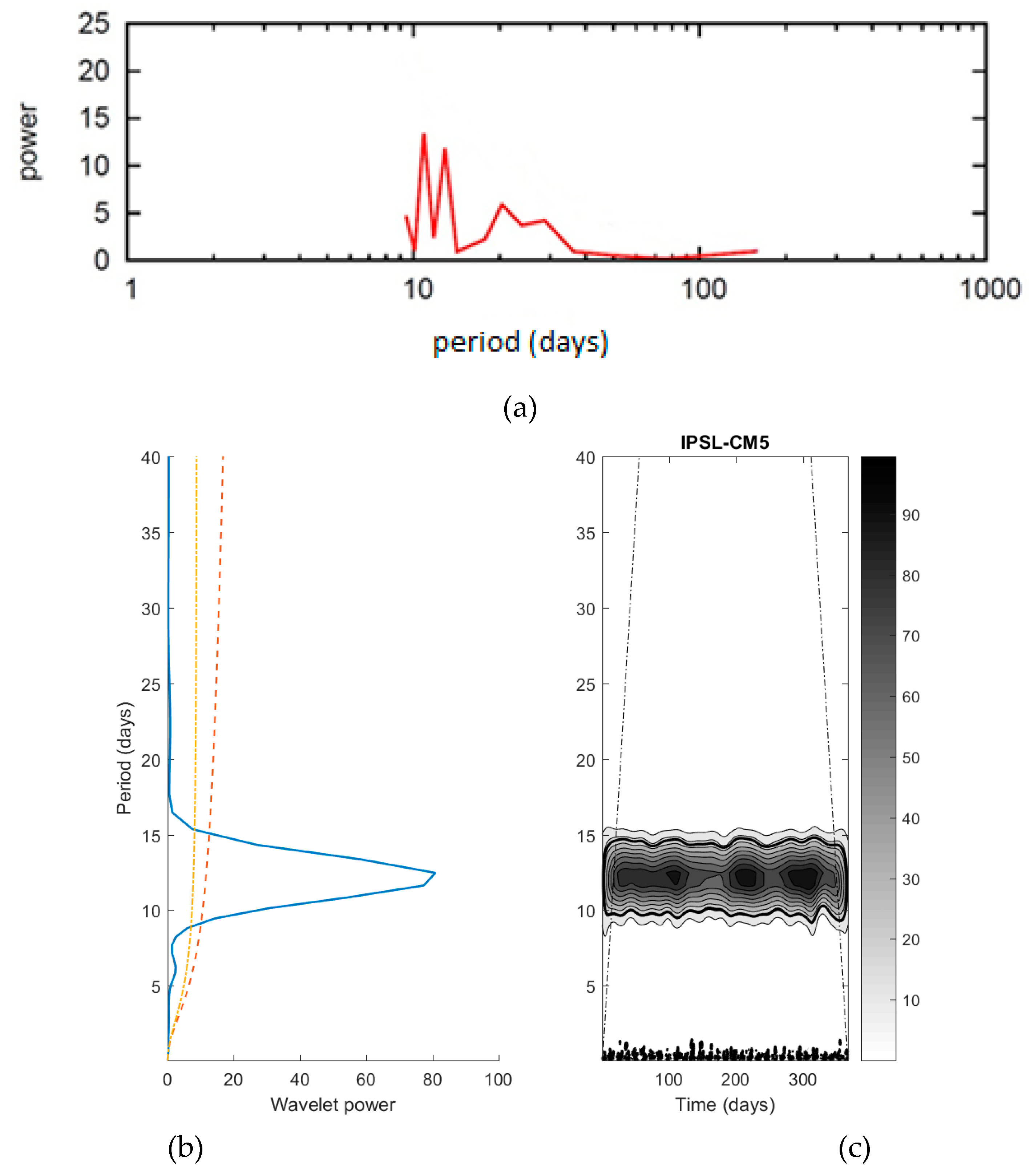
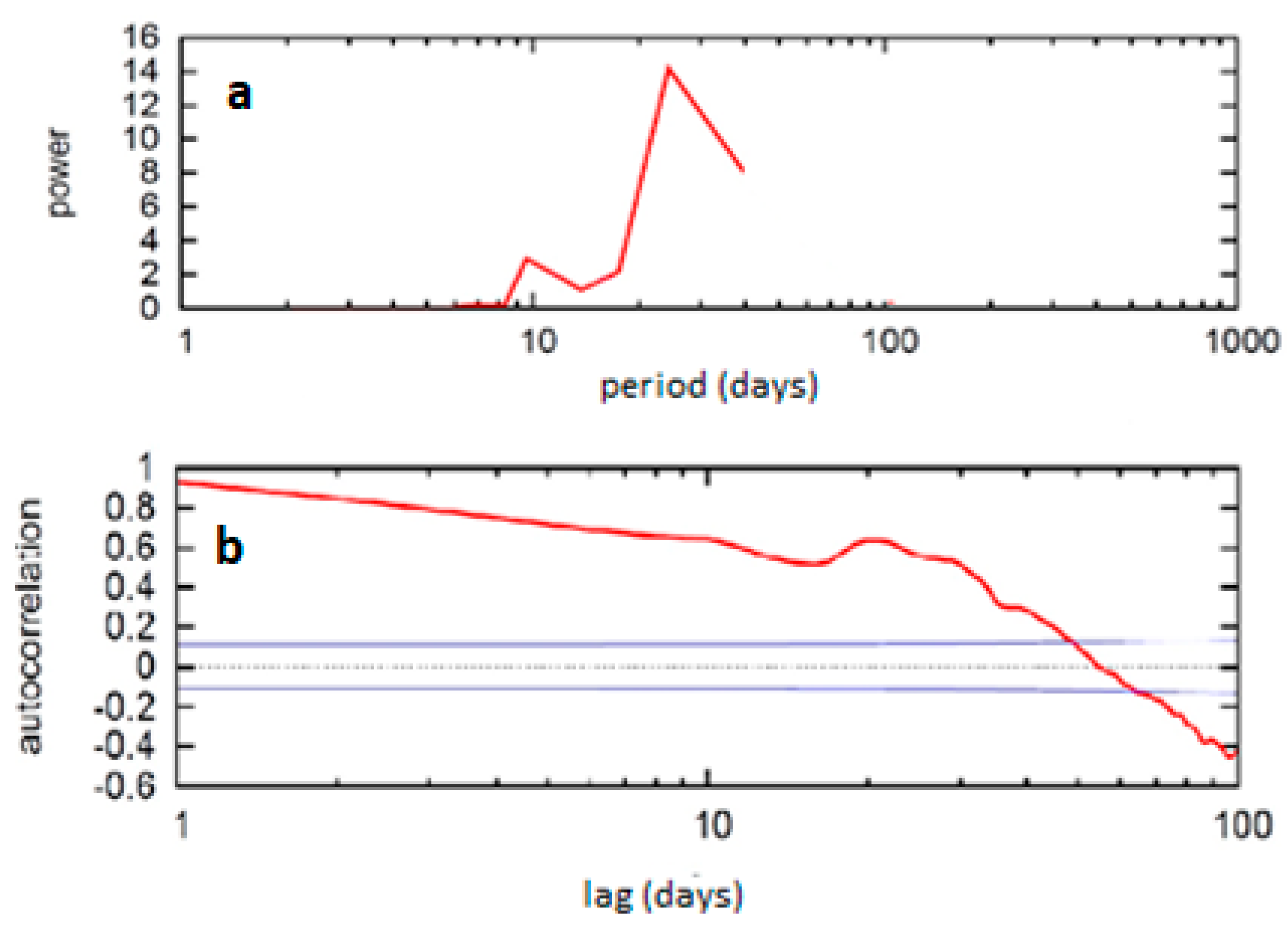
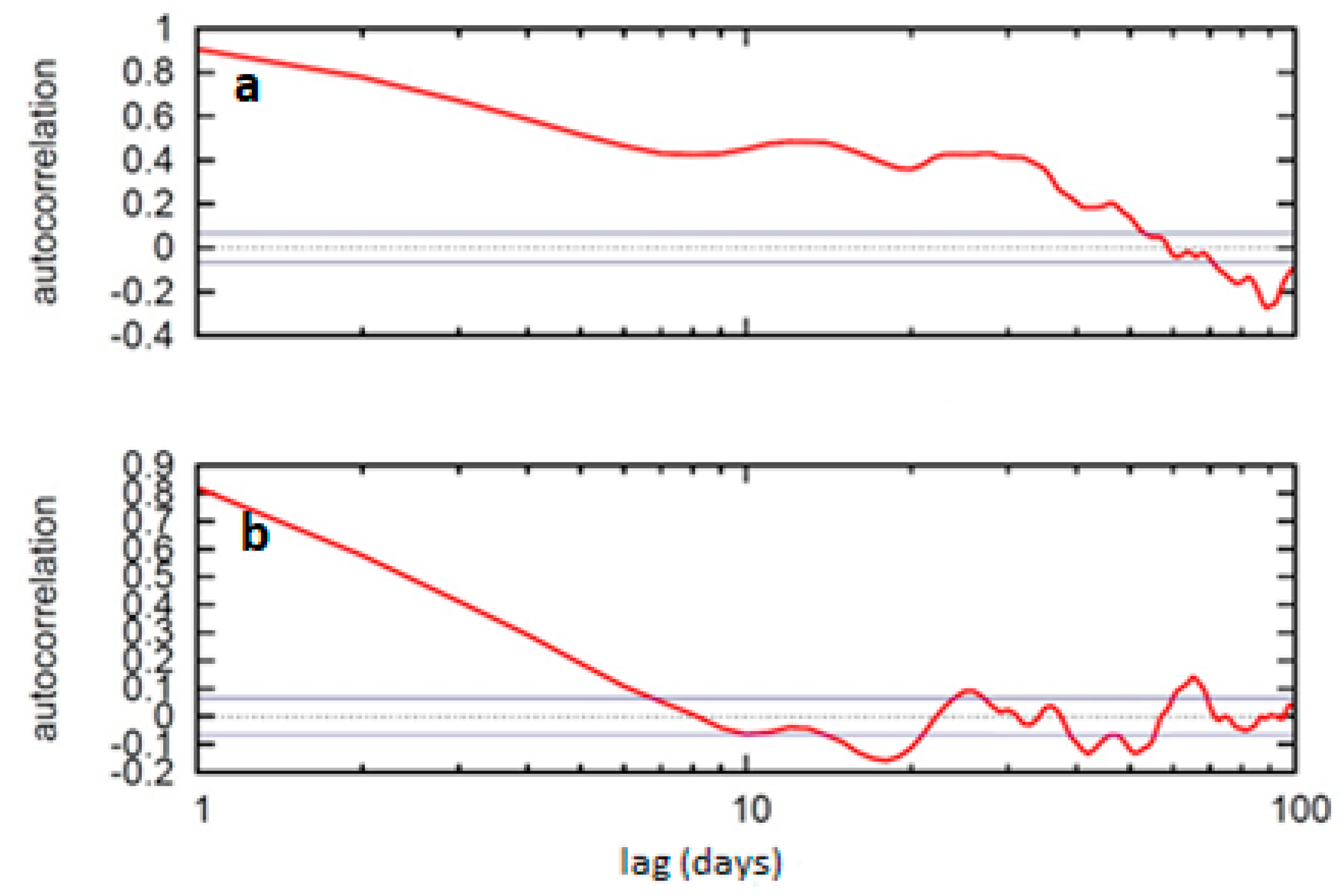
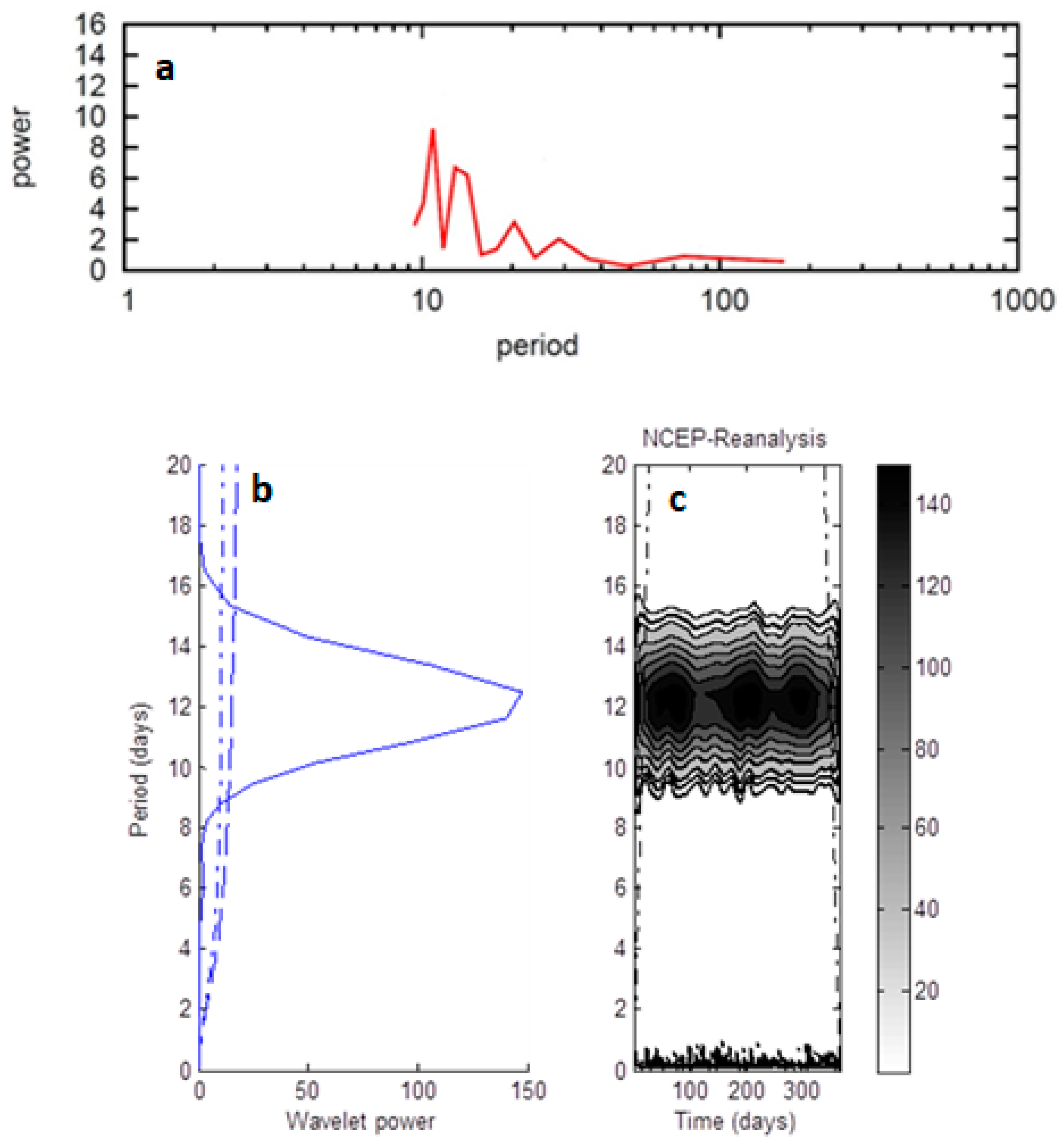
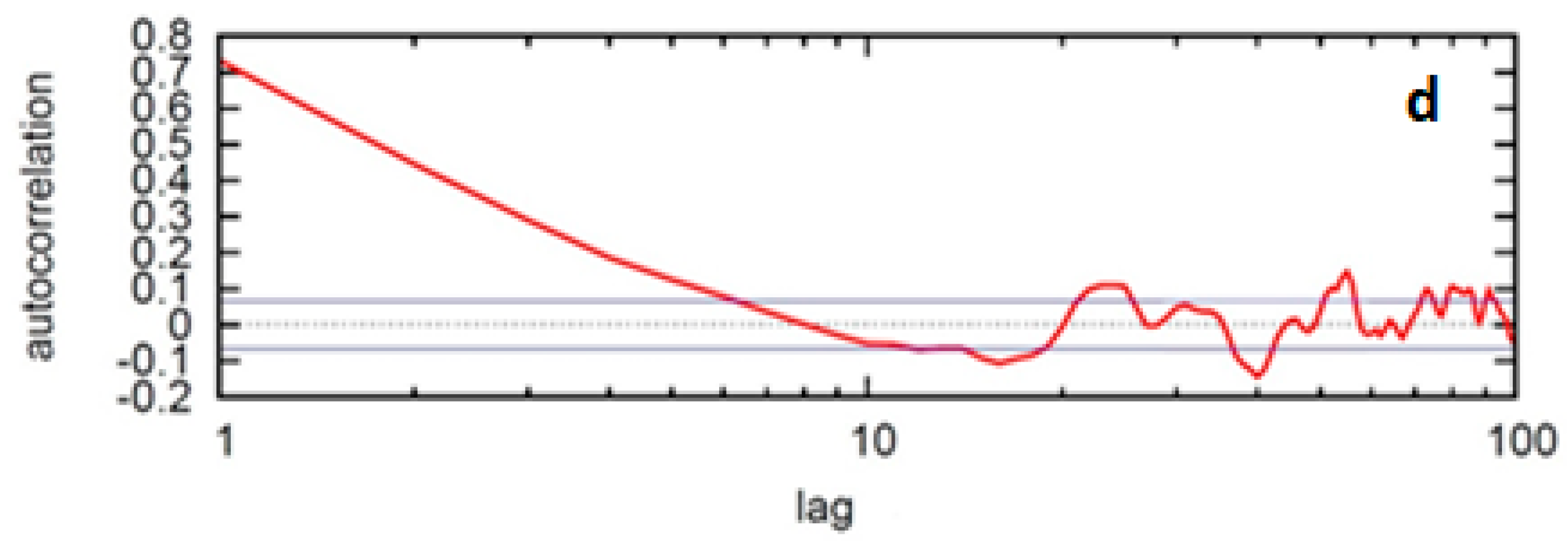
3. Results

The raw time series of the modelled RCP 4.5 Northern Hemisphere IE for 2020–2050 is shown in Figure 1 (IPSL-CM4 Figure 1a, IPSL-CM5 Figure 1b). Time series from both models exhibit an approximate annual cycle, which is a reflection of seasonality in the distribution of the 500 hPa height field. To determine if there are other significant spectral peaks, apart from the clear annual periodicity in IE, as indicated in Figure 1, a bandpass filter was used to filter out frequencies outside the 5–40 day range. The power spectra (both Fourier and Wavelet) obtained after filtering, smoothing, and detrending the time series from both model simulations are shown in Figure 2 and Figure 3. In Figure 2, the power spectra for the IPSL-CM4 time series of IE have a clear spectral peak in the 10–12 day range. This implies that a hemispheric flow regime persists for about 10–12 days before a transition occurs, as identified by the IE diagnostic. The same result is evident for the IPSL-CM5 time series (Figure 3). This persistence is consistent with the results of [6,7] and others for large-scale flow regimes.
A comparison of the near future model RCP 4.5 time series (Figure 2 and Figure 3) with the control model, using the IPSL-CM5 as an example, shows a smaller peak near 10–12 days (Figure 4a) consistent with the model simulations. However, there is a large peak in Figure 4a, near 20–30 days, that is apparent in the IPSL-CM5 control run (but not the IPSM-CM4). It is not immediately obvious why the peak at 20–30 days is strong in the control model simulation for the IPSL-CM5, and a possible explanation will be discussed in section four below.
The autocorrelation (see Figure 5a) of the IPSL-CM4 RCP 4.5 time series decays rapidly, but there is a “bump” at a lag correlation of approximately 10 days, as suggested by the spectral peak in Figure 2a. In Figure 3, the power spectrum for the IPSL-CM5 time series of the IE has a spectral peak at approximately 10–12 days, as shown above, but also has peaks beyond the 10-day period (around 20–30 days) that were not captured as strongly in the IPSL-CM4 time series of the IE. However, the autocorrelation in the time series for both versions of the IPSL model (Figure 5) are qualitatively similar. The autocorrelation of the control model simulation, as represented by IPSL-CM4 (Figure 4b), is also consistent with the RCP 4.5 IPSL-CM4 and CM5 model (Figure 5).
A comparison of the IE derived from the NCEP/NCAR re-analyses (Figure 6) for the period 1981–2010 demonstrates that the IPSL-CM5 represents the character of the large-scale dynamic flow regime properties more faithfully than that of the IPSL-CM4, and this is true for the control runs as well (Figure 5). These will be discussed further below. Additionally, there were no qualitative differences noted in the seasonal cycle between Figure 1 and the control run or NCEP re-analyses.
As explained in section two, the IE achieves a relative maximum during flow regime transitions. The results of the spectral analysis of both models indicate that flow regimes persist for approximately 10 days, which suggests that the IE diagnostic may support, on average, up to approximately 35 flow regime transitions per year in a warmer climate. This number (35) is greater than the number of blocking events found in [26,29]. In spite of this, both studies found that the average duration for blocking is close to 10 days in the IPSL-CM4 and IPSL-CM5 simulations. As discussed in sections one and two, not every flow regime can be associated with the occurrence of blocking, since it has been shown that occasionally blocking occurs simultaneously in two different locations of the Northern Hemisphere [30,48]. This is an important reason for the difference in the annual average number of blocking events in the climatologies of [26,29] (approximately 22 events), and the approximately 30–35 flow regime transition events found here.

4. Discussion and Conclusions

This study examines the behavior of an enstrophy-based diagnostic (IE) and Northern Hemisphere flow regime dynamics described above, in two near-future moderate emission simulations from the IPSL-CM4 and IPSL-CM5 GCMs. The use of the IE diagnostic to study flow regime dynamics in the NCEP/NCAR re-analyses and climate simulations had not been performed previously. The time series of IE for the re-analyses, control simulations, and the 2020–2050 simulations does have an annual cycle. After filtering out low and high frequencies, there is a clear peak of IE at approximately 10–12 days in both the IPSL-CM4 and IPSL-CM5, and this corresponds well to the control run and re-analyses from the most recent 30-year period (1981–2010) derived from observations. Flow regime transition means that a particular atmospheric flow regime persists for 10–12 days, before transitioning to another flow regime. The spectral density peaks also in the 20–30 day range, especially in the NCEP/NCAR re-analyses and the IPSL-CM5 model as shown using FFT analysis. This spectral peak was not statistically significant in the wavelet analysis. Based on previous research ([33,36,46] and others), the IE reaches a maximum during large-scale flow regime transitions, or at the onset and demise of blocking events. This work supported 30–35 flow regime transitions per year in the large-scale Northern Hemisphere flow for the IPSL-CM4 and CM5 simulations, while the annual mean number of blocking events in these same data sets was fewer [26,27,28,29].
Since these results imply that the IE indicates approximately 30–35 flow regime transitions per year on average in a near-future warmer climate, the implication is that the well-known dynamic predictability wall for large-scale flow (e.g., [49,50]) would still be similar to the present day. Further, the implication is that the dynamic character of the near-future large-scale flow regime in a moderate CO2 emissions scenario would be similar to that for the immediate past 30 years, or that the “predictability wall” for short-term weather forecasting does not change appreciably. In a future climate, weather and climate prediction beyond 10–12 days is still only possible using primarily statistical methodologies. While the dynamic character of the large-scale flow, as determined using the IE diagnostic, may not change significantly in the near-future, this does not preclude further changes in regional or global sensible climate that is expected to occur [28].
Support for this conclusion might be inferred from modern studies of jet stream behavior under increased CO2 conditions (e.g., [25,51,52]). All three of these studies [25,51,52] used the CMIP5 model ensembles, including the IPSL-CM4 and CM5 runs, in the RCP4.5 and RCP8.5 scenarios. In [25] they found a poleward shift for the Atlantic jet, and less variability in the latitudinal position of the jet in the increased CO2 runs (but there was also less variability in the control runs). This is supported by [51,52], which also found that the Atlantic basin jet stream included less positional variability, and what they described as more “pulsing” behavior (i.e., stronger variations in scalar wind speed). They [51,52] found the opposite result in the Pacific Region, and speculated that the connection between positional variability versus “pulsating type” behavior may be Rossby wave breaking. Thus, we speculate, based on these studies, that the hemispheric-scale “preferred mode” behavior can be expressed as variability in the position or speed of the jet stream (meridional or zonal), or both. The IE diagnostic is integrated over the whole of the Northern Hemisphere, and thus will reflect the changes in the combined variability across both the Atlantic and Pacific Ocean basins. This may be because enstrophy is the square of the vorticity, and in natural coordinates vorticity can be expressed as the sum of the speed shear and curvature. Thus, if in an increased CO2 atmosphere the preferred mode behavior is represented more by a “pulsating” jet, with less positional variability (at least in the Atlantic), the IE diagnostic should be able to capture this behavior as well.
However, it is conceded here that the discussion in relation to the studies above is within the context of projections for the end of the 21st century ([51,52]). Nonetheless, [52] shows near-term (2020–2044) scenarios in relation to arctic amplification, and the trend toward a more poleward and less variable jet stream is evident, but less than that for the end-of-the-century projections. It is presumed the more “pulsating” type behavior described these studies is also occurring, though it is difficult to determine from the near-term statistics presented by [52]. Additionally, it is noted here that [53] demonstrated that lower resolution models may not represent regional large-scale flow regimes and transitions as faithfully as much higher resolution simulations.
The spectral peak in the modelled IE time series, at approximately 10–12 days, compares favorably with the results of [26,29] for the projected duration of blocking in the mid-to-late 21st century, for the IPSL-CM4 and IPSL-CM5 simulations the peaks were close to 10 days. The model spectral peaks were also consistent with the re-analysis 500-hPa height data, as well as the control run. However, as discussed in section three, large-scale atmospheric flow regimes may occur with the absence of blocking, and at other times with simultaneously occurring blocking events. Simultaneous blocking does occur about nine percent of the time ([30,48]) in the Northern Hemisphere. This is an important reason for the difference in the average number of blocking events in the climatology of [26,29] (approximately 22 events), and the result of approximately 30–35 flow regime transition events, as found here. Additionally, this work did not focus exclusively on atmospheric blocking, as there are several published studies on the future occurrence of these events in increased CO2 climate scenarios, some of which show conflicting results e.g., [29,54].
Lastly, there was a strong spectral peak in the 20–30 day time period in the control model run that is also evident in the IPSL-CM5 simulation and the re-analyses. This peak is evident in the autocorrelation of the IE figures as well. While this time period is beyond the scope of our work here, predictability in the 20–30 day period was discussed in a recent study [55]. That study found statistically significant peaks in this time frame, using the FFT and autocorrelation analysis applied to a 67-year time series of the Pacific North America Index [55]. They attributed these to persistent and quasi-stationary Rossby wave trains occurring within the Pacific Ocean basin, and this information can be used to make weather predictions in the 2–4 week time period.

Acknowledgments

The authors would like to thank the three anonymous reviewers for their suggestions in making this paper a stronger contribution. I.I. Mokhov and M.G. Akperov were supported by the Russian Ministry of Education and Science, agreement No. 14.616.21.0082 (RFMEFI61617X0082). The authors have no conflict of interest to declare.

Author Contributions

A.D. Jensen and A.R. Lupo conceived and designed the experiments; A.D. Jensen, M.G. Akperov, I.I. Mokhov performed the experiments; all five authors analyzed the data, contributed analysis tools, and wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Allen, R.A.; Fletcher, R.; Holmboe, J.; Namais, J.; Willett, H.C. Report on an Experiment on Five-Day Weather Forecasting; Papers in Physical Oceanography and Meteorology; Massachussetts Institute of Technology/Woods Hole Institute of Oceanography (MIT/WHOI): Woods Hole, MA, USA, 1940; Volume 8, 94p. [Google Scholar]
  2. Namias, J. The great Pacific anticyclone of the winter 1948–50: A case study in the evolution of climatic anomalies. J. Meteorol. 1951, 8, 251–261. [Google Scholar] [CrossRef]
  3. Lorenz, E.N. Seasonal and irregular variations of the Northern Hemisphere sea-level pressure profile. J. Meteorol. 1951, 8, 52–59. [Google Scholar] [CrossRef]
  4. Rex, D.F. Blocking action in the middle troposphere and its effect on regional climate II: The climatology of blocking action. Tellus 1950, 3, 275–301. [Google Scholar]
  5. Lorenz, E.N. Deterministic, non-periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
  6. Hansen, A.R. Observational characteristics of atmospheric planetary waves with bimodal amplitude distributions. Adv. Geophys. 1986, 29, 101–134. [Google Scholar]
  7. Sutera, A. Probability density distribution of large-scale atmospheric flow. Adv. Geophys. 1986, 29, 227–250. [Google Scholar]
  8. Charney, J.G.; DeVore, J.G. Multiple flow equilibria in the atmosphere and blocking. J. Atmos. Sci. 1979, 36, 1205–1216. [Google Scholar] [CrossRef]
  9. Mo, K.; Ghil, M. Cluster analysis of multiple planetary flow regimes. J. Geophys. Res. 1988, 93, 10927–10952. [Google Scholar] [CrossRef]
  10. Molteni, F.; Tibaldi, S.; Palmer, T.N. Regimes in the wintertime circulation over northern extratropics. I: Observational evidence. Q. J. R. Meteorol. Soc. 1990, 116, 31–67. [Google Scholar] [CrossRef]
  11. Smyth, P.; Ide, K.; Ghil, M. Multiple Regimes in Northern Hemisphere Height Fields via Mixture Model Clustering. J. Atmos. Sci. 1999, 56, 3704–3723. [Google Scholar] [CrossRef]
  12. Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the northern hemisphere winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
  13. Vautard, R. Multiple weather regimes over the North Atlantic: Analysis of precursors and successors. Mon. Weather Rev. 1990, 118, 2056–2081. [Google Scholar] [CrossRef]
  14. Franzke, C.; Woollings, T.; Martius, O. Persistent circulation regimes and preferred regime transitions in the North Atlantic. J. Atmos. Sci. 2011, 68, 2809–2825. [Google Scholar] [CrossRef]
  15. Michel, C.; Rivière, G. The link between Rossby wave breakings and weather regime transitions. J. Atmos. Sci. 2011, 68, 1730–1748. [Google Scholar] [CrossRef]
  16. Huang, W.; Chen, R.; Wang, B.; Wright, J.S.; Yang, Z.; Ma, W. Potential vorticity regimes over East Asia during winter. J. Geophys. Res. Atmos. 2016, 122. [Google Scholar] [CrossRef]
  17. Lau, K.M.; Sheu, P.J.; Kang, I.S. Multiscale low frequency circulation modes in the global atmosphere. J. Atmos. Sci. 1994, 51, 1169–1193. [Google Scholar] [CrossRef]
  18. O’Kane, T.J.; Monselesan, D.P.; Risbey, J.S. A Multiscale Reexamination of the Pacific–South American Pattern. Mon. Weather Rev. 2017, 145, 379–402. [Google Scholar] [CrossRef]
  19. Kravtsov, S.; Robertson, A.W.; Ghil, M. Bimodal Behavior in the Zonal Mean Flow of a Baroclinic β-Channel Model. J. Atmos. Res. 2005, 62, 1746–1769. [Google Scholar] [CrossRef]
  20. Luo, D.; Lupo, A.R.; Wan, H. Dynamics of eddy-driven low-frequency dipole modes. Part I: A simple model of North Atlantic Oscillations. J. Atmos. Sci. 2007, 64, 29–51. [Google Scholar] [CrossRef]
  21. Luo, D.; Gong, T.; Lupo, A.R. Dynamics of eddy-driven low-frequency dipole modes. Part II: Free mode characteristics of NAO and diagnostic study. J. Atmos. Sci. 2007, 64, 3–28. [Google Scholar] [CrossRef]
  22. Luo, D.; Cha, J.; Zhong, L.; Dai, A. A nonlinear multiscale interaction model for atmospheric blocking: The eddy-blocking matching mechanism. Q. J. R. Meteorol. Soc. 2014, 140, 1785–1808. [Google Scholar] [CrossRef]
  23. Lorenz, D.J.; DeWeaver, E.T. Tropopause height and wind response to global warming in IPCC scenario integrations. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
  24. Hannachi, A.; Straus, D.M.; Franzke, C.L.E.; Corti, S.; Woollings, T. Low-frequency nonlinearity and regime behavior in the Northern Hemisphere extratropical atmosphere. Rev. Geophys. 2017, 55, 199–234. [Google Scholar] [CrossRef]
  25. Iqbal, W.; Leung, W.N.; Hnannachi, A. Analysis of the variability of the North Atlantic eddy-driven jet stream in CMIP5. Clim. Dyn. 2017. [Google Scholar] [CrossRef]
  26. Mokhov, I.I.; Akperov, M.G.; Prokofyeva, M.A.; Timazhev, A.V.; Lupo, A.R.; Le Treut, H. Blockings in the northern hemisphere and Euro-atlantic region: Estimates of changes from reanalysis data and model simulations. Dokl. Earth Sci. 2013, 449, 430–433. [Google Scholar] [CrossRef]
  27. Marti, O.; Braconnot, P.; Dufresne, J.-L.; Bellier, J.; Benshila, R.; Bony, S.; Brockmann, P.; Cadule, P.; Caubel, A.; Codron, F.; et al. Key features of the IPSL ocean atmosphere model and its sensitivity to atmospheric resolution. Clim. Dyn. 2010, 34, 1–26. [Google Scholar] [CrossRef]
  28. Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Scientific Basis; Contributions of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2013; Available online: http://www.ipcc.ch (accessed on 20 December 2017).
  29. Mokhov, I.I.; Timazhev, A.V.; Lupo, A.R. Changes in atmospheric blocking characteristics within Euro-Atlantic region and Northern Hemisphere as a whole in the 21st century from model simulations using RCP anthropogenic scenarios. Glob. Planet. Chang. 2014, 122, 265–270. [Google Scholar] [CrossRef]
  30. Wiedenmann, J.M.; Lupo, A.R.; Mokhov, I.I.; Tikhonova, E.A. The climatology of blocking anticyclones for the Northern and Southern Hemispheres: Block Intensity as a diagnostic. J. Clim. 2002, 15, 3459–3473. [Google Scholar] [CrossRef]
  31. Lupo, A.R.; Mokhov, I.I.; Akperov, M.G.; Cherokulsky, A.V.; Athar, H. A dynamic analysis of the role of the planetary and synoptic scale in the summer of 2010 blocking episodes over the European part of Russia. Adv. Meteorol. 2012, 2012, 584257. [Google Scholar] [CrossRef]
  32. Dymnikov, V.P.; Kazantsev, Y.V.; Kharin, V.V. Information entropy and local Lyapunov exponents of barotropic atmospheric circulation. Izv. Atmos. Oc. Phys. 1992, 28, 425–432. [Google Scholar]
  33. Jensen, A.D.; Lupo, A.R. Using enstrophy advection as a diagnostic to identify blocking regime transition. Q. J. R. Meteorol. Soc. 2013. [Google Scholar] [CrossRef]
  34. Newberry, R.G.; Lupo, A.R.; Jensen, A.D.; Rodgriges Zalipynis, R.A. An Analysis of the Spring-to-Summer Transition in the West Central Plains for Application to Long Range Forecasting. Atmos. Clim. Sci. 2016, 6, 373–393. [Google Scholar] [CrossRef]
  35. Molteni, F.; Palmer, T.N. Predictability and finite-time instability of the northern winter circulation. Q. J. R. Meteorol. Soc. 1993, 119, 269–298. [Google Scholar] [CrossRef]
  36. Lupo, A.R.; Mokhov, I.I.; Dostoglou, S.; Kunz, A.R.; Burkhardt, J.P. The impact of the planetary scale on the decay of blocking and the use of phase diagrams and enstrophy as a diagnostic. Izv. Atmos. Oc. Phys. 2007, 42, 45–51. [Google Scholar] [CrossRef]
  37. Dufresne, J.-L.; Foujols, M.-A.; Denvil, S.; Caubel, A.; Marti, O.; Aumont, O.; Balkanski, Y.; Bekki, S.; Bellenger, H.; Benshila, R.; et al. Climate change projections using the IPSL-CM5 Earth System Model: From CMIP3 to CMIP5. Clim. Dyn. 2013, 40, 2123–2165. [Google Scholar] [CrossRef][Green Version]
  38. Athar, H.; Lupo, A.R. Scale and stability analysis of blocking events from 2002–2004: A case study of an unusually persistent blocking event leading to a heat wave in the Gulf of Alaska during August 2004. Adv. Meteorol. 2010, 2010, 610263. [Google Scholar] [CrossRef]
  39. Lupo, A.R. A Diagnosis of two blocking events that occurred simultaneously in the Mid-Latitude Northern Hemisphere. Mon. Weather Rev. 1997, 125, 1801–1823. [Google Scholar] [CrossRef]
  40. Lupo, A.R.; Smith, P.J. Planetary and Synoptic-Scale Interactions during the Life Cycle of a Mid-Latitude Blocking Anticyclone over the North Atlantic. Tellus Spec. Issue Life Cycles Extr. Cyclones 1995, 47A, 575–596. [Google Scholar]
  41. Gu, D.; Philander, S.G.H. Secular changes of annual and interannual variability in the tropics during the past century. J. Clim. 1995, 8, 864–876. [Google Scholar] [CrossRef]
  42. Hu, Q.; Woodruff, C.M.; Mudrick, S.E. Interdecadal variations of annual precipitation in the Central United States. Bull. Am. Meteorol. Soc. 1998, 79, 221–230. [Google Scholar] [CrossRef]
  43. Birk, K.; Lupo, A.R.; Guinan, P.E.; Barbieri, C.E. The interannual variability of midwestern temperatures and precipitation as related to the ENSO and PDO. Atmosfera 2010, 23, 95–128. [Google Scholar]
  44. Jensen, A.D.; Lupo, A.R. Using enstrophy-based diagnostics in an ensemble for two blocking events. Adv. Meteorol. 2013, 2013, 693859. [Google Scholar] [CrossRef]
  45. Hansen, A.R.; Sutera, A. A comparison between planetary-wave flow regimes and blocking. Tellus 1993, 45A, 281–288. [Google Scholar] [CrossRef]
  46. Jensen, A.D.; Lupo, A.R. The role of deformation and other quantities in an equation for enstrophy as applied to atmospheric blocking. Dyn. Atmos. Oceans 2014, 66, 151–159. [Google Scholar] [CrossRef]
  47. Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
  48. Lejenas, H.; Okland, H. Characteristics of Northern Hemisphere blocking as determined from a long time series of observational data. Tellus 1983, 35A, 350–362. [Google Scholar] [CrossRef]
  49. Lorenz, E.N. A study of the predictability of a 28-variable model. Tellus 1965, 17, 321–333. [Google Scholar] [CrossRef]
  50. Palmer, T.N. Predictability of the atmosphere and oceans: From days to decades. Decadal Clim. Var. 1990, 44, 83–155. [Google Scholar]
  51. Barnes, E.A.; Polvani, L.M. Response of the midlatitude jets, and of their variability, to increased greenhouse gases in the CMIP5 models. J. Clim. 2013, 26, 7117–7135. [Google Scholar] [CrossRef]
  52. Barnes, E.A.; Polvani, L.M. CMIP5 projections of Arctic amplification, of the North American/North Atlantic circulation, and of their relationship. J. Clim. 2015, 28, 5254–5271. [Google Scholar] [CrossRef]
  53. Dawson, A.; Palmer, T.N.; Corti, S. Simulating regime structures in weather and climate prediction models. Geophys. Res. Lett. 2012, 39, L21805. [Google Scholar] [CrossRef]
  54. Sillmann, J.; Croci-Maspoli, M. Present and future atmospheric blocking and its impact on European and extreme climate. Geophys. Res. Lett. 2009, 36, L10702. [Google Scholar] [CrossRef]
  55. Renken, J.D.; Herman, J.J.; Bradshaw, T.R.; Market, P.S.; Lupo, A.R. The utility of the Bering Sea and Typhoon Rules in long range forecasting. Adv. Meteorol. 2017, 2017, 1765428. [Google Scholar] [CrossRef]
Atmosphere 09 00027 g001 550
Figure 1. The Integrated Regional Enstrophy (IE) (× 10−6 m2s−2—ordinate) diagnostic derived from the Northern Hemisphere 500 hPa heights over the period 2020–2050 (abscissa), from the (a) Institut Pierre Simon Laplace Climate Model version 4 (IPSL-CM4) (left), and (b) Institut Pierre Simon Laplace Climate Model version 5 (IPSL-CM5) (right) model runs, and using a moderate emissions scenario.
Figure 1. The Integrated Regional Enstrophy (IE) (× 10−6 m2s−2—ordinate) diagnostic derived from the Northern Hemisphere 500 hPa heights over the period 2020–2050 (abscissa), from the (a) Institut Pierre Simon Laplace Climate Model version 4 (IPSL-CM4) (left), and (b) Institut Pierre Simon Laplace Climate Model version 5 (IPSL-CM5) (right) model runs, and using a moderate emissions scenario.
Atmosphere 09 00027 g001
Atmosphere 09 00027 g002 550
Figure 2. The Integrated Regional Enstrophy (IE) (× 10−6 m2s−2—ordinate) diagnostic derived from the Northern Hemisphere 500 hPa heights for the (a) band passed (5–40 day) Fast Fourier Transform (FFT) power spectra (ordinate) versus spectral period (days—abscissa) (top), and (b), and (c) the wavelet power spectra (time period is days) (bottom). In (b) and (c) the dashed lines represent statistical significance at 90 and 95%, and regions where edge effects become important [47], respectively. Only peaks with statistically significant power are shown in (c).
Figure 2. The Integrated Regional Enstrophy (IE) (× 10−6 m2s−2—ordinate) diagnostic derived from the Northern Hemisphere 500 hPa heights for the (a) band passed (5–40 day) Fast Fourier Transform (FFT) power spectra (ordinate) versus spectral period (days—abscissa) (top), and (b), and (c) the wavelet power spectra (time period is days) (bottom). In (b) and (c) the dashed lines represent statistical significance at 90 and 95%, and regions where edge effects become important [47], respectively. Only peaks with statistically significant power are shown in (c).
Atmosphere 09 00027 g002
Atmosphere 09 00027 g003 550
Figure 3. Same as in Figure 2, except with the IPSL-CM5 model power spectra.
Figure 3. Same as in Figure 2, except with the IPSL-CM5 model power spectra.
Atmosphere 09 00027 g003
Atmosphere 09 00027 g004 550
Figure 4. The control model run (IPSL-CM5) for (a) IE band passed (5–40 day) FFT power spectra (ordinate) versus spectral period (days—abscissa) (top), and (b) the autocorrelation of the IE diagnostic (ordinate), where the lag is presented in days (abscissa). The blue dashed line is the zero correlation line, and the solid line is the 95% confidence level.
Figure 4. The control model run (IPSL-CM5) for (a) IE band passed (5–40 day) FFT power spectra (ordinate) versus spectral period (days—abscissa) (top), and (b) the autocorrelation of the IE diagnostic (ordinate), where the lag is presented in days (abscissa). The blue dashed line is the zero correlation line, and the solid line is the 95% confidence level.
Atmosphere 09 00027 g004
Atmosphere 09 00027 g005 550
Figure 5. The autocorrelation of the IE diagnostic (ordinate), where the lag is presented in days (abscissa) for (a) the representative concentration pathway (RCP) 4.5 IPSL-CM4 (top), and (b) the RCP 4.5 IPSL-CM5 (bottom).
Figure 5. The autocorrelation of the IE diagnostic (ordinate), where the lag is presented in days (abscissa) for (a) the representative concentration pathway (RCP) 4.5 IPSL-CM4 (top), and (b) the RCP 4.5 IPSL-CM5 (bottom).
Atmosphere 09 00027 g005
Atmosphere 09 00027 g006a 550Atmosphere 09 00027 g006b 550
Figure 6. Same as in Figure 2 and Figure 4, except using the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) re-analyses for the period 1981–2010. The top, middle, and bottom diagrams are the Fourier, Wavelet, and autocorrelation diagrams, respectively.
Figure 6. Same as in Figure 2 and Figure 4, except using the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) re-analyses for the period 1981–2010. The top, middle, and bottom diagrams are the Fourier, Wavelet, and autocorrelation diagrams, respectively.
Atmosphere 09 00027 g006aAtmosphere 09 00027 g006b
Back to TopTop