A Matrix-Free Posterior Ensemble Kalman Filter Implementation Based on a Modified Cholesky Decomposition
Abstract
:1. Introduction
2. Preliminaries
2.1. The Ensemble Kalman Filter
2.2. Localization Methods
2.3. Efficient EnKF Implementations: Accounting for Localization
3. A Posterior Ensemble Kalman Filter Based On Modified Cholesky Decomposition
3.1. General Formulation of the Filter
- drawing samples from the Normal distribution (15),where is given by the solution of an upper triangular system of equations,and the columns of are samples from a multivariate standard Normal distribution, or
- using the synthetic data (9b),where is given by the solution of the next linear system of equations,
3.2. Computing the Cholesky Factors of the Precision Analysis Covariance
| Algorithm 1 Rank-one update for the factors and . |
|
| Algorithm 2 Computing the factors and of . |
|
3.3. Computational Cost of the Analysis Step
| Algorithm 3 Assimilation of observations via the posterior ensemble Kalman filter (16). |
|
| Algorithm 4 Assimilation of observations via the posterior ensemble Kalman filter (17) . |
|
3.4. Inflation Aspects
3.5. Main Differences Between the EnKF-MC, the P-EnKF, and the P-EnKF-S
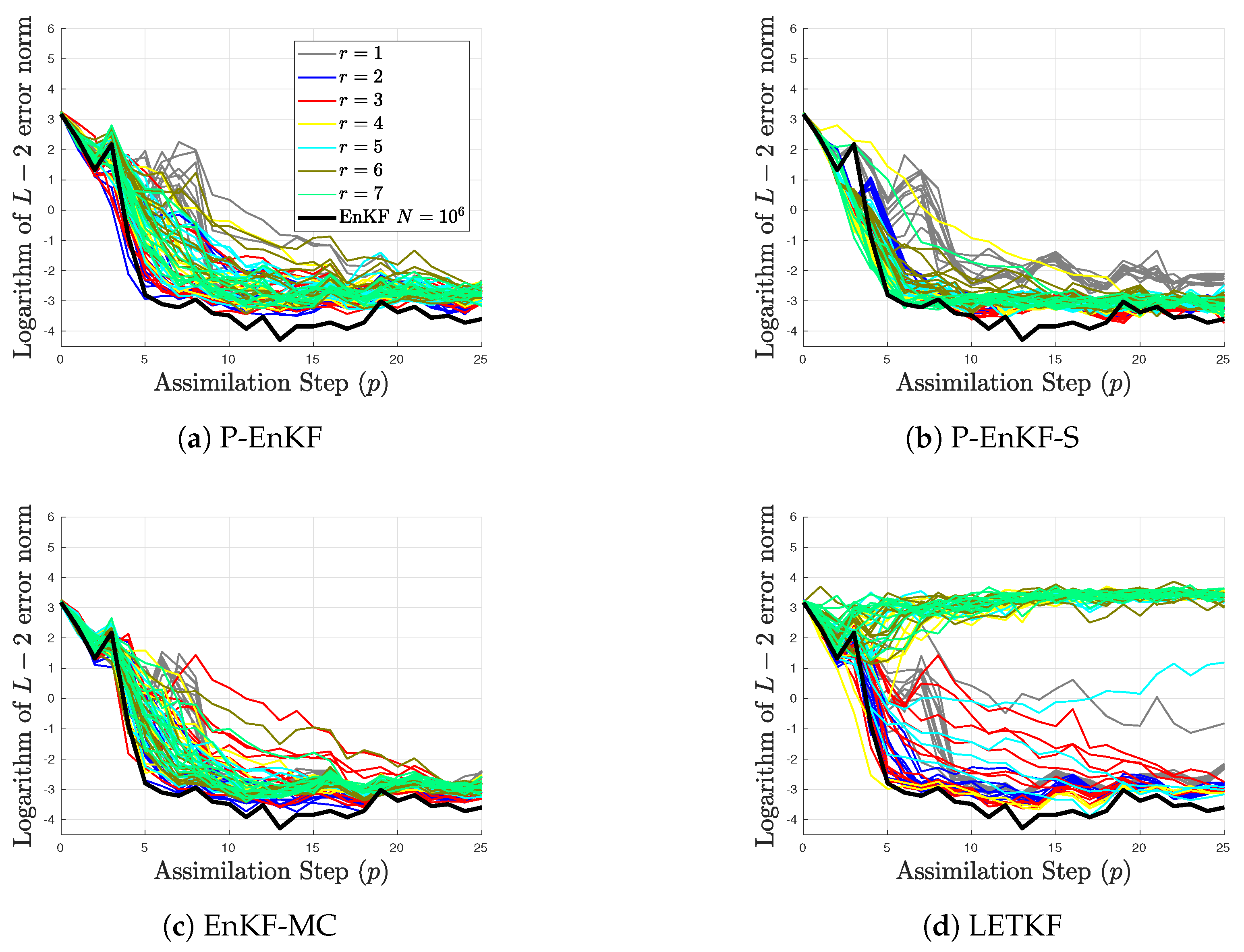
4. Experimental Results
- An initial random solution is integrated over a long time period in order to obtain an initial condition dynamically consistent with the model (22).
- A perturbed background solution is obtained at time by drawing a sample from the Normal distribution,this solution is then integrated for 10 time units (equivalent to 70 days in the atmosphere) in order to obtain a background solution consistent with the numerical model.
- An initial perturbed ensemble is built about the background state by taking samples from the distribution,and in order to make them consistent with the model dynamics, the ensemble members are propagated for 10 time units, from which the initial ensemble members are obtained. We create the initial pool of members.
- The assimilation window consists of observations. These are taken every 3.5 days and their error statistics are associated with the Gaussian distribution,where the number of observed components from the model space is . The components are randomly chosen at the different assimilation steps. Thus, is randomly formed at the different assimilation cycles.
- Values of the inflation factor are ranged in .
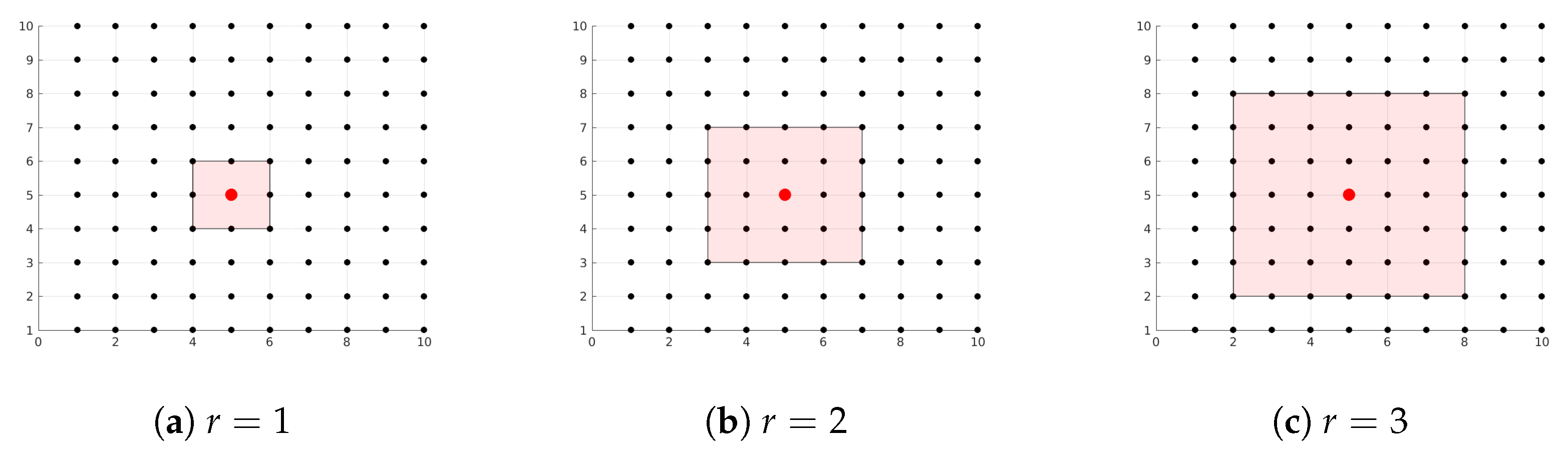
- We try different values for the radii of influence r, these range in .
- The ensemble size for the benchmarks is . These members are randomly chosen from the pool for the different pairs in order to form the initial ensemble for the assimilation window. Evidently, .
- The assimilation steps are also performed by the EnKF with full size of in order to obtain a reference solution regarding what to expect from the EnKF formulations. Note that, the ensemble size is large enough in order to dissipate the impact of sampling errors. No inflation is needed as well.
- The L-2 norm of the error is utilized as a measure of accuracy at the assimilation step p,where and are the reference and the analysis solutions, respectively.
- The Root-Mean-Square-Error (RMSE) is utilized as a measure of performance, in average, on a given assimilation window,
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Buehner, M.; Houtekamer, P.; Charette, C.; Mitchell, H.L.; He, B. Intercomparison of variational data assimilation and the ensemble Kalman filter for global deterministic NWP. Part I: Description and single-observation experiments. Mon. Weather Rev. 2010, 138, 1550–1566. [Google Scholar] [CrossRef]
- Buehner, M.; Houtekamer, P.; Charette, C.; Mitchell, H.L.; He, B. Intercomparison of variational data assimilation and the ensemble Kalman filter for global deterministic NWP. Part II: One-month experiments with real observations. Mon. Weather Rev. 2010, 138, 1567–1586. [Google Scholar] [CrossRef]
- Caya, A.; Sun, J.; Snyder, C. A comparison between the 4DVAR and the ensemble Kalman filter techniques for radar data assimilation. Mon. Weather Rev. 2005, 133, 3081–3094. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Sandu, A. Ensemble Kalman filter implementations based on shrinkage covariance matrix estimation. Ocean Dyn. 2015, 65, 1423–1439. [Google Scholar] [CrossRef]
- Anderson, J.L. Localization and Sampling Error Correction in Ensemble Kalman Filter Data Assimilation. Mon. Weather Rev. 2012, 140, 2359–2371. [Google Scholar] [CrossRef]
- Jonathan, P.; Fuqing, Z.; Weng, Y. The Effects of Sampling Errors on the EnKF Assimilation of Inner-Core Hurricane Observations. Mon. Weather Rev. 2014, 142, 1609–1630. [Google Scholar]
- Buehner, M. Ensemble-derived Stationary and Flow-dependent Background-error Covariances: Evaluation in a Quasi-operational NWP Setting. Q. J. R. Meteorol. Soc. 2005, 131, 1013–1043. [Google Scholar] [CrossRef]
- Nino-Ruiz, E.D.; Sandu, A.; Deng, X. A parallel ensemble Kalman filter implementation based on modified Cholesky decomposition. In Proceedings of the 6th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems, Austin, TX, USA, 15–20 November 2015; p. 4. [Google Scholar]
- Nino-Ruiz, E.D.; Sandu, A.; Deng, X. A parallel implementation of the ensemble Kalman filter based on modified Cholesky decomposition. J. Comput. Sci. 2017. [Google Scholar] [CrossRef]
- Bickel, P.J.; Levina, E. Regularized estimation of large covariance matrices. Ann. Stat. 2008, 36, 199–227. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical Formulation and Practical Implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Lorenc, A.C. The potential of the ensemble Kalman filter for NWP—A comparison with 4D-Var. Q. J. R. Meteorol. Soc. 2003, 129, 3183–3203. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Snyder, C. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter. Mon. Weather Rev. 2001, 129, 2776–2790. [Google Scholar] [CrossRef]
- Cheng, H.; Jardak, M.; Alexe, M.; Sandu, A. A Hybrid Approach to Estimating Error Covariances in Variational Data Assimilation. Tellus A 2010, 62, 288–297. [Google Scholar] [CrossRef]
- Chatterjee, A.; Engelen, R.J.; Kawa, S.R.; Sweeney, C.; Michalak, A.M. Background Error Covariance Estimation for Atmospheric CO2 Data Assimilation. J. Geophys. Res. Atmos. 2013, 118. [Google Scholar] [CrossRef]
- Keppenne, C.L. Data Assimilation into a Primitive-Equation Model with a Parallel Ensemble Kalman Filter. Mon. Weather Rev. 2000, 128, 1971–1981. [Google Scholar] [CrossRef]
- Buehner, M. Evaluation of a Spatial/Spectral Covariance Localization Approach for Atmospheric Data Assimilation. Mon. Weather Rev. 2011, 140, 617–636. [Google Scholar] [CrossRef]
- Sakov, P.; Bertino, L. Relation between two common localisation methods for the EnKF. Comput. Geosci. 2011, 15, 225–237. [Google Scholar] [CrossRef]
- Tippett, M.K.; Anderson, J.L.; Bishop, C.H.; Hamill, T.M.; Whitaker, J.S. Ensemble Square Root Filters. Mon. Weather Rev. 2003, 131, 1485–1490. [Google Scholar] [CrossRef]
- Bishop, C.H.; Toth, Z. Ensemble Transformation and Adaptive Observations. J. Atmos. Sci. 1999, 56, 1748–1765. [Google Scholar] [CrossRef]
- Ott, E.; Hunt, B.R.; Szunyogh, I.; Zimin, A.V.; Kostelich, E.J.; Corazza, M.; Kalnay, E.; Patil, D.J.; Yorke, J.A. A local ensemble Kalman filter for atmospheric data assimilation. Tellus A 2004, 56, 415–428. [Google Scholar] [CrossRef]
- Hunt, B.R.; Kostelich, E.J.; Szunyogh, I. Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter. Phys. D: Nonlinear Phenom. 2007, 230, 112–126. [Google Scholar] [CrossRef]
- Ott, E.; Hunt, B.; Szunyogh, I.; Zimin, A.V.; Kostelich, E.J.; Corazza, M.; Kalnay, E.; Patil, D.J.; Yorke, J.A. A Local Ensemble Transform Kalman Filter Data Assimilation System for the NCEP Global Model. Tellus A 2008, 60, 113–130. [Google Scholar]
- Nino, E.D.; Sandu, A.; Deng, X. An Ensemble Kalman Filter Implementation Based on Modified Cholesky Decomposition for Inverse Covariance Matrix Estimation. arXiv, 2016; arXiv:arXiv:1605.08875. [Google Scholar]
- Sakov, P.; Evensen, G.; Bertino, L. Asynchronous data assimilation with the EnKF. Tellus A 2010, 62, 24–29. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter for combined state and parameter estimation. IEEE Control Syst. 2009, 29. [Google Scholar] [CrossRef]
- Anderson, J.L. An ensemble adjustment Kalman filter for data assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar] [CrossRef]
- Smailbegovic, F.; Gaydadjiev, G.N.; Vassiliadis, S. Sparse matrix storage format. In Proceedings of the 16th Annual Workshop on Circuits, Systems and Signal Processing, Veldhoven, The Netherlands, 17–18 November 2005; pp. 445–448. [Google Scholar]
- Langr, D.; Tvrdik, P. Evaluation criteria for sparse matrix storage formats. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 428–440. [Google Scholar] [CrossRef]
- Dongarra, J.J.; Demmel, J.W.; Ostrouchov, S. LAPACK: A Linear Algebra Library for High-Performance Computers. In Computational Statistics: Volume 1, Proceedings of the 10th Symposium on Computational Statistics; Springer Science & Business Media: Berlin, Germany, 2013; p. 23. [Google Scholar]
- Westgate, P.M. A covariance correction that accounts for correlation estimation to improve finite-sample inference with generalized estimating equations: A study on its applicability with structured correlation matrices. J. Stat. Comput. Simul. 2016, 86, 1891–1900. [Google Scholar] [CrossRef] [PubMed]
- Lei, L.; Whitaker, J.S. Evaluating the tradeoffs between ensemble size and ensemble resolution in an ensemble-variational data assimilation system. J. Adv. Model. Earth Syst. 2017. [Google Scholar] [CrossRef]
- Lee, Y.; Majda, A.J.; Qi, D. Preventing catastrophic filter divergence using adaptive additive inflation for baroclinic turbulence. Mon. Weather Rev. 2017, 145, 669–682. [Google Scholar] [CrossRef]
- Putnam, B.J.; Xue, M.; Jung, Y.; Snook, N.A.; Zhang, G. Ensemble Probabilistic Prediction of a Mesoscale Convective System and Associated Polarimetric Radar Variables using Single-Moment and Double-Moment Microphysics Schemes and EnKF Radar Data Assimilation. Mon. Weather Rev. 2017. [Google Scholar] [CrossRef]
- Ruiz, E.D.N.; Sandu, A.; Anderson, J. An efficient implementation of the ensemble Kalman filter based on an iterative Sherman—Morrison formula. Stat. Comput. 2015, 25, 561–577. [Google Scholar] [CrossRef]
- Lorenz, E.N. Designing Chaotic Models. J. Atmos. Sci. 2005, 62, 1574–1587. [Google Scholar] [CrossRef]
- Fertig, E.J.; Harlim, J.; Hunt, B.R. A comparative study of 4D-VAR and a 4D ensemble Kalman filter: Perfect model simulations with Lorenz-96. Tellus A 2007, 59, 96–100. [Google Scholar] [CrossRef]
- Karimi, A.; Paul, M.R. Extensive chaos in the Lorenz-96 model. Chaos: An Interdiscip. J. Nonlinear Sci. 2010, 20, 043105. [Google Scholar] [CrossRef] [PubMed]
- Gottwald, G.A.; Melbourne, I. Testing for chaos in deterministic systems with noise. Phys. D: Nonlinear Phenom. 2005, 212, 100–110. [Google Scholar] [CrossRef]


© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nino-Ruiz, E.D. A Matrix-Free Posterior Ensemble Kalman Filter Implementation Based on a Modified Cholesky Decomposition. Atmosphere 2017, 8, 125. https://doi.org/10.3390/atmos8070125
Nino-Ruiz ED. A Matrix-Free Posterior Ensemble Kalman Filter Implementation Based on a Modified Cholesky Decomposition. Atmosphere. 2017; 8(7):125. https://doi.org/10.3390/atmos8070125
Chicago/Turabian StyleNino-Ruiz, Elias D. 2017. "A Matrix-Free Posterior Ensemble Kalman Filter Implementation Based on a Modified Cholesky Decomposition" Atmosphere 8, no. 7: 125. https://doi.org/10.3390/atmos8070125
APA StyleNino-Ruiz, E. D. (2017). A Matrix-Free Posterior Ensemble Kalman Filter Implementation Based on a Modified Cholesky Decomposition. Atmosphere, 8(7), 125. https://doi.org/10.3390/atmos8070125




