The Weather Generator Used in the Empirical Statistical Downscaling Method, WETTREG
Abstract
:1. Introduction
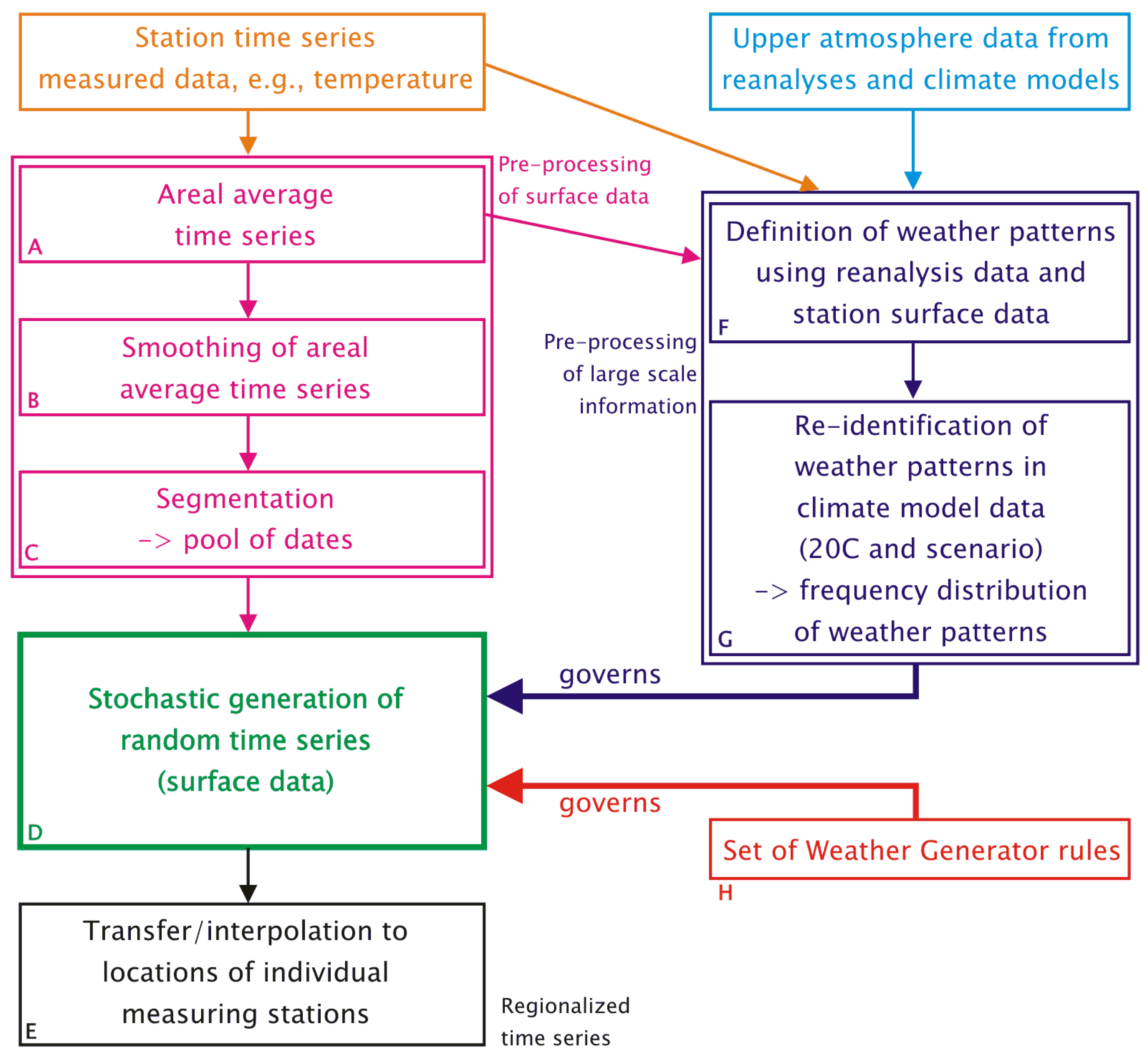
2. Before the WG is Launched
2.1. Data
- Surface observations from the region of interest. This encompasses a number of weather elements (e.g., daily values of temperature, precipitation, sunshine duration, cloudiness, humidity, air pressure, wind) measured at climate stations or precipitation stations. In the course of the pre-processing towards the usage in the WG (boxes A, B and C in Figure 1), surface data are aggregated into regional averages, which are subsequently segmented into episodes. Moreover, the particular method by which WETTREG defines its circulation patterns (see Section 2.2 and Section 3.3), requires aggregated surface observation data, too.
- Atmosphere data based on measurements and homogenized by reanalysis form a kind of three-dimensional climatology of the recent past. Several reanalysis products were developed and are in frequent use: NCEP (National Center for Environmental Prediction) [32], ERA40 [33] and, most recently, ERA-Interim [34]. The philosophy and strategies of reanalysis are described, e.g., in [35] and [36]. In order to cover a period from the 1970s to the early 21st century, NCEP reanalyses are used in the pattern-development stage of WETTREG (cf. box F in Figure 1 and Section 3.3).
- Atmosphere data for the European region from a Global Circulation Model (GCM). Recently, also, Regional Climate Models (RCMs) have been run for a similarly large area, enabling WETTREG to use them as an alternative input data source [24].Eight upper air fields, i.e., geopotential height (at 1,000, 850, 700 and 500 hPa), temperature and humidity at 850 and 500 hPa are extracted for the description of the 12 UTC conditions, as is simulated by the circulation model. So called 20C data are used for the model’s re-simulation of the current climate, and data from the model forced by a scenario, e.g., an emission scenario GCM run, based on the Special Report on Emissions Scenarios (SRES) [37] or representative concentration pathways (RCPs) [38] type, are used for the assessment of future climate conditions. As indicated by box G of Figure 1 and described in Section 3.3, the circulation model data are analyzed with respect to the frequency of the aforementioned circulation patterns—for details, please refer to Section 2.2. The changing frequency distribution is a governing factor for the WG.
2.2. Circulation Patterns
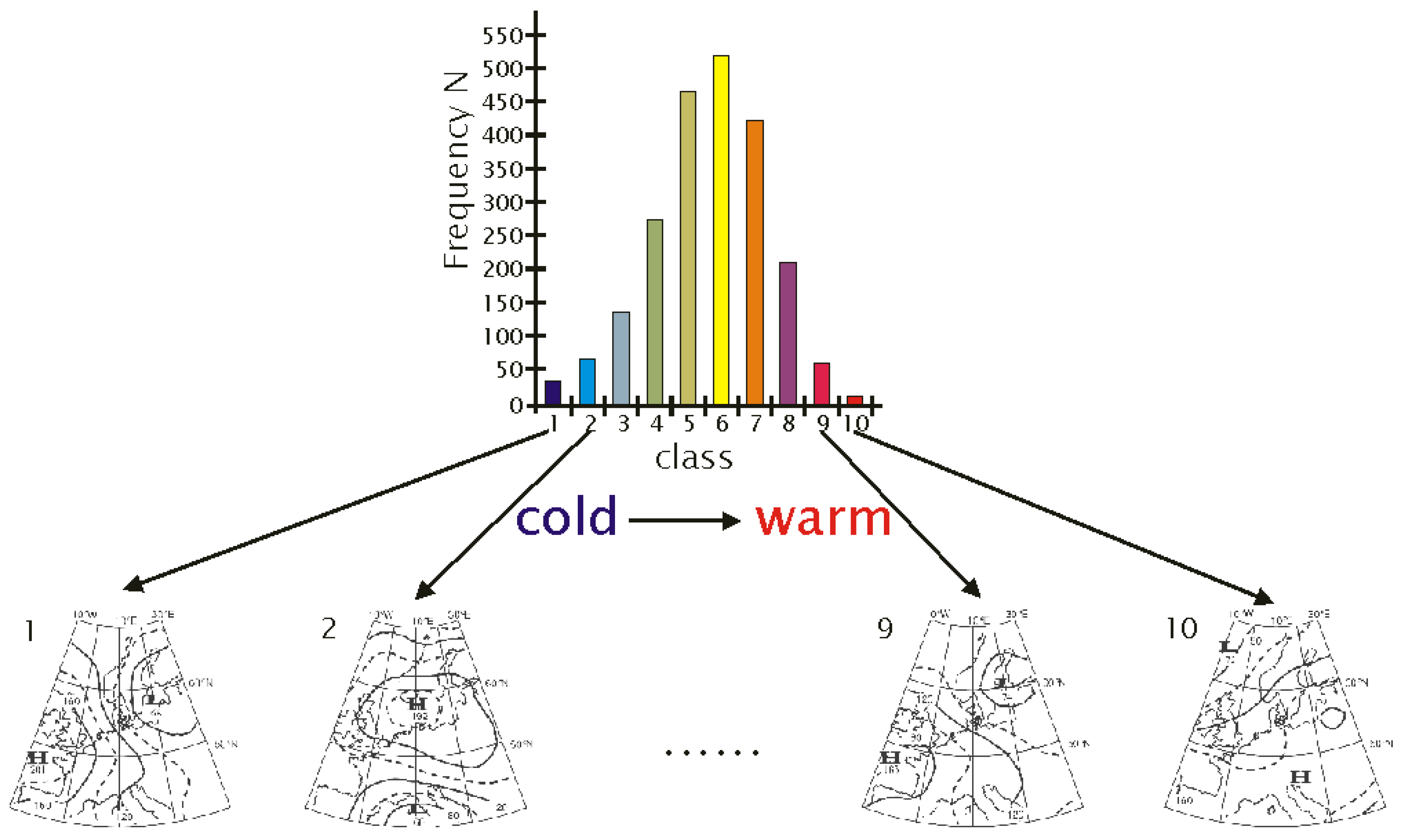
3. Description of the Weather Generator
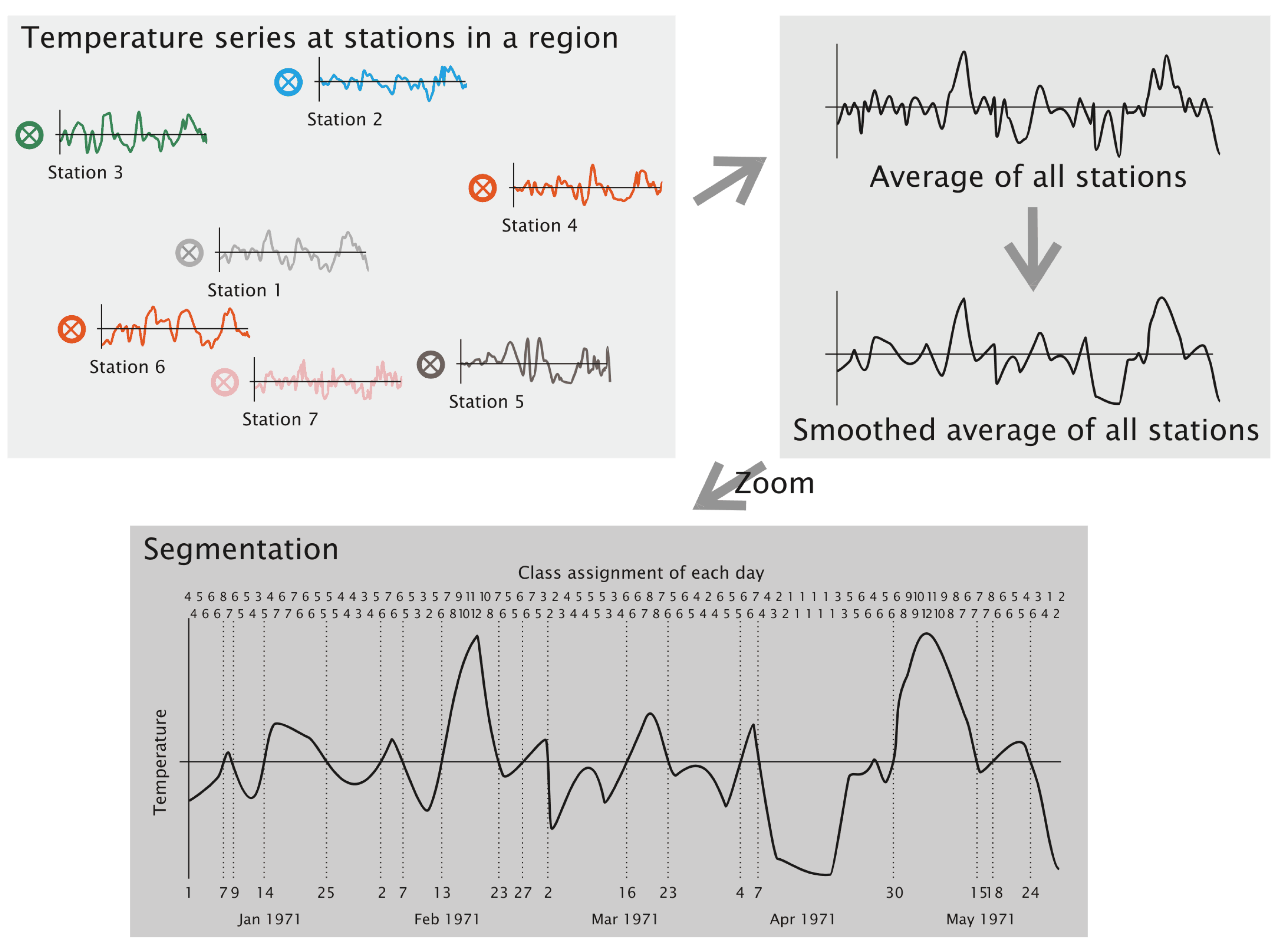
- A target area is selected, and time series of surface climate parameters are identified. However, only the temperature is used for the subsequent pre-processing steps. It is the aim of the authors to keep the method description as simple and straightforward as possible. Therefore, the examples are build up using temperature time series. In the method’s implementation, time series of deviation from the annual temperature cycle are used, which is, however, of little relevance for understanding the method’s principles.
- Areal averages—the arithmetic means of all stations from the target area—of the temperature are computed for each day.
- A five-point smoothing using equal weights is applied (example: the temperature on January 10 is replaced by the average temperature of January 8 to 12). Beginnings and endings of the time series use the average computed from three or four days, respectively.
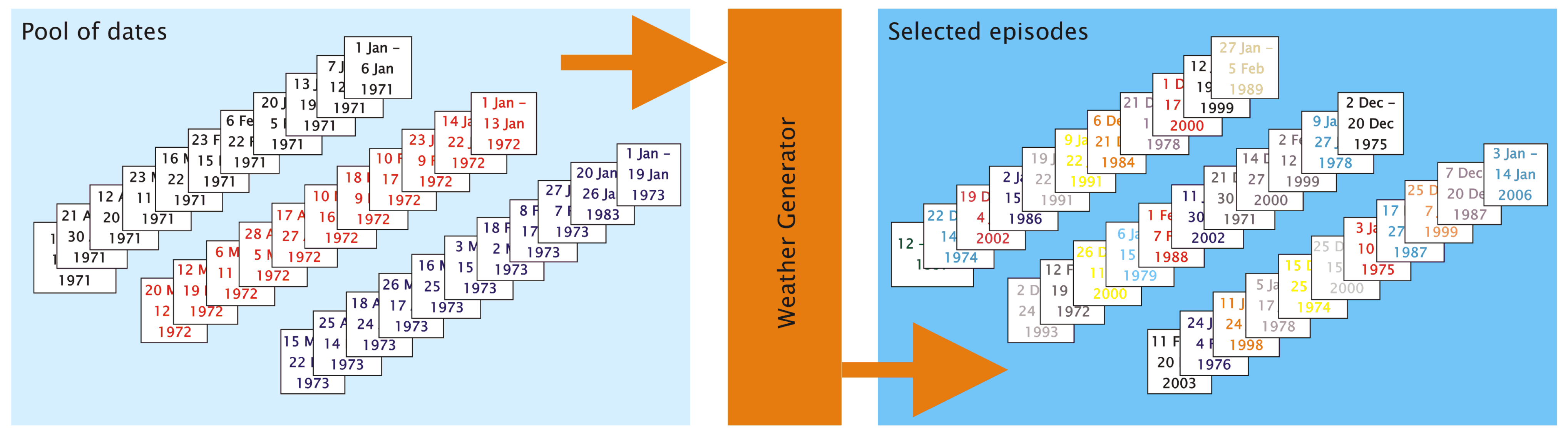
- The smoothed time series is cut into segments whenever a pass through zero occurs.
- Usage of an areal average to generate the pool of dates instead of a station-wise series synthesizing procedure (Section 3.1);
- assembly of episodes of and days-length (Section 3.2);
- frequency of circulation patterns as the main governing factor for optimizing the time series synthesized by the WG (Section 3.3);
- measures to ensure the stochasticity of the the synthesizing process (Section 3.4);
- approximation of synoptical and statistical climate properties (Section 3.5);
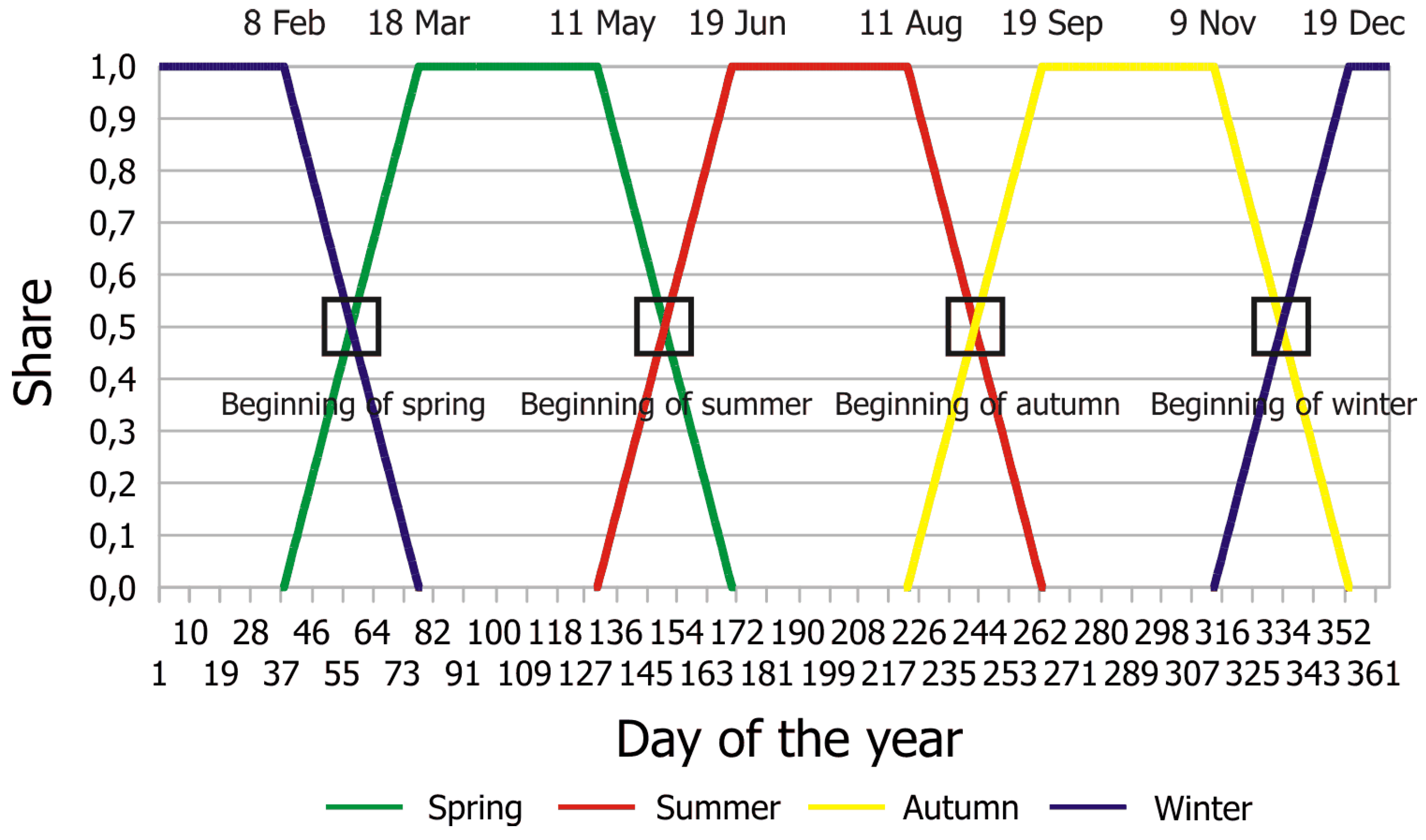
- overlapping frequency distribution as a measure of dealing with seasonality (Section 3.6).

3.1. Why Areal Averaging?
3.2. Episodes and Their Length
3.3. The Synthesizing Process Controlled by Pattern Distributions
- No matter if the individual days are from reanalysis data, 20C simulations or climate model scenario runs, each day had been assigned to a circulation pattern (cf. Section 2.2) during the patterns-matching phase (cf. Equation (1)).
- -
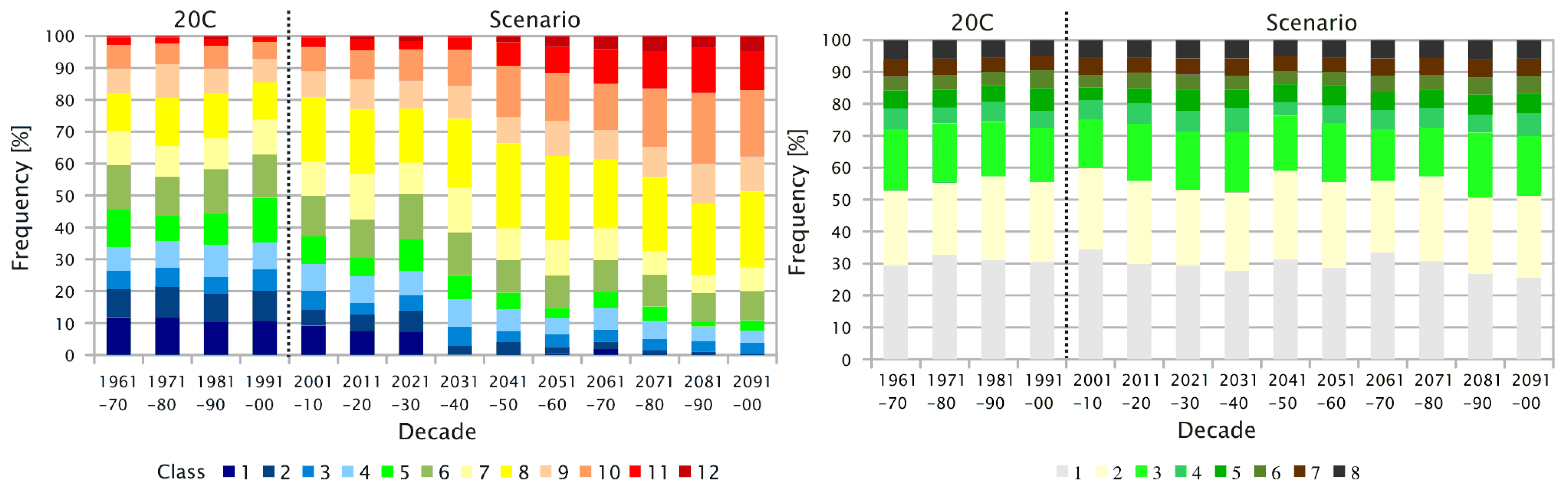
- The sequence of days that belongs to an episode (determined from the current climate conditions as they were measured) carries a frequency distribution of these patterns, as shown in Figure 6. Since the WG strings together episodes that actually occurred, to form new time series, these episodes constitute the building blocks of the emerging time series. Their inherent pattern frequency distribution is evaluated.
- -
- Concerning the days of the 20C runs from a climate model, the determined frequency distribution of circulation patterns constitute the model’s ability to reproduce what was established by way of analyzing reanalysis data and surface measurements.
- -
- Concerning the days of the scenario runs from a climate model, the determined frequency distribution of circulation patterns constitute the model’s projection of a future climate, adhering to the circulation patterns established by way of analyzing reanalysis data and surface measurements.
- The underlying (or target) frequency distribution of the circulation patterns determined from a circulation model is determined (20C or scenario run, depending on the time frame of interest). An example is given in Figure 3.
- The synthesizing process successively generates a string of episodes and is represented by the loop below. The members of the episodes pool are tested one by one if they help optimize the goodness-of-fit between the pattern frequency distribution of the synthesized time series, on the one hand, and the target frequency distribution, on the other hand. One “optimal” episode is determined per pass.
- Selection process for adding the Nth episode to the synthesized time series is launched.
- Episode from the pool of p dates is selected. This is the “candidate episode”.
- If it is the very first episode () in the synthesizing procedure, the subsequent evaluation steps are carried out using the frequency distribution, of (cf. Equation (2)) this candidate episode alone vs. the underlying (target) frequency distribution.
- If a successful candidate has been assigned to the emerging synthesized time series (), a pooled frequency distribution of all members, accepted so far into the series, emerges, as well. Each new “candidate episode”, , is provisionally added to that pooled distribution, and the evaluation steps are then carried out with the provisionally generated frequency distribution until an optimal candidate has been determined.
- The goodness-of-fit measure, (see Equation (2)), is used to determine the degree of match between the pattern frequency distribution within the synthesized time series (including the candidate episode) and that of the circulation model data for a certain time horizon (the prescribed target frequency distribution, shown in the gray shaded area of Figure 6).
- It is evaluated if adding that episode to the time series synthesized so far improves or deteriorates the fit to the prescribed target frequency distributions, by determining if for this pass. Track is kept on the pass number s and its measure.
- If the counter, s, is below or equal to the number of episodes in the pool of dates, i.e., p, then s is increased by one. The loop is repeated, starting at entry number 2 above. It should be noted that at each pass, the entire pool of dates is evaluated, i.e., the same episode can be selected repeatedly.
- When all p episodes have been tested, the candidate episode, , that yielded the minimum of all values for the s passes is added to the emerging synthesized time series.
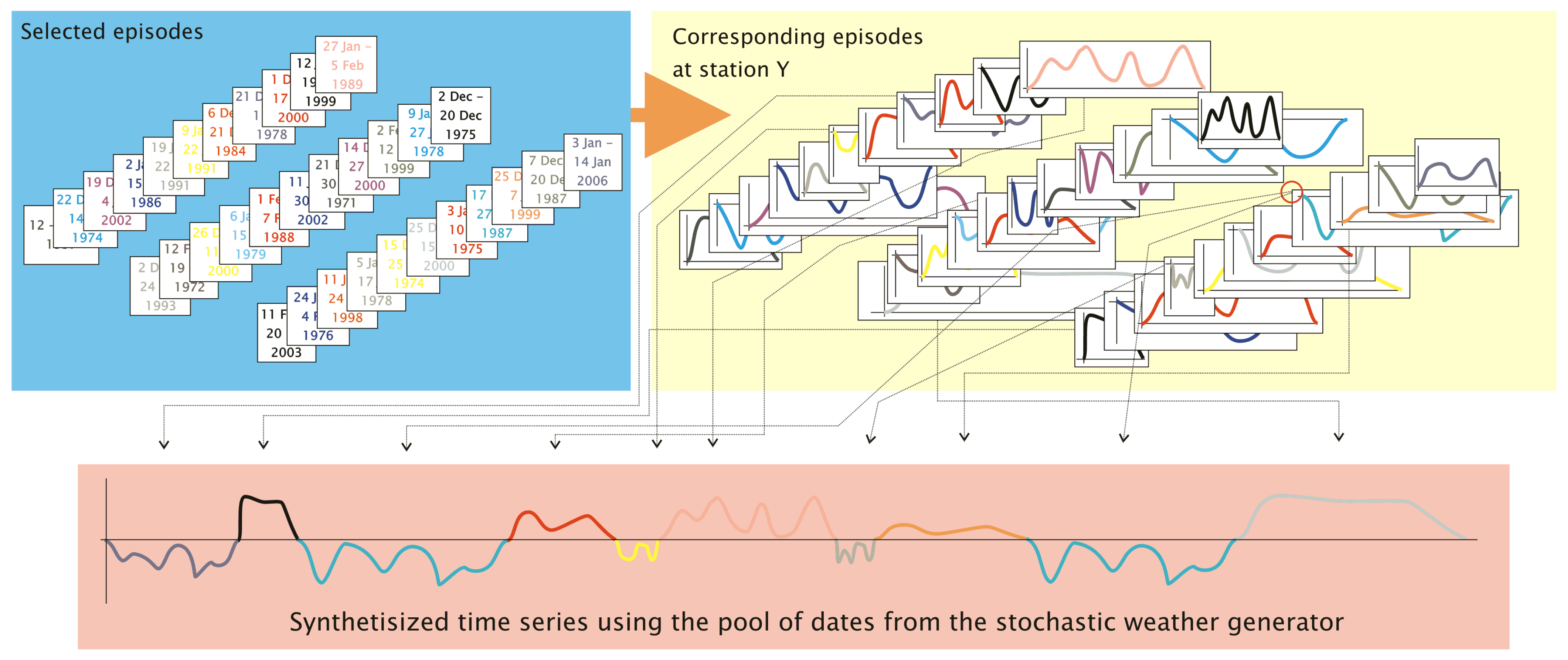
- Track is kept on the origin of the episode (i.e., day, month and year of its beginning, as well as its length, all extracted from the pool of dates), the date in the synthesized series for which the inserted episode is being used and information pertaining to the newly added episode (such as measured meteorological parameters or assigned circulation pattern).
- As long as the final day, initially specified for the synthesized time series, has not been reached, the counter, N, is increased by one. The loop process is repeated starting at entry number 1, above.

3.4. Randomness of the Episode Selection
3.5. Further Governing Factors of the WG
3.6. Reducing the Effects of Season Breaks
4. From the WG to the Production of Local Time Series
5. Comparison to Other Methods
6. Remarks
6.1. Effects of the Changing Frequency of Circulation Patterns
- An extended database of episodes. The idea is based on the delta method. Using the observed time series, an additional set of episodes is generated. Due to the fact that the temperature (i) is causing the problem and (ii) is of high relevance, all temperature values will be increased by a certain value. If needs be, an adjustment of other weather elements is carried out to ensure physical consistency, for example, a higher temperature necessitates the adjustment of the water vapour pressure.To find an appropriate increment, the difference between the mean value of the neighbour temperature classes need to be determined. Based on the assigned class number, each temperature value receives a class-specific correction. Then, the class number, which was originally assigned to a day, needs to be stepped up by one (except for those days that were in the highest class already). The result is an “upward shift” in class membership without changing the value boundaries of the classes themselves (except for the topmost class). Consequently, the episodes in the pool then contain an increased number of days with high temperature class assignments.This has a physical rationale, because it can be argued that the same dynamic atmospheric conditions will be, in the future, linked, e.g., with a higher temperature range, making them the “more extreme relatives” of current patterns. If this alternative pool of shifted episodes is gradually allowed to be used towards the end of the 21st century, i.e., when the frequency of the patterns that needs to be met is gradually deforming, there will be two consequences: (i) the quite frequent usage of just a few episodes is reduced and (ii) an increase in the goodness-of-fit ensues.
- A modified definition of the episodes. In the ‘standard’ version of the WG, an episode is beginning and ending with a zero-crossing, i.e., a transition from below-average to above-average conditions (or vice versa), as described in Section 3.2 and visualized in Figure 4. If the threshold is shifted upwards, episodes are allowed to occur that contain a smaller share of classes associated with rather low temperature ranges.The physical rationale would be that it can be argued that a future annual cycle might shift, as well. These episodes are clearly shorter than the ones derived the standard way; so, the minimum length criterion (cf. Section 3.2) needs to be taken into account. Introducing this measure has two consequences: (i) the effect caused by the introduction of excess days with patterns in the mid-range is reduced and (ii) an increase in the goodness-of-fit ensues.
6.2. Extremes
6.3. User Requirements vs. Deliver-Ability of a WG
7. Summary and Outlook
Authors’ Contributions
Acknowledgments
Conflict of Interest
References
- Wilks, D. Use of stochastic weather generators for precipitation downscaling. WIREs Clim. Chang. 2010, 1, 898–907. [Google Scholar] [CrossRef]
- Semenov, M. Simulation of extreme weather events by a stochastic weather generator. Clim. Res. 2008, 35, 203–212. [Google Scholar] [CrossRef]
- Richardson, C. Stochastic simulation of daily precipitation, temperature, and solar radiation. Water Resour. Res. 1981, 17, 182–190. [Google Scholar] [CrossRef]
- Richardson, C.; Wright, D. WGEN: A Model for Generating Daily Weather Variables; Technical Report; USDA/ARS, ARS-8; Agricultural Research Service: Washington, DC, USA, 1984.
- Hantel, M.; Acs, F. Physical aspects of the weather generator. J. Hydrol. 1998, 212–213, 393–411. [Google Scholar] [CrossRef]
- Global International Geosphere–Biosphere Programme (IGBP) Change. Available online: www.igbp.net (accessed on 31 May 2013).
- Bass, B. BAHC Focus 4: The Weather Generator Project; Technical Report; BAHC Report No. 4; BAHC Core Project Office, Freie Universität Berlin: Berlin, Germany, 1994. [Google Scholar]
- Waymire, E.; Gupta, V. The mathematical structure of rainfall representations—1. A review of the stochastic rainfall models. Wat. Resour. Res. 1981, 17, 1261–1272. [Google Scholar] [CrossRef]
- Katz, R.; Parlange, M. Mixtures of stochastic processes: Application to statistical downscaling. Clim. Res. 1996, 7, 185–193. [Google Scholar] [CrossRef]
- Gabriel, K.; Neumann, J. A Markov chain model for daily rainfall occurrence at Tel Aviv. Quart. J. Roy. Met. Soc. 1962, 88, 90–95. [Google Scholar] [CrossRef]
- Todorovic, P.; Woolhiser, D. A stochastic model of n-day precipitation. J. Appl. Meteorol. 1975, 14, 17–24. [Google Scholar] [CrossRef]
- Busuioc, A.; von Storch, H. Conditional stochastic model for generating daily precipitation time series. Clim. Res. 2003, 24, 181–195. [Google Scholar] [CrossRef]
- Wilks, D. Adapting stochastic weather generation algorithms for climate change studies. Clim. Res. 1992, 22, 67–84. [Google Scholar] [CrossRef]
- Semenov, M.; Barrow, E. Use of a stochastic weather generator in the development of climate change scenarios. Clim. Change 1997, 35, 397–414. [Google Scholar] [CrossRef]
- Schubert, S. A weather generator based on the European “Grosswetterlagen”. Clim. Res. 1994, 4, 191–202. [Google Scholar] [CrossRef]
- Gerstengarbe, F.; Werner, P. Katalog der Großwetterlagen Europas (1881–2004) nach P. Hess und H. Brezowsky; Technical Report 100; PIK-Reports; Potsdam Institut für Klimafolgenforschung: Potsdam, Germany, 2005. [Google Scholar]
- Corte-Real, J.; Xu, H.; Qian, B. A weather generator for obtaining daily precipitation scenarios based on circulation patterns. Clim. Res. 1999, 13, 61–75. [Google Scholar] [CrossRef]
- Wilks, D.; Wilby, R. The weather generation game: A review of stochastic weather models. Progr. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Orlowsky, B.; Gerstengarbe, F.W.; Werner, P. A resampling scheme for regional climate simulations and its performance compared to a dynamical RCM. Theor. Appl. Climatol. 2008, 92, 209–223. [Google Scholar] [CrossRef]
- Hayhoe, H. Improvements of stochastic weather data generators for diverse climates. Clim. Res. 2000, 14, 75–87. [Google Scholar] [CrossRef]
- Mason, S. Simulating climate over Western North America using stochastic weather generators. Clim. Change 2004, 62, 155–187. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G. Copula based multisite model for daily precipitation simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef]
- Spekat, A.; Kreienkamp, F.; Enke, W. An impact-oriented classification method for atmospheric patterns. Phys. Chem. Earth 2010, 35, 352–359. [Google Scholar] [CrossRef]
- Kreienkamp, F.; Baumgart, S.; Spekat, A.; Enke, W. Climate signals on the regional scale derived with a statistical method: Relevance of the driving model’s resolution. Atmosphere 2011, 2, 129–145. [Google Scholar] [CrossRef]
- Enke, W.; Spekat, A. Verbundprojekt: Klimavariabilität und Signalanalyse. Teilthema: Signalanalyse zur Regionalisierung von Klimamodell-Outputs mit Hilfe der Erkennung Synoptischer Muster und Statistischer Analysemethoden; Technical Report 07KV01/1 (161/30); Bundesministerium für Bildung und Forschung (BMBF): Bonn, Germany, 1994. [Google Scholar]
- Enke, W.; Spekat, A. Downscaling climate model outputs into local and regional weather elements by classification and regression. Clim. Res. 1997, 8, 195–207. [Google Scholar] [CrossRef]
- Enke, W.; Deutschländer, T.; Schneider, F.; Küchler, W. Results of five regional climate studies applying a weather pattern based downscaling method to ECHAM4 climate simulations. Meteorol. Z. 2005, 14, 247–257. [Google Scholar] [CrossRef]
- Spekat, A.; Enke, W.; Kreienkamp, F. Neuentwicklung von regional hoch aufgelösten Wetterlagen für Deutschland und Bereitstellung Regionaler Klimaszenarios auf der Basis von Globalen Klimasimulationen mit dem Regionalisierungsmodell WETTREG auf der Basis von Globalen Klimasimulationen mit ECHAM5/MPI-OM T63L31 2010 bis 2100 für die SRES-Szenarios B1, A1B und A2 (Endbericht). Im Rahmen des Forschungs- und Entwicklungsvorhabens: Klimaauswirkungen und Anpassungen in Deutschland—Phase I: Erstellung regionaler Klimaszenarios für Deutschland des Umweltbundesamtes; Technical Report Förderkennzeichen 204 41 138; Umweltbundsamt, Dessau, 2007. [Google Scholar]
- Kreienkamp, F.; Spekat, A.; Enke, W. Weiterentwicklung von WETTREG Bezüglich Neuartiger Wetterlagen; Technical Report. CEC-Potsdam on Behalf of a Consortium of Environment Agencies from German Federal States, 2010. Available online: klimawandel.hlug.de/fileadmin/dokumente/klima/inklim_a/TWL_Laender.pdf (accessed on 31 May 2013).
- Mehrotra, R.; Sharma, A. Evaluating spatio-temporal representations in daily rainfall sequences from three stochastic multi-site weather generation approaches. Adv. Wat. Res. 2009, 32, 948–962. [Google Scholar] [CrossRef]
- Kreienkamp, F.; Hübener, H.; Linke, C.; Spekat, A. Good practice for the usage of climate model simulation results—A discussion paper. Env. Syst. Res. 2012, 1, 9–37. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Met. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Uppala, S.M.; Kållberg, P.W.; Simmons, A.J.; Andrae, U.; da Costa Bechtold, V.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.; et al. The ERA-40 re-analysis. Quart. J. Roy. Met. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. Roy. Met. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Woods, A. Medium-Range Weather Prediction—The European Approach. The Story of the European Center for Medium-Range Weather Forecasts; Springer: New York, NY, USA, 2006. [Google Scholar]
- Edwards, P. A Vast Machine—Computer Models, Climate Data, and the Politics of Global Warming; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Nakićenović, N.; Alcamo, J.; de Vries, B.; Fenhann, J.; Gaffin, S.; Gregory, K.; Grübler, A.; Jung, T.; Kram, T.; Rovere, E.L.; et al. Emissions Scenarios; A Special Reports of IPCC Working Group III; Cambridge University Press: Cambridge, UK, 2000; p. 570. [Google Scholar]
- Moss, R.; Babiker, M.; Brinkman, S.; Calvo, E.; Carter, T.; Edmonds, J.; Elgizouli, I.; Emori, S.; Erda, L.; Hibbard, K.; Jones, R.; et al. Towards New Scenarios for Analysis of Emissions, Climate Change, Impacts, and Response Strategies. In Proceedings of Expert Meeting Report, Noordwijkerhout, The Netherlands, 19–21 September 2007; p. 132.
- Jones, P.; Kilsby, C.; Harpham, C.; Glenis, V.; Burton, A. UK Climate Projections Science Report: Projections of Future Daily Climate for the UK from the Weather Generator; Technical Report; University of Newcastle: Newcastle, UK, 2009. [Google Scholar]
- Benestad, R.; Hanssen-Bauer, I.; Cheng, D. Empirical-Statistical Downscaling; World Scientific Publishing Co. Pte. Ltd.: Singapore, Singapore, 2008. [Google Scholar]
- Enke, W.; Schneider, F.; Deutschländer, T. A novel scheme to derive optimized circulation pattern classifications for downscaling and forecast purposes. Theor. Appl. Climatol. 2005, 82, 51–63. [Google Scholar] [CrossRef]
- Christensen, J.H. Prediction of Regional Scenarios and Uncertainties for Defining European Climate Change Risks and Effects (PRUDENCE), Final Report; Technical Report EVK2-CT2001-00132; Danish Meteorological Institute (DMI): Copenhagen, Denmark, 2005. [Google Scholar]
- Yarnal, B. Synoptic Climatology in Environmental Analysis; Belhaven Press: London, UK, 1993. [Google Scholar]
- Philipp, A.; Bartholy, J.; Beck, C.; Erpicum, M.; Esteban, P.; Huth, R.; James, P.; Jourdain, S.; Krennert, T.; et al. COST733CAT—A database of weather and circulation type classifications. Phys. Chem. Earth 2010, 35, 360–373. [Google Scholar] [CrossRef]
- Huth, R. Synoptic-climatological applicability of circulation classifications from the COST733 collection: First results. Phys. Chem. Earth 2010, 35, 388–394. [Google Scholar] [CrossRef]
- Roeckner, E.; Baeuml, G.; Bonaventura, L.; Brokopf, R.; Esch, M.; Giorgetta, M.; Hagemann, S.; Kirchner, I.; Kornblueh, L.; Manzini, E.; et al. The Atmospheric General Circulation Model ECHAM5—Part 1: Model Description; Report No. 349, MPI-Berichte; Max-Planck-Institut für Meteorologie: Hamburg, Germany, 2003. [Google Scholar]
- Roeckner, E.; Brokopf, R.; Esch, M.; Giorgetta, M.; Hagemann, S.; Kornblueh, L.; Manzini, E.; Schlese, U.; Schulzweida, U. The Atmosphere General Circulation Model ECHAM5—Part 2: Sensitivity of Simulated Climate to Horizontal and Vertical Resolution; Report No. 354, MPI-Berichte; Max-Planck-Institut für Meteorologie: Hamburg, Germany, 2004. [Google Scholar]
- World Meteorological Organization (WMO). Guide to Climatological Practices, 3rd ed.; Technical Report (WMO-No. 100); WMO: Geneva, Switzerland, 2010. [Google Scholar]
- Regional Climate Modelling. Available online: www.remo-rcm.de (accessed on 31 May 2013).
- Climate Limited-Area Modelling COmmunity. Available online: www.clm-community.eu (accessed on 31 May 2013).
- Linke, C.; Grimmert, S.; Hartmann, I.; Reinhardt, K. Auswertung Regionaler Klimamodelle für das Land Brandenburg; Technical Report; Fachbeiträge des Landesumweltamtes, Heft 113; Ministerium für Umwelt, Gesundheit und Verbraucherschutz: Land Brandenburg, Germany, 2010. [Google Scholar]
- Linke, C.; Grimmert, S.; Hartmann, I.; Reinhardt, K. Auswertung Regionaler Klimamodelle für das Land Brandenburg. Teil 2; Technical Report; Fachbeiträge des Landesumweltamtes, Heft 115; Ministerium für Umwelt, Gesundheit und Verbraucherschutz: Land Brandenburg, Germany, 2010. [Google Scholar]
- Arbeitskreis KLIWA. Regionale Klimaszenarien für Süddeutschland. Abschätzung der Auswirkungen auf den Wasserhaushalt. Technical Report; LUBW, KLIWA-Berichte Heft 9. 2006. Available online: http://www.kliwa.de/download/KLIWAHeft9.pdf (accessed on 31 May 2013).
- The Weather Research and Forecasting Model. Available online: www.wrf-model.org (accessed on 31 May 2013).
- Kreienkamp, F.; Spekat, A.; Enke, W. Ergebnisse eines regionalen Szenarienlaufs für Deutschland mit dem statistischen Modell WETTREG2010; Technical Report; Climate and Environment Consulting Potsdam GmbH im Auftrag des Umweltbundesamtes: Dessau, Germany, 2010. [Google Scholar]
- Kreienkamp, F.; Spekat, A.; Enke, W. Ergebnisse Regionaler Szenarienläufe für Deutschland mit der Statistischen Methode WETTREG auf der Basis der SRES Szenarios A2 und B1 Modelliert mit ECHAM5/MPI-OM; Technical Report; Climate and Environment Consulting Potsdam GmbH, Climate Service Center: Hamburg, Germany, 2011. [Google Scholar]
- Kreienkamp, F.; Spekat, A.; Enke, W. Sensitivity studies with a statistical downscaling method—The role of the driving large scale model. Meteorol. Z. 2009, 18, 597–606. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kreienkamp, F.; Spekat, A.; Enke, W. The Weather Generator Used in the Empirical Statistical Downscaling Method, WETTREG. Atmosphere 2013, 4, 169-197. https://doi.org/10.3390/atmos4020169
Kreienkamp F, Spekat A, Enke W. The Weather Generator Used in the Empirical Statistical Downscaling Method, WETTREG. Atmosphere. 2013; 4(2):169-197. https://doi.org/10.3390/atmos4020169
Chicago/Turabian StyleKreienkamp, Frank, Arne Spekat, and Wolfgang Enke. 2013. "The Weather Generator Used in the Empirical Statistical Downscaling Method, WETTREG" Atmosphere 4, no. 2: 169-197. https://doi.org/10.3390/atmos4020169
APA StyleKreienkamp, F., Spekat, A., & Enke, W. (2013). The Weather Generator Used in the Empirical Statistical Downscaling Method, WETTREG. Atmosphere, 4(2), 169-197. https://doi.org/10.3390/atmos4020169



