An atmospheric chemical transport model (CTM) solves the mass balance equations for concentrations x_(i) of tracer species 1 ≤ i ≤ s. The tracer species can be in gas, liquid, or particulate phases, and their concentrations are continuously changed by multiple physical and chemical processes, (1) ∂ x ( i ) ∂ t = − u ⋅ ∇ x ( i ) + 1 ρ ∇ ⋅ ( ρ K ∇ x ( i ) ) + 1 ρ f ( i ) ( ρ x ) + E ( i ) , 1 ≤ i ≤ s , t 0 ≤ t ≤ t F x ( i ) ( t 0 , x ) = x ( i ) initial ( x ) x ( i ) ( t , x ) = x ( i ) inflow ( t , x ) on Γ inflow K n n ∂ x ( i ) ∂ n = 0 on Γ outflow K n n ∂ x ( i ) ∂ n = V ( i ) deposition x ( i ) − Q ( i ) on Γ ground

Here u represents the wind velocity vector, K is the turbulent diffusion tensor, and ρ is the air density These variables are typically prescribed from simulations with a numerical weather prediction model, or are part of the prognostic variables for meteorological models with online chemistry. The concentrations x_(i) are expressed as a mole fraction (e.g., the number of molecules of tracer per 1 billion molecules of air); the absolute concentration of tracer i is ρx_(i) (molecules/cm³). f_(i) is the rate of transformations of species i and depends on all other concentrations at the same spatial location. Such local transformations are determined by gas and liquid phase chemical kinetics, by inter-phase mass transfer, by aerosol dynamic processes (coagulation and growth), by thermodynamic processes, etc. The elevated emissions of species i are E_(i) and the ground level emissions are Q_(i). The deposition velocity is V ( i ) deposition. The model has prescribed initial conditions x^initial, and is subject to Neumann boundary conditions [23] at the ground level boundary Γ^ground. Dirichlet boundary conditions [23] are imposed at the inflow boundary Γ^inflow (along the top and, for regional models, along the lateral boundary as well). A no diffusive flow condition is imposed at the outflow boundary Γ^outflow (along the top and, for regional models, along the lateral boundary as well).

The numerical solution to (1) is represented by the discrete model (2) x i = ℳ t i − 1 → t i ( u , K , E , Q , V deposition , x inflow ; x i − 1 ) , i = 1 , 2 , … ; x 0 = x initial

In (2), the solution x_i is the discrete state vector containing the concentrations of chemical species sampled at the grid points at time t_i. The discrete initial condition x₀ is obtained by sampling x^initial at the grid points. The model solution operator ℳ depends on model parameters such as emission rates, deposition velocities, and boundary fluxes. In principle, all the model parameters, as well as the initial conditions x₀, can be retrieved through data assimilation if there are enough observations. However, we have to limit the number of model parameters to be determined as the observations in reality are lacking to accurately constrain the problem.

While there are numerous CTMs available for both regional and global applications, the community Multiscale Air Quality (CMAQ) model is primarily used to provide examples in Section 5. As an open-source community model, CMAQ is widely used by the air quality community worldwide and continuously updated with support from the U.S. Environmental Protection Agency (EPA) and Community Modeling & Analysis System (CMAS) [24]. CMAQ model was developed by the U.S. EPA to meet the needs of both environmental managers and scientists to improve their ability to evaluate the impact of air quality management practices and to probe, understand, and simulate chemical and physical interactions in the atmosphere. CMAQ model has been designed to model multiple air quality issues, such as tropospheric ozone, fine particles, toxics, acid deposition, and visibility degradation as a whole; and it has capabilities to solve air quality problems in multiple scales including the urban and regional scales [25,26]. CMAQ has been used in numerous chemical data assimilation studies. A 4D-Var data assimilation system, including an adjoint model for CMAQ, has been developed for version 4.5 [27]. The assimilation of AIRNow ozone observations [28] proved to be beneficial for improving ozone predictions [29]. Zubrow et al. [30] presented an ensemble adjustment Kalman filter (EAKF) approach using a a single tracer version of the CMAQ model to assimilate surface measurements of carbon monoxide and showed its ability to provide skillful model results.

Measurements of atmospheric chemical fields have been significantly increasing for the past years throughout the world. Many ground-based networks have been established to routinely monitor the air quality on the surface level. For instance, in the U.S. the AIRNow network has been reporting ozone and fine particle observation (PM2.5, i.e., particulate matter less than 2.5 micrometers in diameter) in near-real-time [28]. However, surface measurements have to be combined with vertical profiles to obtain the three-dimensional states of the atmospheric constituents. Jeuken et al. shows that assimilating ozone columns alone has little impact on the shape of the vertical ozone profile which is mainly determined by the transport [31]. To complement the surface measurements, there are observations regularly taken by balloon and lidar networks. In adding the vertical profiles the chemical and dynamical processes of the atmospheric chemistry can be better understood. Such networks include SHADOZ (Southern Hemisphere Additional Ozonesondes) which has operated since 1998 [32–34]. Lidar networks contribute to the atmospheric chemistry studies by providing vertically resolved data in an extended area. Using observations from 14 Japan National Institute for Environmental Studies (NIES) lidars [35] and RAMS/CFORS-4DVAR assimilation system, Yumimoto et al. investigated mineral dust transport and emission in East Asia during a spring dust event in 2007 [36].

In addition to the in-situ measurement networks, multiple satellite instruments with capability to measure the troposphere and stratosphere atmospheric chemical fields have been operating to provide real-time measurements [37,38]. For instance, Aura [39], a multi-national NASA Earth Observing System (EOS) satellite to study atmospheric chemistry following Terra (launched in 1999) and Aqua (launched in 2002), was launched in 2004. Aura carries a High Resolution Dynamics Limb Sounder (HIRDLS, which stopped operating in 2008), an Ozone Monitoring Instrument (OMI), a Tropospheric Emission Spectrometer (TES), and a Microwave Limb Sounder (MLS) [40]. The retrieval of Envisat-SCIAMACHY (Scanning Imaging Absorption Spectrometer for Atmospheric Chartography) by European Space Agency provides various atmospheric constituents [41]. Moderate resolution imaging spectroradiometer (MODIS) aboard Terra (EOS AM) and Aqua (EOS PM) satellites provides near real time aerosol optical depth (AOD) observations with good spatial resolution and coverage [42,43] and they have been used in many aerosol assimilation applications [44–47]. One of the earlist efforts in chemical data assimilation was a OI type statistical analysis scheme to assimilate the Total Ozone Mapping Spectrometer (TOMS) total ozone data and the Solar Backscatter Ultraviolet/2 (SBUV/2) partial ozone profile observations into an off-line ozone transport model by Štajner et al. [48]. With a broad horizontal coverage, satellite observations are complementary to in-situ measurements that are often located at places of interest. Nassar et al. showed the benefit of combining the two types of observations together in chemical data assimilation systems by assimilating both satellite observations of CO₂ from TES and surface flask measurements [49].

In recent years, many field experiments have been carried out with intensive measurement activities. For instance, the International Consortium for Atmospheric Research on Transport and Transformation (ICARTT) field campaign took place in the northeastern United States and the Maritime Provinces of Canada during summer 2004 [50]. Over 300 government-agency and university participants from U.S., Canada, UK, Germany, and France carried out eleven independent but highly coordinated field experiments with various objectives. Among them, the U.S. National Oceanic and Atmospheric Administration (NOAA) New England Air Quality Study - Intercontinental Transport and Chemical Transformation [51] 2004 experiment studied air quality along the Eastern Seaboard and transport of North American emissions into the North Atlantic [52]. The European International Transport of Ozone and Precursors (EU-ITOP) field program aimed at understanding the factors determining air quality over America and Europe and over remote regions of the North Atlantic [53,54]. As another component of ICARTT, NASA Intercontinental Chemical Transport Experiment - North America Phase A (INTEX-A), focused on the transport and transformation of gases and aerosols on transcontinental/intercontinental scales and their impact on air quality and climate. The continued NASA INTEX project, Phase B, coincided with MIRAGE-Mex (Megacities Impact on Regional and Global Environment-Mexico) in the spring of 2006 [55,56]. In the field experiments, coordinated measurements were made by multiple in-situ instruments on board aircrafts in flights, additional ozonesondes on ground or a research vessel, and airborne ozone lidars. Using ICARTT/INTEX-A data, Chai et al. [11] shows that the combined ozone observations provide a much better representation of the ozone distributions when assimilated simultaneously.

We now summarize some of the previous work in the field of chemical data assimilation. The field has accumulated a large body of work from contributions by many authors. Among those, many excellent papers were products of the Global and Regional Earth-System Monitoring Using Satellite and In situ Data (GEMS [57]) project funded by European Commission to develop comprehensive data analysis and modelling systems for greenhouse gases, global reactive gases, and aerosol, with a focus on Europe from March 2005 to May 2009. Since June 2009, GEMS and the Protocol Monitoring for the GMES Service Element: Atmosphere (PROMOTE [58]) merged into Monitoring Atmospheric Composition and Climate (MACC [59]) project to continue the operation and improvement of the forecasting and assimilation developed during GEMS [60]. Some excellent previous work will inevitably end up not being included in this paper's citation list, and we apologize for this.

Two approaches to data assimilation have become widely used in applications: variational methods, rooted in control theory, and Kalman filter methods, rooted in statistical estimation theory. The base concepts of the variational approach to chemical data assimilation are discussed in [1,10,27,29,61,62]. Early work in chemical data assimilation using variational techniques has been reported in [63,64]. A growing number of applications employ the 3D-Var technique [3,65–72]. The 4D-Var approach has been used to adjust gas phase chemical tracer initial conditions [10,11,61,69,73–77], to improve estimates of pollutant emissions, i.e., emission inversion, [15,78,79], and to improve aerosol fields [80–82]. Suboptimal Kalman filters have been employed successfully in chemical data assimilation for over a decade [63,83–89]. More recently, the ensemble Kalman filter [90] has been studied in the context of chemical data assimilation [91–93]. Several studies compare the relative merits and performance of different approaches [93–98].

EnKF, extended Kalman filter [99] and reduced rank square root Kalman filter [100,101] have been used in chemical data assimilation to recover ozone [99], and various ways of accurately quantifying the uncertainty in sources have been investigated.

The background (prior) probability density 𝒫^b(x) encapsulates our current knowledge of the tracer distribution. Specifically, 𝒫^b(x) describes the uncertainty with which one knows x^t at the present, before any (new) measurements are taken. The mean taken with respect to this probability density is denoted by 𝔼 b [ f ] = ∫ f ( x ) 𝒫 b ( x ) d x

The current best estimate of the true state is called the apriori, or the background state x^b ∈ ℝⁿ. (This is often taken to be the mean of the background distribution x^b = ^b [x].) A typical assumption is that the random background errors ε^b = x^b − x^t are unbiased and have a normal probability density, i.e.. (3) ɛ b = x b − x t ∈ 𝓝 ( 0 , B )

Here B = ^b [ε^b (ε^b)^T] ∈ ℝ^n×n is the background error covariance matrix. With many nonlinear models (e.g., in the presence of nonlinear chemical kinetics) the normality assumption (3) might not always be valid. Nevertheless, it is widely used because of its convenience.

The model (1) encapsulates our knowledge about physical and chemical laws that govern the evolution of the atmospheric composition. The model evolves an initial state x₀ ∈ ℝⁿ at the initial time t₀ to future state values x_i ∈ ℝⁿ at future times t_i (4) x i = ℳ t 0 → t i ( x 0 )

The size of the state space in realistic chemical transport models is very large, typically n ∈ (10⁷) variables for regional models and n ∈ (10⁸) for global models. The model is a first order Markov process, meaning that the probability distribution of the state at time t_i depends only on the probability as time t_i−1: (x_i ∣ [x₀,…, x_i−1]) = (x_i ∣ x_i−1).

Observations represent snapshots of reality available at several discrete time moments. Specifically, measurements y_i ∈ ℝ^m of the physical state are taken at times t_i, i = 1,…, N (5) y i = ℋ t ( c t ( t i ) ) − ɛ i meas , i = 1 , … , N

The observation operator ℋ^t maps the physical state space onto the observation space. The measurement (instrument) errors are denoted by ɛ i meas.

In order to relate the model state to observations we also consider the relation (6) y i = ℋ ( x i t ) − ɛ i obs , i = 1 , … , N

where the observation operator ℋ maps the model state space onto the observation space. In many practical situations ℋ is a highly nonlinear mapping (as is the case, e.g., with satellite observation operators). At present the chemical observations are sparsely distributed, and their number is small compared to the dimension of the state space, m ≪ n.

The observation error term ɛ i obs accounts for both the measurement errors ɛ i meas, as well as the representativeness errors ɛ i repres (i.e., errors in the accuracy with which the model can reproduce reality, and with which the numerical operator ℋ approximates ℋ^t) ɛ i repres = ℋ ( x i t ) − ℋ t ( c t ( t i ) ) = ℋ ( S ( c t ( t i ) ) ) − ℋ t ( c t ( t i ) )

Typically observation errors are assumed to be unbiased and normally distributed (7) ɛ i obs ∈ N ( 0 , R i ) , i = 1 , … , N

Observation errors at different times ( ɛ i obs and ɛ j obs for i ≠ j) are assumed to be independent. Often, the observation errors are also assumed to be spatially uncorrelated. In matrix form this is equivalent to assume that the observation error covariance matrix is diagonal. Moreover, observation errors and background errors are assumed independent of each other.

Based on these three sources of information data assimilation computes the analysis (posterior) probability density ^a(x). Specifically, ^a(x) describes the uncertainty with which one knows x^t after all the information available from measurements has been accounted for. The mean taken with respect to this probability density is denoted by ^a [f] = ∫ f(x) ^a(x) dx.

The best estimate x^a of the true state obtained from analysis distribution is called the aposteriori, or the analysis state. (This estimate can be the posterior mean x^a = ^a [x], but this is not necessary; in the maximum likelihood approach the refined estimate of the true state is obtained from the analysis distribution mode). The analysis estimation errors ε^a = x^a − x^t are characterized by the analysis mean error (bias) β^a = ^a [ε^a] and by the analysis error covariance matrix A = ^a [(ε^a − β^a) (ε^a − β^a)^T] ∈ ℝ^n×n. By design, the analysis errros are also normally distributed if the background and observation errors are assumed such.

The chemical data assimilation problem is formulated in a Bayesian framework. The analysis probability density is the probability density of the state conditioned by all the available observations y = [y₁, …,y_N]. Bayes Theorem allows one to express the analysis probability density as follows: (8) P a ( x ) = P ( x | y ) = P ( y | x ) ⋅ P b ( x ) P ( y )

The denominator (y) is the marginal probability density of the observations and plays the role of a scaling factor. The probability of the observations conditioned by the states (y∣x) is the probability that the observation errors in (6) assume the values ℋ (x^b) − y P ( y | x ) = P obs ( ɛ obs = ℋ ( x b ) − y )

Since the observation errors ɛ 1 obs , … , ɛ N obs at different times t₁,…, t_N are (considered to be) independent, we have that: (9) P ( y | x ) = ∏ i = 1 N P obs ( ɛ i obs ) = ∏ i = 1 N P obs ( ℋ ( x i ) − y i )

Bayes' theorem (8) completely describes the posterior error distribution. In large scale models a direct application of (8) is not possible, since it involves multidimensional probability densities defined over very large spaces (recall that n ∼ 10⁷). Approximations are needed in order to represent such densities. One approach is to approximate all probabilities involved by normal distributions, in which case closed form solutions for the posterior density are possible, see Section 2.3. Practical algorithms based on normal approximations are the suboptimal Kalman filters, discussed in Section 3.2. Another possible approximation is the Monte Carlo approach, where all the probability densities involved are represented by samples in the state space. In this case the application of Bayes' theorem (8) results in a random sample from the posterior distribution. Practical algorithms based on the Monte Carlo approach include ensemble Kalman filters (discussed in Section 3.4) and particle filters [102]. Finally, a less ambitious goal is to obtain only the first several moments of the posterior probability density based on (8).

In practice we want to use (8) to define estimators x^a of the true state x^t that are optimal in a certain sense. One way to define a best estimator is to minimize the expected values of the mean square error min ^a [‖x^a − x^t‖²]. The resulting minimum mean square error (MMSE) estimator is given by the mean of the posterior distribution, x^a = ^a [x]. This estimator is not practical for large scale systems, as it requires an integration in the high dimensional state space. Practical estimators are obtained by taking the mean of an approximation of the posterior distribution, see for example Section 3.4. A computationally feasible estimator is given by the mode of the posterior distribution, and is called the maximum aposteriori estimator (MAP), as discussed in Section 2.4. Of particular interest are unbiased estimators, which are characterized by a zero posterior error mean (i.e., zero bias, β^a = 0). A minimum variance unbiased (MVUE) estimator x^a has the smallest total variance (min trace ^a [ (x^a − ^a [x^a])(x^a − ^a [x^a])^T]) among all unbiased estimators. MVUE estimators are not guaranteed to exist, and when they do, they are difficult to compute for practical problems.

Consider a time invariant ideal case where the observation operator is linear (10) ℋ ( x ) = H ⋅ x , H ∈ ℝ m × nand both the background errors (3) and the observation errors (7) are normally distributed (11a) P b ( x ) = ( 2 π ) − n / 2 ( detB ) − 1 / 2 exp ( − 1 2 ( x − x b ) T B − 1 ( x − x b ) ) (11b) P obs ( y | x ) = ( 2 π ) − m / 2 ( detR ) − 1 / 2 exp ( − 1 2 ( Hx − y ) T R − 1 ( Hx − y ) )

After inserting (11a) and (11b) in (8) a direct calculation shows that the posterior probability density is also Gaussian, ^a(x) = (x^a, A) (11c) P a ( x ) = ( 2 π ) − n / 2 ( detA ) − 1 / 2 exp ( − 1 2 ( x − x a ) T A − 1 ( x − x a ) )

with the analysis mean x^a and covariance A given by the Kalman filter [103] formulas: (12a) K = BH T ( HB H T + R ) − 1 = ( B − 1 + H T R − 1 H ) − 1 H T R − 1 (12b) x a = x b + K ( y − H x b ) (12c) A = ( I − KH ) B

where I is the identity matrix. The matrix K ∈ ℝ^n×m is called the “Kalman gain” operator. A is the covariance matrix of analysis error. Note that in the linear Gaussian case the estimate (12b) represents both the MMSE estimator and the MAP estimator. In general, however, the MMSE and the MAP estimates are distinct.

In the maximum likelihood approach one looks for the argument that maximizes the posterior distribution, or equivalently, minimizes its negative logarithm: (13) x a = arg max x P a ( x ) = arg min x J ( x ) , J ( x ) = − ln P a ( x )

Equation (13) defines the maximum aposteriori estimator (MAP). In this context the data assimilation problem is formulated as an optimization problem. Using (8) the minimization cost function can be written as (14) J ( x ) = − ln P a ( x ) = − ln P b ( x ) − ln P ( y | x ) + const

The scaling factors of the probability densities, as well as the term – ln (y), are constants in x and do not influence the result of the minimization. Under the assumption that the background errors are normally distributed (11a) we have that (15) − ln P b ( x ) = 1 2 ( x − x b ) T B − 1 ( x − x b ) + const

Similarly, under the assumption that observation errors are independent (9) and normally distributed (11b) we have that (16) − ln P ( y | x ) = − ln P obs ( ɛ obs ) = 1 2 ( ℋ ( x ) − y ) T R − 1 ( ℋ ( x ) − y ) + const

The maximum likelihood estimator is obtained as the minimizer of the cost function (17) J ( x ) = 1 2 ( x − x b ) T B − 1 ( x − x b ) + 1 2 ( ℋ ( x ) − y ) T R − 1 ( ℋ ( x ) − y )

where the constant terms have been left out.

Note that if, in addition, the observation operator is linear (10) then the function (17) is quadratic, and the minimizer can be computed explicitly from setting the gradient to zero (18) ∇ x J ( x a ) = B − 1 ( x a − x b ) + H T R − 1 w ( H x a − y ) = 0

The result is the Kalman filter estimate for the mean (12b). Moreover, the Hessian of the cost function coincides with the inverse of the Kalman filter analysis covariance matrix (12c) (19) ∇ x , x 2 J = B − 1 + H T R − 1 H = A − 1

Typical data assimilation applications are concerned with time dependent systems, e.g., the evolution of the chemical composition of the atmosphere. In such applications the interest is not focused on one analysis at one time, but on a series of analyses for times t₁,…, t_N when observations are available.

There are two approaches to obtain the analysis probability densities ^a(x_i). In the smoothing (simultaneous) data assimilation approach all observations at all times t₁, …, t_N are considered at once. Corrections of the concentration state vectors at all times are determined in the same analysis step. The result is a sequence of posterior probabilities of states, (x_i ∣ [y₁,…, y_N]), i = 1,…, N, each conditioned by all available observations. The application of (12) in the simultaneous setting leads to the Kalman smoother approach, while the maximum likelihood estimator obtained from (17) leads to the four dimensional variational (4D-Var) assimilation method.

In the filtering (sequential) data assimilation approach [63] the observations (6) are considered successively at times t₁,…, t_N. Corrections of the concentration state vector are computed and applied at each t_i as soon as observations become available. The result is a sequence of posterior probabilities of states (x_i ∣ [y₁,…, y_i]), i = 1,…, N, each conditioned by all past and current observations (but not by the future observations). The application of (12) in the sequential setting leads to the Kalman filter approach, while the maximum likelihood estimator obtained from (17) leads to the three dimensional variational (3D-Var) assimilation method.

We now discuss the Kalman filter approach in the ideal case where the observation operator is linear (10), and, in addition, the model dynamics (4) is also linear, ℳ_ti−1→ti (x) = M_ti−1→ti · x.

The background state (i.e., the best state estimate) at time t_i is given by the model forecast, starting from the analysis (i.e., the best estimate at the previous time t_i−1): (20a) x i b ≡ x i f = M t i − 1 → t i ⋅ x i − 1 a

Note that a model forecast starting from the true state at t_i−1 does not reproduce the true state at t_i since the model only approximates the dynamics of the physical system. Specifically, we have that x i t = M t i − 1 → t i ⋅ x i − 1 t − η i

where η_i is the model error. Typically the model error is assumed to be a normal random variable η_i ∈ (0, Q_i), where the zero mean represents the unbiased model assumption.

The background error at t_i has two components: the analysis error at t_i−1, transported through the model equations, and the model error ɛ i b = M t i − 1 → t i ⋅ ɛ i − 1 a − η i

The model error η_i and the solution error ɛ i − 1 a are typically assumed to be independent. Consequently, the background error covariance at t_i (the forecast error covariance matrix P i f) is obtained by transporting the analysis covariance at t_i−1 to t_i through the linearized dynamics, and adding the model error covariance (20b) B i ≡ P i f = M t i − 1 → t i P i − 1 a M t i → t i − 1 T + Q i

For every observation time t_i, the filter starts with the model forecast state ( x i f ) and provides an analysis state ( x i a ) that reduces the discrepancy between the model forecast and the observations y_i. The analysis state vector is obtained from (12b) (20c) x i a = x i f + K i ( y i − H x i f )

with the Kalman gain matrix given by (12a) (20d) K i = P i f H i T ( H i P i f H i T + R i ) − 1

where R_i is the observation error covariance matrix at time t_i. At each observation time, along with the analysis state, the analysis error covariance matrix P i a is also calculated via (12c) (20e) A i ≡ P i a = ( I – K i H i ) P i f

The extended Kalman filter (EKF) generalizes the original Equations (20) to nonlinear systems (4) and nonlinear observations (6) by linearization about the forecast state. Consider the linearized model and observation operators M t i − 1 → t i = ℳ ′ ( x f ) , H i = ℋ ′ ( x i f )

The EKF approach modifies (20) as follows. The forecast state equation uses the nonlinear model ℳ, while the forecast covariance equation uses the linearized dynamics M. Similarly, the analysis equation uses the nonlinear observation operator ℋ, but both the gain equation and the analysis covariance equation use the linearized operator H. The resulting EKF equations are: (21a) x i f = ℳ t i − 1 → t i ( x i − 1 a ) (21b) P i f = M t i − 1 → t i P i − 1 a M t i → t i − 1 T + Q i (21c) x i a = x i f + K i ( y i − ℋ ( x i f ) (21d) K i = P i f H T ( H i P i f H i T + R i ) − 1 (21e) P i a = ( I − K i H i ) P i f

The extended Kalman filter is not practical for large systems because of the (n²) memory size needed to store full covariance matrices, and the prohibitive computational costs associated with inverting large matrices in (21c)–(21d), and with propagating the covariance matrices in time via (21e). Suboptimal Kalman filters designate a wide class of assimilation algorithms which are based on EKF formulas (21), but approximate the covariance matrices as well as the covariance propagation Equation (21e) in order to obtain computationally feasible algorithms. The approximations lead to suboptimal solutions, even in the case of linear Gaussian systems. There are multiple ways in which this analysis covariance matrix is made available to the next observation window, and different approximation strategies lead to different suboptimal filters.

A low memory approximation of a covariance matrix B can store only the diagonal terms (the variances B ( ℓ ) , ( ℓ ) = σ ( ℓ ) 2of the error in state variables x_(ℓ) for ℓ = 1,…,n), and use a model to represent the error correlation structure. For example, the correlation between the errors in x_(ℓ) and x_(k) can be modeled as decreasing with the distance between the gridpoints of ℓ and k. When a Gaussian de-correlation formula is used, with a correlation distance of L (space units), the {(ℓ), (k)} entry of the approximate covariance matrix is (22) B ( ℓ ) , ( k ) = σ ( ℓ ) σ ( k ) exp ( − distance { gridpoint ( ℓ ) , gridpoint ( k ) 2 } / L 2 )

Polynomial models of spatial correlations [104] are also widely used.

The simplest approach to avoid the cost of (21e) is to keep the forecast covariance equal to the background covariance for the entire assimilation period, P i f = B 0 for i = 1,…, N [89]. A more complex approach is to build diagonal approximations to P i f by transporting the standard deviations σ_(ℓ) as passive tracers from t_i−1 to t_i [83]. The propagated variances can be used together with a model of the correlation structure to reconstruct P i f .

The reduced rank Kalman filter approach [105] is based on the observation that the symmetric positive definite matrix B can be completely described in terms of its eigenvalues λ_i and its orthonormal eigenvectors υ_i. A rank r approximation of the matrix can be constructed from the dominant eigenvalue-eigenvector pairs as follows: (23) B = ∑ i = 1 n λ i υ i υ i T ≈ ∑ i = 1 r λ i υ i υ i T = V V T , V = [ λ 1 υ 1 , … , λ r υ r ] ∈ ℜ n × r

Using a rank r approximation for the analysis covariance matrix at t_i−1 P i − 1 a = V i − 1 a ( V i − 1 a ) T

leads to the following forecast covariance (21b) (24) P i f = ( M t i − 1 → t i V i − 1 a ) ( M t i − 1 → t i V i − 1 a ) T + Q i ≈ V i f ( V i f ) T

The terms M t i − 1 → t i V i − 1 a are evaluated by propagating the r vectors through the linearized model dynamics. A rank r approximation of the forecast covariance is obtained via (23). Using this approximation, the Kalman gain matrix (21d) becomes W i f = H ⋅ V i f , K i = V i f ( W i f ) T ( W i f ⋅ ( W i f ) T + R i ) − 1

and the analysis covariance (21e) reads P i a = ( V i f − K i W i f ) ( V i f ) T = V i a ( V i a ) T , V i a = V i f ( I − ( W i f ) T ( W i f ⋅ ( W i f ) T + R i ) − 1 W i f ) 1 / 2

It is immediate that the analysis increments x i a − x i f in (21c) are restricted to the r-dimensional subspace spanned by the columns of V i f (the so-called “rank problem”). In particular, the r degrees of freedom available to the analysis may be insufficient to produce a good fit to observations. One way to overcome this problem is to perform local analyses, as discussed in Section 3.3. Another way is through covariance localization [106], where an assumed correlation structure is overimposed to the low rank approximation. For example, using (22), the {(ℓ), (k)} entry of the forecast covariance matrix (24) becomes ( P i f ) ( ℓ ) , ( k ) = ( V i f ) ( ℓ ) ( V i f ) ( k ) exp ( − distance { gridpoint ( ℓ ) , gridpoint ( k ) 2 } / L 2 )

Localization improves the accuracy of the approximation by removing spurious long-distance correlations, and results in a full rank forecast covariance matrix.

Optimal interpolation [107] simplifies the extended Kalman filter formulation (21) by assuming that, during the analysis process, each model variable is influenced by only a subset of observations. Consider, without loss of generality, that only μ ≪ m observations have an impact on the model variable x_(ℓ). For example, these can be observations located sufficiently close to the the grid point where x_(ℓ) is defined. Let I_l ∈ ℝ^μ×m be the operator that selects the important μ components out of the m-dimensional vector of observations, y_ℓ = I_ℓy ∈ ℝ^μ. Then H_ℓ = I_ℓH ∈ ℝ^μ×n is the observation operator associated with the locally important observations, and R ℓ = I ℓ R I ℓ T ∈ ℝ μ × μis the corresponding observation error covariance matrix.

Let ⅇ_ℓ ∈ ℝⁿ be the ℓ-th column of the identity matrix. From (12a) and (12b) the analysis of variable x_(ℓ) is given by x ( ℓ ) a = x ( ℓ ) b + e ( ℓ ) T B H T ( HB H T + R ) − 1 ( y − H x b ) ≈ x ( ℓ ) b + e ( ℓ ) T B H ℓ T ( H ℓ B H ℓ T + R ℓ ) − 1 ( y ℓ − H ℓ x b )

The cost of forming and solving the matrix H ℓ B H ℓ T + R ℓ is (μ³), instead of (m³) for the complete matrix H B H^T + R. Only the increments y_l − H_l x^b of the important observations are used. The weight ⅇ ℓ T B H ℓ T is a row vector obtained by applying the relevant part of the observation operator to the ℓ-th column of the background covariance H_ℓ (Bⅇ_ℓ), and transposing the result. The analyses for different components ℓ can be computed in parallel.

When approximations of B are employed this is easy to compute. For example, using the approximation (22), the weight vector reads ( H ℓ B ⅇ ℓ ) ( j ) = σ ( ℓ ) ∑ k ( H ℓ ) ( j ) , ( k ) σ ( k ) exp ( − distance { gridpoint ( ℓ ) , gridpoint ( k ) 2 } / L 2 )

The ensemble Kalman filter (EnKF) [90,105,108] uses a Monte-Carlo approach to propagate covariances. An ensemble of E states (labeled e = 1,…,E) is used to sample the probability distribution of the error. The analysis probability density at time t_i−1 is represented by the sample points x i − 1 a [ e ] , e = 1,…, E, in the state space. Each member of the ensemble is propagated to t_i using the model (4) to obtain the “forecast” ensemble (25) x i f [ e ] = ℳ t i − 1 → t i x i − 1 a [ e ] + η i [ e ] , e = 1 , … , E

where the random variable η_i represents the model error, and is typically assumed to be Gaussian and unbiased, η_i ∈ (0, Q_i). The forecast error covariance P i f is estimated from the statistical samples (26) 〈 x i f 〉 = 1 E ∑ e = 1 E x i f [ e ] , P i f ≈ 1 E − 1 ∑ e = 1 E ( x i f [ e ] − 〈 x i f 〉 ) ( x i f [ e ] − 〈 x i f 〉 ) Tand the Kalman gain matrix is computed computed using Equation (20d).

Each member forecast ensemble is processed separately using (20c) to obtain the “analysis” ensemble (27) x i a [ e ] = x i f [ e ] + K i ( y i [ e ] − ℋ i ( x i f [ e ] ) ) , e = 1 , … , E

To obtain the correct posterior statistics, a different set of perturbed observations is used for each ensemble member, y_i [e] = y_i + θ_i [e], with perturbations drawn from the real observation error statistics θ_i [e] ∈ (0, R_i) [90,108]. The analysis covariance is estimated from the statistical samples x i a [ e ] , e = 1,…, E, using the formula (26).

The ensemble Kalman filter raises several issues. First the rank of the estimated covariance matrix (26) is typically several orders of magnitude smaller than the dimension of the matrix, and additional approximations are needed to fix the rank-deficiency problem [106]. Next, the random errors in the statistically estimated covariance decrease slowly, with only the square-root of the ensemble size E. Furthermore, the subspace spanned by random vectors for expressing the forecast error is not optimal.

In spite of the problems, ensemble Kalman filter has many attractive features. The effects of non-linear dynamics are captured by the use of the forward model (25). This model is used as is, and there is no need for the tangent linear or adjoint models. EnKF allows one to easily account for model errors, and the calculations are almost ideally parallelizable.

Numerous improvements of the original EnKF [90,109] have been proposed in the literature to alleviate inbreeding [110], to increase computational efficiency [105,106,111], to relax the normal error distribution assumptions [112,113], and to allows observations to occur at times different than assimilation times [114,115]. The square-root implementations of EnKF [116,117] update the ensemble by applying linear transformations to the prior ensemble, and avoid adding perturbations to observations (e.g., the ensemble adjustment [118], the variance reduced [119], and the ensemble transform [120] Kalman filters).

The use of EnKF [90] in chemical data assimilation has been studied in [91–93,121–124]. Three techniques have proved essential for the practical performance of the EnKF. Due to the small ensemble size many entries in the forecast covariance matrix are poorly approximated; such sampling errors are referred to as spurious correlations. Covariance localization scales each entry P ( k , ℓ ) f by a function that decreases with the physical distance between the gridpoints where x_(ℓ) and x_(k) are defined in Equation (22). Covariance localization alleviates the effect of spurious correlations, and improves the rank of P^f. It has been observed in practice that, after a number of assimilation cycles, all ensemble members tend to be close to one another in the state space. In this case the estimated forecast covariance (26) is small, and the filter trusts the model too much and starts rejecting the observations. This situation is referred to as filter divergence. Covariance inflation scales P^f by a factor α > 1 at each cycle. The scaling has the net effect of accounting for larger model errors, and helps prevent filter divergence. It has also been observed in practice that the inflation goes uncorrected in data-sparse regions, and the ensemble spread continues to grow to unreasonable values. To alleviate this, the third important technique is adaptive inflation (inflation is localized to data-rich areas) [93].

Variational methods solve the data assimilation problem in an optimal control framework [125–127]. Specifically, one finds the control variable values (e.g., initial conditions) which minimize the discrepancy between model forecast and observations; the minimization is subject to the governing equations, which are imposed as strong constraints in most practical applications. Similar as OI, 3D-Var does not consider evolution of the model in the assimilation. Thus, it is possible to have a dual formulation of OI/3D-Var [128]. In OI applications, analysis is often solved in blocks due to the computation difficulties of the large size matrix inversion problems. Complicated observation operators are often obstacles to use OI in practice. In this discussion, for simplicity of presentation, we focus on discrete models where the initial conditions are the control variables.

In the 3D-Var data assimilation the observations (6) are considered successively at times t₁,…, t_N. The background state (i.e., the best state estimate at time t_i) is given by the model forecast, starting from the previous analysis (i.e., best estimate at time t_i−1) x i b = ℳ t i − 1 → t i ( x i − 1 a )

The discrepancy between the model state x_i and observations at time t_i, together with the departure of the state from the model forecast x i b, are measured by the 3D-Var cost function (17): (28) J ( x i ) = 1 2 ( x i − x i b ) T B i − 1 ( x i − x i b ) + 1 2 ( ℋ ( x i ) − x i obs ) T R i − 1 ( ℋ ( x i ) − x i obs )

While in principle a different background covariance matrix should be used at each time, in practice the same matrix is re-used throughout the assimilation window, B_i = B, i = 1,…, N. The 3D-Var analysis is the MAP estimator, and is computed as the state which minimizes (28) (29) x i a = argmin J ( x i )

Typically a gradient-based numerical optimization procedure is employed to solve (29). The gradient ▽ of the cost function (28) is (30) ∇ J ( x i ) = B i − 1 ( x i − x i b ) + H i T R i − 1 ( ℋ ( x i ) − x i obs )

Note that the gradient requires to computation of the adjoint H i T of the linearized observation operator H_i = ℋ′(x_i) about the current state.

Preconditioning is often used to improve convergence of the numerical optimization problem (29). A change of variables is performed by shifting the state and scaling it with the square root of covariance: (31) x ^ i = B i 1 / 2 ( x i − x i b )and carrying out the optimization with the new variables x̂_i.

In strongly-constrained 4D-Var data assimilation all observations (6) at all times t₁,…, t_N are considered simultaneously over the assimilation window. The control parameters are the initial conditions x₀; they uniquely determine the state of the system at all future times via the model Equation (4). The background state is the prior value of the initial conditions x 0 b.

Given the background value of the initial state x 0 b, the covariance of the initial background errors B₀, the observations y_i at t_i and the corresponding observation error covariances R_i, i = 1,…, N, the 4D-Var problem looks for the MAP estimate x 0 a of the true initial conditions by solving the optimization problem (13). Combining (14), (15), and (16) leads to the 4D-var cost function: (32) J ( x 0 ) = 1 2 ( x 0 − x 0 b ) T B 0 − 1 ( x 0 − x 0 b ) + 1 2 ∑ i = 1 N ( ℋ ( x i ) − y i ) T R i − 1 ( ℋ ( x i ) − y i )

Note that the departure of the initial conditions from the background is weighted by the inverse background error covariance matrix, while the differences between the model predictions H(x_i) and observations y_i are weighted by the inverse observation error covariance matrices. The 4D-Var analysis is computed as the initial condition which minimizes (32) subject to the model equation constraints (4) (33) x 0 a = argmin J ( x 0 ) subject to : x i = ℳ t 0 → t i ( x 0 ) , i = 1 , … , N

The model (4) propagates the optimal initial condition (32) forward in time to provide the analysis at future times, x i a = ℳ t 0 → t i x 0 a.

The large scale optimization problem (33) is solved numerically using a gradient-based technique. The gradient of (32) reads (34) ∇ J ( x 0 ) = B 0 − 1 ( x 0 − x 0 b ) + ∑ i = 1 N ( ∂ x i ∂ x 0 ) T H i T R i − 1 ( ℋ ( x i ) − y i )

The 4D-Var gradient requires not only the linearized observation operator H_i = ℋ′(x_i), but also the transposed derivatives of future states with respect to the initial conditions ( ∂ x i / ∂ x 0 ) T = M t 0 → t i T. It can be demonstrated that the solution of the adjoint equations at the initial time provides the gradient of the cost function with respect to the initial condition in a computationally efficient way The 4D-Var gradient can be obtained effectively by forcing the adjoint model with observation increments, and running it backwards in time. The construction of an adjoint model is a nontrivial task.

In the incremental formulation of 4D-Var [129,130], the estimation problem is linearized around the background trajectory. By expressing the state as x i = x i b + δ x i, i = 1,…, N we have (35) J ′ ( x 0 ) δ x 0 = 1 2 δ x 0 T B 0 − 1 δ x 0 + 1 2 ∑ i = 0 N ( H i δ x i + d i b ) T R i − 1 ( H i δ x i + d i b ) d i b = ℋ ( x i b ) − y i

where δx_i = M_t0→ti · δx₀, and H_i is the linearized observation operator. The incremental 4D-Var problem (35) uses linearized operators and leads to a quadratic cost function ′ whose minimizer is δ x 0 a. The incremental 4D-Var estimate is x 0 a = x 0 b + δ x 0 a. A new linearization can be performed about this estimate and the incremental problem (35) can be solved again to improve the resulting analysis. The iterated incremental 4D-Var is nothing but a sequential quadratic programming approach [131] to solve the constrained optimization problem (33).

Weakly constrained 4D-Var avoids the assumption of a perfect model, implicit in the formulation (33), at the expense of solving a larger optimization problem. The state x_i at t_i is allowed to differ from the model prediction; the difference is the model error, considered to be a random variable. With the assumption that the model is not biased, and the model error is normally distributed, we have that x i = ℳ t i − 1 → t i ( x i − 1 ) + η i , η i ∈ N ( 0 , Q i ) , i = 1 , ⋯ , N

The weakly constrained 4D-Var estimate of x = [x₀, x₁,…, x_N] is the unconstrained minimizer of the following cost function: (36) J weak ( x ) = 1 2 ( x 0 − x 0 b ) T B 0 − 1 ( x 0 − x 0 b ) + 1 2 ∑ i = 1 N ( ℋ ( x i ) − y i ) T R i − 1 ( ℋ ( x i ) − y i ) + 1 2 ∑ i = 1 N ( x i − ℳ t i − 1 → t i ( x i − 1 ) ) T Q i − 1 ( x i − ℳ t i − 1 → t i ( x i − 1 ) )

The optimization variables are the model states at all times x ∈ ℝ^n(N+1), and therefore the resulting optimization problem is of larger dimension than that for strongly-constrained 4D-Var.

Insightful comparisons of the relative merits of EnKF and 4D-Var [132–134], and of EnKF and 3D-Var [95] have been reported in the context of numerical weather prediction. Similar arguments hold in the context of CTMs. A comprehensive comparison of the performance of several methods applied to the assimilation of ozone satellite measurements in a global chemistry and transport framework has recently been carried out [17].

EnKF is simple to implement, while 4D-Var requires the construction of adjoint models, a non-trivial task in the presence of stiff chemistry [61]. EnKF allows for a simple integration of model errors, whereas strong-constrained 4D-Var assumes a perfect model. The ensemble propagates the forecast covariance and an estimate of the background covariance is readily available at the beginning of the next assimilation cycle.

On the other hand the 4D-Var optimal solution is consistent with model dynamics throughout the assimilation window. 4D-Var naturally incorporates asynchronous observations while for EnKF asynchronous observations require a more involved framework [114]. A consistent derivation of the initial ensemble in EnKF is difficult. Moreover, in the presence of stiff chemistry, each application of the filter throws the model state off balance; consequently, after each assimilation cycle a new stiff transient will be introduced, and this may considerably impact the computational time needed to advance the model state for each ensemble member.

Very recent wok has focused on the development of hybrid data assimilation methods, that attempt to combine the advantages of both variational and ensemble techniques [135,136].

Running chemical transport models requires several essential components. Firstly, model-ready emission files have to be processed using emission inventories. Secondly, meteorological states are needed for commonly-used off-line CTMs. Lastly, the realistic initial concentrations for various constituents are required. A spin-up period is often chosen to generate such initial fields when no previous run results are available. Chemical data assimilation adds two more components to these, i.e., the observational inputs and model background error statistics.

Obtaining and utilizing atmospheric chemical observations remains a challenge. Currently atmospheric chemical observations come from many different sources. They vary greatly in their dissemination methods, availability, data reliability due to different validation and quality control methods, instrument descriptions and measurement uncertainties, temporal and spatial resolutions, and data formats. “Integrated Global Atmospheric Chemistry Observations” (IGACO) is an ongoing effort as a component of the Integrated Global Observing Strategy (IGOS) partnership [137]. To manage and utilize the observational data from various sources, preprocessing is often required. In the preprocessing, the observations with higher spatial and temporal resolutions can be re-gridded into the model grid and model representative errors can be approximated in such steps [11,15].

The most important challenge posed by 4D-Var data assimilation is the need to construct and maintain an adjoint of the chemical transport model. The construction of adjoint models is a labor intensive and error prone task. Moreover, the adjoint is specific to the chemical transport model version at hand; any new release of an improved version of the code requires changes in the adjoint model to reflect the changes in the forward model. The construction of the adjoint model is a continuous process that follows closely the development of the forward chemical transport model.

The adjoint of a chemical transport model consists of adjoints of all the individual science processes [61,138,139]. Two routes can be taken toward building science process adjoints. In the continuous adjoint approach the mathematical equations governing the science model are differentiated analytically, in an appropriate framework, to obtain a new set of “adjoint” mathematical equations. The latter system is discretized with the numerical methods of choice. In the discrete adjoint approach one starts with the numerical implementation of the science process, as available in the CTM, and differentiates it in the discrete setting. The resulting computational process yields the sensitivities of the numerical solution. Discrete adjoints can be obtained with the help of automatic differentiation [140,141].

The two approaches lead to different results, since taking the adjoint and discretization operations do not commute. Considerable work has been done to understand the theoretical properties of different types of adjoint models, and the implications they have on sensitivity analysis and chemical data assimilation [142–149]. A good choice is to use continuous adjoints for advection, and discrete adjoints for other processes like chemistry and particles [16]. Recent work has proposed the use of simplified adjoint models for 4D-Var chemical data assimilation [150].

Specialized tools have been developed to assist the construction of chemical transport adjoint models. The chemical kinetic preprocessor KPP produces efficient code for the simulation of stiff chemistry, together with efficient tangent linear and discrete adjoint chemical kinetic models [151–153]. Sustained effort from several research groups in the past few years has lead to the construction of complete adjoints for the widely used chemical transport models STEM [1,61], CMAQ [27], and GEOS-Chem [62,154].

The quality of the assimilation depends on the accuracy with which the background and observation error covariances are known; misspecification of these covariances directly impacts the accuracy of the analysis [155]. Models of observation errors include information about the measuring instrument noise and bias (measurement error), and about the resolution with which the model reproduces the pointwise variability of the physical system and the quality of the observation operator (representativeness error).

Background error covariances determine the relative weighting between observations and a priori data, and dictate how the information is spread in space and among variables. Background error covariances are based on models of the error at the current time (or at initial time in 4D-Var). In case of cyclic data assimilation the analysis error covariance from the previous cycle, transported to the current time, may be used as the new background error covariance. Background error covariance matrices need to:

capture the spatial error correlations created by the flow (transport and diffusion),

Reasonable approximations and representations of the background error are crucial to data assimilation applications. Chai [11] has estimated the CTM error statistics through both the NMC (National Meteorological Center) and the Hollingsworth-Lönnberg methods. The statistics were successfully implemented through a truncated singular vector decomposition regularization method in 4D-Var data assimilation applications with the STEM model.

An autoregressive (AR) model approach to represent background error covariance matrices has been proposed in [156]. The background error field is assumed to have zero mean 〈ε^b〉 = 0, and background covariance B. The background state error field is modeled as a multilateral autoregressive (AR) process [157] of the form (37) δ x i , j , k b = α i ± 1 , j , k δ x i , j , k b + β i , j ± 1 , k δ x i , j ± 1 , k b + γ i , j , k ± 1 δ x i , j , k ± 1 b + σ i , j , k ξ i , j , k

Here (i, j, k) are gridpoint indices on a three dimensional structured grid. The model (37) captures the correlations among neighboring grid points, with α, β, γ representing the correlation coefficients in the x, y and z directions respectively. The last term represents the additional uncertainty at each grid point, with ξ ∈ (0,1) normal random variables and σ local error variances. The AR model coefficients α, β, γ depend on the wind field vector at each point and are obtained from a monotonic discretization of the linearized dynamics on the structured grid. Relation (37), with proper coefficients, is nothing but a finite difference approximation of the advection-diffusion equation. This approach accurately captures the flow dependent correlations, does not need any prior assumptions regarding correlation lengths, can be extended to include chemical correlations, is computationally inexpensive, and results in well conditioned covariance matrices.

A simplified approach proposed in [158] constructs multidimensional correlation matrices as tensor products of one-dimensional correlations. This method has resulted in improved chemical data assimilation results with GEOS-Chem.

In the context of 4D-Var chemical data assimilation the hybrid approach discussed in [159] estimates the analysis covariance at the end of one assimilation window (i.e., the background covariance at the beginning of the next window). An ensemble drawn from the background distribution is run side by side with the optimization process, the subspace of errors corrected by 4D-Var is identified, and this information is used to transform the background ensemble into one that samples the analysis distribution.

At the end of any data assimilation calculation one would like to estimate the quality of the analysis, i.e., the magnitude of the posterior estimate error, and its impact on given aspects of the subsequent forecast. The most robust way is to use an independent data set (not used directly in assimilation, and not correlated with the assimilated observations). The discrepancy between the model results and the independent data set, before and after data assimilation, gives a good indication of the error reduction through assimilation.

In operational data assimilation the goal is to improve forecasts. The model is initialized with the analysis that incorporates information from all past observations; the model is run, and the forecast is compared against the new observations that become available in the subsequent time window. Well established metrics for model-observation discrepancies in forecast mode are the forecast skill scores [107]. To estimate the quality of the analysis in hindcast (reanalysis) mode one can withhold part of the data from the assimilation system, and use it to assess the accuracy of the result.

The data assimilation system itself has the ability to provide estimates of the posterior error magnitude. If an ensemble Kalman filter is used, estimates of the analysis covariance matrices P i a are readily available at each assimilation time t_i. For variational methods additional calculations are necessary. The second order adjoint (SOA) of the chemical transport model [160,161] computes matrix vector products between the Hessian of the 3D/4D-Var cost function ∇ x 0 , x 0 2 J and user-supplied vectors. The SOA model provides information about the aposteriori error via the observation that the Hessian inverse approximates the posterior error covariance [162] A 0 ≈ ( ∇ x 0 , x 0 2 J ( x 0 a ) ) − 1

In [160] the smallest Hessian eigenvalues, and the associated eigenvectors, were computed using a Lanczos approach for an ozone data assimilation problem. (The Lanczos approach uses only matrix-vector products, provided by the SOA). The inverses of the smallest eigenvalues, and their eigenvectors, approximate the principal components of the 4D-Var analysis error.

As described in Section 4.3, model background error statistics are crucial in data assimilation applications. It is important to gain knowledge of model uncertainties for a CTM with its specific setups, including the gas phase chemistry mechanism and aerosol module, model resolution, emission inventories, etc. In the following vertical ozone error statistics estimation and ozone OI data assimilation test runs, the CMAQ model is from the released version 4.6 with the Carbon Bond IV (CBIV) gas-phase chemical mechanism and aerosol module version 4 (AERO-4) [163,164]. In the aerosol optical depth assimilation test cases presented in Section 5.3, an updated Carbon Bond version (CB05) is used with the same AERO-4 aerosol module [165]. The 2001 National Emission Inventory (NEI) with recent updates is used.

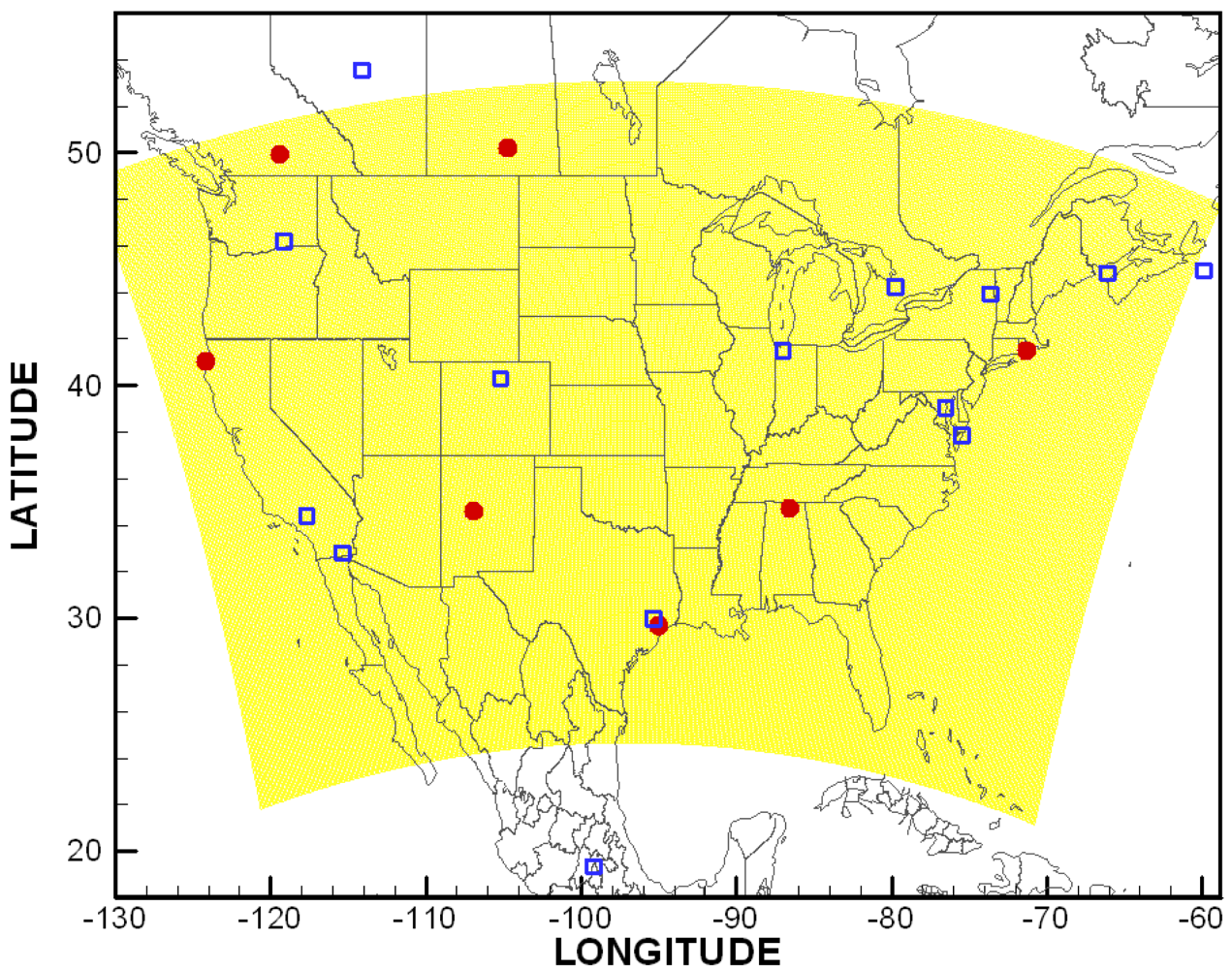
A computational grid with a 12-km resolution covering the contiguous United States (CONUS, shown in Figure 1) used in the United States National Air Quality Forecast Capability (NAQFC) is adopted here [166]. A sub-domain covering the Mid-Atlantic region (see [29] for detail) is used in ozone data assimilation tests and the horizontal error statistics estimation. The aerosol optical depth (AOD) assimilation tests in Section 5.3 and vertical error statistics estimation using the ozonesondes are carried out over the CONUS domain. The grid has a 22 sigma pressure hybrid vertical layers spanning from surface to 100 hPa.

Repeating the steps described in [11], the CMAQ error statistics were estimated using the Hollingsworth-Lönnberg method. AIRNow hourly ozone observations in the sub-domain were used to calculate the horizontal error statistics.

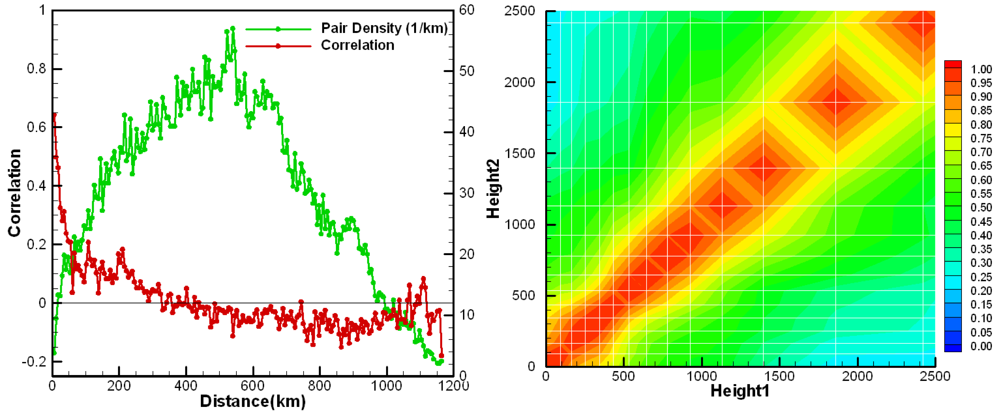
Model error correlation coefficients are shown in Figure 2 (left) as a function of horizontal distance between pairs of two surface stations. Pair density is also shown to indicate the number of station pairs used in the calculation. The CMAQ background model error for ozone is about 14 ppbv and its horizontal correlation length is around 50 km. Ozonesonde profiles from the measurements sites shown in Figure 1 were used to calculate the vertical model error statistics shown in Figure 2 (right) as a correlation coefficient contour plot.

Two CMAQ data assimilation systems are built with 4D-Var and OI approaches separately. The data assimilation time window is set to start from 1200Z on August 5, 2007 until 1200Z on August 6, 2007. In this 24-h period, the AIRNow hourly-averaged observations are assimilated and the observations are assumed to be un-correlated with each other and have a uniform root-mean-square error set as 3.3 ppbv. To check the effect of the data assimilation tests, an additional “forecast” day, starting from 1200Z on August 6, 2007 until 1200Z on August 7, 2007 is continuously run and will be evaluated against the AIRNow observations that are not assimilated in any of the assimilation tests.

In the 4D-Var data assimilation, the initial ozone concentrations are chosen as the only control parameters to be adjusted. Currently, the ozone background error covariance matrix B is assumed to be diagonal, with the root-mean-square errors set as 14.3 ppbv at every grid point. A quasi-Newton limited memory L-BFGS [167,168] is used in the cost functional minimization. The maximum number of iterations is set to be 15.

For the OI data assimilation runs, the assimilation happens every hour by combining the model results with the observations. To illustrate the effect of the background error covariance, we designed a case that eliminates the spatial correlation usage, both horizontally and vertically. It is listed in Table 1 as Case 3. In the other OI case, i.e., Case 4 in Table 1, the horizontal background error covariance is approximated as (38) B = H ⊗ V ⊗ C

where H and V are matrices that represent the error correlation in horizontal and vertical directions respectively. C is the error covariance matrix at a single grid point that represents the error variances. ⊗ denotes the Kronecker product [169]. The horizontal correlation between two grid points are calculated using a simple function e − Δ l h, where Δ is the horizontal distance between the two grid pointsand l_h is set as 48 km. The background error variances are 14.3² ppbv². Instead of using a constant vertical correlation structure obtained in Section 5.1, we use the boundary layer depth information available from the meteorological inputs. In Case 4, the vertical correlation coefficients are set as 1.0 for any two model grid layers inside the boundary layers. Otherwise, it is assumed there is no correlation for the background error.

Figure 3 shows the comparisons between the model predictions and observations of ozone during the assimilation and forecast periods for the base case and the OI case with spatial correlation accounted, i.e., Cases 1 and 4 in Table 1 respectively. After assimilation, the model has a much better agreement with AIRNow ozone measurements. The correlation coefficient improved from 0.59 to 0.81 during the daytime, 1300-2400Z on August 5, 2007. For the next day “forecast” run, the improvement of model ozone predictions is also apparent, with the daytime correlation coefficient between model and observations changed from 0.56 to 0.68.

Table 1 lists the comparisons between the different assimilation cases and the base case run. All three assimilation cases prove to be able to generate better results not only in the assimilation day, but also in the next day “forecast”. Without fully accounting for the background error covariance, the 4D-Var case still generates the best results during the first day in terms of the model biases and root-mean-square errors (RMSEs) against the AIRNow observations. By utilizing the error statistics obtained from Section 5.1, Case 4 with the simple OI method provides the best “forecast” for the second day, where the model bias and RMSE are reduced from 8.7 ppbv to 3.1 ppbv and from 16.3 ppbv to 12.8 ppbv respectively. Without using the model background error spatial correlations, Case 3 is only slightly better than the base case for the “forecast” day. From Table 1, we can see that the 4D-Var case has comparable results as Case 3, which implements the simple OI method. As indicated by the comparison between Case 3 and Case 4, replacing the diagonal background error covariance used in Case 2 with one accounting for the spatial correlation is expected to improve next day forecast for the 4D-Var case. It cannot be generalized to conclude the 4D-Var system has the same performance as OI approach. It has to be noted that the 4D-Var system is based upon CMAQ version 4.5 and the other cases implement CMAQ version 4.6.

Compared to ozone predictions, CMAQ PM2.5 predictions are much worse for the NAQFC experimental runs [170]. MODIS AOD observations can be used to constrain the model input parameters such as emissions or initial concentrations. As a test case here, we assimilate the MODIS AOD using OI approach.

In the test, the MODIS AOD fine mode products are used. The model counterpart can be reconstructed by integrating the hourly extinction coefficients over the whole vertical columns. The extinction coefficients calculated from two visibility methods, Mie theory approximation and mass reconstruction method [171], are quite similar and we chose to use the results from the mass reconstruction method. Both Terra and Aqua fine mode AOD data are used during the assimilation time period (August 14–20, 2009). Before the data assimilation tests, the AOD background error statistics is first estimated using Hollingsworth-Lönnberg approach. As an integrated quantity, only horizontal correlation is needed in constructing the error statistics. The horizontal correlation between two grid points are modeled as a function e − Δ l h, where l_h is set as 84 km. The AOD background error is assumed to be 0.6× AOD_MODIS. In the OI assimilation, the analysis process takes place once a day, at 1700Z, which is close to the midpoint of the Terra and Aqua observation time. The adjust factor of AOD at each grid point is then uniformly applied to mass concentrations of all the aerosol species.

Figure 4 shows the AOD distributions from MODIS and CMAQ simulation with and without data assimilation. The differences after assimilation are also shown. Note that the MODIS AOD data are quite sparse, but the OI assimilation spreads the information using the obtained horizontal correlations between AOD background errors. The CMAQ PM2.5 predictions before and after AOD assimilations are evaluated using the AIRNow PM2.5 observations for each day. Table 2 shows the correlations between the MODIS observed and CMAQ predicted AOD before and after OI in the upper Midwest and Northeast of the U.S. (see [172] for region definition), where most of data reside. It is seen that the R² improve over four out of six days in both regions. It is encouraging as the correlation between the column quantity of AOD and the surface PM2.5 is not linear. A better reconstructed AOD cannot guarantee better predictions of surface aerosol. The current simplification of placing the observations at a single time each day and adjusting all the aerosol species using a single factor will be modified in the future. In addition, switching OI approach to 3D-Var or 4D-Var method is expected to generate better assimilation results.