An Analytical Simple Formula for the Ground Level Concentration from a Point Source
Abstract
: The Advection-Diffusion Equation is solved for a constant pollutant emission from a point-like source placed inside an unstable Atmospheric Boundary Layer. The solution is obtained adopting the novel analytical approach: Generalized Integral Laplace Transform Technique. The concentration solution of the equation is expressed through an infinite series expansion. After setting a realistic scenario through the wind and diffusivity parameterizations, the Ground Level Concentration (GLC) is determined, and an explicit approximate expression is provided for it, allowing an analytically simple expression for the position and value of the maximum. Remarks arise regarding the ability to express value and position of the GLC as explicit functions of the parameters defining the Atmospheric Boundary Layer scenario and the source height.1. Introduction
Irreversible consequences of air pollution in the Atmospheric Boundary Layer (ABL) and instances of environmental accidents or even catastrophes demand increasing real time environmental monitoring and control as a routine instrument. In order to evaluate such scenarios one needs efficient procedures, which yield immediate results, for instance evaluating the ground level concentration of pollutants, and especially the maximum concentration and its position. Numerical simulation approaches may in fact still be too slow to provide a map of concentrations in real time, when immediate decisions are necessary. However, analytical solutions for theoretical models are independent of a specific situation and function by parameter estimation. The computational evaluation of numerical data of the concentration field or for a set of positions is an instant task. In view of this, the current work presents a derivation of compact phenomenological formula extracted from the analytical GILTT (Generalized Integral Laplace Transform Technique) [1] approach which permits determination of the ground level concentration in terms of physical parameters.
2. A Short Review of Solutions of the Advection-Diffusion Equation
The analytical solution of the Advection-Diffusion Equation (ADE) has been performed following different approaches based on Gaussian and non-Gaussian solutions. Gaussian solutions represent a rather easy operative tool to handle. Non-Gaussian analytical solutions represent a more realistic approach to represent atmospheric diffusion. However, solutions using non-Gaussian approaches are much harder to achieve, and are often restricted only to rather simple parameterization profiles. A short review in analytically solving the ADE is provided.
A two-dimensional (2-D) steady-state solution of the ADE is shown by [2] for ground source only. Parameterization of the ABL is realized through a power law for the wind u(z) and the diffusivity kz (z), respectively. A solution for elevated sources has been provided by [3] but only considering linear profiles of the diffusivity. Van Ulden [4] presented a solution based on the Monin-Obukhov similarity theory, the ABL parameterizations of which follow power law profiles. Such a solution upgrades that given in [2] allowing it to be applied to higher source heights inside the surface layer. The solution was implemented in a Skewed Puff Model [5].
Another 2-D solution has been worked out by Smith [6] where both u(z) and kz (z) follow a power law profile satisfying the conjugate law of Schmidt (that is: “wind exponent” = 1 − “kz (z) exponent”). An alternative solution uses constant u(z) and a piecewise continuous power law function for kz (z) [7].
Scriven and Fisher [8] proposed a solution solving the stationary ADE for long-range distances. Results were provided for constant u(z) and linear profiles of kz (z) inside the surface layer, and constant above, dry and wet deposition effects were included. References [9] and [10] presented 2-D solutions of the ADE for elevated source and with power profiles for both u(z) and kz (z). However, the solution assumes infinite height of the ABL.
Demuth [11] provided a further solution with power law parameterizations with the more realistic assumption of a bounded ABL. Such a solution involves a series expansion of the concentration in terms of the Bessel functions. The solution has been implemented in the KAPPAG model [12]. Then [13] extended the solution of [11] with boundary conditions suitable for simulating dry deposition to the ground.
Nieuwstadt [14] presented a one-dimensional (1-D) time-dependent solution. A further extended solution accounting for a growing ABL height was given in terms of Jacobi polynomials [15].
Koch [16] developed a 2-D analytical solution for a ground level source with power law profiles for wind and eddy diffusion coefficients accounting for the effects of ground level absorption. The deposition term of the solution includes the Kummer function [17], which has the drawback that it requires continuous checking for computational overflow.
In the work [18], an analytical solution was proposed adopting a constant wind and a diffusivity depending on the horizontal distance from the source.
Due to the limitedness of generality and to the increasing development of Large Eddy Simulation (LES) models, analytical approaches to solve the ADE have been largely ignored. In this paper, a complete and coherent analytical solution of the ADE is presented. The solution is based on the GILTT method [1]. The solution in analytical closed form introduces progress in the field of the study of concentrations. Due to the non-explicit dependence on the set of variables defining the ABL scenario and the source features, an explicit analytical approximation would represent a useful reference when application purposes are required. Moreover, it provides a simple formula for the value and position of maximum ground level concentration in function of source characteristic and meteorological variables.
3. The Solution by GILTT
The two dimensional steady-state ADE for an emitting point-like source in a stationary ABL reads:
Where, along the x -direction, the longitudinal diffusion term has been neglected in respect to the advection term. In the above Equation (1),C(x, z) represents the cross-wind integrated three-dimensional time-independent concentration:
The horizontal wind u(z) is the horizontal mean wind and kz (z) is the vertical diffusivity. Both depend on the vertical coordinate z. The boundary conditions impose the flux to vanish at the extremes of the ABL (z = 0, h), and the source condition is set to represent the point-like source placed at the height hs above the ground level, namely:
The GILTT technique provides a solution for Equation (1) which is written in terms of a converging infinite series expansion [1]:
4. Turbulent Parameterization
The choice of the turbulent parameterization is set to account for the dynamic processes occurring in the ABL. In the following, we restrict our discussion to simple vertical profiles of wind and eddy diffusivity still a reasonably realistic, but more specifically for an unstable regime. For an extension including stable regimens we refer to a future work. The choice of the vertical profile for the wind u(z) is set to follow a power law [20]:
The vertical diffusivity parameterization is chosen according to reference [23], which for an unstable ABL is given as:
The chosen profiles ensure simple functions whilst maintaining rather realistic horizontal wind u(z) and diffusivity kz (z) inside and at both edges of the ABL.
5. Ground Level Concentration
From the solution of the ADE, the Ground Level Concentration (GLC) is obtained after setting z = 0 inside the solution C(x, z). Results will be reported in terms of the dimensionless GLC as follows:
If we consider the definition of u profile in Equation (5) we have .
Equation (11) has been introduced to obtain the unitary limit independent of a specific parameter choice
It would be redundant to compare the GILTT results with experimental data as outcomes have already been extensively reported in the literature [25,26]. Instead, the scope of this paper is to provide a simple explicit expression for the maximum GLC CMGLC(xM) occurring at the horizontal distance xM as a function of the setting parameters for the ABL scenario and source emission. As previously mentioned, in fact, although Equation (4) represents the exact solution of the ADE (1) except for a round-off error, the series expansion misses manifest dependencies on ABL parameters and source height. On the other hand, the main advantage of the GILTT technique is that it allows the step from a differential-like approach, traditionally adopted to solve the ADE numerically, into a matrix algebra approach after applying the generalized Laplace transform. Then the core of the problem leads to the investigation of the behavior of the series (4) after setting z = 0, and using the property of the Sturm-Liouville eigenfunctions for which φi(0) = 1 regardless of the index i. An analysis of the behavior and properties of the series (4) will indicate how to synthesize the considerable expression into a more compact formula. The results based on such an approach are still profile-dependent and a general approximation is beyond the scope of the present work. Nevertheless, the choice of a profile-dependent approximation still maintains the advantage of simplicity and allows for a specific case for exploring the functional behaviors of the main physical parameters that drive atmospheric diffusion. To this end we introduce empirical parameters which are determined by fit procedures to best reproduce the exact solution.
Based on these facts, and bearing in mind the Gaussian solution and the GLC obtained with power low profile of wind and eddy diffusivity, the dimensionless GLC defined in Equation (11) can be approximated as follows:
Due to the negative values assumed by the Monin-Obukhov length, it will be defined in the following calculations as the positive dimensionless parameter L̃ MO = –LMO / h. Parameters b, c, κ and λ have been determined by least squares fittings procedures in Equation (14) against the analytical solution. These are:
Equations (15)–(18) give the explicit dependency on the source height hs, the wind parameters α (it compares in κ and λ), u1 and the convection scaling parameter w* (it compares in λ, see Equation (18)) which is related to the Monin-Obukhov length LMO and the friction parameter u* by the relationship (7).
From the explicit approximation for CGLC(x) one may evaluate the position where the maximum GLC occurs. In fact, putting the derivative of Equation (14) equal to 0 with respect to x, and with the assumption that:
Finally, putting xM in Equation (14), the corresponding Maximum Ground Level Concentration (CMGLC (xM)) is:
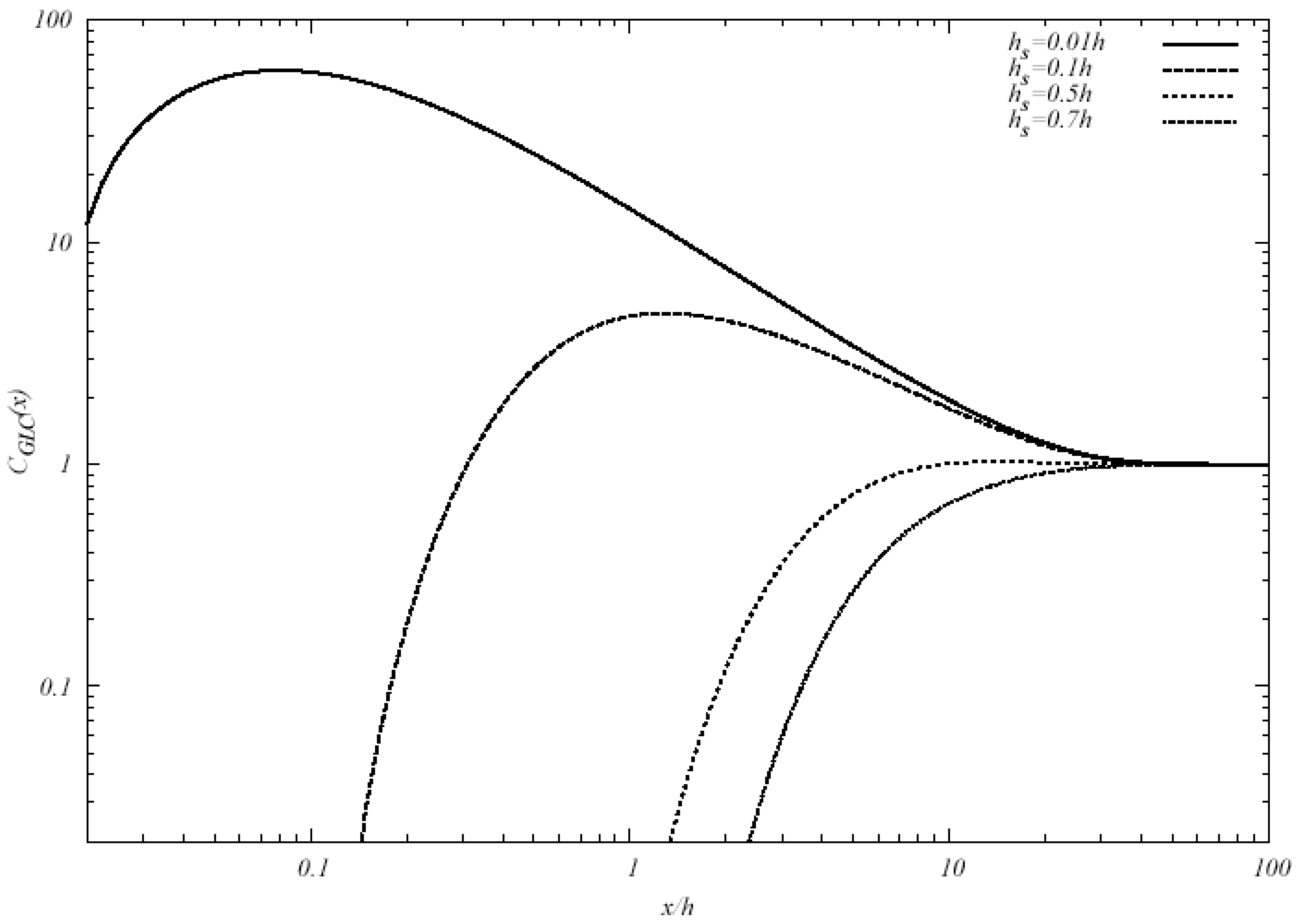
Two considerations are important here. Firstly, the expression for the position xM is valid provided that it is in the range of horizontal distances where a position xM occurs. Such approximation affects an error when high sources are concerned (above h̃s ≈ 0.35), but high convection-driven turbulence enforces condition (19). Secondly, because no maximum is reached for any h̃s > 0.5, the position of maxima in these cases has to be expected at x→∞ (due to the predominant weight of the exponential function compared to the first factor in Equation (14)). For this reason, the study of the maximum GLC will be limited to sources placed below the ABL center level. The omission of maxima will be explicitly shown in Figure 1 (see next section).
6. Results
Figure 1 shows plots of the GLC versus the horizontal distance from the source x̃ for near surface source (h̃s = 0.01), a low source (h̃s = 0.1) (at the top of the surface layer z̃sl = 0.1), center source (h̃s= 0.5), and high source (h̃s = 0.7) (above ABL center) with L̃M0 = 0.03. Except for the plot h̃s = 0.7, all show a maximum, where the sharpness of the peak reduces as h̃s increases, until a critical source height is reached (slightly above 0.5h), then value 1 becomes an upper asymptote for the GLC. When the emitting source height decreases, the maximum GLC increases, and occurs at a closer distance, turning into a well-pronounced peak.
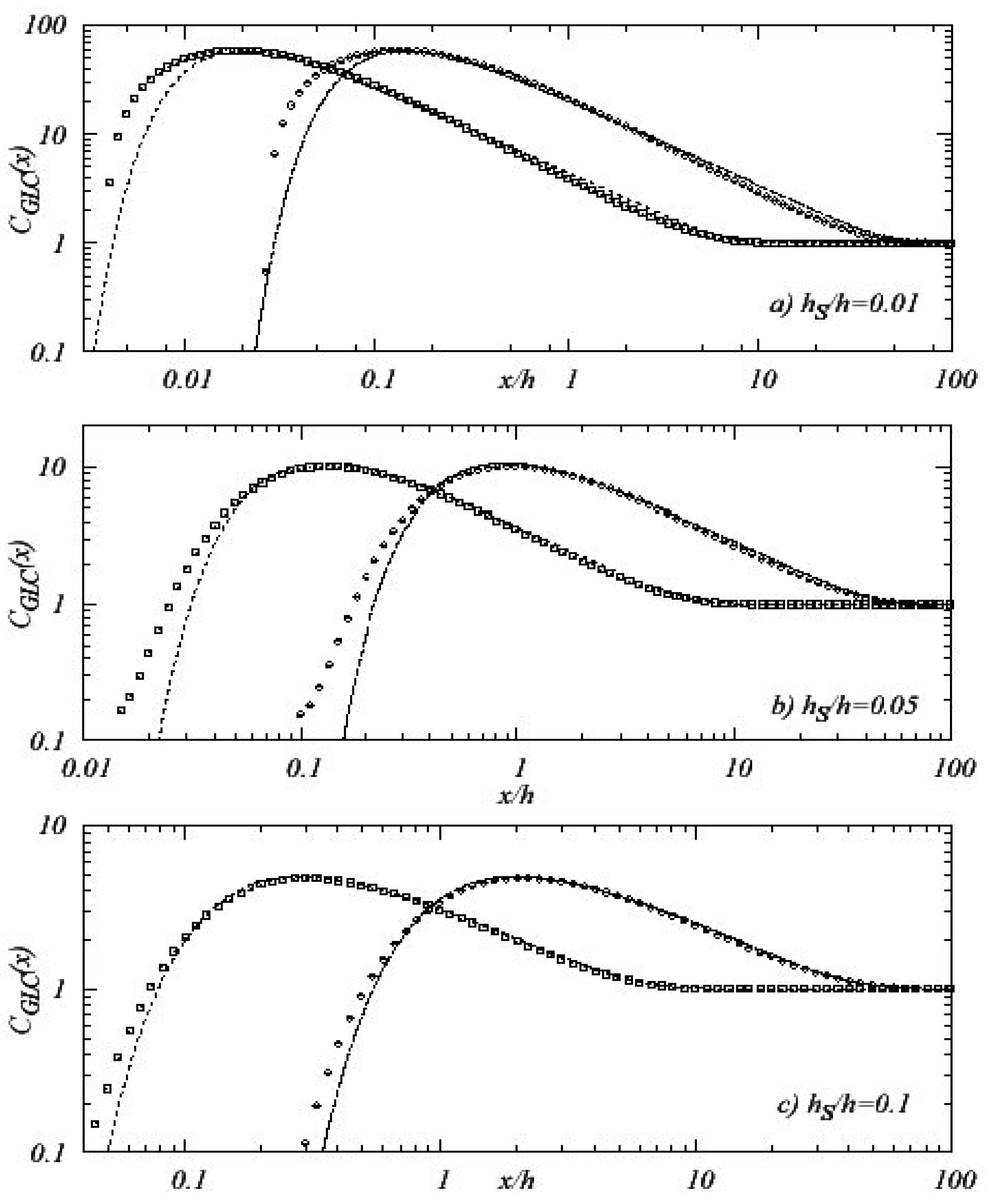
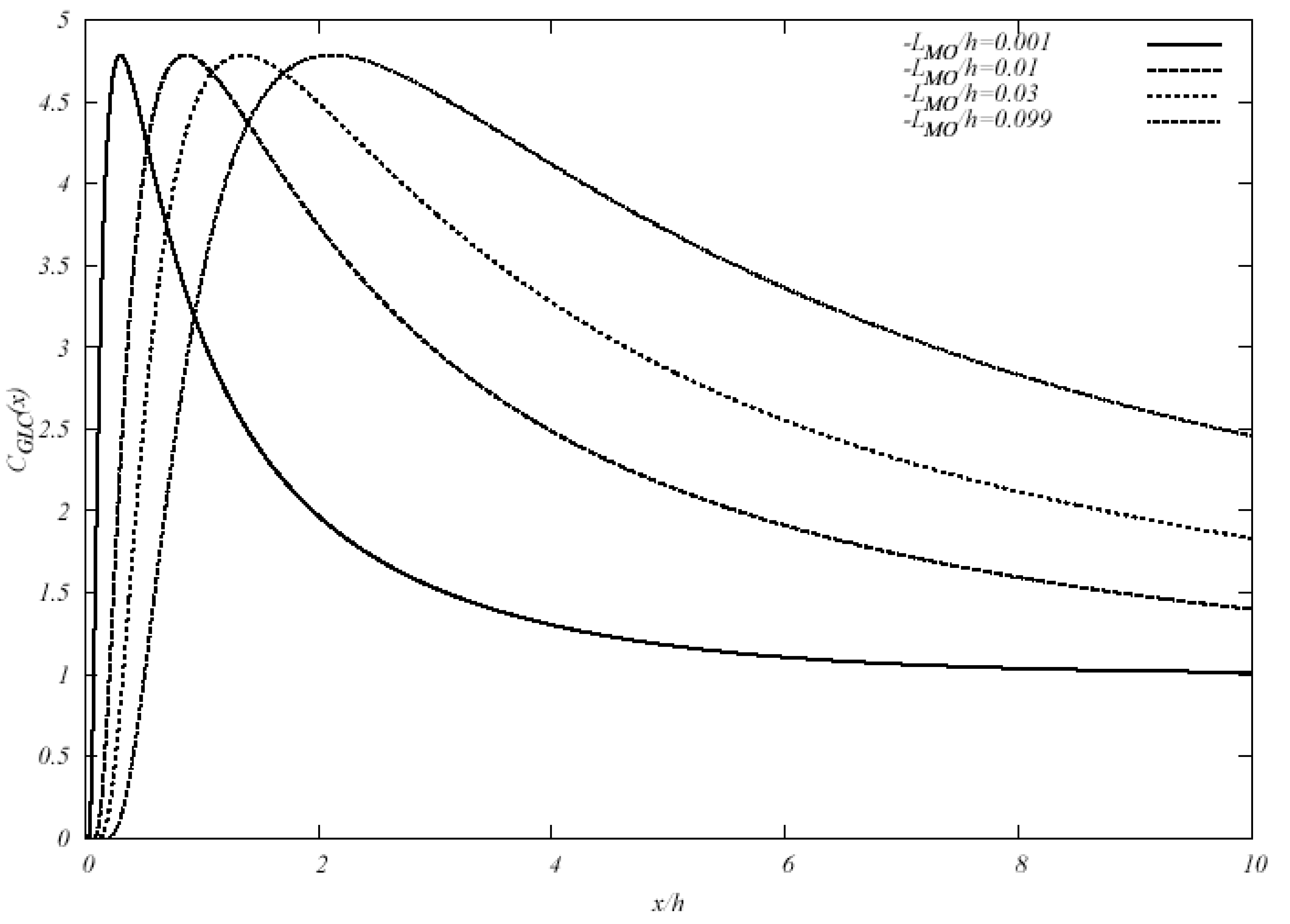
In Figure 2a–2c, the GLC versus x̃ is shown for three values of h̃s (h̃s = 0.01,0.05,0.1). For each source height, two extreme Monin-Obukhov lengths are used with L̃M0 = 0.001, 0.099 (empty squares and triangles, respectively). The second value for L̃M0 reflects the limit imposed by the Pleim and Chang diffusivity introduced in Equation (6). The GILTT-based GLC are superimposed on the approximation of Equation (14) (dotted lines). The plots show that for near surface sources there is a slight difference between points and lines near the source position. Where the horizontal gradient is most pronounced, a logarithmic scale enhances such a discrepancy.
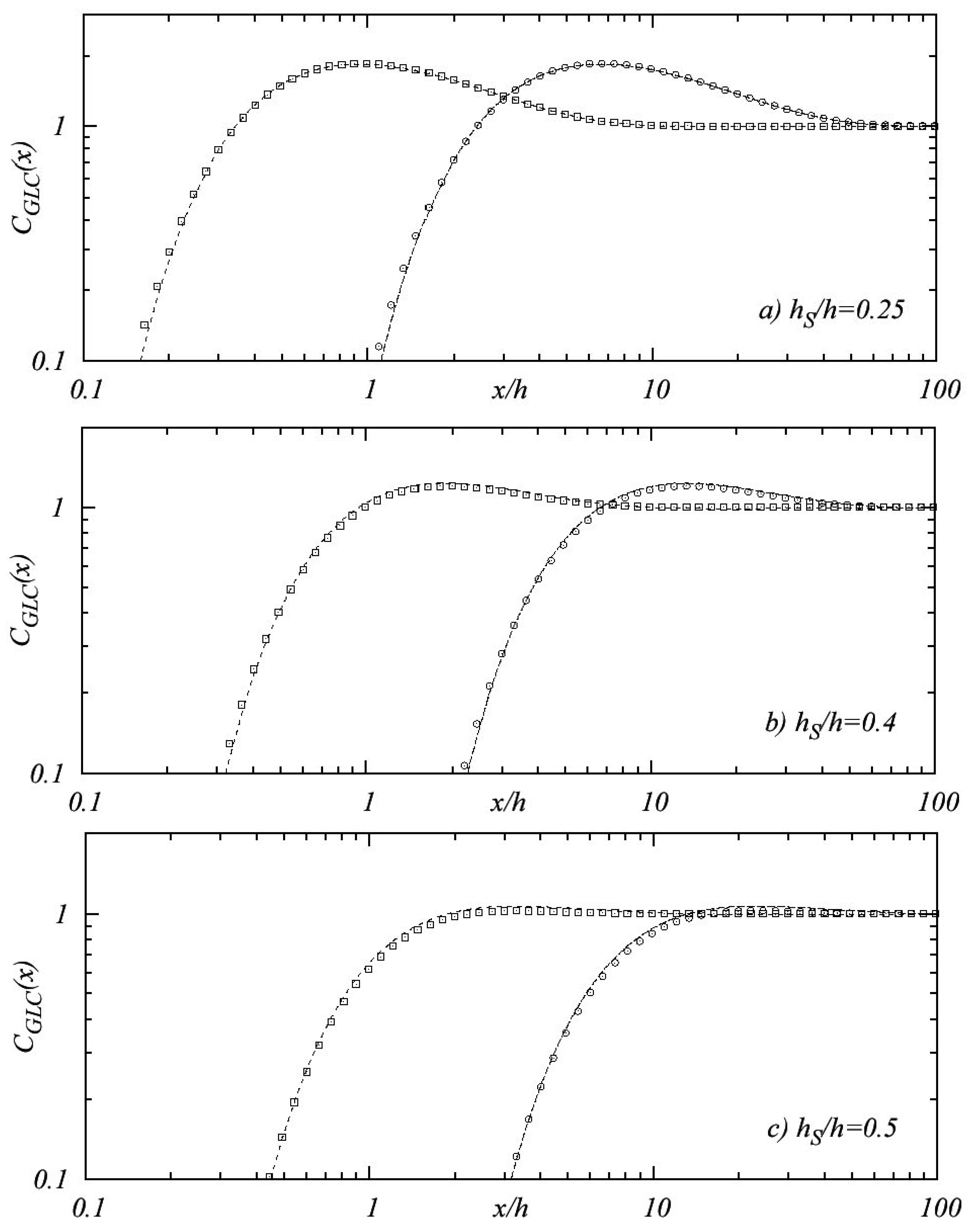
Figures 3a–3c refer to higher sources with h̃s = 0.25,0.4,0.5. These plots show well-matching results as well as a good reproduction of the position where the maximum GLC occurs. As the emitting source height h̃s increases, the approximated function slightly underestimates the GILTT-based maximum. This discrepancy reflects the fact that condition (19) is no longer satisfied. Nonetheless, through the whole range of source heights 0 < h̃s ≤ 0.25 the function CGLC (x) reproduces the GILTT results fairly well.
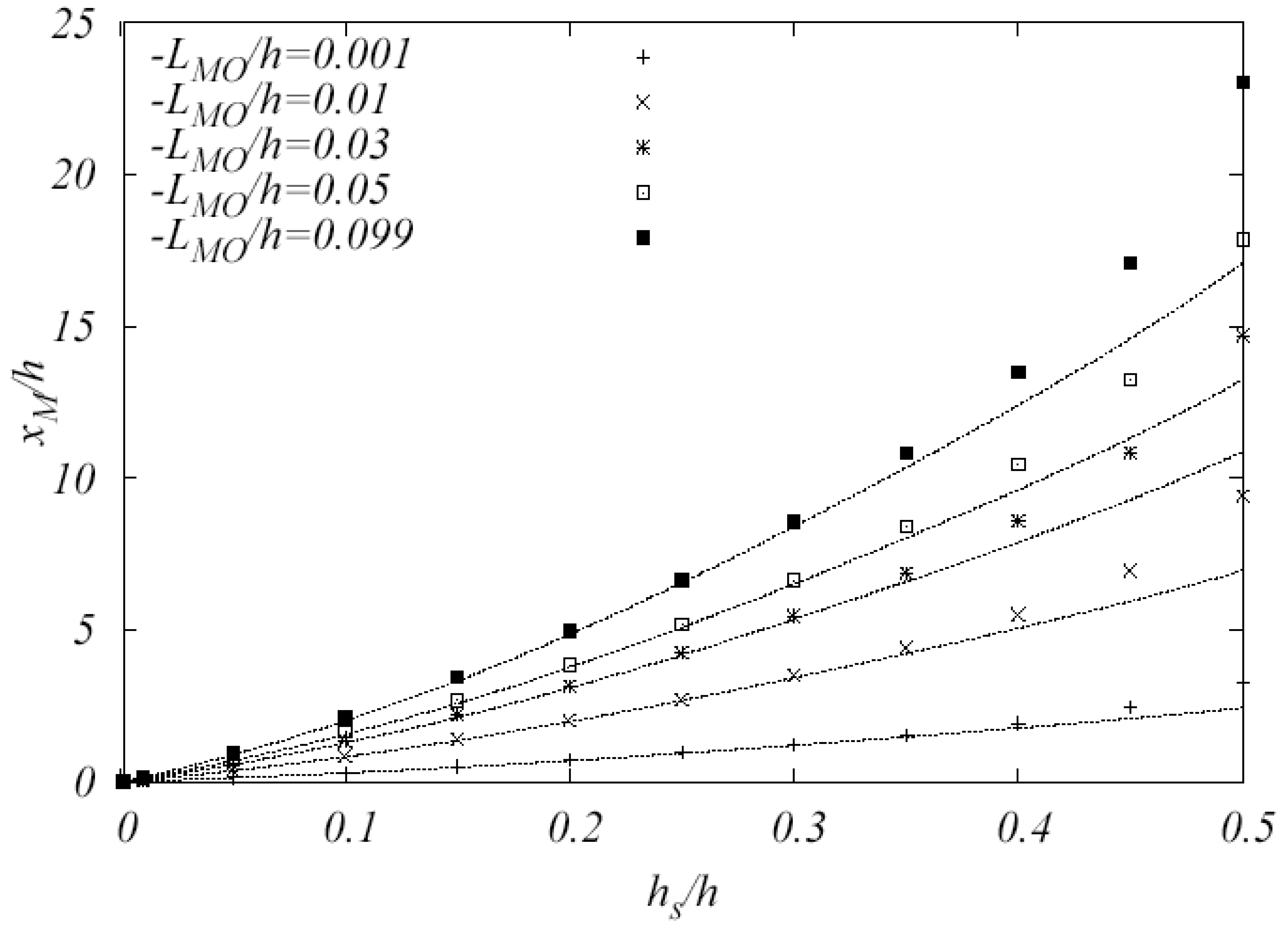
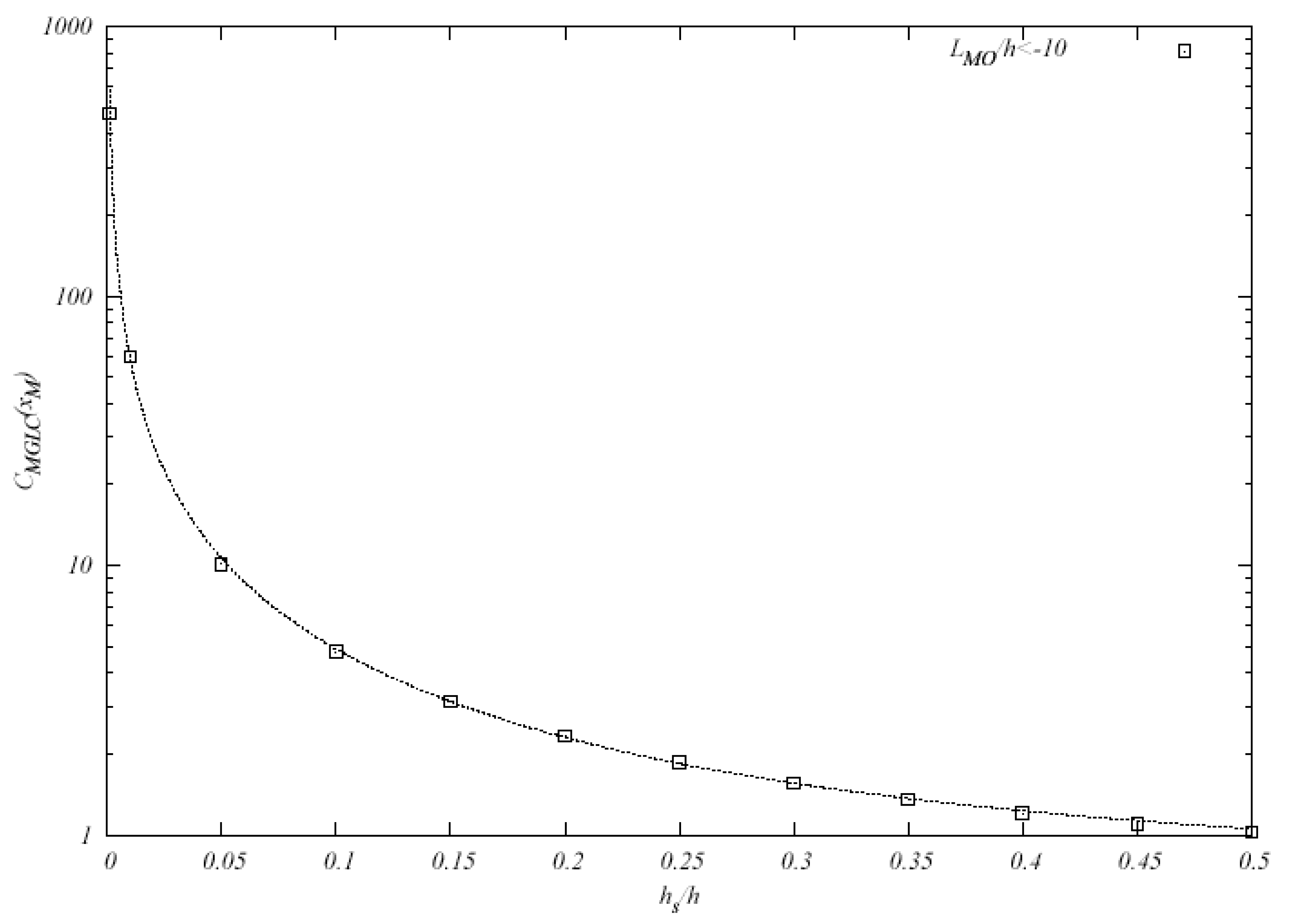
Figures 4 and 5 show plots of the maximum GLC CMGLC (xM) and its position xM for several source heights h̃s and for a selection of turbulence parameters L̃MO. In both figures the GILTT results (points) are superimposed on the approximations (20) (dotted lines). Figure 5 depicts the position where the maximum occurs for low sources, where GILTT results (dotted lines) and our approximations (solid lines) show well-matching results, regardless of the turbulence regime. When higher sources are considered, a difference is visible and increases as convective turbulence reduces its strength. This fact follows from the condition of (19). The turbulence dependency shows that, for a fixed h̃s, the strength of convection causes xM to get closer to the source. From the physics point of view this result agrees with the mixing effect of turbulence.
A final remark should be made in regard to Figure 5. Both GILTT and Equation (21) confirm that the maximum GLC value depends on the source height, regardless of the turbulence. Based on the Equation (21) and the parameters definitions (15)–(16) for b, c and κ, the leading term for the maximum GLC results:
Note that for the three-dimensional case this is no longer true. It is evident that diffusive parameters do not play a part and it confirms that turbulence has the only effect that determines the distance where maximum GLC occurs. The results shown above can be generalized (see Figure 6 as an example) to the case of vertical diffusivities defined with a multiplicative Monin-Obukhov length:
7. Conclusions
The results presented in this paper show the possibility of expressing the GLC from an emitting point-like source in a steady convective ABL by a compact analytical expression. The function was determined analyzing the behavior of the series expansion provided by the GILTT solution, the predictive power of which has been extensively demonstrated in the literature when applied to several experimental data sets. Despite the simplifications due to restricting only to unstable ABL regimes, the analysis allows a high level of understanding of the form of the ground level concentration.
The main progress worth emphasizing is the following: for a function given in Equation (14), within the setting choice for the ABL parameter set, the maximum GLC depends only on the source height, regardless of the Monin-Obukhov length. However, turbulence can still affect the position where the maximum GLC occurs, which is also confirmed by the GILTT solution. A further notable point shown in the result that no maxima occurs for all sources placed above the ABL center level; the limit becomes an upper-bound limit. The existence of a non-zero limit is one of the main properties of the two-dimensional ADE.
From the operative point of view, Equation (14) and its related features are useful as an additional tool for decisional as well as emergency responses.
Acknowledgments
The authors thank Brazilian CNPq, Italian CNR and ENVIREN for the partial financial support of this work.
References and Notes
- Moreira, D.M.; Vilhena, M.T.; Tirabassi, T.; Buske, D.; Cotta, R.M. Near souce atmospheric pollutant dispersion using the new GILTT method. Atmos. Environ. 2005, 39, 6289–6294. [Google Scholar]
- Roberts, O.F.T. The theoretical scattering of smoke in a turbulent atmosphere. Proc. Roy. Soc. 1923, 104, 640. [Google Scholar]
- Rounds, W. Solutions of the two -dimensional diffusion equation. Trans. Am. Geoph. Union 1955, 36, 395–405. [Google Scholar]
- Van Ulden, A.P. A surface-layer similarity model for the dispersion of a skewed passive puff near the ground. Atmos. Environ. 1992, 26A, 681–692. [Google Scholar]
- Tirabassi, T.; Rizza, U. A practical model for the dispersion of skewed puffs. J. Appl. Meteor. 1995, 34, 989–993. [Google Scholar]
- Smith, F.B. The diffusion of smoke from a continuous elevated point-source into a turbulent atmosphere. J. Fluid Mech. 1957, 2, 49–76. [Google Scholar]
- Smith, F.B. Convection-Diffusion Processes below a Stable Layer; Meteorological Research Committee N. 1048 and N. 10739: London, UK, 1957. [Google Scholar]
- Scriven, R.A.; Fisher, B.E.A. Long-range transport of airborn material and its removal by deposition and washout .2. Effect of turbulent-diffusion. Atmos. Environ. 1975, 9, 59–69. [Google Scholar]
- Yeh, G.T.; Huang, C.H. Three-dimensional air pollutant modeling in the lower atmosphere. Boundary-Lay. Meteorol. 1975, 9, 381–390. [Google Scholar]
- Berlyand, M.Y. Contemporary Problems of Atmospheric Diffusion and Pollution of the Atmosphere; Translated version by United State Environmental Protection Agency (USEPA): Raleigh, NC, USA, 1975. [Google Scholar]
- Demuth, C. A contribution to the analytical steady solution of the diffusion equation. Atmos. Environ. 1978, 12, 1255–1258. [Google Scholar]
- Tirabassi, T.; Tagliazucca, M.; Zannetti, P. KAPPA-G, a non-Gaussian plume dispersion model: description and evaluation against tracer measurements. JAPCA 1986, 36, 592–596. [Google Scholar]
- Lin, J.S.; Hildemann, L.M. A generalised mathematical scheme to analytically solve the atmospheric diffusion equation with dry deposition. Atmos. Environ. 1997, 31, 59–71. [Google Scholar]
- Nieuwstadt, F.T.M. An analytical solution of the time-dependent, one-dimensional diffusion equation in the atmospheric boundary-layer. Atmos. Environ. 1980, 14, 1361–1364. [Google Scholar]
- Nieuwstadt, F.T.M.; de Haan, B.J. An analytic solution of the one-dimensional diffusion equation in a nonstationary boundary-layer with an application to inversion rise fumigation. Atmos. Environ. 1981, 15, 845–851. [Google Scholar]
- Koch, W. A solution of the two-dimensional atmospheric diffusion equation with height-dependent diffusion-coefficient including ground-level absorption. Atmos. Environ. 1989, 23, 1729–1732. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover Publications, Inc.: New York, NY, USA, 1972; p. 1047. [Google Scholar]
- Sharan, M.; Singh, M.P.; Yadav, A.K. Mathematical model for atmospheric dispersion in low winds with eddy diffusivities as linear functions of downwind distance. Atmos. Environ. 1996, 30, 1137–1145. [Google Scholar]
- Tirabassi, T.; Tiesi, A.; Buske, D.; Vilhena, M.T. Some characteristics of a plume from a point source based on an analytical solution of the two-dimensional advection-diffusion equation. Atmos. Environ. 2009, 43, 2221–2227. [Google Scholar]
- Panofsky, H.A.; Dutton, J.A. Atmospheric Turbulence; John Wiley & Sons: New York, NY, USA, 1988. [Google Scholar]
- Irwin, J.S. A theoretical variation of the wind profile power-low exponent as a function of surface roughness and stability. Atmos. Environ. 1979, 13, 191–194. [Google Scholar]
- Pasquill, F.; Smith, F.B. Atmospheric Diffusion; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Pleim, J.E.; Chang, J.S. A nonlocal closure.model for vertical mixing in the convective boundary-layer. Atmos. Environ. 1992, 26, 965–981. [Google Scholar]
- Zannetti, P. Air Pollution Modelling; Computational Mechanics Publications: Southampton, UK, 1990; p. 444. [Google Scholar]
- Moreira, D.M.; Vilhena, M.T.; Buske, D.; Tirabassi, T. The GILTT solution of the advection-diffusion equation for an inhomogeneous and nonstationary ABL. Atmos. Environ. 2006, 40, 3186–3194. [Google Scholar]
- Buske, D.; Vilhena, M.T.; Moreira, D.M.; Tirabassi, T. Simulation of pollutant dispersion for low wind conditions in stable and convective planetary boundary layer. Atmos. Environ. 2007, 41, 5496–5501. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tirabassi, T.; Tiesi, A.; Vilhena, M.T.; Bodmann, B.E.J.; Buske, D. An Analytical Simple Formula for the Ground Level Concentration from a Point Source. Atmosphere 2011, 2, 21-35. https://doi.org/10.3390/atmos2020021
Tirabassi T, Tiesi A, Vilhena MT, Bodmann BEJ, Buske D. An Analytical Simple Formula for the Ground Level Concentration from a Point Source. Atmosphere. 2011; 2(2):21-35. https://doi.org/10.3390/atmos2020021
Chicago/Turabian StyleTirabassi, Tiziano, Alessandro Tiesi, Marco T. Vilhena, Bardo E.J. Bodmann, and Daniela Buske. 2011. "An Analytical Simple Formula for the Ground Level Concentration from a Point Source" Atmosphere 2, no. 2: 21-35. https://doi.org/10.3390/atmos2020021



