Atmospheric CO₂ Isotopic Variations, with Estimation of Ocean and Plant Source Contributions

Abstract

This analysis uses both atmospheric CO₂ concentrations and the accompanying δ¹³C isotopic measurements of CO₂ over 40 years from 1978 to 2015 observed at ten different latitudes from 90° S to 82 °N. Atmospheric CO₂ is separated into two components of CO₂ attributable to deep ocean and to plant (including fossil fuel) sources. The isotopic values assigned to the two components are δ¹³C = 0‰ and −26‰, respectively. The latitude variations in residual source component CO₂ show the ocean source component peaking at the equator. This contrasts with the residual plant source component that peaks in the Arctic Circle region. Seasonal comparisons show no change in the ocean component peaking at the equator and no significant changes in its variation with latitude, while the plant component shows seasonal changes of the order of 15 ppm at high latitudes. The ocean component shows clear anomalous behavior in the three years following the 1989 Pacific Ocean regime shift (a shift independently identified from the changed biological time series). By contrast, the residual plant component shows a correlation in the timing of maxima in its annual variations with the timing of El Nino events over the time span of 1985–2015. It also shows a discontinuity in annual variation coinciding with the 1995 AMO phase change. We conclude that the ocean and plant components of atmospheric CO₂ relate to independent sources of atmospheric CO₂ and have approximately equal magnitudes. The observations are consistent with a hypothesis that variations in the ocean components have an origin from upwelling water from deep ocean currents, and variations in plant components are dominated by a combination of fossil fuel CO₂, phytoplankton productivity, and forest and peat fires, which primarily occur in the northern hemisphere.

1. Introduction

It has been previously shown that the apparent smooth and continuous rise in atmospheric CO₂ concentrations can be broken into a series of trend changes associated with ocean decadal phase changes [1]. We extend that association through the separation of CO₂ concentrations on the basis of carbon isotopes in order to distinguish between variations in CO₂ concentrations associated with Pacific Ocean regime changes and variations associated with sea-surface temperature variations as represented in the Nino 3.4 index [2].

This paper does not study the bidirectional carbon cycle, which involves the bidirectional flux of CO₂ from land to atmosphere, and ocean to atmosphere (see, for example, [3,4]). Rather, we use the observed isotopic composition of CO₂ observed at ten globally distributed stations in order to obtain estimates of annual and decadal variations in atmospheric CO₂ attributable to plant origins (both natural and anthropogenic processes) and to CO₂ transfer into the atmosphere from upwelling deep ocean waters. This global perspective is thus different from, for example, the work of [5] who used carbon isotope studies on plant matter from a single location (Baragui River, Parana, Brazil) in order to deduce local climatic and vegetation composition changes over the past 400 years.

The measure of the ratio of ¹²C to ¹³C found in a sample of CO₂ is expressed as δ¹³C, where the ¹³C/¹²C abundance ratio is of the order of 0.01. Variations in δ¹³C are attributable to variations in the molecular weight of CO₂, which affect the rate of chemical reactions and photosynthesis.

There are now about 60 years of atmospheric CO₂ concentration measurements available from the Scripps Institution of Oceanography (SIO) [6] and 40 years of δ¹³C isotope measurements of CO₂ commencing in 1978. The SIO stations and years with both CO₂ and δ¹³C measurements are listed in

Table 1. SIO stations and years for CO₂ and δ¹³C measurements, from [6].

	Latitude	Longitude	Elevation	Years with	% Months with no Data
			(meters)	CO2 and d13C	All	1986–2015
Alert	82° N	63° W	210	1986–2018	4.55%	4.72%
Point Barrow	71° N	157° W	11	1983–2018	4.17%	4.72%
La Jolla	33° N	117° W	10	1979–2018	14.38%	10.28%
Kumukahi	19° N	155° W	3	1981–2018	1.10%	0.28%
Mauna Loa	19° N	156° W	3397	1981–2018	2.19%	0.00%
Christmas Island *	2° N	157° W	2	1978–2018	32.11%	26.67%
American Samoa	14° S	171° W	30	1985–2018	3.92%	3.33%
Kermadec	29° S	178° W	2	1985–2018	53.43%	51.94%
Baring Head	41° S	175° E	85	1986–2018	40.91%	39.17%
South Pole	90° S		2810	1978–2018	7.52%	3.06%

* Note that Christmas Island is part of the Republic of Kiribati in the Pacific Ocean.

. The additional column shows the percentage of months with no data from 1986 to 2015. In the following analysis, we select the time period of 1986–2015 as having the most complete records. In particular, we avoid a 32-month period from 2016 to 2018 on Christmas Island, which has no data.

This analysis uses the CO₂ concentration and isotope measurements after 1978 to divide the atmospheric CO₂ concentration into an “ocean” and a “plant” component by assuming values for the isotopic composition for the two components. The purpose of this study is to demonstrate a means of computing the fraction of gaseous CO₂ in atmospheric samples that can be attributed to a plant origin.

The isotopic approach used in this paper allows a phenomenological study of atmospheric CO₂ origins from upwelling deep ocean sources, and from plant sources including both anthropogenic and natural sources that release CO₂ into the atmosphere. This approach does not require assumptions or estimations of the dissolved inorganic carbon content of the ocean surface waters, nor does it quantify the uptake by the oceans of atmospheric CO₂. It does, however, provide quantitative data on seasonal, annual and latitudinal variations in fractions of atmospheric CO₂ attributable to ocean and plant sources.

2. Method, Model and Data

2.1. Deep Ocean and Plant Contributions to CO₂

The basis of this analysis is that contributions to CO₂ derived from deep ocean and from plant sources take discrete and different values. For SIO δ¹³C data, the standard ratio R(¹³C/¹²C)_std is from the Vienna Peedee Belemnite (VPDB) isotope [7] where R_std = 0.011180.

Deviations in the isotope ratio as measured in air samples are expressed as

δ¹³C_meas = ((R_meas/R_std) − 1) × 1000.

For this analysis, we use two reference points as follows. For deep oceans:

¹³C_ocean = 0‰

as given by [8,9,10], and for plants, we use

δ¹³C_plant = −26‰.

The plant value is representative of C3 plants [11]; phytoplankton for north and south, high latitudes [12]; and fossil fuels [13,14].

The separation of deep ocean and plant contributions can be quantified using the two relations defined in Equations (1) and (2):

A_meas = A_ocean + A_plant

(1)

δ¹³C_meas = (δ ¹³C_ocean × A_ocean+ δ¹³C_plant × A_plant)/A_meas

(2)

where:

• A_meas is the measured atmospheric concentration of CO₂ in ppm;
• A_ocean is the component of deep ocean origin, in ppm;
• A_plant is the component of plant origin, in ppm;
• δ¹³C_meas is the isotopic value of measured atmospheric CO₂;
• δ¹³C_ocean is the isotopic value of “ocean” component atmospheric CO₂;
• δ¹³C_plant is the isotopic value of “plant” component atmospheric CO₂.

So, the separate components calculated using the measured values for atmospheric CO₂, and assuming isotopic values for “deep ocean” and “plant” components, are given by Equations (3) and (4) as follows.

A_ocean = A_meas × (δ¹³C_meas − δ¹³C_plant)/(δ¹³C_ocean − δ¹³C_plant),

(3)

and

A_plant = A_meas − A_ocean.

(4)

Measured atmospheric concentrations are recorded in parts per million (ppm) by volume. Thus, separating an ocean and a plant source component requires converting ppm by volume to ppm by mass.

So,

δ¹³C = {R(¹³C/¹²C) _meas/R(¹³C/¹²C)_std − 1} × 1000

(5)

and

R(¹³C/¹²C) _meas = (1 + δ¹³C/1000) × R(¹³C/¹²C)_std

(6)

where:

• R(¹³C/¹²C) _meas is the ratio for the sample carbon-13 to carbon-12;
• R(¹³C/¹²C)_std is the ratio for the standard carbon-13 to carbon-12.

Then, the carbon mass may be calculated in atomic mass units as

Carbon = {12 + 13 × R(¹³C/¹²C) _meas}/(1 + R(¹³C/¹²C) _meas).

(7)

So, the mass of CO₂ can be calculated, hence the conversion of ppm by volume to ppm by mass.

The mass correction is small, of the order of 0.0005 ppm compared with measurement errors of the order of 0.1 ppm. Although not significant, these mass corrections are applied to this data.

For the remainder of this paper, we use the term “ocean component” and “ocean source” to refer to that fraction of atmospheric CO₂ having the isotopic signature of deep ocean water.

2.2. Ocean and Plant Source Component Analysis for Monthly Values

The monthly measurements for the South Pole and Christmas Island from 1978 to 2015 and Point Barrow from 1980 to 2015 are shown in Figure 1. The ocean and plant source components of atmospheric CO₂ are found using Equations (3) and (4), respectively. The results from the monthly measurements of atmospheric CO₂ concentrations and δ ¹³C are shown in Figure 2 and Figure 3, respectively, for the South Pole and Christmas Island from 1978 to 2015 and for Point Barrow from 1983 to 2015.

The seasonal variations seen in the measured CO₂ concentrations for the South Pole, Christmas Island and Point Barrow are found in the respective plant components but not to any significant extent in the corresponding ocean components.

There are two observations that follow from this analysis:

(a)

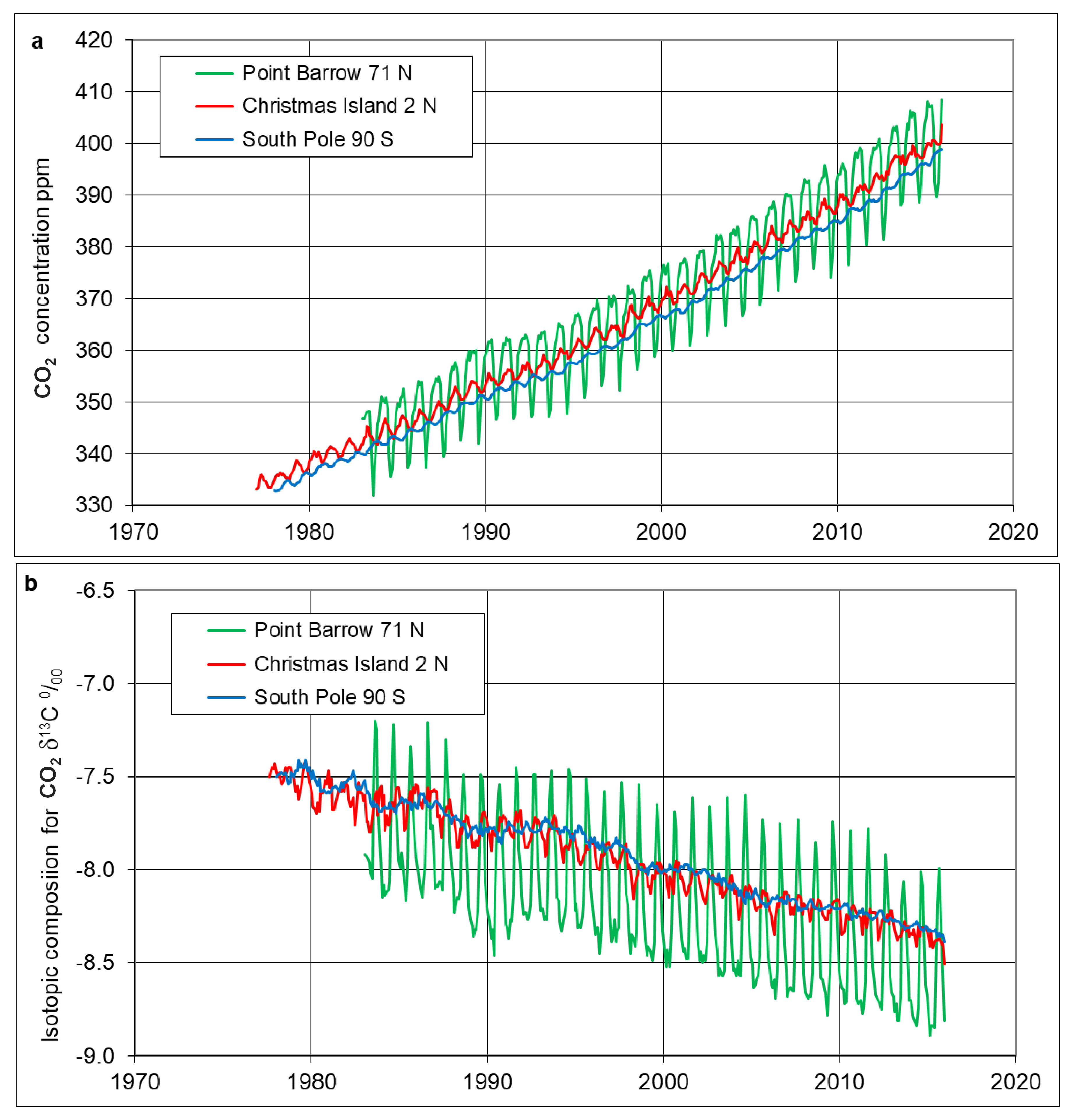
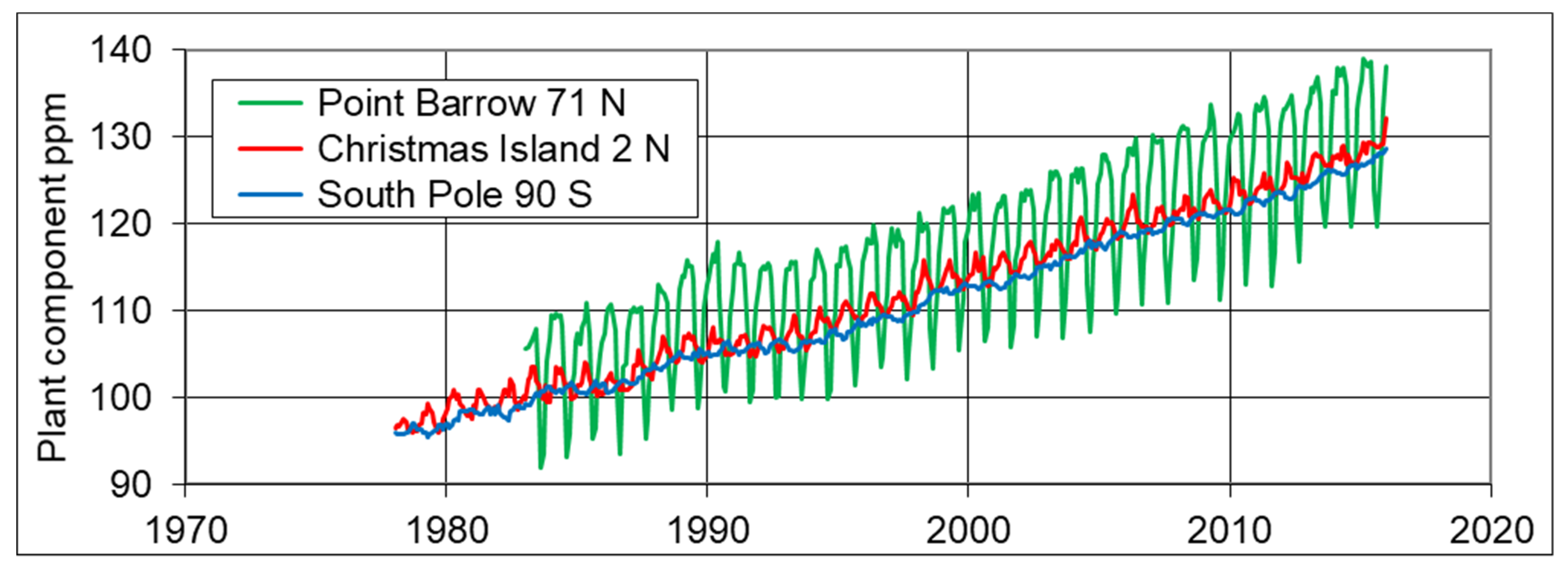
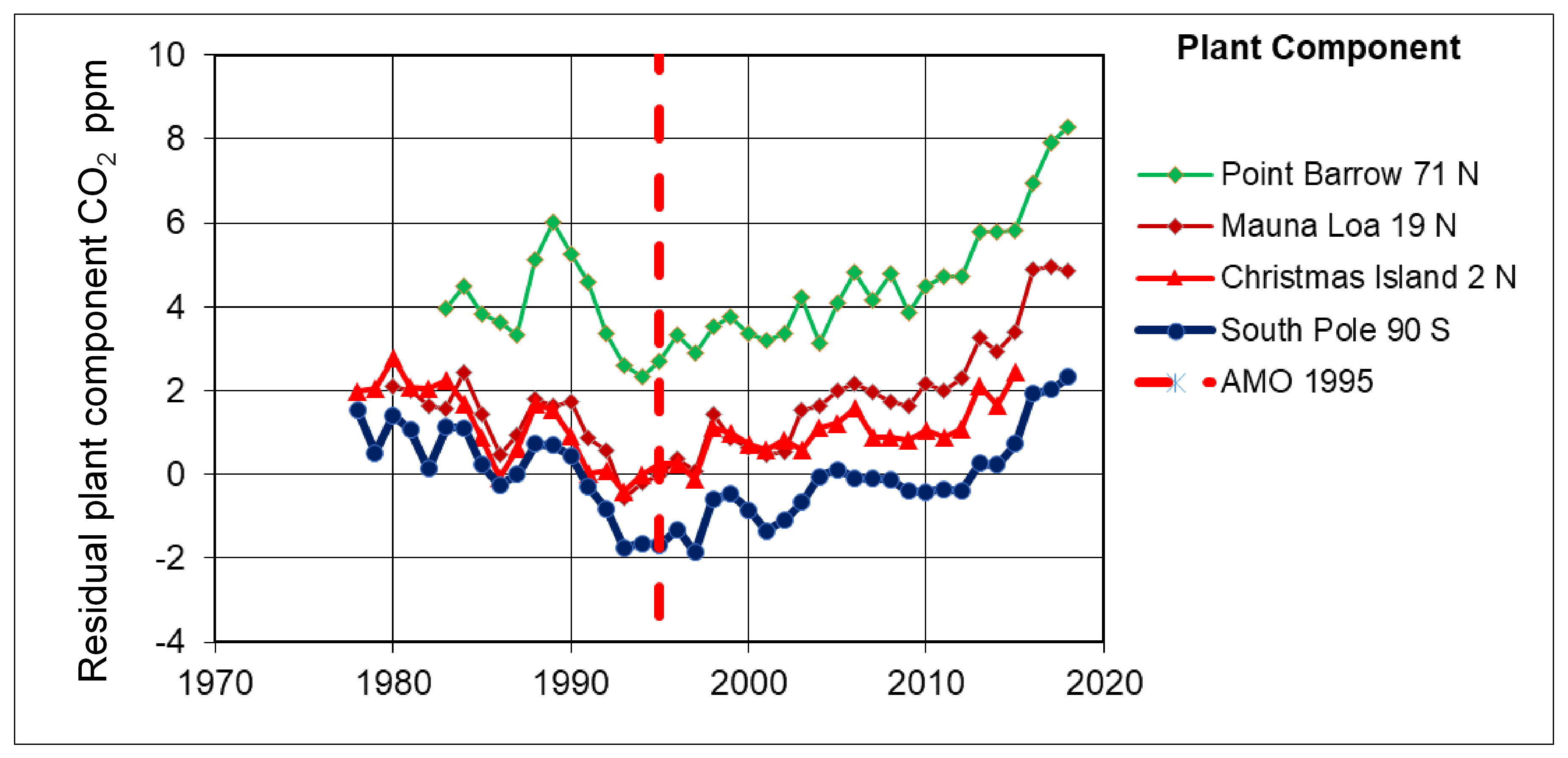
A subtle increase above the trend in the measured CO₂ concentrations is visible in Figure 1a for times around 1988–1991. This feature is clear in the plot of isotopic composition shown in Figure 1b (referred to as the “bubble” in later paragraphs) and overlaps in time the 1989 Regime Shift described by [15]. That 1989 event was clearly evident in biological records although only weakly shown in indices of the Pacific climate. Consistent with that prior finding of an event in biological records, we see that the “bubble” is present in the plant component of atmospheric CO2 as deduced from the isotopic analysis (Figure 2). However, the “bubble” is not evident in Figure 3, which shows the equivalent plot of the ocean component of atmospheric CO2. This feature is discussed in additional detail below in Section 4.

(b)

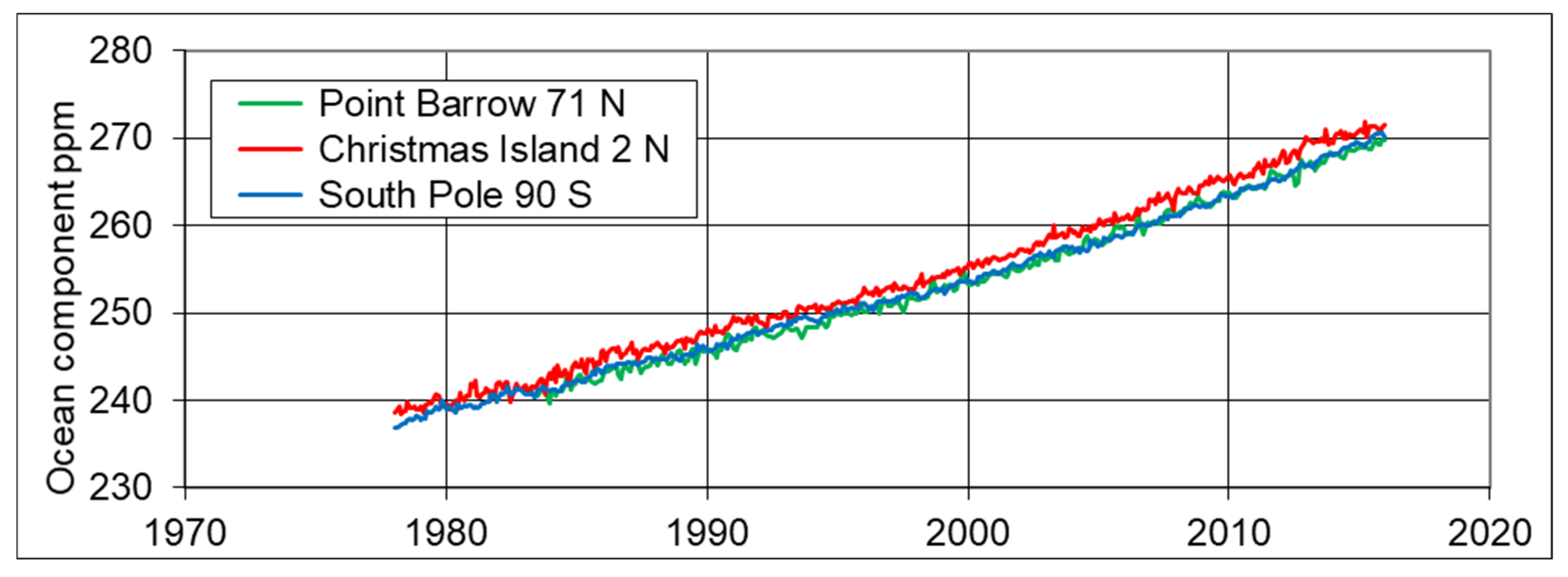
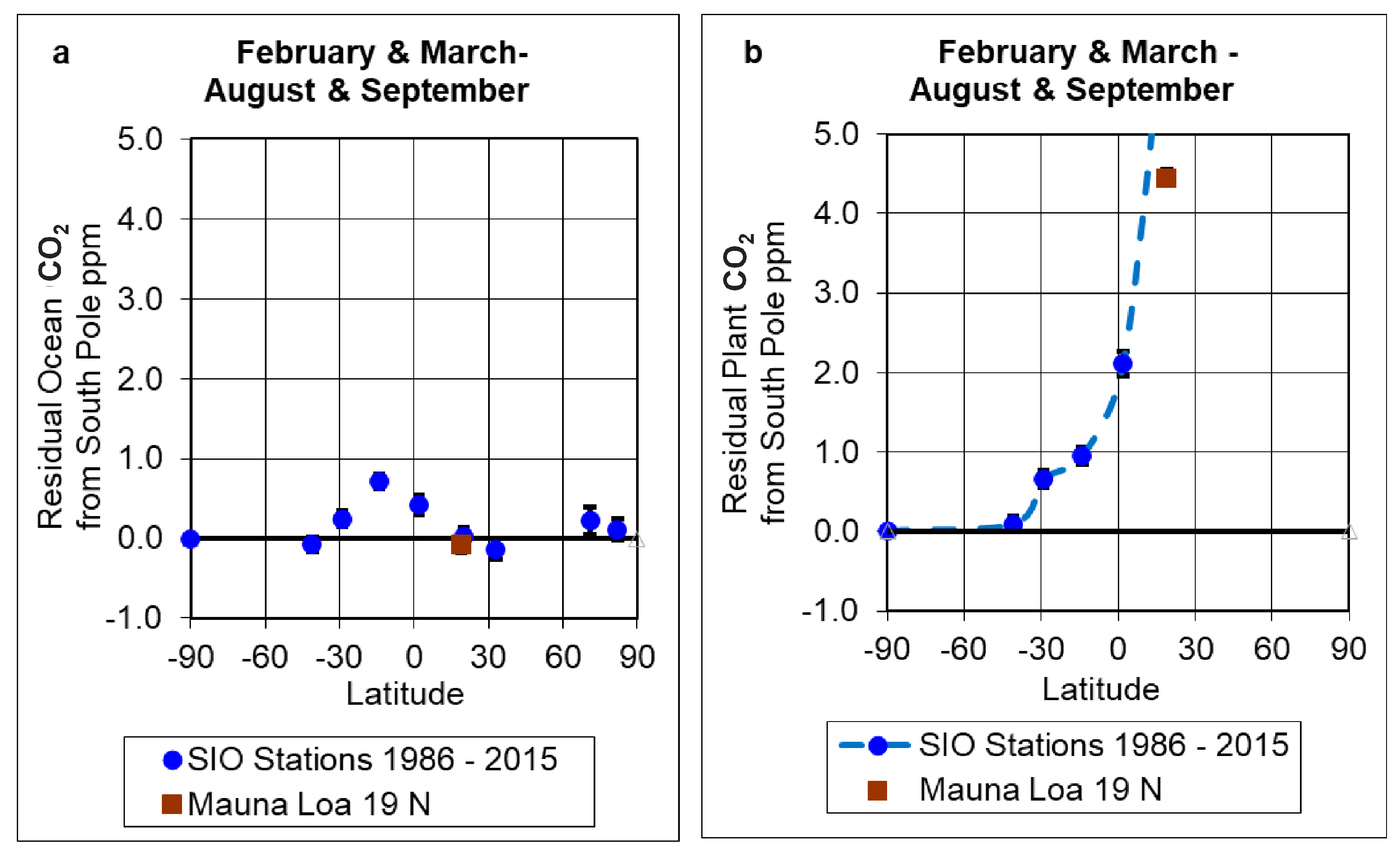
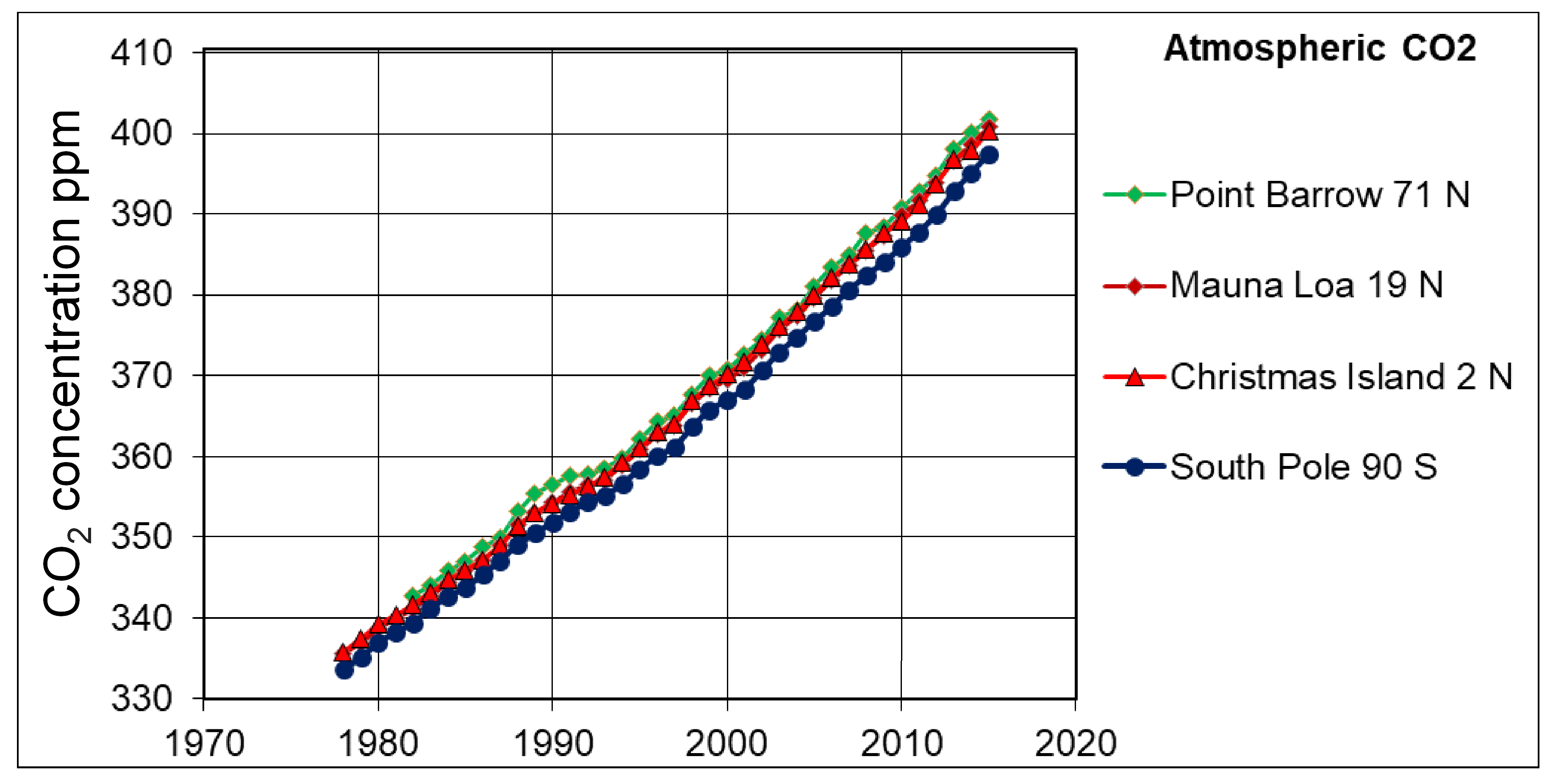
For the ocean components shown in Figure 2, Christmas Island (2° N) near the equator shows higher values for the entire time span of 1978–2015, while Point Barrow (71° N) in the Arctic shows the lowest values. We discuss the significance of these observations in the context of ocean currents, in Section 3.2.

The average annual increases for each of the stations in Figure 1, computed for the time span from 1986 to 2015, are found through a least-squares fit to the measurements; these are listed in

Table 2. Annual CO₂ increases using monthly data, averaged over the years of 1986 to 2015.

	Annual Increases in ppm
Stations	CO2 Concentration	Ocean Component	Plant Component
South Pole 90° S	1.769 +/− 0.008	0.886 +/− 0.005	0.883 +/− 0.005
Christmas Island 2° N	1.819 +/− 0.009	0.910 +/− 0.005	0.909 +/− 0.007
Point Barrow 71° N	1.800 +/− 0.038	0.902 +/− 0.005	0.898 +/− 0.038

. The most remarkable result is that, for each site, the ocean and plant average annual increases are similar, to within 0.3%.

3. Ocean and Plant Source Component Latitude Analysis

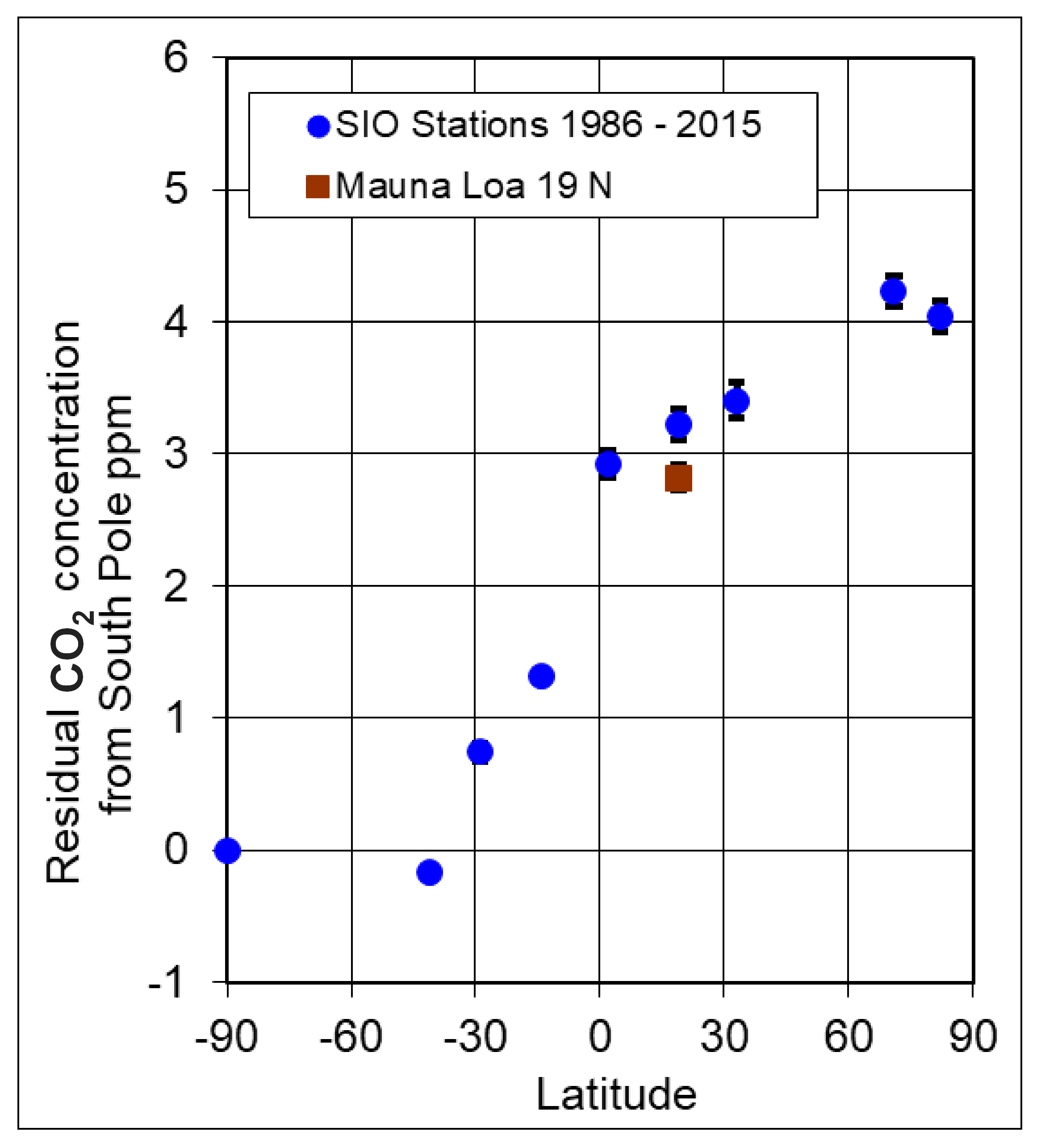
3.1. Annual Values

The behavior of the ocean and plant components are further explored through analysis of each of the ten SIO latitudes listed in Table 1.

The variation in atmospheric CO₂ measurements shows increasing concentrations from the lowest values at the South Pole 90° S to a peak at Point Barrow 71° N. Figure 4 shows the residual annual variations of total CO₂ less the value at the South Pole, for each station, averaged over 1986 to 2015. This is the time span where there are concentration and isotopic composition CO₂ measurements available for all latitudes shown in Table 1.

The latitude variations in the residual annual variations of total CO₂ concentrations are quite different when separated into ocean and plant components. The component values, standard deviations and errors of the mean are listed in

Table 3. Residual ocean component values for 1986 to 2015.

SIO Stations	Latitude	Longitude	Elevation (Meters)	Residual Values from South Pole Value in ppm
				Mean	Standard Deviation	Error of Mean
Alert	82° N	63° W	210	−0.29	0.33	0.06
Point Barrow	71° N	157° W	11	−0.30	0.39	0.06
La Jolla	33° N	117° W	10	0.36	0.40	0.07
Kumukahi	19° N	155° W	3	0.70	0.39	0.07
Mauna Loa	19° N	156° W	3397	0.99	0.24	0.04
Christmas Island	2° N	157° W	2	1.62	0.42	0.08
American Samoa	14° S	171° W	30	0.94	0.26	0.05
Kermadec	29° S	178° W	2	0.43	0.34	0.06
Baring Head	41° S	175° E	85	0.16	0.27	0.05
South Pole	90° S		2810	0.00

and

Table 4. Residual plant component values for 1986 to 2015.

SIO Stations	Latitude	Longitude	Elevation (Meters)	Residual Values from South Pole Value in ppm
				Mean	Standard Deviation	Error of Mean
Alert	82° N	63° W	210	4.33	0.57	0.10
Point Barrow	71° N	157° W	11	4.54	0.58	0.11
La Jolla	33° N	117° W	10	3.04	0.74	0.14
Kumukahi	19° N	155° W	3	2.52	0.52	0.09
Mauna Loa	19° N	156° W	3397	1.83	0.59	0.11
Christmas Island	2° N	157° W	2	1.31	0.48	0.09
American Samoa	14° S	171° W	30	0.37	0.30	0.05
Kermadec	29° S	178° W	2	0.31	0.33	0.06
Baring Head	41° S	175° E	85	−0.32	0.24	0.04
South Pole	90° S		2810	0.00

and shown in Figure 5. The ocean component peaks near the equator (Figure 5a). However, the plant component peaks at the Arctic Circle latitudes of Point Barrow 71° N and Alert 82° N (Figure 5b).

The analysis also shows significantly different residual values at Mauna Loa at an elevation of 3397 m compared to Kumukahi at the same latitude but at an elevation of 3 m (highlighted in Table 3 and Table 4). The ocean component residual at Mauna Loa is significantly greater than the Kumukahi residual and the sign of this difference of residuals is reversed for the corresponding plant components. These differences are shown in Figure 5.

The differences may be due to the elevation at which Mauna Loa measurements are made; we suggest that the elevation of 3397 m is above the sub-tropical inversion, having the effect that the atmosphere is locally more mixed with contributions from the equatorial region. This would have the effect of increasing the residual ocean component relative to that found at Kumukahi at an elevation of 3 m. Likewise, the residual plant component values at the elevated Mauna Loa site are mixed to a lower value than the Kumukahi residual plant value.

We also note from Figure 5 and Figure 6 that the negative values of CO₂ relative concentration, and of plant source component CO₂, as observed at Baring Head (latitude 41° S between the north and south islands of New Zealand), are associated with a location between the Southern Ocean and south Pacific Ocean. This is consistent with an understanding that the expanse of ocean in the southern hemisphere acts as a sink for atmospheric CO₂, and further, that an absence of upwelling deep ocean currents in southern latitudes [9] is associated with an absence of an anomaly in the ocean source component of CO₂ at Baring Head.

3.2. Latitude Analysis for Seasonal Values

If the ocean source component is independent of the plant source component, then the ocean source peaking at the equator should be independent of seasonal variations. Figure 6 shows residual seasonal variations restricted to the end of the boreal winter and to the end of the boreal summer. Averaging is performed for the two months of February–March, and for August–September. As for Figure 5, we obtain ocean and plant components of CO₂ for all latitudes, but restricted to the two seasons. There is little change in the ocean components for the seasonally separated values relative to the residual annual averages. The stability of the ocean source CO₂ concentrations can be seen by comparing the latitude seasonal changes for February–March with those of August–September (Figure 6a,b).

The residual seasonal variations in the plant component of CO₂ are quite different when compared to the ocean component, as seen in plots of Figure 6b,d. Plant components show changes of up to 16 ppm from the end of the boreal winter (February–March) to end of summer (August–-September) at the far-north stations of Point Barrow and Alert.

The hypothesis for this seasonal difference is that plant source component variations in the Northern Hemisphere are due to the influence on the carbon cycle of the boreal forests. The trees start to grow in spring, drawing CO₂ from the atmosphere until autumn when the end of summer growth reduces the draw-down of CO₂. In addition, it is expected that decaying plants will return CO₂ to the atmosphere.

The seasonal differences of end boreal winter less boreal summer are shown in Figure 7 for ocean and plant components. The ocean component (Figure 7a) shows that seasonal differences are not statistically different with the exception of Christmas Island 2° N, American Samoa 14° S and Kermadec Island 29° S. The peak in the ocean component for the boreal winter (Figure 6a) is shifted about 15° S in Figure 7a. This may be explained as a result of transport by atmospheric winds comparatively enriched in the ocean component as there are strong wind systems, particularly the trade winds in the equatorial region.

The plant component also shows evidence of atmospheric transport from the northern hemisphere to southern hemisphere during the boreal winter, seen at latitudes 15° S to 30° S (Figure 6b,d and Figure 7b). It is seen most clearly in Figure 7b at 30° S where the residual plant component is approximately 0.5 ppm above the trend, consistent with atmospheric transport from north to south.

This analysis shows that at Point Barrow, 71° N, and at Alert, 82° N, the ocean component varies only slightly by 0.3 ± 0.2 ppm and 0.1 ± 0.1 ppm from boreal winter to summer, whereas there are large variations of 16 ppm and 15 ppm for the plant component, respectively. At lower latitudes in the northern hemisphere, there are reduced differences from winter to summer. The spatial and seasonal distribution in ocean and plant source components differs by up to a factor of 50, and leads us to the conclusion that the ocean source of CO₂ is an independent source of atmospheric CO₂ and is decoupled from the plant source component.

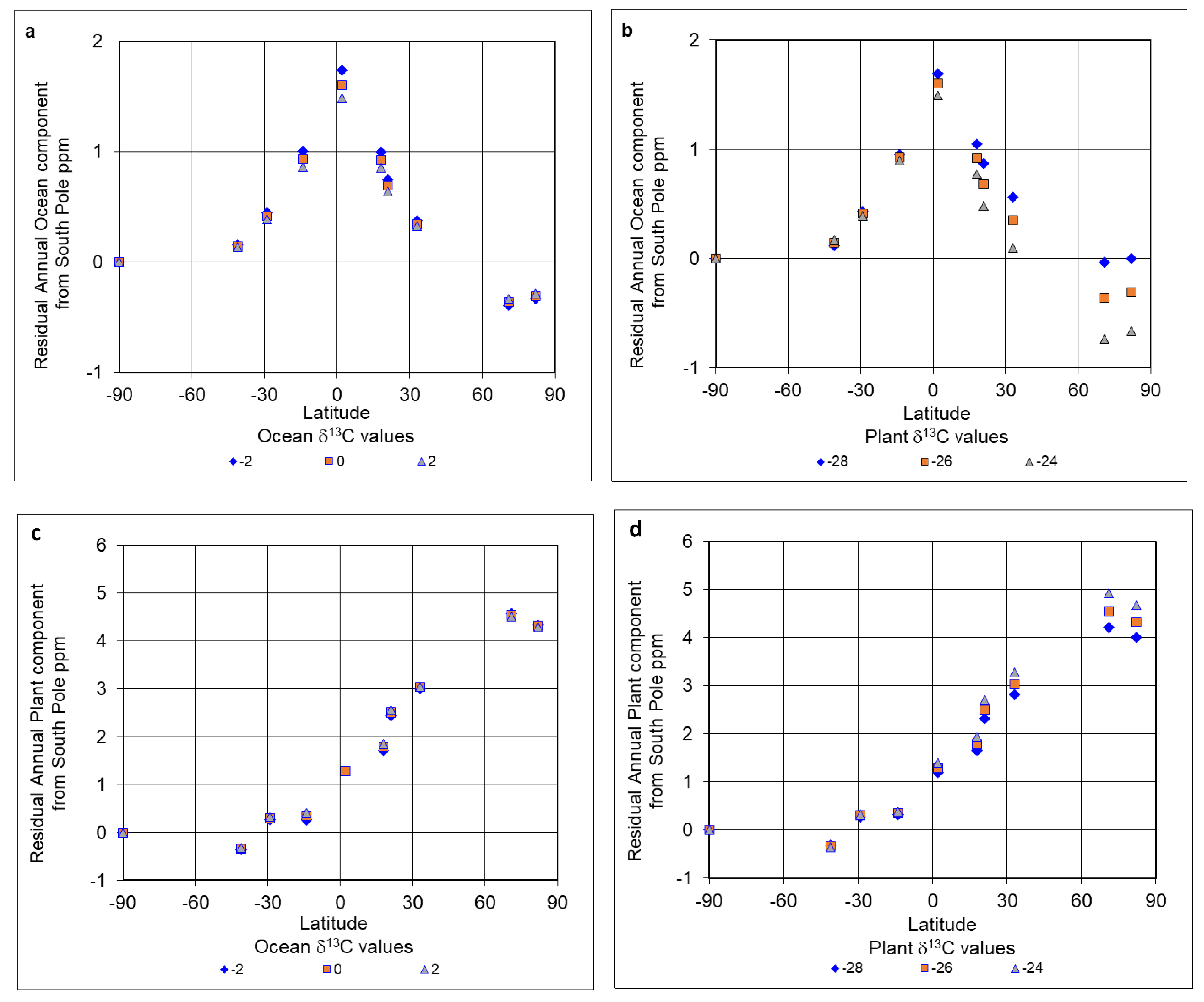
3.3. Sensitivity of Latitude Analysis to Assumptions of Isotopic Composition

The separation of observations of atmospheric CO₂ content into ocean and plant source components is made using assumptions that the CO₂ ocean component δ¹³C is 0‰ and the plant component δ¹³C is −26‰. The sensitivity to this choice is assessed by independently varying each component δ¹³C by ±2. The results are shown in Figure 8 for station variations less the source contributions at the South Pole, for the time span of 1986 to 2015.

The perturbed values of δ¹³C_ocean in Figure 8 give a maximum component variation of 0.1 ppm, while the corresponding perturbations in δ¹³C_plant give a maximum component variation of 0.4 ppm.

These perturbation studies demonstrate that the patterns of ocean and plant component changes with latitude are not significantly affected by variations of ±2‰ in the assumed baseline values used for δ¹³C.

4. Annual Differences of Ocean and Plant CO₂ Components

4.1. Annual Differences for Individual Stations

Figure 1, Figure 2 and Figure 3 show plots of monthly variations in total CO₂ and its isotopically separated ocean and plant components. Additional features of ocean and plant source components of CO₂ can be seen in an analysis of annually averaged measured CO₂ concentrations and corresponding ocean and plant components. These are shown in Figure 9, Figure 10 and Figure 11. Figure 10 and Figure 11 show that there is more annually averaged variability in the plant components compared to the ocean components. The simplest demonstration of variability comes from the standard deviations for the year-on-year changes. The results, given in

Table 5. Station variability, measured as standard deviations of annually averaged CO₂, ocean and plant components.

	Year-on-Year Changes: Standard Deviations in ppm
Stations	CO2 Concentration	Ocean Component	Plant Component
South Pole 90° S	0.46 +/− 0.08	0.31 +/− 0.06	0.48 +/− 0.09
Christmas Island 2° N	0.57 +/− 0.10	0.38 +/− 0.07	0.53 +/− 0.10
Mauna Loa 19° N	0.54 +/− 0.10	0.32 +/− 0.06	0.59 +/− 0.10
Point Barrow 71° N	0.86 +/− 0.14	0.28 +/− 0.05	0.74 +/− 0.14

, show that the ocean components are consistently less variable than the plant components. We suggest that this may be attributable to the fact that the ocean dynamics change more slowly than the atmospheric dynamics, affecting plant components.

The quantitative annual increases for atmospheric CO₂ and components from 1986 to 2015 are given in

Table 6. Annual CO₂ increases using annual data, averaged over the years of 1986 to 2015.

	Annual Increases in ppm
Stations	CO2 Concentration	Ocean Component	Plant Component
South Pole 90° S	1.77 +/− 0.03	0.89 +/− 0.02	0.88 +/− 0.02
Christmas Island 2° N	1.82 +/− 0.03	0.91 +/− 0.02	0.91 +/− 0.02
Mauna Loa 19° N	1.82 +/− 0.03	0.88 +/− 0.02	0.94 +/− 0.02
Point Barrow 71° N	1.81 +/− 0.03	0.90 +/− 0.02	0.91 +/− 0.02

. The ocean component and plant components are approximately equal at 50% of the annual CO₂ concentration increase.

We note that the annual values in Table 2 are directly from monthly values that have seasonal variations, while the values in Table 6 come from annual averages; hence, the latter do not show seasonal variations. This difference is illustrated in a comparison of the plant component at Point Barrow, which has a larger standard deviation of 0.038 ppm from the monthly seasonal variations, compared with 0.02 ppm for the annual averages.

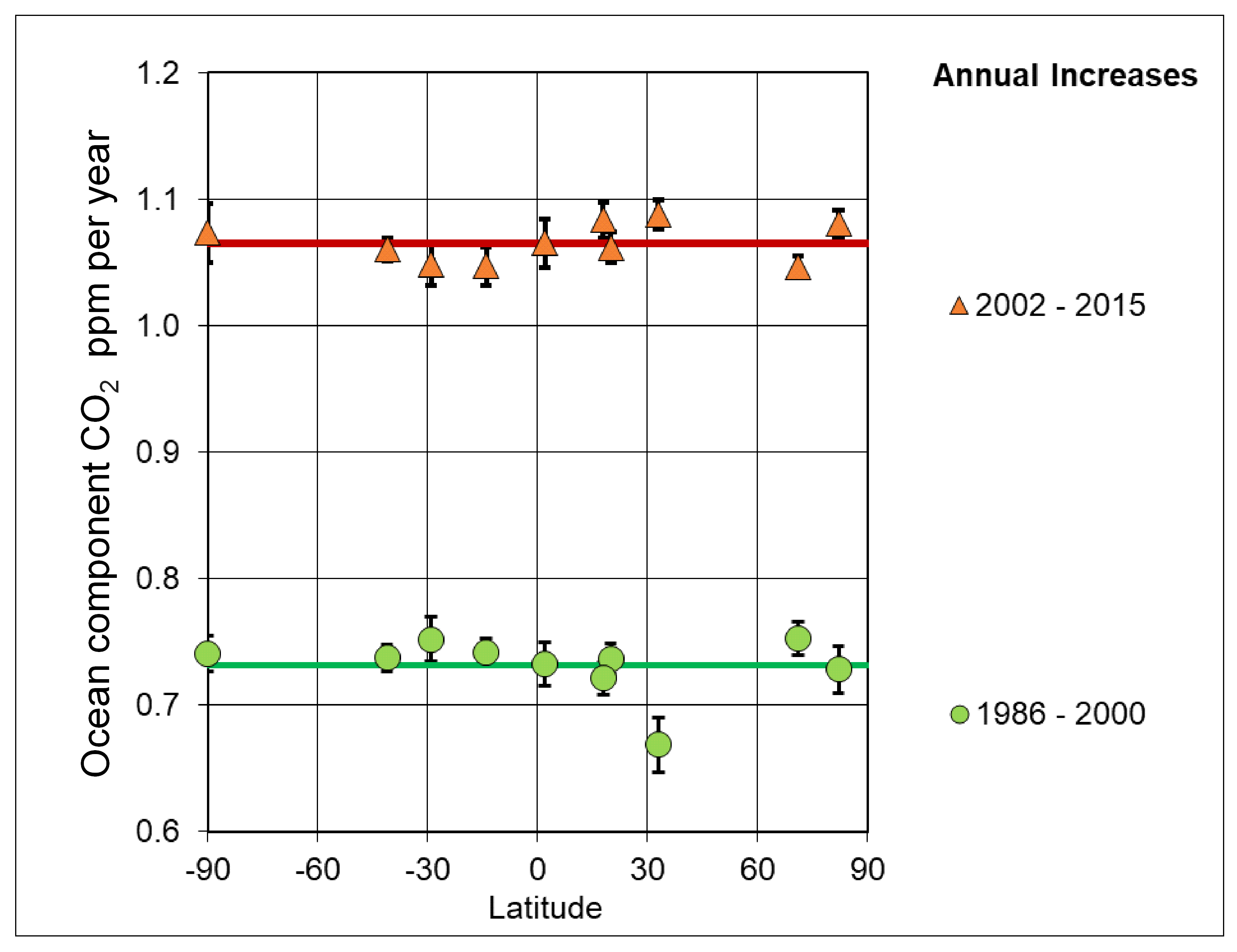
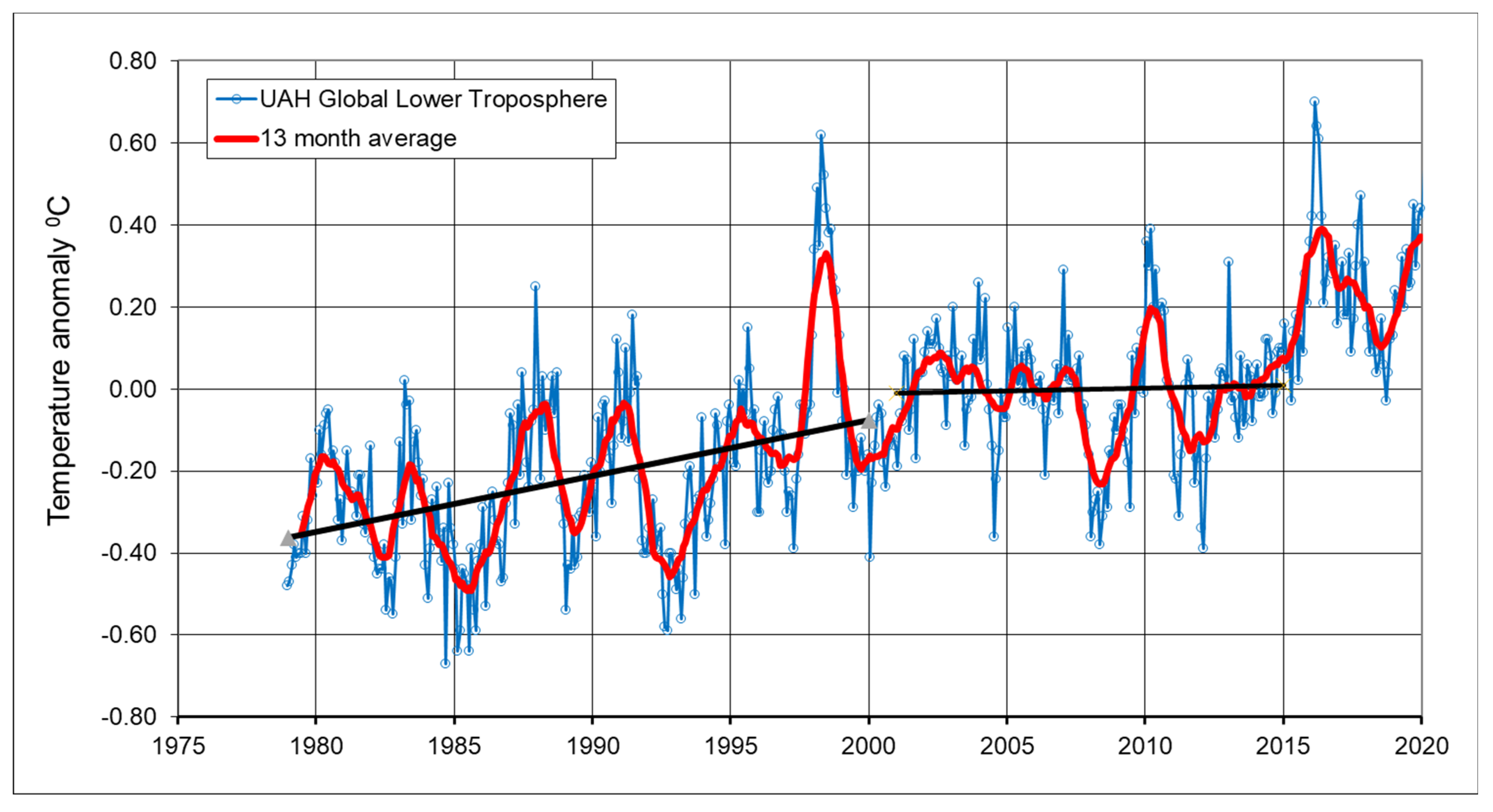
4.2. Trend Breaks in Annual Differences for the Ocean Component

The annually averaged CO₂ concentration values are shown in Figure 9. It is obvious that there is a slight excursion from 1988 to 1991 for Point Barrow CO₂ concentrations (the “bubble” referred to above).

For the ocean component shown in Figure 10, the Christmas Island values are above those at the South Pole and Point Barrow. Further, a straight-line fit for the South Pole component from 1979 to 2001 projected to 2018 shows a trend change in ocean component data at about year 2000.

We use the Chow Break Test [16] on each of the curves plotted in Figure 10. The Chow Break Test is used on a data series, and it uses a linear least-squares straight-line fit to show whether there is a statistically significant break for two straight lines to be a better fit than one straight line. This example shows that the ocean component for each of the South Pole, Christmas Island, Mauna Loa and Point Barrow has a break point in its trend at year 2001 ±2.

This break in the ocean component is present at all latitudes, as shown in Figure 11, where the average ocean component of CO₂ increases by 0.731 ± 0.008 ppm per year for 1986 to 2000 and 1.066 ± 0.005 per year for 2002 to 2015.

In searching for an explanation, or at least an association, with the break in the ocean component, we observe that the break in ocean component CO₂ after 2001 is coincident with an inflection in global lower troposphere temperatures measured by satellites [17]. The inflection is obvious in Figure 12 where separate straight-line fits for 1979 to 2000 and 2001 to 2015 are identified. Tropospheric temperatures show a rising trend of the order of 0.15 °C per decade before 2001, and a temperature plateau starting in 2000 to 2002, extending to approximately 2015 (the duration of this study).

An analysis of the global carbon cycle by [4] also shows a change in trend following the year of 2000. That analysis used measured and modeled data (but not isotopic data) to estimate the movement of CO₂ from the atmosphere into the ocean and found an increase in CO₂ absorbed into the ocean from about 2000 to 2019. In contrast to [4], the results in Figure 11 and Figure 12 demonstrate a change in the trend of movement of CO₂ from ocean to atmosphere, which is based on observational data only.

A hypothesis consistent with the observed break in the trends of atmospheric ocean-component CO₂ and tropospheric temperature around 2001 is that there is an increased upwelling of cold water in the oceans, which may then reduce global temperature and release CO₂ with an increased ocean-component isotopic mix into the atmosphere.

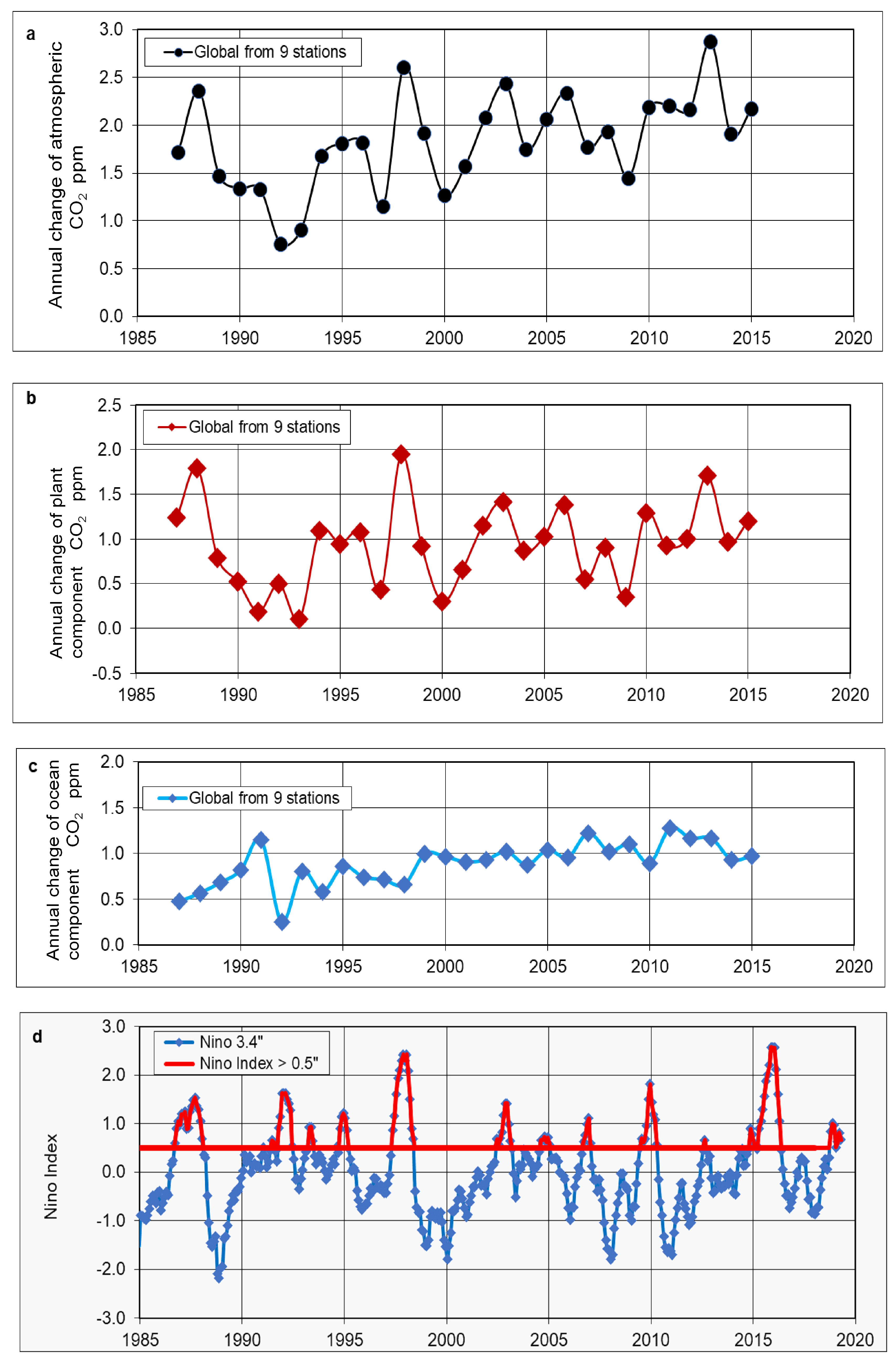
4.3. Annual Differences in the Plant Component CO₂; Correlation with a Phase Change in the AMO

The plant component CO₂ also shows an observed temporal change associated with ocean and atmospheric temperature shifts. Figure 13 shows annual changes including the “bubble” for the years 1988–1992 associated with the 1989 Regime Shift described by [15]. Replotting these data in Figure 14 after trend removal shows not only the “bubble” but a correlation of plant component CO₂ with increasing latitude—a regional rather than global change. The residual plant CO₂ values show increases in a northerly direction from the South Pole to Point Barrow 71° N. The obvious hypothesis to explain this variation is that the source of atmospheric plant CO₂ is a combination of fossil fuel CO₂, phytoplankton productivity in the oceans, and forest and peat fires, which occur primarily in the northern hemisphere. Figure 14 is consistent with this combination of sources.

Figure 14 also shows a clear inflection in the residual trends of the annual change in plant component CO₂ near the year of 1995. This coincides with a phase change in the Atlantic Multi-decadal Oscillation (AMO) from negative to positive, as described by [18]. That phase change is also associated with synchronous changes in numbers of small pelagic fishes [19]. These observational changes are consistent with an interpretation of decreased phytoplankton productivity after 1995, which in turn may explain the observed decrease in numbers of small pelagic fishes.

The pelagic fish time series shows an increase from 1995 to 2010 and, with phytoplankton at the bottom of the ocean food chain, implies increasing phytoplankton productivity. Such an increase would cause the increased removal of CO₂ in the ocean; this outcome in turn is associated with a decrease in the plant component of atmospheric CO₂. Thus, variable ocean sinks for CO₂ are directly coupled to the atmosphere as the concentration and isotopic composition of the atmosphere are varied.

4.4. Correlation of Global Plant Component CO₂ Variations with the ENSO

It is possible to estimate the annual changes in global atmospheric CO₂ concentrations and the separate ocean and plant CO₂ components, using the nine surface stations listed in Table 1 (where Mauna Loa is excluded, being at an altitude of 3397 m above sea level). The nine stations are taken to represent values in latitude bands defined by the average of the station latitudes, with the exception of the latitude extremes represented by Alert and the South Pole. The band latitudes are then used to calculate the fraction of the global surface within the bands, as shown in

Table 7. Latitude bands for global CO₂ concentrations.

Station	Latitude	Latitude Band	Band width Degrees	Fraction of Global Surface
Alert	82° N	90° N to 76.5° N	13.5	1.38%
Point Barrow	71° N	76.5° N to 52° N	24.5	9.22%
La Jolla	33° N	52° N to 26° N	26.0	17.48%
Kumukahi	19° N	26° N to 10.5° N	15.5	12.81%
Christmas Island	2° N	10.5° N to 6° S	16.5	14.34%
American Samoa	14° S	6° S to 21.5° S	15.5	13.10%
Kermadec Island	29° S	21.5° S to 35° S	13.5	10.35%
Baring Head	41° S	35° S to 65.5° S	30.5	16.82%
South Pole	90° S	65.5° S to 90° S	24.5	4.50%
Total			180.0	100.00%

.

Figure 15a–c show the year-on-year annual changes in global atmospheric CO₂ concentrations and annual changes in global plant and ocean CO₂ components. For comparison, the El Nino southern Oscillation (ENSO) variation is shown in Figure 15d via the Nino 3.4 SST Index [2,20]. The strong 1997–1998 and 2016–2017 El Nino events are obvious. Between 1989 and 2013, there are 10 El Nino peaks, which correlate in time with peaks in the annual plant component of CO₂, although the two time series are clearly not linearly related in their magnitude.

5. Discussion and Conclusions

For the time span of 1978 to 2015, the division of atmospheric CO₂ concentrations into two components having separate origins from deep ocean sources and from plants including fossil fuel emissions, shows a differing geographical distribution of the components. This indicates that variations in deep ocean components and in plant components of atmospheric CO₂ concentrations are attributable to independent mechanisms. These results are not significantly affected by variations in the assumed baseline values of δ¹³C, which characterize the isotopic composition of carbon in CO₂.

We find that the ocean component and plant components as derived from isotopic data are approximately equal at 50% of the annual CO₂ concentration increase. This result is similar to the outcome of a recent study [21] that used an ocean circulation model (without isotopic data) to track emitted carbon through the atmosphere–ocean system from pre-industrial times to the present (1780 to 2020). That study provided an estimate of 55% ocean source in atmospheric CO₂ despite using a very different methodology compared with this paper. It is of interest that the two different approaches yield estimates of those contributions to atmospheric CO₂ concentrations that are similar within a few percentage points.

Four essential conclusions may be drawn from this study using carbon isotopes.

• Annual increases in atmospheric CO₂ concentrations over 1978–2015 when split into plant and deep ocean sources via the isotopic signatures show approximately equal parts when averaged over all latitudes.
• The deep ocean component of CO₂ has its maximum value at the equator and we conclude that it is an independent source of atmospheric CO₂. This is further demonstrated by its limited year-on-year variability. We hypothesize that the observations of changes in ocean source CO₂ are attributable to the upwelling of CO₂-rich water transported across the sea floor via the global thermohaline circulation of the oceans.
• The plant source CO₂ in the atmosphere shows strong seasonal variability in northern latitudes up to the Arctic circle. It also shows more temporal year-by-year variability than that of the ocean source CO₂ and shows maximum variations coincident with the timing of El Nino events. It also shows a change in trend associated with the 1995 AMO phase change. These spatial and temporal variations are consistent with the plant source CO₂ being associated with multiple variations in fossil fuel CO₂ emissions, together with natural variations in the net primary productivity of oceanic phytoplankton, and forest and peat fires.
• The differing variations by year and by latitude of plant source and deep ocean source CO₂ as measured from the analysis of carbon isotopes in atmospheric CO2 samples, suggest that inclusion of such isotopic data in full carbon cycle models for the Earth may provide additional constraints on the modeling of bidirectional atmosphere–ocean transfers of CO₂.