Are There Knots in Chromosomes?
Abstract
1. Introduction
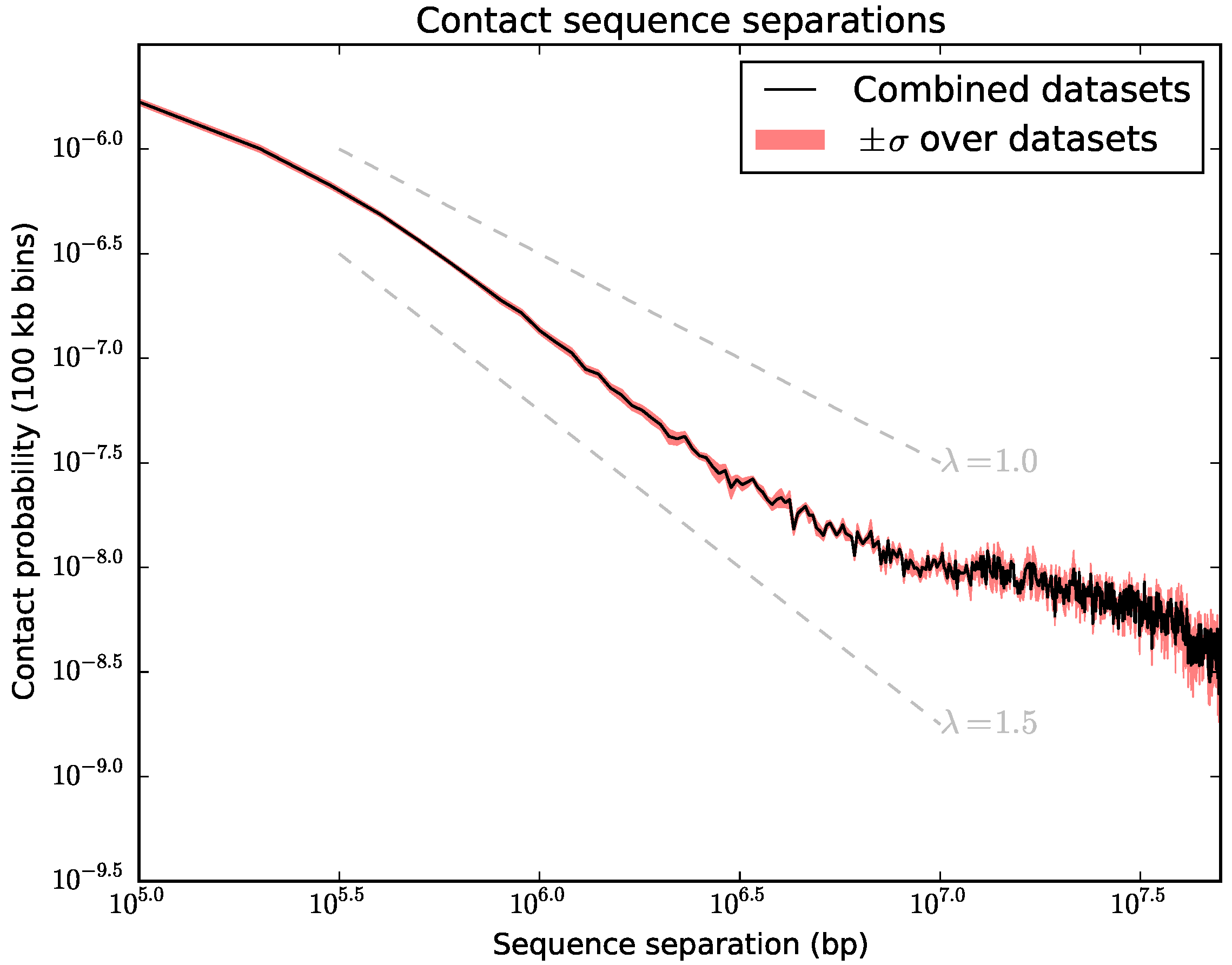
2. Methods
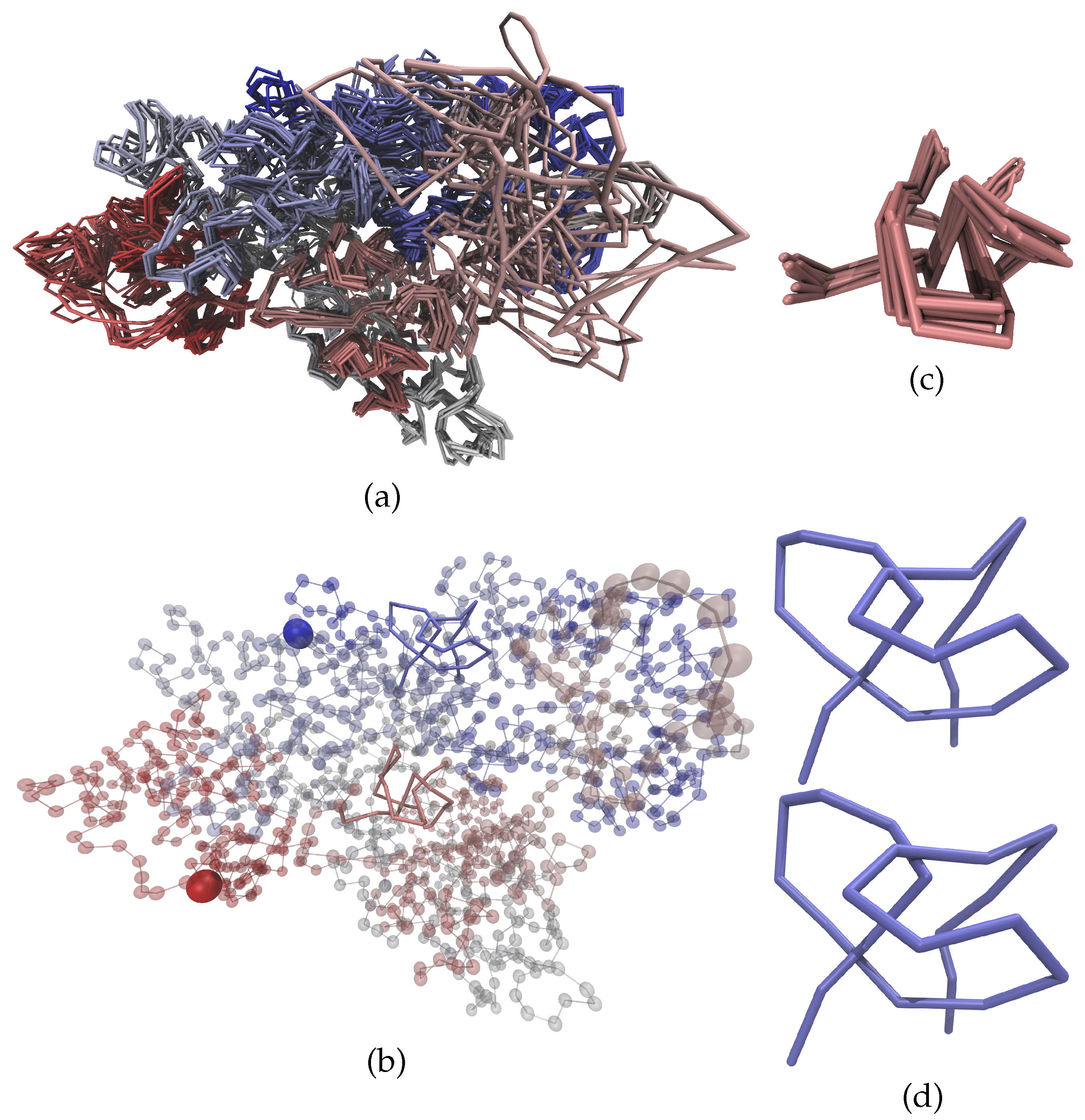
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bickmore, W.A.; van Steensel, B. Genome architecture: Domain organization of interphase chromosomes. Cell 2013, 152, 1270–1284. [Google Scholar] [CrossRef] [PubMed]
- Cremer, T. The 4D nucleome: Evidence for a dynamic nuclear landscape based on co-aligned active and inactive nuclear compartments. FEBS Lett. 2015, 589, 2931–2943. [Google Scholar] [CrossRef] [PubMed]
- Dixon, J.R. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature 2012, 485, 376–380. [Google Scholar] [CrossRef] [PubMed]
- Kalhor, R.; Tjong, H.; Jayathilaka, N.; Alber, F.; Chen, L. Genome architectures revealed by tethered chromosome conformation capture and population-based modeling. Nat. Biotechnol. 2011, 30, 90–98. [Google Scholar] [CrossRef] [PubMed]
- Lieberman-Aiden, E. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 2009, 326, 289–293. [Google Scholar] [CrossRef] [PubMed]
- Naumova, N. Organization of the mitotic chromosome. Science 2013, 342, 948–953. [Google Scholar] [CrossRef] [PubMed]
- Nora, E.P. Spatial partitioning of the regulatory landscape of the X-inactivation centre. Nature 2012, 485, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Phillips-Cremins, J.E. Architectural protein subclasses shape 3D organization of genomes during lineage commitment. Cell 2013, 153, 1281–1295. [Google Scholar] [CrossRef] [PubMed]
- Rao, S.S. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 2014, 159, 1665–1680. [Google Scholar] [CrossRef] [PubMed]
- Sexton, T. Three-dimensional folding and functional organization principles of the Drosophila genome. Cell 2012, 148, 458–472. [Google Scholar] [CrossRef] [PubMed]
- Tjong, H. Population-based 3D genome structure analysis reveals driving forces in spatial genome organization. Proc. Natl. Acad. Sci. USA 2016, 113, E1663–E1672. [Google Scholar] [CrossRef] [PubMed]
- Zuin, J. Cohesin and CTCF differentially affect chromatin architecture and gene expression in human cells. Proc. Natl. Acad. Sci. USA 2014, 111, 996–1001. [Google Scholar] [CrossRef] [PubMed]
- Bolzer, A.; Kreth, G.; Solovei, I.; Koehler, D.; Saracoglu, K.; Fauth, C.; Müller, S.; Eils, R.; Cremer, C.; Speicher, M.R.; et al. Three-dimensional maps of all chromosomes in human male fibroblast nuclei and prometaphase rosettes. PLoS Biol. 2005, 3, e157. [Google Scholar] [CrossRef] [PubMed]
- Kschonsak, M.; Haering, C.H. Shaping mitotic chromosomes: From classical concepts to molecular mechanisms. BioEssays 2015, 37, 755–766. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.F.; Liu, C.C.; Alberts, B.M. Type II DNA topoisomerases: Enzymes that can unknot a topologically knotted DNA molecule via a reversible double-strand break. Cell 1980, 19, 697–707. [Google Scholar] [CrossRef]
- Uemura, T.; Ohkura, H.; Adachi, Y.; Morino, K.; Shiozaki, K.; Yanagida, M. DNA topoisomerase II is required for condensation and separation of mitotic chromosomes in S. pombe. Cell 1987, 50, 917–925. [Google Scholar] [CrossRef]
- Gilbert, N.; Allan, J. Supercoiling in DNA and chromatin. Curr. Opin. Genet. Dev. 2014, 25, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Halverson, J.D.; Smrek, J.; Kremer, K.; Grosberg, A.Y. From a melt of rings to chromosome territories: The role of topological constraints in genome folding. Rep. Progress Phys. 2014, 77, 22601. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, M.L. Knots in Hamilton cycles. Macromolecules 1994, 27, 5924–5926. [Google Scholar] [CrossRef]
- Virnau, P.; Kantor, Y.; Kardar, M. Knots in globule and coil phases of a model polyethylene. J. Am. Chem. Soc. 2005, 127, 15102–15106. [Google Scholar] [CrossRef] [PubMed]
- Klotz, A.R.; Narsimhan, V.; Soh, B.W.; Doyle, P.S. Dynamics of DNA Knots during Chain Relaxation. Macromolecules 2017, 50, 4074–4082. [Google Scholar] [CrossRef]
- Tang, J.; Du, N.; Doyle, P.S. Compression and self-entanglement of single DNA molecules under uniform electric field. Proc. Natl. Acad. Sci. USA 2011, 108, 16153–16158. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, M.L. Are there knots in proteins? Nat. Struct. Mol. Biol. 1994, 1, 213–214. [Google Scholar] [CrossRef]
- Takusagawa, F.; Kamitori, S. A real knot in protein. J. Am. Chem. Soc. 1996, 118, 8945–8946. [Google Scholar]
- Taylor, W.R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R. Protein knots and fold complexity: some new twists. Comput. Biol. Chem. 2007, 31, 151–162. [Google Scholar] [CrossRef] [PubMed]
- Virnau, P.; Mirny, L.A.; Kardar, M. Intricate knots in proteins: Function and evolution. PLoS Comput. Biol. 2006, 2, e122. [Google Scholar] [CrossRef] [PubMed]
- Potestio, R.; Micheletti, C.; Orland, H. Knotted vs. unknotted proteins: evidence of knot-promoting loops. PLoS Comput. Biol. 2010, 6, e1000864. [Google Scholar] [CrossRef] [PubMed]
- Bölinger, D.; Sułkowska, J.I.; Hsu, H.P.; Mirny, L.A.; Kardar, M.; Onuchic, J.N.; Virnau, P. A Stevedore’s protein knot. PLoS Comput. Biol. 2010, 6, e1000731. [Google Scholar] [CrossRef] [PubMed]
- Sułkowska, J.I.; Sułkowski, P.; Onuchic, J. Dodging the crisis of folding proteins with knots. Proc. Natl. Acad. Sci. USA 2009, 106, 3119–3124. [Google Scholar] [CrossRef] [PubMed]
- Virnau, P.; Mallam, A.; Jackson, S. Structures and folding pathways of topologically knotted proteins. J. Phys. Condens. Matter 2011, 23, 33101. [Google Scholar] [CrossRef] [PubMed]
- Mallam, A.L.; Jackson, S.E. Knot formation in newly translated proteins is spontaneous and accelerated by chaperonins. Nat. Chem. Biol. 2012, 8, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.F.; Perkocha, L.; Calendar, R.; Wang, J.C. Knotted DNA from bacteriophage capsids. Proc. Natl. Acad. Sci. USA 1981, 78, 5498–5502. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.F.; Davis, J.L.; Calendar, R. Novel topologically knotted DNA from bacteriophage P4 capsids: Studies with DNA topoisomerases. Nucleic Acids Res. 1981, 9, 3979–3989. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vázquez, M.; Trigueros, S.; Roca, J.; Sumners, D.W. Knotting probability of DNA molecules confined in restricted volumes: DNA knotting in phage capsids. Proc. Natl. Acad. Sci. USA 2002, 99, 5373–5377. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vazquez, M.; McGuirk, P.; Trigueros, S.; Roca, J.; Sumners, D.W. DNA knots reveal a chiral organization of DNA in phage capsids. Proc. Natl. Acad. Sci. USA 2005, 102, 9165–9169. [Google Scholar] [CrossRef] [PubMed]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E.; Sumners, D. Simulations of knotting in confined circular DNA. Biophys. J. 2008, 95, 3591–3599. [Google Scholar] [CrossRef] [PubMed]
- Marenduzzo, D.; Micheletti, C.; Orlandini, E.; Sumners, D.W. Topological friction strongly affects viral DNA ejection. Proc. Natl. Acad. Sci. USA 2013, 110, 20081–20086. [Google Scholar] [CrossRef] [PubMed]
- Reith, D.; Cifra, P.; Stasiak, A.; Virnau, P. Effective stiffening of DNA due to nematic ordering causes DNA molecules packed in phage capsids to preferentially form torus knots. Nucleic Acids Res. 2012, 40, 5129–5137. [Google Scholar] [CrossRef] [PubMed]
- Rybenkov, V.V.; Cozzarelli, N.R.; Vologodskii, A.V. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl. Acad. Sci. USA 1993, 90, 5307–5311. [Google Scholar] [CrossRef] [PubMed]
- Shaw, S.Y.; Wang, J.C. Knotting of a DNA chain during ring closure. Science 1993, 260, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Rieger, F.C.; Virnau, P. A Monte Carlo study of knots in long double-stranded DNA chains. PLoS Comput. Biol. 2016, 12, e1005029. [Google Scholar] [CrossRef] [PubMed]
- Plesa, C.; Verschueren, D.; Pud, S.; van der Torre, J.; Ruitenberg, J.W.; Witteveen, M.J.; Jonsson, M.P.; Grosberg, A.Y.; Rabin, Y.; Dekker, C. Direct observation of DNA knots using a solid-state nanopore. Nat. Nanotechnol. 2016, 11, 1093–1097. [Google Scholar] [CrossRef] [PubMed]
- Rosa, A.; Everaers, R. Structure and dynamics of interphase chromosomes. PLoS Comput. Biol. 2008, 4, e1000153. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Nechaev, S.K.; Shakhnovich, E.I. The role of topological constraints in the kinetics of collapse of macromolecules. J. Phys. 1988, 49, 2095–2100. [Google Scholar] [CrossRef]
- Lieberman-Aiden, E.; Van Berkum, N.L.; Williams, L.; Imakaev, M.; Ragoczy, T.; Telling, A.; Amit, I.; Lajoie, B.R.; Sabo, P.J.; Dorschner, M.O.; et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 2009, 326, 289–293. [Google Scholar] [CrossRef] [PubMed]
- Mirny, L.A. The fractal globule as a model of chromatin architecture in the cell. Chromosom. Res. 2011, 19, 37–51. [Google Scholar] [CrossRef] [PubMed]
- Stevens, T.J.; Lando, D.; Basu, S.; Atkinson, L.P.; Cao, Y.; Lee, S.F.; Leeb, M.; Wohlfahrt, K.J.; Boucher, W.; O’Shaughnessy-Kirwan, A.; et al. 3D structures of individual mammalian genomes studied by single-cell Hi-C. Nature 2017, 544, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Gr. 1996, 14, 33–38. [Google Scholar] [CrossRef]



| Knot Type | Frequency | Corrected Frequency |
|---|---|---|
| Unknot | 17.9% | |
| 14.8% | 12.3% | |
| 2.4% | 1.8% | |
| 1.3% | 1.0% | |
| 1.6% | 1.1% | |
| 4.6% | ||
| 2.6% | ||
| More complicated | 54.8% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siebert, J.T.; Kivel, A.N.; Atkinson, L.P.; Stevens, T.J.; Laue, E.D.; Virnau, P. Are There Knots in Chromosomes? Polymers 2017, 9, 317. https://doi.org/10.3390/polym9080317
Siebert JT, Kivel AN, Atkinson LP, Stevens TJ, Laue ED, Virnau P. Are There Knots in Chromosomes? Polymers. 2017; 9(8):317. https://doi.org/10.3390/polym9080317
Chicago/Turabian StyleSiebert, Jonathan T., Alexey N. Kivel, Liam P. Atkinson, Tim J. Stevens, Ernest D. Laue, and Peter Virnau. 2017. "Are There Knots in Chromosomes?" Polymers 9, no. 8: 317. https://doi.org/10.3390/polym9080317
APA StyleSiebert, J. T., Kivel, A. N., Atkinson, L. P., Stevens, T. J., Laue, E. D., & Virnau, P. (2017). Are There Knots in Chromosomes? Polymers, 9(8), 317. https://doi.org/10.3390/polym9080317





