Efficient Sampling of Knotting-Unknotting Pathways for Semiflexible Gaussian Chains
Abstract
:1. Introduction
2. Methods
2.1. The Conditioned Langevin Equation
2.2. Polymer Chain
2.3. Circular Permutations
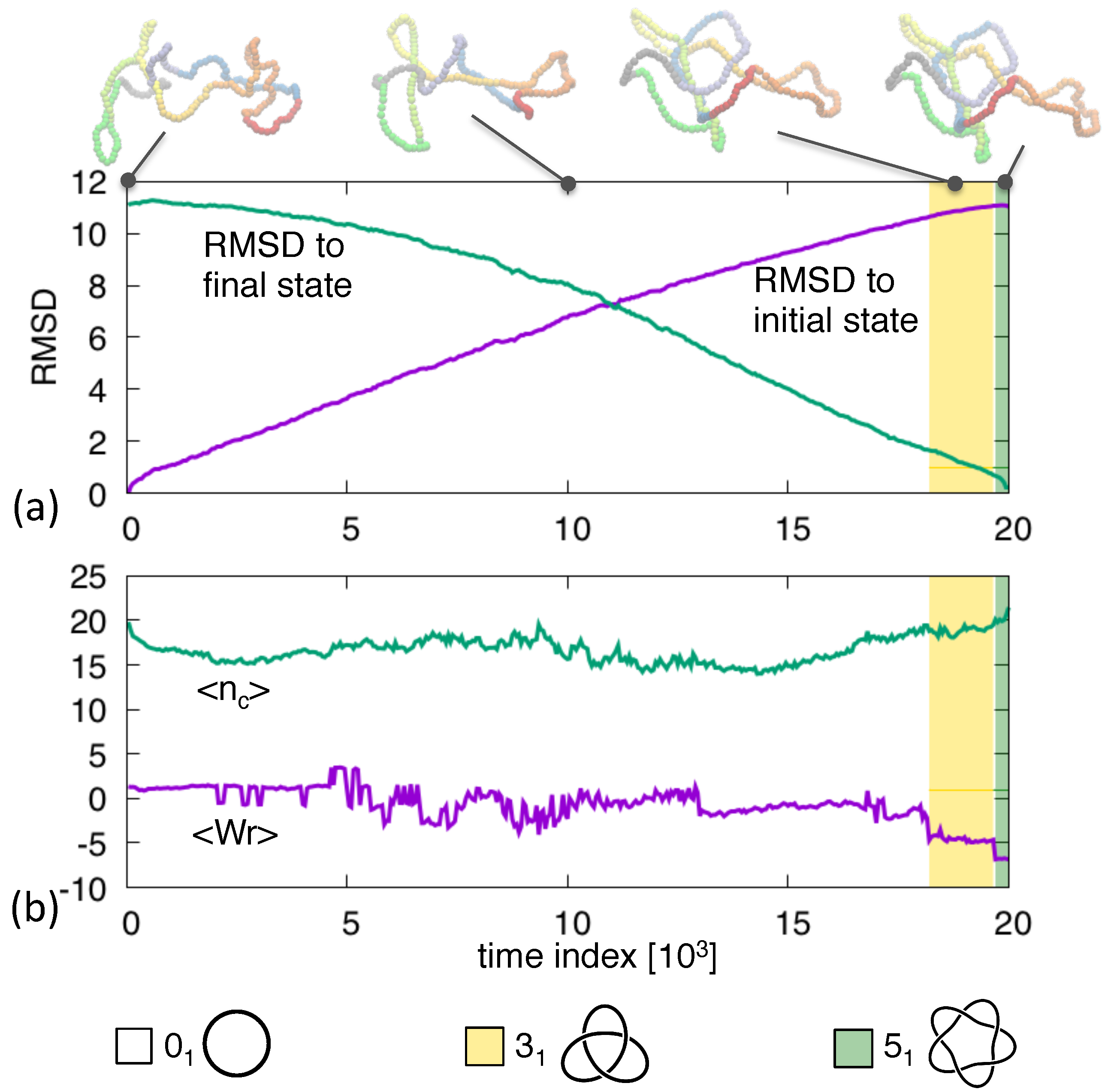
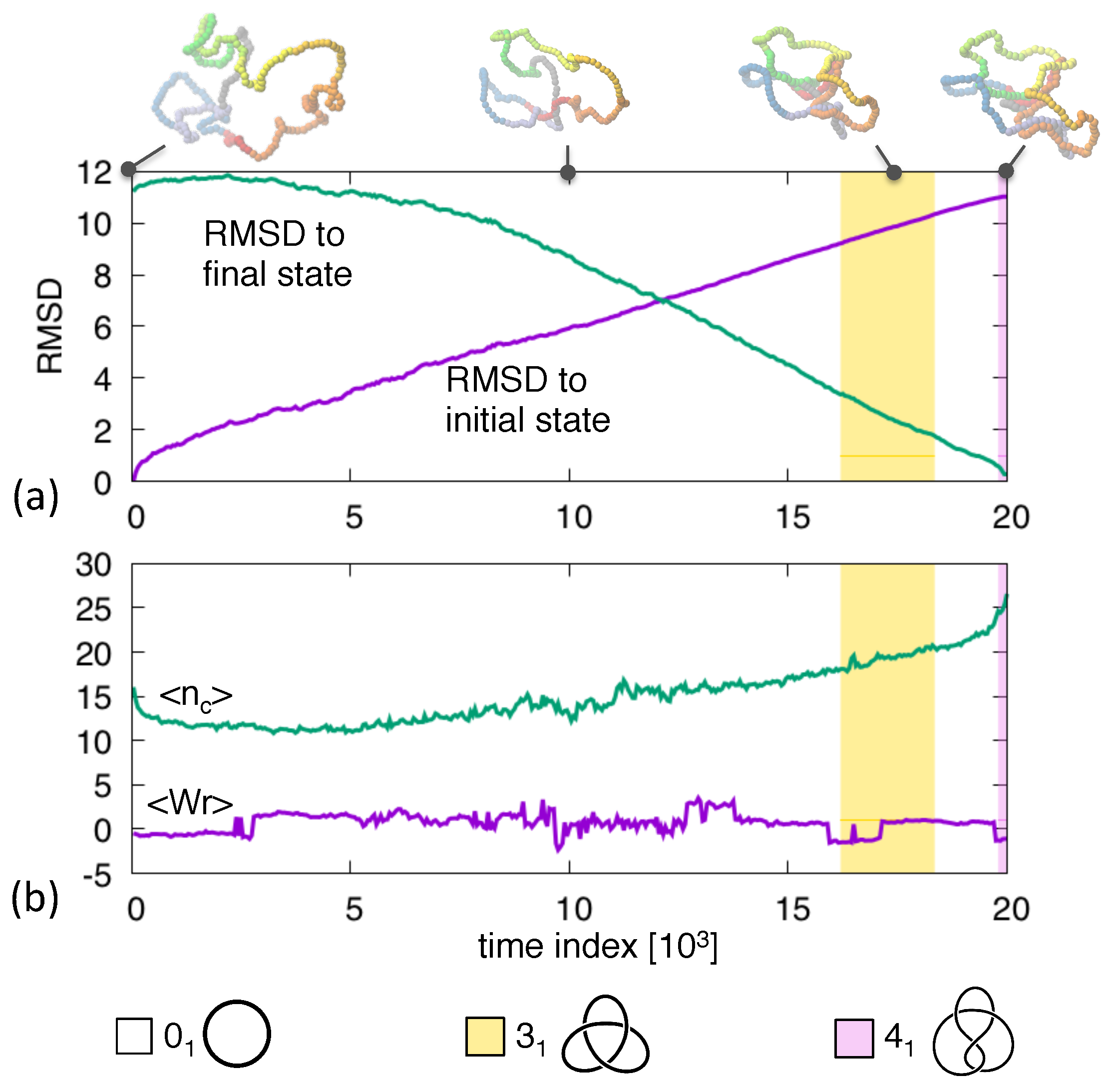
3. Results and Discussion
4. Concluding Remarks
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Desyatnikov, A.S.; Buccoliero, D.; Dennis, M.R.; Kivshar, Y.S. Spontaneous knotting of self-trapped waves. Sci. Rep. 2012, 2, 771. [Google Scholar] [CrossRef] [PubMed]
- Kedia, H.; Bialynicki-Birula, I.; Peralta-Salas, D.; Irvine, W.T.M. Tying knots in light fields. Phys. Rev. Lett. 2013, 111, 150404. [Google Scholar] [CrossRef] [PubMed]
- Kleckner, D.; Irvine, W.T.M. Creation and dynamics of knotted vortices. Nat. Phys. 2013, 9, 253–258. [Google Scholar] [CrossRef]
- Kedia, H.; Foster, D.; Dennis, M.R.; Irvine, W.T.M. Weaving knotted vector fields with tunable helicity. Phys. Rev. Lett. 2016, 117, 274501. [Google Scholar] [CrossRef] [PubMed]
- Tkalec, U.; Ravnik, M.; Copar, S.; Zumer, S.; Musevic, I. Reconfigurable knots and links in chiral nematic colloids. Science 2011, 333, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Jampani, V.S.R.; Škarabot, M.; Ravnik, M.; Čopar, S.; Žumer, S.; Muševič, I. Colloidal entanglement in highly twisted chiral nematic colloids: Twisted loops, Hopf links, and trefoil knots. Phys. Rev. E 2011, 84, 031703. [Google Scholar] [CrossRef] [PubMed]
- Martinez, A.; Ravnik, M.; Lucero, B.; Visvanathan, R.; Zumer, S.; Smalyukh, I.I. Mutually tangled colloidal knots and induced defect loops in nematic fields. Nat. Mater. 2014, 13, 258–263. [Google Scholar] [CrossRef] [PubMed]
- Machon, T.; Alexander, G.P. Knots and nonorientable surfaces in chiral nematics. Proc. Natl. Acad. Sci. USA 2013, 110, 14174–14179. [Google Scholar] [CrossRef] [PubMed]
- Irvine, W.T.M.; Kleckner, D. Liquid crystals: Tangled loops and knots. Nat. Mater. 2014, 13, 229–231. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M.G.; Tasinkevych, M.; Smalyukh, I.I. Topological polymer dispersed liquid crystals with bulk nematic defect lines pinned to handlebody surfaces. Phys. Rev. Lett. 2014, 112, 197801. [Google Scholar] [CrossRef] [PubMed]
- Laing, C.E.; Ricca, R.L.; Sumners, D.W.L. Conservation of writhe helicity under anti-parallel reconnection. Sci. Rep. 2015, 5, 9224. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Ricca, R.L. Knots cascade detected by a monotonically decreasing sequence of values. Sci. Rep. 2016, 6, 24118. [Google Scholar] [CrossRef] [PubMed]
- Scheeler, M.W.; Kleckner, D.; Proment, D.; Kindlmann, G.L.; Irvine, W.T.M. Helicity conservation by flow across scales in reconnecting vortex links and knots. Proc. Natl. Acad. Sci. USA 2014, 111, 15350–15355. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.J.; Dennis, M.R. Vortex knots in tangled quantum eigenfunctions. Nat. Commun. 2016, 7, 12346. [Google Scholar] [CrossRef] [PubMed]
- Kleckner, D.; Kauffman, L.H.; Irvine, W.T.M. How superfluid vortex knots untie. Nat. Phys. 2016, 12, 650–655. [Google Scholar] [CrossRef]
- Shishido, K.; Komiyama, N.; Ikawa, S. Increased production of a knotted form of plasmid pBR322 DNA in Escherichia coli DNA topoisomerase mutants. J. Mol. Biol. 1987, 195, 215–218. [Google Scholar] [CrossRef]
- Ullsperger, C.; Cozzarelli, N.R. Contrasting enzymatic activities of topoisomerase IV and DNA gyrase from Escherichia coli. J. Biol. Chem. 1996, 271, 31549–31555. [Google Scholar] [CrossRef] [PubMed]
- Rybenkov, V.V.; Ullsperger, C.; Vologodskii, A.V.; Cozzarelli, N.R. Simplification of DNA topology below equilibrium values by type II topoisomerases. Science 1997, 277, 690–693. [Google Scholar] [CrossRef] [PubMed]
- Hua, X.; Nguyen, D.; Raghavan, B.; Arsuaga, J.; Vazquez, M. Random state transitions of knots: A first step towards modeling unknotting by type II topoisomerases. Topol. Appl. 2007, 154, 1381–1397. [Google Scholar] [CrossRef] [PubMed]
- Grainge, I.; Bregu, M.; Vazquez, M.; Sivanathan, V.; Ip, S.C.Y.; Sherratt, D.J. Unlinking chromosome catenanes in vivo by site-specific recombination. EMBO J. 2007, 26, 4228–4238. [Google Scholar] [CrossRef] [PubMed]
- Vologodski, A. Disentangling DNA molecules. Phys. Life Rev. 2016, 18, 118–134. [Google Scholar] [CrossRef] [PubMed]
- Olender, R.; Elber, R. Calculation of classical trajectories with a very large time step: Formalism and numerical examples. J. Chem. Phys. 1996, 105, 9299–9315. [Google Scholar] [CrossRef]
- Elber, R. Reaction paths and rates. In Encyclopedia of Biophysics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 2186–2191. [Google Scholar]
- Bello-Rivas, J.M.; Elber, R. Exact milestoning. J. Chem. Phys. 2015, 142, 094102. [Google Scholar] [CrossRef] [PubMed]
- Pan, A.C.; Sezer, D.; Roux, B. Finding transition pathways using the string method with swarms of trajectories. J. Phys. Chem. B 2008, 112, 3432–3440. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.; Shukla, D.; Pande, V.S.; Roux, B. Transition path theory analysis of c-Src kinase activation. Proc. Natl. Acad. Sci. USA 2016, 113, 9193–9198. [Google Scholar] [CrossRef] [PubMed]
- Banisch, R.; Conrad, N.D.; Schütte, C. Reactive flows and unproductive cycles for random walks on complex networks. Eur. Phys. J. Spec. Top. 2015, 224, 2369–2387. [Google Scholar] [CrossRef]
- Faccioli, P.; Sega, M.; Pederiva, F.; Orland, H. Dominant pathways in protein folding. Phys. Rev. Lett. 2006, 97, 108101. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.G.; Chandler, D.; Dellago, C.; Geissler, P.L. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. [Google Scholar] [CrossRef] [PubMed]
- Daldrop, J.O.; Kim, W.K.; Netz, R.R. Transition paths are hot. Europhys. Lett. 2016, 113, 18004. [Google Scholar] [CrossRef]
- Schlitter, J.; Engels, M.; Krüger, P.; Jacoby, E.; Wollmer, A. Targeted molecular dynamics simulation of conformational change-application to the T-R transition in insulin. Mol. Simul. 1993, 10, 291–308. [Google Scholar] [CrossRef]
- Grubmüller, H.; Heymann, B.; Tavan, P. Ligand binding: Molecular mechanics calculation of the streptavidin-biotin rupture force. Science 1996, 271, 997–999. [Google Scholar] [CrossRef] [PubMed]
- Isralewitz, B.; Gao, M.; Schulten, K. Steered molecular dynamics and mechanical functions of proteins. Curr. Opin. Struct. Biol. 2001, 11, 224–230. [Google Scholar] [CrossRef]
- Yunger Halpern, N.; Jarzynski, C. Number of trials required to estimate a free-energy difference, using fluctuation relations. Phys. Rev. E 2016, 93, 052144. [Google Scholar] [CrossRef] [PubMed]
- Paci, E.; Karplus, M. Forced unfolding of fibronectin type 3 modules: An analysis by biased molecular dynamics simulations. J. Mol. Biol. 1999, 288, 441–459. [Google Scholar] [CrossRef] [PubMed]
- Camilloni, C.; Broglia, R.A.; Tiana, G. Hierarchy of folding and unfolding events of protein G, CI 2, and ACBP from explicit-solvent simulations. J. Chem. Phys. 2011, 134, 01B632. [Google Scholar] [CrossRef] [PubMed]
- Orland, H. Generating transition paths by Langevin bridges. J. Chem. Phys. 2011, 134, 174114. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, S.N.; Orland, H. Effective Langevin equations for constrained stochastic processes. J. Stat. Mech. Theory Exp. 2015, 2015, P06039. [Google Scholar] [CrossRef]
- Adams, C.C. The Knot Book; An Elementary Introduction to the Mathematical Theory of Knots; American Mathematical Soc.: Williamstown, MA, USA, 2004. [Google Scholar]
- Darcy, I.K.; Sumners, W.D. Applications of topology to DNA. In Knot Theory; Banach Center Publications: Warsaw, Poland, 1998; Volume 42. [Google Scholar]
- Flammini, A.; Maritan, A.; Stasiak, A. Simulations of action of DNA topoisomerases to investigate boundaries and shapes of spaces of knots. Biophys. J. 2004, 87, 2968–2975. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Micheletti, C.; Orland, H. Efficient Sampling of Knotting-Unknotting Pathways for Semiflexible Gaussian Chains. Polymers 2017, 9, 196. https://doi.org/10.3390/polym9060196
Micheletti C, Orland H. Efficient Sampling of Knotting-Unknotting Pathways for Semiflexible Gaussian Chains. Polymers. 2017; 9(6):196. https://doi.org/10.3390/polym9060196
Chicago/Turabian StyleMicheletti, Cristian, and Henri Orland. 2017. "Efficient Sampling of Knotting-Unknotting Pathways for Semiflexible Gaussian Chains" Polymers 9, no. 6: 196. https://doi.org/10.3390/polym9060196





